Search Advanced

AIMS Biophysics

2017, Volume 4, Issue 1: 121-151. doi: 10.3934/biophy.2017.1.121
Previous Article Next Article
Review Special Issues

Fluorescent probes for detecting cholesterol-rich ordered membrane microdomains: entangled relationships between structural analogies in the membrane and functional homologies in the cell

  • 1.
    Theranyx SA, Marseille, France
  • 2.
    Université Toulouse III, UMR 1048 INSERM, Toulouse, France
  • 3.
    Plateau Technique d’Imagerie Cellulaire, INSERM U1043, Toulouse, France
  • 4.
    Université Toulouse III, Toxalim UMR 1331 INRA, ENVT, Toulouse, France
  • 5.
    IBiTecS/SB2SM CEA and I2BC UMR 9198 CNRS, Université Paris-Saclay, Gif-sur-Yvette, France
  • Received: 20 December 2016 Accepted: 15 February 2017 Published: 21 February 2017

  • This review addresses the question of fluorescent detection of ordered membrane (micro) domains in living (cultured) cells, with a “practical” point of view since the situation is much more complicated than for studying model membranes. We first briefly recall the bases of model membrane structural organization involving liquid-ordered and -disordered phases, and the main features of their counterparts in cell membranes that are the various microdomains. We then emphasize the utility of the fluorescent probes derived from cholesterol, and delineate the respective advantages, limitations and drawbacks of the existing ones. In particular, besides their intra-membrane behavior, their relevant characteristics should integrate their different cellular fates for membrane turn-over, trafficking and metabolism, in order to evaluate and improve their efficiency for in-situ probing membrane microdomains in the cell physiology context. Finally, at the present stage, it appears that Bdp-Chol and Pyr-met-Chol display well complementary properties, allowing to use them in combination to improve the reliability of the current experimental approaches. But the field is still open, and there remains much work to perform in this research area.

    Citation: Gérald Gaibelet, François Tercé, Sophie Allart, Chantal Lebrun, Xavier Collet, Nadège Jamin, Stéphane Orlowski. Fluorescent probes for detecting cholesterol-rich ordered membrane microdomains: entangled relationships between structural analogies in the membrane and functional homologies in the cell[J]. AIMS Biophysics, 2017, 4(1): 121-151. doi: 10.3934/biophy.2017.1.121

    Related Papers:

  • This review addresses the question of fluorescent detection of ordered membrane (micro) domains in living (cultured) cells, with a “practical” point of view since the situation is much more complicated than for studying model membranes. We first briefly recall the bases of model membrane structural organization involving liquid-ordered and -disordered phases, and the main features of their counterparts in cell membranes that are the various microdomains. We then emphasize the utility of the fluorescent probes derived from cholesterol, and delineate the respective advantages, limitations and drawbacks of the existing ones. In particular, besides their intra-membrane behavior, their relevant characteristics should integrate their different cellular fates for membrane turn-over, trafficking and metabolism, in order to evaluate and improve their efficiency for in-situ probing membrane microdomains in the cell physiology context. Finally, at the present stage, it appears that Bdp-Chol and Pyr-met-Chol display well complementary properties, allowing to use them in combination to improve the reliability of the current experimental approaches. But the field is still open, and there remains much work to perform in this research area.


    加载中
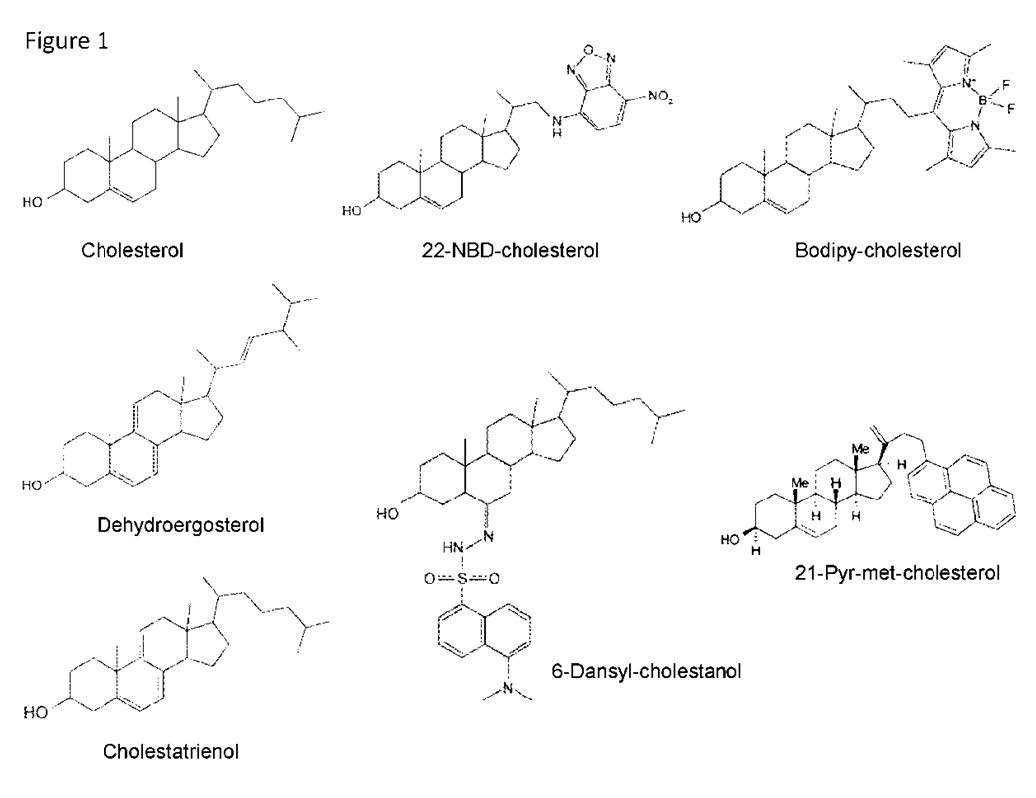
    [1] Klymchenko AS, Kreder R (2014) Fluorescent probes for lipid rafts: from model membranes to living cells. Chem Biol 21: 97-113. doi: 10.1016/j.chembiol.2013.11.009
    [2] Sankaram MB, Thompson TE (1991) Cholesterol-induced fluid-phase immiscibility in membranes. Proc Natl Acad Sci USA 88: 8686-8690. doi: 10.1073/pnas.88.19.8686
    [3] Veatch SL, Keller SL (2005) Seeing spots: complex phase behavior in simple membranes. Biochim Biophys Acta 1746: 172-185. doi: 10.1016/j.bbamcr.2005.06.010
    [4] Daly TA, Wang M, Regen SL (2011) The origin of cholesterol's condensing effect. Langmuir 27: 2159-2161. doi: 10.1021/la105039q
    [5] Hakobyan D, Heuer A (2014) Key molecular requirements for raft formation in lipid/cholesterol membranes. PLoS One 9: e87369. doi: 10.1371/journal.pone.0087369
    [6] Krause MR, Regen SL (2014) The structural role of cholesterol in cell membranes: from condensed bilayers to lipid rafts. Acc Chem Res 47: 3512-3521. doi: 10.1021/ar500260t
    [7] Feigenson GW (2006) Phase behavior of lipid mixtures. Nat Chem Biol 2: 560-563. doi: 10.1038/nchembio1106-560
    [8] Rog T, Pasenkiewicz-Gierula M, Vattulainen I, et al. (2009) Ordering effects of cholesterol and its analogues. Biochim Biophys Acta 1788: 97-121. doi: 10.1016/j.bbamem.2008.08.022
    [9] Garcia-Saez AJ, Schwille P (2010) Stability of lipid domains. FEBS Lett 584: 1653-1658. doi: 10.1016/j.febslet.2009.12.036
    [10] Shaw JE, Epand RF, Epand RM, et al. (2006) Correlated fluorescence-atomic force microscopy of membrane domains: structure of fluorescence probes determines lipid localization. Biophys J 90: 2170-2178. doi: 10.1529/biophysj.105.073510
    [11] Mouritsen OG, Zuckermann MJ (2004) What's so special about cholesterol? Lipids 39: 1101-1113. doi: 10.1007/s11745-004-1336-x
    [12] Wang J, Megha, London E (2004) Relationship between sterol/steroid structure and participation in ordered lipid domains (lipid rafts): implications for lipid raft structure and function. Biochemistry 43: 1010-1018. doi: 10.1021/bi035696y
    [13] Wenz JJ, Barrantes FJ (2003) Steroid structural requirements for stabilizing or disrupting lipid domains. Biochemistry 42: 14267-14276. doi: 10.1021/bi035759c
    [14] Xu X, Bittman R, Duportail G, et al. (2001) Effect of the structure of natural sterols and sphingolipids on the formation of ordered sphingolipid/sterol domains (rafts) Comparison of cholesterol to plant, fungal, and disease-associated sterols and comparison of sphingomyelin, cerebrosides, and ceramide. J Biol Chem 276: 33540-33546. doi: 10.1074/jbc.M104776200
    [15] Xu X, London E (2000) The effect of sterol structure on membrane lipid domains reveals how cholesterol can induce lipid domain formation. Biochemistry 39: 843-849. doi: 10.1021/bi992543v
    [16] Bernardino de la Serna J, Schutz GJ, Eggeling C, et al. (2016) There is no simple model of the plasma membrane organization. Front Cell Dev Biol 4: art106.
    [17] van Meer G, Stelzer EH, Wijnaendts-van-Resandt RW, et al. (1987) Sorting of sphingolipids in epithelial (Madin-Darby canine kidney) cells. J Cell Biol 105: 1623-1635. doi: 10.1083/jcb.105.4.1623
    [18] Simons K, Ikonen E (1997) Functional rafts in cell membranes. Nature 387: 569-572. doi: 10.1038/42408
    [19] Gupta N, DeFranco AL (2007) Lipid rafts and B cell signaling. Semin Cell Dev Biol 18: 616-626. doi: 10.1016/j.semcdb.2007.07.009
    [20] Ikonen E (2001) Roles of lipid rafts in membrane transport. Curr Opin Cell Biol 13: 470-477. doi: 10.1016/S0955-0674(00)00238-6
    [21] Lasserre R, Guo XJ, Conchonaud F, et al. (2008) Raft nanodomains contribute to Akt/PKB plasma membrane recruitment and activation. Nat Chem Biol 4: 538-547. doi: 10.1038/nchembio.103
    [22] Orlowski S, Comera C, Terce F, et al. (2007) Lipid rafts: dream or reality for cholesterol transporters? Eur Biophys J 36: 869-885. doi: 10.1007/s00249-007-0193-8
    [23] Orlowski S, Martin S, Escargueil A (2006) P-glycoprotein and 'lipid rafts': some ambiguous mutual relationships (floating on them, building them or meeting them by chance?). Cell Mol Life Sci 63: 1038-1059. doi: 10.1007/s00018-005-5554-9
    [24] Owen DM, Magenau A, Williamson D, et al. (2012) The lipid raft hypothesis revisited—new insights on raft composition and function from super-resolution fluorescence microscopy. Bioessays 34: 739-747. doi: 10.1002/bies.201200044
    [25] Simons K, Toomre D (2000) Lipid rafts and signal transduction. Nat Rev Mol Cell Biol 1: 31-39.
    [26] Carquin M, D'Auria L, Pollet H, et al. (2016) Recent progress on lipid lateral heterogeneity in plasma membranes: From rafts to submicrometric domains. Prog Lipid Res 62: 1-24. doi: 10.1016/j.plipres.2015.12.004
    [27] Jacobson K, Mouritsen OG, Anderson RG (2007) Lipid rafts: at a crossroad between cell biology and physics. Nat Cell Biol 9: 7-14. doi: 10.1038/ncb0107-7
    [28] Mayor S, Rao M (2004) Rafts: scale-dependent, active lipid organization at the cell surface. Traffic 5: 231-240. doi: 10.1111/j.1600-0854.2004.00172.x
    [29] Pike LJ (2004) Lipid rafts: heterogeneity on the high seas. Biochem J 378: 281-292. doi: 10.1042/bj20031672
    [30] Simons K, Gerl MJ (2010) Revitalizing membrane rafts: new tools and insights. Nat Rev Mol Cell Biol 11: 688-699. doi: 10.1038/nrm2977
    [31] Wustner D (2007) Fluorescent sterols as tools in membrane biophysics and cell biology. Chem Phys Lipids 146: 1-25. doi: 10.1016/j.chemphyslip.2006.12.004
    [32] Baker BY, Epand RF, Epand RM, et al. (2007) Cholesterol binding does not predict activity of the steroidogenic acute regulatory protein, StAR. J Biol Chem 282: 10223-10232. doi: 10.1074/jbc.M611221200
    [33] Honigmann A, Pralle A (2016) Compartmentalization of the Cell Membrane. J Mol Biol 428: 4739-4748. doi: 10.1016/j.jmb.2016.09.022
    [34] Lenne PF, Wawrezinieck L, Conchonaud F, et al. (2006) Dynamic molecular confinement in the plasma membrane by microdomains and the cytoskeleton meshwork. EMBO J 25: 3245-3256. doi: 10.1038/sj.emboj.7601214
    [35] van Zanten TS, Mayor S (2015) Current approaches to studying membrane organization. F1000Research: 6868.
    [36] Lingwood D, Simons K (2010) Lipid rafts as a membrane-organizing principle. Science 327: 46-50. doi: 10.1126/science.1174621
    [37] Devaux PF, Morris R (2004) Transmembrane asymmetry and lateral domains in biological membranes. Traffic 5: 241-246. doi: 10.1111/j.1600-0854.2004.0170.x
    [38] Lorent JH, Levental I (2015) Structural determinants of protein partitioning into ordered membrane domains and lipid rafts. Chem Phys Lipids 192: 23-32. doi: 10.1016/j.chemphyslip.2015.07.022
    [39] Chum T, Glatzova D, Kvicalova Z, et al. (2016) The role of palmitoylation and transmembrane domain in sorting of transmembrane adaptor proteins. J Cell Sci 129: 95-107. doi: 10.1242/jcs.175190
    [40] Levental I, Grzybek M, Simons K (2010) Greasing their way: lipid modifications determine protein association with membrane rafts. Biochemistry 49: 6305-6316. doi: 10.1021/bi100882y
    [41] Anderson RG, Jacobson K (2002) A role for lipid shells in targeting proteins to caveolae, rafts, and other lipid domains. Science 296: 1821-1825. doi: 10.1126/science.1068886
    [42] Kaiser HJ, Orlowski A, Rog T, et al. (2011) Lateral sorting in model membranes by cholesterol-mediated hydrophobic matching. Proc Natl Acad Sci USA 108: 16628-16633. doi: 10.1073/pnas.1103742108
    [43] Nyholm TK (2015) Lipid-protein interplay and lateral organization in biomembranes. Chem Phys Lipids 189: 48-55. doi: 10.1016/j.chemphyslip.2015.05.008
    [44] Fujiwara T, Ritchie K, Murakoshi H, et al. (2002) Phospholipids undergo hop diffusion in compartmentalized cell membrane. J Cell Biol 157: 1071-1081. doi: 10.1083/jcb.200202050
    [45] Braccia A, Villani M, Immerdal L, et al. (2003) Microvillar membrane microdomains exist at physiological temperature. Role of galectin-4 as lipid raft stabilizer revealed by "superrafts". J Biol Chem 278: 15679-15684.
    [46] Hansen GH, Immerdal L, Thorsen E, et al. (2001) Lipid rafts exist as stable cholesterol-independent microdomains in the brush border membrane of enterocytes. J Biol Chem 276: 32338-32344. doi: 10.1074/jbc.M102667200
    [47] Danielsen EM, Hansen GH (2003) Lipid rafts in epithelial brush borders: atypical membrane microdomains with specialized functions. Biochim Biophys Acta 1617: 1-9. doi: 10.1016/j.bbamem.2003.09.005
    [48] Meder D, Moreno MJ, Verkade P, et al. (2006) Phase coexistence and connectivity in the apical membrane of polarized epithelial cells. Proc Natl Acad Sci USA 103: 329-334. doi: 10.1073/pnas.0509885103
    [49] Lingwood D, Ries J, Schwille P, et al. (2008) Plasma membranes are poised for activation of raft phase coalescence at physiological temperature. Proc Natl Acad Sci USA 105: 10005-10010. doi: 10.1073/pnas.0804374105
    [50] Mizuno H, Abe M, Dedecker P, et al. (2011) Fluorescent probes for superresolution imaging of lipid domains on the plasma membrane. Chem Sci 2: 1548-1553. doi: 10.1039/c1sc00169h
    [51] Carquin M, Conrard L, Pollet H, et al. (2015) Cholesterol segregates into submicrometric domains at the living erythrocyte membrane: evidence and regulation. Cell Mol Life Sci 72: 4633-4651. doi: 10.1007/s00018-015-1951-x
    [52] Carquin M, Pollet H, Veiga-da-Cunha M, et al. (2014) Endogenous sphingomyelin segregates into submicrometric domains in the living erythrocyte membrane. J Lipid Res 55: 1331-1342. doi: 10.1194/jlr.M048538
    [53] D'Auria L, Van der Smissen P, Bruyneel F, et al. (2011) Segregation of fluorescent membrane lipids into distinct micrometric domains: evidence for phase compartmentation of natural lipids? PLoS One 6: e17021. doi: 10.1371/journal.pone.0017021
    [54] Frisz JF, Klitzing HA, Lou K, et al. (2013) Sphingolipid domains in the plasma membranes of fibroblasts are not enriched with cholesterol. J Biol Chem 288: 16855-16861. doi: 10.1074/jbc.M113.473207
    [55] Frisz JF, Lou K, Klitzing HA, et al. (2013) Direct chemical evidence for sphingolipid domains in the plasma membranes of fibroblasts. Proc Natl Acad Sci USA 110: E613-622. doi: 10.1073/pnas.1216585110
    [56] Magenau A, Benzing C, Proschogo N, et al. (2011) Phagocytosis of IgG-coated polystyrene beads by macrophages induces and requires high membrane order. Traffic 12: 1730-1743. doi: 10.1111/j.1600-0854.2011.01272.x
    [57] Stancevic B, Kolesnick R (2010) Ceramide-rich platforms in transmembrane signaling. FEBS Lett 584: 1728-1740. doi: 10.1016/j.febslet.2010.02.026
    [58] Garcia-Ruiz C, Morales A, Fernandez-Checa JC (2015) Glycosphingolipids and cell death: one aim, many ways. Apoptosis 20: 607-620. doi: 10.1007/s10495-015-1092-6
    [59] Contreras FX, Sot J, Ruiz-Arguello MB, et al. (2004) Cholesterol modulation of sphingomyelinase activity at physiological temperatures. Chem Phys Lipids 130: 127-134. doi: 10.1016/j.chemphyslip.2004.02.003
    [60] Cheng JP, Nichols BJ (2016) Caveolae: One Function or Many? Trends Cell Biol 26: 177-189. doi: 10.1016/j.tcb.2015.10.010
    [61] Parton RG, del Pozo MA (2013) Caveolae as plasma membrane sensors, protectors and organizers. Nat Rev Mol Cell Biol 14: 98-112. doi: 10.1038/nrm3512
    [62] Parton RG, Simons K (2007) The multiple faces of caveolae. Nat Rev Mol Cell Biol 8: 185-194. doi: 10.1038/nrm2122
    [63] Shvets E, Ludwig A, Nichols BJ (2014) News from the caves: update on the structure and function of caveolae. Curr Opin Cell Biol 29: 99-106. doi: 10.1016/j.ceb.2014.04.011
    [64] Fridolfsson HN, Roth DM, Insel PA, et al. (2014) Regulation of intracellular signaling and function by caveolin. FASEB J 28: 3823-3831. doi: 10.1096/fj.14-252320
    [65] Banning A, Tomasovic A, Tikkanen R (2011) Functional aspects of membrane association of reggie/flotillin proteins. Curr Protein Pept Sci 12: 725-735. doi: 10.2174/138920311798841708
    [66] Ortegren U, Yin L, Ost A, et al. (2006) Separation and characterization of caveolae subclasses in the plasma membrane of primary adipocytes; segregation of specific proteins and functions. FEBS J 273: 3381-3392. doi: 10.1111/j.1742-4658.2006.05345.x
    [67] Sinha B, Koster D, Ruez R, et al. (2011) Cells respond to mechanical stress by rapid disassembly of caveolae. Cell 144: 402-413. doi: 10.1016/j.cell.2010.12.031
    [68] Roper K, Corbeil D, Huttner WB (2000) Retention of prominin in microvilli reveals distinct cholesterol-based lipid micro-domains in the apical plasma membrane. Nat Cell Biol 2: 582-592. doi: 10.1038/35023524
    [69] Zimmerman B, Kelly B, McMillan BJ, et al. (2016) Crystal structure of a full-length human tetraspanin reveals a cholesterol-binding pocket. Cell 167: 1041-1051. doi: 10.1016/j.cell.2016.09.056
    [70] Hemler ME (2005) Tetraspanin functions and associated microdomains. Nat Rev Mol Cell Biol 6: 801-811. doi: 10.1038/nrm1736
    [71] Yanez-Mo M, Barreiro O, Gordon-Alonso M, et al. (2009) Tetraspanin-enriched microdomains: a functional unit in cell plasma membranes. Trends Cell Biol 19: 434-446. doi: 10.1016/j.tcb.2009.06.004
    [72] Zhang XA, Huang C (2012) Tetraspanins and cell membrane tubular structures. Cell Mol Life Sci 69: 2843-2852. doi: 10.1007/s00018-012-0954-0
    [73] Hugel B, Martinez MC, Kunzelmann C, et al. (2005) Membrane microparticles: two sides of the coin. Physiology (Bethesda) 20: 22-27. doi: 10.1152/physiol.00029.2004
    [74] Raposo G, Stoorvogel W (2013) Extracellular vesicles: exosomes, microvesicles, and friends. J Cell Biol 200: 373-383. doi: 10.1083/jcb.201211138
    [75] van der Pol E, Boing AN, Harrison P, et al. (2012) Classification, functions, and clinical relevance of extracellular vesicles. Pharmacol Rev 64: 676-705. doi: 10.1124/pr.112.005983
    [76] Kravets FG, Lee J, Singh B, et al. (2000) Prostasomes: current concepts. Prostate 43: 169-174.
    [77] Llorente A, van Deurs B, Sandvig K (2007) Cholesterol regulates prostasome release from secretory lysosomes in PC-3 human prostate cancer cells. Eur J Cell Biol 86: 405-415. doi: 10.1016/j.ejcb.2007.05.001
    [78] Arvidson G, Ronquist G, Wikander G, et al. (1989) Human prostasome membranes exhibit very high cholesterol/phospholipid ratios yielding high molecular ordering. Biochim Biophys Acta 984: 167-173. doi: 10.1016/0005-2736(89)90212-5
    [79] Llorente A, de Marco MC, Alonso MA (2004) Caveolin-1 and MAL are located on prostasomes secreted by the prostate cancer PC-3 cell line. J Cell Sci 117: 5343-5351. doi: 10.1242/jcs.01420
    [80] Kastelowitz N, Yin H (2014) Exosomes and microvesicles: identification and targeting by particle size and lipid chemical probes. ChemBioChem 15: 923-928. doi: 10.1002/cbic.201400043
    [81] Bagnat M, Keranen S, Shevchenko A, et al. (2000) Lipid rafts function in biosynthetic delivery of proteins to the cell surface in yeast. Proc Natl Acad Sci USA 97: 3254-3259. doi: 10.1073/pnas.97.7.3254
    [82] Dupre S, Haguenauer-Tsapis R (2003) Raft partitioning of the yeast uracil permease during trafficking along the endocytic pathway. Traffic 4: 83-96. doi: 10.1034/j.1600-0854.2003.40204.x
    [83] Lauwers E, Andre B (2006) Association of yeast transporters with detergent-resistant membranes correlates with their cell-surface location. Traffic 7: 1045-1059. doi: 10.1111/j.1600-0854.2006.00445.x
    [84] Malinska K, Malinsky J, Opekarova M, et al. (2003) Visualization of protein compartmentation within the plasma membrane of living yeast cells. Mol Biol Cell 14: 4427-4436. doi: 10.1091/mbc.E03-04-0221
    [85] Malinska K, Malinsky J, Opekarova M, et al. (2004) Distribution of Can1p into stable domains reflects lateral protein segregation within the plasma membrane of living S. cerevisiae cells. J Cell Sci 117: 6031-6041. doi: 10.1242/jcs.01493
    [86] Spira F, Mueller NS, Beck G, et al. (2012) Patchwork organization of the yeast plasma membrane into numerous coexisting domains. Nat Cell Biol 14: 640-648. doi: 10.1038/ncb2487
    [87] Bagnat M, Simons K (2002) Lipid rafts in protein sorting and cell polarity in budding yeast Saccharomyces cerevisiae. Biol Chem 383: 1475-1480.
    [88] Wachtler V, Balasubramanian MK (2006) Yeast lipid rafts?—an emerging view. Trends Cell Biol 16: 1-4.
    [89] Klose C, Ejsing CS, Garcia-Saez AJ, et al. (2010) Yeast lipids can phase-separate into micrometer-scale membrane domains. J Biol Chem 285: 30224-30232. doi: 10.1074/jbc.M110.123554
    [90] Aresta-Branco F, Cordeiro AM, Marinho HS, et al. (2011) Gel domains in the plasma membrane of Saccharomyces cerevisiae: highly ordered, ergosterol-free, and sphingolipid-enriched lipid rafts. J Biol Chem 286: 5043-5054. doi: 10.1074/jbc.M110.154435
    [91] Mongrand S, Stanislas T, Bayer EM, et al. (2010) Membrane rafts in plant cells. Trends Plant Sci 15: 656-663. doi: 10.1016/j.tplants.2010.09.003
    [92] Tapken W, Murphy AS (2015) Membrane nanodomains in plants: capturing form, function, and movement. J Exp Bot 66: 1573-1586. doi: 10.1093/jxb/erv054
    [93] Malinsky J, Opekarova M, Grossmann G, et al. (2013) Membrane microdomains, rafts, and detergent-resistant membranes in plants and fungi. Annu Rev Plant Biol 64: 501-529. doi: 10.1146/annurev-arplant-050312-120103
    [94] Lopez D, Kolter R (2010) Functional microdomains in bacterial membranes. Genes Dev 24: 1893-1902. doi: 10.1101/gad.1945010
    [95] Lopez D (2015) Molecular composition of functional microdomains in bacterial membranes. Chem Phys Lipids 192: 3-11. doi: 10.1016/j.chemphyslip.2015.08.015
    [96] Saenz JP, Grosser D, Bradley AS, et al. (2015) Hopanoids as functional analogues of cholesterol in bacterial membranes. Proc Natl Acad Sci USA 112: 11971-11976. doi: 10.1073/pnas.1515607112
    [97] Huang Z, London E (2016) Cholesterol lipids and cholesterol-containing lipid rafts in bacteria. Chem Phys Lipids 199: 11-16. doi: 10.1016/j.chemphyslip.2016.03.002
    [98] Haidekker MA, Theodorakis EA (2007) Molecular rotors--fluorescent biosensors for viscosity and flow. Org Biomol Chem 5: 1669-1678. doi: 10.1039/B618415D
    [99] Demchenko AP, Mely Y, Duportail G, et al. (2009) Monitoring biophysical properties of lipid membranes by environment-sensitive fluorescent probes. Biophys J 96: 3461-3470. doi: 10.1016/j.bpj.2009.02.012
    [100] Bagatolli LA (2006) To see or not to see: lateral organization of biological membranes and fluorescence microscopy. Biochim Biophys Acta 1758: 1541-1556. doi: 10.1016/j.bbamem.2006.05.019
    [101] Gaus K, Zech T, Harder T (2006) Visualizing membrane microdomains by Laurdan 2-photon microscopy. Mol Membr Biol 23: 41-48. doi: 10.1080/09687860500466857
    [102] Gaus K, Gratton E, Kable EP, et al. (2003) Visualizing lipid structure and raft domains in living cells with two-photon microscopy. Proc Natl Acad Sci USA 100: 15554-15559. doi: 10.1073/pnas.2534386100
    [103] Sezgin E, Sadowski T, Simons K (2014) Measuring lipid packing of model and cellular membranes with environment sensitive probes. Langmuir 30: 8160-8166. doi: 10.1021/la501226v
    [104] Kucherak OA, Oncul S, Darwich Z, et al. (2010) Switchable nile red-based probe for cholesterol and lipid order at the outer leaflet of biomembranes. J Am Chem Soc 132: 4907-4916. doi: 10.1021/ja100351w
    [105] Baumgart T, Hunt G, Farkas ER, et al. (2007) Fluorescence probe partitioning between Lo/Ld phases in lipid membranes. Biochim Biophys Acta 1768: 2182-2194. doi: 10.1016/j.bbamem.2007.05.012
    [106] Solanko KA, Modzel M, Solanko LM, et al. (2015) Fluorescent sterols and cholesteryl esters as probes for intracellular cholesterol transport. Lipid Insights 8: 95-114.
    [107] Gimpl G, Gehrig-Burger K (2007) Cholesterol reporter molecules. Biosci Rep 27: 335-358. doi: 10.1007/s10540-007-9060-1
    [108] Fujimoto T, Hayashi M, Iwamoto M, et al. (1997) Crosslinked plasmalemmal cholesterol is sequestered to caveolae: analysis with a new cytochemical probe. J Histochem Cytochem 45: 1197-1205. doi: 10.1177/002215549704500903
    [109] Shimada Y, Maruya M, Iwashita S, et al. (2002) The C-terminal domain of perfringolysin O is an essential cholesterol-binding unit targeting to cholesterol-rich microdomains. Eur J Biochem 269: 6195-6203. doi: 10.1046/j.1432-1033.2002.03338.x
    [110] Liu SL, Sheng R, Jung JH, et al. (2017) Orthogonal lipid sensors identify transbilayer asymmetry of plasma membrane cholesterol. Nat Chem Biol 13: 268-274.
    [111] Koivusalo M, Alvesalo J, Virtanen JA, et al. (2004) Partitioning of pyrene-labeled phospho- and sphingolipids between ordered and disordered bilayer domains. Biophys J 86: 923-935. doi: 10.1016/S0006-3495(04)74168-5
    [112] Koivusalo M, Jansen M, Somerharju P, et al. (2007) Endocytic trafficking of sphingomyelin depends on its acyl chain length. Mol Biol Cell 18: 5113-5123. doi: 10.1091/mbc.E07-04-0330
    [113] Pagano RE, Watanabe R, Wheatley C, et al. (1999) Use of N-[5-(5,7-dimethyl boron dipyrromethene difluoride-sphingomyelin to study membrane traffic along the endocytic pathway. Chem Phys Lipids 102: 55-63. doi: 10.1016/S0009-3084(99)00075-4
    [114] Scheidt HA, Muller P, Herrmann A, et al. (2003) The potential of fluorescent and spin-labeled steroid analogs to mimic natural cholesterol. J Biol Chem 278: 45563-45569. doi: 10.1074/jbc.M303567200
    [115] Smutzer G, Crawford BF, Yeagle PL (1986) Physical properties of the fluorescent sterol probe dehydroergosterol. Biochim Biophys Acta 862: 361-371. doi: 10.1016/0005-2736(86)90239-7
    [116] Ohvo-Rekila H, Akerlund B, Slotte JP (2000) Cyclodextrin-catalyzed extraction of fluorescent sterols from monolayer membranes and small unilamellar vesicles. Chem Phys Lipids 105: 167-178. doi: 10.1016/S0009-3084(00)00122-5
    [117] Hao M, Lin SX, Karylowski OJ, et al. (2002) Vesicular and non-vesicular sterol transport in living cells The endocytic recycling compartment is a major sterol storage organelle. J Biol Chem 277: 609-617. doi: 10.1074/jbc.M108861200
    [118] Wustner D, Herrmann A, Hao M, et al. (2002) Rapid nonvesicular transport of sterol between the plasma membrane domains of polarized hepatic cells. J Biol Chem 277: 30325-30336. doi: 10.1074/jbc.M202626200
    [119] Wustner D, Mondal M, Tabas I, et al. (2005) Direct observation of rapid internalization and intracellular transport of sterol by macrophage foam cells. Traffic 6: 396-412. doi: 10.1111/j.1600-0854.2005.00285.x
    [120] Frolov A, Petrescu A, Atshaves BP, et al. (2000) High density lipoprotein-mediated cholesterol uptake and targeting to lipid droplets in intact L-cell fibroblasts A single- and multiphoton fluorescence approach. J Biol Chem 275: 12769-12780. doi: 10.1074/jbc.275.17.12769
    [121] Wustner D, Mondal M, Huang A, et al. (2004) Different transport routes for high density lipoprotein and its associated free sterol in polarized hepatic cells. J Lipid Res 45: 427-437.
    [122] Liu J, Chang CC, Westover EJ, et al. (2005) Investigating the allosterism of acyl-CoA:cholesterol acyltransferase (ACAT) by using various sterols: in vitro and intact cell studies. Biochem J 391: 389-397. doi: 10.1042/BJ20050428
    [123] Mukherjee S, Zha X, Tabas I, et al. (1998) Cholesterol distribution in living cells: fluorescence imaging using dehydroergosterol as a fluorescent cholesterol analog. Biophys J 75: 1915-1925. doi: 10.1016/S0006-3495(98)77632-5
    [124] Sato SB, Ishii K, Makino A, et al. (2004) Distribution and transport of cholesterol-rich membrane domains monitored by a membrane-impermeant fluorescent polyethylene glycol-derivatized cholesterol. J Biol Chem 279: 23790-23796. doi: 10.1074/jbc.M313568200
    [125] Mazeres S, Schram V, Tocanne JF, et al. (1996) 7-nitrobenz-2-oxa-1,3-diazole-4-yl-labeled phospholipids in lipid membranes: differences in fluorescence behavior. Biophys J 71: 327-335. doi: 10.1016/S0006-3495(96)79228-7
    [126] Loura LM, Fedorov A, Prieto M (2001) Exclusion of a cholesterol analog from the cholesterol-rich phase in model membranes. Biochim Biophys Acta 1511: 236-243. doi: 10.1016/S0005-2736(01)00269-3
    [127] Sezgin E, Can FB, Schneider F, et al. (2016) A comparative study on fluorescent cholesterol analogs as versatile cellular reporters. J Lipid Res 57: 299-309.
    [128] Gaibelet G, Allart S, Terce F, et al. (2015) Specific cellular incorporation of a pyrene-labelled cholesterol: lipoprotein-mediated delivery toward ordered intracellular membranes. PLoS One 10: e0121563. doi: 10.1371/journal.pone.0121563
    [129] Dagher G, Donne N, Klein C, et al. (2003) HDL-mediated cholesterol uptake and targeting to lipid droplets in adipocytes. J Lipid Res 44: 1811-1820. doi: 10.1194/jlr.M300267-JLR200
    [130] Sparrow CP, Patel S, Baffic J, et al. (1999) A fluorescent cholesterol analog traces cholesterol absorption in hamsters and is esterified in vivo and in vitro. J Lipid Res 40: 1747-1757.
    [131] Wiegand V, Chang TY, Strauss JF, 3rd, et al. (2003) Transport of plasma membrane-derived cholesterol and the function of Niemann-Pick C1 Protein. FASEB J 17: 782-784.
    [132] Shrivastava S, Haldar S, Gimpl G, et al. (2009) Orientation and dynamics of a novel fluorescent cholesterol analogue in membranes of varying phase. J Phys Chem B 113: 4475-4481. doi: 10.1021/jp808309u
    [133] Huang H, McIntosh AL, Atshaves BP, et al. (2010) Use of dansyl-cholestanol as a probe of cholesterol behavior in membranes of living cells. J Lipid Res 51: 1157-1172. doi: 10.1194/jlr.M003244
    [134] Li Z, Mintzer E, Bittman R (2006) First synthesis of free cholesterol-BODIPY conjugates. J Org Chem 71: 1718-1721. doi: 10.1021/jo052029x
    [135] Bergstrom F, Mikhalyov I, Hagglof P, et al. (2002) Dimers of dipyrrometheneboron difluoride (BODIPY) with light spectroscopic applications in chemistry and biology. J Am Chem Soc 124: 196-204. doi: 10.1021/ja010983f
    [136] Marks DL, Bittman R, Pagano RE (2008) Use of Bodipy-labeled sphingolipid and cholesterol analogs to examine membrane microdomains in cells. Histochem Cell Biol 130: 819-832. doi: 10.1007/s00418-008-0509-5
    [137] Ariola FS, Li Z, Cornejo C, et al. (2009) Membrane fluidity and lipid order in ternary giant unilamellar vesicles using a new bodipy-cholesterol derivative. Biophys J 96: 2696-2708. doi: 10.1016/j.bpj.2008.12.3922
    [138] Wustner D, Solanko L, Sokol E, et al. (2011) Quantitative assessment of sterol traffic in living cells by dual labeling with dehydroergosterol and BODIPY-cholesterol. Chem Phys Lipids 164: 221-235. doi: 10.1016/j.chemphyslip.2011.01.004
    [139] Solanko LM, Honigmann A, Midtiby HS, et al. (2013) Membrane orientation and lateral diffusion of BODIPY-cholesterol as a function of probe structure. Biophys J 105: 2082-2092. doi: 10.1016/j.bpj.2013.09.031
    [140] Holtta-Vuori M, Uronen RL, Repakova J, et al. (2008) BODIPY-cholesterol: a new tool to visualize sterol trafficking in living cells and organisms. Traffic 9: 1839-1849. doi: 10.1111/j.1600-0854.2008.00801.x
    [141] Mazeres S, Lagane B, Welby M, et al. (2001) Probing the lateral organization of membranes: fluorescence repercussions of pyrene probe distribution. Spectrochim Acta A Mol Biomol Spectrosc 57: 2297-2311. doi: 10.1016/S1386-1425(01)00486-3
    [142] Le Guyader L, Le Roux C, Mazeres S, et al. (2007) Changes of the membrane lipid organization characterized by means of a new cholesterol-pyrene probe. Biophys J 93: 4462-4473. doi: 10.1529/biophysj.107.112821
    [143] Lagane B, Mazeres S, Le Grimellec C, et al. (2002) Lateral distribution of cholesterol in membranes probed by means of a pyrene-labelled cholesterol: effects of acyl chain unsaturation. Biophys Chem 95: 7-22. doi: 10.1016/S0301-4622(01)00235-6
    [144] Lecompte MF, Gaibelet G, Lebrun C, et al. (2015) Cholesterol and sphingomyelin-containing model condensed lipid monolayers: heterogeneities involving ordered microdomains assessed by two cholesterol derivatives. Langmuir 31: 11921-11931. doi: 10.1021/acs.langmuir.5b02646
    [145] Astarie-Dequeker C, Le Guyader L, Malaga W, et al. (2009) Phthiocerol dimycocerosates of M. tuberculosis participate in macrophage invasion by inducing changes in the organization of plasma membrane lipids. PLoS Pathog 5: e1000289.
    [146] Rohrl C, Meisslitzer-Ruppitsch C, Bittman R, et al. (2012) Combined light and electron microscopy using diaminobenzidine photooxidation to monitor trafficking of lipids derived from lipoprotein particles. Curr Pharm Biotechnol 13: 331-340. doi: 10.2174/138920112799095338
    [147] Holtta-Vuori M, Sezgin E, Eggeling C, et al. (2016) Use of BODIPY-Cholesterol (TF-Chol) for Visualizing Lysosomal Cholesterol Accumulation. Traffic 17: 1054-1057. doi: 10.1111/tra.12414
    [148] Gaibelet G, Terce F, Bertrand-Michel J, et al. (2013) 21-Methylpyrenyl-cholesterol stably and specifically associates with lipoprotein peripheral hemi-membrane: a new labelling tool. Biochem Biophys Res Commun 440: 533-538. doi: 10.1016/j.bbrc.2013.09.101
    [149] Storey SM, Gallegos AM, Atshaves BP, et al. (2007) Selective cholesterol dynamics between lipoproteins and caveolae/lipid rafts. Biochemistry 46: 13891-13906. doi: 10.1021/bi700690s
    [150] Ohsaki Y, Cheng J, Suzuki M, et al. (2009) Biogenesis of cytoplasmic lipid droplets: from the lipid ester globule in the membrane to the visible structure. Biochim Biophys Acta 1791: 399-407. doi: 10.1016/j.bbalip.2008.10.002
    [151] Mukherjee S, Soe TT, Maxfield FR (1999) Endocytic sorting of lipid analogues differing solely in the chemistry of their hydrophobic tails. J Cell Biol 144: 1271-1284. doi: 10.1083/jcb.144.6.1271
    [152] Prinz WA (2007) Non-vesicular sterol transport in cells. Prog Lipid Res 46: 297-314. doi: 10.1016/j.plipres.2007.06.002
  • Reader Comments
  • © 2017 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索
AIMS Biophysics
1.5

Metrics

Article views(4498) PDF downloads(1355) Cited by(1)

Preview PDF
Download XML
Export Citation
Article outline

Figures and Tables

Figures(3)  /  Tables(1)

Other Articles By Authors

Related pages

Tools

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return

Catalog