A novel model for intersections of vehicular traffic flow

1.   Introduction

Some millennia ago, epidemics were mainly of interest to historians. The last 95 years has resulted in a dramatic turn in events. From the outbreak of the Spanish flu in 1918–1919 [1], to herpes and legionnaires disease in the early 70s to the discovery of acquired immunodeficiency syndrome (AIDS) and Ebola, the world has witnessed highly contagious diseases that have threatened human existence [2]. A complete historical account of outbreaks was documented by Brauer [1]. According to Velevan and Meyer [3], coronaviruses were initially identified in 1966 by Tyrell et al. [4]. Recently, according to Guarner [5], the world has witnessed the emergence of three coronaviruses that have led to outbreaks, causing troubling worldwide health and economic concerns. The first two are the severe acute respiratory syndrome (SARS) and the Middle East respiratory syndrome coronavirus (MERS-CoV) that both have case fatality rates of about 9.5 and $35\%$, respectively. The most recent disease currently ravaging the world population is COVID-19. Though the virus was recognized in December 2019 [6], the first official case was reported on the 7th of January 2020. Due to several factors, the spread of the virus has been rapid. It has led the leadership of the World Health Organization (WHO) Emergency Committee to declare the infection a pandemic and a global health emergency [3]. A slight solace is that COVID-19 fatality rate is at $2-3\%$, unlike the other coronaviruses.

The use of mathematical models in aiding effective decision making in public health and clinical medicine has been acknowledged by Porgo et al. [7]. Several modelling frameworks are often proposed to understand the spread of diseases within a population and develop short- and long-term control strategies [8]. One of such is the use of mathematical models, which are often deployed to capture the dynamics of the disease at different stages [9]. Several authors such as Kassa et al. [10], Ndairou et al. [11], Zhang et al. [12] among others have come up with several models that fully capture the different transmission modes of the Covid-19 infection and inculcated several intervention strategies. Their results show that mathematical models are imperative in the fight against the spread of the disease.

Given that COVID-19 was officially reported in January 2020 and months later, several countries are yet to experience the peak of the disease and vaccine has been unavailable, it is imperative to consider the influence of several non-pharmaceutical interventions. Several scientists such as Zhang et al. [12] evaluated interventions like social distancing, school closures, isolation and quarantine. While their studies revealed the positive influence of these measures on reducing the spread, their findings do not represent the situation worldwide. Based on statistics provided by Bargain and Ulugbek [13] and Olopade et al. [14], among others, several countries have more than half the population living below the poverty line. It is also important to note that some of these countries are densely and highly populated.

In light of the above observation, it is essential to consider various mitigation factors in poverty-ravaged countries where most of the population live below the poverty line, where unemployment is rife, and a high number of people share a small space and limited facilities exist. In such countries, the disparity in wealth means only a small percentage of the population can afford to execute all the mitigation processes comfortably without being a risk to others. Taking South Africa as a case in point, which this study will focus on, 14% of the population lives in an informal settlement, and there is an unemployment rate of 29% with a significant percentage having menial employment [15]. A rigorous study conducted by Garba et al. [16] within the South African context found that if all the control measures implemented by the government were put in place early and for a sustained period, the disease would subsequently die out, which is excellent. The downside, however, is that a particular set of the population, especially the unemployed and the low-income earners, would find it even harder to survive economically.

The study by Stiegler and Bouchard [15] found that the phased approach used by the government worked, but given that the study was conducted in May 2020 and 6 months later, South Africa went into a second wave means that the strategy needs revisiting. Based on the respondents reported in the study, it is clear that people's attitude to the government response to the COVID-19 situation differs for the middle-class and poor respondents. Furthermore, Arndt et al. [17] conducted a study focusing on the impact of government response on food security. They found that the mitigation approach of distancing directly impacted the wage income, particularly for low-skilled workers, and suggested that the initial lockdown policies had a detrimental impact on the food security of low-income households. These studies highlight the need to construct a model that focuses on measures that can help curb the spread of the virus while allowing unemployed and low-income earners to go about their daily business. Therefore, there is a need to apply a two-pronged approach to curb the spread of COVID-19. Therein lies the objective of this study.

We aim to construct a model that caters for non-pharmaceutical measures and also takes into consideration the impact of vaccination in anticipation of the arrival of vaccines and the significant number of people against vaccination (see Megget [18] and De Roo et al. [19]). We also investigate the potential impact of vaccine efficacy on the reproduction number. We carry out the stability analysis of the disease-free equilibrium point and sensitivity of the effective reproduction number to the model's parameters. We investigate the impact of combining both pharmaceutical and non-pharmaceutical measures in curbing the spread of the infection.

2.   Mathematical models

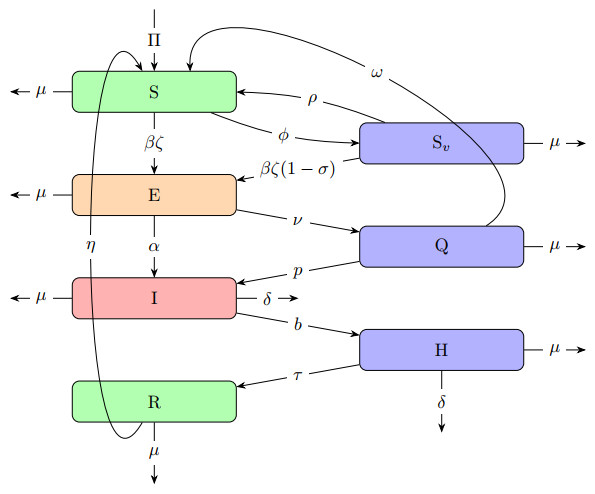
In this section, we propose a mathematical model of the dynamics of COVID-19 and mitigation measures. This model assumes that the total population $N(t)$ is divided into seven classes; namely, the susceptible class $S(t)$, the vaccinated class $S_v(t)$, the exposed class $E(t)$, the quarantined class $Q(t)$, the infected class $I(t)$, the hospitalized class $H(t)$ and recovered class $R(t)$. We assume that the susceptible class is vaccinated at a rate $\phi$ and the vaccine has an efficacy rate $(1-\sigma)$, where $\sigma = 0$ indicates a failed vaccination and $\sigma = 1$ depicts a perfectly effective vaccination. The vaccine is assumed to dwindle at a constant rate $\rho$, such that individuals that are vaccinated have immunity for a period of $1/\rho$ time unit. It is assumed that individuals who have failed vaccination may become exposed and inadvertently become infected at a lower infection rate $\beta\zeta(1-\sigma)IS_v/N$ than individuals from the susceptible population who are unvaccinated, who become infected at a rate $\beta\zeta IS/N$, where $\beta$ is the probability of transmission and $\zeta$ is the effective contact rate. Individuals exposed to the virus are kept in quarantine at a rate $\nu$ and those who show clinical symptoms are hospitalized and treated for COVID-19 symptoms at a constant rate $b$, with a recovery rate $\tau$. However, quarantined individuals who show no symptoms during the fourteen-day incubation period rejoin the susceptible compartment at a rate $\omega$, while individuals who show clinical symptoms progress to the infected class at $p$. We considered natural death and assumed that the mortality rate is $\mu$, while COVID-19 related mortality rate is $\delta$.

The system of differential equations describing the model is derived using the assumptions mentioned above and the flow diagram in Figure 1, and are expressed as follow:

with the initial conditions

2.1.   Parameter estimation and model fitting

We use the daily number of COVID-19 infections reported in South Africa to estimate some of the parameter values in the system of Eq (2.1). Figure 2 shows the trend of the daily number of new infections reported [20]. We consider two stages, the first stage represents the onset of the disease and the phase when mitigation strategies were first implemented. The second stage represents the stage when the implementation of mitigation strategies was at its peak. We use the genetic algorithm optimization technique to estimate the parameters. For both stages, we consider Eq (2.1) without the vaccinated component or the vaccination parameters, such that the model reduces to

For the first stage, we consider the COVID-19 data from 05/03/2020 until 17/07/2020, and the second stage from 17/07/2020 to 24/10/2020. To estimate the parameters for the first stage, given that there were very few known cases, we assumed that the initial number of exposed individuals is $20$, that is $E(0) = 20$. The infected class initial value $I(0)$ is $5$, the number of cases reported on the 5th of March 2020. The recruitment rate $\Pi$ is evaluated using $\mu N$, where $N = 58.56\times 10^6$ is South Africa total population and $\mu = 1/(63.86\times365)$ is the natural mortality rate [21]. The initial values of the $Q$ and $R$ components are assumed to be zero, and $S(0) = N-E(0)-I(0)$. For the second stage, the components initial values are taken to be the terminal values of the first stage. Figure 3 shows the curves of the daily number of infections simulated by model (2.3) and the reported data. In Table 1, we present the estimated parameter values in both stages. Because the implementation of mitigation strategies was at its peak, contact rate and transmission probability in the second stage are lower than the corresponding values in the first stage.

3.   Mathematical analysis

This section presents some theoretical results wherein we obtain the disease-free equilibrium point and analyze its local stability. We prove that the model Eq (2.1) is well-posed, bounded, and its solutions are positive, and then proceed to obtain the effective reproduction number at the disease-free equilibrium point.

3.1.   Positivity and boundedness

Theorem 1. Assume that $\{S(0) \geq 0, S_v(0) \geq 0, E(0) \geq 0, Q(0) \geq 0, I(0) \geq 0, H(0) \geq 0, R(0) \geq 0\}$ are the initial values of the solutions of equations (2.1). The solution set

are all non-negative for all $t \geq 0$, provided all parameters are positive.

Proof. By continuous dependence of the solutions on initial conditions, we only need to show the solution set is positive, given that the initial conditions are positive. From Eq (2.1d), and by using the method of integrating factor, we have

Similarly, from Eq (2.1f)

Similar approach can be used for the other equations, and this guarantees the positivity of the solutions. Therefore, the system is positively invariant in ${\mathbb{R}}^{7}_+$.

Theorem 2. The model (2.1) is well-posed, and the solution is bounded and invariant in the region

Proof: We know that

Assume that there is no disease-induced death, then

Therefore,

where $N(0)$ is the initial value of the total population. Equation (3.7) implies that the model is well-posed, and solutions are bounded in $\Lambda$.

3.2.   Disease-free equilibrium

Assume that there are no infectious individuals at the disease-free state, then $E^0 = I^0 = 0$. Consequently, $Q^0 = H^0 = R^0 = 0$, and

Therefore, the disease-free equilibrium point is obtained as

3.3.   Effective reproduction number

For the study of the stability properties of the model (2.1), we will use the effective reproduction number, which is the average number of secondary cases produced by one infected individual during its entire infectious period in an otherwise uninfected population [22]. From a mathematical viewpoint, the value of the effective reproduction number associated with the epidemiological model Eq (2.1a) to (2.1g) can be computed as the spectral radius of the next–generation matrix (see Heesterbeek and Dietz [22] and Van den Driessche and Watmough [23] for more details). We do this by decomposing the infectious compartments of the model into $\mathcal{F}-\mathcal{V}$, and finding the next-generation matrix $FV^{-1}$ at the disease-free equilibrium point. $F$ and $V$ are respectively the Jacobian of the matrices $\mathcal{F}$ and $\mathcal{V}$ defined as:

Therefore,

and the next generation matrix (NGM) is obtained as

The effective reproduction number is the spectral radius of the next generation matrix. In this case, the spectral radius of $NGM$ is the matrix's only non-zero eigenvalues. Thus, the effective reproduction number of the epidemiological model (2.1) is obtained as follow:

The linear relationship between the reproduction number and the probability of transmission is quite apparent. We can decompose the effective reproduction number into two parts such that

where

$\mathcal{R}_i$ represents the contribution of individuals who are exposed and subsequently become infected to the spread of the infection. In contrast, $\mathcal{R}_q$ represents the contribution of individuals who progressed to the infected compartment from quarantine to the spread of the disease. We can define the effective reproduction number in terms of the basic reproduction number $\mathcal{R}_0$ without vaccination as

where

Given the positivity of the parameters, $1-{\scriptstyle{}^{\sigma \phi }\!\!\diagup\!\!{}_{(\phi +\rho +\mu)}\; } < 1$, and it corresponds to the vaccine administration rate. If $\mathcal{R}_0$ is less than unity, we can easily see that $\mathcal{R}_{vac} < 1$. However, if $\mathcal{R}_0$ is greater than one, it is imperative to ask if the administration of a vaccine would make $\mathcal{R}_{vac} < 1$. In that case, the vaccination rate must satisfy the following inequality

for which $\mathcal{R}_0(\sigma - 1) + 1 > 0$, which implies that the vaccine efficacy rate $\sigma$ must be greater than $1 - 1/\mathcal{R}_0$. This simply means that; given the critical vaccination rate $\phi_c$ defined as

There is a region in the domain of the parameters where we can make the effective reproduction number less than one. We illustrate this using the parameter values estimated from the model fitting process. We calculate the basic reproduction number from the two stages and present them in Table 2. The values obtained in Table 2 show that strict implementation of the mitigation strategies significantly reduces the basic reproduction number. In the shaded region in Figure 4, $\mathcal{R}_{vac} < 1$. By assuming that vaccinated individuals are immune for $365$ days, we can see that with about $75\%$ vaccine efficacy and a good vaccination rate, it is possible to make the effective reproduction number less than unity. This implies that if a reoccurrence of stage 1 happens in South Africa, utilizing non-pharmaceutical measures, such as quarantine and reducing contact rate, combined with a vaccine that has $75\%$ efficacy, the rate of secondary infection can be kept to the minimum.

3.4.   Local stability of the disease-free equilibrium point

Theorem 3. The disease-free equilibrium point is asymptotically stable whenever ${\mathcal{R}}_{vac} < 1$ and unstable otherwise.

Proof. Evaluating the linearized Jacobian at the disease-free equilibrium point, we have

where

are non-negative. To show that the disease–free equilibrium point is locally asymptotically stable, we must show that the eigenvalues of $J(\zeta^0)$ have negative real part if $\mathcal{R}_{vac} < 1$. The characteristics polynomial of the Jacobian $J(\zeta^0)$ is given as

where

To show that the disease-free equilibrium point is locally asymptotically stable, it suffices to prove, by the Routh–Hurwitz stability criterion for fourth–order polynomials, that $\lambda_0 > 0, \; \lambda_1 > 0, \; \lambda_4 > 0, \; \lambda_1\lambda_2 - \lambda_0\lambda_3 > 0$ and $\left(\lambda_1\lambda_2 - \lambda_0\lambda_3\right)\lambda_3 - \lambda_1^2\lambda_4 > 0$. These conditions are satisfied whenever $\mathcal{R}_{vac} < 1$ as shown in Appendix A.1. Therefore, the disease-free equilibrium point is locally asymptotically stable.

3.5.   Global stability of the disease-free equilibrium point

This section uses the application of the Lyapunov function to establish the global stability of the disease-free equilibrium.

Definition 1. Given the dynamical system, $\dot{X} = \mathcal{G}(X)$, with equilibrium point, $X^*$, such that $\mathcal{G} : \mathbb{R}^n \mapsto \mathbb{R}^n$. We define a continuous scalar function $\mathcal{L} : \mathbb{R}^n \mapsto \mathbb{R}^n$. $\mathcal{L}$ is said to be positive definite if the conditions

are satisfied. If $\mathcal{L}(X) \to \infty$ as $\Vert X \Vert \to \infty$, then $\mathcal{L}(X)$ is radially unbounded [24].

Theorem 4 (Lyapunov's Stability Theorem).The equilibrium point, $X^*$, is globally stable if $\mathcal{L}(X)$ is a Lyapunov function such that $\dot{\mathcal{L}}(X) < 0$ for all $X \neq X^*$.

An extension of the Lyapunov stability theorem is the LaSalle invariance principle which partially states that, given a dynamical system $\dot{X} = \mathcal{G}(X)$ with equilibrium, $X^*$, such that $\mathcal{G}(X^*) = 0$, $X^*$ is globally stable if there is a continuously differentiable Lyapunov function which satisfies

This allows us to define an invariant set $\left\{X \in \mathbb{R}^n_+ \; st \; \dot{\mathcal{L}} = 0 \right\}$, such that the only maximal compact set in the invariant set is the equilibrium point, $X^*$. See Martcheva [24] for the proof of this theorem.

Theorem 5. The disease free equilibrium point, $\xi^0$, is globally asymptotically stable whenever $\mathcal{R}_{vac} < 1$.

Proof. To prove this theorem, we define a Lyapunov function

where the constants, $\iota_1, \iota_2$ and $\iota_3$, are to be determined. Differentiating Eq (3.24) with respect to time and substituting $\dot{E}, \dot{Q}, \dot{I}, \dot{H}$ from Eq (2.1), we have

If the coefficients of $E, Q$ and $H$ are equated to zero, we obtain the following positive values for $\iota_1, \iota_2$ and $\iota_3$

Therefore, we can define a Lyapunov, $\mathcal{L}$, for the disease-free equilibrium point, $\xi^0$, as follow

Differentiating Eq (3.26) with respect to $t$ and substituting $\dot{E}, \dot{Q}, \dot{I}$ from Eq (2.1) gives

whenever $\mathcal{R}_{vac} < 1$.

Furthermore, $\dot{\mathcal{L}}(\xi^0) = 0 \iff (E = Q = I = H = 0)$. Therefore, the singleton set $\{\xi^0\}$ is the only compact set in the invariant set $\left\{ (S, S_v, E, Q, I, H, R) \in \mathbb{R}^7_+ \; st \; \dot{\mathcal{L}} = 0 \right\}$, and thus by the LaSalle invariance principle, the disease-free equilibrium, $\xi^0$, is globally asymptotically stable if $\mathcal{R}_{vac} < 1$.

4.   Numerical simulation

This study deals with a model for the dynamics of COVID-19 with vaccination. Numerical simulations were carried out for the system of equations (2.1) with the range of parameter values detailed in Table 1. The parameter values were sampled using the Latin Hypercube Sampling, and these samples were used to carry out a series of numerical simulations for the model. 2500 values were sampled for each parameter. A partial rank correlation analysis was carried out between the sampled values of the parameters and the values of important response variables, such as the effective reproduction number, the cumulative vaccinated population, the cumulative infected population and the cumulative hospitalized population. In Table 3, the partial rank correlation coefficient (PRCC) for each response variable for the parameters are presented. The PRCC values show the important parameters in the dynamics of the administration of control and preventive measures on the infection rate of COVID-19. We note here that the parameters with large PRCC values, that is $> 0.5$ or $< - 0.5$ and p-value $\leq 0.05$ are the most significant parameters. The closer the PRCC value is to positive or negative unity, the higher their influence on the measured variable. The sign of the PRCC value indicates the qualitative relationship between the parameter and the response function. A positive sign means a direct relationship between the parameter and measured variable, while a negative sign indicates otherwise.

In Table 4, we ordered the PRCC values of each measured function for each parameter in descending order of ranking. For the effective reproductive number, it can be seen that the top three ranked parameters are the probability of transmission, vaccine efficacy rate, and effective contact rate. In contrast, the bottom-ranked parameter is the vaccination waning rate. The two highest-ranked parameters for the cumulative vaccinated population are the vaccination rate and the vaccine waning rate. In contrast, the lowest-ranked parameter is the rate at which quarantined individuals are confirmed non-infectious, which is insignificant in the dynamics of the vaccinated population. Amongst the topmost ranked parameters in the infected compartment is the vaccination rate and effective contact rate. This show how significant pharmaceutical measures such as vaccination and non-pharmaceutical measures like reducing contact between infected and susceptible individuals can affect the dynamics of the infected individuals in South Africa and inadvertently affect the dynamics of the hospitalized compartment. The results in Table 4 show that the degree of efficacy of a vaccine would be significant in the dynamics of the rate of infection of COVID-19, as this parameter is highly ranked and statistically significant for each response function. For instance, the vaccine efficacy rate is second in significance to the transmission probability for the effective reproduction number. This indicates that the efficacy of the anticipated vaccine would be as significant or, to some extent, more important than the rate of administration of the vaccine.

4.1.   Sensitivity analysis of $\mathcal{R}_{vac}$

We use sensitivity analysis to determine the relative importance of each parameter in the effective reproduction number. We define the sensitivity index for any parameter, say $x$, as

Therefore, the sensitivity indexes of the parameters with respect to effective reproduction number are given as follow:

A positive sensitivity index, on the one hand, of the model output $\mathcal{R}_{vac}$ for any parameter, say $x$, implies that a percentage increase/decrease in $x$ will result in a $\Gamma\%$ increase/decrease in $\mathcal{R}_{vac}$. On the other hand, a negative sensitivity index implies that a percentage increase/decrease in parameter $x$ will lead to a $\Gamma\%$ decrease/increase in $x$. $\mathcal{R}_{vac}$ grows at the same proportion with the transmission probability and effective contact rate. In contrast, control parameters such as hospitalization rate, quarantine rate, vaccination rate and vaccination efficacy rate are inversely proportional to the reproduction number.

The sensitivity indexes in Table 5 are arranged in descending order of magnitude, placing the most significant parameter at the top. In this case, we used the parameter values obtained from fitting the model and assumed that a vaccine with $75\%$ efficacy, giving immunity for $365$ days, is administered at a $50\%$ ratio. The table shows that the vaccine's efficacy, $\sigma$, is the most significant parameter. The obtained sensitivity index of $\mathcal{R}_{vac}$ for $\sigma$ indicates that a $1\%$ increase in the vaccine effectiveness will lead to an approximately $3\%$ decrease in the number of secondary infections. Other control measures, such as limiting the contact rate between the susceptible and infected population, maximizing the treatment of infected individuals, and isolating exposed individuals, are also pivotal in minimizing the number of secondary infections. We already know that if there is no vaccination and using the values in Table 5, we obtain a basic reproduction number of $3.5655$. However, including vaccination and vaccine efficacy significantly reduces the reproduction number to $0.9062$. Figure 5 presents the effective reproduction number as a function of transmission probability ($\beta$) and contact rate ($\zeta$). The figure shows the significance of the transmission probability in bringing the effective reproduction number below unity. It shows that a drastic reduction in the transmission probability to about $0.05$, which can be facilitated by personal hygiene, sanitation and wearing of a mask, can significantly reduce the infection rate as seen in Figure 5b. In Figure 6a, the reproduction number is plotted as a function of vaccination rate and vaccine efficacy. Again, we can see in Figure 6a that a vaccine with about $75\%$ efficacy can reduce the reproduction number to less than $1$, while Figure 6b shows the importance of combining both pharmaceutical and non-pharmaceutical approaches in reducing the spread of the virus.

5.   Conclusions

In this study, a model describing the transmission of COVID-19 with the implementation of pharmaceutical and non-pharmaceutical mitigation measures was proposed. To contextualize the South African situation, emphasis has been placed on more adaptable measures like personal hygiene, sanitation, wearing of mask, social distancing, and vaccination. The disease-free equilibrium point analysis was obtained, and the local stability analysis of the point was performed. We obtained the reproduction number at the disease-free equilibrium point and further analyzed the sensitivity of the reproduction number to some of the parameters considered in the model.

The results obtained indicate that, in the South African context, a vaccine with at least $75\%$ efficacy coupled with other non-pharmaceutical measures that minimize the probability of infection such as personal hygiene and protective gear can significantly decrease the rate of secondary infection. The importance of quarantine and isolation of exposed individuals has been established in studies. Still, we have also established the importance of adhering to measures that mitigate the risk of infection even if they have contact with an exposed or infected individual.

As we await the production and administration of the vaccine for the general public, the results of this study indicate that control measures such as personal hygiene, use of protective gear, limiting physical and social interactions should be adhered to to reduce the transmission of the virus.

Acknowledgement

The authors would like to acknowledge the support of the School of Computer Science and Applied Mathematics, University of Witwaterstrand.

Conflict of interest

The authors declare that there are no conflicts of interest.

A.   Appendix

A.1.   Routh-Hurwitz criterion for the characteristics polynomial (3.22)

In this section, we show the positivity of the sequence of determinants of the principal sub-matrices of the Hurwitz matrix of the characteristics polynomial (3.22). That is, given the polynomial (3.22)

where

we want to show that $\lambda_0, \; \lambda_1, \; \lambda_4, \; \lambda_1\lambda_2 - \lambda_0\lambda_3, \; \left(\lambda_1\lambda_2 - \lambda_0\lambda_3\right)\lambda_3 - \lambda_1^2\lambda_4$ are all non-negative whenever $\mathcal{R}_{vac}$ is less than unity. $\lambda_0$ is obviously positive. Note that the parameters $k_1, \; k_2, \; k_3$ and $k_4$ Equation (3.21) are positive. Since this is the case, $\lambda_1$ and $\lambda_4$ are non-negative whenever $\mathcal{R}_{vac} < 1$. It remains to show that $\lambda_1\lambda_2 - \lambda_0\lambda_3 > 0$ and $\left(\lambda_1\lambda_2 - \lambda_0\lambda_3\right)\lambda_3 - \lambda_1^2\lambda_4 > 0$. If we can show that $\left(\lambda_1\lambda_2 - \lambda_0\lambda_3\right)\lambda_3 - \lambda_1^2\lambda_4$ is positive whenever $\mathcal{R}_{vac} < 1$, then $\lambda_1\lambda_2 - \lambda_0\lambda_3 > 0$ whenever $\mathcal{R}_{vac} < 1$. After some algebraic calculations, $\left(\lambda_1\lambda_2 - \lambda_0\lambda_3\right)\lambda_3 - \lambda_1^2\lambda_4$ was obtained as

where

From Equation (3.15), $\mathcal{R}_i$ and $\mathcal{R}_q$ are non-negative, and given the positivity of $k_1, k_2, k_3, k_4$, we can conclude that $\left(\lambda_1\lambda_2 - \lambda_0\lambda_3\right)\lambda_3 - \lambda_1^2\lambda_4 > 0$ whenever $\mathcal{R}_{vac} < 1$.

We now show the positivity of $\lambda_1\lambda_2 - \lambda_0\lambda_3$ whenever $\mathcal{R}_{vac} < 1$. Since $\left(\lambda_1\lambda_2 - \lambda_0\lambda_3\right)\lambda_3 - \lambda_1^2\lambda_4 > 0$ whenever $\mathcal{R}_{vac} < 1$, we have

It is obvious that $\frac{\lambda_1^2\lambda_4}{\lambda_3} > 0$ whenever $\mathcal{R}_{vac} < 1$. Therefore, $\lambda_1\lambda_2 - \lambda_0\lambda_3$ is positive whenever $\mathcal{R}_{vac} < 1$. However, for completeness, $\lambda_1\lambda_2 - \lambda_0\lambda_3$ was obtained as

whenever $\mathcal{R}_{vac} < 1$.