Traveling fronts of pyramidal shapes in competition-diffusion systems

1.   Introduction

In the last decades, many researchers have formulated various mathematical models to characterize the human immune system reaction on invading viruses ^{[1,2,3,4,5,6]}. The two mean immune system reactions are the cell-mediated immunity and the humoral immunity. The cell-mediated immunity is based on Cytotoxic T Lymphocytes (CTLs) which kill the infected cells, while the humoral immunity is based on antibodies which are produced by B cells and neutralize the free viruses from the plasma. Some existing models describe the virus dynamics under the effect of cell-mediated immune response (see e.g., ^[7,8,9,10], see also ^[11] and the references therein) or humoral immune response ^{[12,13,14,15,16,17]}. Wodarz ^[18] has formulated a virus dynamics model with five compartments; susceptible cells ($ S $), infected cells ($ I $), virus particles ($ V $), B cells ($ A $) and CTL cells ($ B $) as:

The model has been extended in ^{[19,20,21,22,23]}, but with virus-to-cell transmission. Cell-to-cell infection plays an important role in increasing the number of infected cells. Mathematical models of virus dynamics with both virus-to-cell and cell-to-cell transmissions have been studied in several works (see e.g., ^{[24,25,26,27,28,29,30,31,32,33,34]}). In very recent works ^[35], both CTL cells and B cells have been incorporated into the viral infection models with both cell-to-cell and virus-to-cell transmissions. However, in ^[35], only one class of infected cells (actively infected cells) is considered. It has been reported in ^[36] and ^[37] that the time from the contact of viruses and susceptible cells to the death of the cells can be modeled by dividing the process into $ n $ short stages $ I_{1}\rightarrow I_{2}\rightarrow....\rightarrow I_{n} $. In ^[38], virus dynamics models with multi-staged infected cells, humoral immunity and with only virus-to-cell infection have been studied.

The aim of the present paper is to formulate a virus dynamics model by incorporating (ⅰ) multi-staged infected cells, (ⅱ) both cell-mediated and humoral immune responses (ⅱ) both cell-to-cell and virus-to-cell infections as:

where, $ I_{k} $, $ k = 1, 2, ..., n $ represents the concentration of the $ i $-th stage of infected cells. The model assumes that the susceptible cells are infected by virus particles at rate $ \eta_{1}S(t)V(t) $ and by infected cells at rate $ \eta_{2}S(t)I_{n}(t) $.

2.   Well-Posedness of solutions

Let $ \Omega_{j} > 0 $, $ j = 1, 2, ..., n+3 $ and define

Proposition 1. The compact set $ \Theta $ is positively invariant for system (1.2).

Proof. We have

This insures that, $ S(t) > 0 $, $ I_{k}(t)\geq0, $ $ k = 1, ..., n, $ $ V(t)\geq0, $ $ A(t)\geq0 $, and $ C(t)\geq0 $ for all $ t\geq0 $.

To show the boundedness of $ S(t) $ and $ I_{1}(t) $ we let $ \Psi_{1} (t) = S(t)+I_{1}(t), $ then

where $ \phi_{1} = \min\{ \alpha, b_{1}\} $. It follows that,

Hence, $ 0\leq\Psi_{1}(t)\leq\Omega_{1} $ if $ \Psi_{1}(0)\leq\Omega_{1} $ for $ t\geq0, $ where $ \Omega_{1} = \frac{\rho}{\phi_{1}}. $ Since $ S(t) > 0 $ and $ I_{1}(t)\geq0 $, then $ 0\leq S(t), I_{1}(t)\leq\Omega_{1} $ if $ S(0)+I_{1} (0)\leq\Omega_{1} $. From the fourth equation of system (1.2) in case of $ k = 2 $, we have

It follows that, $ 0\leq I_{2}(t)\leq\Omega_{2} $ if $ I_{2}(0)\leq\Omega_{2} $, where $ \Omega_{2} = \dfrac{d_{1}\Omega_{1}}{b_{2}} $. Similarly, we can show$ \, 0\leq I_{k}(t)\leq\Omega_{k} $ if $ I_{k}(0)\leq\Omega_{k} $, where $ \Omega_{k} = \dfrac{d_{k-1}\Omega_{k-1}}{b_{k}}, $ $ k = 3, ..., n-1 $. Further, we let $ \Psi_{2}(t) = I_{n}(t)+\frac{\mu}{\sigma}C(t) $, then

where $ \phi_{2} = \min\{b_{n}, \pi\} $. It follows that, $ 0\leq\Psi_{2} (t)\leq\Omega_{n} $ if $ \Psi_{2}(0)\leq\Omega_{n} $, where $ \Omega_{n} = \dfrac{d_{n-1}\Omega_{n-1}}{\phi_{2}} $. Since $ I_{n}(t)\geq0 $ and $ C(t)\geq 0 $, then $ 0\leq I_{n}(t)\leq\Omega_{n} $ and $ 0\leq C(t)\leq\Omega_{n+1} $ if $ I_{n}(0)+\frac{\mu}{\sigma}C(0)\leq\Omega_{n} $, where $ \Omega_{n+1} = \frac{\sigma}{\mu}\Omega_{n} $. Finally, let $ \Psi_{3}(t) = V(t)+\frac{\gamma }{\tau}A(t) $, then

where $ \phi_{3} = \min\{ \varepsilon, \zeta\} $. It follows that, $ 0\leq\Psi _{3}(t)\leq\Omega_{n+2} $ if $ \Psi_{3}(0)\leq\Omega_{n+2} $, where $ \Omega _{n+2} = \dfrac{d_{n}\Omega_{n}}{\phi_{3}} $. It follows that, $ 0\leq V(t)\leq\Omega_{n+2} $ and $ 0\leq A(t)\leq\Omega_{n+3} $ if $ V(0)+\frac{\gamma }{\tau}A(0)\leq\Omega_{n+2} $, where $ \Omega_{n+3} = \frac{\tau}{\gamma} \Omega_{n+2} $.

3.   Threshold parameters and equilibria

In this section, we derive five threshold parameters which guarantee the existence of the equilibria of the model.

Lemma 1. System (1.2) has five threshold parameters $ \Re_{0} > 0 $, $ \Re_{1}^{A} > 0 $, $ \Re_{1}^{C} > 0 $, $ \Re_{2}^{C} > 0 $ and $ \Re_{2}^{A} > 0 $ with $ \Re_{1}^{C} < \Re_{0} $ such that

(ⅰ) if $ \Re_{0}\leq1, $ then there exists only one steady state $Ɖ_{0} $,

(ⅱ) if $ \Re_{1}^{A}\leq1 $ and $ \Re_{1}^{C}\leq1 < \Re_{0}, $ then there exist only two equilibria $Ɖ_{0} $ and ${\bar Ɖ}$,

(ⅲ) if $ \Re_{1}^{A} > 1 $ and $ \Re_{2}^{C}\leq1, $ then there exist only three equilibria $Ɖ_{0} $, ${\bar Ɖ}$ and $\hat Ɖ$,

(ⅳ) if $ \Re_{1}^{C} > 1 $ and $ \Re_{2}^{A}\leq1, $ then there exist only three equilibria $Ɖ_{0} $, ${\bar Ɖ}$ and $\mathop Ɖ\limits^ \vee $, and

(ⅴ) if $ \Re_{2}^{A} > 1 $ and $ \Re_{2}^{C} > 1, $ then there exist five equilibria $Ɖ_{0} $, ${\bar Ɖ}

$$, $ $\hat Ɖ$$ , $ $\mathop Ɖ\limits^ \vee $ and $\tilde Ɖ$.

Proof. Let $ (S, I_{1}, ..., I_{n}, V, A, C) $ be any equilibrium of system (1.2) satisfying the following equations:

We find that system (1.2) admits five equilibria.

(ⅰ) Infection-free equilibrium $Ɖ_{0} = (S_{0}, \overset{n+3}{\overbrace {0, ..., 0, 0}}) $, where $ S_{0} = \rho/\alpha $.

(ⅱ) Chronic-infection equilibrium with inactive immune response $\bar Ɖ = (\bar{S}, \bar{I}_{1}, ..., \bar{I}_{n}, \bar{V}, 0, 0), $ where

Therefore, ${\bar Ɖ}$ exists when

At the equilibrium ${\bar Ɖ}$ the disease persists while the immune response is inhibited. The basic infection reproductive ratio for system (1.2) is defined as:

The parameter $ \Re_{0} $ determines whether the disease will progress or not. In terms of $ \Re_{0} $, we can write

(ⅲ) Chronic-infection equilibrium with only active humoral immune response $\hat Ɖ$$ = (\hat{S}, \hat{I}_{1}, ..., \hat{I}_{n}, \hat{V}, \hat{A}, 0) $, where

where

is the positive solution of

with

We note that $\hat Ɖ$ exists when $ \frac{d_{n}\tau}{\varepsilon\zeta}\hat {I}_{n} > 1 $. Let us define the active humoral immunity reproductive ratio

which determines when the humoral immune response is activated. Thus, $ \hat {A} = \dfrac{\varepsilon}{\gamma}\left(\Re_{1}^{A}-1\right) $.

(ⅳ) Chronic-infection equilibrium with only active cell-mediated immune response $\mathop Ɖ\limits^ \vee $$ = (\check{S}, \check{I}_{1}, ..., \check{I}_{n}, \check {V}, 0, \check{C}) $, where

We note that $\mathop Ɖ\limits^ \vee $ exists when $ \dfrac{\sigma\rho\left(\eta_{1}d_{n} +\eta_{2}\varepsilon\right) }{d_{n}\left[\pi\left(\eta_{1}d_{n}+\eta _{2}\varepsilon\right) +\alpha\varepsilon\sigma\right] }\left(\mathop {\mathop \prod \limits^n }\limits_{i = 1} \frac{d_{i}}{b_{i}}\right) > 1 $. The active cell-mediated immunity reproductive ratio is stated as:

The parameter $ \Re_{1}^{C} $ determines when the cell-mediated immune response is activated. Thus, $ \check{C} = \dfrac{b_{n}}{\mu}(\Re_{1}^{C}-1) $ and $ \Re _{1}^{C} < \Re_{0} $.

(ⅴ) Chronic-infection equilibrium with both active humoral and cell-mediated immune responses $\tilde Ɖ$$ = (\tilde{S}, \tilde{I}_{1}, ..., \tilde{I}_{n}, \tilde {V}, \tilde{A}, \tilde{C}) $, where

It is obvious that $\tilde Ɖ$ exists when $ \dfrac{\sigma\rho\left(\eta_{1} \zeta\sigma+\eta_{2}\tau\pi\right) }{d_{n}\pi\left[\alpha\tau\sigma +\eta_{1}\zeta\sigma+\eta_{2}\tau\pi\right] }\left(\mathop {\mathop \prod \limits^n }\limits_{i = 1} \frac{d_{i}}{b_{i}}\right) > 1 $ and $ \frac{d_{n}\pi\tau }{\varepsilon\sigma\zeta} > 1 $. Now we define

where $ \Re_{2}^{C} $ refers to the competed cell-mediated immunity reproductive ratio and appears as the average number of T cells activated due to infectious cells in the scene that the humoral immune response has been constructed, while, $ \Re_{2}^{A} $ refers to the competed humoral immunity reproductive ratio and appears as the average number of B cells activated due to mature viruses in the scene that the cell-mediated immune response has been constructed. Clearly, $\tilde Ɖ$ exists when $ \Re_{2}^{C} > 1 $ and $ \Re_{2}^{A} > 1 $ and we can write $ \tilde{C} = \dfrac{b_{n}}{\mu}\left(\Re_{2}^{C}-1\right) $ and $ \tilde{A} = \dfrac{\varepsilon}{\gamma}\left(\Re_{2}^{A}-1\right). $

The five threshold parameters are given as follows:

We define the active humoral immunity reproductive ratio $ \Re_{humoral}^{A} $ which comes from the limiting (linearized) $ A $-dynamics near $ A = 0 $ as:

Lemma 2. (ⅰ) if $ \Re_{1}^{A} < 1, $ then $ \Re_{humoral}^{A} < 1 $,

(ⅱ) if $ \Re_{1}^{A} > 1, $ then $ \Re_{humoral}^{A} > 1 $,

(ⅲ) if $ \Re_{1}^{A} = 1, $ then $ \Re_{humoral}^{A} = 1 $,

Proof. (ⅰ) Let $ \Re_{1}^{A} < 1, $ then from Eq. 3.10 we have $ \hat{I}_{n} < \frac{\varepsilon\hat{V}}{d_{n}}. $ Then, using Eq. 3.8 we get

which leads to

Using Eq. 3.9 we derive

Thus, $ \Re_{humoral}^{A} < 1 $. Using the same argument one can easily confirm part (ⅱ) and (ⅲ).

4.   Global stability analysis

The global stability of the each equilibria will be investigated by constructing Lyapunov functions using the method presented ^{[39,40,41,42,43,44,45]}. Let us define the function $ \digamma:\mathbb{(} 0, \infty\mathbb{)}\rightarrow\mathbb{[}0, \infty\mathbb{)} $ as $ \digamma (\upsilon) = \upsilon-1-\ln\upsilon $. Denote $ (S, I_{1}, ..., I_{n}, V, A, C) = (S(t), I_{1}(t), ..., I_{n}(t), V(t), A(t), C(t)) $. The following equalities will be used:

where $ I^{\ast}\in\left\{ \bar{I}, \hat{I}, \check{I}, \tilde{I}\right\}. $

Theorem 1. If $ \Re_{0}\leq1 $, then the infection-free equilibrium $Ɖ_{0} $ is globally asymptotically stable.

Theorem 2. Suppose that $ \Re_{1}^{A}\leq1 $ and $ \Re_{1}^{C}\leq 1 < \Re_{0} $, then the chronic-infection equilibrium with inactive immune response ${\bar Ɖ}$ is globally asymptotically stable.

Theorem 3. If $ \Re_{1}^{A} > 1 $ and $ \Re_{2}^{C}\leq1 $, then the chronic-infection equilibrium with only active humoral immune response $\hat Ɖ$ is globally asymptotically stable.

Theorem 4. Suppose that $ \Re_{1}^{C} > 1 $ and $ \Re_{2}^{A}\leq1 $, then the chronic-infection equilibrium with only active cell-mediated immune response $\mathop Ɖ\limits^ \vee $ is globally asymptotically stable.

Theorem 5. If $ \Re_{2}^{A} > 1 $ and $ \Re_{2}^{C} > 1 $, then the chronic-infection equilibrium with both active humoral and cell-mediated immune responses $\tilde Ɖ$ is globally asymptotically stable.

The proofs of Theorems 1–5 are given in a Supplementary.

5.   Numerical simulations

In this section, we perform some numerical simulations in case of three stages of infected cells i.e. $ n = 3 $.

The threshold parameters $ \Re_{0}, $ $ \Re_{1}^{A}, $ $ \Re_{1}^{C}, $ $ \Re_{2} ^{C}, $ and $ \Re_{2}^{A} $ for system (5.1) are given by:

where

Table 1 contains the values of the parameters of model (5.1).

The results of Theorems 1–5 will be investigated by choosing the values of $ \eta_{1} $, $ \eta_{2} $, $ \tau $ and $ \sigma $ under three different initial conditions for model (5.1) as follows:

Initial–1: $ (S(0), I_{1}(0), I_{2}(0), I_{3} (0), V(0), A(0), C(0)) = (800, 3, 1, 1, 2, 3, 10) $, (Solid lines in the figures)

Initial–2: $ (S(0), I_{1}(0), I_{2}(0), I_{3} (0), V(0), A(0), C(0)) = (700, 0.5, 2, 2, 3, 4, 5), $ (Dashed lines in the figures)

Initial–3: $ (S(0), I_{1}(0), I_{2}(0), I_{3} (0), V(0), A(0), C(0)) = (300, 0.1, 0.5, 0.5, 1.5, 2, 2.5) $. (Dotted lines in the figures)

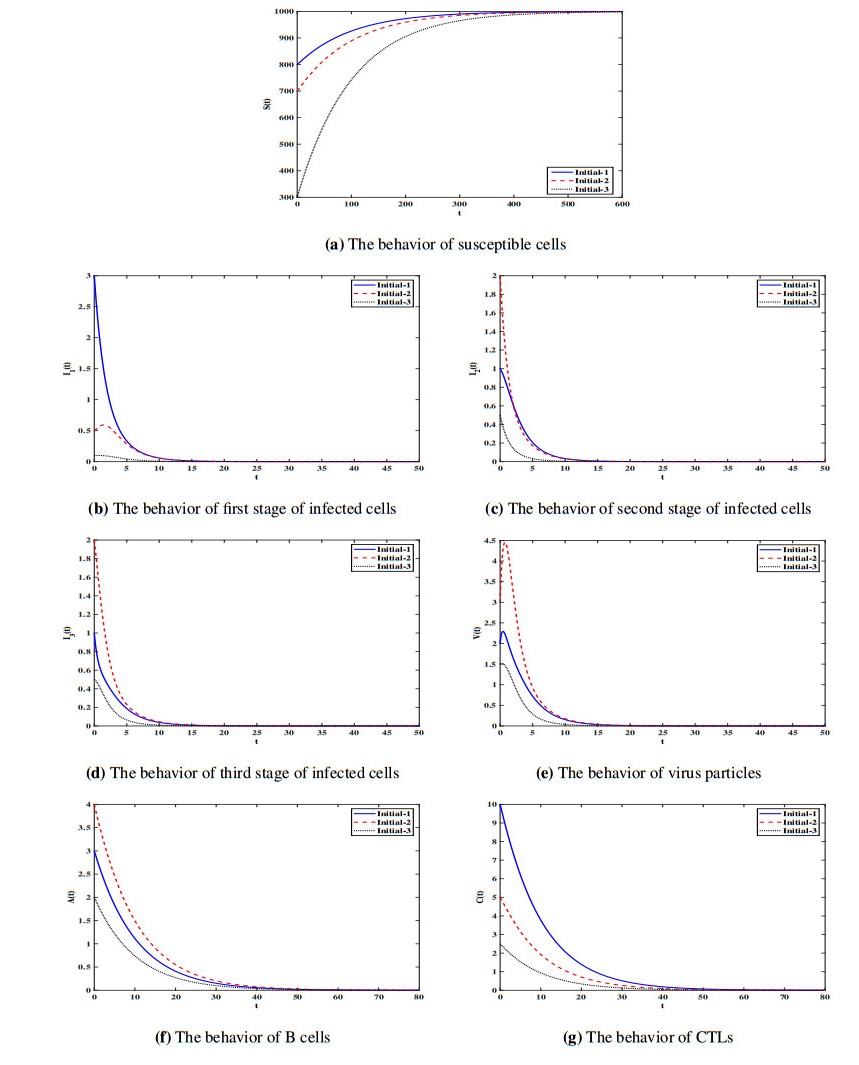
Stability of $Ɖ_{0} $: $ \eta_{1} = \eta_{2} = 0.0001 $, $ \tau = 0.001 $ and $ \sigma = 0.01 $. For this set of parameters, we have $ \Re _{0} = 0.26 < 1, $ $ \Re_{1}^{A} = 0.10 < 1 $, $ \Re_{1}^{C} = 0.18 < 1 $ and $ \Re_{2} ^{C} = 0.31 < 1 $. Figure 1 illustrates that the solution trajectories starting from different initial conditions reach the equilibrium $Ɖ_{0} = (1000, 0, 0, 0, 0, 0, 0) $. This ensures that $Ɖ_{0} $ is globally asymptotically stable according to the result of Theorem 1. In this situation the viruses will be died out.

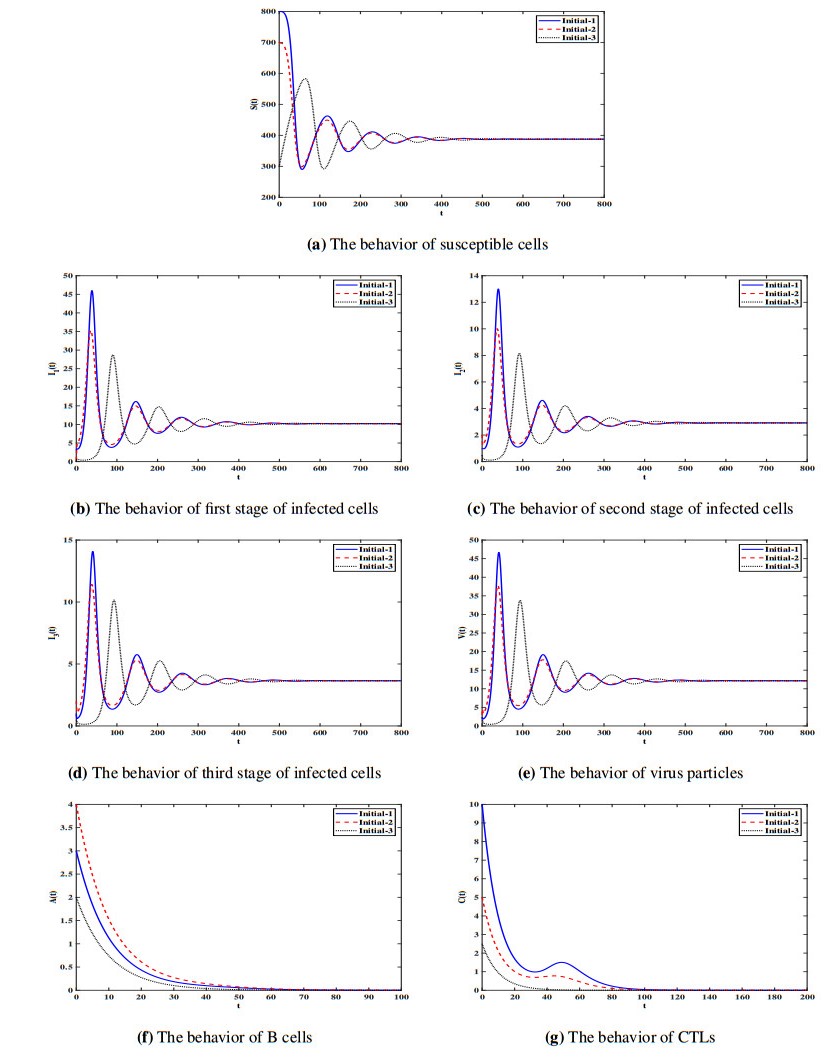
Stability of ${\bar Ɖ}$: $ \eta_{1} = \eta_{2} = 0.001 $, $ \tau = 0.001 $ and $ \sigma = 0.01 $. With such choice we get, $ \Re_{1}^{A} = 0.18 < 1 $ and $ \Re_{1}^{C} = 0.48 < 1 < \Re_{0} = 2.58 $ and ${\bar Ɖ}$ exists with $\bar Ɖ = (387.68, 10.21, 2.92, 3.65, 12.15, 0, 0). $ Thus, Lemma 1 is verified. Figure 2 shows that the solution trajectories starting from different initial conditions tend to ${\bar Ɖ}$ and this support Theorem 2. This case represents the persistence of the viruses but with inhibited humoral and cell-mediated immune responses.

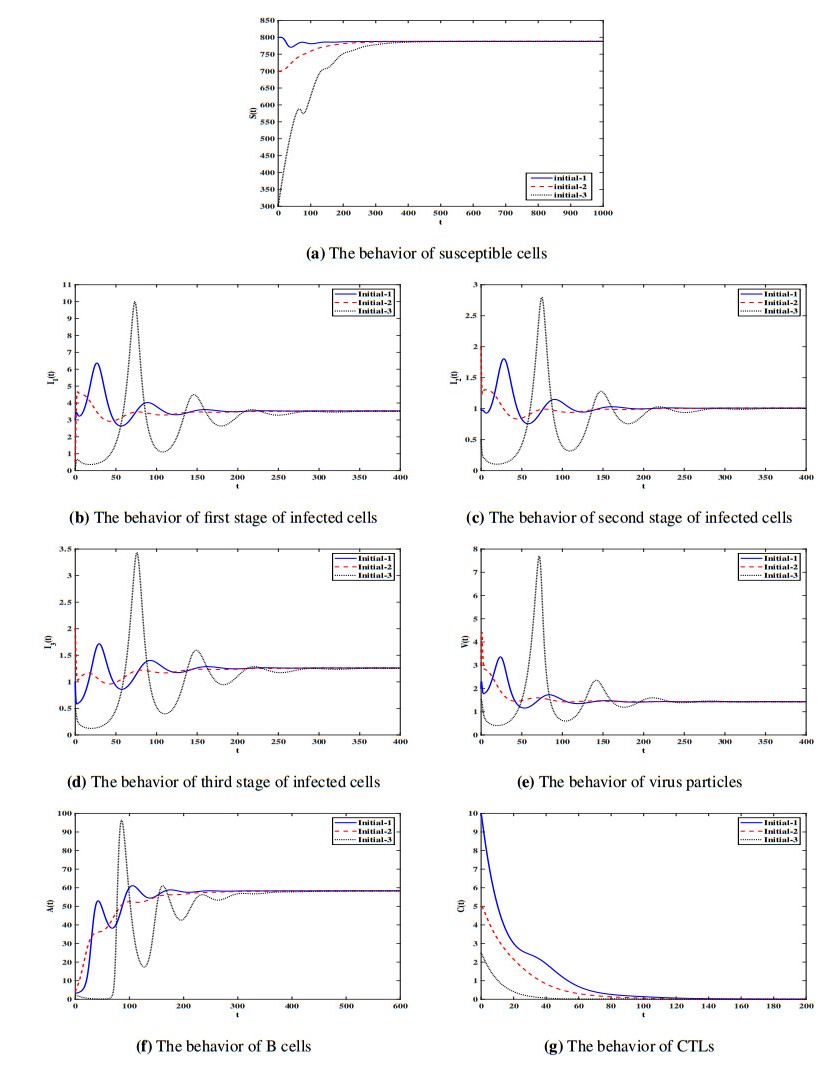
Stability of $\hat Ɖ$: $ \eta_{1} = \eta_{2} = 0.001 $, $ \tau = 0.07 $ and $ \sigma = 0.05 $. Then, we calculate $ \Re_{0} = 2.58 > 1 $, $ \Re_{1}^{A} = 2.94 > 1 $ and $ \Re_{2}^{C} = 0.76 < 1 $. The numerical results show that $\hat Ɖ = (787.99, 3.53, 1.01, 1.26, 1.43, 58.34, 0) $ which confirm Lemma 1. The global stability result given in Theorem 3 is illustrated by Figure 3. This situation represents the case when the infection is chronic and the humoral immune response is active, while the cell-mediated immune response is inhibited.

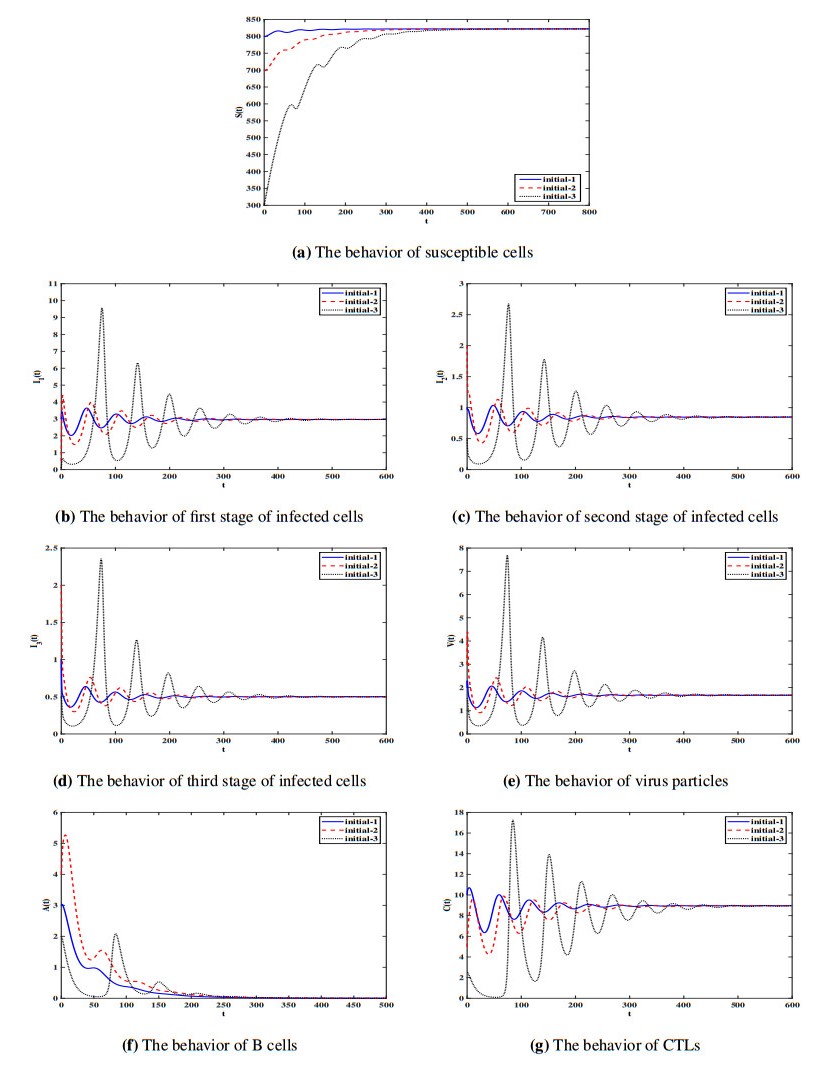
Stability of $\mathop Ɖ\limits^ \vee $: $ \eta_{1} = \eta_{2} = 0.001 $, $ \tau = 0.05 $ and $ \sigma = 0.2 $. Then, we calculate $ \Re_{0} = 2.58 > 1 $, $ \Re _{1}^{C} = 2.12 > 1 $ and $ \Re_{2}^{A} = 0.83 < 1 $. The results presented in Lemma 1 and Theorem 4 show that the equilibrium $\mathop Ɖ\limits^ \vee $ exists and it is globally asymptotically stable. Figure 4 supports the results of Theorem 4, where the solution trajectories of the system starting from different initial conditions reach the equilibrium point $\mathop Ɖ\limits^ \vee $ $ = (821.91, 2.97, 0.85, 0.50, 1.67, 0, 8.96) $. This situation represents the case when the infection is chronic and the cell-mediated immune response is active, while the humoral immune response is inhibited.

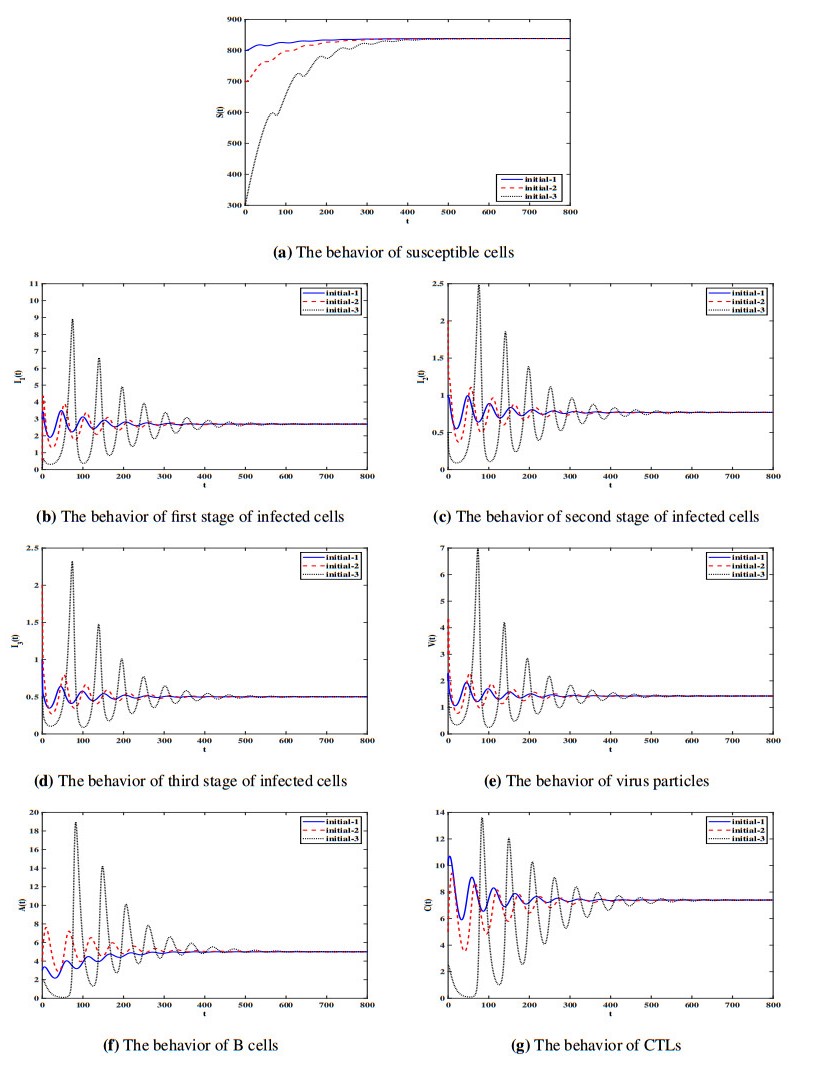
Stability of $\tilde Ɖ$: $ \eta_{1} = \eta_{2} = 0.001 $, $ \tau = 0.07 $ and $ \sigma = 0.2 $. Then, we calculate $ \Re_{0} = 2.58 > 1 $ and $ \Re_{2} ^{A} = 1.17 > 1, $ $ \Re_{2}^{C} = 1.92 > 1 $. The numerical results show that $\tilde Ɖ = (838.32, 2.69, 0.77, 0.50, 1.43, 5.00, 7.40) $ which ensure Lemma 1. Moreover, the global stability result given in Theorem 5 is demonstrated in Figure 5. It can be seen that the solution trajectories of the system starting from different initial conditions converge to the equilibrium $\tilde Ɖ$. This situation represents the case when the infection is chronic and both immune responses are active.

5.1.   Comparison results

We consider system (5.1) under the effect of two types of treatment as:

where, the parameter $ \epsilon_{1}\in\lbrack0, 1] $ is the efficacy of antiretroviral therapy in blocking infection by virus-to-cell mechanism, and $ \epsilon_{2}\in\lbrack0, 1] $ is the efficacy of therapy in blocking infection by cell-to-cell mechanism ^[47].

The basic reproduction number of system (5.2) is given by

where

When the cell-to-cell transmission is neglected, system (5.2) leads to the following system:

The basic reproduction number of system (5.3) is given by

Without loss of generality we let $ \epsilon_{1} = \epsilon_{2} = \epsilon $. Now we calculate the minimum drug efficacy $ \epsilon $ which stabilize the infection-free equilibrium for systems (5.2) and (5.3). For system (5.2) one can determine the minimum drug efficacy $ \epsilon _{(5.2)}^{\min} $ such that $ \Re_{0, (5.2)}(\epsilon)\leq1 $ for all $ \epsilon_{(5.2)}^{\min}\leq\epsilon\leq1 $ as:

For system (5.3) the minimum drug efficacy $ \epsilon_{(5.3)} ^{\min} $ such that $ \Re_{0, (5.3)}(\epsilon)\leq1 $, $ \epsilon _{(5.3)}^{\min}\leq\epsilon\leq1 $ is given by:

Comparing Eqs. (5.5) and (5.4) we get that $ \epsilon_{(5.3)}^{\min}\leq\epsilon_{(5.2)}^{\min} $. Therefore, if we apply drugs with $ \epsilon $ such that $ \epsilon_{(5.3)}^{\min}\leq\epsilon < \epsilon _{(5.2)}^{\min} $, this guarantee that $ \Re_{0, (5.3)}(\epsilon)\leq1 $ and then $Ɖ_{0} $ of system (5.3) is globally asymptotically stable, however, $ \Re_{0, (5.2)} > 1 $ and then $Ɖ_{0} $ of system (5.2) is unstable. Therefore, more accurate drug efficacy $ \epsilon $ is determined when using the model with both virus-to-cell and cell-to-cell transmissions. This shows the importance of considering the effect of the cell-to-cell transmission in the virus dynamics.

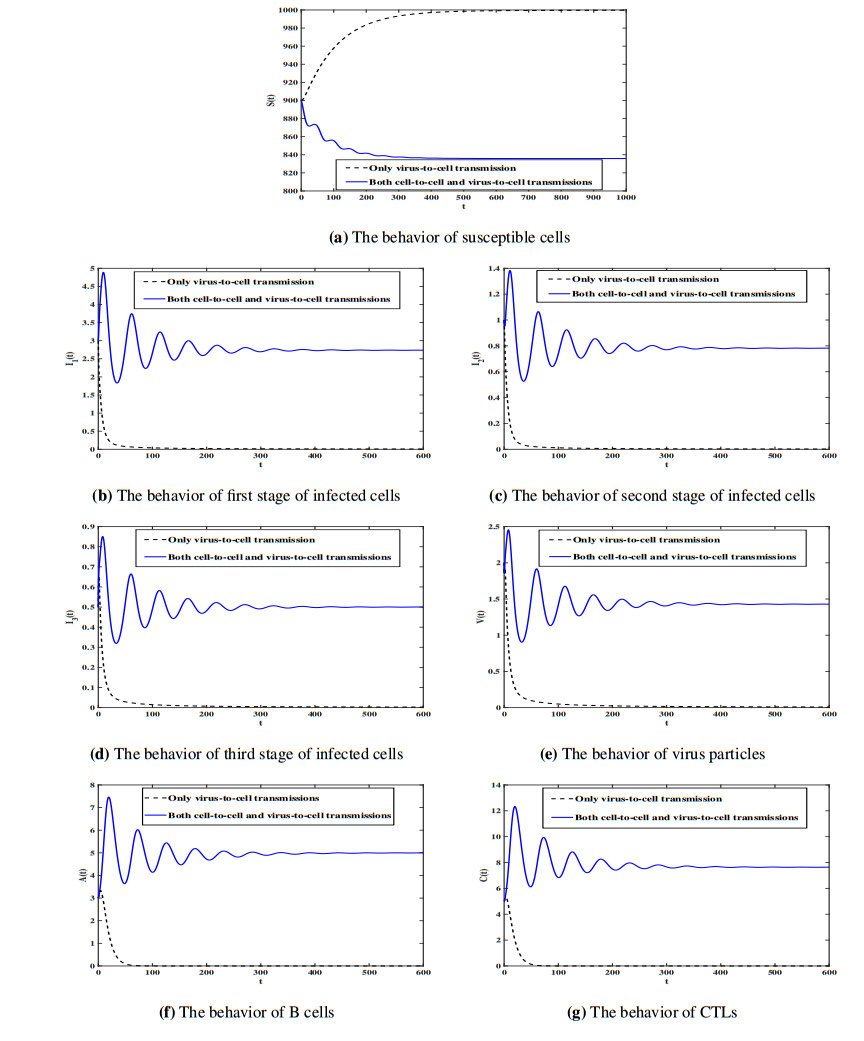
Now we perform numerical simulation for both systems (5.2) and (5.3). Using the values given in Table 1 and choosing $ \eta_{1} = 0.001 $, $ \eta_{2} = 0.005 $, $ \tau = 0.07 $ and $ \sigma = 0.2 $. Then we get

Now we select $ \epsilon = 0.5 $ and choose the initial condition as follows:

Initial–4: $ (S(0), I_{1}(0), I_{2}(0), I_{3} (0), V(0), A(0), C(0)) = (900, 3, 1, 0.5, 2, 3, 5) $.

From Figure 6 we can see that the trajectory of model (5.3) tends to $Ɖ_{0} $, while the trajectory of model (5.2) tends to $\tilde Ɖ$. It means that if one design treatment using model (5.3) where the cell-to-cell transmission is neglected, then this treatment will not suffice to clear the viruses from the body.

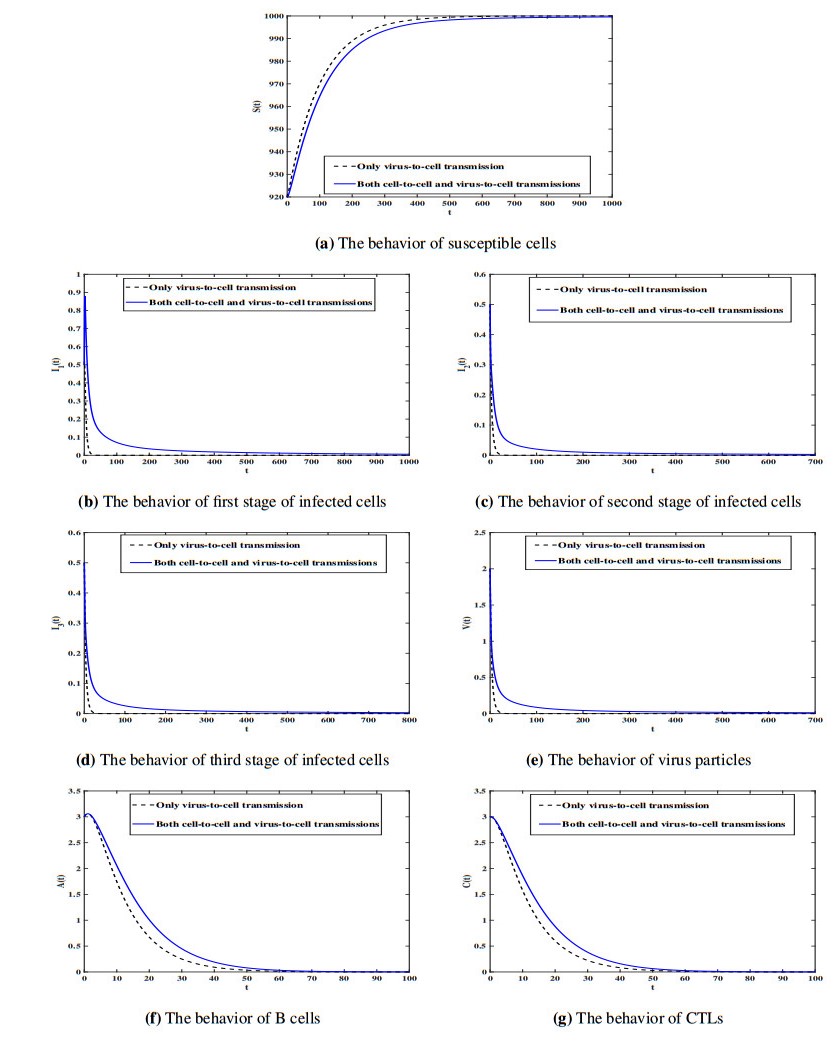
On the other hand, we choose $ \epsilon = 0.8 $ and consider the following initial condition:

Initial–5: $ (S(0), I_{1}(0), I_{2}(0), I_{3} (0), V(0), A(0), C(0)) = (920, 0.5, 0.5, 0.5, 2, 3, 3) $.

From Figure 7 we can see that the trajectories of both systems (5.2) and (5.3) tend to $Ɖ_{0} $. Therefore, this treatment will suffice to clear the viruses from the body.

6.   Conclusion and discussion

In this paper, we formulated and analyzed a virus dynamics model with both CTL and humoral immune responses. We incorporated both virus-to-cell and cell-to-cell transmissions. We assumed that the infected cells pass through $ n $ stages to produce mature viruses. We showed that the solutions of the system are nonnegative and bounded, which ensures the well-posedness of the proposed model. Further, we obtained five threshold parameters, $ \Re_{0} $ (the basic infection reproductive ratio), $ \Re_{1}^{A} $ (the active humoral immunity reproductive ratio), $ \Re_{1}^{C} $ (the active cell-mediated immunity reproductive ratio), $ \Re_{2}^{C} $ (the competed cell-mediated immunity reproductive ratio), and $ \Re_{2}^{A} $ (the competed humoral immunity reproductive ratio). The global asymptotic stability of the five equilibria $Ɖ_{0}, $ $\bar Ɖ, $ $\hat Ɖ$, $\mathop Ɖ\limits^ \vee $, $\tilde Ɖ$ was investigated by constructing Lyapunov functions and applying LaSalle's invariance principle. To support our theoretical results, we conducted some numerical simulations. We note that the incorporation of cell-to-cell transmission mechanism into the viral infection model increases the basic reproduction number $ \Re_{0} $, since $ \Re_{0} = \Re_{01}+\Re_{02} > \Re_{01} $. Therefore, neglecting the cell-to-cell transmission will lead to under-evaluated basic reproduction number. Model with two types of treatment was presented. We showed that more accurate drug efficacy which is required to clear the virus from the body is calculated by using our proposed model.

There are some factors that can extend our model (1.2):

a. The infected cells may begin to present the viral antigen earlier than when they reach the terminal stage $ n $ (i.e. at stage $ m $ where $ m\leq n $). Therefore, infected cells $ I_{m} $, $ I_{m+1}, ..., I_{n} $ are subject to be targeted by the CTL immune response.

b. Model (1.2) is formulated by assuming that the virus is purely lytic, that is, only the bursting cells are capable of releasing the free virions. However, many viruses are somewhat mixed, in the sense that they are partially lytic and partially budding, where the release of free virions can be from the infected cells $ I_{m} $, $ I_{m+1}, ..., I_{n} $.

c. The cell-to-cell infection mechanism can also be expanded to the contact between susceptible cells with infected cells $ I_{m} $, $ I_{m+1}, ..., I_{n} $.

d. The loss of virions upon the infection could also be added to the model. In fact, there is some speculation that the virions may be indiscriminately entering not only the susceptible cells, but also the cells that are already infected ^[26,53].

Then, taking into account the above factors will leads to the following model:

where, $ \sum\limits_{k = m}^{n}\eta_{k}SI_{k} $ represent the incidence rates due to the contact of the infected cells $ I_{m}, I_{m+1}, ..., I_{n} $ with susceptible cells. The term $ \bar{\eta}_{1}SV $ is the loss of virus upon entry of a susceptible cell. The term $ V\sum\limits_{k = 1}^{n}\varkappa_{k}I_{k} $ represents the absorption of free virions into already infected cells $ I_{1}, I_{2}, ..., I_{n} $. The production rate of the viruses and the activation rate of the CTL cells are modeled by $ \sum\limits_{k = m}^{n}\delta_{k}I_{k} $ and $ \sum\limits_{k = m}^{n}\sigma_{k}CI_{k} $, respectively. The $ k $-stage infected cells $ I_{k}, $ are attacked by CTL cells at rate $ \mu_{k}CI_{k}, $ $ k = m, m+1, ..., n $. Analysis of system (6.1) is not straightforward, therefore we leave it for future works.

It is commonly observed that in viral infection processes, time delay is inevitable. Herz et al. ^[59] formulated an HIV infection model with intracellular delay and they obtained the analytic expression of the viral load decline under treatment and used it to analyze the viral load decline data in patients. Several viral infection models presented in the literature incorporated discrete delays (see, e.g., ^[36] and ^[44]) or distributed delays (see, e.g., ^[7,23] and ^[48,49,50]). In these papers, the global stability of equilibria was proven by utilizing global Lyapunov functional that was motivated by the work in ^[51] and ^[52]. Model (6.1) can be extended to incorporate distributed time delays. Moreover, considering age structure of the infected class or diffusion in the virus dynamics model will lead to PDE model ^{[54,55,56,57,58]}. These extensions require more investigations, therefore we leave it for future works.

Acknowledgements

This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (DG–14–247–1441). The authors, therefore, gratefully acknowledge the DSR technical and financial support.

Conflict of interest

There is no conflicts of interest.

Supplementary

Proof of Theorem 1. Constructing a Lyapunov function:

It is seen that, $ \Phi_{0}(S, I_{1}, ..., I_{n}, V, A, C) > 0 $ for all $ S, I_{1}, ..., I_{n}, V, A, C > 0, $ and $ \Phi_{0} $ has a global minimum at $Ɖ_{0} $. We calculate $ \frac{d\Phi_{0}}{dt} $ along the solutions of model (1.2) as:

Using (4.3), we have

Then,

Using $ S_{0} = \rho/\alpha $, we obtain

Therefore, $ \frac{d\Phi_{0}}{dt}\leq0 $ for all $ S, I_{n}, A, C > 0 $ with equality holding when $ S(t) = S_{0} $ and $ I_{n}(t) = A(t) = C(t) = 0 $ for all $ t. $ Let $ \Upsilon_{0} = \left\{ (S(t), I_{1}(t), ..., I_{n}(t), V(t), A(t), C(t)):\frac {d\Phi_{0}}{dt} = 0\right\} $ and $ \Upsilon_{0}^{^{\prime}} $ is the largest invariant subset of $ \Upsilon_{0} $. We note that, the solutions of system (1.2) are confined to $ \Upsilon_{0} $ ^[46]. The set $ \Upsilon_{0} $ is invariant and contains elements which satisfy $ I_{n}(t) = 0 $. Then, $ \dot {I}_{n}(t) = 0 $ and from Eq. 3.4 we have

It follows that, $ I_{n-1}(t) = 0 $ for all $ t $. Since we have $ I_{n-1}(t) = 0 $, then $ \dot{I}_{n-1}(t) = 0 $ and from Eq. 3.3, we have $ \dot{I} _{n-1}(t) = d_{n-2}I_{n-2} = 0 $ which yields $ I_{n-2}(t) = 0 $. Consequently, we obtain $ I_{k}(t) = 0, $ where $ k = 1, ..., n $. Moreover, since $ S(t) = S_{0} $ we have $ \dot{S}(t) = 0 $ and Eq. 3.1 implies that

which insures that $ V(t) = 0 $. Noting that $ \Re_{0}\leq1 $, then $Ɖ_{0} $ is globally asymptotically stable using LaSalle's invariance principle.

Proof of Theorem 2. Let us define a function $ \Phi_{1}(S, I_{1}, ..., I_{n}, V, A, C) $ as:

Calculating $ \frac{d\Phi_{1}}{dt} $ as:

Collecting terms of Eq. 6.5 and using Eqs. 4.2 and 4.3, we derive

Using the equilibrium conditions for ${\bar Ɖ}$:

We obtain

Since we have

then

Also we have when $ k = n $,

Therefor Eq. 6.7 becomes

Since the arithmetical mean is greater than or equal to the geometrical mean, then

From Lemma 2 we have $ \bar{V} < \hat{V} $ and since $ \Re_{1}^{C}\leq1 < \Re_{0} $ then $ \frac{d\Phi_{1}}{dt}\leq0 $ for all $ S, I_{k}, V, A, C > 0 $ with equality holding when $ S(t) = \bar{S} $, $ I_{k}(t) = \bar{I}_{k} $, $ k = 1, 2, ..., n, $ $ V(t) = \bar{V}, $ and $ A(t) = C(t) = 0 $ for all $ t. $ It can be easily verified that $ \Upsilon_{1}^{\prime} = \left\{ \text{${\bar Ɖ}$}\right\} $ is the largest invariant subset of $ \Upsilon_{1} = \left\{ (S(t), I_{1}(t), ..., I_{n} (t), V(t), A(t), C(t)):\frac{d\Phi_{1}}{dt} = 0\right\} $^[46]. Then, ${\bar Ɖ}$ is globally asymptotically stable using LaSalle's invariance principle.

Proof of Theorem 3. The candidate Lyapunov function is

We calculate $ \frac{d\Phi_{2}}{dt} $ as:

Collecting terms of Eq. 6.10 and using Eqs. 4.2 and 4.3, we derive

Using the equilibrium conditions for $\hat Ɖ$:

We obtain

Using Eq. 6.12 in case of $ k = n $ we get

Thus, Eq. 6.13 will become

Eq. 6.14 can be written as

Thus, if $ \Re_{2}^{C}\leq1 $, then $\tilde Ɖ$ dose not exist since $ \tilde {C} = \dfrac{b_{n}}{\mu}\left(\Re_{2}^{C}-1\right) \leq0. $ This guarantee that $ \dot{C}(t) = \sigma\left(I_{n}(t)-\frac{\pi}{\sigma}\right) C(t) = \sigma\left(I_{n}(t)-\tilde{I}_{n}\right) C(t)\leq0 $ for all $ C > 0 $, which implies that $ \hat{I}_{n} < \tilde{I}_{n} $. Hence $ \frac{d\Phi_{2}} {dt}\leq0 $ for all $ S, I_{k}, V, A, C > 0 $ with equality holding when $ S(t) = \hat{S} $, $ I_{k}(t) = \hat{I}_{k} $, $ k = 1, 2, ..., n, $ $ V(t) = \hat{V}, $ and $ C(t) = 0 $ for all $ t. $ We note that, the solutions of system (1.2) are tend to $ \Upsilon_{2}^{^{\prime}} $ the largest invariant subset of $ \Upsilon _{2} = \left\{ (S(t), I_{1}(t), ..., I_{n}(t), V(t), A(t), C(t)):\frac{d\Phi_{2}} {dt} = 0\right\} $ ^[46]. For each element of $ \Upsilon_{2}^{^{\prime}} $ we have $ I_{n}(t) = \hat{I}_{n}, $ $ V(t) = \hat{V} $, then $ \dot{V}(t) = 0 $ and from Eq. 3.5 we have

which gives $ A(t) = \hat{A}. $ Therefore, $ \Upsilon_{2}^{^{\prime}} = \left\{ \text{$\hat Ɖ$}\right\} $. Applying LaSalle's invariance principle we get $\hat Ɖ$ is globally asymptotically stable.

Proof of Theorem 4. Define a function $ \Phi_{3}(S, I_{1}, ..., I_{n}, V, A, C) $ as:

We calculate $ \frac{d\Phi_{3}}{dt} $ as:

Collecting terms of Eq. 6.16 and using Eqs. 4.2 and 4.3, we derive

Using the equilibrium conditions for $\mathop Ɖ\limits^ \vee $:

we obtain

Since we have in case of $ k = n $:

Then,

Hence, if $ \Re_{2}^{A} = \frac{\tau\check{V}}{\zeta}\leq1 $, then $ \frac {d\Phi_{3}}{dt}\leq0 $ for all $ S, I_{k}, V, A, C > 0 $ with equality holding when $ S(t) = \check{S} $, $ I_{k}(t) = \check{I}_{k} $, $ k = 1, 2, ..., n, $ $ V(t) = \check{V} $ and $ A(t) = 0 $ for all $ t. $ It can be easily verified that the largest invariant subset of $ \Upsilon_{3} = \left\{ (S(t), I_{1}(t), ..., I_{n} (t), V(t), A(t), C(t)):\frac{d\Phi_{3}}{dt} = 0\right\} $ is $ \Upsilon _{3}^{^{\prime}} = \left\{ \text{$\mathop Ɖ\limits^ \vee $}\right\} $ ^[46]. Applying LaSalle's invariance principle we get that $\mathop Ɖ\limits^ \vee $ is globally asymptotically stable.

Proof of Theorem 5. Define $ \Phi_{4}(S, I_{1}, ..., I_{n}, V, A, C) $ as:

Calculating $ \frac{d\Phi_{4}}{dt} $ as:

Collecting terms of Eq. 6.20 and using Eqs. 4.2 and 4.3, we obtain

Using the equilibrium conditions for $\tilde Ɖ$:

We obtain

Since we have

and

Then, Eq. 6.22 will be reduced to the form

Hence, $ \frac{d\Phi_{4}}{dt}\leq0 $ for all $ S, I_{k}, V, A, C > 0 $ with equality holding when $ S(t) = \tilde{S} $, $ I_{k}(t) = \tilde{I}_{k} $, $ k = 1, 2, ..., n, $ and $ V(t) = \tilde{V} $ for all $ t. $ It can be easily verified that the largest invariant subset of $ \Upsilon_{4} = \left\{ (S(t), I_{1}(t), ..., I_{n} (t), V(t), A(t), C(t)):\frac{d\Phi_{3}}{dt} = 0\right\} $ is $ \Upsilon _{4}^{^{\prime}} = \left\{ \tilde Ɖ\right\} $ ^[46]. LaSalle's invariance principle implies that $\tilde Ɖ$ is globally asymptotically stable.