Stability analysis of general delayed HTLV-I dynamics model with mitosis and CTL immunity

1.   Introduction

Human T-cell lymphotropic virus class I (HTLV-I) is one of the most dangerous viruses that infect the human body and causes inflammatory and malignant diseases. It was estimated that about 10 to 25 million humans infected with HTLV-I worldwide ^[1]. HTLV-I can be transferred via bodily fluids including blood and semen. Further, HTLV-I can be transferred from mother to child via breast-feeding ^[2]. The high transmission of HTLV-I was reported in Caribbean Islands, Central Africa, Northeast South America and Southwestern Japan ^[3]. HTLV-I can progress to serious diseases, adult T-cell leukemia (ATL) and HTLV-I-associated myelopathy/tropical spastic paraparesis (HAM/TSP) ^[4]. HTLV-I is a single-stranded RNA virus which infects the most important component of the immune system, CD$4^{+}$T cells ^[5]. There are two modes of within-host transmission, vertical or mitotic transmission of actively HTLV-I infected cells and horizontal by infectious transmission through direct cell-to-cell touch ^[6].

Mathematical modeling of HTLV-I was established since 1990 to understand the pathogenesis of the HTLV-I infection inside the host cell that has a critical ramifications for the movement of remedial measures and for the acknowledgment of hazard elements of the advancement of HAM/TSP. A lot of mathematical models were planned by numerous scientists to epitomize the intuitive dynamics within-host among HTLV-I infection to depict the pathogenesis of HTLV-I related infection ^{[7,8,9,10,11,12]}.

Stilianakis and Seydel ^[7] constructed a four-dimensional system of ODEs which describes the within-host HTLV-I dynamics as:

where $U$, $L$, $A\ $and $Q$ (cells mm$^{-3}$) are the concentrations of healthy or uninfected CD$4^{+}$T cells, latently CD$4^{+}$T infected cells, actively CD$4^{+}$T infected cells and leukemia cells (ATL cells), respectively. The variable $t$ denotes to the time (days). Uninfected cells are created at a constant rate $\nu$. The bilinear incidence term $\beta UA\ $accounts for the rate of infectious via horizontal transmission appears by cell-to-cell touch between uninfected and actively infected cells. $\pi L$ is the activation rate of latently infected cells, and $\varkappa A$ is the conversion rate of actively infected cells to ATL cells. $Q_{\max }$ is the maximal growth of ATL cells and $\lambda$ is the maximum proliferation rate of ATL cells. The death rates of the uninfected cells, latently infected cells, actively infected cells and ATL cells are indicated by $\bar{\nu}U$, $\mu L$, $\delta ^{\ast }A$ and $\ell Q$, respectively.

As mentioned before HTLV-I has two modes of transmission, horizontal and vertical. Actively infected cells propagate faster than uninfected and latently infected cells. This causes an increasing in the proviral load. As a consequence, mitotic transmission plays an instrumental role in the persistence of HTLV-I infection ^[3]. Li and Lim ^[10] developed an HTLV-I infection model by considering both horizontal and vertical transmissions as:

where $\epsilon \in(0, 1)$ is the probability of new HTLV-I infections via horizontal route become latently infected. The vertical transmission is represented in proliferating the actively infected cells at rate $\varepsilon^{\ast}A\left(1-\frac{U+L}{U_{\max}}\right)$, where $U_{\max}$ is the CD$4^{+}$T cells carrying capacity. The actively infected cells become latent at rate $\omega \varepsilon^{\ast}A\left(1-\frac{U+L}{U_{\max} }\right)$, where $\omega \in(0, 1)$. It was shown in ^[13] that $U+L < U_{\max}$. Therefore, in ^[14], the logistic term $\varepsilon^{\ast}A\left(1-\frac{U+L}{U_{\max}}\right)$ was replaced by an exponential growth term $\varepsilon^{\ast}A$.

Cytotoxic T lymphocyte (CTL) is identified as the tremendous element of human immunity in killing viral infections. It represses viral reproduction and kills the cells which can be tainted by infections. It was mentioned in ^[13,15] that the CTLs assume a strong part in controlling the HTLV-I related diseases. CTLs can realize and kill the actively infected CD$4^{+}$T cells, further, they able to lessen the proviral load. The effect of CTL immunity was included in several models for HTLV-I infection (e.g., ^{[4,16,17,18,19,20,21,22,23,24,25]}).

To incorporate both CTL immunity and mitosis into the HTLV-I dynamics model, Lim and Maini ^[14] proposed the following system:

where $C$ denotes the concentration of CTLs. The removal rate of actively infected by CTLs is represented by $\alpha AC$, where $\alpha$ represents the CTL-mediated lysis constant ^[5]. The term $\rho A$ indicates the proliferation rate of CTLs. The death rate of the CTLs is denoted by $\gamma C$. The authors studied the global stability of equilibrium points by utilizing Lyapunov approach. Models (1.8)–(1.11) was developed and modified in ^[26,27,28]. Recently, Khajanchi et al. ^[1] modified models (1.8)–(1.11) by replacing Eq (1.11) by

The authors investigated the global stability for chronic infection equilibrium point via two approaches Lyapunov and geometric.

In the above models, it was assumed that the uninfected CD$4^{+}$T cells become latently infected instantaneously. Moreover, the transition from latently infected to actively infected is also instantaneously. However, there exist delays in the infection process and activation of latently infected cells. Therefore, ignoring these time delays is biologically unrealistic. In addition, these time intracellular delays have an important effect on the stability of system ^[29,30]. HTLV-I infection models have been incorporated with intracellular delay ^{[23,24,31,32,33]} or immune response delay ^{[16,20,21,34,35]}. Both intracellular and immune response delays were considered in ^[25,29,36]. Katri and Ruan ^[31] modified models (1.1)–(1.4) by including a discrete-time intracellular delay $\tau _{1}$ which describes the time between the initial infection of uninfected CD$4^{+}$T cells to become latently CD$4^{+}$T infected cells. Equation (1.2) was replaced by

The delayed HTLV-I infection models presented in the literature included either discrete-time delay ^{[16,20,21,24,25,32,33,34,35,36]}, or distributed-time delay ^[23]. All these models neglected the latently infected cells.

In the literature of HTLV-I infection models, the intrinsic growth rate of uninfected cells was given by two main forms, linear form $\Phi \left(U\right) = \nu -\bar{\nu}U$ ^{[7,11,23,24,25]}, and logistic function $\Phi (U) = \nu -\bar{\nu}U+\varsigma U\left(1-\frac{U}{ U_{\max }}\right)$ ^[16], where $\varsigma > 0$ is the maximum propagation rate of uninfected cells and $U_{\max } > 0$ is maximal population level of uninfected cells.

The incidence rate that models the touch between the uninfected cells and actively infected cells presented in models (1.1)–(1.4), (1.5)–(1.7) and (1.8)–(1.11) was given by bilinear incidence $\beta UA$. This bilinear form may not be completely characterize the incidence between uninfected cells and actively infected cells ^[37]. Several HTLV-I infection models were introduced in the literature by considering different incidence rate forms such as: (ⅰ) saturated incidence $\frac{\beta UA}{1+\upsilon A}$ ^[11], $\frac{\beta UA}{1+\eta U}$ ^[27], standard incidence $\frac{\beta UA}{U+A}$ ^[38], Beddington-DeAngelis incidence $\frac{\beta UA}{1+\eta U+\upsilon A}$ ^[29], Crowley Martin incidence $\frac{\beta UA}{(1+\eta U)(1+\upsilon A)}$ ^[23], and nonlinear incidence in the form $\beta U^{q}A^{p}$ ^[28]; $\beta U\Lambda(A)$ ^[24] and ^[39]; $\Lambda(U, A)A$ ^[26], where $\beta, \upsilon, \eta, p$ and $q$ are positive constants and $\Lambda$ is a general function satisfies some conditions.

In models (1.1)–(1.4), (1.5)–(1.7) and (1.8)–(1.11) and most of the HTLV-I models introduced in the literature, the death rate of the cells is given by linear function of their concentration. However, the death rate of the cells is generally not known.

Our aim of the present paper is to formulate and analyze a general delayed HTLV-I mathematical model under the following generalizations:

G1: We assume that the intrinsic growth rate of the uninfected CD$4^{+}$T cells is given by a general function $\Phi(U)$.

G2: We consider a general incidence rate in the form $\Lambda(U, A)$.

G3: We assume that the death rates of the latently infected cells, actively infected cells and CTLs are given by general nonlinear functions $\mu \Psi_{1}\left(L\right)$, $\delta^{\ast}\Psi_{2}\left(A\right)$ and $\gamma \Psi_{3}\left(C\right)$, respectively.

G4: We assume that the transition rate from latently infected phase to actively infected phase is given by a general nonlinear function in the form $\pi \Psi_{1}\left(L\right)$.

G5: We assume that actively infected cells proliferate at rate $\varepsilon^{\ast}\Psi_{2}\left(A\right)$, with $\left(1-\omega \right) \varepsilon^{\ast}\Psi_{2}\left(A\right)$, $\omega \in(0, 1)$ staying in the actively infected cells compartment, while $\omega \varepsilon^{\ast}\Psi _{2}\left(A\right)$ being latent and therefore escaping from the CTL immunity.

G6: We assume that the replenishment rate of CTLs and the elimination of actively infected cells by CTLs are given by $\rho \Psi_{2}\left(A\right) \Psi_{3}\left(C\right)$ and $\alpha \Psi_{2}\left(A\right) \Psi _{3}\left(C\right)$, respectively.

G7: We include distributed intracellular delay which describes the cell mutates from uninfected to latent.

G8: We include distributed delay in the activation of latently infected.

2.   HTLV-I dynamics model with delay-distributed

With the above generalizations G1–G8 we propose the following HTLV-I dynamics model with two types of distributed-time delays:

Here, $\varpi$ is a random variable generated from probability distribution functions $\mathit{f}_{i}(\varpi)$, $i = 1, 2$ over the time interval $\left[0, \kappa _{i}\right]$, $i = 1, 2$ where $\kappa _{i}$ is the upper limit of the delay period. Here $\mathit{f}_{1}(\varpi)e^{-\xi _{1}\varpi }$ represents the probability of surviving the cells from time $t-\varpi$ to time $t$. The factor $\mathit{f}_{2}(\varpi)e^{-\xi _{2}\varpi }$ represents the probability that latently infected cells is survived $\varpi$ time units to become actively infected cells. Functions $\mathit{f} _{i}(\varpi)_{i = 1, 2}$ satisfy the following conditions:

(a) $\mathit{f}_{i}(\varpi) > 0, i = 1, 2,$

(b) $\int \limits_{0}^{\kappa_{i}}\mathit{f}_{i}(\varpi)d\varpi = 1, i = 1, 2,$

(c) $\int \limits_{0}^{\kappa_{i}}e^{-\xi_{i}\varpi}\mathit{f} _{i}(\varpi)d\varpi < \infty,$ $\xi_{i} > 0,$ $i = 1, 2.$

Here, $\Phi$, $\Lambda$, $\Psi_{i}$, $\ i = 1, 2, 3$ are continuously differentiable functions, in addition they satisfy a set of conditions:

Condition(C1):(a) there exists a $U_{0} > 0$ such that $\Phi(U_{0}) = 0$ and $\Phi(U) > 0$ for $U\in \lbrack0, U_{0})$.

(b)$\ \Phi^{\prime}(U) < 0$ for all $U > 0$.

(c) there exists $\nu > 0$ and $\bar{\nu} > 0$ such that $\Phi(U)\leq \nu-\bar{ \nu }U$, for all $U\geq0$.

Condition(C2):(a) $\Lambda(U, A) > 0$ and $\Lambda (0, A) = \Lambda(U, 0) = 0,$ for all $U > 0, A > 0$.

(b) $\frac{\partial \Lambda(U, A)}{\partial U} > 0$, $\frac{\partial \Lambda (U, A)}{\partial A} > 0$ and $\frac{\partial \Lambda(U, 0)}{\partial A} > 0,$ for all $U > 0$, $A > 0$.

(c) $\frac{d}{dU}\left(\frac{\partial \Lambda(U, 0)}{\partial A}\right) > 0,$ for all $U > 0.$

Condition(C3): (a) $\Psi_{i}(s) > 0$ for all $s > 0$, $\Psi _{i}(0) = 0,$ $i = 1, 2, 3$.

(b) $\Psi_{i}^{\prime}(s) > 0,$ for all $s > 0$, $i = 1, 3$, $\ \Psi_{2}^{\prime }(s) > 0,$ for all $s\geq0$.

(c) there is $\alpha_{i} > 0$, $i = 1, 2, 3$ such that $\Psi_{i}(s)\geq \alpha_{i}s,$ for all $s\geq0$.

Condition(C4): $\frac{\Lambda(U, A)}{\Psi_{2}(A)}$ is decreasing w.r.t $A,$ for all $A > 0$.

Let $\kappa = \max \left \{ \kappa _{1}, \kappa _{2}\right \}$ and assume the initial conditions of systems (2.1)–(2.4) having the following form:

where $\phi \in$ $\mathbb{C}$ and $\mathbb{C} = \mathbb{C} \left(\left[-\kappa, 0\right], \mathbb{R} _{+}^{4}\right)$ is the Banach space of continuous mapping the interval $\left[-\kappa, 0\right]$ into $\mathbb{R} _{+}^{4}$ with the norm $\left \Vert \phi _{i}\right \Vert = \sup \limits_{-\kappa \leq \theta \leq 0}\left \vert \phi _{i}(\theta)\right \vert$ for $\phi _{i}\in \mathbb{C}$, $i = 1, 2, 3, 4,$ where $\mathbb{R} _{+}^{4} = \left \{ \left(U, L, A, C\right) :U\geq 0, L\geq 0, A\geq 0, C\geq 0\right \}$. We note that the systems (2.1)–(2.4) with initial conditions (2.5) by the fundamental theory of functional differential equations has a unique solution ^[40].

The parameters presented in models (2.1)–(2.4) are positive. In ^[14,41,42], it was assumed that $\varepsilon ^{\ast } < \min \{ \bar{\nu}, \mu, \delta ^{\ast }\}$. Since $\varepsilon ^{\ast } < \delta ^{\ast }$ and $0 < \omega < 1$, so $(1-\omega)\varepsilon ^{\ast } < \delta ^{\ast }$. Let's assume that $\delta = \delta ^{\ast }-(1-\omega)\varepsilon ^{\ast } > 0$ and $\varepsilon = \omega \varepsilon ^{\ast }.$ Hence, $\delta -\varepsilon = \delta ^{\ast }-\varepsilon ^{\ast } > 0$. Then the systems (2.1)–(2.4) will take the following form:

Let us define $\digamma _{i}$ as:

Clearly $0 < \digamma _{i}\leq 1,$ $i = 1, 2$.

Remark 1. If the time delay is not considered, $\varpi = 0$, all proliferated actively infected by mitosis become latent, $\omega = 1$, the intrinsic growth rate of the uninfected CD$4^{+}$T cells is given by linear function, $\Phi (U) = \nu - \bar{\nu}U$, the infection rate is given by bilinear incidence, $\Lambda (U, A) = \beta UA$, the death rates of the compartments are given by linear functions $\Psi _{i}\left(x\right) = x$, $i = 1, 2, 3$, and the CTL immune response is given by linear form, $\rho A$, then systems (2.1)–(2.4) will lead to the ODEs systems (1.8)–(1.11). In addition, if the CTL immune response is given by a nonlinear form, $\rho AC$, then systems (2.1)–(2.4) will reduce to the model presented in ^[1]. Thus, systems (2.1)–(2.4) can be considered a generalization of the systems presented in ^[1,14]. We mention that functions $\Phi \left(U\right)$, $\Lambda (U, A)$ and $\Psi _{i}$, $i = 1, 2, 3$, include and generalize many forms presented in the literature. The general distribution functions $f_{i},$ $i = 1, 2$ considered in our work allows us to include several special forms of intracellular delays existing in the literature (see ^{[24,31,32,33]}). Finally, models (2.1)–(2.4) can be considered as a generalization of the model presented in ^[23] which neglected the latently infected cells.

2.1.   Properties of solutions

Proposition 1. Suppose that Conditions C1–C3 are valid. Then thesolutions of (2.6)–(2.9) are non-negative and ultimately bounded.

Proof. We assume that systems (2.6)–(2.9) can be written in matrix form $\dot{X} = Y(X(t)),$ where

Clearly, $Y(X(t))$ satisfies the following: $\left. Y_{i}(X(t))\right \vert _{X_{i} = 0, X(t)\in \mathbb{R} _{+}^{4}}\geq 0, i = 1, 2, 3, 4.$ From Lemma 2 in ^[43] we get that the solutions of systems (2.6)–(2.9) with initial conditions (2.5) satisfies $(U(t), L(t), A(t), C(t))\geq 0$ for all $t\geq 0.$ Hence, the $\mathbb{R} _{\geq 0}^{4}$ is positively invariant for systems (2.6)–(2.9). Now, we show that the solutions of the system are bounded. The non-negativity of the system's solution implies that $\limsup \limits_{t \longrightarrow \infty }U\left(t\right) \leq \frac{\nu }{\bar{\nu}} = M_{1}.$ We define

Then

By using Conditions C1 and C3, we get

It follows that

where $\sigma = \min \left \{ \bar{\nu}, \mu \alpha _{1}, (\delta ^{\ast }-\varepsilon ^{\ast })\alpha _{2}, \xi _{2}, \gamma \alpha _{3}\right \}$. The non-negativity of the model's solutions imply that $\limsup \limits_{t\longrightarrow \infty }L\left(t\right) \leq M_{1},$ $\limsup \limits_{t\longrightarrow \infty }A\left(t\right) \leq M_{1}$ and $\limsup \limits_{t\longrightarrow \infty }C(t)\leq M_{2}$, where$\ M_{2} = \frac{\rho }{\alpha }M_{1}$. Therefore, $U(t), L(t), A(t)$ and $C(t)$ are all ultimately bounded.

According to Proposition 1, we can establish that the region $\Omega = \{(U, L, A, C)\in \mathbb{C} _{\geq 0}^{4}:\left \Vert U\right \Vert \leq M_{1},$ $\left \Vert L\right \Vert \leq M_{1},$ $\left \Vert A\right \Vert \leq M_{1},$ $\left \Vert C\right \Vert \leq M_{2}\}$ is positively invariant for systems (2.6)–(2.9).

2.2.   Equilibrium points and threshold parameters

Here, we look at the model's equilibrium points and deduce the conditions that allow them to exist.

Lemma 1. Suppose that C1–C4 are valid, then there exist twopositive threshold numbers $R_{0}$ and $R_{1}$ with $R_{0} > R_{1}$ such that:

(a) if $R_{0}\leq1$, then there exists a single equilibrium point $EP_{0} = \left(U_{0}, 0, 0, 0\right)$.

(b) if $R_{1}\leq1 < R_{0}$, then there exist two equilibrium points $EP_{0}$ and $EP_{1} = \left(U_{1}, L_{1}, A_{1}, 0\right)$.

(c) if $R_{1} > 1$, then there exist three equilibrium points $EP_{0}$, $EP_{1}$ and $EP_{2} = \left(U_{2}, L_{2}, A_{2}, C_{2}\right)$.

Proof. Any equilibrium point $EP = (U, L, A, C)$ satisfies

Equation (2.13) has two possibilities $\Psi_{3}(C) = 0$ and $\Psi_{2}\left(A\right) = \frac{\gamma}{\rho}$.

If $\Psi_{3}(C) = 0$, then from Condition C3 we obtain $C = 0$. From Condition C3 we have $\Psi_{i}^{-1}$, $i = 1$, $2$ exist, moreover, these functions are strictly increasing. Define

Therefore, Eqs (2.11) and (2.12) imply that

Obviously, from Condition C1 we have $\Xi(0), \Pi(0) > 0$ and $\Xi (U_{0}) = \Pi(U_{0}) = 0$.

From Eqs (2.10)–(2.12) we get

where $\varrho = \frac{\pi \digamma_{1}\digamma_{2}}{\pi \left(\delta -\varepsilon \digamma_{2}\right) +\delta \mu}$.

Equation (2.15) admits a solution $U = U_{0}$ which yields $L = A = C = 0$ and provides the infection-free equilibrium point $EP_{0} = (U_{0}, 0, 0, 0)$. Let

It is clear from Conditions C1–C3 that,

Moreover,

We note from Condition C1 that, $\frac{\partial \Lambda \left(U_{0}, 0\right) }{\partial U} = 0.$ Then

Since$\ \Psi_{2}\left(\Pi(U)\right) = \varrho \Phi(U)$ then $\Psi_{2}^{\prime}\left(\Pi(U)\right) \Pi^{\prime}(U) = \varrho \Phi^{\prime}(U)$. Substituting by $U = U_{0},$ we get $\Psi_{2}^{\prime} \left(0\right) \Pi^{\prime}(U_{0}) = \varrho \Phi^{\prime}(U_{0})$. Therefore,

Condition C1 implies that $\Phi^{\prime}(U_{0}) < 0$, thus if $\frac{\varrho}{\Psi_{2}^{\prime}\left(0\right) }\frac{\partial \Lambda \left(U_{0}, 0\right) }{\partial A} > 1$, then $\Gamma_{1}^{\prime }(U_{0}) < 0$ and there exists $U_{1}\in(0, U_{0})$ such that $\Gamma_{1}(U_{1}) = 0$. It follows from Eq (2.14) that, $L_{1} = \Xi(U_{1}) > 0$ and $A_{1} = \Pi(U_{1}) > 0$. This shows that, an infected equilibrium point without CTL immunity $EP_{1} = (U_{1}, L_{1}, A_{1}, 0)$ exists when $\frac{\varrho}{ \Psi_{2}^{\prime}\left(0\right) }\frac{\partial \Lambda \left(U_{0}, 0\right) }{\partial A} > 1.$ We denote

which defines the basic infection reproductive number and decides when the HTLV-I infection will be chronic. The second possibility of Eq (2.13) is $\Psi_{3}(C)\neq0$ and $\Psi_{2}(A_{2}) = \frac{\gamma}{\rho}$. This yields that $A_{2} = \Psi_{2}^{-1}(\frac{\gamma}{\rho}) > 0$. We insert the value of $A_{2}$ in Eq (2.10) and let

Based on Conditions C1 and C2, $\Gamma_{2}$ is a strictly decreasing function of $U$. Clearly, $\Gamma_{2}(0) = \Phi(0) > 0$ and $\Gamma _{2}(U_{0}) = -\Lambda(U_{0}, A_{2}) < 0$. Thus, there exists a unique $U_{2}\in(0, U_{0})$ such that $\Gamma_{2}(U_{2}) = 0$. From Eq (2.11) we get

From Eq (2.12) we get

Clearly, $C_{2} > 0$ when $\varrho \frac{\Lambda \left(U_{2}, A_{2}\right) }{ \Psi_{2}\left(A_{2}\right) } > 1$. Let us denote

which represents the CTL immunity stimulation number and determines when CTL immunity can be activated. Therefore, $C_{2}$ can be written as:

Thus, there exists an infected equilibrium point with CTL immunity $EP_{2} = (U_{2}, L_{2}, A_{2}, C_{2})$ when $R_{1} > 1$.

Conditions C2 and C4 imply that

2.3.   Global stability analysis

Stability analysis of equilibrium points is at the heart of dynamical system analysis. Stable solutions can only be observed experimentally. Thus, we demonstrate the global asymptotic stability of all equilibrium points in this section by establishing appropriate Lyapunov functions ^[44,45,46] and applying Lyapunov-LaSalle asymptotic stability theorem (L-LAST) ^[47,48,49]. We define the function $\mathcal{H}(x)\geq 0$ for all $x > 0$ as: $\mathcal{H} (x) = x-1-\ln x,$ where $\mathcal{H}(x) = 0$ if and only if $x = 1.$ Hence,

Denote $\left(U, L, A, C\right) = \left(U\left(t\right), L\left(t\right), A\left(t\right), C\left(t\right) \right).$

We will use the follow equations:

Let $T_{j}(U, L, A, C)$ be a Lyapunov function candidate and define a set

and $\Upsilon _{j}^{^{\prime }}$ be the largest invariant subset of $\Upsilon _{j}.$

Theorem 1. If $R_{0}\leq 1$ and Conditions C1–C4 are satisfied, then the equilibrium point $EP_{0}$ is globally asymptotically stable (GAS).

Proof. Let $T_{0}$ be defined as:

Obviously, $T_{0}(U, L, A, C) > 0$ for all $U, L, A, C > 0$, while $T_{0}(U_{0}, 0, 0, 0) = 0$. The time derivative of $T_{0}$ along the trajectories of systems (2.6)–(2.9) is calculated as follows:

Since $\Phi (U_{0}) = 0,$ then

Using Condition C4 we obtain

Therefore, if $R_{0}\leq 1$, then $\frac{dT_{0}}{dt}\leq 0$ and $\frac{dT_{0} }{dt} = 0$ when $U = U_{0}$ and $A = C = 0.$ The solutions of systems (2.6)–(2.9) are limited $\Upsilon _{0}^{\prime }$ which contains elements with $A(t) = 0$ and$\ C(t) = 0$. Then from Eq (2.8)

It follows that $\Upsilon _{0}^{\prime } = \left \{ EP_{0}\right \}$ and using L-LAST, we derive that $EP_{0}$ is GAS ^[47,48,49].

Remark 2. We know from Conditions C2 and C4 that

which provides us

Lemma 2. Let $R_{0} > 1$ and Conditions C1–C4 aresatisfied, then

Proof. From C1 and C2, for $U_{1}, U_{2}, A_{1}, A_{2} > 0$, we obtain

Using Condition C4, we get

First, assume that $sgn(U_{2}-U_{1}) = sgn(A_{2}-A_{1})$. We have

Hence, from Inequalities (2.19)–(2.21) we get:

which leads to a contradiction and hence, $sgn(U_{2}-U_{1}) = sgn(A_{1}-A_{2}).$ Utilizing the equilibrium pointconditions for $EP_{1}$ we obtain $\varrho \frac{\Lambda \left(U_{1}, A_{1}\right) }{\Psi _{2}\left(A_{1}\right) } = 1,$ then

Thus, from Inequalities (2.20) and (2.22) we obtain $sgn(R_{1}-1) = sgn(U_{2}-U_{1}) = sgn(A_{1}-A_{2}).$

Theorem 2. If $R_{1}\leq 1 < R_{0}$ and Conditions C1-C4 are satisfied, then the infected equilibrium point without CTL immunity $EP_{1}$ is GAS.

Proof. Let $T_{1}$ be defined as:

Clearly $T_{1}(U, L, A, C) > 0$ for all $U, L, A, C > 0$ and $T_{1}(U_{1}, L_{1}, A_{1}, 0) = 0$. Calculate $\frac{dT_{1}}{dt}$ as

Collecting terms we get

Using $\Phi (U_{1}) = \Lambda \left(U_{1}, A_{1}\right)$ we obtain

Utilizing the equilibrium point conditions for $EP_{1}$:

we obtain

Therefore $\frac{dT_{1}}{dt}$ can be written as:

Equation (2.23) can be written as:

Equation (2.24) can be simplified as:

Lemma 2 implies that, if $R_{1}\leq 1$, then $A_{1}\leq A_{2}$ and from Condition C3 we get $\Psi _{2}(A_{1})\leq \Psi _{2}(A_{2})$. Therefore, if $R_{1}\leq 1$, then $\frac{dT_{1}}{dt}\leq 0$, where $\frac{dT_{1}}{dt} = 0$ occurs at the equilibrium point $EP_{1}$. Hence $\Upsilon _{1}^{\prime } = \left \{ EP_{1}\right \}$ and then L-LAST guarantees the global asymptotic stability of $EP_{1}$.

Theorem 3. If $R_{1} > 1$ and Conditions C1–C4 are satisfied, thenthe infected equilibrium point with CTL immunity $EP_{2}$ is GAS.

Proof. We define $T_{2}$ as:

Clearly, $T_{2}(U, L, A, C) > 0$ for all $U, L, A, C > 0$ and $T_{2}(U_{2}, L_{2}, A_{2}, C_{2}) = 0$. Calculate $\frac{dT_{2}}{dt}$ as:

Collecting terms we get

Using $\Phi (U_{2}) = \Lambda (U_{2}, A_{2})$ we obtain

Using the equilibrium point conditions for $EP_{2}$:

we obtain

Equation (2.26) can be written as:

Using Eqs (2.16) and (2.18) we get

Hence, if $R_{1} > 1$, then $U_{2}$, $L_{2}$, $A_{2}$, $C_{2} > 0$. From Conditions C1, C2 and C4, we get that $\frac{dT_{2}}{dt} \leq 0$ and $\frac{dT_{2}}{dt} = 0$ when $U = U_{2}, L = L_{2}$ and $A = A_{2}.$ The solutions of the system converge to $\Upsilon _{2}^{\prime }$ which has elements with $U = U_{2},$ $L = L_{2}$ and $A = A_{2}.$ It follows that $\dot{A} = 0$ and Eq (2.8) becomes

and hence $\Upsilon _{2}^{\prime } = \left \{ EP_{2}\right \}.$ L-LAST implies the global asymptotic stability of $EP_{2}$.

3.   Special case of the distributed-time delay

In this section, we take a particular form of the probability distributed functions as:

where $\Delta (.)$ is the Dirac delta function and $\tau _{i}$, $i = 1, 2\ $ are constants. When $\kappa _{i}\rightarrow \infty, i = 1, 2$, we have

Moreover,

Hence, models (2.6)–(2.9) will reduce to the following model with discrete-time delays:

Similar to the proof of Proposition 1, one can show that the solutions of systems (3.1)–(3.4) are non-negative and ultimately bounded.

Corollary 1. Consider systems (3.1)–(3.4) and suppose that C1–C4 are satisfied, then there exist two positive threshold numbers $R_{0}$ and $R_{1}$ with $R_{0} > R_{1}$ such that:

(a) If $R_{0}\leq 1$, then there exists a single equilibrium point $EP_{0}$.

(b) If $R_{1}\leq 1 < R_{0}$, then there exist two equilibrium points $EP_{0}$ and $EP_{1}$.

(c) If $R_{1} > 1$, then there exist three equilibrium points $EP_{0}$, $EP_{1}$ and $EP_{2}$.

The proof can be completed as the same as given in Lemma 1 by replacing $\digamma _{i}$ by $e^{-\xi _{i}\tau _{i}}, i = 1, 2$. The parameters $R_{0}$ and $R_{1}$ for system (3.1)-(3.4) are given by

where $\varrho ^{S} = \frac{\pi e^{-\xi _{1}\tau _{1}-\xi _{2}\tau _{2}}}{\pi \left(\delta -\varepsilon e^{-\xi _{2}\tau _{2}}\right) +\delta \mu }$.

We can obtain the global dynamics of models (3.1)–(3.4) as follows:

Corollary 2. Consider systems (3.1)–(3.4) and suppose that Conditions C1–C4 are satisfied.

(ⅰ) If $R_{0}\leq 1$, then the equilibrium point $EP_{0}$ is GAS.

(ⅱ) If $R_{1}\leq 1 < R_{0}$, then the infected equilibrium point without CTL immunity $EP_{1}$ is GAS.

(ⅲ) If $R_{1} > 1$, then the infected equilibrium point with CTL immunity $EP_{2}$ is GAS.

Proof. (ⅰ) We consider the Lyapunov function $T_{0}$ as:

Following the proof of Theorem 1 we obtain $\frac{dT_{0}}{dt}$ as:

(ⅱ) We define the Lyapunov function $T_{1}$ as:

Then, we follow the proof of Theorem 2 to get

(ⅲ) We define the Lyapunov function $T_{2}$ as:

Following the proof of Theorem 3 we obtain $\frac{dT_{2}}{dt}$ as:

Similar to the proofs of Theorems 1–3 one can complete the proof.

4.   Numerical simulations

To illustrate and validate our theoretical results we present some numerical simulations for systems (3.1)–(3.4) with the following specific shapes of the general functions:

● Logistic function for the intrinsic growth rate of uninfected cells

● Crowley-Martin incidence rate

● Linear death rate of the cells

Thus, systems (3.1)–(3.4) become

Clearly $\Phi(0) = \nu > 0$ and $\Phi(U_{0}) = 0$, where $U_{0} = \frac{U_{\max}}{2 \varsigma}\left(\varsigma-\bar{\nu}+\sqrt{(\varsigma-\bar{\nu })^{2}+\frac{4\nu \varsigma}{U_{\max}}}\right).$ It was mentioned in ^[16] that the term $\varsigma-\bar{\nu}$ is not necessary to be positive, therefore we assume that $\varsigma < \bar{\nu}.$ We see that $\Phi^{\prime}(U) = -\bar{\nu}+\varsigma-\frac{2\varsigma U}{U_{\max}} < 0.$

Obviously, $\Phi(U) > 0$ for all $U\in \lbrack0, U_{0})$. Hence, Condition C1 is satisfied. We note that $\Lambda(U, A) > 0$ for all $U, A > 0$ and $\Lambda(U, 0) = \Lambda(0, A) = 0.$ Moreover, for all $U > 0, A > 0$ we have

Then Condition C2 is satisfied.

Also, we can see that $\Psi _{i}(s) > 0$, for all $s > 0$ and $\Psi _{i}(0) = 0, i = 1, 2, 3$. Moreover, $\Psi _{i}^{\prime }(s) = 1 > 0,$ $i = 1, 2, 3$ for all $s\geq 0$. Thus, Condition C3 is satisfied. Finally, we have

Thus, Condition C4 is satisfied as well. We can also see that our example satisfied the global stability results (Theorems 1–3) with, $R_{0}$ and $R_{1}$ given by

where $U_{2}$ is the positive root of the equation

We present some numerical results for models (4.1)–(4.4) to address the stability of equilibrium points. Further, we address the effect of time delays on the dynamical behavior of the system. All the simulations are done using the solver dde23 MATLAB.

4.1.   Stability of equilibrium points

In this subsection, we illustrate our global stability results given in Theorems 1–3 by showing that from any selected initial conditions, the solution of the HTLV-I infection model will tend to one of the three equilibrium points. Let us select three initial conditions as:

We fix the time delays $\tau _{1}$ and $\tau _{2}$ to become $\tau _{1} = \tau _{2} = 0.1$. We use the values of some parameters of models (4.1)–(4.4) given in Table 1 and establish the effect of the other parameters, $\beta$ and $\rho$ on the stability of the three equilibrium points. We investigate three cases as follows:

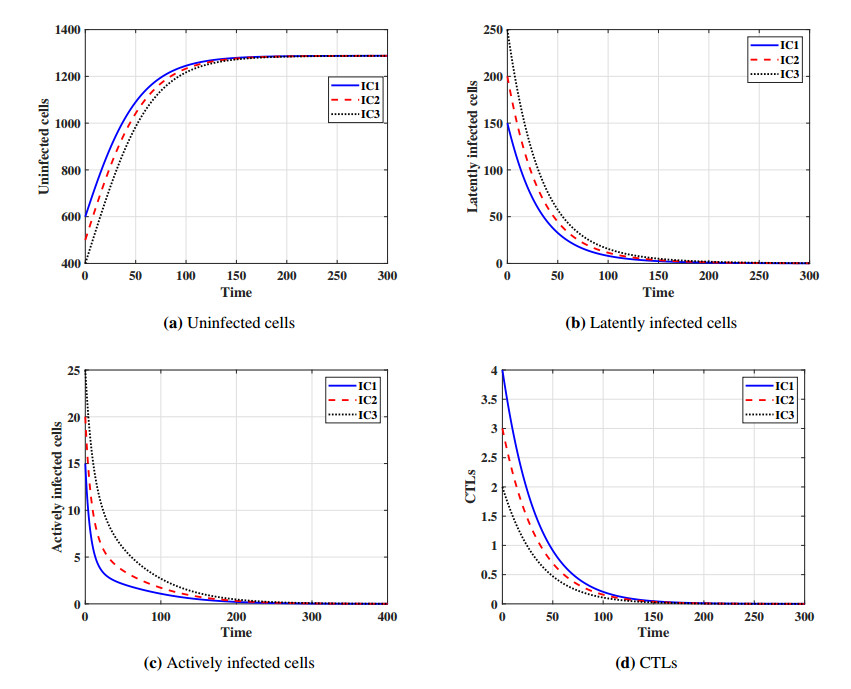
Case 1. ($R_{0}\leq1$): Choosing $\beta = 0.0001$ and $\rho = 0.0001$ which gives $R_{0} = 0.1276 < 1$ and $R_{1} = 0.0332 < 1.$ Lemma 1 and Theorem 1 prove that the system has a single equilibrium point, $EP_{0}$ and it is GAS. Figure 1 shows that for all the threeinitials IC1-IC3, the concentrations of latently infected cells, activelyinfected cells and CTLs are tending to zero. In the mean time, theconcentration of the uninfected cells tends to its healthy value $U_{0} = 1288.15$. This case means that there is no HTLV-I infection in thebody.

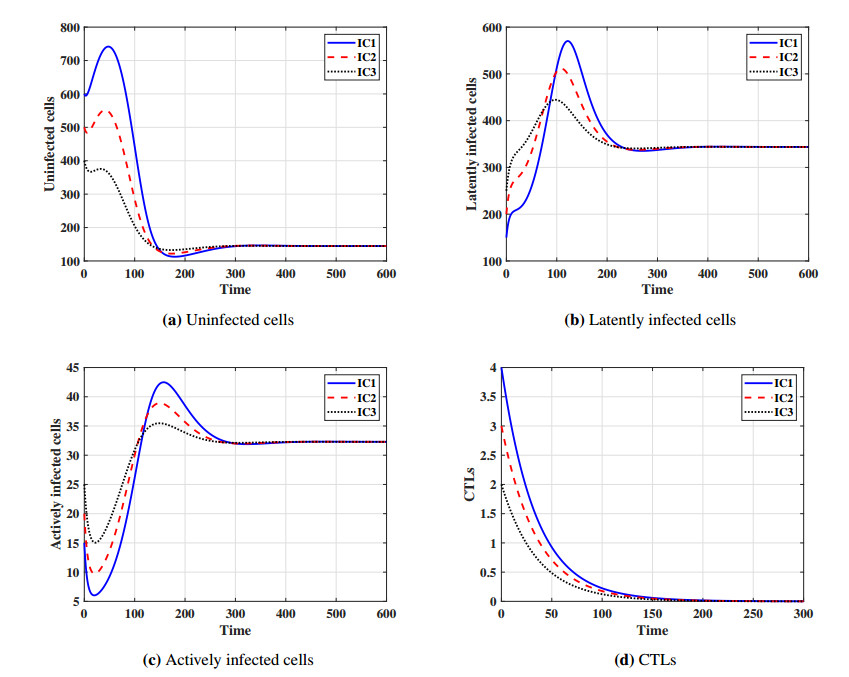
Case 2. ($R_{1}\leq1 < R_{0}$): We take $\beta = 0.004$ and $\rho = 0.0001.$ So, we get $R_{0} = 5.1054 > 1$ and $R_{1} = 0.0936 < 1.$ Based on Lemma 1 and Theorem 2, the infected equilibrium point withoutCTL immunity $EP_{1}$ exists. In such case, $EP_{1}$ is GAS. Figure 2 shows that the numerical simulations illustrate our theoreticalresult given in Theorem 2. The system'ssolutions converge to the equilibrium point $EP_{1} = (144.65,343.80, 32.29, 0)$ for all the three initials IC1-IC3. In this situation, the HTLV-I-patienthas non-active CTL immunity.

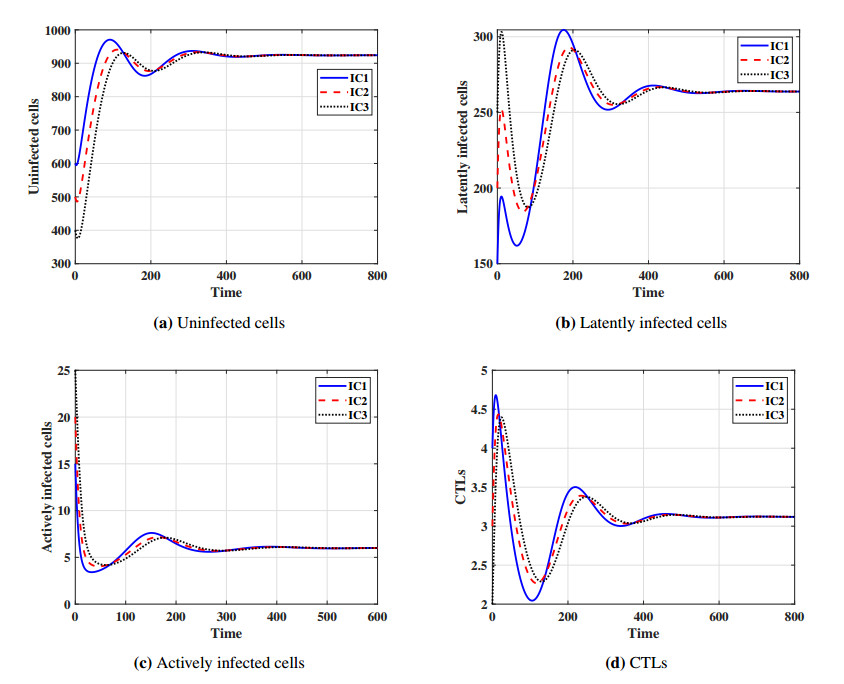
Case 3. ($R_{1} > 1$): We choose $\beta = 0.004$ and $\rho = 0.005$. Then, we calculate $R_{0} = 5.1054 > 1$ and $R_{1} = 4.2216 > 1$. Lemma 1 and Theorem 3 state that the infected equilibrium pointwith CTL immunity $EP_{2} = \left(923.92,263.87, 6, 3.12\right)$ exists and isGAS. Figure 3 displays the numerical solutions of the systemconverge to $EP_{2}$ for all the three initials IC1-IC3. The results supportthe theoretical results presented in Theorem 3. This case corresponds to an HTLV-I chronic infection with active CTLimmunity.

4.2.   Impact of the CTL immunity on the dynamics of HTLV-I

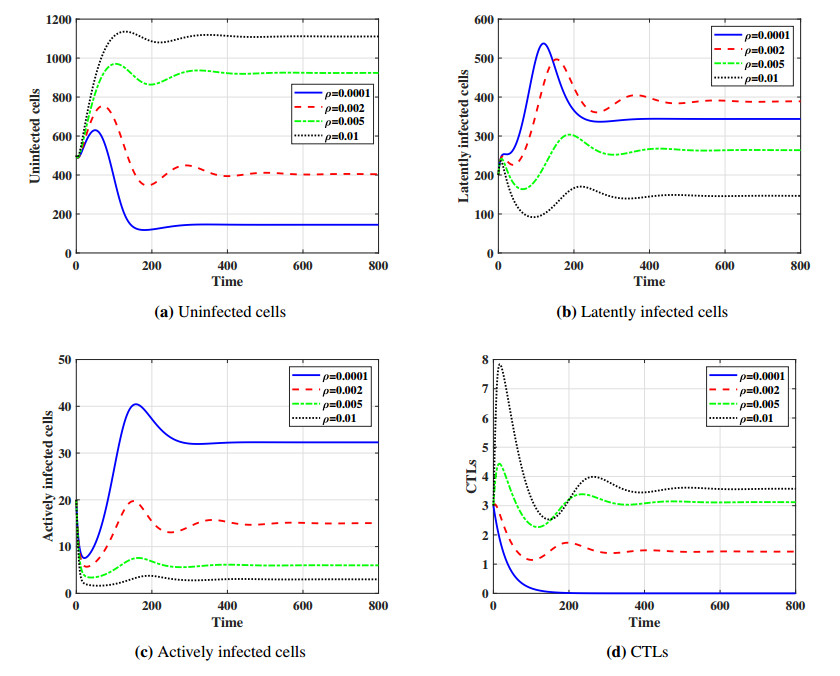
We observe that the values of the parameter $\alpha, \rho$ and $\gamma$ have no effect on the value of $R_{0}$. It means that, CTL immunity has no effect on the stability of the infection-free equilibrium point $EP_{0}$. Now we address the effect of the proliferation rate constant of CTL $\rho$ on the HTLV-I dynamics. Using the values of the parameters in Table 1 to solve the model (4.1)-(4.4) with initial condition IC2. We choose $\beta = 0.004$, $\tau _{1} = \tau _{2} = 0.1$. We can see from Table 2 that $R_{1}$ can be increased by increasing the value of $\rho$. We can see from Figure 4 when $\rho$ is increased, the concentrations of uninfected cells and CTLs are increased, while the concentration of actively infected cells is decreased. Therefore, CTL immunity does not play the role in deleting the virus, but it has an important role in controlling the HTLV-I infection.

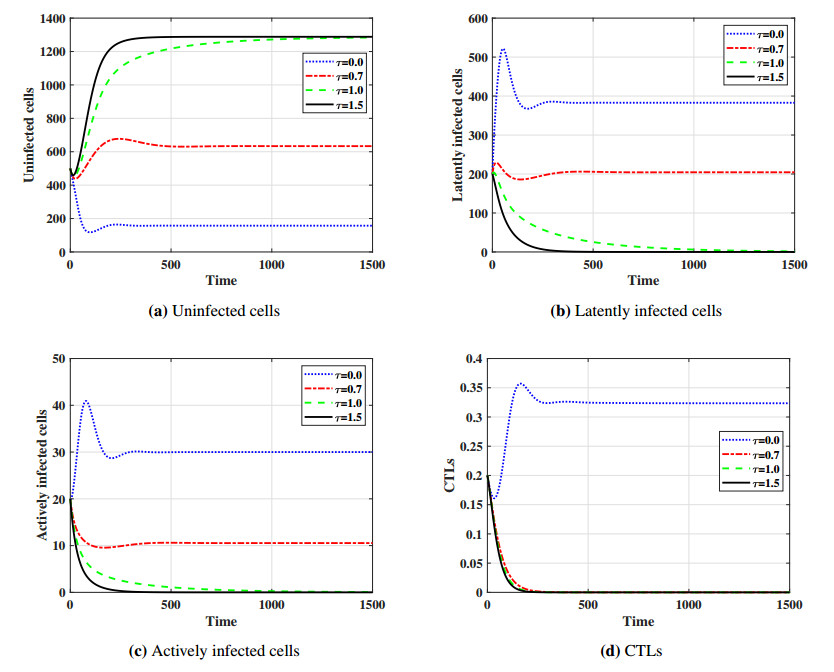
4.3.   Impact of time delays $\tau _{1}$ and $\tau _{2}$ on the dynamics of HTLV-I

In this part, we study the effect of vary the time delays $\tau _{1}$ and $\tau _{2}$ on the HTLV-1 dynamics. Using the values of the parameters in Table 1 and considering $\beta = 0.004$ and $\rho = 0.001\ $to solve the models (4.1)–(4.4) with initial condition:

Consider $\tau = \tau _{1} = \tau _{2}$, then $R_{0}$ and $R_{1}$ can be given as functions of $\tau$ as follows:

We note that $R_{0}$ and $R_{1}$ are decreasing functions of $\tau$. Let $\tau _{CR_{0}}$ and $\tau _{CR_{1}}$ be such that $R_{0}\left(\tau _{CR_{0}}\right) = 1$ and $R_{1}\left(\tau _{CR_{1}}\right) = 1.$ Using the values of the parameters in Table 1 and considering $\beta = 0.004$ and $\rho = 0.001,$ we obtain $\tau _{CR_{0}} = 0.907187$ and $\tau _{CR_{1}} = 0.142356.$ Therefore, we have the following cases:

(a) if $\tau \geq0.907187,$ then $R_{0}\left(\tau \right) \leq1$ and $EP_{0 }$ is GAS;

(b) if $0.142356\leq \tau < 0.907187,$ then $R_{1}\left(\tau \right) \leq1 < R_{0}\left(\tau \right)$ and $EP_{1 }$ is GAS;

(c) if $\tau < 0.142356,$ then $R_{1}\left(\tau \right) > 1$ and $EP_{2 }$ is GAS.

It is clear from Figure 5 that as $\tau$ increases, the concentration of uninfected CD4$^{+}$T cells is increased and the other concentrations are decreased. In Table 3 we calculate the values of $R_{0}\ $and $R_{1}$ as functions of $\tau$. We note that, when $\tau$ is increased, the values of both $R_{0}$ and $R_{1}$ are decreased. We can see from the above discussion that increasing time delays values can have similar effect as antiviral treatments.

5.   Conclusions and discussion

In this work, we proposed and examined a general HTLV-I infection models with CTL immunity and mitotic transmission of actively infected cells. We introduce two intracellular distributed-time delays into the models: (ⅰ) delay in the formation of latently infected cells, (ⅱ) delay in the activation of latently infected cells. We constructed the model with more general nonlinear functions for the generation/stimulation and clearance rates of all compartments as well as the incidence rate of infection. We established some conditions on such general functions and determined two threshold numbers $R_{0}$ and $R_{1}$ which control the existence and global stability of the three equilibrium points. We formulated Lyapunov functions and used L-LAST to establish the global asymptotic stability of the equilibrium points. We proved that

● If $R_{0}\leq 1$, then the infection-free equilibrium point $EP_{0}$ is GAS. This result suggests that when $R_{0}\leq 1$, the HTLV-I infection is predicted to die out regardless of the initial conditions. From a control viewpoint, making $R_{0}\leq 1$ will be an ideal way but HTLV-I infection is lifelong, and the viruses are rarely cleared.

● If $R_{1}\leq 1 < R_{0}$, then the infected equilibrium point without CTL immunity $EP_{1}$ is GAS. This result establishes that when $R_{1}\leq 1 < R_{0}$, the HTLV-I infection with inactive CTL immunity is always established regardless of the initial conditions.

● If $R_{1} > 1$, then the infected equilibrium point with CTL immunity $EP_{2}$ is GAS. This result illustrates that when $R_{1} > 1$, the HTLV-I infection with active CTL immunity is always established regardless of the initial conditions. This implies that the infection becomes chronic and the CTL immune response is persistent. In cases $R_{1}\leq 1 < R_{0}$ and $R_{1} > 1$, the individuals have a high risk of developing HAM/TSP and can be characterized as the HAM/TSP patients.

We studied the global stability of a general HTLV-I model with discrete-time delays as a special case of the model with distributed-time delays when the probability distributed function is given by Dirac delta function. To support the obtained theoretical results, we conducted numerical simulations for the model with discrete-time delays, logistic form for the intrinsic growth rate of uninfected cells, Crowley-Martin incidence rate and linear death rate of the cells. We discussed the impacts of the proliferation of CTLs on the HTLV-I dynamics. We noted that the CTL immunity does not play the role in deleting the virus from the body, but it has an important role in controlling and suppressing the HTLV-I infection. We showed that the parameter $\rho$ has a significant effect of the dynamical behavior of the HTLV-I. The effect of the time delays on the HTLV-I dynamics was discussed. We established that, when all other parameters are fixed and delays are sufficiently large, $R_{0}$ becomes less than one, which makes the infection-free equilibrium point $EP_{0}$ globally asymptotically stable. From a biological viewpoint, time delays play positive roles in the HTLV-I infection process in order to eliminate the virus. Sufficiently large time delays makes the HTLV-I development slower, and the HTLV-I is controlled and disappears. This gives us some suggestions on new drugs to prolong the time of formation of latent infected cells, or the time of activation of latent infected cells.

We mention that models (1.8)–(1.11) presented by Lim and Maini ^[14] considered a linear proliferation rate of the CTLs, $\rho A$. In comparison with our proposed model, models (1.8)–(1.11) admits only two equilibrium points, infection-free equilibrium point $\widetilde{EP}_{0} = (\frac{\nu }{\bar{\nu}}, 0, 0, 0)$ and infected equilibrium point $\widetilde{EP}_{1} = (\tilde{U}_{1}, \tilde{L}_{1}, \tilde{A} _{1}, \tilde{C}_{1})$. The existence and stability of $\widetilde{EP}_{0}$ and $\widetilde{EP}_{1}$ are determined by the basic reproductive number

We note that, $\tilde{R}_{0}$ does not depends on the proliferation rate constant of the CTLs, $\rho$. As a result, $\rho$ does not play any role on the existence and stability of both equilibria. In this case, the effect of the CTL immune response on the dynamical behavior of the HTLV-I does not appear explicitly. In our model, by considering a nonlinear proliferation rate of the CTLs, the role of the CTLs in controlling the HTLV-I infection is well presented. In ^[1], an HTLV-I infection model was presented with a nonlinear proliferation rate of the CTLs, $\rho AC$, however, the intracellular time delay was neglected. In addition, the infection rate was given by bilinear incidence which may not be completely characterize the incidence between uninfected cells and actively infected cells ^[37]. Overall, our proposed model helps to better understand the dynamical behavior of HTLV-I infection with CTL immunity and time delays.

The model presented in this paper can be extended in many directions such as (ⅰ) including the reaction diffusion ^[55], (ⅱ) considering the stochastic interactions ^[56], (ⅲ) modeling the coinfection with HTLV-I and other types of viruses.

Acknowledgements

This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under grant no. (KEP-PHD-38-130-43). The authors, therefore, acknowledge with thanks DSR technical and financial support.

Conflict of interest

The authors declare there is no conflict of interest.