Follow-the-Leader models can be viewed as a numerical approximation to the Lighthill-Whitham-Richards model for traffic flow

1.   Introduction

There are two paradigms in the mathematical modeling of traffic flow. One is based on an individual modeling of each vehicle with the dynamics governed by the distance between adjacent vehicles. The other is based on the assumption of dense traffic where the vehicles are represented by a density function, and individual vehicles cannot be identified. The dynamics is governed by a local velocity function depending solely on the density. The first model is denoted the Follow-the-Leader (FtL) model, and the second is called the Lighthill-Whitham-Richards (LWR) model [13,14] for traffic flow. Further refinements and extensions of these models are available. Intuitively, it is clear that the the FtL model should approach or approximate the LWR model in the case of heavy traffic, and that is what is proved here. This problem has been extensively studied, see [1,2,3,5,0,7,8,9,10,12,15].

This paper is based upon the observation that the FtL model coincides with a semi-discrete (continuous time, discrete space) numerical model for the LWR model in Lagrangian coordinates. This allows us to use theory from numerical methods for scalar conservation laws to show that FtL models appear naturally as a numerical approximation of the LWR model. This constitutes a short and direct proof that the FtL model converges to the LWR model, and our analysis is based on a careful study of the relationship between weak solutions in Lagrangian and Eulerian variables. Our point here is not to pretend that this would be an optimal numerical method; rather our emphasis here is that by identifying that FtL can be viewed as numerical approximation of LWR, we can apply known results from numerical analysis to analyze the approximation.

In the LWR model vehicles are described by a density $\rho = \rho(t, x)$ where $x$ is the position along the road, and $t$ as usual denotes time. Locally, one assumes that the velocity is given by a function $v$ that depends on the density only, that is, $v = v(\rho)$. If we consider unidirectional traffic on a homogenous road without exits or entries, conservation of vehicles requires that the dynamics is governed by the scalar conservation law

which constitutes the LWR model. It is often denoted as "traffic hydrodynamics" due to its resemblance with fluid dynamics.

The FtL model can be described as follows. Consider $N$ vehicles with length $\ell$ and position $z_1(t) < \dots < z_N(t)$ on the real axis with dynamics given by

Here $v$ denotes a given velocity function with maximum $v_{\max}$, perhaps the speed limit. Our proofs are considerably simpler when we have a uniform bound on $z_{i+1}(t)-z_i(t)$. Having empty road ahead of the first car would mean that "$z_{N+1}-z_N = \infty$". This is the same as imposing $\dot{z}_N = v_{\max}$, and in this case $z_{i+1}(t)-z_i(t)$ would not be bounded by a constant independent of time. Therefore we will in this paper assume that we model one of two alternatives:

Periodic case: We are in the periodic case in which $z_i\in [a, b]$ for some interval $[a, b]$, and

Non-periodic case: We imagine that there are infinitely many vehicles to the right of $z_N$, the distance between each of these vehicles is $M\ell$, for a finite, but arbitrary, constant $M>1$. In this case

Introduce $y_i = (z_{i+1}-z_i)/\ell$ for $i = 1, \dots, N-1$, to obtain

In this paper we analyze the limit of this system of ordinary differential equations when $N\to\infty$ and $\ell\to 0$. There are two ways to proceed.

We may analyze this system directly, in what we call the semi-discrete case, see Section 2.1. By using methods from the theory of numerical methods for scalar conservation laws we show that the sequence $\{ y_i(t) \}_{i = 1}^{N-1}$ converges, as $\ell\to 0$ and $N\to\infty$, to a function $y(t, x)$ that satisfies the equation

where $V(y) = v(1/y)$, and with boundary condition

Note that $x$ is the Lagrangian mass coordinate, so that the integer part of $x/\ell$ measures how many cars there are to the left of $x$.

Equation (1.1) is an example of a hyperbolic conservation law. It is well-known that solutions develop singularities, denoted shocks, in finite time independent of the smoothness of the initial data. Thus one needs to study weak solutions, and design so-called entropy conditions to identify the unique weak physical solution. For a scalar conservation law $u_t+f(u)_x = 0$ with initial data $u|_{t = 0} = u_0$, the unique weak entropy solution $u = u(t, x)$, which is an integrable function of bounded variation, satisfies the Kružkov entropy condition

for all real constants $k\in\mathbb{R}$, and all non-negative test functions $\phi\in C^\infty_0(\mathbb{R}\times [0, \infty))$. See [11].

As an alternative approach, see Section 2.2, we may discretize the time derivative by a small positive $\Delta t$ and write $z^n_j \approx z_j(n\Delta t)$, $y_j^{n}\approx y_j(n\Delta t)$, we have that

where $V^n_j = V(y^n_j)$. The key observation is that this is an approximation of the hyperbolic conservation law $y_t-V(y)_x = 0$ by a monotone scheme, and from the classical result of Crandall-Majda [4], see also [11,Thm. 3.9], we know that this scheme converges, as $\ell\to0$, $N\to \infty$, and $\Delta t\to 0$, to the entropy solution of equation (1.1), namely $y_t-V(y)_x = 0$. Thus in both cases we obtain convergence to the same hyperbolic conservation law in Lagrangian coordinates. The approach here avoids some of the more technical machinery employed in [8].

Next we have to transform the result of the two approaches, both in Lagrangian coordinates, to Eulerian coordinates. For smooth solutions this is nothing but a simple exercise in calculus, but for weak entropy solutions this is a deep result due to Wagner [16]. To be specific, we introduce the Eulerian space coordinate $z = z(t, x)$, with $z_x = y$ and $z_t = V(y)$. A straightforward (but formal) calculation reveals that the Eulerian functions satisfy

and hence

which is nothing but the LWR model. These formal transformations are not valid in general for weak entropy solutions. However, thanks to the fundamental result of Wagner [16], weak entropy solutions in Lagrangian coordinates transform into weak entropy solutions in Eulerian variables. The approach here bears some resemblance to the approach in [12], where the proof is obtained in a grid-less and very direct manner, and it does not depend on the use of Crandall-Majda and Wagner. In the present paper we introduce and analyze a discrete Lagrange-to-Euler mapping that we think is of independent interest.

2.   The model

Let us first introduce the FtL model. Consider $N$ vehicles moving on a one-dimensional road. Their position is given as a function of time $t$ as $z_1(t), \dots, z_N(t)$. For the moment (we shall actually show that this is so below) we assume that $z_1(t) < z_2(t)< \cdots < z_N(t)$. We introduce the "local inverse density" by

where $\ell$ is the length of each vehicle. The velocity of the vehicle at $z_j$ is assumed to be a function of the distance to the vehicle in front, at $z_{j+1}$. This means that

Regarding the first vehicle, located at $z_N$, we either assume that there are infinitely many equally spaced vehicles in front of it, i.e., $y_N = M$, or that we are in the periodic setting in an interval $[a, b]$, so that the distance from the vehicle at $z_N$ to the vehicle at $z_1$ is $b-z_N + z_1 -a$, i.e., $y_N = (b-z_N+z_1-a)/\ell$. We have

Regarding the velocity function $v$, we assume it to be a decreasing Lipschitz continuous function such that

The prototypical example is $v(\rho) = v_{\max}\max\{ 0, 1-\rho \}$. We define the velocity in Lagrangian variables by $V(y) = v(1/y)$. Observe that $V$ is globally bounded, Lipschitz continuous and increasing for $y\ge 1$, with a bounded Lipschitz constant $L_v$.

Rewriting (2.1) in terms of $\{ y_j \}$ we get

and

Let us define the Lagrangian grid $\{ x_{j-1/2} \}_{j = 1}^N$ by $x_{j-1/2} = (j-1)\ell$. We shall also assume throughout that there is a constant $1\le K < \infty$, $K$ independent of $N$ and $\ell$, such that

2.1.   The semi-discrete case

In this section we show that the solution of the system (2.4) of ordinary differential equations converges to an entropy solution of (1.1) as $\ell\to 0$, and that "$\rho = 1/y$" converges to an entropy solution of (1.3).

Concretely, we define the piecewise constant function

We shall also use the notation

for the forward difference. Let

and let $H$ denote the Heaviside function

Lemma 2.1.  Let $y_j(t)$ solve the system (2.4). Then

for any constant $k$.

Proof.Throughout we use the notation $V_j = V(y_j)$. We have that

Now

since $y\mapsto V(y)$ is increasing. This proves (2.8a); estimate (2.8b) is proved similarly.

Now define $y_j(t) = y_{N}(t)$ for $j>N$ in the non-periodic case. In the periodic case we define $y_j(t)$ for $j>N$ by periodic extension. Then (2.8a) and (2.8b) holds for all $j\ge 1$. To save space, we also use the convention that in the non-periodic case, sums over $j$ range over all $j\ge 1$, while in the periodic case, sums range over $j = 1, \ldots, N-1$.

Lemma 2.2.  If $1\le y_j(0)\le K$, then $1\le y_j(t)\le K$ for $t>0$.

Proof. We claim that

In the non-periodic case we get

In the periodic case we have

Thus if $y_j(0)\le K$ for all $j$, then $y_j(t)<k$ for any constant $k>K$. Similarly $y_j(t)>k$ for any constant $k<1$ if $y_j(0)\ge 1$ for all $j$.

Lemma 2.3.  If $\{ \tilde{y}_j(t) \}_{j = 1}^{N-1}$ is another solution of (2.4) and (2.5) with initial data $\tilde{y}_j(0)$, then

for $T>0$.

Proof.Adding (2.8a) and (2.8b), and observing that

we find that

Choosing $k = \tilde{y}_j(\tau)$ in the inequality for $y_j(t)$ and $k = y_j(t)$ in the inequality for $\tilde{y}_j(\tau)$, and adding the two inequalities, give

Summing over $j$, multiplying with a non-negative test function $\varphi(t, \tau)$, where $\varphi\in C^\infty_0((0, \infty)^2)$, and integrating by parts yield

Now we can use Kružkov's trick, see [11,Sec. 2.4], and choose

where $\psi\in C^\infty_0((0, \infty))$, $\psi\ge 0$ and $\omega_\varepsilon$ is a standard mollifier, to obtain, as $\varepsilon\to0$, that

Choose $\psi$ to be a smooth approximation to the characteristic function of the interval $(t_1, t_2)\subset (0, T)$, to get

The lemma follows by letting $t_1\downarrow 0$ and $t_2\uparrow T$. For details, see [11,Sec. 2.4].

Lemma 2.4. Assume that $1\le y_j(0)\le K$ and that $\sum_j|y_{j+1}(0)-y_j(0)|\le K$ for some constant $K$ independent of $\ell$. Then there is a sequence $\{ \ell_i \}$, where $\ell_i \to 0$ as $i\to \infty$, and there exists a function $y\in C([0, T];L^1([0, 1])$ such that $y_{\ell_i}$ converges to $y$ in $C([0, T];L^1([0, 1])$.

Proof. Lemma 2.2 shows that $\{ y_\ell \}_\ell$ is bounded independently of $\ell$; choosing $\tilde{y}_j = y_{j+1}$ and using Lemma 2.3 yields the $BV$ bound on $\{ y_\ell(t) \}_\ell$ uniformly in $\ell$ and $t$. Choosing $\tilde{y}_j(t) = y_j(t-\sigma)$ in Lemma 2.3 for some $0<\sigma<t$ gives

Hence the map $t\mapsto y_\ell(t, \cdot)$ is $L^1$ Lipschitz continuous, with a Lipschitz constant independent of $\ell$. Thus by [11,Thm. A.11], the family $\{ y_\ell \}_{\ell>0}$ is compact in $C([0, \infty);L^1([0, 1]))$.

Furthermore we assume that as $N$ increases, the initial positions of the vehicles are such that there is a function $y_0(x)$ such that

and that this convergence is in $L^1([0, 1])$. We also assume that $||y_0||_{L^\infty([0, 1])}\le K$, without loss of generality we can then also assume that $||y_\ell(0, \cdot)||_{L^\infty([0, 1])}\le K$.

It is now straightforward, starting from the discrete entropy inequality (2.10), to show that any limit of $\{ y_\ell \}_{\ell>0}$ is the unique entropy solution to (2.20) by following a standard Lax-Wendroff argument, see [11,Thm. 3.4].Thus the whole sequence $\{ y_\ell \}$ converges, and the unique entropy solution to (1.1) is the limit

Introduce the Eulerian spatial coordinate $z$, given by the equations

and the variable $\rho = 1/y$. We can now proceed following the argument of Wagner [16] to obtain that $\rho$ is the unique weak entropy solution to the LWR model

We can also study the convergence in Eulerian coordinates directly by defining a discrete version of the transformation from Lagrangian to Eulerian coordinates. To define the discrete version of $\rho$, we need the approximate Eulerian coordinate; $z_\ell(t, x)$. Define

where $\{ z_j(t) \}$ solves (2.1). Then

for $x\in (x_{j-1/2}, x_{j+1/2})$. The sequence $\{ z_\ell \}_{\ell>0}$ is uniformly Lipschitz continuous. Hence by the Arzel{á}-Ascoli theorem, it converges uniformly to a Lipschitz continuous limit $z(t, x)$ satisfying $z_t = V(y)$ and $z_x = y$ almost everywhere. Furthermore the map $x\mapsto z_\ell(t, x)$ is invertible, with inverse $x_\ell(t, z)$. In the periodic case we set

otherwise we define

Observe that $z_{l, \ell}(t) = z_\ell(t, 0)\to z(t, 0) = z_l(t)$ as $\ell\to 0$. Define

In the periodic case, we define $\rho_\ell$ by periodic continuation, while in the non-periodic case we define

Next we claim that

in $L^1([z_l, z_r])$ as $\ell\to 0$. To see this, define $\tilde\rho_\ell(t, x) = 1/y_\ell(t, x)$, and compute

We have that

Since $\tilde\rho_\ell$ and $\tilde\rho$ are both bounded by $1$, and $z_{l, \ell}\to z_l$ as $\ell\to 0$, the first of these integrals tend to zero. Since $x_\ell\to x$ uniformly, the integrand tends to zero almost everywhere, and is bounded by $2$. Hence by the dominated convergence theorem, the last integral tends to zero. The same argument applies to $B$. Thus the claim (2.15) is justified.

Summing up, we have shown the following result.

Theorem 2.5. Assume that the function $v$ satisfies (2.3). Let $\{ y_j \}_{j = 1}^{N-1}$ satisfy (2.4), with either periodic boundary conditions; $y_N(t) = y_1(t)$, or $y_N(t) = M$ for some fixed constant $M>1$. Assume that the initial positions of the vehicles $\{ z_i(0) \}_{i = 1}^{N}$ are such the we can define a bounded function $y_0$ by (2.11), and that (2.6) holds, namely that the initial data are bounded with finite total variation.

(i) The piecewise constant (in space) function $y_\ell(t, x)$ defined by (2.7) converges in $C([0, T];L^1([0, 1])$ as $\ell\to0$ to the unique weak entropy solution $y$ of (1.1). The function $\rho = 1/y$ satisfies the LWR model (2.12) in Eulerian variables.

(ii) The function $\rho_\ell$ defined by (2.14) converges in $C([0, T];L^1([0, 1])$ as $\ell\to0$ to the unique weak entropy solution $\rho$ of (2.12).

2.2.   Analysis of the Euler scheme for (2.1)

The simplest numerical method to approximate solutions of (2.1) is the forward Euler scheme, viz.,

where $\Delta t$ is a (small) positive number.

If we write the Euler scheme (2.16) in the $y$ variable, we get

where $y^n_j = y_j(t^n)$, $t^n = n\Delta t$, $\lambda = \Delta t/\ell$ and $V^n_j = V(y^n_j)$. As a (right) boundary condition we use

For $t\ge 0$ and $x\in [0, (N-1)\ell]$ define the function

Observe that we can rewrite (2.17) as

where

and since $V$ is Lipschitz continuous, $\theta^n_{i+1/2}\le L_v$. Hence if the CFL-condition

holds, then $y^{n+1}_j$ is a convex combination of $y^n_j$ and $y^n_{j+1}$. Thus the scheme (2.17) is monotone. In passing, we note that a consequence is that if $1\le y^0_j\le K$ for all $i$, then $1\le y^n_j\le K$ for all $i$. Regarding the position of vehicles, this means that if $z_{j}(0)\le z_{j+1}(0)-\ell$, then $z_{j}(t^n)\le z_{j+1}(t^n)-\ell$. So from a road safety perspective, the model is rather optimistic.

We are now interested in taking the limit as $\ell\to 0$. We do this by increasing the number of vehicles such that $(N-1)\ell = 1$; furthermore we assume that (2.11) holds. Now the conditions are such that fundamental results of Crandall and Majda [4], see also [11,Thm. 3.9], can be applied. Thus we know that there is a function $y\colon\mathbb{R}_0^+\times [0, 1] \to \mathbb{R}$, with $y\in C(\mathbb{R}^+;L^1([0, 1]))$, such that

with the limit being in $C(\mathbb{R}^+;L^1([0, 1]))$, and that $y$ is the unique entropy solution to the Cauchy problem

If we do not have periodic conditions, this is supplemented with the boundary condition

We remark that since the characteristic speeds of (2.20) are strictly negative, this boundary condition can be enforced strictly.

Note that the convergence of $y_\ell$ and the bounds $1\le y_\ell \le M$, imply the convergence of $\tilde\rho_\ell = 1/y_\ell$ to some function $\tilde\rho$. We now proceed to show how $\tilde\rho$ is related to the solution of the LWR model.

We also define the discrete "Lagrange to Euler" map $\tilde{z}_\ell$ as follows. Let

Since $z^n_j$ solves (2.16), we also have that

Define $\tilde{z}_\ell(t^n, x_{i+1/2}) = \tilde{z}^n_{j+1/2}$, and by bilinear interpolation between these points. For later use we employ the notation for the value of $\tilde{z}_\ell$ at the edges of the "Lagrangian grid",

Observe that $\tilde{z}_{j-1/2}(t)$ coincides with the approximate trajectory of the vehicle starting at $z_j(0)$ calculated by the Euler method (2.16). Since $y_\ell$ is bounded, we can invoke the Arzel{á}-Ascoli theorem to establish the convergence

with the limit being in $C([0, T]\times[0, 1])$ and $z\in\ C([0, T]\times[0, 1])$, and that

weakly. We have that the map $x \mapsto \tilde{z}_\ell(t, x)$ is invertible for each $t$, we denote the inverse map by $x_\ell$, so that $x_\ell(t, z_\ell(t, x)) = x$. Define $z_{l, \ell}$ and $z_r$ as in (2.13) and $\rho_\ell$ as in (2.14).

Note that if $z\in (z_{j-1/2}(t), z_{j+1/2}(t)]$ and $t\in [t^n, t^{n+1})$, then

As before we have that

in $L^1([z_l, z_r])$ as $\ell\to 0$.

By Wagner's result [16], we have proved the following theorem.

Theorem 2.6.   Assume that the function $v$ satisfies (2.3). Let $\ell>0$ and $N\in\mathbb{N}$, let $\{ z_j \}_{j = 1}^N$ satisfy (2.16), and assume that either we are in the periodic case $z_j\in [0, 1]$, or that $z_N$ satisfies the boundary condition (2.2), with $y_N = M$. Assume that the initial positions of the vehicles $\{ z_i(0) \}_{i = 1}^{N}$ are such the we can define a bounded function $y_0$ by (2.11), and that (2.6) holds.

Define the function $\rho_\ell(t, z)$ by (2.14).Let $N$ and $\ell$ satisfy $(N-1)\ell = 1$ and assume that the CFL-condition (2.19) holds.

As $\ell\to 0$, $\rho_\ell$ converges in $C([0, \infty);L^1)$ to the unique entropy solution $\rho$ of the conservation law (2.12).

To illustrate the ideas in this paper we show how the method works in a concrete example. We have a periodic road in the interval $z\in [-1, 1]$, and choose to position $N$ vehicles in this interval so that

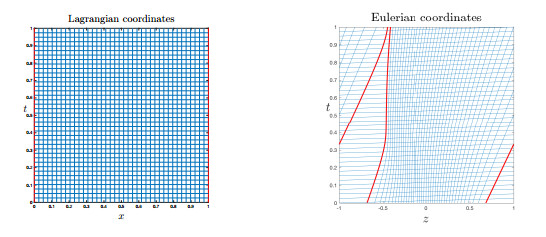
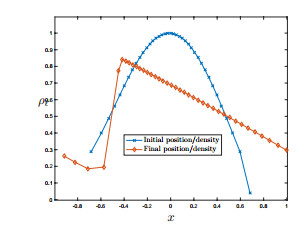
In Figure 1 we show the Lagrangian grid and the corresponding mapping to Eulerian coordinates for $N = 40$, and $t\in [0, 1]$. The "vertical" lines in the Eulerian coordinates are also the paths followed by the vehicles, and the grid in Eulerian coordinates is the result of applying the map $z_\ell$ to the rectangular grid depicted in Lagrangian coordinates on the left. In Figure 2, we show the approximate density $\rho_\ell$ at $t = 0$ and $t = 1$ in Eulerian coordinates. We see that the solution at $t = 2$ approximates the ubiquitous "$N$-wave".

3.   Conclusion

We have shown how to view the standard Follow-the-Leader (FtL) model as a numerical approximation of the Lighthill-Whitham-Richards (LWR) model for traffic flow in the case of dense traffic. Standard numerical techniques of hyperbolic conservation laws then apply. We show convergence (as the number of vehicles increases, while the length of individual vehicles decreases) in the semi-discrete case in Theorem 2.5, and in the fully discrete case in Theorem 2.6. An important step in our analysis is the equivalence [16] of weak entropy solutions in the Lagrangian and Eulerian formulation. We analyze a discrete Lagrange-to-Euler map, and illustrate the result in a numerical example, see Figures 1 and 2. The analysis here contrasts the one in [12] where a grid-less approach is introduced and the convergence is proved directly in the Kružkov entropy formulation.