1.
Introduction
In this paper we obtain convergence rates for the homogenization of the Poisson problem in a bounded domain of Rd, d⩾3, that is perforated by many small random holes Hε. We impose Dirichlet boundary conditions on the boundary of the set and of the holes Hε. In other words, given f∈H−1(D) and D⊆Rd bounded and regular, we define the perforated set Dε:=D∖Hε and study the boundary value problem
We assume that, for ε>0, the holes Hε are a union of spherical holes having random centres and radii. Let (Φ,R) be marked point process where Φ is either the lattice Zd or a Poisson point process of intensity λ>0. We assume that the associated marks R={ρz}z∈Φ are independent and identically distributed random variables that satisfy the moment condition
Here and below, Eρ[⋅] denotes the expectation under ρ. The set Hε is thus defined by
As shown in [13], if β=0 in (1.2), then for P-almost every realization of the random set Hε, the solutions to (1.1) converge weakly in H10(D) to the homogenized problem
The constant C0>0 is the limit of the density of harmonic capacity generated by the set Hε: If Sd denotes the d-dimensional unit sphere and Hd is the d-dimensional Hausdorff measure, then
In this paper, we strengthen the condition (1.2) on the integrability of the marks R from β=0 to β>0 and study the convergence rates of uε to the homogenized solution u.
By the Strong Law of Large Numbers, assumption (1.2) with β=0 is minimal in order to ensure that for P-almost every realization of Hε, its density of capacity admits a finite limit. However, it does not prevent the balls in Hε from having radii that are much bigger than εdd−2. This gives rise to clustering phenomena with overwhelming probability. In particular the expected number of balls of Hε that intersect, namely such that their radius εdd−2ρz is bigger than the typical distance ε between the centres, is of order ε−d+2 (over an expected total of ε−d balls). The analogue holds also under assumption (1.2) for values β<(d−2)22, with the expected number of overlapping balls being of order ε−d+2+2d−2β.
The presence of balls that overlap is the main challenge in the proof of the qualitative homogenization statement obtained in [13] and is one of the challenges of the current paper. It requires a careful treatment of the set Hε to ensure that the presence of long chains of overlapping balls does not destroy the homogenization process. For a more detailed discussion on this issue we refer to the introductory section in [13] and to Subsection 2.2 of the present paper.
The main results contained in this paper provide an annealed (i.e. averaged in probability) estimate for the H1-norm of the homogenization error uε−Wεu. The function Wε is a suitable corrector function that is related to the so-called oscillating test function [6,23]. We assume that Φ is the lattice Zd or that it is a Poisson point process in dimension d=3. For a comment on the case d>3, we refer to Remark 2.2. If E[⋅] denotes the expectation under the probability measure associated to the process (Φ,R), we show that1
1 In the case of Φ being a Poisson point process, there is a factor logε on the right-hand side. We refer to Theorem 2.1 for the precise statement.
We stress that in the case of periodic holes, namely when Φ=Zd and the radii ρz=r, r>0 are constant and deterministic, the optimal rate on the right-hand side of (1.6) is ε [18]. In the current setting, the unboundedness and randomness of the radii seems to yield slower convergence rates. We refer to Subsection 2.2 for a discussion on the exponents obtained in (1.6) and how they relate to the techniques used in the present paper to treat the case of unbounded and random radii.
The main quantity that governs the decay of the homogenization error uε−Wεu is the convergence of the capacity density of Hε to the constant term C0 that appears in the homogenized equation (1.4). In the periodic case mentioned in the previous paragraph, the term C0=cdrd−2 (c.f. (1.5)) is close to the density of capacity of Hε already at scale ε. Heuristically, indeed, if A⊆D we have
and this chain of identities is true as long as |A| is at least of order ε. On the other hand, in the random setting, this identity is expected to hold at scales that are larger than ε due to the fluctuations of the process (Φ,R). We also remark that the threshold d−2 in the parameter β obtained in (1.6) is related to the L2-nature of the norm considered for the homogenization error. Roughly speaking, the norm considered in (1.6) requires a control on the expectation of the square of the capacity generated by the balls in Hε. This quantity depends on the 2(d−2)-moments of the random variable ρ.
Starting with [6] and [21], there is a large amount of literature devoted to the homogenization of (1.1), both for deterministic and random holes Hε [3,20]; similar problems have also been studied in the case of the fractional laplacian (−Δ)s, [2] or for nonlinear elliptic operators [4,24]. All the models considered in the deterministic case contain assumptions that ensure that, for ε small enough, the holes in Hε do not to overlap. In the random models mentioned above, a non-overlapping condition is as well imposed, at least for P-almost every realization and ε>0 small enough. For a complete and more detailed description of these works, we refer to the introduction of [13].
For what concerns quantitative rates of convergence for (1.1) to (1.4), the first result in the periodic case is contained in [18]. When the holes are randomly distributed, the first quantitative result has been obtained in [9]. In this paper, the authors study the analogue of (1.1) for the operator −Δ+λ in an unbounded domain of R3, that is perforated by m spherical holes of identical radius ∼m−1. The centres of the holes are independent and distributed according to a compactly supported and continuous potential V. If um denotes the analogue of uε, when the massive term λ is big enough compared to the size of V, the authors provide rates of convergence for the L2-norm of the difference um−u in the limit m→+∞. Furthermore, they prove the Gaussianity of the fluctuations of um around the homogenized solution u in the CLT-scaling. In [16], this result has been obtained in the same setting of [9] without any constraint on the massive term λ>0.
The quantitative estimates developed in this paper are also used in [10] to obtain homogenization results for solutions to (1.1) and the analogous Stokes system in the regimes leading to Darcy's law. In [10], the radii in (1.3) are rescaled by a factor εα, 1<α<dd−2 and the random variables {ρz}z∈Φ satisfy a suitable moment condition. Like (1.2), also this condition does not prevent the holes from overlapping and give rise to clusters.
We conclude this introduction mentioning that the analogue of (1.1) for a Stokes (and Navier-Stokes) system with no-slip boundary conditions on the holes Hε has been considered in [1,22] in the periodic case and then extended to more general configurations of holes (see, e.g., [5,8,15]). In the case of the Stokes operator, the limit equation contains an additional zero-th order term similar to C0 in (1.4). Under the same assumptions of this paper, the analogue of the homogenization result contained in [13] has been proven for a Stokes system in [11,12]. We believe that techniques similar to the one of this paper may be used to prove the same result of (1.6) also in the case of a Stokes system. However, in this case, we expect that the role played by the pressure would yield a less explicit definition of the corrector function Wε.
2.
Setting and main result
Let d⩾3 and D⊆Rd be a bounded and smooth domain that is star-shaped with respect to the origin. For ε>0, we define the punctured set Dε=D∖Hε, with Hε as in (1.3). We assume that the union of balls Hε is generated by a marked point process (Φ,R) on Rd×R+: We generate the centres of the balls in Hε via a point process Φ. To each point z∈Φ, we associate a mark ρz⩾0 that determines the radius of the ball. We refer to [7,Chapter 9,Definitions 9.1.I-9.1.IV] for an extensive and rigorous definition of marked point processes and their associated measures on Rd×R+.
We denote by (Ω;F,P) the probability space associated to (Φ,R), so that the random sets in (1.3) and the random field solving (1.1) may be written as Hε=Hε(ω), Dε=Dε(ω) and uε(ω;⋅), respectively. The set of realizations Ω may be seen as the set of atomic measures ∑n∈Nδ(zn,ρn) in Rd×R+ or, equivalently, as the set of (unordered) collections {(zn,ρn)}n∈N⊆Rd×R+.
Throughout this paper we assume that (Φ,R) satisfies the following conditions:
(i) Φ is either the lattice Zd or Φ=Poi(λ), i.e. a Poisson point process of intensity λ>0;
(ii) The marks {ρz}z∈Φ are independent and identically distributed: The marginal of the marks with respect to the process Φ, has n-correlation function, n∈N, that may be written as the product
(iii) The marks R have finite (d−2+β)-moment, namely the density function g in (ii) satisfies
We stress that conditions (i)-(ii) yield that (Φ,R) is stationary. In the case Φ=Poi(λ), the process (Φ,R) is stationary with respect to the action of the group of translations {τx}x∈Rd. This means that the probability measure P is invariant under the action of the transformation τx:Ω→Ω, ω={(zi;ρzi)}i∈N↦τxω:={(zi+x;ρzi)}i∈N. In the case Φ=Zd the same holds under the action of the group {τz}z∈Zd.
Notation. When no ambiguity occurs, we skip the argument ω∈Ω in the notation for Hε(ω),Dε(ω), uε(ω;⋅) and in all the other random objects. We denote by E[⋅] and EΦ[⋅] the expectations under the total probability measure P and the probability measure PΦ associated to the point process Φ, respectively. For ε>0 and a set A⊆Rd, we define
and the random variables
For any μ∈H−1(D), we write ⟨⋅;⋅⟩ for the duality product with H10(D); we use the notation 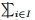 for the averaged sum #(I)−1∑i∈I and ≲ and ≳ instead of ⩽C and ⩾C with the constant C depending on the dimension d, the domain D and, in the case of Φ=Poi(λ), the intensity rate λ.
for the averaged sum #(I)−1∑i∈I and ≲ and ≳ instead of ⩽C and ⩾C with the constant C depending on the dimension d, the domain D and, in the case of Φ=Poi(λ), the intensity rate λ.
For two sets A⊆B⊆Rd, we denote by Cap(A;B) the relative harmonic capacity of the set A in B (c.f., for instance, [13][(4.17)]).
2.1. Main result
Before stating the main results, we need to define a suitable corrector function Wε that appears in the homogenization error uε−Wεu. For x∈Rd we set
Note that, if Φ=Zd, then Rε,x=ε4 for every x∈Φ. For δ>0, we denote by Φεδ(D)⊆Φε(D) the set
where here and through out the paper a∨b=max{a;b}.
For each z∈Φεδ(D), let wε,z∈H1(Bε4(εz)) be the solution to
We thus define
We stress that (2.5) ensures that definitions (2.6) and (2.7) are well-posed since the set {BRε,z(εz)}z∈Φεδ(D) is made of disjoint balls and, for every z∈Φεδ(D), it holds Bεdd−2ρz(εz)⊆BRε,z(εz). Note that in the above definition the function Wε∈H1(D) depends on the choice of the parameter δ used to select the subset Φεδ(D). The optimal parameter δ will be fixed in Theorem 2.1. We finally stress that, in the periodic case Φ=Zd and ρz≡r, for any δ>0 and ε small enough, the function Wε coincides with the oscillating test function constructed in [6,18].
Theorem 2.1. Let (Φ,R) satisfy conditions (i)-(iii). For ε>0 and p>d, let f∈W1,p(D) with ‖f‖W1,p(D)=1 and uε and u be as in (1.1) and (1.4), respectively. We consider the random field Wε in (2.7) with
(a) If Φ=Zd, there exists a constant C=C(d,D,p)>0 such that
(b) If Φ=Poi(λ) with λ>0 and d=3, there exists a constant C=C(λ,D,p)>0 such that
Remark 2.2. As shown throughout Section 4, the argument of Theorem 2.1 (b) applies also to higher dimensions d⩾4. In this case, the homogenization error decays as εα, for an exponent α=α(d,β). The exponent α, however, is generally smaller than the one in the periodic case and it is the same only for β small enough (β⩽2d−1(d−2)).
We expect that the techniques used to prove Theorem 2.1 do extend to other examples of stationary random distributions of centres. For instance, to point processes that satisfy a finite-range of dependence assumption and for which the expected number of elements in a finite set A scales like its (Lebesgue-)measure. We also believe that Theorem 2.1 may be adapted to sets of holes Hm, m∈N that are a collection of m balls having centres that are independently distributed according to a fixed density Ψ∈C∞c(D). In this case, the balls have random radii rescaled by m−1d−2 and the homogenization limit is obtained for m→∞. For this choice of holes, the deterministic control on the cardinality of the set of centres simplifies some of the estimates.
Remark 2.3. As it becomes apparent in the proof of Theorem 2.1, the choice of Wε is not unique. The same result holds, for instance, if Wε is replaced with the oscillating test function wε constructed in [13,Section 3] and in Subsection 3.2 of the present paper. The function Wε, however, has a simpler and more explicit construction that may be implemented numerically with more efficiency. It is, indeed, an oscillating test function basically restricted to the balls of Hε that do not overlap and have radius smaller than ε1+δ. We emphasize that the condition on the minimal distance being at least ε2 is purely technical and may be avoided by either assuming that the radii {ρz}z∈Φ are (uniformly) bounded from below, or that their inverse ρ−1z satisfies a suitable moment condition.
2.2. Ideas of the proofs
The proof of Theorem 2.1 is inspired to the proof of the same result in the case of periodic holes shown in [18]. The latter, in turn, upgrades the result of [6] from the qualitative statement uε⇀u in H10(D) to an estimate on the convergence of the homogenization error. Both arguments rely on the construction of suitable oscillating test functions {wε}ε>0⊆H1(D). In the qualitative statement of [6], these functions allow to pass to the limit ε↓0 in the weak formulation of (1.1) and infer the homogenized equation (1.4).
The functions {wε}ε>0 may be constructed as Wε in (2.7), where the set Φεδ coincides with the whole set Φ=Zd and the functions {wε,z}z∈Φε(D) introduced in (2.6) satisfy wε,z(⋅)=wε,0(⋅+z). The additional term C0=cdrd−2 that appears in the homogenized equation (1.4) is the limit of the measures −Δwε when tested against the function ρuε∈H10(Dε), ρ∈C∞0(D). It is not hard to see from (2.7) that, for functions that vanish on the holes Hε, the action of −Δwε reduces the periodic measure
that is concentrated on the spheres {∂Bε4(εz)}z∈Zd. Here, ∂n is the outer normal derivative on ∂Bε4(εz).
In [18], the corrector Wε is chosen as the oscillating test function wε itself. As a first step, it is shown that the decay of ‖uε−Wεu‖H10(D) boils down to controlling the convergence of the density of capacity of Hε to its limit C0 (c.f. (1.5)). The latter is expressed in terms of the decay of the norm ‖με−C0‖H−1(D), with με as in (2.8). As a second step, the authors appeal to a result of [19] to estimate the decay of ∥με−C0D∥H−1(D) in terms of the size ε of the periodic cell Cε:=[−ε2;ε2] of με. The crucial feature is that, up to a correction of order ε2, the measure με−C0 has zero average in Cε. In other words, we have
In this paper we adapt to the random setting the previous two-step argument. The first main difference is strictly related to the randomness of the radii in Hε and needs to be addressed also in the case of bounded radii (i.e. if β=+∞ in (2.1)) and periodic centres. In this case, the measure με is defined as in (2.8) but, on each sphere ∂Bε4(εz), the term ∂nwε depends on the random mark ρz. Therefore, contrarily to the periodic case, (2.9) may not hold in each cube εz+Cε. Nevertheless, by the Law of Large Numbers, we may expect that the average of με−C0 is close to zero over cubes of size kε, k>>1, as the left-hand side in (2.9) turns into an averaged sum of kd random variables. This motivates the introduction of a partition of the set D into cubes of mesoscopic size kε (c.f. Section 3.1) that plays the role of the cells εz+Cε of the periodic case. This allows us to adapt the result by [19] and obtain
Here, the last term accounts for the difference between the average of με in each cube of size (kε), k∈N and the value C0. This inequality, implies an estimate of the form:
The optimal choice of k yields the exponent dd+2 of Theorem 2.1. If ρz≡r for all z∈Zd, then the second term vanishes and the above estimate with k=1 gives the optimal rate of [18].
In the case of centres distributed according to a Poisson point process, the argument for Theorem 2.1 follows the same ideas sketched above. Although the centres of the holes in Hε have random positions, their typical distance is still of size ε. This feature gives rise to the additional logarithmic factor in the rate of Theorem 2.1. The main technical challenge is related to the construction of the mesoscopic partition of D that allows to obtain the analogue of (2.10). In contrast with the case Φ=Zd, indeed, there are (P-many) realizations of Hε where the support of the measure με defined in (2.8) intersects the boundary of the covering. In other words, the spheres {∂Bε4(εz)}z∈Φεδ(D) might fall across two cubes of size εk that cover D. This, in particular, implies that to the covering does not correspond to a well-defined partition of the spheres where the measure με is supported. We tackle this issue by constructing a suitable random covering. We refer to Subsection 3.1 for the precise construction.
A second challenge that arises in the proof of Theorem 2.1 is related to the presence of overlapping holes in the case β<+∞ in (2.1). The strategy to deal with this issue is very similar to the one used in [13]: We partition, indeed, the set of holes as Hε=Hεb∪Hεg, where the subset Hεb contains all the holes that overlap (c.f. Lemma 3.1). As shown in [13], the contribution of Hεb to the density of capacity is negligible in the limit ε↓0. As a consequence, we may modify the estimates of [18], to prove that ∥uε−Wεu∥H10(D) is controlled by the norm ‖με−C01D‖H−1(D), where the measure με is now only related to the union of disjoint balls Hεg.
3.
Proof of Theorem 2.1, (a)
3.1. Partition of the holes Hε and mesoscopic covering of D
This subsection contains some technical tools that will be crucial to prove the main result: The first one is an adaptation of [13] and provides a suitable way of dividing the holes Hε between the ones that may overlap due to the unboundedness of the marks {ρz}z∈Φ and the ones that, instead, are disjoint and have radii εdd−2ρz much smaller than the distance ε between the centres.
Lemma 3.1. Let δ∈(0,2d−2] be fixed. There exists an ε0=ε0(δ,d) such that for every ε⩽ε0 and ω∈Ω we may find a partition of the realization of the holes
with the following properties:
● There exists a subset of centres nε(D)⊆Φε(D) such that
● There exists a set Dεb⊆{x∈R3:dist(x,D)⩽2} satisfying
and
Proof of Lemma 3.1. The construction for the sets Hεg,Hεb and Dεb is the one implemented in the proof of [13,Lemma 2.2]. We fix δ∈(0,2d−2] throughout the proof.
We denote by Ibε⊆Φε(D) the set that generates the holes Hεb. We construct it in the following way: We first set Jεb:=Φε(D)∖Φεδ(D) with Φεδ as in (2.5). Since Φ=Zd, this turns into
Given the holes ˜Hεb:=⋃z∈JεbB2(εdd−2ρz∧1)(εz), we include in Iεb also the set of points in Φε(D)∖Jεb that are "too close'' to the set ˜Hεb, i.e.
We define
It remains to show that the sets defined above satisfy properties (3.1)-(3.3). Property (3.1) is an immediate consequence of definition (3.4). The first inclusion in (3.2) follows by the definition of Hεb and Dεb in (3.6); for the inequality in (3.2) we instead appeal to the subadditivity of the capacity to bound
Moreover, by the monotonicity property Cap(A;C)⩽Cap(A;B) for every A⊆B⊆C, this turns into
i.e. the estimate in (3.2).
To conclude the proof of this lemma, it remains to argue (3.3): By construction (see (3.6)), it holds that
On the one hand, by (3.5) and the definition of nε(D) in (3.6), for each z∈nε(D) we have that
On the other hand, by (3.4) and (3.5), if w∈˜Iεb, then 4εdd−2ρw⩽ε1+δ so that
whenever ε is such that εδ<14. Hence, also
Combining this with (3.8) and (3.7), we infer (3.3). The proof of Lemma 3.1 is complete.
We now construct a suitable covering of D that, as explained in Subsection 2.2, plays a fundamental role in the proof of Theorem 2.1. We recall that, by our assumption, the set D is any smooth domain that is star-shaped with respect to the origin.
For z∈Rd, we define the "microscopic cubes''
while for k∈N and any z∈Zd we set
Let Nk⊆Zd be such that the collection {Qk,z}z∈Nk is an essentially disjoint covering of D. Since D is bounded, we may assume that
Let
Since is smooth and has compact boundary, it is easy to see that there exist such that, whenever it holds
Finally, for each we denote by the set of points of that, when rescaled, are contained into the cube , i.e. such that
Note that, since in this section we assumed that , it follows that for every , we have where are defined as in (3.9). Morevoer, for every , the collection provides a refinement of .
3.2. Quenched estimates for the homogenization error
All the results contained in this subsection are quenched, in the sense that they hold for any fixed realization of the holes . The main result of this section is Lemma 3.2 that allows to control the norm of the homogenization error in terms of suitable averaged sums of the random marks .
Before giving the statement of Lemma 3.2, we recall the construction of the oscillating test function implemented in [13]. As mentioned in the introduction and in Subsection 2.2, the main feature of this function is to vanish on the holes and "approximate'' the density of the capacity of . We note that the unboundedness of the marks implies that the set and that the function in (2.7) does not vanish in all the holes contained in .
Let and be as in Lemma 3.1. For every , let2
2 We assume that the minimizer exists. If this is not the case, it suffices to take in the minimizing class such that .
We pick as oscillating test function
where and are defined as follows:
and
For each , the function is as in (2.6). We remark that each admits the explicit formulation
For , let be the covering of constructed at the end of Subsection 3.1. For every , we define the random variables
Lemma 3.2. Let be fixed. Then for every and with the following inequality holds: If are as in Theorem 2.1 and as in , then
Lemma 3.2 relies on the next lemma, that is an adaptation of [18][Theorem 3.2] and shows that controlling the error considered in Theorem 2.1 boils down to controlling the convergence to of the density of capacity generated by .
Lemma 3.3. Let be fixed; let and be as in Lemma 3.2. Let be as in . Then
with
Proof of Lemma 3.2. The statement follows from Lemma 3.3, provided that we show that
and that for every and such that
We first argue (3.21): By definition (3.16) for and Lemma 3.1, we have that
Since by Lemma 3.1 the sets and are disjoint, we appeal to (3.15) to estimate
The function vanishes on : Since the balls are all disjoint, Poincaré's inequality in each ball yields
Using definitions (3.17), (2.6) and property (3.1) of Lemma 3.1, we may rewrite
and, inserting this into (3.24), also
To conclude the proof of (3.21) for , it thus remains to estimate the last term on the right-hand side. By construction (c.f. (3.16)), it holds on ; appealing to Lemma 3.1, we also have that . We thus apply Poincaré's inequality in this set and conclude that
To establish (3.21) for , it only remains to combine this last inequality with (3.25).
We now argue (3.21) for : By definition (2.5) and (3.1) of Lemma 3.1, it holds
Thanks to definition (3.15) for and the fact that, by Lemma 3.1 the support of and is disjoint, we use the triangle inequality to infer that
Comparing definition (3.17) for with definition (2.7) for and using inclusion (3.26), we observe that
Since the balls are disjoint, the previous identity and the triangle inequality imply that
Inserting this bound into (3.27) yields (3.21) also for the norm of .
We now turn to (3.22) and claim that we may apply Lemma 5.1 with , , and for every . We use as covering the sets . Conditions (5.1) and (5.3) are satisfied thanks to (2.5) and by construction (see Subsection 3.1), respectively. Appealing to Lemma 5.1, we therefore have that
By the triangle inequality and the previous estimate, we thus bound
so that, to prove (3.22), it only remains to control the last term on the right-hand side above. We do this by observing that, since is a disjoint covering of , for each we have
By the triangle inequality, also
We claim that
This is an easy consequence of the properties of the covering of , (3.11), together with Cauchy-Schwarz's inequality and Poincaré's inequality for in .
We now turn to the second term in (3.29). We note that, by definition (3.12), the set
Since and is a smooth and bounded set, we may appeal to Poincaré's inequality in the previous set on the right-hand side to bound
Appealing once again to Cauchy-Schwarz's inequality and using the above estimate, we control
Hence, provided , we may appeal to (3.13) and infer that
Combining this with (3.30) and (3.29) allows us to infer that for every
or, equivalently, that
This, together with (3.28), establishes (3.22). The proof of Lemma 3.2 is complete.
Proof of Lemma 3.3. The argument for this lemma is very similar to the one of [18,Theorem 3.1]. Since , and since is smooth, by standard elliptic regularity we infer that the solution of (1.4) satisfies . By computing the (distributional) Laplacian of we obtain that in
We now smuggle the term in the right-hand side so that the previous identity turns into
We stress that, since , , , the above equation holds in the sense that for every
Since the balls are all mutually disjoint, by definition (2.7) and equations (2.6) we have that
Since and therefore it vanishes on the spheres , the above identity implies that
Inserting this last identity in (3.32), we infer that
We now choose and apply Hölder's and Poincaré's inequalities to bound
To obtain the claim of Lemma 3.3 it remains to use that, by the triangle inequality and Hölder's inequality, we have
and that, by definitions (2.7) and (3.15), the difference is compactly supported in (see also Lemma 3.1).
3.3. Annealed estimates (Proof of Theorem 2.1, )
In this subsection we rely on the quenched estimate of Lemma 3.2 to prove the statement of Theorem 2.1 in the case of periodic centres. The first ingredient is the following annealed bound:
Lemma 3.4. Let satisfy the assumptions of Theorem 2.1, . For every , let be the random subset constructed in Lemma 3.1. Then
Proof of Theorem 2.1, . By the assumptions on , we may assume that for and such that , the cube . We restrict to the values of satisfying the previous bound.
Combining Lemma 3.2 and Lemma 3.4, we bound for every and as above
Since the sets are deterministic and are identically distributed, we infer that
We observe that, by (2.5), (2.1) and the inequality (c.f. (2.3)), we have that
Since , the previous two displays thus imply
We now claim that for every such that with as in (3.13), then
where is defined as in (3.19). We begin by showing how to conclude the proof of the theorem provided (3.34) holds.
Let us first assume that (2.1) holds with ; in this case, we have that
and therefore that
Estimate of Theorem 2.1 for follows from this inequality if we minimize the right-hand side above in , i.e. if we choose , and set as in Theorem 2.1.
Let us now assume that in (2.1): In this case, we bound
so that (3.34) turns into
Also in this case, we infer the estimate of Theorem 2.1 by minimizing the right-hand side in and , i.e. choosing and as in Theorem 2.1.
To complete the proof of the theorem it only remains to argue (3.34) from (3.33). We first tackle the second term on the right-hand side of (3.33) and show that
This may be done after noticing that the left-hand side may be written, up to an error, as the sum of centred and independent random variables: Definitions (2.5) and (3.14) for and imply that
Since , this, (3.19) and the triangle inequality allows us to bound
Thanks to Chebyshev's inequality and assumption (2.1) we have
and thus we may rewrite (3.37) as
Since
the independence of the random variables , and the fact that (c.f. (2.3)), allows us to obtain (3.35), by means of standard CLT arguments.
We now turn to the remaining term in (3.33) and argue that
By the triangle inequality and assumption (2.1), the left-hand side is bounded by
To establish (3.39) from this it suffices to remark that, by (3.19) and (3.36), we have
so that this, and the fact that the random variables are identically distributed, yields
Inserting this into (3.40) implies (3.39). To establish (3.34) it remains to combine (3.39), (3.35) and (3.33). The proof of Theorem 2.1, is complete.
Proof of Lemma 3.4. We resort to the construction of the set implemented in Lemma 3.1: By (3.6), (3.4) and (3.5) in the proof of Lemma 3.1 we decompose
and prove the statement of Lemma 3.4 for each one of the two sums. We begin with the first one: Using (3.4) we write
Taking the expectation and using that are identically distributed and that , we immediately bound
i.e. the claim of Lemma 3.4 for the first sum in (3.41).
We now turn to the second sum in (3.41): By definition (3.5), if , then and there exists an element such that . This allows us to bound
We now take the expectation and use that and that are independent and identically distributed: This implies that
Since for every , the set
we obtain that
This, together with identities (3.41) and (3.42), establishes Lemma 3.4.
4.
Proof of Theorem 2.1,
In this section we adapt the argument of the previous section to Theorem 2.1 in case . As mentioned in Subsection 2.2, the main challenge is related to the construction of a mesoscopic covering that plays the same role of of Subsection 3.1. In the present case, the random positions of the centres imply that (with positive probability) there are configurations in which some of the spheres intersect the boundary of . This prevents us from appealing to Lemma 5.1 as condition (5.3) is violated.
All the results contained in this section besides hold for any dimension . However, in the proof of Theorem 2.1, we obtain the same decay rate of case only in . In higher dimensions we obtain a slower (but still algebraic) rate. In order to best appreciate this dimensional constraint, in the whole section we work in a general dimension .
Throughout this section we set as in Theorem 2.1 and define the parameters
4.1. Partition of the holes and mesoscopic covering of
This subsection contains an adaptation to the case of random centres of Lemma 3.1 and of the sets .
Lemma 4.1. Let be as in Theorem 2.1. We recall the definition of . For , we consider a realization of the marked point process and of the associated set of holes . Then, there exists a partition
with the following properties:
● There exists a subset of centres such that
and such that , for every .
● There exists a set satisfying
and for which , for every .
Proof of Lemma 4.1. The construction for the sets and is analogous to the one implemented in the proof of Lemma 3.1, with the only difference that in this case, we set
and in the definition (3.5) of the ball is replaced by .
For as in (4.1), let be as in Subsection 3.1. For every we define the sets as in (3.14). We stress that, in this case, (3.14) is ill-defined for the realizations of such that there are points in that fall on the boundary of the cubes . This issue may be easily solved by fixing a deterministic rule to assign these points to a particular cube that shares the boundary considered. We stress that all the arguments of this section do not depend on this rule since the set of the boundaries of the covering has zero (Lebesgue)-measure.
For and , we define the modification of the minimal distance :
We aim at obtaining a (random) collection of disjoint sets having size and such that for every and
We modify as follows: For as in (4.1), any and , we consider the cubes
Note that, by definition (2.4), all the cubes above are disjoint. For every , we thus set (see Figure (1))
Since the cubes are disjoint we have that
We emphasize that the previous properties hold for every realization of the point process . The introduction of the modified random variable is needed to ensure that the second property in (4.4) holds with instead of . This yields that the difference between the volume of the set and the cube is of order instead of . This condition plays a crucial role in the proof of the theorem (see (4.14)) and is the main term that forces the dimensional constraint in the rates of convergence.
4.2. Quenched estimates for the homogenization error
In this section we adapt Lemma 3.2 to the current setting. As in the case of Lemma 3.2, the next result relies on a variation of Lemma 3.3 that allows us to replace in the definition (3.20) of the radii with defined in (4.2).
We define the oscillating test function as done in Subsection 3.2, this time using the sets and of Lemma 4.1 with as in Theorem 2.1, and instead of in (3.17). We also define the analogues of (3.19), this time associated to the covering constructed in the previous subsection: For every we indeed set
Lemma 4.2. Let be as in and let as in Theorem 2.1. Then, for every and such that we have that
Lemma 4.3. Let and be as in Lemma 3.2 and let be as defined above. Then
where is defined as in with substituted by . Furthermore, in this case
with as in with instead of .
Proof of Lemma 4.2. Analogously to the proof of Lemma 3.2, we appeal to Lemma 4.3 and reduce to showing that
and
Inequality (4.6) may be argued exactly as done for (3.21) in the proof of Lemma 3.2, this time appealing to Lemma 4.1 instead of Lemma 3.1.
We thus turn to (4.7). We begin by remarking that is well-defined: Indeed, by definition (2.4) and (4.5), we have that for every . Furthermore, since (c.f. (4.1) and Theorem 2.1), it follows from (2.5) that , for every . Therefore, comparing the two definitions of and , we use (4.2) to bound:
Since, if , then , we have that
Appealing to (2.7), (2.6) and the adaptation of (3.18) for both and , the previous integrals may be bounded by
Since , we have that so that
Inserting this into (4.9) and appealing to (4.1) for yields (4.7).
We finally tackle (4.8): As done for (3.22) of Lemma 3.2, we aim at applying Lemma 5.1. We thus pick and . As shown above before the argument for (4.7), condition (5.1) is satisfied. Moreover, thanks to (4.3), the collection satisfies (5.3). Hence, by Lemma 5.1, we have that
where, thanks to (4.5), we have that . By the triangle inequality it thus only remains to control the norm . Using (4.4), this may be done exactly as in the proof of Lemma 3.2. The proof of Lemma 4.2 is complete.
Proof of Lemma 4.3. This lemma may be argued as done for Lemma 3.3. The only difference is that, in (3.31), we smuggle in instead of and apply the triangle inequality to bound .
4.3. Annealed estimates (Proof of Theorem 2.1, )
As in case , the next lemma provides annealed bounds for some of the quantities appearing in the right-hand side of Lemma 4.2.
Lemma 4.4. Let the (random) subset constructed in Lemma 4.1. Then
Proof of Theorem 2.1, . We recall that satisfies (4.1). Combining Lemma 4.2 and Lemma 4.4, we bound
As done in the proof of Theorem 2.1 (a), this also turns into
We now claim that, thanks to (4.1), the previous estimate reduces to
If the previous estimate holds, by the choice of and (4.1), we infer that
which establishes Theorem 2.1, if .
To conclude the proof, we only need to obtain (4.11) from (4.10). The sum over may be treated as in (3.39). We thus obtain inequality (4.11) provided that
and
We argue (4.13): Recalling the definition of the covering , we decompose
and rewrite
Since the process is stationary, we bound
Let us partition the cube into cubes of size and let be as in (3.10); the definitions of and (c.f. (2.5), (4.5)) and the stationarity of imply that
We now apply Lemma 5.2 with to infer that
We rewrite
We claim that
This inequality, indeed, is obtained by decomposing the indicator function above into
and using that, by definition (2.4), it holds
where is the ball of radius centred at the origin. Hence,
Inserting this into (4.17) we obtain that for
Thus, inequality (4.15) turns into
This yields (4.13) provided that
Let be the cube of size centred at the origin. Using (2.5) we bound
Since we may decompose the set into unitary cubes, we use again the stationarity of and infer that
where is any unitary cube that is contained in 3. We now decompose with
3 In this last step one should distinguish between unitary cubes according to the number of faces that they share with . However, the argument shown below is immediately adapted to any of the previous cubes.
and use (4.2) to rewrite
We now appeal again to Lemma 5.2 as for (4.16) to reduce to
Arguing as for (4.18) and using the stationarity of we infer that
To establish (4.19) it only remains to combine the previous inequality with (4.20) and use (4.1). The proof of (4.13) is therefore complete.
Inequality (4.12) may be obtained in a similar way as to that of (4.13): Since we may decompose the set into disjoint cubes of size , we use definition (2.5) and the stationarity of to bound
so that, again by Lemma 5.2, we obtain
We establish (4.12) after observing that, thanks to (4.1), it holds .
We now tackle (4.14): As in the proof of case , we may assume that for the set . By construction (see definition (4.3)), the (random) set satisfies
where is, as above, the cube of size centred at the origin. Hence, decomposing into unitary cubes, definitions (4.5) and (2.5) allow us to rewrite
with
We rewrite
so that the triangle inequality, assumption (2.1) and the quenched bounds in (4.4) yield
Appealing to definitions (4.21), (4.5) and (2.4), we observe that and are independent whenever are such that and are not adjacent. We emphasize that they are not identically distributed as in definition (4.21) the random variables contain the modified radii (see (4.5) and (4.2)). Hence, by taking the expectation in the previous inequality, we estimate
To establish (4.14) from (4.22) it suffices to bound
We emphasize that in the first bound the right-hand side may be bounded by .
Inequality (4.23) follows from Cauchy-Schwarz's inequality, the triangle inequality and definitions (4.21) and (4.5). We thus turn to (4.24) and fix . Since by definition (4.5) it holds
we use this and (4.21) to rewrite
Observing that , and writing
we infer that
We now appeal to Lemma 5.2 with to infer that
By the properties of the Poisson point process and definition (2.4) this yields
Hence
To establish (4.24) it remains to bound the last term above by : By stationarity we have
We now observe that if , then by (4.2) we have that : In this case, the expectation on right-hand side above may be bounded similarly to (4.18) so that
If, otherwise, , then (4.2) and a decomposition of similar to the one performed in (4.20) implies that
Using that, if , we have (c.f. (4.1)) and dealing with the remaining expectation as done in (4.26), yields that
Combining (4.27) and (4.26) with (4.25) implies (4.24) and, in turn, (4.14). The proof of Theorem 2.1 is complete.
Proof of Lemma 4.4. The proof of this lemma follows the same lines of the argument for Lemma 3.4. We resort to the construction made in Lemma 4.1 (c.f. (3.6)) to decompose
The expectation of the first sum may be bounded by by by arguing in a way analogue to the one for (3.42) in Lemma 3.4. In this case, besides (2.1), we also appeal to assumption and to the properties of the Poisson point process. Hence, it only remains to estimate the last sum in (4.28). As done for the same sum in (3.41), we use the definiton of and the stationarity of to rewrite
By Lemma 5.2 applied to
we infer that
Since the marks are identically distributed and independent, we use (2.1) to bound
Since , the term corresponding to the first sum on the right-hand side above is easily bounded by
We now turn to the second term in (4.29): Since this term reduces to the values , we have that
Using Hölder's inequality with exponents { and in the inner expectation, definition (2.4) and the fact that is a Poisson point process, this implies that
We control the last term by
Since and , the last term on the right-hand side above is bounded by . Combining this with (4.31), (4.29) and (4.30) yields . This concludes the proof of Lemma 4.4.
5.
Auxiliary results
Let be a collection of points and let . We assume that
We define the measure
where each solves (2.6) with and replaced by and , respectively.
The next lemma is a generalization of the result by [19] used in [18] to show the analogue of Theorem 2.1 in the case of periodic holes .
Lemma 5.1. Let , and be as above and let be as in . Then, there exists a constant such that for every Lipschitz and (essentially) disjoint covering of such that
we have that
with
Here, the constant is as in (1.5).
The next result is a consequence of the assumptions (i)-(iii) on the marked point process . Since it is used extensively in the proof of Theorem 2.1, in the sake of a self-contained presentation, we give below the statement and its brief proof. Let the underlying probability space for . Let be a stationary random field. This means that for almost every , the expectation .
Lemma 5.2. Let be bounded and such that . Let satisfy (i)-(iii) with . For every and , let be as in . Then for every stationary it holds
Proof of Lemma 5.1. With no loss of generality, we give the proof for . We start by remarking that, thanks to (5.3), we may rewrite the measure in (5.2) as
By the definition of the capacitary functions (see also (3.18)), in (5.4) satisfies
For every , we thus define as the (weak) solution to
We stress that exists since is a Lipschitz domain and, thanks to (5.3) and (5.5)-(5.6), the compatibility condition is satisfied.
By (5.7) and (5.5)-(5.6), we thus have that
The statement of Lemma 5.1 holds, provided that we show that for each
We argue (5.8) as follows: testing (5.7) with itself and using that , we obtain
By Cauchy-Schwarz's inequality and by the definition of (see also (3.18)), this implies that
By the trace estimate for functions ,
inequality (5.9) turns into
Since by (5.3) we have , we infer that
This, Cauchy-Schwarz's inequality, and (5.1) further yield
Since by (5.7) the function has zero mean, we may apply Poincaré-Wirtinger's inequality to conclude that
This establishes (5.8) and, in turn, concludes the proof of Lemma 5.1.
Proof of Lemma 5.2. Without loss of generality we assume that . By the assumption (i)-(ii) on and by symmetry we have that
Appealing to Fubini's theorem and relabelling the elements , this implies
i.e. . Since is stationary, the above equality immediately implies Lemma 5.2.
Acknowledgments
The author thanks the anonymous referees for the helpful comments and suggestions on the first version of the paper.

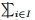 for the averaged sum
for the averaged sum 