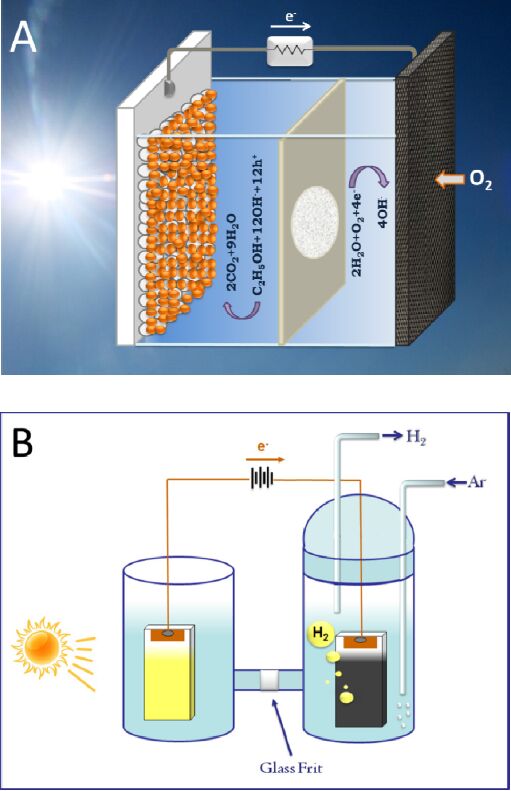
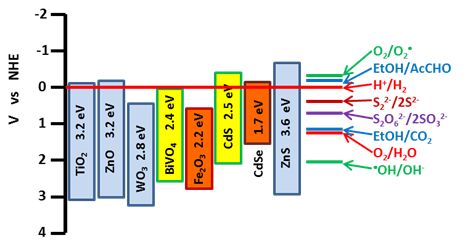
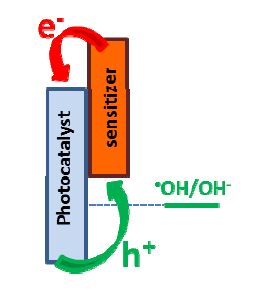
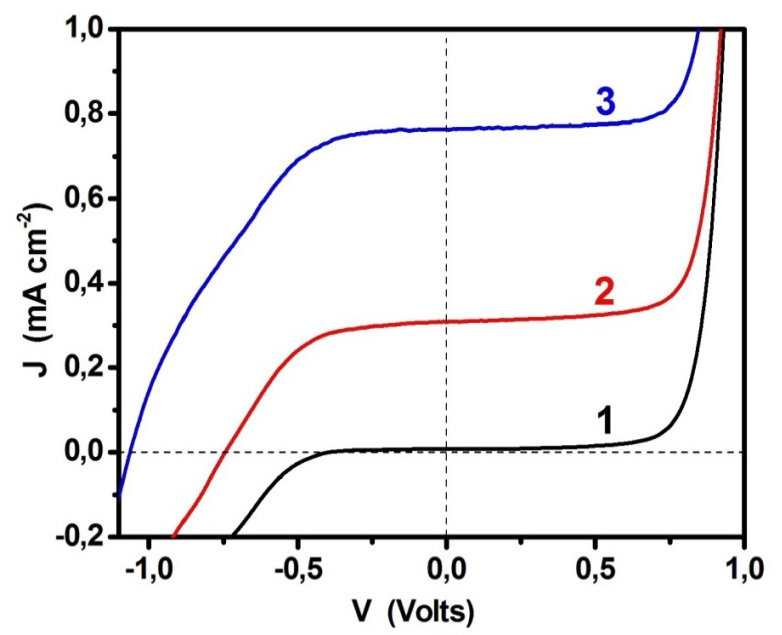
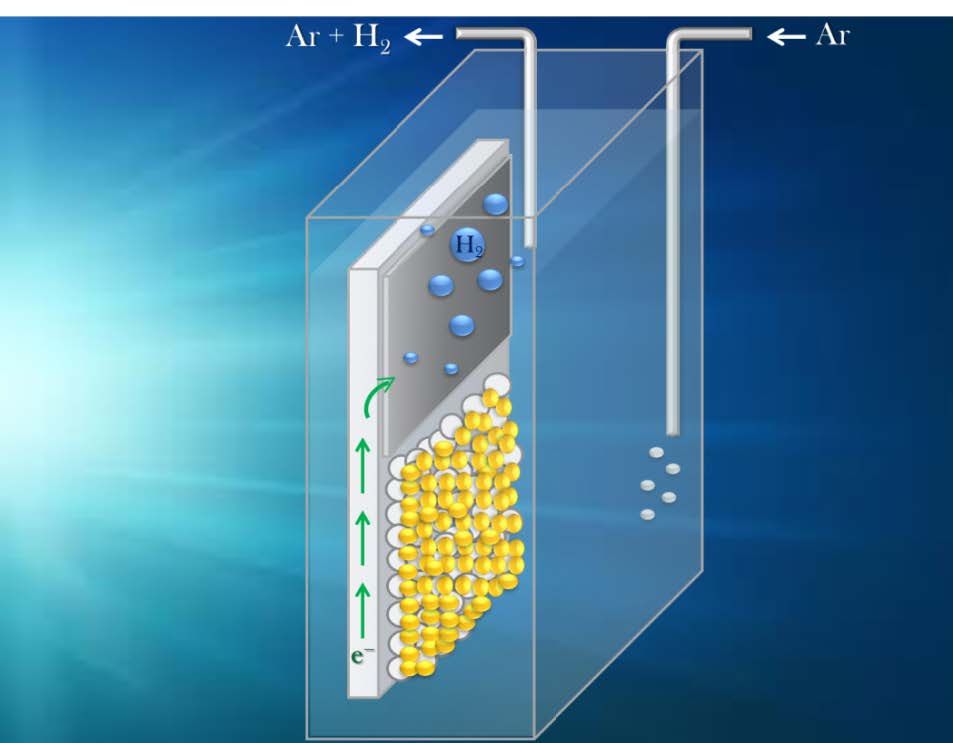
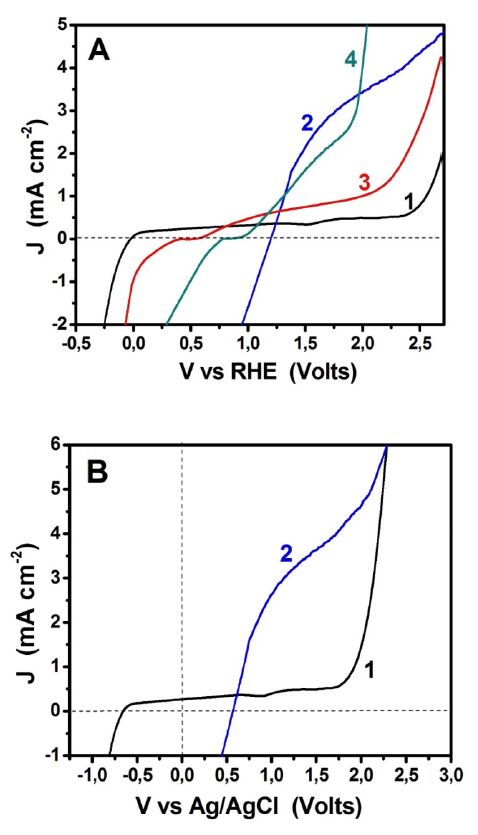
This work is a short review of Photoactivated Fuel Cells, that is, photoelectrochemical cells which consume an organic or inorganic fuel to produce renewable electricity or hydrogen. The work presents the basic features of photoactivated fuel cells, their modes of operation, the materials, which are frequently used for their construction and some ideas of cell design both for electricity and solar hydrogen production. Water splitting is treated as a special case of photoactivated fuel cell operation.
1.
Introduction
In scientific research and engineering technology, many problems, such as the deformation of engineering building beams and the load of turbine blades under the impact of airflow in fluid mechanics, can be attributed to the existence of solutions of differential equations. And in elastic mechanics and engineering physics, elastic beam is one of the basic components of engineering building. The nonlinear boundary value problem of the fourth order differential equation with different boundary conditions can describes the deflection of elastic beam under external force, the reflects, and the stress. The static beam equation:
is most studied under the following boundary conditions:
or
where $ f:[0, 1]\times[0, \infty) \to [0, \infty) $ is continuous. They are often used to describe the equilibrium state of the elastic beams. While the problem (1.1), (1.2) describes the static beam with simple support at both ends, the problem (1.1), (1.3) describes the static beam with simple support at one end and sliding support at the other end. These two types of problems, can be converted into second-order equation by simple transformation. Therefore, some methods of studying ordinary differential equations can be applied to the study of problems (1.1), (1.2) and (1.1), (1.3).
The problem (1.1), (1.2) has been investigated in many literutures, see [1,2,3,4,5,6]. Among them, Bai [1] used a new maximum principle to give the solutions for the problem. Gabriele [2] used a local minimum theorem to give the existence of at least one non-trivial solution. Li [3] got the existence of positive solutions based on the fixed point index theory. And Yao [6] used the approximation by operators of completely continuous operator sequence and the Guo-Krasnosel'skii fixed point theorem for cone expansion and compression.
The problem (1.1), (1.3) also has been investigated by many authors, see [7,8,9]. Yao gave the existence of $ n $ solutions by choosing suitable cone and using the Krasnosel'skii fixed point theorem in [7]. Yao and Li [8] used the Leray-schauder fixed point theorem to get the existence of positive solutions. Zhao [9] used the fixed point theorem due to Avery-Peterson and Leggett-williams to get the existence of positive solutions. The upper and lower solution method and the fixed-point techniques have been used to study many other problems. We provide reference alone this line for some research on beam equation [10,11].
The typical static elastic beam equation with fixed ends can be described by Eq (1.1) with boundary condition
Compared with the above two type problems, this problem can not be solved by directly converting it into some second-order problems. But due to its wide application, many authors set out to find a positive solution to problem (1.1), (1.4). In 1984, Agarwal [12] first considered the problem, and used the compression mapping principle and numerical iteration method to study the existence of solutions. Later, Wu and Ma [13,14] used the Krasnoselskii's fixed point theorem to get the existence results under the following conditions:
Caballero [15] applied a fixed point theorem in partially ordered metric spaces to get a unique symmetric positive solution for problem (1.1), (1.4), where $ f(x, y) $ is a nondecreasing function with respect to $ y $ for each $ x\in[0, 1] $, and satisfy the Lipschitz type condition. Obviously the function $ f(x, y) $ has strong constraints in above literatures.
This paper study the existence of positive solutions for the following fourth-order two-point boundary value problem:
where $ f: [0, 1]\times[0, \infty) \to [0, \infty) $ is continuous. In section 2, the Green's function is given by the use of the Laplace transform, and some preliminary lemmas also be obtained. In section 3, the eigenvalue of the linear equation corresponding to problem (1.5), (1.6) is given by Ritz method in calculus of variations with the help of the mathematical tool software. The fixed point index value is obtained by using the theory of the self-adjoint operator, and the existence of positive solutions is given by the use of the fixed point index theorem. In section 4, an examples is given to illustrate the main results.
Compared with other literature, in this paper, the way to get the eigenvalue of problem considered is new. We use Laplace transform to get the Green function of this problem, this way is more convenient and easier. And the constraint of $ f(t, u) $ in this paper is more weaker than which get in other paper.
2.
Preliminaries
For convenience, we introduce some symbols,
Lemma 2.1. Given $ h\in C[0, 1] $, the unique solution of
is
where
Proof. By the use of Laplace transform on equation (2.1), one has
where $ Y(s) = £ [y(x)], H(s) = £ [h(x)] $. Thus,
By the use of the inverse Laplace transform and the boundary condition (2.2), one has
then
Let $ x = 1 $ in (2.5) and (2.6), then we can get
Put them into Eq (2.5), we get
The proof is completed.
Remark 2.1. The Green's function (2.4) have been obtained before in some literatures, but to my best knowledge, the way to get it by Laplace transform hadn't been mentioned yet. Obviously, this way is more convenient and easier.
Lemma 2.2. [13] Let $ a(s): [0, 1] \to [0, 1] $ define as
then $ a(s) = \frac{1}{3-2s} $, for $ 0\leq s\leq \frac{1}{2}; a(s) = \frac{2}{1+2s} $, for $ \frac{1}{2}\leq s\leq 1 $.
Lemma 2.3. [13] The function $ G(x, s) $ defined by (2.4) satisfies:
$ (i) $ $ G(x, s) = G(s, x) > 0 $, for $ x, s \in[0, 1] $;
$ (ii) $ $ \frac{G(x, s)}{G(a(s), s)}\geq q(x) $, where $ q(x) = \min\{\frac{2}{3}x^2, \frac{2}{3}(1-x)^2\} $, for $ x, s\in[0, 1] $;
$ (iii) $ $ G(x, s)\geq\frac{1}{24}G(a(s), s) $, for $ x\in [\frac{1}{4}, \frac{3}{4}], s\in[0, 1] $.
Let $ C^+[0, 1] $ be the cone of all nonnegative functions in $ C[0, 1] $ which is a Banach space with $ \|y\| = \max\limits_{x\in[0, 1]}|y(x)| $. And the cone
Then denote
and define $ T: C^+[0, 1] \to C^+[0, 1] $ by
Lemma 2.4. [13] By Lemma 2.3 and formula (2.7), there holds
Lemma 2.5. Let $ f: [0, 1]\times[0, \infty) \to [0, \infty) $ be continuous, then
$ (1) $ the operator $ T: D \to D $ is completely continuous,
$ (2) $ the solution of boundary value problem (1.5), (1.6) $ y(x) $ satisfies
Proof. The positive solution of problem (1.5), (1.6) is equivalent to the nonzero fixed point of $ T $. On the one hand,
By the arbitrariness of $ y $ and $ G(x, s)\geq 0 $, we obtain $ T(D)\subset D $. Then by the continuity of $ f $ and Arzela-Ascoli Theorem, we get $ (1) $ holds. On the other hand, by the definition of the operator $ T $ and the function $ a(s) $, we have
Suppose $ y\in D $ is a solution of problem (1.5), (1.6), then
The proof is completed.
Given $ b > 0 $, let
Lemma 2.6. [16] Suppose $ T: D \to D $ is completely continuous and
$ (i)\; \inf\limits_{y\in \partial D_{b}}\|Ty\| > 0, $
$ (ii)\; \alpha Ty\neq y $ for $ \forall y\in \partial D_{b} $ and $ \alpha \geq1 $.
Then $ i(T, D_{b}, D) = 0 $.
Lemma 2.7. [16] Suppose $ T: D \to D $ is completely continuous. If $ \alpha Ty\neq y $ for $ \forall y\in \partial D_{b} $ and $ 0 < \alpha \leq1 $, then $ i(T, D_{b}, D) = 1. $
Lemma 2.8. Assume that $ G(x, s) $ is defined as formula (2.4). Then the operator $ H: C[0, 1] \to C[0, 1] $,
is a self-adjoint operator.
Proof. By Lemma 2.1, it is clear that $ G(x, s) $ is a real symmetric function, that is to say that, $ G(x, s) = G(s, x) $ for $ 0 \le s, x \le 1 $. Thus, for $ \forall z_1 = z_1(s), z_2 = z_2(s)\in C[0, 1] $, there holds
So, the operator $ H $ is a self-adjoint operator.
3.
Main results
Lemma 3.1. The first eigenvalue $ \lambda_1 $ of the problem
is $ \lambda_1\approx 500.564 $.
Proof. Define the linear differential operator $ L: \{y \in C^4[0, 1] \mid y(0) = y(1) = y'(0) = y'(1) = 0\} \to C[0, 1] $ as
With Ritz method, the problem which to get the first eigenvalue $ \lambda_1 $ can be transformed to get the extreme value of the functional
under the normalization condition
Combing the definition of the functional $ J $ and the boundary condition (3.2), one has
Choose the primary function as
then, the $ n $-th order approximate solution of the functional extremum function is
By (3.4), (3.5), there is
Then the Lagrangian function
Now, we solve the following equation system by the use of the mathematical tool software Mathematica,
Firstly, we get $ a_{i} (i = 1, 2, 3, \cdots, n) $ and $ \tau $, then, plug them into (3.6) to get $ y_{n}(x) $. By Eq (3.7) we get the corresponding eigenvalue $ \lambda_1 = J[y_{n}(x)] \approx 500.564 $ for $ n \geq 6 $. The proof is completed.
Remark 3.1. Although some authors mentioned the eigenvalue before, but to my best knowledge, the eigenvalue of problem (3.1), (3.2) hadn't been obtained yet. However, we use the Ritz-Method to get the concrete eigenvalue $ \lambda_1 $ here.
Theorem 3.1. Suppose one of the following relation is true:
$ (i) $ $ \bar{f}_0 < \lambda_1, $ $ \underline{f}_{\infty} > \lambda_1 $;
$ (ii) $ $ \underline{f}_0 > \lambda_1, \; \; \bar{f}_{\infty} < \lambda_1. $
Then boundary value problem (1.5), (1.6) has at least one positive solution.
Proof. $ (i) $ By $ \bar{f}_0 < \lambda_1 $, for $ \epsilon\in(0, \lambda_1) $, there exists $ b_0 > 0 $ such that
Set $ b\in(0, b_0) $. Assume there exist $ y_0\in \partial D_{b} $ and $ \alpha _0\in(0, 1] $ such that $ \alpha_0Ty_0 = y_0 $. Then $ y_0 $ satisfies
Taking into account (3.9) and (3.10), there is
Due to the fact that the inverse operator of a self-adjoint operator is self-adjoint and Lemma 2.8, the operator $ L $ defined by (3.3) is a self-adjoint operator. Suppose $ \hat{y}\in D $ is a eigenfunction of $ L $ with respect to $ \lambda_1 $ such that $ \int_0^1 \hat y(x)dx = 1 $, that is to say that
Then
So we get
obviously this is a contradictory. Hence Lemma 2.7 yields that
Since $ \underline{f}_{\infty} > \lambda_1 $, for given $ \epsilon > 0 $, there exists $ K > 0 $ such that
suppose $ C = \max\limits_{0\leq x\leq1, 0\leq y\leq K} |f(x, y)-(\lambda_1 + \epsilon)y|+1 $, then
Let $ r > r_0 : = max\{24K, b_0\} $. For $ y\in\partial D_r $, there is $ y(s)\geq \frac{1}{24} \|y\| > K $ for $ s\in \left[\frac{1}{4}, \frac{3}{4}\right] $, then, by (3.12)
So $ \inf\limits_{y\in\partial D_r}\|Ty\| > 0 $.
Suppose there exist $ y_0 \in D_r $ and $ \mu_0 \ge 1 $ such that $ \mu_0 T y_0 = y_0 $, then
Thus,
So,
Similar to the proof of Lemma 2.5, by $ \mu_0Ty_0 = y_0 $, one has
So,
Thus,
Now set $ r > max\{\bar{r}, b_0\} $, then there is $ \mu Ty\neq y $ for $ \forall y\in\partial D_{r} $ and $ \mu\geq1 $. Consequently, two conditions of Lemma 2.6 all hold, thus
By (3.11) and (3.15) there is
Hence $ T $ has a fixed point in $ D_r\backslash \overline{D_b} $.
$ (ii) $ Since $ \underline{f}_0 > \lambda_1 $, for $ \epsilon > 0 $, there exists $ h_0 > 0 $ such that
Set $ h\in(0, h_0) $, similar to (3.13), one has
so $ \inf\limits_{y\in\partial D_{b}}\|Ty\| > 0 $.
Assume there exist $ y_1 \in \partial D_h $ and $ \alpha_1 \ge 1 $ such that $ \alpha_1 Ty_1 = y_1 $, then
Obviously this is a contradiction, because $ (y_1, \hat y) > 0 $. Therefore, Lemma 2.5 yields that
On the other hand, since $ \bar{f}_{\infty} < \lambda_1 $, for $ \epsilon \in(0, \lambda_1) $, there exists $ K_2 > 0 $ such that
Let $ C = \max\limits_{0\leq x\leq1, 0\leq y\leq K_2}|f(x, y) - (\lambda_1-\epsilon)y|+1 $, then
Assume there exist $ y_2 \in D $ and $ \alpha_2 \in (0, 1] $ such that $ \alpha_2 Ty_2 = y_2 $, then
Similar to the previous proof, one has $ \|y_2\| \le \bar r $. Set $ r > max\{\bar{r}, h_0\} $, we get $ \alpha Ty\neq y $ for $ \forall y\in \partial D_r $ and $ \alpha \in(0, 1] $. Hence by Lemma 2.7,
then
In conclusion, the boundary value problem (1.5), (1.6) has at least one positive solution.
Remark 3.2. Compared with literatures [14,15] and so on, the constraint of $ f(x, y) $ in our results is weaker.
4.
Example
Example 4.1. Consider the problem:
It's obviously that $ \frac{f(x, y)}{y} = y^{\theta-1}+300-x $.
Case $ (1) $: $ \theta > 1 $, there are
Case $ (2) $: $ \theta < 1 $, there are
By Theorem 3.1, for $ \theta\neq1 $, Problem (4.1), (4.2) has at least one positive solution.
5.
Conclusions
The fourth order differential equations have been applied in different aspects of applied mathematics and physics, especially in the theory of elastic beams and stability. In this paper, the fourth-order two-point boundary value problem is studied, which can describe some changes when the elastic beam deforms or rotates when it is subjected to external forces, and provides an important theoretical basis for solving the problem. And compare with other literature, our method in this paper makes the equation more widely used and describes the equilibrium state of the elastic beam better.
Acknowledgments
This work is supported by Natural Science Foundation of China (Grant No.11571207), the Taishan Scholar project, and SDUST graduate innovation project SDKDYC190237.
Conflict of interest
The authors declare no conflict of interest in this paper.













 DownLoad:
DownLoad: