A new DNA coding and hyperchaotic system based asymmetric image encryption algorithm

1.   Introduction

With the rapid development of smart phones and other intelligent terminals, multimedia communication is becoming more and more important and indispensable in today's society, for example, image, video, and audio. However, the openness and sharing of networks bring many security risks to digital communication. As an important medium of multimedia communication, digital image plays an important role in military, medical, biological and social life. Digital image carries a lot of useful information, which is widely spread communicated over the open Internet. However, some of them are private or contain sensitive information. So, it is an urgent task to protect the security of image content. Compared with traditional texts or words, images have some special characteristics such as large amount of data, high redundancy, strong correlation between adjacent pixels, and low information entropy. Therefore, persons need a long keystream to encrypt images ^[1] for security requirement.

Recently, chaos as a new interdisciplinarity has shown its inherent advantages such as pseudo-random and ergodic. It is a deterministic but unpredictable nonlinear system, which is very sensitive to each initial condition and parameter. Therefore, many image encryption algorithms, techniques and methods based on chaotic systems have been proposed. In ^[2], Ye et al. proposed a new meaningful image encryption algorithm based on compressive sensing ^[3] and random numbers insertion using information hiding technology, in which the measurement matrix for compressive sensing is generated by a low dimensional complex chaotic tent-sine system. In ^[4], a novel multi-image visually encryption algorithm based on compressive sensing and Schur decomposition was proposed. Chaotic logistic sine coupling map was employed to confuse the part Hadamard matrix. By regarding two secret images as the real part and imaginary part respectively, a double image encryption ^[5] by using random binary encoding and gyrator transform was proposed. Liu and Wang ^[6] proposed an image encryption algorithm based on one-time keys. The piecewise linear chaotic map was used to produce pseudo-random keystream sequences. By designing a dynamic random growth technique ^[7], a chaotic block image encryption algorithm was proposed with a diffusion process depending on both the key and the plain image. Although those schemes take some measurements to improve the security during the encryption process, they cannot completely resist the chosen plaintext and known plaintext attacks. For example, Ma et al. ^[8] gave a thorough security analysis on the algorithm ^[9] and made successful break on it. Moreover, many pixel-level based encryption algorithms or improved schemes have been proposed such as ^[10].

To solve the above problem, a new local image encryption scheme ^[14] was proposed, in which the scheme encrypted only the necessary part of the sensitive information in the frequency domain of lifting wavelet transform (LWT). Due to the advantages of bit-level operation, some image encryption algorithms using bit-level permutation have been proposed ^[15,16,17]. The reason is that it can change pixel position and alter their values at the same time. For example, in^[18], heterogeneous bit-permutation was employed to reduce computation cost and change pixel values at the permutation stage. Li et al. ^[19] presented a new bit-level based image encryption algorithm. They diffused two binary sequences mutually in the diffusion stage. Moreover, An new image cryptosystem adopting bit-level permutation by Arnold cat map with a diffusion was designed in ^[20].

Considering the complex biological structure, some cryptographic algorithms based on DNA coding have also been proposed ^[21,22,23] for image encryption. DNA molecule has the advantages of high information density, good parallelism and ultra-low energy consumption, which is suitable in the field of cryptography ^[24,25]. The core of these algorithms is DNA coding and DNA operating, including DNA complementarity, DNA addition, DNA subtraction and DNA XOR. Yildirim ^[26] studied a DNA encoding based image encryption algorithm together with neuron model, circuit design with memristor, and chaos theory. In ^[27], an image encryption algorithm based on DNA coding and two Logistic maps was proposed. However, Hermassi et al. ^[28] pointed out that the encryption method ^[27] has serious defects, that is, it is non-invertible even having correct keys, and cannot resist the known plaintext attack. Furthermore, the key can be recovered by a pair of plain images and corresponding cipher images. The encryption process is also not sensitive to the change of plain image or key. In addition, the rules of DNA coding and DNA decoding are fixed. To improve the sensitivity, hash values of the plain image were also seen as a part of the key ^[29]. However, one needs to transfer the corresponding image hash values when decrypting the cipher images.

For symmetric ciphers such as ^{[30,31,32,33]}, the sender and the receiver should share the same keys for communication. Therefore, it is hard to ensure the secure exchange of keys in a special channel. On the contrary, asymmetric ciphers can solve the problems of key transmission and management. So, the public cryptosystem based encryption algorithms have been introduced in the protection of image content ^[34,35]. For example, the El-Gamal encryption algorithm ^[34] was employed to encrypt the permuted image followed by scrambling to pixel locations in the confusion and diffusion stages. However, the keystream is only with key dependence in these algorithms. So, it cannot frustrate the known plaintext and chosen plaintext attacks. Furthermore, traditional modular multiply operation suffers much time cost. The new methods to improve the operation speed have also been studied more and more in recent years ^{[36,37,38,39]}. For example, Huang and Wang ^[36] proposed a novel and efficient design for an RSA cryptosystem with a large key space, in which a new modular multiplier architecture was proposed different from traditional method. In ^[37], a high frequency as well as low latency RSA cryptosystem was presented to perform efficient hardware implementation. By an improved processor architecture and software implementation, Reference ^[38] designed new hardware stages at the same time uses an open-source big number library to execute the operation. Adiono et al ^[39] proposed a Montgomery multiplier hardware design with primitive gates, adders, shifters, multiplexers, and registers to compute RSA. All these are aiming to speed up the computation.

In this paper, to avoid the problems seen above, an asymmetric image encryption scheme based on RSA and a four-dimensional hyperchaotic system is proposed. Firstly, using RSA to generate initial values for hyperchaotic system and produce the random number sequences needed for image encryption. Especially, the plaintext related messages are extracted from odd rows, even rows, odd columns, and even columns respectively as the input of RSA. Then, pixel-level permutation is employed to permute the plain image. Secondly, using DNA coding and DNA operation to diffuse the permuted image. The combination of pixel-level permutation and DNA coding diffusion can improve the security of our cryptosystem. Moreover, different DNA decoding rules are used to fetch the cipher image. Compared with the existing image encryption algorithms based on hyperchaotic systems, the proposed algorithm has three advantages: (1) Different DNA coding and DNA decoding rules are designed. (2) The rules of DNA coding, DNA decoding and DNA operating are all related to chaotic sequences dynamically. (3) The initial values of the hyperchaotic system are related to the plain image by using the RSA algorithm and a mathematical map. As a result, the sender in our algorithm does not need to transfer the extra transmission to the receiver. Both sender and receiver do not need to manage the secret keys.

This paper is organized as follows. In Section 2, some preliminary knowledge are introduced, which are used in the proposed algorithm including RSA, DNA, and hyperchaotic system. The proposed image encryption scheme is described in detail in Section 3. In Section 4, some simulations are carried out with test results displayed. In Section 5, many security analyses are evaluated. Section 6 gives some conclusions for this paper.

2.   Preliminary knowledge

2.1.   Hyperhaotic system

Hyperchaotic can show good sensitivity to initial conditions ^[40] and has the characteristics of random like behavior, which provides a new way to improve the security of encryption system. A new four-dimensional hyperchaotic system was studied in ^[41] which can be defined by the following equation.

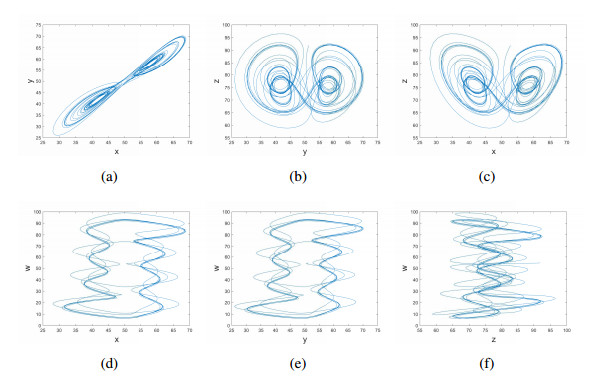
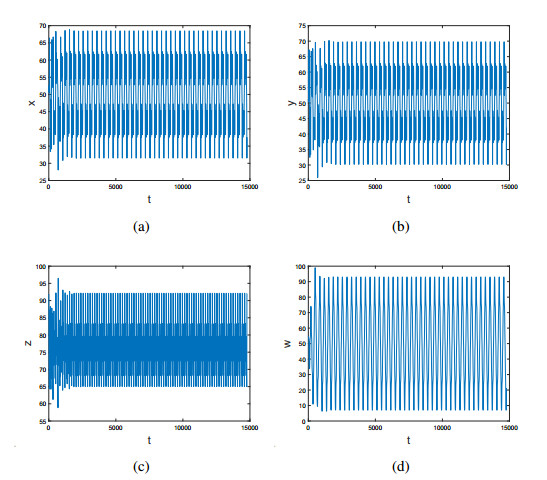
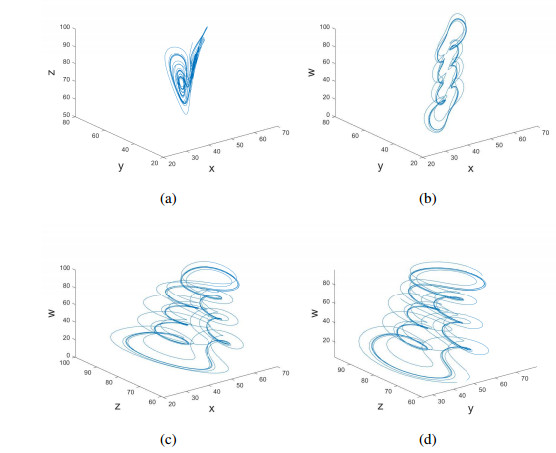
where $a$, $b$, $c$ and $k$ are the system parameters. If one set $a$, $b$, $c$, and $k$ be 35, 83, 28, and 5, respectively, the Lyapunov exponents of above hyperchaotic system are ^[41]: $\lambda_1 = 0.3997$, $\lambda_2 = 0.3113$, $\lambda_3 = 0$ and $\lambda_4 = -14.3776$. Apparently, the above system is in a hyperchaotic state due to double positive Lyapunov exponents. With parameters $a$ = 35, $b$ = 83, $c$ = 28, $k$ = 5 and all initial conditions $(x_0, y_0, z_0, w_0)$ = $(-10, -10, -10, -10)$, Figure 1 and Figure 2 depict chaotic attractors by different real axis, while Figure 3 shows the time series for differen planes.

To further show the good statistical properties: unpredictability, randomness, independence, and uniform distribution, the NIST SP800-22 is tested for the above hyperchaotic system with results listed in Table 1. So, we can see that all items can pass the NIST SP800-22 test and it is suitable to be the randomness of random number generator (TRNG) and pseudorandom number generator (PRNG).

2.2.   RSA cryptography

RSA algorithm is a public key cryptosystem widely used in data security transmission, in which the public key is open for doing encryption which is different to the decryption key seen as private key. Anyone can encrypt the message with the public key, but it can only be decrypted correctly by the person who knows the private key. The security of RSA cryptography is dependent on the difficulty of factoring the product of large primes. Algorithm 1 gives the process of RSA as follows.

2.3.   Operation of xnor

The xnor operation is defined binary numbers 0 and 1 as: if the input variables are the same, the output is 1, while the input variables are different, the output is 0. The calculation results are presented in Table 2.

2.4.   DNA coding

A DNA sequence contains four bases, i.e., A (adenine), C (cytosine), G (guanine) and T (thymine), in which A and T are one pair, and C and G are another pair. In order to comply with the complement rules, eight coding schemes are commonly considered as listed in Table 3.

In the process of image encryption, the gray pixel value can be represented by a 8-bit binary number and with a 4-bit DNA sequence. For example, a pixel value is 210, then its binary number is expressed as 11010010. Using DNA rules, we can get eight combinations: TCAG, TGAC, ACTG, AGTC, GACT, GTCA, CAGT and CTGA. In addition, operations for DNA addition, subtraction, xor and xnor are listed in Tables 4, 5, 6, and 7, respectively.

3.   Algorithm description

3.1.   Encryption algorithm

Step 1: For an plain image $A$ with size $M \times N$, suppose the operation of RSA is $Rfunction$, the initial values of the hyperchaotic system are computed with a mathematical model as seen in Algorithm 2.

Step 2: Generate four chaotic sequences by iterating the initial values $x_0$, $y_0$, $z_0$, and $w_0$ into hyperchaotic system to get $\{ x$, $y$, $z$, $w \}$.

Step 3: Use the following equation for $x$, $y$, $z$ and $w$ to obtain new sequences $x'$, $y'$, $z'$, and $w'$ as,

Step 4: Confuse the plain image using Algorithm 3 to scramble all the pixel positions.

Although the four sequences are not the same, the repeated permutation of pixels may occur, resulting in the degradation of encryption effect, so it is necessary to remove the repeated permutation.

Step 5: Construct a sequence $x'' = mod(floor(x\times10^{14}), 256)$, and do the xor operations for each row and column in $A'$ as Algorithm 4,

Step 6: Convert $A''$ to a binary number matrix to obtain matrix $B$.

Step 7: Construct four sequences as,

Step 8: By using $xx$ as index to choose DNA encoding rule, perform it on $B$ to obtain matrix $B'$ with $M$ rows and $4 \times N$ columns. Algorithm 5 shows the process, where $D\_encode(R, s)$ is a function that implements DNA encoding on $R$ using $xx$ by eight combinations in Table 3.

Step 9: Convert sequence $yy$ to a matrix $H$ of $M$ rows and $N$ columns, and perform similarly on $H$ using DNA encoding according to coding rule $xx$ to obtain matrix $H'$ with $M$ rows and $4 \times N$ columns, seeing following algorithm 6.

Step 10: Perform a DNA operation on the each row of matrix $B'$ and matrix $H'$ according to the corresponding operation rule in $zz$ to obtain matrix $C$. Algorithm 7 shows the process with function $D\_opera(P, Q, k)$ for performing DNA operations, where $P$ and $Q$ represent DNA coding sequences with the same dimensions. Set $k = 1, 2, 3, 4$, in which the number 1 represents the addition of $P$ and $Q$, the number 2 represents the subtraction of $P$ and $Q$, the number 3 represents the xor operation of $P$ and $Q$, and the number 4 represents the xnor operation of $P$ and $Q$.

Step 10: Decode matrix $C$ into an image $E$ with decimal numbers according to decoding rule $ww$, and get the cipher image. Algorithm 8 shows the process with function $D\_decode(R, s)$ to implement DNA sequence decoding, where $R$ is a DNA sequence to be decoded, and $s = 1, 2, 3, 4, 5, 6, 7, 8$ respectively represent the eight combinations in Table 3.

3.2.   Decryption algorithm

Decryption is the inverse of encryption. First, we need to compute the chaotic sequences generated by the hyperchaotic system using private key and cipher message $c_i, i = 1, 2, 3, 4$. Then, the inverse operation of decoding is performed on the cipher image $E$. Next, the inverse operation of DNA operations is performed. Finally, we get the plain image $A$ through the inverse operation of pixel permutation.

4.   Experimental results

MATLAB of 2019b version including Main Toolbox, Control System Toolbox, Image Processing Toolbox, and Signal Processing Toolbox is used to perform encryption and decryption to test images on a computer Windows 10 with AMD FX-8300 3.3 GHz CPU, and 8GB RAM. Lena image with size $256\times 256$ is randomly selected. Figure 4 shows the results of encryption and decryption.

5.   Performance analysis

5.1.   Information entropy analysis

Information entropy ^[42] can display a quantitative reflection of the uncertainty for an image. The greater the information entropy, the greater the uncertainty, that is, the stronger randomness of the image. The calculation formula of image information entropy is following.

where $p(x_i)$ is the probability of symbol $x_i$ and $L$ is the total number of $x_i$. The ideal value of entropy for an 8-bit gray scale image is 8. If the value is closer to 8, the more uncertain the image is.

The information entropy tests for different images, Lena$_{ (256\times256) }$, Lena$_{ (512\times512) }$, male$_{ (1024\times1024) }$, Bridge$_{ (512\times5126) }$, brick wall$_{ (512\times512) }$, and brick wall$_{ (1024\times1024) }$, are listed in Table 8 with test images shown in Figure 5. Therefore, the simulation results tell us that the pixel distribution in the cipher image is very random by using the proposed algorithm.

5.2.   Key space analysis

For a secure algorithm, the key space should keep large enough to resist brute force attacks. Moreover, the keys should be easy to establish and exchange ^[43] for practical communication. In our algorithm, the keys consist of the four plain messages extracted from the plain image. Then, they are converted into the initial conditions of the hyperchaotic system. To simply compute, the size of the key space is determined by the initial value of the hyperchaotic system indirectly. The hyperchaotic system has four initial values $x_0$, $y_0$, $z_0$, $w_0$. When the precision is set to be $10^{-14}$, the key space can reach $10^{56}$, which is about $2^{186}$ and bigger than $2^{100}$. Therefore, the key space of our algorithm is large, and it can resist the brute force attack.

5.3.   Histogram analysis

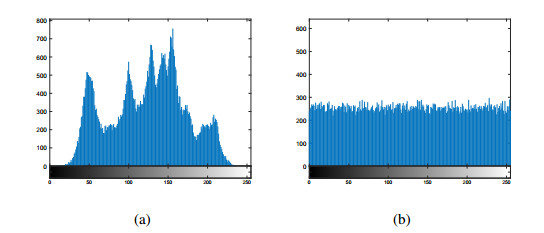
Histogram describes the distribution of pixel values for an image visually, which is an important feature to reflect whether the designed algorithm can resist the attack of statistical analysis. If the distribution is not uniform, attackers can obtain a certain amount of plain information through statistical analysis. So, as a good encryption system, the histogram of cipher image should be evenly distributed. Figure 6 shows the histograms before and after encryption for the image Lena. Obviously, one can find that the histogram of plain image before encryption is not uniform, while the histogram of cipher image becomes uniform. Therefore, the proposed algorithm shows good performance.

5.4.   Correlation coefficients analysis

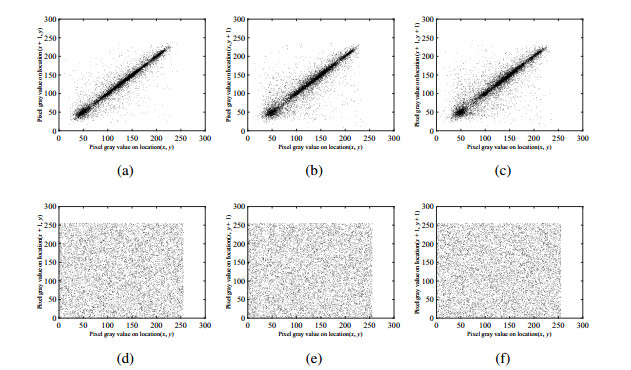
Generally, there is a strong correlation between adjacent pixels of a natural meaningful plain image. In order to analyze and compare the correlation between adjacent pixels in the plain image and its corresponding cipher image, 10000 pairs of adjacent pixels in each direction are randomly selected for test. Figure 7 shown the correlation distribution of two adjacent pixels in three directions. It can be seen that the adjacent pixels of the plain image have a strong linear relationship, while the adjacent pixels of the cipher image have a random relationship, which indicates that the redundancy and correlation of the cipher image are removed by using our method.

More specially, for calculating the correlation coefficient for a message, the equations can be seen as following.

where $x$ and $y$ are the gray values of two adjacent pixels in the image and $k$ is the total number of pixels. Table 9 lists the test results. So, we can see that the correlation coefficient of the plain image is close to 1, while the correlation coefficient of the cipher image is close to 0. Therefore, the proposed algorithm can effectively resist statistical attacks.

5.5.   Chosen plaintext attack and known plaintext attack analysis

In this paper, the plain message is extracted from the plain image, then, the RSA algorithm is employed to compute the cipher message. Both of them are designed to generate the initial values for the hyperchaotic system. Consequently, the keystream used in our encryption algorithm has a high connection with the plain image. Fortunately, due to the public key cryptosystem, the sender and receiver do not need to save and manage the same secret key. Different images will produce different keystreams, that is to say, the chosen plaintext attack and known plaintext attack are difficult to break the proposed algorithm.

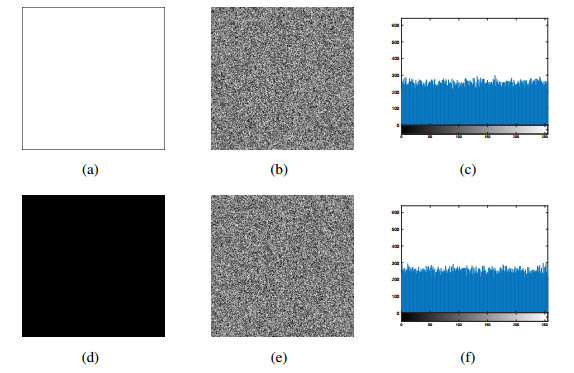
Besides, some attacks may use a black image or white image as a special pure image to attack encryption algorithms. Figure 8 shows the plain images with pure black and white images, cipher images with their histograms. So, the pixels in the cipher image are uniformly distributed with random noise, and it is impossible to obtain useful information from the image to crack the encryption algorithm. Therefore, our encryption algorithm can effectively resist the chosen plaintext attack and known plaintext attack.

5.6.   UACI and NPCR analysis

To measure quantitatively the difference between two images, The number of pixels change rate (NPCR) and the unified average changing intensity (UACI) defined as the following equations are commonly used as test tools.

where $P_1$ is the cipher image, and $P_2$ is another cipher image just with a pixel changed in the same plain image. If $P_1(i, j)$ is equal to $P_2(i, j)$, then $F(i, j)$ is equal to 0; otherwise, $F(i, j)$ is equal to 1. Lena image is randomly chosen for test. The pixel value in the first row and the first column is changed from 165 to 166. The NPCR value is 99.6185%, and the UACI is 33.4058%. Table 10 also lists the results of some other images. Therefore, our algorithm has a strong ability to resist differential attacks.

5.7.   Comparisons

As mentioned above, the proposed encryption algorithm based on the idea RSA, permutation, confusion, and DNA operation is presented. The beauty of our work is that we have achieved very competitive and promising results. To show better performance, some other similar studies ^{[44,45,46,47]} are also compared (by Lena image) with our work as listed in Table 11 and Table 12. So, one can see that the proposed algorithm has a good effect for image encryption.

6.   Conclusions

Combing with the RSA algorithm and DNA coding, a new asymmetric image encryption algorithm has been proposed in this paper. Compared with current encryption schemes, our contributions are: (1) The process of DNA coding, operation, and decoding are not fixed but dynamically. (2) Odd rows, even rows, odd columns, and even columns in the plain image are extracted as plain message and as the input of RSA. (3) A new mathematical model is established to map both plain message and cipher message got from RSA into initial values for the hyperchaotic system. The advantages are: (1) The proposed encryption algorithm can make the encryption process be associated with the plain image by RSA. (2) No extra transmission is needed because of the open of the cipher messages produced from plain messages by RSA. (3) Different plain images would generate different keystreams with respect to different plain messages. Due to the binary operations in DNA codes like most current DNA based image encryption algorithms, our algorithm still needs much time to encrypt larger images. So, in the future, we will focus on improving the operation time for the encryption process and hardware implement.

Acknowledgments

The authors would like to thank the reviewers for their valuable comments and the editor's helpful suggestions. This work was supported in part by the National Natural Science Foundation of China (No.61972103); the Natural Science Foundation of Guangdong Province of China (No.2019A1515011361); and the Key Scientific Research Project of Education Department of Guangdong Province of China (No.2020ZDZX3064).

Conflict of interest

The authors declare that they have no conflict of interest.