A novel quantity for identifying the repelling structures of continuous dynamical systems

1.   Introduction

In recent decades, people from various fields have been working on developing useful tools to analyze, visualize, and then extract important information in time-varying continuous dynamical systems, especially the fluid flows ^{[1,2,4,5,11,16,17,19,20,21,23]}. Mathematically, a dynamical system is modelled as an ordinary differential equation (ODE) given by

with the initial condition ${\bf{x}}(t_0) = {\bf{x}}_0$ and a Lipschitz velocity field ${\bf{u}}:\mathbb{R}^d \times \mathbb{R} \rightarrow \mathbb{R}^d$. Among all, the Lagrangian coherent structure (LCS) is one of most useful and interesting approaches, which partitions the space-time domain into subregions based on certain quantity measured along with the passive tracer advected according to the associated dynamical system.

The most commonly used way to extract the LCS is based on the so-called finite time Lyapunov exponent (FTLE) ^{[5,6,8,9,10,13,14,15,21]}. It measures the rate of change in the distance between neighboring particles across a finite interval of time with an infinitesimal perturbation in the initial position. Define the flow map $\Phi_{t_0}^{t_0+T}:\mathbb{R}^d \rightarrow \mathbb{R}^d$ as the mapping which takes the point ${\bf{x}}_0$ to the particle location at the final time $t = t_0+T$, i.e $\Phi_{t_0}^{t_0+T}({\bf{x}}_0) = {\bf{x}}(t_0+T)$ with ${\bf{x}}(t)$ satisfying (1.1). The FTLE can then be computed using the largest eigenvalue of the deformation matrix based on the Jacobian of this resulting flow map. For example, the FTLE $\sigma_0^T({\bf{x}})$ from time $t = 0$ to time $t = T$ is computed as $\sigma_0^T({\bf{x}}) = \frac{1}{T}\ln\sqrt{\lambda_{max}(\Delta_0^T({\bf{x}}))}$ where $\Delta_0^T({\bf{x}}) = (\nabla\Phi_0^T({\bf{x}}))^T(\nabla\Phi_0^T({\bf{x}}))$ is the deformation matrix and $(\cdot)^T$ denotes the matrix transpose. Following the definition of Haller ^[5,7,8], one can see that the LCS is closely related to the ridges of the FTLE fields.

From the definition of the FTLE, however, one can see that the FTLE computed over a time interval, say $[t_0, t_0+T]$, only concerns the particle positions at the initial time $t = t_0$ and the terminal time $t = t_0+T$. In other words, it does not care about where these particle trajectories travel at the intermediate times $t\in (t_0, t_0+T)$. In this paper, we propose an alternative tool called the Lagrangian Averaged Repelling Rate (LARR), to measure the averaged repelling rate of each particular particle trajectory in the whole time interval. In particular, we trace the particle evolution and compute the trajectory integral of its maximum repelling rate against nearby trajectories within the whole time intervel $[t_0, t_0+T]$. It means that, the proposed LARR takes the repelling behavior of the trajectory at any intermediate time $t\in (t_0, t_0+T)$ into account. A counterpart for measuring the attracting behaviors of particle trajectories can be similarly defined and discussed and we omit it in this paper.

Finally, we want to point out that compared to the traditional FTLE, the LARR actually measures the repelling properties of trajectories from a different perspective. People might make a choice depending on their need or the particular application. If they care about the ultimate growth rate of distances between particle trajectories at the single final time, then only the initial and final positions of these trajectories are concerned and the FTLE should be used. However, if they want to measure the averaged growth rate of distances between particle trajectories during the whole time interval, then LARR might be a better choice.

2.   The proposed LARR

In this section, we first give two simple examples to illustrate that the FTLE values only depend on the initial and final locations of particle trajectories and then propose an alternative quantity called LARR. After that, the objectivity of the LARR is shown and an efficient Eulerian algorithm for computing the LARR is developed.

2.1.   Two illustrative examples

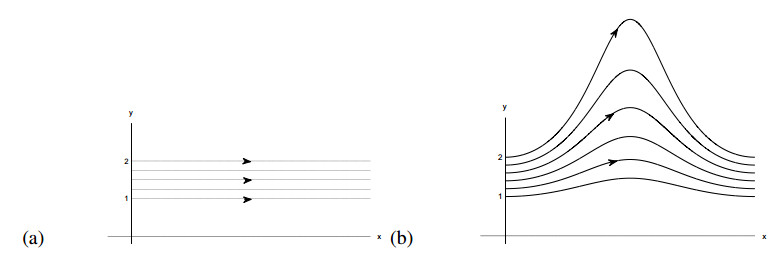
Before giving the definition of the LARR, we first consider two examples to show that the FTLE only focuses on the initial and final particle locations and thus might not be enough in measuring the averaged separation or repelling behaviors of particle trajectories. The first example is a constant velocity model given by ${\bf{u}}({\bf{x}}) = (1, 0)^T$, where all particles travel with the constant speed $1$ towards the positive $x$-axis as shown in Figure 1(a). It is easy to see that the deformation matrix is the second order identity matrix and hence the FTLE $\sigma_0^1({\bf{x}})$ from $t = 0$ to $t = 1$ equals to zero at any point ${\bf{x}}$ in the phase space. Then we consider a little more complex dynamical system with the velocity field ${\bf{u}}({\bf{x}}) = (1, y^2\sin(2\pi t))^T$, from which we can obtain an analytical flow map $\Phi_0^T({\bf{x}}) = (x+T, \pi y/(\pi-y\sin^2(\pi T)))^T$. In particular, the flow map at $T = 1$ is given by $\Phi_0^1({\bf{x}}) = (x+1, y)^T$ and the resulting FTLE is also zero at any point ${\bf{x}}$. Figure 1(b) shows several trajectories within the time interval $[0, 1]$ of particles taking off from the points on the line segment with endpoints $(0, 1)$ and $(0, 2)$. In both subfigures, we can see that the distance between any two nearby trajectories at time $t = 1$ does not change compared to their initial distance. As we said, the FTLE only cares about the particle states at the initial time $t = 0$ and the terminal time $t = 1$. As a result, it is not surprising that the FTLE $\sigma_0^1({\bf{x}})$ constantly equals to zero at any point ${\bf{x}}$ in both examples. However, we can see from Figure 1(b) that those particle trajectories do not always keep a constant distance from each other during the evolution process in the intermediate time levels $t\in [0, 1]$. On average, the upper trajectories have higher repelling rates than the lower ones.

Figure 1.  Several particle trajectories starting from the points $(0, y_0)$ with $y_0\in [1, 2]$ corresponding to (a) the first example, and (b) the second example.

DownLoad: Full-Size Img PowerPoint

2.2.   The construction of the LARR

Inspired by the second example in Section 2.1, we here propose a novel tool to measure the averaged repelling rate along the whole particle trajectory under consideration. In particular, we have to consider the repelling rate of the trajectory at any time level $\tau\in [t_0, t_0+T]$, not only the initial and the terminal time levels. To measure the repelling rate of the particle trajectory ${\bf{x}}(t)$ at a particular time level $\tau\in [t_0, t_0+T]$, we consider another particle trajectory ${\bf{x}}^*(t)$ which is infinitesimally close to ${\bf{x}}(t)$ at time $\tau$, i.e. $|\xi(\tau)|\ll 1$, where $\xi(t)\triangleq {\bf{x}}^*(t)- {\bf{x}}(t)$ denotes the difference between the two trajectories at time $t$. According to (1.1), we have

where $G$ is the high order nonlinear terms of $\xi(\tau)$. Ignoring the nonlinear terms, we will simply have $\dot{\xi}(\tau) = \nabla {\bf{u}}({\bf{x}}(\tau), \tau)\xi(\tau)$.

Define the separation rate between ${\bf{x}}(t)$ and ${\bf{x}}^*(t)$ at time $\tau$ as $V(\tau)\triangleq \frac{1}{2}\frac{d}{dt}|\xi(t)|^2|_{t = \tau}$, then we have $V(\tau) = \langle \xi(t), \dot{\xi(t)}\rangle|_{t = \tau} = \langle \xi(\tau), \nabla {\bf{u}}({\bf{x}}(\tau), \tau)\xi(\tau)\rangle = \langle \xi(\tau), S({\bf{x}}(\tau), \tau)\xi(\tau)\rangle$ where $S({\bf{x}}, t)$ is the rate-of-strain tensor given by $S = (\nabla {\bf{u}}+\nabla {\bf{u}}^T)/2$. If $V < 0$, the two trajectories get closer over time while $V > 0$ indicates their separation. As a result, the separation rate between ${\bf{x}}(t)$ and ${\bf{x}}^*(t)$ at $t = \tau$ is bounded by $V(\tau)\leq \lambda_{max}(S({\bf{x}}(\tau), \tau))|\bf{e}(\tau)|^2$, where $\bf{e}(\tau)$ aligns with the eigenvector associated with the largest eigenvalue of the rate-of-strain tensor $\lambda_{max}(S({\bf{x}}(\tau), \tau))$. In other words, the maximum repelling rate of the trajectory ${\bf{x}}(t)$ at time $t = \tau$ against any nearby trajectory is actually measured by the quantity $\lambda_{max}(S({\bf{x}}(\tau), \tau))$. The LARR of the trajectory ${\bf{x}}(t)$ within the time interval $[t_0, t_0+T]$ is then defined as the integral

where ${\bf{x}}_0 = {\bf{x}}(t_0)$ is the initial location of ${\bf{x}}(t)$ at time $t = t_0$. We can see that the proposed LARR concerns the repelling behavior of the trajectory at any intermediate time.

Now we get back to the two examples given in Section 2.1 and consider the corresponding LARR values. For the first example, the rate-of-strain tensor $S({\bf{x}}, t)$ is constantly equal to zero and therefore $\text{LARR}_{t_0}^{t_0+T}({\bf{x}}) = 0$ for any ${\bf{x}}$ in the spatial domain, which indicates that no particle trajectory repels the nearby trajectories. This satisfies our expectation since all particle trajectories have kept their distance from each other during the whole time interval $[t_0, t_0+T]$. In the second example, the trajectory of the particle initially located at ${\bf{x}}_0 = (x_0, y_0)$ can be analytically given by ${\bf{x}}(t) = (x_0+t, \pi y_0/(\pi-y_0\sin^2(\pi t)))^T$. The LARR of the trajectories within the time interval $[0, 1]$ starting from the line segment $(0, 1)\rightarrow (0, 2)$ is given by $\text{LARR}_0^1(x_0, y_0) = 2\ln\frac{\pi}{\pi-y_0}$ with $1\leq y_0\leq 2$, which indicates that the upper the trajectory, the larger the LARR. This result is very reasonable as shown in Figure 1(b), since the upper trajectories repel the nearby trajectories more during the evolution process. This example suggests that the LARR is more valid and reasonable in measuring the averaged repelling behaviors of the whole particle trajectory.

2.3.   The objectivity of the LARR

Since LARR is used to measure the intrinsic repelling behaviors of particle trajectories, a basic requirement is that it is objective, i.e. remains invariant under coordinate changes of the form

where $Q(t)$ is a time-varying orthogonal matrix and ${\bf{b}}(t)$ is a time-varying translation vector. The following theorem guarantees this objectivity of the LARR.

Theorem 2.1. The LARR defined as in (2.1) is invariant under any coordinate change given by (2.2).

Proof. According to the definition of the flow map, we have ${\bf{x}}(t) = \Phi_{t_0}^t({\bf{x}}_0)$. Plugging (2.2) into this formula gives $Q(t)\tilde{ {\bf{x}}}(t)+ {\bf{b}}(t) = \Phi_{t_0}^t(Q(t_0)\tilde{ {\bf{x}}}_0+ {\bf{b}}(t_0))$, or equivalently,

where we use $\tilde{\cdot}$ to denote the operations in the transformed framework. Differentiating this equation with respect to $\tilde{ {\bf{x}}}_0$ gives $\tilde{\nabla}\tilde{\Phi}_{t_0}^t(\tilde{ {\bf{x}}}_0) = Q^T(t)\nabla\Phi_{t_0}^t({\bf{x}}_0)Q(t_0)$. Differentiating this formula with respect to time $t$ and recalling that $\frac{d}{dt}\nabla\Phi_{t_0}^t({\bf{x}}) = \nabla {\bf{u}}(\Phi_{t_0}^t({\bf{x}}), t)\nabla\Phi_{t_0}^t({\bf{x}})$, we have

Adding the transpose of both sides yields

That is, $\tilde{S}(\tilde{x}(t), t)$ is similar to $S({\bf{x}}(t), t)$ and thus $\lambda_{max}(\tilde{S}(\tilde{x}(t), t)) = \lambda_{max}(S({\bf{x}}(t), t))$.

2.4.   An efficient Eulerian algorithm for computing the LARR

Since the LARR is a quantity defined along each particular particle trajectory, a natural way to compute it is using the Lagrangian ray tracing approach. In particular, one numerically solves the integral (2.1) and the ODE system (1.1) simultaneously from the initial time $t = t_0$ to the terminal time $t = t_0+T$. In this paper, we propose an efficient Eulerian-type algorithm to compute the LARR where only one single partial differential equation (PDE) needs to be solved. For simplicity, suppose $[0, T]$ is the time interval of interest and the value of $\text{LARR}_0^T({\bf{x}})$ is required at each mesh point ${\bf{x}}$. According to (2.1), we have $\text{LARR}_0^T({\bf{x}}) = \frac{1}{T}\int_0^T \lambda_{max}(S(\Phi_0^t({\bf{x}}), t)) dt$. Then we define a real-valued function $F({\bf{x}}, t):\Omega \times [0, T] \rightarrow \mathbb{R}$ as

with $\Omega$ the computational domain. Indeed, $F({\bf{x}}, t)$ denotes the line integral of the maximal repelling rate along the particle trajectory starting from the location ${\bf{x}}$ at time $t$ and terminating at time $T$. It is obvious that $F({\bf{x}}, T) = 0$ and $\text{LARR}_0^T({\bf{x}}) = F({\bf{x}}, 0)/T$ for any ${\bf{x}}\in\Omega$. Furthermore, $F({\bf{x}}, t)$ decreases along any particle trajectory since

where $\frac{D(\cdot)}{Dt}$ denotes the material derivative, or equivalently,

Compared to the Lagrangian approach, the proposed Eulerian approach is more efficient. In particular, our Eulerian approach only needs to solve one single PDE (2.4) using any well-developed high order numerical methods like WENO5-TVDRK2 ^[3,18,22] backward in time from $t = T$ to $t = 0$ with the terminal condition $F({\bf{x}}, T) = 0$. The required LARR is then obtained by assigning $\text{LARR}_0^T({\bf{x}}) = F({\bf{x}}, 0)/T$. In contrast, the Lagrangian approach propose to solve the integral (2.1) and the ODE system (1.1) simultaneously from the initial time $t = 0$ to the terminal time $t = T$. That is, $d+1$ equations are solved together in the Lagrangian approach where $d$ is the dimension of the underlying velocty field. Our Eulerian approach is even more efficient if the velocity data is only available at discrete mesh points. All computations are implemented only on the mesh in our Eulerian approach. As a result, we only need discrete velocity data at mesh points and no interpolation is required. For the Lagrangian approach, however, since ${\bf{x}}(t)$ is in general not a mesh point, integration of ODEs (1.1) will require interpolation on the discrete velocity data at each time step. Furthermore, the computation of the integral (2.1) involves the computation of the velocity gradient along each particle trajectory. One has to first solve the velocity gradient at mesh points by using the finite difference scheme upon the discrete velocity data and then use the interpolation scheme to obtain the velocity gradient data at off-grid points. All these extra interpolation routines could be quite time-consuming. Even worse, as mentioned in ^[24], one needs to use high-order numerical algorithms to implement the integration and interpolation, otherwise some small scale flow features might not be accurately extracted.

3.   Numerical examples

We give four examples to support our claims. The first three are analytical examples while the last one is a real data example.

3.1.   The double gyre flow

This example is taken from ^[21] to describe a periodically varying double-gyre. The flow is modeled by the stream-function $\psi(x, y, t) = A \sin[ \pi k(x, t) ] \sin(\pi y)$, where $k(x, t) = a(t) x^2 + b(t) x$ with $a(t) = \epsilon \sin(\omega t)$ and $b(t) = 1- 2\epsilon \sin(\omega t)$. Here we set the parameters $A = 0.1$ and $\omega = 2\pi/10$.

3.1.1.   The solution of LARR using our proposed algorithm

In this part, we compute the LARR field $\text{LARR}_0^{10}({\bf{x}})$ using our Eulerian algorithm by assigning $\epsilon = 0.3$ and using only the velocity data at mesh points. The solution is shown in Figure 2(a) where $\Delta x = \Delta y = 1/256$. In the implementation, we only need to solve the single PDE (2.4) backward from $t = 10$ to $t = 0$ with the terminal condition $F({\bf{x}}, 10) = 0$. To show the convergence of our Eulerian algorithm, we have shown the $L_1$ errors of $\text{LARR}_0^{10}({\bf{x}})$ using the red solid line in Figure 2(b) with $\Delta x$ varying from $1/32$ to $1/512$ while keeping $\Delta t/\Delta x$ fixed. As a comparison, the errors of the solutions of $\text{LARR}_0^{10}({\bf{x}})$ computed using the Lagrangian approach are also shown using a blue dashed line in the same figure where the TVD-RK4 scheme is used for the integration of corresponding ODEs and the third order cubic spline method is used as the interpolation operator for solving the velocity and velocity gradient at off-grid points. As can be seen, our Eulerian approach is a little more accurate than the Lagrangian approach and our proposed Eulerian approach shows second order accuracy with respect to $\Delta x$. For the Lagrangian approach, since we have used high order numerical schemes to implement the integration, interpolation and finite difference, the second order accuracy can also be observed. However, once lower order interpolation schemes are used, the Lagrangian approach will no longer show second order accuracy. Regarding the computational efficiency, our Eulerian approach will behave much better than the traditional Lagrangian approach. The comparison is given in Table 1 which shows that the Lagrangian approach requires twice to three times the computational time of our Eulerian approach.

Figure 2.  (Section 3.1) (a) The $\text{LARR}_0^{10}({\bf{x}})$ field computed with our proposed Eulerian approach with $\epsilon = 0.3$. (b) The $L_1$ errors of the numerical approximation to $\text{LARR}_0^{10}({\bf{x}})$ computed with our proposed Eulerian approach (red solid line) and also the traditional Lagrangian approach (blue dashed line) with respect to different $\Delta x$'s. We also plot a solid black line with slope 2 as a reference.

DownLoad: Full-Size Img PowerPoint

Table 1.  The computational time of our proposed Eulerian approach and the Lagrangian approach with different $\Delta x$'s and fixed $\Delta t/\Delta x$.

$\Delta x$	1/32	1/64	1/128	1/256	1/512
Eulerian approach	0.9s	3.2s	20.6s	179.8s	1453.1s
Lagrangian approach	1.5s	8.5s	51.2s	502.3s	3985.2s

---

 | Show Table

DownLoad: CSV

Now we look further into Figure 2(a), from which we can observe sharp structures which correspond to the initial locations of the trajectories with high repelling rates. In particular, we have marked on this figure point $A = (1.15625, 0.34375)$ which has a high LARR value and point $B = (1, 0.5)$ which has a low LARR value. From the definition of LARR, the particle trajectories starting from point $A$ and $B$ at time $t = 0$ and terminating at time $t = 10$ must repel the nearby trajectories with a high and low rate, respectively. In Figure 3(a), we have shown the evolution of the distances between the trajectories starting from point $A$ and four neighboring mesh points during the time period $[0, 10]$. A counterpart for point $B$ is shown in Figure 3(b). To have a clearer comparison, in Figure 3(c) we have used a red (blue) line to show the temporal evolution of the maximum distance between the trajectories starting from point $A$ (point $B$) and four neighboring mesh points. All the results support our claim that the higher LARR value suggests the more repelling particle trajectory.

Figure 3.  (Section 3.1) The distances between the trajectories starting from (a) point $A$, (b) point $B$ and four neighboring mesh points during the time period $[0, 10]$. (c) The maximum distance between the trajectories starting from point $A$ (point $B$) and four neighboring mesh points is shown using a red (blue) line.

DownLoad: Full-Size Img PowerPoint

3.1.2.   Comparison between the proposed LARR and the traditional FTLE

Then we turn $\epsilon$ to 0.1 and compare our LARR field with the traditional FTLE field in detail. Figure 4(a) and (b) show the LARR field and the FTLE field, respectively. We can observe that the macroscopic topological structures of these two fields are similar. However, there do exist some differences between them, especially at the ridge locations. The FTLE field seems to have a sharper ridge and the FTLE values on the ridge have little difference. In contrast, the LARR values on its ridge have obvious differences, which implies that trajectories starting from the points on the LARR ridge have different levels of repelling properties. To have a better explanation, we first choose two points $A_1 = (1.0430, 0.1680)$ and $A_2 = (1.0820, 0.9219)$ on the FTLE ridge which have been marked using small black circles as shown in Figure 5. The LARR values at $A_1$ and $A_2$ are 0.8248 and 0.7127, respectively, i.e. $\text{LARR}_0^{10}(A_1) = 0.8248$ and $\text{LARR}_0^{10}(A_2) = 0.7127$. And the FTLE values are given by $\sigma_0^{10}(A_1) = 0.4988$ and $\sigma_0^{10}(A_2) = 0.5604$, respectively. Interestingly we have $\sigma_0^{10}(A_1) < \sigma_0^{10}(A_2)$ but $\text{LARR}_0^{10}(A_1) > \text{LARR}_0^{10}(A_2)$. As introduced in Section 1, the proposed LARR and the traditional FTLE measure the repelling properties of trajectories from different perspectives. The FTLE only concerns the particle positions at the initial time $t = 0$ and the final time $t = 10$ and does not care about where these particle trajectories have traveled at the intermediate times $t\in (0, 10)$. The proposed LARR, however, measures the averaged repelling rate of each particular particle trajectory against nearby trajectories in the whole time interval $t\in [0, 10]$. It means that, the LARR traces the repelling behavior of the trajectory at any time $t\in [0, 10]$. More intuitively, in Figure 6(a) we have shown the temporal evolution of the maximum distance between the trajectories starting from point $A_i$ ($i = 1, 2$) and four neighboring mesh points during the time period $[0, 10]$. We can see that the red line is beyond the blue line until about $t = 9.2$ and then the blue line goes beyond the red line. This means that, in most of the time during $t\in[0, 10]$ or averagely, the trajectory starting from $A_1$ is more repelling than that from $A_2$. As a result, we have $\text{LARR}_0^{10}(A_1) > \text{LARR}_0^{10}(A_2)$. In contrast, the FTLE does not care about the intermediate process and only focuses on the initial and final states. At the final time $t = 10$, the blue line is beyond the red line. Therefore, it gives $\sigma_0^{10}(A_1) < \sigma_0^{10}(A_2)$, although the blue line is under the red line in most of the time.

Figure 4.  (Section 3.1) (a) The $\text{LARR}_0^{10}({\bf{x}})$ field and (b) the FTLE field $\sigma_0^{10}({\bf{x}})$ of the double gyre flow with $\epsilon = 0.1$.

DownLoad: Full-Size Img PowerPoint

Figure 5.  (Section 3.1) $A_1$, $A_2$ are marked using small black circles and $B_1$, $B_2$ are marked using small black stars on Figure 4.

DownLoad: Full-Size Img PowerPoint

Figure 6.  (Section 3.1) The maximum distance between the trajectories starting from (a) $A_i$ ($i = 1, 2$), (b) $B_i$ ($i = 1, 2$) and four neighboring mesh points as a function of time $t\in [0, 10]$.

DownLoad: Full-Size Img PowerPoint

We have also chosen another two points $B_1 = (0.6563, 0.9492)$ and $B_2 = (1.0586, 0.4766)$ on the ridge as marked using small black stars in Figure 5. The corresponding LARR values are $\text{LARR}_0^{10}(B_1) = 0.6617$, $\text{LARR}_0^{10}(B_2) = 0.7664$ and the FTLE values at the two points are almost the same given by $\sigma_0^{10}(B_1) = 0.5430$, $\sigma_0^{10}(B_2) = 0.5441$. Figure 6(b) gives the temporal evolution of the maximum distance between the trajectories starting from point $B_i$ ($i = 1, 2$) and four neighboring mesh points within $t\in [0, 10]$. We can see that the blue line is always beyond the red line but finally they are very close at $t = 10$. This means that, the trajectory from $B_2$ is more repelling than that from $B_1$ during the whole time interval $t\in[0, 10]$ and surely $\text{LARR}_0^{10}(B_2) > \text{LARR}_0^{10}(B_1)$. However, since they are very close at the final time $t = 10$, we have $\sigma_0^{10}(B_1)\approx\sigma_0^{10}(B_2)$, although the blue line is always beyond the red line.

3.1.3.   Extension of the LARR to identify attracting trajectories

At the end of this example, we extend the use of the proposed LARR to identify the most attracting trajectories. Recalling that backward FTLE measures the level of compression ^[8,14], we here take a similar idea and propose to compute the backward LARR from the current time $t = t_0$ back to an earlier time $t = t_0-T$. Figure 7(a) shows the backward LARR field $\text{LARR}_{20}^0({\bf{x}})$ from the current time $t = 20$ back to $t = 0$. The higher the LARR value, the more attracting the underlying particle trajectory. To show this, we have particularly marked two points $C_1 = (0.9492, 0.7109)$ and $C_2 = (1.4727, 0.4297)$ as shown in Figure 7(b) where the backward LARR values at $C_1$ and $C_2$ are high and low, respectively. In particular, we have $\text{LARR}_{20}^0(C_1) = 0.7899$ and $\text{LARR}_{20}^0(C_2) = 0.0652$. As a result, the particle trajectory reaching $C_1$ at $t = 20$ should be very attracting while the trajectory getting to $C_2$ at $t = 20$ can hardly exhibit attraction. This claim is verified in Figure 8 which shows some neighbouring trajectories near $C_1$ and $C_2$, respectively. In Figure 8(a) all the nearby trajectories get closer and closer to the trajectory reaching $C_1$. In contrast, the trajectory arriving at $C_2$ has not obviously attracted the nearby trajectories.

Figure 7.  (Section 3.1) (a) The backward $\text{LARR}_{20}^0({\bf{x}})$ field. (b) Two points $C_1$ and $C_2$ are marked.

DownLoad: Full-Size Img PowerPoint

Figure 8.  (Section 3.1) Some neighbouring trajectories near (a) $C_1$ and (b) $C_2$.

DownLoad: Full-Size Img PowerPoint

3.2.   Rayleigh-B$\acute{e}$nard convection cells

As the second example, we consider a model of Rayleigh-B$\acute{e}$nard convection cells as introduced in ^[12]. The stream-function of this model is given by

Following ^[12], we here use a quasi-periodic roll motion $g(t) = 0.3\sin(4\pi t)+0.1\sin(2t)$. The $\text{LARR}_0^1({\bf{x}})$ field computed using our proposed algorithm is shown in Figure 9(a), with the mesh size $\Delta x = \Delta y = 1/256$. As a comparison, we have also plotted the FTLE field $\sigma_0^1({\bf{x}})$ in Figure 9(b). The two fields do exhibit some similarity to certain extent. However, like the double gyre flow in Section 3.1.2, we can observe some differences between them. For example, the FTLE values are very close at the two points $A = (1.5117, 0.1523)$ and $B = (1.1836, 0.5469)$ located on the FTLE ridge, which have been marked using small black circles in Figure 9(a), (b). In particular, we have $\sigma_0^1(A) = 5.2240$ and $\sigma_0^1(B) = 5.2536$. In contrast, the LARR values at the two points are $\text{LARR}_0^1(A) = 5.8381 < \text{LARR}_0^1(B) = 7.3802$. In Figure 9(c) we have shown the temporal evolution of the maximum distance between the trajectories starting from point $A$ and four neighboring mesh points within $t\in[0, 1]$, using the red line. A counterpart for point $B$ is plotted using the blue line. We can see that the red line is always under the blue line and even far from the blue line during a subinterval of $[0, 1]$. This indicates that averagely the particle trajectory starting from $B$ is more repelling than that from $A$ in the whole time period $t\in [0, 1]$. There is no doubt that $\text{LARR}_0^1(B)$ should be greater than $\text{LARR}_0^1(A)$ since the LARR measures the averaged repelling rate of the particle trajectory against nearby trajectories in the whole time interval. However, as we can see from Figure 9(c), the red line almost catches the blue line at the final time $t = 1$. As a result, the FTLE values at the two points are very close since the the FTLE only focuses on the final states of particle trajectories.

Figure 9.  (Section 3.2) (a) The $\text{LARR}_0^1({\bf{x}})$ field and (b) the FTLE field $\sigma_0^1({\bf{x}})$ marked by two points $A$ and $B$. (c) The maximum distance between the trajectories starting from point $A$ (point $B$) and four neighboring mesh points as a function of time $t\in [0, 1]$ is plotted using the red (blue) line.

DownLoad: Full-Size Img PowerPoint

3.3.   Spiral focus ridge

Then we take the spiral focus ridge for example to test our proposed Eulerian algorithm for computing the LARR and also the effectiveness of the LARR in revealing the repelling properties of particle trajectories. The example starts with a trivial field ${\bf{v}}({\bf{x}}, t) = (0, x)^T$ and its flow map is given by $(\Phi_{{\bf{v}}})_0^{\tau}({\bf{x}}) = (x, y+\tau x)^T$. Let

with $\gamma = p_0/(1+\left|x^2+y^2 \right|)$. Then the velocity field ${\bf{w}}$ of the spiral focus ridge flow is constructed as

We set the parameter $p_0 = 12$ and the computational domain as $[-1, 1]\times[-1, 1]$. The LARR field $\text{LARR}_0^3({\bf{x}})$ computed using the proposed algorithm is shown in Figure 10(a) with the mesh size $\Delta x = \Delta y = 1/128$. We can see that the fine structures can be captured. Then we mark two points $A = (0.5, -0.6953)$ and $B = (0.3594, -0.6719)$ on Figure 10(a) with a high and low LARR value, respectively. The maximum distance between the trajectories starting from $A$ and four neighboring mesh points is plotted using the red line in Figure 10(b). A counterpart for $B$ is also shown using a blue line. As can be seen, the blue line is beyond the red line at the beginning. However, as time goes the red line rises and goes far beyond the blue line. As a result, the trajectory starting from point $A$ is averagely more repelling than that from point $B$, which again verifies the effectiveness of the LARR.

Figure 10.  (Example 3.3) (a) The LARR field $\text{LARR}_0^3({\bf{x}})$ computed using the proposed Eulerian algorithm. (b) The maximum distance between the trajectories starting from point $A$ (point $B$) and four neighboring mesh points as a function of time $t\in [0, 3]$ is plotted using the red (blue) line.

DownLoad: Full-Size Img PowerPoint

3.4.   Ocean Surface Current Analyses Real-time (OSCAR)

To test the effectiveness of the LARR in measuring the repelling behaviors of particle trajectories and also the robustness of our proposed Eulerian algorithm, finally we consider a more challenging case, which is the Ocean Surface Current Analyses Real-time (OSCAR) data. In ^[25], we have used this dataset to compute the FTLE field and the ISLE field. Here we compute the LARR field of this dataset. As in ^[25], we also choose an ocean region near the Line Islands as our computational region, which is enclosed by $S17^{\circ}$ ($17$ degrees South) to $N8^{\circ}$ ($8$ degrees North) latitude and $E180^{\circ}$ ($180$ degrees East) to $E230^{\circ}$ longitude. We have re-processed the dataset to have a finer resolution of $0.25$ days in the temporal direction and $1/12^{\circ}$ in each spatial direction. The velocity data of the ocean surface current within the first 50 days in year 2015 is used and then the corresponding LARR field $\text{LARR}_0^{50}({\bf{x}})$ is computed using our Eulerian algorithm. Figure 11(a) shows the solution of $\text{LARR}_0^{50}({\bf{x}})$ from which we can observe fine structures with high LARR values. Again we have marked two points $A = (E215.25^{\circ}, S1.25^{\circ})$ and $B = (E217.5^{\circ}, N2.25^{\circ})$ on this figure which have a high LARR value and a low LARR value, respectively. From the definition of LARR, the particle trajectories starting from point $A$ and $B$ at time $t = 0$ and terminating at time $t = 50$ must repel the nearby trajectories with a high and low rate, respectively. In Figure 11(b) we have used a red (blue) line to show the temporal evolution of the maximum distance between the trajectories starting from point $A$ (point $B$) and four neighboring mesh points, which also indicates that the higher LARR value does suggest the more repelling particle trajectory.

Figure 11.  (Section 3.4) (a) The $\text{LARR}_0^{50}({\bf{x}})$ field computed with our proposed Eulerian approach. (b) The maximum distance between the trajectories starting from point $A$ (point $B$) and four neighboring mesh points is shown using a red (blue) line.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

In this study, we have proposed a novel quantity called LARR to measure the averaged repelling rate along each particle trajectory against nearby trajectories. The LARR equally treats the repelling behavior of the trajectory during the whole time period, unlike the traditional FTLE which only concerns the initial and the terminal states of particle trajectories. The LARR is shown to be framework-independent and we have also proposed a simple yet efficient Eulerian algorithm to compute it. All the analytical and real data examples have shown the effectiveness of the proposed LARR in measuring the repelling behaviors of particle trajectories and the accuracy and efficiency of our proposed Eulerian algorithm. We believe that the LARR should be closely related to the LCS or even an alternative to LCS might be developed based on the LARR, which will be further subjects of future research.

Conflict of interest

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with this work.