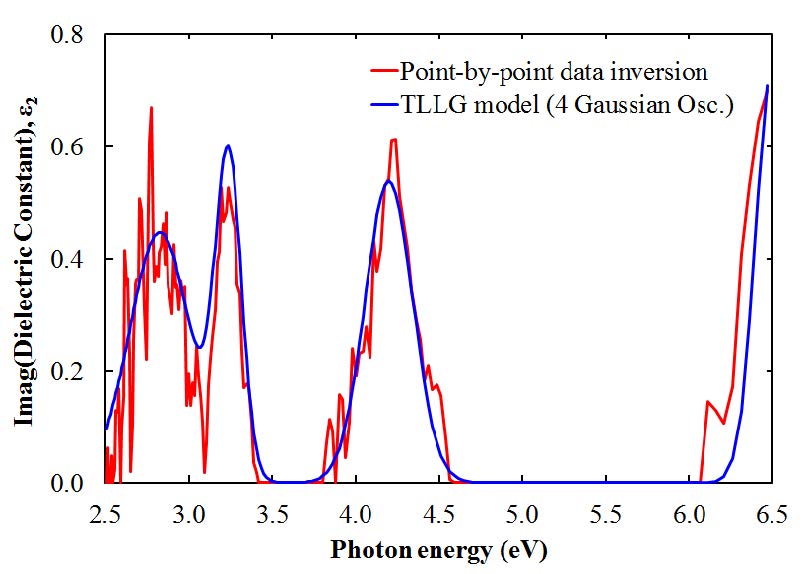
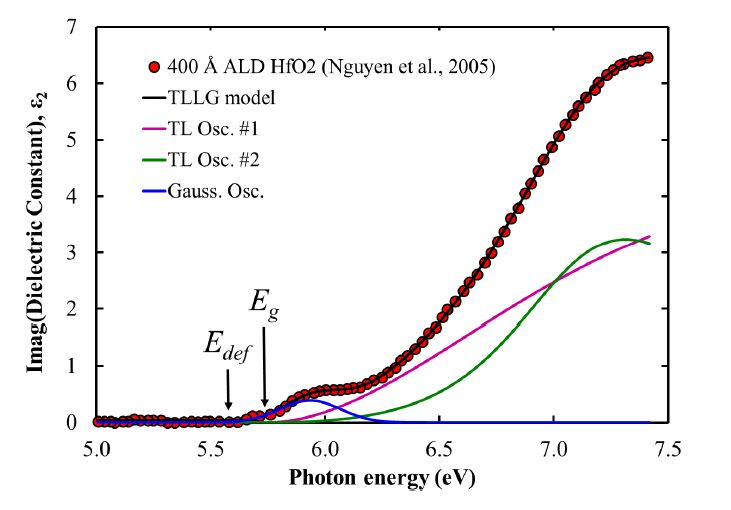
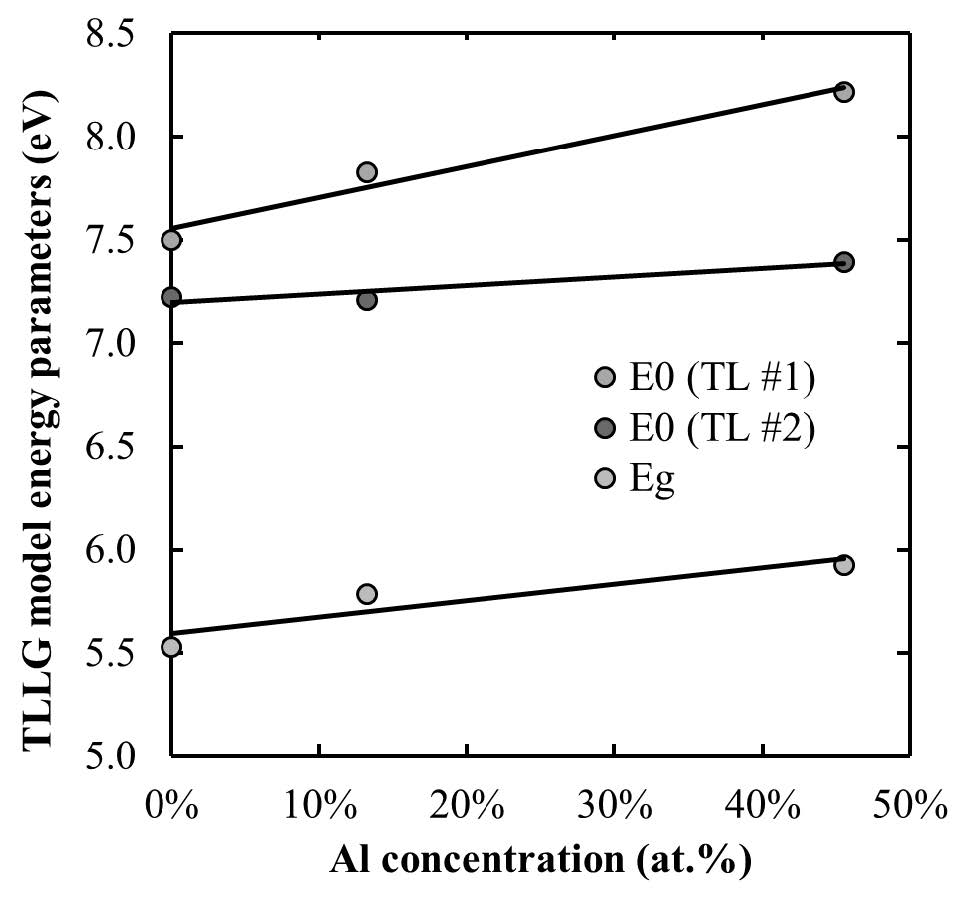
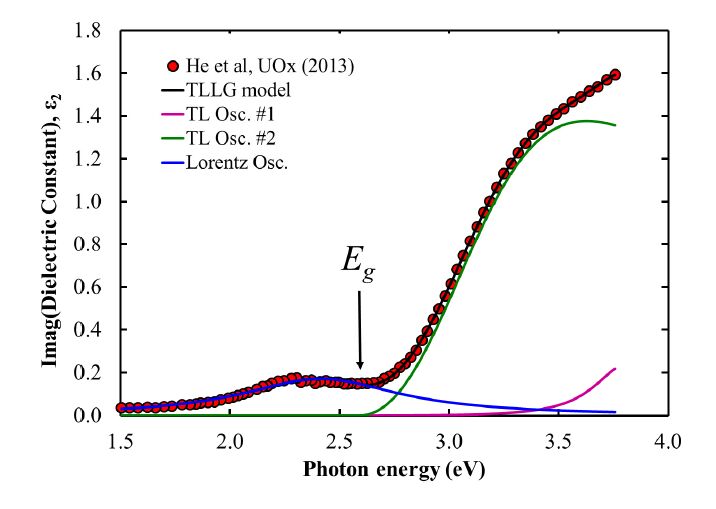
Analytic representations of the complex dielectric function, which describe various types of materials, are needed for the analysis of optical measurements, in particularly, ellipsometric data. Here, we examine an improved multi-oscillator Tauc-Lorentz (TL) model with a constraint on the band-gap parameter Eg, which forces it to be common for all TL oscillators, and possibility to represent reasonably weak absorption features below the bandgap by inclusion of additional unbounded Lorentz and/or Gaussian oscillators with transition energies located below Eg. We conclude that the proposed model is the most appropriate for the characterization of various materials with sub-band absorption features and provides meaningful value for the energy bandgap. A few examples to illustrate the use of modified model have been provided.
1.
Introduction
Let $ \Omega\subset \mathbb{R}^{2} $ be a bounded convex polygonal domain covered by a thin flat plate, and $ \Gamma = \partial\Omega $ be the Lipschitz continuous boundary of $ \Omega $. For a given loading function $ f\in L^2(\Omega), \; f\leq0 \; a.e.\; \hbox{in}\; \Omega $, and an elastic obstacle $ \psi\in L^2(\Omega) $, we consider the following clamped Kirchhoff plate problem with elastic unilateral obstacle (refer to [1,2]):
where
Here $ J(v) $ is the total energy, $ a(v, v) $ represents the strain energy corresponding to displacement $ v $ of the plate, $ j(v) $ can be interpreted as the contribution from the contact with $ \psi $ and $ (f, v) $ is the potential energy. Moreover, the symbol $ v_{-} = \min \{v, 0\} $, $ \nu\in(0, 1/2) $ is the Poisson's ratio, $ \kappa\in L^{\infty}(\Omega) $ describes the stiffness of the obstacle and satisfies $ \; \kappa\geq\kappa_{0} > 0 \; a.e.\; \hbox{in}\; \Omega $. In the limiting case $ \kappa\rightarrow \infty $, the obstacle becomes rigid and the problem (1.1) reduces to a constrained minimisation:
with $ K^* = \{v\in V: v\geq \psi\ \mbox{in}\ \Omega\} $. (1.2) is a classical displacement obstacle model of clamped Kirchhoff plate (cf.[3]) and equivalent to a fourth-order variational inequality:
Different with the displacement obstacle model (1.2), the elastic obstacle problem (1.1) can be investigated based on the following weak formulation [1]:
which has a unique solution [2] and is equivalent to another fourth-order variational inequality:
As we all know, analytical solutions to obstacle problems are always difficult to obtain. In this case, the study of numerical solutions has attracted a lot of attention. The finite element method (FEM) is a popular numerical method to solve obstacle problems [3–8]. In the last decades, more efforts have devoted to FEM analysis for the limit form of elastic obstacle problem (1.1), i.e., displacement obstacle problem (1.2), see [9–17] and references therein. But works focusing on FEMs of the elastic obstacle problem (1.1) are relatively rather few in the existing literature. From [1], the convergence analysis of a mixed FEM for the elastic obstacle problem (1.1) was obtained, where elements employed must satisfy $ C^0 $ continuous. In [18], a stabilized FEM was constructed for (1.1) with a $ C^1 $ continuous requirement. [2] provided a general framework of optimal error estimates for FEM, where the continuous requirement is relatively relaxed but continuity at each element's vertex of the subdivision is indispensable. In this situation, a natural question is whether these requirements for continuity can be completely removed. In other words, a key difficulty is how to get the optimal error estimates for a strongly discontinuous element dissatisfying above continuity requirements, which is just the motivation of this work.
In this paper, as an attempt, we will investigate the FEM approximation for the elastic obstacle problem (1.1) by using Bergan's energy-orthogonal element. This element is constructed through an energy-orthogonal free formulation (cf. [19,20]), which is convergent for arbitrary meshes. Its degrees of freedom are all defined on the element's vertex, including the function values and the two first derivatives at the three vertices of each element, which are very simple and can be used conveniently. Moreover, the global dimension of the vector of unknowns is only $ 3NP $ ($ NP $ denotes the number of vertex in mesh subdivision), about 25 percent fewer than that of the famous triangular Morley element (about $ 4NP $). This property is very useful for a reduction the amount of computation. But the element has strong discontinuous, that is, the shape function and its first derivatives are no longer continuous at the element's the vertex. This element does not satisfy the above mentioned continuity requirements. Despite so high discontinuity, Bergan's energy-orthogonal plate element has been applied to the FEM approximate for the displacement obstacle problem (1.2) (see [12]). The authors developed a convergence analysis method and obtained the optimal error estimate of order $ O(h) $ in [12]. We note that the convergence analysis relied on two additional introduced tools, i.e., an approximation subset and an enriching operator from Bergan's energy-orthogonal FE space to $ C^{1} $-conforming Bell FE space and the process is very complicated.
This paper aims to develop a new error analysis of Bergan's energy-orthogonal element approximation for the elastic obstacle problem (1.1). Unlike the convergence analysis in [12], we make full use of some special approaches, including interpolation operator splitting and energy orthogonality, to derive the optimal error estimates of order $ O(h) $ in the broken energy norm. The theoretical analysis is very simple and clear. The numerical results demonstrate the proposed method not only enjoys one-order accuracy but also can well reflect the influence brought by the obstacle stiffness parameter $ \kappa $.
The organization of this paper is as follows: In Section 2, Bergan's energy-orthogonal plate element and its typical properties are briefly introduced. Then we propose a novel error analysis approach and obtain the optimal error estimate of order $ O(h) $ successfully in Section 3. At last, Section 4 provides some numerical results to illustrate the validity of the theoretical analysis.
2.
The Bergan's energy-orthogonal plate element approximation scheme
Bergan's energy-orthogonal element was first proposed by Bergan et al. in [19] using the free formulation scheme. Then Shi et al. [20] proved that this element is equivalent to a nonconforming element constructed based on a specific interpolation $ {\Pi}_{K} $ (see Eq (2.3) below), where $ {\Pi}_{K} $ is introduced to form the shape function. It is shown in [20] that the special construction of interpolation $ {\Pi}_{K} $ makes the two components of the shape function energy-orthogonal and the stiffness matrix consistent with that in the free formulation scheme. In the following, we will introduce Bergan's energy-orthogonal plate element briefly, and the readers can refer to [19,20] for details.
Assume that $ {T}_{h} $ is a regular triangulation of $ \Omega $ with mesh size $ h $. For a given $ K\in {T}_{h} $, let its diameter be $ h_{K} $, three vertices be $ p_{i}(x_{i}, y_{i}) $ and the area coordinates be $ \lambda_{i} $ for $ i = 1, 2, 3 $. Firstly, we select nine nodal parameters set as $ \Sigma(v) = \{{v}_1, {v}_{1x}, {v}_{1y}, {v}_2, {v}_{2x}, {v}_{2y}, {v}_3, {v}_{3x}, {v}_{3y}\}, $ where $ {v}_i = v(p_{i}), \, {v}_{ix} = \frac{\partial v}{\partial x}(p_{i}), \, {v}_{iy} = \frac{\partial v}{\partial y}(p_{i}), \; i = 1, 2, 3. $ The shape function space is taken as same as that of Zienkiewicz element, i.e., $ \widetilde{{P}}(K) = span\{\widetilde{N}_{1}, \widetilde{N}_{2}, \cdots, \widetilde{N}_{9}\}, $ here $ \widetilde{N}_{j} = \lambda_{j}, \, \widetilde{N}_{4+j} = \lambda_{j}\lambda_{j+1}, \, \widetilde{N}_{6+j} = \lambda_{j}^{2}\lambda_{j+1}-\lambda_{j+1}\lambda_{j}^{2}, \, j = 1, 2, 3 $ and $ \lambda_{4} = \lambda_{1}\nonumber $. Then the associated conventional interpolation operator $ \widetilde{\Pi}_{K}: H^{3}(K) \rightarrow \widetilde{{P}}(K) $ satisfies
where $ \overline{r}_{K}(v) $ and $ r_{K}'(v) $ are the quadratic and cubic terms respectively, and the coefficients $ \alpha_{i}(v) $ can be written as: $ \alpha_{j}(v) = v_{j}, \ \alpha_{3+j}(v) = \frac{c_{(j+2)}}{2}({v}_{jx}-{v}_{(j+1)x})-\frac{b_{(j+2)}}{2}({v}_{jy}-{v}_{(j+1)y}), \ \alpha_{6+j}(v) = {v}_j-{v}_{(j+1)}+\frac{c_{(j+2)}}{2}({v}_{jx}+{v}_{(j+1)x})-\frac{b_{(j+2)}}{2}({v}_{jy}+{v}_{(j+1)y}) $ with $ b_{j} = y_{(j+1)}-y_{(j+2)} $ and $ c_{j} = -(x_{(j+1)}-x_{(j+2)}) $ for $ j = 1, 2, 3, $ here and later subscripts $ (j+i) $ will be replaced with $ (j+i)(mod\; 3) $ when $ (j+i) > 3 $ for $ i = 1, 2 $.
Next we introduce another shape function space $ P(K) = span\{N_{1}, N_{2}, \cdots, N_{9}\}, $ where $ N_{i} = \widetilde{N}_{i}, \, i = 1, 2, \cdots, 6, \, \, N_{6+j} = (\lambda_{j}-\lambda_{(j+1)})^{3}, \, j = 1, 2, 3 $ and $ \lambda_{4} = \lambda_{1} $. It is easy to verify that
and the associated traditional interpolation operator $ {\hat{{\Pi}}}_{K}: H^{3}(K) \rightarrow {P}(K) $ is defined by
where $ \beta_{i}(v), \; i = 1, 2, ..., 9, $ can be expressed as:
for $ j = 1, 2, 3. $
Now employing Eq (2.1) and Eq (2.3), we introduce an interpolation operator $ {\Pi}_{K} $ as
Then taking $ {\Pi}_{K}v $ as the shape function on $ K $ and $ \Sigma(v) $ as its associated nodal parameters (vanishing at nodes on the boundary $ \Gamma $), and defining an interpolation operator $ {\Pi}_{h} $ for every $ v \in H^{3}(\Omega) $ with $ ({\Pi}_{h}v)|_{K} = {\Pi}_{K}v, $ we can obtain a piecewise cubic polynomial space on $ \Omega $ denoted by $ V_h $. It has been shown in [20] that $ V_{h} $ is equivalent to the Bergan's energy-orthogonal plate element first proposed by Bergan etal through the free formulation scheme. Obviously, the construction process of $ V_h $ is quite different from conventional element spaces. Herein the shape function on $ K $ is formulated through the operator $ {\Pi}_{K} $ involving two interpolation operators $ \widetilde{{\Pi}}_{K} $ and $ {\hat{{\Pi}}}_{K} $.
It follows from Eqs (2.1), (2.4) and the formulas of $ \alpha_i(v) $ and $ \beta_i(v)\; (i = 1, 2, \cdot\cdot\cdot, 9) $ that
for $ j = 1, 2, 3 $, where $ \triangle $ represents the area of $ K $. Thus $ {\Pi}_{K}v $ and its two first derivatives are discontinuous at vertices $ p_j $ $ (j = 1, 2, 3) $. Moreover, the mean value of $ {\Pi}_{K}v $ along the element's each edge $ F $ can be calculated as
Obviously, it is not continuous neither. In spite of so high discontinuity of the interpolation $ {\Pi}_{K}v $, the element space possesses the following special features (cf.[20]), which will play an important role in the follow-up convergence analysis.
Lemma 2.1. $ (\mathcal{R}1) $ For any $ v_{h}\in {{V}}_h $, there exists a $ v\in H^{3}(K) $ such that
When $ {v}_{h}|_{K}\in \mathbb{{P}}_2(K) $, there holds $ {v}_{h} = \bar{v}_{h} $. Moreover, $ {\partial_{xx}}\overline{r}_{K}(v) $, $ {\partial_{xy}}\overline{r}_{K}(v) $ and $ {\partial_{yy}}\overline{r}_{K}(v) $ are constants, which together with Eq (2.2) imply that $ \overline{r}_{K}(v) $ and $ S_{K}'(v) $ are energy-orthogonal, thus the element is called energy-orthogonal. Let $ \nabla^2{v}_{h} $ be the Hessian matrix of $ {v}_{h} $, then we have $ \int_{K}\nabla^2\bar{v}_{h}:\nabla^2v_{h}'dxdy = 0 $.
$ (\mathcal{R}2) $ For $ j = 1, 2, 3 $, the quadratic term $ \overline{r}_{K}(v) $ satisfies
i.e., for any $ v_{h}\in {{V}}_h $, its quadratic term $ \bar{v}_{h} $ is continuous at the element's vertices and midpoints of edges. In other words, $ \bar{v}_{h}\in C^0(\Omega) $.
$ (\mathcal{R}3) $ For any $ v\in H^{3}(K) $ and integer $ m $ $ (0\leq m\leq 3) $, there holds
Here and later, $ C $ denotes a positive constant independent of $ h $ and may be different at each appearance.
We consider the Bergan's energy-orthogonal plate element discrete approximation form of the variational inequality (1.5) as:
where $ a_h(w_{h}, v_{h}) = \sum\limits_{K\in T_h} \int_{ K}\Delta w_{h} \Delta v_{h}+ (1-\nu)(2w_{hxy}v_{hxy}-w_{hxx}v_{hyy}-w_{hyy}v_{hxx})]dxdy. $
3.
The optimal error estimate
In this section, we will establish error estimates of Bergan's energy-orthogonal FEM for the elastic obstacle problem (1.1) in the energy norm.
Firstly, using the the similar argument to [2], we have
Theorem 3.1. The problem (2.11) is equivalent to the discrete approximation of plate problem:
which has a unique solution $ u_h $. Moreover, $ \|u_h\|_h $ and $ \|(u_{h}-\psi)_{-}\|_0 $ are uniformly bounded independently of $ h $, where $ \left\| \cdot \right\|_{h} = (\sum\limits_{K\in T_h}\left| \cdot \right|_{2, K}^{2})^{\frac{1}{2}} $ can be shown to be a norm over $ V_{h} $ by using $ (\mathcal{R}1) $ and $ (\mathcal{R}2) $ in Lemma 2.1.
In what follows, we will give error estimate for Eq (2.11).
Theorem 3.2. Assume that $ u $ and $ u_{h} $ are the solutions of Eqs (1.5) and (2.11) respectively, $ u\in H^3(\Omega) $ and $ f, \; \psi\in L^{2}(\Omega) $, then we have
where the constant $ C $ depends on the stiffness of the obstacle $ \kappa $.
Proof. Since $ \left\| u-u_{h} \right\|_{h}\leq \left\| u-{{\Pi}_{h}u} \right\|_{h}+\left\| {{\Pi}_{h}u}-u_{h} \right\|_{h}, $ in view of Eq (2.9) in $ (\mathcal{R}3) $ of Lemma 2.1, we only need to estimate the second term $ \left\| {{\Pi}_{h}u}-u_{h} \right\|_{h} $. In fact, let $ w_h = {{\Pi}_{h}u}-u_{h} $ and employ Eq (3.1), we have
Now we concentrate on the estimate of the second term in the right hand of Eq (3.3). It follows from $ (\mathcal{R}1) $ in Lemma 2.1 that $ w_{h} = \bar{w}_{h}+w_{h}' $ and there exists a $ w\in H^{3}(K) $ such that
Then we can deduce that
On one hand, from [2] we know that the solution $ u $ of the problem (1.5) satisfies
On the other hand, $ (\mathcal{R}2) $ in Lemma 2.1 implies $ \bar{w}_{h} \in H_{0}^{1}(\Omega) $. Thus applying Green formula and Eq (3.6) yields
here $ \textbf{n} $ and $ \textbf{s} $ are the unit outward normal vector and tangential vector respectively.
Substituting Eq (3.7) into Eq (3.5) leads to
In what follows, we will estimate $ (Er)_j $ one by one for $ j = 1, 2, ..., 6. $
Firstly, applying Lemmas 3.5 and 3.6 in [21] yields
By use of Eq (3.4), we get
At the same time, employing Eq (2.10) in $ (\mathcal{R}3) $ and the inverse estimate gives
which in conjunction with Eq (3.10) leads to $ \label{zz50}|(Er)_1|\leq Ch\| u\|_{3}\|w_{h}\|_h. $
Secondly, the fact $ \bar{w}_{h} \in H_{0}^{1}(\Omega) $ implies $ \label{xzz50} (Er)_2 = 0. $
Thirdly, from Eq (2.2), we have $ a_{h}(\overline{{\Pi}_{h}u}, w_{h}') = 0 $, which together with the Eq (2.10) in $ (\mathcal{R}3) $ and Eq (3.10) gives
Moreover, it follows from Eq (3.4), Eq (2.10) in $ (\mathcal{R}3) $ and the inverse estimate that
which reveals
Finally, by use of the elementary inequality $ (t_{-}-s_{-})(t-s)\geq 0 $ and Theorem 3.1, we have
Then combining Eq (3.8) and the above bounds of $ (Er)_1 $–$ (Er)_6 $ results in
Therefore, the desired result Eq (3.2) follows from $ (\mathcal{R}3) $, Eqs (3.3) and (3.17) immediately.
Remark. The analysis presented herein is also valid to the elastic obstacle problem (1.1) with $ j(v) = \int_{\Omega}{\kappa}[(v-\psi)_{+}]^{2}dxdy $, $ v_{+} = \max \{v, 0\} $ and $ f\in L^{2}(\Omega), \; f\geq0 \; a.e.\; in\; \Omega $.
4.
Numerical results
We consider the elastic obstacle problem (1.1) with $ \Omega = (0, 1)^2 $, $ f = -10, \ \nu = 0.25 $ and an elastic obstacle defined by the function $ \psi = \left\{0 if(x,y)∈[0.3,0.7]2,−1 otherwise. \right. $ The domain $ \Omega $ is firstly divided into $ N\times N $ rectangles. Then each rectangle is further divided along its diagonal into two equal triangles.
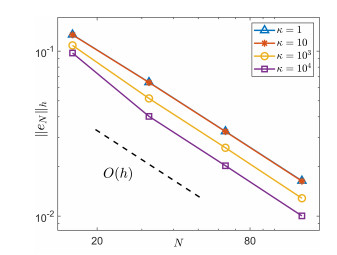
Since it is not easy to derive the exact solution, we denote $ u_N $ as the $ N $-th level discrete solution and take $ \|e_N\|_h = \|u_N-u_{N-1}\|_h $ as the error in the broken energy norm. The numerical results $ \|e_N\|_h $ for different obstacle stiffness parameter $ \kappa = 10^j \ (j = 0, 1, 3, 4) $ with $ N = 16, 32, 64,128 $ are given in Table 1 and further plotted in the logarithm scales in Figure 1. We observed that the errors in the energy norm are indeed convergent at optimal order $ O(\frac{1}{N}) $, i.e., $ O(h) $, as $ h = \frac{\sqrt{2}}{N}\rightarrow 0 $. This result is consistent with the theoretical analysis in Theorem 3.2.
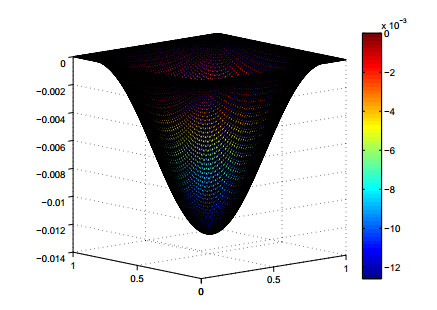
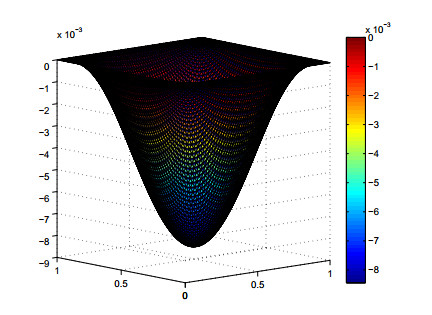
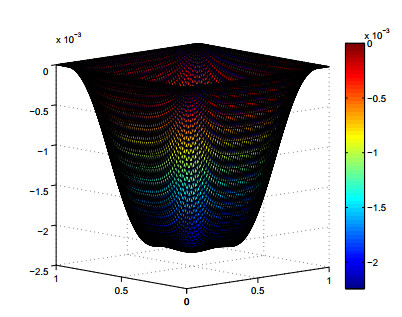
Moreover, the discrete solution $ u_N $ with $ N = 64 $ is also depicted in Figures 2–4, where the parameter $ \kappa $ is chosen as $ 1, 10^3\; $and$ \; 10^4 $, respectively. We can see that the bigger parameter $ \kappa $, the more obvious the influence of obstacles. From Figure 2 ($ \kappa = 1 $) and Figure 3 ($ \kappa = 10^3 $), we observe that the difference of $ \kappa $ makes the minimum value of the discrete solution change, but the shape of the solution does not change significantly. In Figure 4 ($ \kappa = 10^4 $), it is easy to see that the elastic obstacle has a very obvious effect on the solution, which is agrees with the fact that the elastic obstacle will become a rigid obstacle when $ \kappa\rightarrow \infty $. This phenomenon further indicates the proposed numerical method in this paper can also be used for approximated simulation of the displacement obstacle problem by taking a relatively large obstacle stiffness parameter $ \kappa $.
In a word, the numerical results in this section confirm the theoretical analysis in Section 3 and indicate the effectiveness of the numerical method.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No.11701523, 11801527, 11871441).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: