Application of Digital Imaging for Cytopathology under Conditions of Georgia

1.   Introduction

By 1941, Huggins and Hodes ^[1] had demonstrated that castration induces the regression of prostate tumors, which implies that the growth of prostate cancer cells is highly dependent on androgen (male sex hormones). Their work showed, perhaps for the first time, that some cancers potentially could be clinically treatable by chemical means, and Huggins shared the 1966 Nobel Prize in Medicine and Physiology for this discovery ^[2]. Nowadays, hormone therapy—specifically, androgen suppression therapy—is a common treatment for localized and locally advanced prostate cancer and has been shown to have a significant survival benefit, albeit with considerable side effects ^[3]. Typically, continuous androgen suppression (CAS) therapy is given until the tumor evolves resistance, at which point the patient's prognosis becomes unfavorable ^[4,5].

Intermittent androgen suppression (IAS) therapy aims to reduce the side effects of CAS and potentially delay the onset of hormonal resistance ^[6]. During IAS, the patient is put on treatment until his blood serum level of prostate-specific antigen (PSA, a biomarker for prostate cancer) falls below a predetermined lower threshold. Treatment is halted until the patient's PSA level later rises above a predetermined upper threshold, when it is restarted. The on-off cycles are repeated until the tumor becomes resistant. Although IAS reduces the side effects of treatment, its ability to forestall treatment resistance is not yet clear ^[7].

Over the last decade, various mathematical models have been developed to describe the dynamics of prostate cancer under IAS, as measured by clinical time series of blood serum levels of PSA, and possibly also of androgen, of individual patients in clinical trials. The models are clinically validated insofar as initial conditions and rate parameters can be selected so that the numerical solutions reproduce the observed time series with reasonable fidelity. Several such models are described in Section 1.2.

1.1.   Motivating example

One of the main clinical problems in any individual patient case, and one for which a validated mathematical model of prostate cancer might provide insight, is whether another round of IAS therapy will be helpful. Thus it is reasonable to ask, if a given mathematical model accurately reproduces past observations of PSA, can it predict future observations with an acceptable degree of reliability? If not, then why not?

To illustrate, we consider a particular patient in a clinical trial of IAS whose serum PSA levels are measured approximately every 30 days. This patient starts treatment on day 0, goes off treatment around day 300, restarts around day 600, and so on for five intervals of approximately 300 days each. Using a fitting procedure described in Section 2.4, parameters for two models, which we call Model H and Model P in Section 1.2, are selected to provide "optimal" values of the model parameters, insofar as each model solution, starting from a fixed initial condition and integrated for 900 days, yields the smallest root-mean-square difference with the data. In addition, we vary the relative value of one of the model parameters by up to 10 percent from the "optimal" one.

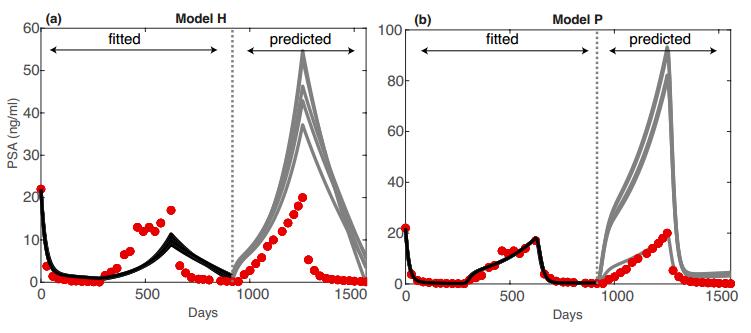
Figure 1 shows the results. The solid curves in each panel show the respective model's solutions obtained from both the "optimal" parameters and from varying one of the parameters slightly as just described. The models are integrated for 1500 days from a suitable initial condition to demonstrate 900 days of approximate agreement with clinical measurements of PSA (the "fitted" interval) and another 600 days of predicted PSA levels (the "predicted" interval), assuming that the last cycle of IAS therapy begins around day 1200. Although Model P (Figure 1(b)) reproduces the observed PSA levels through day 900 better than Model H, its predictions of PSA levels for days 900–1500 are much worse. Both Model H and Model P significantly overestimate—by factors of greater than 2 and 4, respectively—the observed PSA level in the second off-treatment interval, depending on the choice of parameter. One choice of parameter vector for Model P yields a pretty good prediction of the effect of the next cycle of treatment, but the others do not, even though all the choices accurately reproduce the observations over the "fitted" interval.

We investigate two principal mathematical questions in this paper. First, can the parameters of a given model be estimated reliably from available clinical data, which typically consists of serial measurements of serum PSA? This question motivates our investigation into parameter identifiability, which includes issues of structural and practical identifiability ^[8,9]. Second, what are some useful approaches to quantify the uncertainties in parameter estimates and the reliability of "patient-specific" forecasts of treatment response, based on a particular model? This question motivates our use of an ensemble Kalman filter (EnKF), which is widely used for data assimilation and parameter estimation in weather forecasting and similar predictive settings.

Our main conclusions are that, while parameters for a deterministic model may reproduce clinical measurements well, they may be subject to large uncertainties, as may the predictions of such a model. Additional types of clinical measurements, if available, may help constrain the values of more parameters. To be clinically practicable, model design must take into consideration the nature of the available observations. The next sections provide an overview of some dynamical models of IAS therapy and some background on parameter identifiability and uncertainty quantification.

1.2.   Mathematical models of prostate cancer treatment

Jackson ^[10] laid the groundwork for several data-driven mathematical models for prostate cancer ^[11,12,13]. The three models considered in this paper all assume that the tumor is composed of two or more subpopulations of cells that differ in their degree of androgen dependence. However, the models differ in the way they represent the biological details, particularly the role in which androgen fuels the growth of the tumor cells.

1.2.1.   Model H: the Hirata et al. model

Hirata et al. ^[14,15,16] introduced a piecewise-linear model ("Model H") of the dynamics of prostate cancer under IAS therapy. Model H proposes that there are three cancer cell subpopulations, $ x_1 $, $ x_2 $, and $ x_3 $, that represent, respectively, treatment-sensitive, -insensitive, and irreversibly treatment-insensitive cells. It has been used to study parameter estimation and optimal control of IAS therapy as well as forecasting of treatment resistance and uncertainty quantification ^{[14,17,18,19]}.

Model H is constructed by assuming that the rates of biphasic increase and decrease of PSA levels during the respective off- and on-treatment intervals are linear combinations of the tumor cell subpopulations. At any given instant, cells in subpopulation $ j $ grow at the rate $ w_{jj}x_j $; cells transition from subpopulation $ j $ to $ k $ at the rate $ w_{kj}x_j $, $ j, k\in\{1, 2, 3\} $, and $ w_{3j} = 0 $, $ j = 1, 2 $. There are two versions of each parameter: $ w_{jk}^0 $ during the off-treatment intervals and $ w_{jk}^1 $ during treatment. During the on-treatment intervals, Model H takes the form

This form implicitly takes into account the lack of androgen, which retards the growth of the $ x_1 $ and $ x_2 $ subpopulations and also selects for the fully treatment-resistant phenotype, $ x_3 $.

During off-treatment intervals, Model H assumes that the partially treatment-resistant ($ x_2 $) subpopulation reverts back to the sensitive one ($ x_1 $) at a certain rate, while the growth of the $ x_3 $ population depends only on its present size:

Model H also assumes that the level of serum PSA at time $ t $ is proportional to the sum of the three tumor subpopulations,

For simplicity, the units of tumor cell populations and PSA level are scaled such that $ \alpha = 1 $. Although the validity of the biological assumptions in Model H is debatable, it reproduces clinical time series of PSA data well ^[14,16,20].

Model H has 10 parameters and 3 initial conditions that must be estimated from PSA data (androgen is not explicitly incorporated). There are no a priori constraints on the parameters, other than clinically realistic bounds on the net tumor growth rate.

1.2.2.   Model P: The Portz et al. model

In contrast to the phenomenological approach in Model H, Portz, Kuang, and Nagy ^[12] have formulated a mechanistic model ("Model P"), inspired by Droop's nutrient-limiting theory ^[21], that regards androgen as the limiting nutrient for cancer growth and transformation. Model P has inspired several variants ^{[9,20,22,23,24,25]}, but we focus on the original formulation here. Model P presumes that the tumor is comprised of treatment-sensitive and -insensitive prostate cancer cells, each of which requires a minimum level of androgen, called the cell quota. When the available androgen falls below the cell quota, the respective subpopulation declines. Cells may mutate from one subpopulation to the other in response to selection pressure from IAS therapy.

Model P contains explicit equations that govern the intracellular androgen levels, $ Q_1 $ and $ Q_2 $, of the treatment-sensitive and -insensitive subpopulations $ x_1 $ and $ x_2 $, respectively. Androgen data is used to interpolate values for the serum androgen function $ A(t) $, which acts as an external forcing to represent the on- and off-treatment cycles. The growth and transformation rates for both cell subpopulations depend on the intracellular androgen levels, while the death rates are constant ^[12].

Model P is defined by the following system of differential equations:

The cell quota for each subpopulation is $ q_j $, the death rate is $ d_j $, and the mutation rate from subpopulation $ i $ is $ \lambda_j(Q_j) = K_j/(Q_j + K_j) $, $ j = 1, 2 $. Since $ x_2 $ is the less treatment-sensitive subpopulation, $ q_2 < q_1 $. The PSA production rate depends on the tumor cell subpopulations. Further details about the development of this model are found in ^[12].

Model P contains 21 parameters and a 5-dimensional state vector. It is possible to find parameters so that model solutions replicate clinically observed time series of serum PSA levels ^[12,20]. While the PSA data is utilized for estimating the model parameters, the available androgen data is used only for the interpolation of $ A(t) $. The parameters in Model P are biologically meaningful, and ranges for most of them can be found in the literature.

1.2.3.   Model T: the Phan et al. model

One difficulty with Model P is that it cannot reproduce PSA relapse under CAS ^[26] within the parameter ranges given in ^[12]. The problem may arise from the assumption that the cell subpopulations can mutate from one to the other ^[9]. To address these issues, Baez and Kuang ^[22] introduced a simplification of Model P, which has been further refined into Model T, below. (See ^[24] for the derivation.) Key changes include the addition of an irreversibly treatment-resistant tumor subpopulation (similar to that of Model H) and the addition of a compartment for serum androgen, $ A $:

where the respective androgen-dependent death and mutation rates are $ D_j(Q) = d_j R_j/(Q+R_j) $, $ j = 1, 2 $ and $ \lambda(Q) = cK/(Q+K) $. The unit step function $ u(t) $ is $ 1 $ when when the patient is on treatment and is $ 0 $ otherwise; the treatment time intervals are determined directly from the data.

Model T has $ 21 $ parameters and a $ 5 $-dimensional state vector. Biologically realistic estimates of the parameters are given in Table 1. In this paper, we fix the parameters $ c = 0.00015 $, $ K = 1 $, $ \delta_1 = 5 $, $ \delta_2 = 5 $, and $ \gamma_2 = 0.005 $ in all simulations, as their values have relatively little effect on the model output ^[24]. For simplicity, we also set $ \mu_1 = \mu_2 = \mu_m $, which leaves a model with $ 13 $ adjustable parameters that we call T-13. Based on the results of a prior a sensitivity analysis ^[24], we also consider a version of Model T, which we call T-5, in which all but 5 of the parameters are fixed. (The adjustable parameters in Eqs. 1.9–1.13 in Model T-5 are $ \mu_m $, $ q_2 $, $ d_1 $, $ \gamma_1 $, and $ A_0 $.) The parameter estimation and time series prediction procedures processes described in Section 2 are carried out on versions T-13 and T-5 using time series of serum PSA and androgen levels.

2.   Materials and methods

As described in the introduction, we are concerned with two main questions: the reliability with which model parameters can be estimated from the available data, and the trustworthiness of model predictions after the parameters have been selected to maximize the agreement between model observables and prior clinical measurements of PSA. In this section, we briefly survey the data sources that we use and the mathematical approaches that we apply to each question.

2.1.   Data

The data for this study comes from a clinical trial at the Vancouver Prostate Center, which admitted patients who demonstrated a rising serum PSA level after they received radiotherapy and had no evidence of metastasis ^[27]. The study admitted patients who had not had hormonal suppression therapy, with the exception of less than 3 months of neoadjuvant androgen suppression, and who experienced PSA relapses after radiotherapy with no evidence of distant metastasis (e.g., bone metastasis) ^[27]. The study contains patients with high serum PSA levels prior to androgen suppression therapy (i.e., $ \mbox{PSA} > 6\, \mbox{ $\mu$g/L} $).

The data used in the parameter-fitting and prediction efforts in this paper come from two disjoint subsets totaling 54 patients, for whom we have approximately monthly measurements of serum PSA and androgen levels. One subetaoup of 28 patients has data for at least one cycle of androgen-suppression treatment, and the second subetaoup of 26 patients, 2.5 cycles. We do not have imaging data or other independent measures of tumor volume, nor any biopsy, genomic, or cell receptor information from these patients.

2.2.   Parameter identifiability and associated metrics

Each of the models considered here defines a vector field $ \mathbf{F} $ of an $ m $-dimensional state vector $ \mathbf{x}(t) $ that depends upon a fixed $ q $-vector of parameters $ \mathbf{p} $. At each measurement time, the clinical observations are assumed to be a function $ \mathbf{H}: \mathbb{R}^m \to \mathbb{R}^s $ of the tumor state; in this paper, $ s = 1 $ or $ 2 $ depending on whether both androgen and PSA levels are observed. We may represent the mathematical setup as a system of the form

Here $ \mathbf{y}(t, \mathbf{p}) $ represents the observables (predicted observations) from the given initial condition and parameter vector at time $ t $. We represent by the $ s $-vector $ \mathbf{y}^{\mbox{ obs}}(t) $ the actual data (observations) at selected measurement times.

If any component of $ \mathbf{p} $ is an implicit function of some of the others, then, in general, different values of $ \mathbf{p} $ yield the same solution vector $ \mathbf{x}(t, \mathbf{p}) $ for a given initial condition. In such a case, $ \mathbf{p} $ is said to be structurally non-identifiable because $ \mathbf{p} $ cannot be estimated uniquely from a given set of observables. In general, it is not possible to define a confidence interval for numerical estimates of structurally non-identifiable parameters.

If no implicit functional relationship exists between the elements, then $ \mathbf{p} $ is structurally identifiable ^[28,29]. Practical identifiability refers to the question of whether the components of $ \mathbf{p} $ can be estimated with suitably small confidence bounds from observations with noise of finite variance. Structural identifiability is a necessary condition for practical identifiability ^{[30,31,32,33]}.

2.2.1.   The Fisher information matrix

The Fisher information matrix (FIM) measures the sensitivity of the model output at measurement times $ t_n $ with respect to the model's parameter vector. It can detect combinations of identifiable parameters ^[34,35,36]. Given a set of measurements at $ N $ distinct time points and an ODE model with an $ m $-dimensional state vector and $ q $-vector of parameters, the $ Nm\times q $ sensitivity matrix $ \mathbf{S} $ consists of $ N $ time-dependent $ m\times q $ blocks $ \mathbf{A}(t_n) $:

The $ q\times q $ Fisher information matrix is $ \mathbf{M} = \mathbf{S}^{\rm T}\mathbf{S} $. (In practice, each $ A_{jk} $ must be approximated numerically.) The parameter vector $ \mathbf{p} $ is structurally identifiable if and only if $ \mathbf{M} $ has full rank ^[31]. The rank of $ \mathbf{M} $ corresponds to the number of identifiable parameter combinations in $ \mathbf{p} $. The condition number of $ \mathbf{M} $ is a measure of the practical identifiability of the parameters: if the condition number is large, then small amounts of measurement noise can render reliable estimation of $ \mathbf{p} $ impossible.

The Cramér-Rao bound covariance matrix is $ \mathbf{C} = \mathbf{M}^{-1} $. The diagonal element $ C_{jj} $ is the asymptotic variance of the $ j $th parameter; $ C_{jj}^{1/2} $ is the standard deviation ($ SD_j $) of $ p_j $. The coefficient of variation ^[34] for the $ j $th parameter is

If $ CV_j \ge 1 $, then the uncertainty in $ p_j $ is at least as great as its value, which may be considered a useful upper bound for practical identifiability. If $ CV_j $ is large (say, $ CV_j > 10^4 $), then $ p_j $ simply may not be estimable from the data, which renders it structurally unidentifiable ^[8,34].

2.2.2.   The profile likelihood method

The available observations in this study are time series of serum PSA, and, in some cases, of serum androgen, so the observation vector $ \mathbf{y}^{\mbox{ obs}}(t_n) $ has at most 2 components (with respective standard errors $ \sigma_{jn} $). For a fixed time series of such observation vectors, and a given set of observables $ \mathbf{y}(t, \mathbf{p}) $ (Eq. 2.9), the negative log likelihood function takes the form

where $ \mathbf{p} $ is the model parameter vector. There are $ N $ measurement time points and $ s $ observations at each time point ($ s = 1 $ or $ 2 $ for the models discussed here). When the measurement variances $ \sigma_{jn} $ are all equal to the same known constant, the minimization of $ -LL $ is equivalent to the minimization of the third term on the right-hand side of Eq. 2.5, and, thus, parameter estimation with the negative log likelihood is equivalent to least-squares minimization. (We take $ \sigma_{jn} = 1 $ for the PSA and androgen time series used in this paper.)

The profile likelihood is computed by fixing one element of $ \mathbf{p} $ and choosing the remaining elements over appropriate ranges to minimize Eq. 2.5. The profile likelihood $ PL_j $ is computed as

where all but the $ j $th component of $ \mathbf{p} $ is varied over an appropriate interval. The confidence interval $ \alpha $ for the profile likelihood of parameter $ p_j $ is

For a sufficiently large data set, $ \Delta(\alpha) $ takes the following form asymptotically:

Here $ \text{icdf}(\chi^2, \alpha, df) $ is the inverse cumulative distribution function for $ \chi^2 $ with $ \alpha $-quantiles (e.g., $ \alpha = 0.95 $ for a 95% confidence interval) and $ df $ degrees of freedom, which can be taken as $ 1 $ when all but one element of the parameter parameter vector is fixed, or as $ q $ for a simultaneous confidence interval for all components of the model parameter vector ^[8,29,37].

2.3.   Uncertainty quantification: the ensemble transform Kalman filter

The ensemble Kalman filter (EnKF) is a common approach to data assimilation ^[38,39]. It is used to estimate the $ m $-dimensional state vector of a dynamical model given a set of noisy observations that can be regarded as a "predictor-corrector" scheme.

The simulations presented here use the ensemble transform Kalman filter ^[40], which is one of several possible square-root filters. Details of the implementation are given in the appendix, but we briefly summarize the approach here. Starting with a set of $ K $ initial conditions at $ t_n $, we integrate the model to time $ t_{n+1} $ to produce a background ensemble $ \left\{\mathbf{x}(t_{n+1})_{b(k)}\right\}_{k = 1}^K $. Let $ \mathbf{y}^{\mbox{ obs}}(t_{n+1}) $ denote the vector of measurements at $ t_{n+1} $. (Depending on the time series, the measurement is either a 1-vector of serum PSA level or a 2-vector of serum PSA and androgen levels.) Here we assume that the observables (i.e., predicted observations) are related to the model state vector by the function $ \mathbf{H} $, sometimes called the forward operator, as

In the models considered in this paper, $ \mathbf{H} $ may be a linear (e.g., Eq. 1.3) or a nonlinear (e.g., Eqs. 1.8 and 1.13) function of the model state vector.

The objective of the ensemble transform Kalman filter is to find a linear combination of the elements of the background ensemble that best match the data, in the sense that the weight vector $ \mathbf{w} $ minimizes the sum of squares

where

is the ensemble mean, $ \mathbf{X}_b $ is the $ m\times K $ ensemble perturbation matrix whose $ i $th column is $ \mathbf{x}(t_{n+1})_{b(k)}-\overline{\mathbf{x}}_b $, $ k = 1, \ldots, K $, $ \mathbf{R} $ is the covariance matrix of the errors in the observations, and $ \mathbf{H} $ is the forward operator associated with the model. (The ensemble mean and perturbation matrix vary with time, as may $ \mathbf{H} $ and $ \mathbf{R} $, but the explicit time dependence is omitted here to simplify the notation.) The filter produces the analysis ensemble $ \{\mathbf{w}_{a(k)}\}_{k = 1}^K $, which in model space becomes

(See the appendix for further details.) The analysis ensemble defined in Eq. 2.12 forms a new set of initial conditions, which are then integrated to the next observation time $ t_{n+2} $, and the process is repeated until the end of the data series.

The process begins with a preselected set of initial conditions at $ t_0 $. The results described below include patients for whom there are at least $ 20 $ observation time points.

State augmentation. The Kalman filter can be used to estimate $ q $ model parameters with the rest of the $ m $-dimensional state vector by considering the $ (m+q) $-dimensional vector $ \mathbf{x}^* = (\mathbf{x}, \mathbf{p})^{\rm T} $ that solves the augmented system

In our case, the associated forward operator is $ \mathbf{H}^* = (\mathbf{H}, {\bf 0})^{\rm T} $ because the parameter vector is not observed directly. Here $ \mathbf{G} $ can be any model for the evolution of the parameter vector $ \mathbf{p} $. In the simplest case, which is considered here, the parameters are assumed constant over the course of treatment, so $ \mathbf{G} = {\bf 0} $, but a more sophisticated model of parameter drift could be used.

2.4.   Mean-squared-error parameter estimation

Our metric for the agreement between the observations and the model observables at the $ n $th measurement time, $ n = 1, 2, \ldots, N $ is the mean squared error (MSE) defined by

where $ \sigma_{jn} $ is the variance of the measurement error in the $ k $th component of the observation vector at time $ t_n $. (We take $ \sigma_{jn} = 1 $ for the data used in this paper.) If the measurement errors are normally distributed, then $ E $ has a $ \chi^2 $ distribution, and minimizing $ E $ is equivalent to maximum likelihood estimation ^[29]. In the numerical investigations described in Section 3, the parameter estimation is carried out using the MATLAB built-in function $\textsf{fmincon}$.

Because the exact analytical expressions for the solutions of the models in question are difficult or impossible to find, the blocks of the sensitivity matrix $ \mathbf{S} $ (Eq. 2.3) are estimated numerically at the time of each clinical measurement. We illustrate the approach first with Model H, Eqs. (1.1)–(1.2), which has $ 10 $ parameters.

Initially, the total tumor cell population ($ x_1+x_2+x_3 $) in Model H numerically equals the first clinical measurement of serum PSA level. For parameter identification purposes, we fix the initial cell populations $ x_1(0) $, $ x_2(0) $, and $ x_3(0) $ to be $ 0.95\% $, $ 0.05\% $, and $ 0\% $, respectively, of the initial PSA measurement. For our numerical computations, we use the time series of serum PSA data from Patient 1 in the Vancouver Prostate Center public dataset ^[27] (any patient will do). Clinical measurements are taken approximately at monthly intervals; $ P(t_0) $ is the initial clinical measurement of PSA level at the start of treatment, and $ P(t_n) $, the $ n $th subsequent measurement. We select the parameters to minimize $ E(\mathbf{x}_0, \mathbf{p}) $, Eq. (2.14), using the built-in MATLAB function $\textsf{fmincon}$.

All $ 10 $ parameters are minimized simultaneously using the time series of PSA data from the first 1.5 cycles of treatment (i.e., the initial on-off-on treatment intervals). The allowed parameter ranges for Model H, used as constraints in $\textsf{fmincon}$, are taken from ^[20]. The output is an estimated parameter vector,

for which a model integration starting from the initial condition above produces observables (i.e., predicted serum PSA levels, Eq. 1.3), that minimize $ E(\mathbf{x}_0, \mathbf{p}) $.

An analogous procedure is performed for the $ 21 $ parameters of Model P, using the initial condition $ x_1(0) = 99 $, $ x_2(0) = 1 $, $ Q_1(0) = 0.5 $, $ Q_2(0) = 0.5 $. The initial PSA level, $ P(0) $, is taken as the first clinical measurement of PSA. The process is similar for Model T using the initial conditions in Section 3.2.

2.5.   Numerical estimation of the Fisher information matrix

After the parameter estimates are obtained from $\textsf{fmincon}$, we estimate the uncertainty in each parameter as follows. At time $ t_0 $, i.e., at the time of the first clinical measurement of PSA after treatment begins, we perturb the first parameter, $ p_1^* = w_{1, 1}^{1*} $, to generate two new values, $ w_{1, 1}^{1*, \pm} = (1\pm 0.01) w_{1, 1}^{1*} $, from which we integrate the model to the first measurement time, $ t_1 $. Then we approximate

(cf. Eq. 2.3) by finite differencing the two solutions at $ t_1 $ with respect to the $ j $th component of the model state vector, $ j = 1, 2, 3 $. We proceed likewise for $ w_{2, 1}^{1*} $ through $ w_{3, 3}^{1*} $ to estimate the first block $ \mathbf{A}(t_0) $ of the sensitivity matrix. During the on-treatment intervals, the elements of $ \mathbf{A} $ corresponding to parameters $ w_{1, 1}^{0*} $ through $ w_{3, 3}^{0*} $ are zero.

This process begins anew at $ t_1 $, starting with the state vector $ \mathbf{x}(t_1, \mathbf{p}^*) $, to estimate $ \mathbf{A}(t_1) $. When we reach the end of the first on-treatment interval at $ t_{n_1} $, the process continues with components $ w_{1, 1}^{0*} $, $ w_{1, 2}^{0*} $, $ w_{2, 2}^{0*} $, and $ w_{3, 3}^{0*} $ of $ \mathbf{p}^* $ through the first off-treatment interval at $ t_{n_2} $; the elements of $ \mathbf{A} $ corresponding to $ w_{1, 1}^{1*} $ through $ w_{3, 3}^{1*} $ are zero. Finally, we proceed as above with parameters $ w_{1, 1}^{1*} $ through $ w_{3, 3}^{1*} $ for the second on-treatment interval through $ t_{n_3} $. The numerical estimates of $ \mathbf{A}(t_n) $, $ n = 1, \ldots, N_3 $ yield the sensitivity matrix $ \mathbf{S} $, from which we compute the Fisher information matrix $ \mathbf{M} = \mathbf{S}^{\rm T}\mathbf{S} $ and the Cramér-Rao bound covariance matrix, $ \mathbf{C} = \mathbf{M}^{-1} $.

3.   Results and discussion

One naïve way to estimate the uncertainty in model parameters is to run MATLAB's $\textsf{fmincon}$ function to determine a vector of parameters for which the model's observables of PSA agree closely with a given patient's clinical time series. For this purpose, we have used Model T-13 and minimized Eq. 2.14 subject to the biological constraints in Table 1. Such a calculation was run for $ 28 $ different patients over their first on-off-on treatment intervals.

Table 2 shows the sample means and variances of the parameters returned by $\textsf{fmincon}$ for this set of patients. The "optimal" parameter values are about the same for each patient for the most part. One may wonder whether the sample variances obtained in this manner are realistic. The analyses in Sections 3.1–3.2 suggest that they are not, and, in fact, that the actual uncertainties are much larger than the results in Table 2 might suggest.

In this section, we present the results obtained from studying the identifiability and uncertainty quantification of parameters and predictions from Models H, P, T-13, and T-5. We show that, based on the available time series data, the parameters of models H, P, and T-13 are not practically identifiable. The method of profile likelihood shows that the parameters of Model T-5 are identifiable under the biological constraints given in Table 1.

We also use the ensemble Kalman filter on the associated augmented systems to assess the short- and long-term predictive capability of Model T-5. Although we obtain some promising initial results for many patients, there is evidence of significant model error.

3.1.   Parameter identifiability of Model H and Model P

Table 3 shows the rank of the Fisher information matrix $ \mathbf{M} $ obtained using the numerical procedure described in Section 2.5. In particular, the rank of $ \mathbf{M} $ for Models H and P is 9 and 15, respectively. Because the rank is less than the number of model parameters, we conclude that neither model has a parameter vector that can be identified uniquely from the available observations.

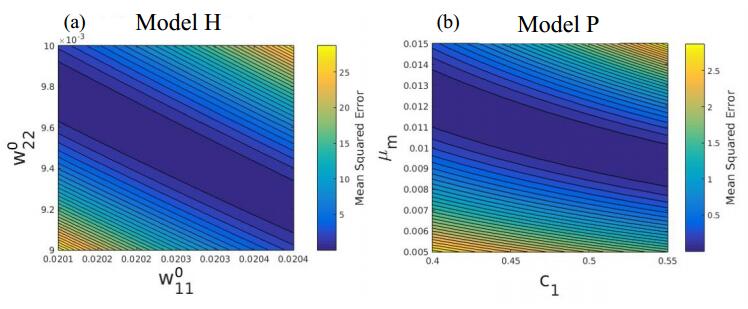
To illustrate one of the implicit functional relationships between some of the model parameters, Figure 2 shows a plot of the profile likelihood (Eq. 2.6) between a selected pair of parameters from each of Models H and P. The negative log likelihood function can be minimized by multiple choices of the two selected parameters within the ranges specified on each graph. The two parameters are related by an implicit function within and beyond the indicated bounds on the axes, and it is not possible to associate a confidence interval to them. These results suggest that the parameters in Models H and P are structurally unidentifiable when the only observables are time series of PSA levels.

Next we turn to the uncertainties in the parameters returned by $\textsf{fmincon}$, as estimated from the Crámer-Rao covariance matrix, $ \mathbf{M}^{-1} $. Table 4 shows the resulting coefficients of variation (Eq. 2.4). The coefficient of variation of all parameters except $ w_{1, 1}^1 $ in Model H and $ \mu_m $ in Model P is greater than unity (i.e., the uncertainty is at least as large as the estimated parameter value). Thus, the parameters are practically unidentifiable given the available clinical time series.

The numerical results presented here are based on time series from one representative patient (Patient 39) in the Vancouver Prostate Center clinical dataset; analogous results are obtained for other patients. Although it is possible to find estimates of the parameter vector for each of Model H and P that provide reasonably good agreement with clinical observations, such estimates are not unique, and they may be subject to large relative errors. The uncertainties in the parameters lead to unreliable predictions for the future clinical course of individual patients (Figure 1).

3.2.   Parameter identifiability in Models T-13 and T-5

The numerical estimation of the Fisher information matrix for these models proceeds in the same manner as described in Section 2.5. We fix the initial values of $ x_1 $ and $ x_2 $ to $ 0.01 $ and $ 0.0001 $, respectively, and $ A(0) $ and $ P(0) $ are taken as the first value of recorded androgen and PSA data; we assume that $ Q(0) = 0.90A(0) $. The results shown in Table 2 indicate that Model T-13 has $ 2 $ unidentifiable parameters, as the rank of the Fisher information matrix is $ 11 $. In contrast, the rank of the Fisher information matrix is $ 5 $ for Model T-5, so all of the adjustable parameters are identifiable.

The coefficients of variation in Table 4 indicate that estimates of all but two of the parameters in Model T-13 are subject to large uncertainties. In contrast, 4 of the 5 adjustable parameters in Model T-5 may be practically identifiable.

The computations reported in Table 4 do not account for biologically realistic bounds on the parameters. To assess the practical identifiability of model T-5 with respect to the biological constraints in Table 1, we use the clinical time series from Patient 39 in the Vancouver database as a representative case to compute the profile likelihood for all 5 model parameters, shown in Figure 3. Each black curve represents the value of the negative log likelihood, Eq. 2.5, when all parameters are set to the values returned by $\textsf{fmincon}$ (Section 2.4) except for the one that is varied within the interval shown on the horizontal axis.

Also shown in the graphs is the 95% confidence threshold, Eq. 2.7, as a dotted red line. The corresponding confidence interval in the parameter consists of those parameter values for which the profile likelihood lies below the dotted line. In some cases, the confidence interval lies outside a biologically realistic range. For example, only nonnegative values of parameter $ d_1 $ (Figure 3(c)) are biologically meaningful, yet the left endpoint of the 95% confidence interval is a negative value. The parameter $ q_2 $ corresponds to the cell quota for the androgen-independent call subpopulation, and, by hypothesis, is less than $ q_1 $. That the right endpoint of the 95% confidence interval extends beyond the biologically meaningful upper limit for $ q_2 $ suggests that $ q_2 $ may not be practically identifiable from the available observational data.

3.3.   Data assimilation for Model T-5

The ensemble Kalman filter (EnKF) provides another way to quantify the uncertainties in model predictions and parameters, provided that the latter are identifiable. As outlined in Section 2.3, the Kalman filter updates the model state vector whenever new observations become available, and the updated state vector becomes the new initial condition for the subsequent time interval. We use an augmented system, Eq. 2.13, for the vector field $ \mathbf{F} $ defined by Model T, Eqs. 1.9–1.13, in the results described here. We consider only version T-5 of this model, as the $ 5 $ adjustable parameters form an identifiable subset. Of these $ 5 $ parameters, we fix $ \mu_m $ and $ d_1 $, as their values do not vary significantly between patients. Only $ A_0 $, $ \gamma_1 $, and $ q_2 $ are estimated as part of the augmented state vector. In general, a smaller state vector helps to reduce the ensemble variance, all other factors being equal. In this case, however, including $ q_2 $ as a parameter to be estimated proves problematic, as we discuss in more detail below.

An open question is a suitable choice of the starting ensemble. The sample variance of the initial conditions should reflect that of the underlying state vector, but we know neither the initial fraction of treatment-resistant cells nor the amount of intracellular androgen in each patient's tumor. Furthermore, the uncertainty in "patient-specific" model parameters may be large. As a guess, we form the ensemble by choosing $ 100 $ initial values of the initial state vector from $ 0.7 $ to $ 1.6 $ times the value of each component of the initial condition $ \mathbf{x}_0 $ estimated for each patient in ^[24]. The initial ensemble mean values of the parameters $ A_0 $ and $ \gamma_1 $ are given by the output of $\textsf{fmincon}$ to minimize Eq. 2.14 for each respective patient, and the standard errors are approximated from the respective 95% confidence intervals in Figure 3. Altogether, the augmented state vector is $ \mathbf{x}^* = (x_1, \ldots, x_5, A_0, \gamma_1, q_2)^{\rm T} $. We assume that the errors in the observations of serum PSA and androgen levels are independent and have variance $ 1 $.

We integrate each initial condition of the 100-member ensemble to the first observation time $ t_1 $, then compute the linear combination of ensemble members that minimizes Eq. 2.10, which becomes the new initial condition. The integration continues to the second observation time $ t_2 $, and the process is repeated until the end of the dataset or until another prespecified ending time. Altogether, we ran the EnKF on time series from $ 26 $ patients from the Vancouver Prostate Center database. This set of patients is disjoint from the set used to estimate model parameters in Sections 3.1–3.2.

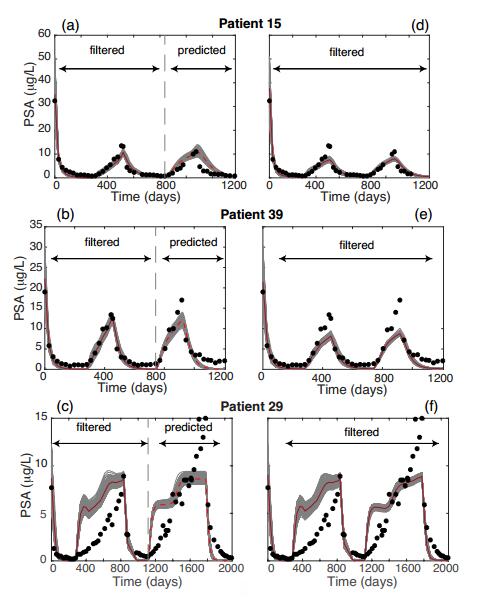
Figure 4 shows some representative results for the PSA component of the ensemble state vectors for 3 different patients using the EnKF as a data assimilation system. The red curve in each plot shows the ensemble mean value of the PSA level, and the gray curves show each ensemble realization of the PSA levels. (Analogous plots can be made of the other components of the model state vector.)

To return to one of the questions asked in the introduction, we consider what happens when the EnKF is run for the first on-off-on treatment intervals to compute an ensemble estimate of the augmented state vector. Using the analysis at the end of the second on-treatment interval, we run the model for a period of 400 to 800 days, depending on the patient, to predict the serum PSA levels for the next cycle, that is, over the next treatment hiatus and subsequent on-treatment interval. The ensemble predictions are shown for each patient to the right of the vertical dotted line in panels (a)–(c).

The panels on the right, Figure 4(d)–(f), show the outputs of the filter as it is run over the entire time series of clinical PSA observations (shown as round circles). At each observation time $ t_n $, we compute the mean of the predicted PSA level from the analysis at $ t_{n-1} $ over all $ 100 $ ensemble members, i.e.,

and, at the end of the time series, the root mean square (RMS) of the one-step ahead prediction error of serum PSA level averaged over all $ N $ observation time points is

The respective values of $ \hat{P} $ for panels (d)–(f) are $ 1.80 $, $ 2.38 $, and $ 2.84\; \mbox{ $\mu$g/L} $.

In the case of Patient 15, the EnKF produces good agreement with observations throughout the clinical data record. When the forecast/update cycle is halted shortly after day 800 and the model is run freely for the next 500 days or so, the model provides a good prediction of the patient's clinical course during the next off- and on-treatment cycle. When the EnKF is run continuously throughout Patient 15's clinical course, the ensemble variance increases notably toward the end of the second off-treatment interval, and the filter takes $ 5 $ or so update cycles for the ensemble mean to settle near the observed clinical PSA values. As mentioned above, the RMS error of the ensemble mean's one-step ahead prediction of serum PSA is about $ 1.80\; \mbox{ $\mu$g/L} $.

The results are similar for Patient 39, panels (b) and (e), although the ensemble mean tends to underestimate the observed serum PSA levels towards the end of each on-treatment interval. As with Patient 15, the EnKF produces an augmented state vector at the end of the second on-treatment interval that yields a reasonable 450-day prediction of Patient 39's clinical course.

Serious problems are evident in the case of Patient 29. It is not clear whether the filter is even convergent after more than a handful of observation time points. How can a filter initialized in the same way as for the other patients produce such poor results? The answer turns on the inclusion of Model T-5's adjustable parameter $ q_2 $, the cell quota for the treatment-resistant tumor cell subpopulation, in the augmented state vector. The analysis in Section 3.2 suggests that $ q_2 $ may not be practically identifiable; in any case, its 95% confidence interval as estimated from the profile likelihood includes values that are not biologically meaningful. A similar problem bedevils the augmented ensemble for this patient case.

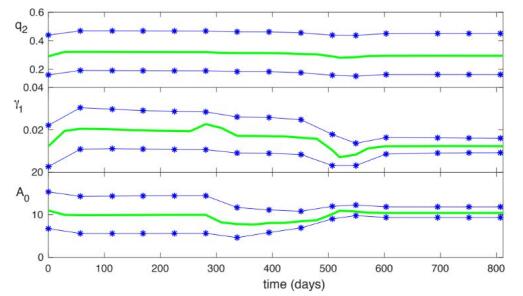
Figure 5 shows the time evolution of the EnKF's estimates of the adjustable parameters $ A_0 $, $ \gamma_1 $, and $ q_2 $ for Patient 15 (Figure 4(a)). The green curve shows the ensemble mean value of each parameter as the forecast/update cycle proceeds, and the blue starred curves at the bottom and top represent the ensemble minimum and maximum values at each analysis time point. In particular, the EnKF's estimate of $ q_2 $ remains within the biologically realistic interval given in Table 1 and is less than the value of $ q_1 = 0.613 $ that is fixed for Model T-5.

In the case of Patient 29, however, the ensemble estimates of $ q_2 $ are much larger. After a few analysis cycles, some of the ensemble estimates of $ q_2 $ exceed $ q_1 $ (not shown in the figure). At this point, the dynamical model no longer makes sense, because for these ensemble members, the model includes a treatment-resistant cell subpopulation with a greater cell quota for androgen than the treatment-sensitive one. The forecast ensemble quickly diverges from reality, and of course the model's predictions are not believable.

We include this last example as a cautionary note in the application of ensemble Kalman filters. One must be careful that the parameters being estimated have a sufficiently small variance so that their ensemble updates remain within a sensible range for the model under consideration. It is possible to modify the EnKF to add a suitable penalty term to Eq. 2.10 to further constrain the parameter values, but the resulting minimization problem becomes nonlinear and is more expensive to solve numerically.

4.   Conclusions

Prostate cancer has attracted the development of numerous mathematical models to study various aspects of the cancer dynamics under different treatment scenarios, especially in the last two decades. However, deterministic ODE models tend to contain many rate parameters ^{[12,15,22,24]}. Because clinical data used for parameter calibration typically is limited to time series of serum PSA and possibly also androgen levels, parameter identifiability is a significant issue. It is not possible to quantify the uncertainty in unidentifiable parameters. Furthermore, the ability of the model to fit prior clinical data with suitable choices of parameters does not imply that the model's predictions of the future clinical course can be trusted.

In this paper, we investigate three existing models (H, P, and T) for prostate cancer, each of which has been validated with clinical data ^[12,15,24]. All of the models divide the tumor cell population into two or more classes that differ in their sensitivity to androgen deprivation therapy and presume an autonomous relationship between the size of the tumor cell classes and the rate of serum PSA production.

The limited set of observables leads to unidentifiable sets of parameters in each of Models H, P, and T. By restricting the set of adjustable parameters in Model T using a sensitivity analysis in ^[24], we show that a 5-parameter version of Model T is identifiable (Table 2) given only clinical time series of PSA levels. Nevertheless, given the available time series, 3 of the 5 identifiable parameters are subject to relative uncertainties of at least $ 40 $ percent (Table 4). Models H and P have only one practically identifiable parameter, i.e., only one of the parameters is estimable from the available data with a relative uncertainty of less than unity.

Past is not prologue. Although it may be possible to find a set of parameters so that the model observables agree well with previous clinical measurements, the model's predictions of future time series of PSA need not be reliable.

In some cases, fixing many of the parameters in a complex model may yield an identifiable version that can produce reasonable predictions of PSA dynamics. This is the approach taken with Model T, which contains $ 21 $ parameters, all but $ 5 $ of which can be fixed to yield an identifiable subset and for which confidence intervals can be constructed using the method of profile likelihood (Section 3.2). However, the confidence intervals may not lie within biologically realistic bounds. Conversely, however, biological constraints may help to reduce the uncertainty in numerical estimates of a given parameter.

The ensemble Kalman filter is a useful way to assimilate data and quantify the uncertainty in model predictions. The EnKF provides a systematic and consistent method to account for new observations and update the associated model state vector accordingly. Nevertheless, for best results, one needs good estimates of the initial uncertainty in the state vector, which are not available for the models considered here. Systematic model errors (biases) can be accounted for in EnKF schemes ^[41], but we have not pursued this approach here.

Improved models are needed. Resistance to androgen deprivation therapy, or, alternatively, the androgen cell quota, probably exists on a continuum in a typical prostate tumor. The division of the tumor cell population into two or three distinct subpopulations may be too much of an oversimplification for clinically useful predictions. Although the notion of a nutrient-limiting mechanism to tumor growth is biologically reasonable, the dynamics of androgen metabolism probably are not well characterized in Models P and T. More work is needed to improve them.

The development of clinically applicable dynamical models of prostate cancer treatment, and of many other cancers, may benefit from the application of observing-system simulation experiments. OSSEs have been widely used in numerical weather prediction for over half a century. Broadly speaking, in an OSSE, synthetic data is assimilated into a complex dynamical model to assess measures like prediction accuracy (forecast skill) as a function of the accuracy, sparsity, and types of observations. An historical overview may be found in ^[42]; one early example was an attempt to test whether the wind field of an atmospheric model could be estimated from measurements of temperature alone. Another important application concerns "the potential improvements in climate analysis and weather prediction to be gained by augmenting the present atmospheric observing system with additional envisioned types of observations that do not yet exist" ^[43]. In the present context, OSSEs might be used to quantify errors in parameter estimates from data with various noise levels or to assess the impact of a new assay or other tumor diagnostic on the predictive ability of a given model. In the authors' view, such efforts will be necessary to develop clinically validated mathematical models that will be useful tools for physicians and patients.

Acknowledgments

The research of this work was partially supported by NSF grants (to YK) DMS-1615879, DMS-1518529 and a grant (to EK and YK) by the Arizona Biomedical Research Commission. ZW was partially supported by a block grant from the Arizona State University Graduate College. We are grateful to the late Dr. Nicholas Bruchovsky for the clinical data set.

Conflict of interest

The authors declare no conflict of interest.

Appendix

Kalman filter algorithm

Here we outline the implementation of the ensemble transform Kalman filter used in the simulations described in Section 3.3. Additional details concerning the motivation and derivation of the filter are given in ^[40].

At time $ t_n $, we begin with an ensemble of initial conditions, which can be regarded as a sample drawn from a normal distribution about a mean state that we wish to estimate. A forecast (often called the background) is made by integrating the model of interest from each ensemble member to time $ t_{n+1} $, at which point additional measurements have become available. The EnKF seeks a linear combination of the forecasts that best fits the data in a weighted least-squares sense; the linear combination serves as a new set of initial conditions, called the analysis, at $ t_{n+1} $ from which the model is integrated to time $ t_{n+2} $, when the process is repeated. The mean of the analysis ensemble is the updated estimate of the "true" state of the system, and the sample covariance represents the uncertainty in the analysis mean.

All the computations below are done at $ t_{n+1} $, so we omit the time dependence to simplify the notation. Let $ \{\mathbf{x}_{b(k)}\}_{k = 1}^K $ be the set of $ K $ state vectors (each of dimension $ m $) that represent the background ensemble, and let $ \overline{\mathbf{x}}_b $ denote the ensemble mean, Eq. 2.11. Let $ \mathbf{X}_b $ be the $ m\times K $ matrix whose $ k $th column is $ \mathbf{x}_{b(k)}-\overline{\mathbf{x}}_b $, $ k = 1, \ldots, K $. If $ \mathbf{w} $ is a Gaussian $ K $-vector with mean $ {\bf 0} $ and covariance $ (K-1)^{-1}\mathbf{I} $, then $ \mathbf{x} = \overline{\mathbf{x}}_b + \mathbf{X}_b \mathbf{w} $ has mean $ \overline{\mathbf{x}}_b $ and covariance $ (K-1)\mathbf{X}_b\mathbf{X}_b^{\rm T} $, which, in model space, is the ensemble estimate of the forecast uncertainty.

Let $ \mathbf{y}^{\mbox{ obs}} $ be the $ s $-vector of observations, which is assumed to be related to the "true" model state vector $ \mathbf{x}_t $ by

where $ \mathbf{\epsilon} $ is a Gaussian random $ s $-vector of mean $ \bf 0 $ and covariance $ \mathbf{R} $ (cf. Eq. 2.9). The ensemble transform Kalman filter minimizes the cost function given in Eq. 2.10, where, as necessary, we approximate a nonlinear forward operator $ \mathbf{H} $ as

where the $ s $-vector $ \overline{\mathbf{y}}_b $ is the mean of the background observation ensemble

and the $ k $th column of the $ s\times K $ matrix $ \mathbf{Y}_b $ is $ \mathbf{y}_{b(k)} - \overline{\mathbf{y}}_b $. The minimizer of Eq. 2.10 is found from

which in model space yields the analysis mean and covariance

As mentioned above, the analysis ensemble is constructed from a linear combination of the background ensemble members. The first step in this procedure is to compute the symmetric square root

One rationale for the symmetric square root in Eq..8 is that the elements of the resulting matrix vary continuously with the observational data. The analysis ensemble $ \{\mathbf{w}_{a(k)}\}_{k = 1}^K $ is formed by adding $ \overline{\mathbf{w}}_a $ to each column of $ \mathbf{W}_a $; in model space, the analysis ensemble is

Further details on the derivation of the ensemble transform Kalman filter are given in ^[40].

In the results described in the paper, we apply the ensemble transform Kalman filter to the augmented dynamical system defined by Eq. 2.13. Let $ \tilde{\mathbf{F}} = (\mathbf{F}, \mathbf{G})^{\rm T} $ denote the augmented vector field ($ \mathbf{F} $ is the vector field representing the ODE model in question, and $ \mathbf{G} $ is the model for the time evolution of the parameters). The $ (m+q) $-dimensional state vector of the augmented system is $ \mathbf{x}^* = (\mathbf{x}, \mathbf{p})^{\rm T} $.

The forecast-update cycle may be expressed in the following steps:

1. Begin with the analysis ensemble at $ t_n $, $ \{\mathbf{x}^{n}_{a(k)}\}_{k = 1}^k $ with the associated analysis covariance matrix $ \mathbf{P}_a^n $, and set each $ \mathbf{x}_{a(k)} $, $ k = 1, \ldots, K $ as the initial condition for the next forecast.

2. Integrate the model $ \tilde{\mathbf{F}}(t, \mathbf{x}^*) $ from $ t_{n} $ to $ t_{n+1} $ for each initial ensemble member $ \mathbf{x}^{n}_{a(k)} $, $ k = 1, \ldots, K $. The $ K $ solutions now become the background ensemble at time $ t_{n+1} $: $ \left\{\mathbf{x}^{n+1}_{b(k)}\right\}_{k = 1}^K $.

3. Interpolate between the background ensemble and observations at time $ t_{n+1} $ by applying the forward operator $ \mathbf{H}^* $ to each of the background ensemble member and form a new ensemble $ \mathbf{y}_{b(k)} = \mathbf{H}^*(\mathbf{x}_{b(k)}) $, $ k = 1, \ldots, K $.

4. Minimize the Kalman filter cost function, Eq. 2.10, of the current time step to produce the analysis at time $ t_{n+1} $: $ \left\{\mathbf{x}^{n+1}_{a(i)}\right\}_{i = 1}^k $ associated with analysis covariance matrix $ \mathbf{P}_a^{n+1}. $

5. Use $ \left\{\mathbf{x}^{n+1}_{a(k)}\right\}_{k = 1}^K $ as the initial conditions for the next background ensemble and repeat the steps.