A short proof of the logarithmic Bramson correction in Fisher-KPP equations

1.   Introduction

With the development of industry and agriculture, a variety of chemical toxins, such as heavy metals and pesticides etc., have been released into aquatic ecosystems. These toxins have the potential to cause an adverse impact on a diverse range of organisms ^[1], which has become a primary concern all over the world. Many countries have made a list of priority chemicals of concern and designated policies and measures to mitigate the adverse effects of chemical toxins on aquatic environments ^[2,3]. Accurately assessing the risks of toxins requires understandings of the effects of toxins on organisms, as well as on complex ecological interactions.

During the last several decades, mathematical models including individual-based model, matrix population models, differential equation models, have been developed to understand the ecological effects of toxin exposure. Bartell ^[4] and Pastorok et al. ^[5] make a complete review on the realism, relevance, and applicability of distinct types of models from the point of view of evaluating risks caused by environmental toxins. A literature search shows that since a series of work by Hallam et al. ^[6,7,8,9], a number of differential equation models have been proposed and studied to examine the effects of toxins on aquatic populations. A common feature of these differential equation models is that they involve three state variables: the population concentration, the concentration of toxins in the population, and the concentration of toxins in the environment, hence these models describe the interactions between populations and environmental toxins. In practice, because toxins contained in populations are extremely small portion of the whole environment, population birth, mortality, and metabolism do not significantly affect the concentration of toxins in the environment where the population habit. Based on this fact, Huang et al. ^[10] developed a body burden-dependent population model in which the concentration of toxins in the environment is treated as an important parameter and the effect of the population on environmental toxins is ignored. The model was then used to understand the toxic effects of methylmercury on the long-term behavior of the rainbow trout (Oncorhynchus mykiss). In terms of the results of model parameterization, the authors provided a threshold concentration of methylmercury in the external environment to maintain population persistence. Moreover, a complete global and bifurcation analysis of the model can be found in ^[11].

Time delays are very common in the biological processes, which can cause complex dynamic phenomena including limit cycle oscillations, quasi-periodic oscillations, and even chaos. Time delayed models are widely used to model biological systems, such as population dynamics ^[12,13,14], predator prey system ^[15,19], tumor immune system ^[18], gut microbiota system ^[20], Escherichia coli Tetrahymena system ^[21], food chain system ^[22] and so on. Recently, many authors have considered time delays in modeling aquatic population dynamics with the effects of environmental toxins ^[16,17,23]. For example, Chattopadhyay et al. ^[16] proposed a toxin-producing phytoplankton and zooplankton interaction model and revealed that the toxin substances produced by the phytoplankton play a significant role in the termination of planktonic blooms. Furthermore, Chattopadhyay et al. ^[17] extended the previous model ^[16] by considering the time delay of the liberation of toxic substances by the phytoplankton population, and investigated the delayed effect of toxic phytoplankton causing oscillation behaviors of phytoplankton and zooplankton populations. Besides, Jiang et al. ^[23] developed a delayed phytoplankton-zooplankton model with the coefficients depending on the delay. They showed that the maturity delay of toxic substances might serve as a key factor in the periodic phytoplankton and algae blooms.

The external changes in the environment have some kind of delayed effects on population dynamics, in particular, when a species live in a polluted aquatic environment, toxins have delayed responses on its growth and death ^[26]. Casarini et al. used Frog Embryo Teratogenesis Assay–Xenopus (FETAX) assay to measure mortality, delayed growth and embryo deformation. The results showed that the growth rate of the embryos was significantly delayed at the concentrations of $ 0.1 $ to $ 10\; nM $ of exposure to Okadaic Acid (OA) ^[27]. And the delayed mortality is observed in several species 4 to 12 d following the exposure to very low toxicant concentrations ^[28]. A delayed model for studying the interaction among phytoplankton, zooplankton, and fish in the presence of toxins has been developed in ^[24]. The delayed effect of toxins in a polluted environment on the growth of the population biomass has been considered in ^[25].

In this work, we extend the above-mentioned body burden-dependent model in ^[10,11] to a delay model by incorporating delayed toxic responses. The extension is based on the fact that the effects of toxins on the growth and mortality maybe not immediate, but time-delayed, especially when the population is subject to sublethal toxin levels ^[29]. We analyze the model in terms of steady states, stability, and bifurcation. By analyzing the transcendental characteristic equation, we investigate the effects of the time delays on the local stability of equilibria. We find that the Hopf bifurcation can occur in the model as the threshold value increases through certain values of the delays.

The paper consists of five sections. In the next section, we propose the toxin-mediated population model with time-delayed toxic responses. Section 3 contains nondimensionalization, existence and local stability of equilibria, and bifurcation analysis. In section 4, we make numerical simulations to verify the theoretical results. The conclusion and discussion are in the final section.

2.   The model

Our model with time delays is based on the following toxin-dependent aquatic population model studied in ^[10,11]:

where $ x(t) $ represents the concentration of population biomass — the mass of the population per unit volume of the aquatic environment — at time $ t $, $ y(t) $ represents the body burden of the population — the mass of toxin per unit population biomass — at time $ t $. The model parameters $ \alpha_{1}, \alpha_{2}, \alpha_{3} $, $ k, m, a, T_e $, and $ \sigma $ are all positive constants. See ^[11] for the detailed model construction.

Equation (2.1a) presents the rate of change of the population biomass under the influence of the toxin. The term, $ \alpha_1\max\{0, 1-\alpha_2y(t)\}/(1+\alpha_3 x(t)) $, describes the population gain rate that depends on the population biomass and the body burden, $ \alpha_1/(1+\alpha_3 x(t)) $, a decreasing function with respect to population biomass, is a density-dependent biomass gain rate due to birth and growth, where $ \alpha_1 $ is the maximum gain rate and $ \alpha_3 $ denotes the crowding effect. The expression, $ \max\{0, 1-\alpha_2y(t)\} $, is a fraction between 0 and 1, which represents linear toxic responses for the gain rate. If there is no toxic effect (i.e., body burden $ y(t) = 0 $), then $ \max\{0, 1-\alpha_2y(t)\} = 1 $, the gain rate of population biomass is $ \alpha_1/(1+\alpha_3 x(t)) $. If the body burden $ y_i $ reaches a threshold level $ 1/\alpha_2 $, then $ \max\{0, 1-\alpha_2y(t)\} = 0 $, the gain rate of population biomass is $ 0 $. In this case, the population stops reproduction and growth. The term, $ ky(t)+m $, means that the population mortality rate linearly depends on the body burden $ y(t) $, where $ k $ is the effect coefficient of toxin on mortality, and $ m $ is the natural mortality rate. If there is no toxic effect, i.e., $ y(t) = 0 $, then the mortality rate is given by the natural mortality rate $ m $.

Equation (2.1b) is a balance equation for the body burden, where $ a $ represents the toxin uptake rate by the population from the environment and $ T_e $ is the concentration of toxin in the environment — the mass of toxin per unit volume of the aquatic environment. $ \sigma $ is the toxin elimination rate due to the metabolic processes of the population. The last term of (2.1b), $ \alpha_1\max\{0, 1-\alpha_2y(t)\}y(t)/(1+\alpha_3x(t)), $ means toxin dilution due to birth and growth.

Model (2.1) assumes that the toxic responses (i.e., the effects of toxin on population growth and mortality) are immediate. In this paper, we extend model (2.1) by considering delayed toxic responses. To this end, we introduce two time delays $ \tau_1 $ and $ \tau_2 $, which are associated with the effects of toxins on growth and mortality, respectively. Then a modified model from (2.1) reads

We non-dimensionalize system (2.2) by introducing the following dimensionless quantities:

Dropping the tildes for notational simplicity, we obtain the following scaled model:

We denote by $ \mathcal{C} $ the Banach space of continuous functions $ \phi:[-\tau, 0]\rightarrow\mathbf{R^2} $ equipped with the suitable norm, where $ \tau = \max\{\tau_1, \tau_2\} $. Furthermore, let

The initial conditions of system (2.3) are given as

3.   Local stability and bifurcation analysis

First of all, we show that solutions of system (2.3) behave in a biologically reasonable manner.

Proposition 3.1. The solutions of system (2.3) are always nonnegative and bounded under the initial conditions (2.4).

Proof. Since the right-hand side of the system (2.3) is locally Lipschitz-continuous in $ \mathbf{R}_{+}^{2} = \{(x(t), y(t))|x(t), y(t)\geq0\} $, we obtain

Using the positive property of solutions, we get

According to the comparison principle, we have

So, any solutions of system (2.3) with the initial conditions (2.4) will stay in the rectangular region:

The existence and stability conditions of equilibria of system (2.3) without time delays were discussed in ^[11]. Here we summarize the results as follows.

Lemma 3.1. Consider system (2.3) when $ \tau_1 = 0 $ and $ \tau_2 = 0 $.

(i) When $ 0 < \sigma < 1 $, system (2.3) has the boundary equilibrium

(ii) When $ \sigma \geq 1 $, system (2.3) has the boundary equilibrium

where

(iii) When

system (2.3) has a unique interior equilibrium

where

Lemma 3.2. Consider system (2.3) when $ \tau_1 = 0 $ and $ \tau_2 = 0 $.

(i) When $ E^0_1 $ exists, it is stable if $ \sigma > \frac{1-(2m+k)}{1+k} $.

(ii) When $ E^0_2 $ exists, it is always unstable.

(iii) When $ E^0_3 $ exists, it is always stable.

(iv) When $ E^* $ exists, it is stable if $ T < k\theta^2+(m+\sigma)\theta : = T_\theta $, where

Next, we discuss the effects of $ \tau_1 $ and $ \tau_2 $ on the stability of the interior equilibrium $ E^*. $ Note that $ 0 < y^* < 1 $, we have $ \max\{0, 1-y^* \} = 1-y^* $.

Case (I) $ \tau_1 > 0, \; \tau_2 = 0 $.

Theorem 3.1. For system (2.3), suppose that $ \tau_1 > 0, \; \tau_2 = 0 $, then when $ E^{*} $ exists, it is locally asymptotically stable if $ T < T_\theta $.

Proof. When $ \tau_1 > 0, \; \tau_2 = 0 $, linearizing system (2.3) at $ E^{*} $, we have

Let $ \vec{Z}(t) = (x(t), y(t))^{T} $, system (3.1) can be transformed as

where

Let $ \vec{Z} = e^{\lambda t}\vec{\xi}, \; \vec{\xi}\neq\vec{0} $ in (3.2), then we obtain

that is,

where $ I $ is an identity matrix. Therefore, the characteristic equation is

which can be written as the form

where

and

Since $ E^* = \left(\dfrac{1-y^*}{ky^*+m} -1, \; y^*\right) $ implies that $ 0 < y^* < 1 $ and $ ky^*+y^*+m < 1 $, we have that $ E_1 > 0, \; D_2 < 0 $.

Let $ \omega > 0 $ and suppose $ \lambda = i\omega $ is a pure imaginary root of equation (3.3). Separating the real and imaginary parts, we have

Thus

where

Then we have

Equation (3.5) has positive roots if and only if

Since $ T < T_\theta $, $ D_1+D_2 > 0 $, we have $ D_1 > 0 $, $ D_1-D_2 > 0 $. Besides, due to $ D_1^2-4E_1-D_2^2 = a_1-2E_1 < 0 $, we have $ \Delta < 0 $. It is a contradiction. So equation (3.5) has no positive root.

Therefore, when $ \tau_1 > 0, \; \tau_2 = 0 $ and $ E^{*} $ exists, it is locally asymptotically stable if $ T < T_\theta $.

Case (II) $ \tau_1 = 0, \tau_2 > 0 $.

Theorem 3.2. For system (2.3), suppose that $ \tau_1 = 0, \tau_2 > 0 $, if $ (A1) $ holds, then there is a positive integer $ m $ such that

$ E^{*} $ is locally asymptotically stable if $ \tau_2\in\left(0, \tau_{2, +}^{(0)}\right)\cup\left(\tau_{2, -}^{(0)}, \tau_{2, +}^{(1)}\right)\cup\cdots\cup\left(\tau_{2, -}^{(m-1)}, \tau_{2, +}^{(m)}\right) $, and $ E^{*} $ is unstable if $ \tau_2\in\left(\tau_{2, +}^{(0)}, \tau_{2, -}^{(0)}\right)\cup\left(\tau_{2, +}^{(1)}, \tau_{2, -}^{(1)}\right)\cup\cdots\cup\left(\tau_{2, +}^{(m)}, \infty\right) $. Furthermore, if $ (A2) $ holds, then system (2.3) undergoes Hopf bifurcation at $ \tau_2^* $, where $ \tau_2^* = \tau_{2}^{(0)} = \min\{\tau_{2, +}^{(0)}, \tau_{2, -}^{(0)}\} $.

Proof. When $ \tau_1 = 0, \; \tau_2 > 0 $, linearizing system (2.3) at $ E^{*} $, we get

Similarly, the characteristic equation is given by

where

and

Since $ 0 < y^* < 1 $ and $ ky^*+y^*+m < 1 $, we have $ G_1 > 0, \; G_2 > 0. $ And since $ T < k \theta^2+(m+\sigma)\theta $, we have $ F_1 > 0 $.

Let $ \omega > 0 $ and suppose $ \lambda = i\omega $ is a pure imaginary root of equation (3.3). Separating the real and imaginary parts, we have

Thus

where

$ \textbf{(A1)}: $ Suppose $ b_1 < 0, (b_1)^2-4b_2 > 0 $.

Equation (3.9) has two positive roots $ \omega_+ $ and $ \omega_- $, where

According to (3.8), we obtain

Then solving equation (3.11) for $ \tau_2 $ yields

Define

Next we obtain the transversality conditions for the Hopf bifurcation at $ \tau_2 = \tau_2^* $.

Let $ \lambda(\tau_2) = \upsilon(\tau_2)+i\omega(\tau_2) $ be the root of equation (3.7). When $ \tau_2 = \tau_2^* $, we have $ \upsilon(\tau_2^*) = 0 $ and $ \omega(\tau_2^*) = \omega^* $.

Differentiating equation (3.7) with respect to $ \tau_2 $, we have

Thus

Hence if the following conditon

$ \textbf{(A2)}:\; h_2'({\omega^*}^2)\neq0 $

holds, then the transversality condition for the Hopf bifurcation is satisfied.

Case (III) $ \tau_1\in(0, \infty), \; \tau_2 > 0 $.

Theorem 3.3. For system (2.3), suppose that for each fixed $ \tau_1\in(0, \infty), \; \tau_2 > 0 $, if $ (A3) $ holds, then there is a positive integer $ n $ such that

$ E^{*} $ is locally asymptotically stable if $ \tau_2\in\left(0, \tau_{2}^{(1, 0)}\right)\cup\left(\tau_{2}^{(2, 0)}, \tau_{2}^{(3, 0)}\right)\cup\cdots\cup\left(\tau_{2}^{(3, n)}, \tau_{2}^{(4, n)}\right) $, and $ E^{*} $ is unstable if $ \tau_2\in\left(\tau_{2}^{(1, 0)}, \tau_{2}^{(2, 0)}\right)\cup\left(\tau_{2}^{(3, 0)}, \tau_{2}^{(4, 0)}\right)\cup\cdots\cup\left(\tau_{2}^{(4, n)}, \infty\right) $. Furthermore, if $ (A4) $ holds, then system (2.3) undergoes Hopf bifurcation at $ \tau^\star_2 $, where $ \tau_2^{\star} = \tau_{2}^{(k_0, 0)} = \min\limits_{k\in\{1, ..., k_m\}}\{\tau_{2}^{(k, 0)}\} $.

Proof. We assume that $ \tau_1 $ is arbitrarily fixed within the stable interval $ \tau_1\in(0, \infty) $, while $ \tau_2 $ is varied as a control parameter. We linearize the system (2.3) at $ E^{*} $ to obtain

Similarly, the characteristic equation is given by

where $ P(\lambda) = \lambda^2+H_1\lambda+I_1 $, $ Q(\lambda) = H_2\lambda $, $ R(\lambda) = I_2 $,

and

The corresponding real and imaginary parts become

We obtain

where $ c_i\; (i = 1, 2, 3, 4) $ are given by

$ \textbf{(A3)}: $ Suppose that (3.16) has at least one positive root.

Let $ k_m $ denote the maximum number of positive real roots of equation (3.16). For $ k \in {1, \cdots, k_m} $, positive roots of equation (3.16) are denoted by $ \omega_k $.

According to (3.15), we obtain

Then solving the equation (3.17) for $ \tau_2 $ yields

We define

By differentiating equation (3.14) with respect to $ \tau_2 $, we get that

where

Consequently, we obtain

Hence, if the conditon

(A4): $ [P_1(\tau_2)R_1(\tau_2)+Q_1(\tau_2)S_1(\tau_2)]|_{\tau_2 = \tau_2^{\star}}\neq0 $

holds, then the transversality condition for Hopf bifurcation is satisfied.

4.   Numerical simulations

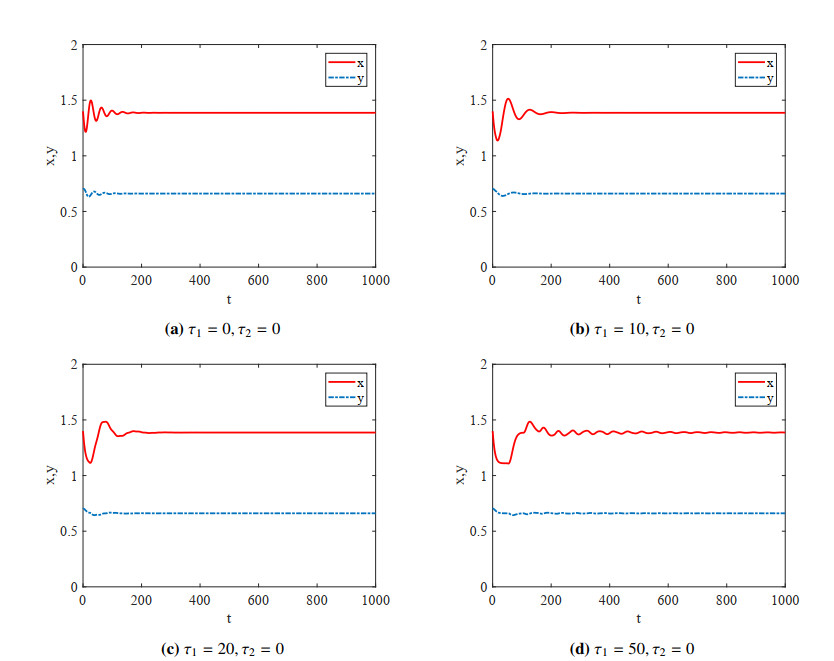
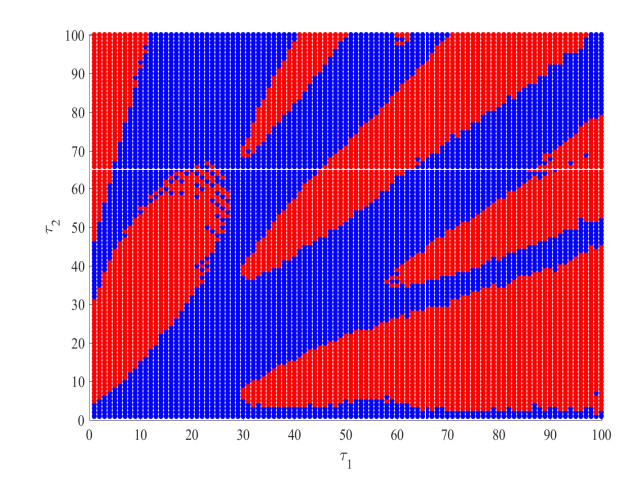
In this section, we numerically study the influence of time delays $ \tau_1 $ and $ \tau_2 $ on the stability of the interior equilibrium $ E^* $ of system (2.3). We choose a set of parameter values as $ k = 0.2, \; m = 0.01, \; \sigma = 0.1, \; T = 0.16 $. By some calculations, we have $ E^* = (1.38658, 0.660748) $, $ T_\theta = 0.170329, \; T_c = 0.226875 $. According to Lemma 3.2, $ E^* $ is stable when $ \tau_1 = \tau_2 = 0 $. Stability regions of the interior equilibrium $ E^* $ of system (2.3) in $ (\tau_1, \tau_2) $ plane are drawn in Figure 1. We then consider the following three cases and plot some graphs of the numerical solutions of system (2.3).

Case(I) $ \tau_1 > 0, \; \tau_2 = 0 $.

From (3.5) and $ (3.6) $, we have $ a_1 = -0.0330221 < 0 $ and $ \Delta = -0.00273187 < 0 $. So equation (3.5) has no positive root. According to Theorem 3.1, $ E^* $ is locally asymptotically stable when $ \tau_1 > 0, \; \tau_2 = 0 $, which means that $ \tau_1 $ can not change the stability of $ E^* $ (see Figure 2).

Case(II) $ \tau_1 = 0, \tau_2 > 0 $.

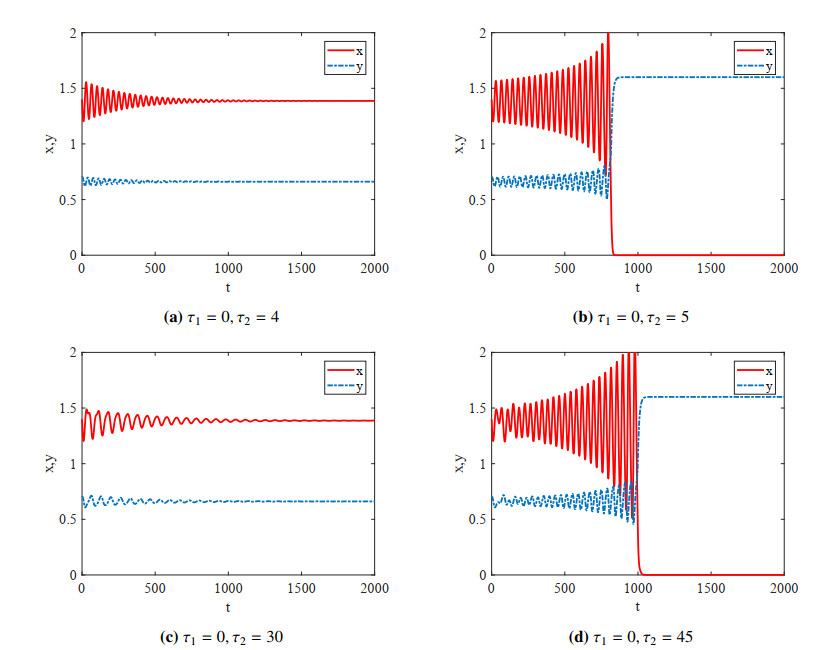
From (3.10a) and (3.10b), we have $ \omega_+ = 0.165797, \omega_- = 0.101075 $. According to Theorem 3.2, there is a positive integer $ m = 1 $ such that $ 0 < \tau_{2, +}^{(0)} < \tau_{2, -}^{(0)} < \tau_{2, +}^{(1)} $, where $ \tau_{2, +}^{(0)} = 4.9121, \; \tau_{2, -}^{(0)} = 26.5368, \; \tau_{2, +}^{(1)} = 42.8089 $. $ E^{*} $ is locally asymptotically stable if $ \tau_2\in\left(0, \tau_{2, +}^{(0)}\right)\cup\left(\tau_{2, -}^{(0)}, \tau_{2, +}^{(1)}\right) $, and $ E^{*} $ is unstable if $ \tau_2\in\left(\tau_{2, +}^{(0)}, \tau_{2, -}^{(0)}\right)\cup\left(\tau_{2, +}^{(1)}, \infty\right) $. When we choose $ \tau_2 = 4 $, $ E^{*} $ is stable (see Figure 3a). However, when $ \tau_2 $ increases to $ 5 > 4.9121 $, $ E^{*} $ becomes unstable and tends to the boundary equilibrium. In this case, the subcritical Hopf bifurcation appears resulting in an unstable limit cycle (see Figure 3b). As $ \tau_2 $ increase to $ 30 $, $ E^{*} $ becomes stable again (see Figure 3c). When $ \tau_2 $ increases to $ 45 > 42.8089 $, $ E^{*} $ becomes unstable again and tends to the boundary equilibrium (see Figure 3d). Furthermore, system (2.3) undergoes Hopf bifurcation at $ \tau^*_2 = \tau_{2, +}^{(0)} = 4.9121 $ (see Figure 1).

Case(III) $ \tau_1 \in(0, \infty), \tau_2 > 0 $.

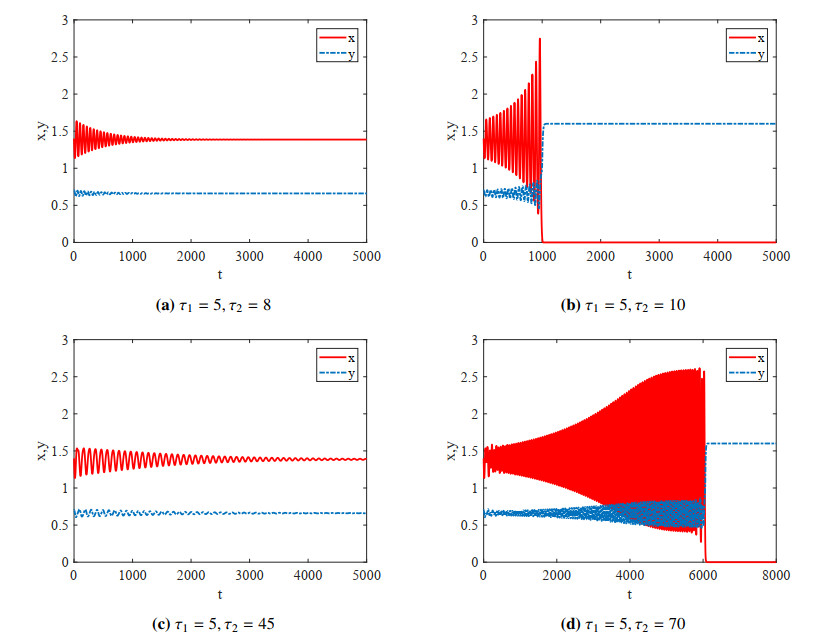
Here we fix $ \tau_1 = 5 $. By calculations, equation (3.16) has two positive roots: $ \omega_1 = 0.105931, \omega_2 = 0.0646036 $. According to Theorem 3.3, there is a positive integer $ n = 1 $ such that $ 0 < \tau_{2}^{(1, 0)} < \tau_{2}^{(2, 0)} < \tau_{2}^{(1, 1)} $, where $ \tau_{2}^{(1, 0)} = 9.29205, \; \tau_{2}^{(2, 0)} = 42.7927, \; \tau_{2}^{(1, 1)} = 68.6063 $. $ E^{*} $ is locally asymptotically stable if $ \tau_2\in\left(0, \tau_{2}^{(1, 0)}\right)\cup\left(\tau_{2}^{(2, 0)}, \tau_{2}^{(1, 1)}\right) $, and $ E^{*} $ is unstable if $ \tau_2\in\left(\tau_{2}^{(1, 0)}, \tau_{2}^{(2, 0)}\right)\cup\left(\tau_{2}^{(1, 1)}, \infty\right) $. When we choose $ \tau_2 = 8 $, $ E^{*} $ is stable (see Figure 4a). However, when $ \tau_2 $ increases to $ 10 > 9.29205 $, $ E^{*} $ becomes unstable and tends to the boundary equilibrium. In this case, the subcritical Hopf bifurcation appears resulting in an unstable limit cycle (see Figure 4b). As $ \tau_2 $ increase to $ 45 $, $ E^{*} $ becomes stable again (see Figure 4c). When $ \tau_2 $ increases to $ 70 > 68.6063 $, $ E^{*} $ becomes unstable again and tends to the boundary equilibrium (see Figure 4d). Furthermore, system (2.3) undergoes Hopf bifurcation at $ \tau^\star_2 = \tau_{2}^{(1, 0)} = 9.29205 $ (see Figure 1). Although the introduction of $ \tau_1 $ has no effects on the stability of $ E^* $, it can increase the critical values of $ \tau_2 $ which can destabilize $ E^* $.

5.   Conclusion and discussion

In order to understand the effects of toxins on the dynamics of populations in polluted environments, a large number of mathematical models have been developed ^[4,5]. The existing models usually assume that the effects of toxins on population reproduction and mortality are instant. However, there are evidences showing that toxic effects on populations may be delayed. This motivates us to propose a new mathematical model (2.3) with delayed toxic responses in this paper. In the model, two discrete delays $ \tau_1 $ and $ \tau_2 $ represent the delayed effects of toxins on the reproduction and mortality of the population, respectively. We mainly focused on the effects of $ \tau_1 $ and $ \tau_2 $ on the stability of interior equilibrium $ E^\ast $, at which the population persists. The results of theoretical analysis showed that the delayed effect on the reproduction of the aquatic population does not change the stability of $ E^\ast $, but the delayed effect on the mortality of the population significantly affects long-term population dynamics. It turns out that the delayed mortality effects not only produces population oscillations, but also change the fluctuation amplitudes. So, we suggest that experimental biologists should pay more attention to the delayed mortality caused by environmental toxins.

An interesting and challenging future work is the global stability analysis of the equilibria of model (2.3). The delay model (2.3) we studied in this work can be extended in several biologically meaningful ways: (1) The delayed toxic responses in our model are constant. Indeed, the delays can depend on toxin levels or some other environmental factors. We can modify our model such that the delays are functions of the body burden. (2) In a population, different development stages may have different sensitivities to toxins and different delayed toxic responses, so it is worth extending the current model to a stage-structured population model by taking these factors into account. (3) Different species living in the same environment may have different vulnerabilities to toxins, the impact of toxins on the interactions between different species in polluted aquatic environments was studied in ^[30] and ^[31]. We plan to investigate how delayed toxic responses affect the long-term dynamics of two interactive species in the future.

Acknowledgments

The first author is supported by the National Natural Science Foundation of China (11901225), the Natural Science Foundation of Hubei Province (2019CFB189), and the Fundamental Research Funds for the Central Universities (CCNU18XJ041). The third author is supported by the National Natural Science Foundation of China (11871060), the Venture and Innovation Support Program for Chongqing Overseas Returnees (7820100158), the Fundamental Research Funds for the Central Universities (XDJK2018B031), and the faculty startup fund from Southwest University (20710948).

Conflict of interest

The author declares no conflicts of interest in this paper.