We consider the Navier-Stokes equations of an incompressible fluid in a three dimensional curved domain with permeable walls in the limit of small viscosity.
Using a curvilinear coordinate system, adapted to the boundary, we construct a corrector function at order $ε^j$, $j=0,1$, where $ε$ is the (small) viscosity parameter.
This allows us to obtain an asymptotic expansion of the Navier-Stokes solution at order $ε^j$, $j=0,1$, for $ε$ small .
Using the asymptotic expansion, we prove that the Navier-Stokes solutions converge, as the viscosity parameter tends to zero, to the corresponding Euler solution in the natural energy norm.
This work generalizes earlier results in [14] or [26], which discussed the case of a channel domain, while here the domain is curved.
1.
Introduction
Regardless of its relatively young age in comparison with other entropy statistics, Permutation Entropy (PE) has soon become one of the most utilised time series entropy–related measures. It was proposed in the well known paper by Bandt and Pompe [1] in 2002, and since then, it has given rise to a number of applications and further algorithm developments. This number is growing exponentially [2], as a clear evidence of the utility of the PE approach.
Regarding PE applications, it has been used mainly in physiological records classification. There are many scientific papers that illustrate this point. For example, we have used PE to successfully classify body temperature records from febrile and healthy patients [3] and to classify glucose records from patients at diabetes risk [4]. More frequent applications are based on electroencephalogram [5,6,7,8] and heart rate variability [9,10,11] analysis.
Other PE fields of application are also receiving a great deal of attention. In econometrics, there are quite many interesting examples already available. In [12], the authors used PE to try to unearth the dynamical properties of time series featuring Dow Jones Industrial Average data from 1901 to 2016, obtaining a very high degree of randomness related to the market efficiency. They also used PE on temporal windows to identify market events. Along this line, [13] applied PE to stock market time series of several countries to estimate their investment attractiveness. Their findings confirmed the validity of this approach, and they also found a clear correlation between market crisis and PE value decline. The paper [14] studied the evolution of stock market efficiency during the last financial crisis. It used some specific stock exchange indices, with its main focus on the differences between pre and post crisis data processed by PE. In the same context, [15] used the complexity-entropy causality plane and a permutation statistical complexity to analyse financial time series. Using permutation Shannon entropy and permutation Fisher information measure, [16] analysed the possible deterministic components in Libor rates time series induced by manipulation. The study in [17] applied a dynamic approach to detect structural changes in time series using different entropy measures related to PE, including Gaussian, Rényi, Tsallis, and Shannon entropies. They first developed a theoretical study over synthetic time series with abrupt changes in order to assess the transition detection power. Then they applied the methods to real time series, seismic data, and economic data (exchange rates between US dollar and gold, and Nasdaq time series).
In mechanical engineering, PE has also clearly demonstrated its usefulness, mainly in the framework of fault diagnosis. This is the case in [18]. This study uses vibration signals for bearing fault diagnosis based on multiscale PE and multinomial logit model. The classification accuracy achieved was close to 100%. The researchers in [19] also used multiscale PE for automatic recognition of weak faults in hydraulic systems from vibration signals as well. All the diagnosis methods tested achieved at least a recognition rate of 89%, and were able to discern among normal state, slight, moderate, and severe leakage.
The basic PE algorithm has also been improved since its initial version. Two possible algorithm weaknesses were almost immediately detected by researchers regarding PE. First, PE is based on relative frequency of ordinal patterns, but it does not take into account the possible influence of amplitude differences. For example, the subsequences $ \left(0.25, -1.7, -0.33\right) $ and $ \left(100, 99, 99.5\right) $ correspond to the same ordinal pattern $ \left(1, 2, 0\right) $, but from an amplitude perspective they are very different. Some PE algorithm improvements have been proposed in the last years to have the amplitude patterns somehow covered in PE. For example, the Weighted Permutation Entropy method [20,21,22] applies a correction factor before computing the relative frequencies, based on the subsequence variance. The Fine Grained Permutation method [23] adds a new symbol to the ordinal motif of the subsequence that accounts for the amplitude differences. The amplitude information overlooked by the standard PE method has been demonstrated to be significant in many classification tests [24].
The other claimed PE flaw is the impossibility to assign a single motif to subsequences that contain equal values or ties. For example, the subsequence $ \left(2, 1, 2\right) $ could be assigned the ordinal pattern or motif $ \left(1, 0, 2\right) $, but also the $ \left(1, 2, 0\right) $. In the seminal paper [1], Bandt and Pompe already acknowledged this possible issue, and proposed to add a small random noise to break ties in the unlikely event that equal values fall within the same subsequence. However, such ties are not that unlikely, and some improvements have also been suggested since then to minimise the possible histogram bias due to ordinal ambiguities. Thus, the modified PE method [11] generates more motifs corresponding to the possible ties. For example, the motif $ \left(0, 1, 2, 3\right) $ generates also ordinal patterns $ \left(0, 1, 22\right) $, $ \left(0, 11, 3\right) $, $ \left(0, 11, 2\right) $, and $ \left(0, 111\right) $. The method in [25] uses a Bayesian missing data imputation to learn from the unambiguous subsequences what are the most likely motifs in case of ties. The presence of such ties can lead to the incorrect interpretation of the chaotic nature of the time series, but they exert a minor impact on classification performance [26].
Another line of research related to PE is the use of complex networks to map time series [27]. Specifically, the use of transition networks with nodes featuring ordinal patterns as for PE, connected by edges based on temporal succession information from a time series, is a very promising research topic for the future in the field of non–linear dynamics analysis [28]. We also have results in this regard already, using Hidden Markov Models to synthetically generate time series based on the transition probabilities between consecutive ordinal patterns [29].
Other methods have been proposed to improve the performance and robustness of PE. Special attention deserves the Amplitude Aware Permutation Entropy method [30], a method that addresses simultaneously the two PE problems described above. This is also the case for the recently published Improved Permutation Entropy method [31], which adds an amplitude quantization stage to account for amplitude differences, ties, and noise. A different approach is the Bubble Entropy (BE) method [32], devised to reduce the dependence of PE on input parameters, such as the data length or the embedding dimension, by counting the number of sample swaps necessary to achieve the ordered subsequences instead of counting order patterns. It seems that BE exhibits more stability and discriminating power than the standard PE method [32].
Since the BE approach could be a game–changer, based on sorting relations instead of order relations, we hypothesized that PE and BE could exhibit some kind of synergy, since they are not looking exactly at the same aspects of the time series dynamics. For example, the patterns $ \left\{0, 2, 1\right\} $ and $ \left\{1, 0, 2\right\} $ are different for PE, but obtained with the same number of swaps (1) from the original ordinal pattern $ \left\{0, 1, 2\right\} $, therefore, they are considered the same from the BE perspective.
2.
Materials and methods
2.1. Permutation Entropy
The present study is based on the original PE algorithm described in [1], for a single time scale. This method computes a normalised histogram of ordinal patterns found in the subsequences drawn from a time series, when sorted in ascending order, from which the Shannon Entropy is calculated. The length of these subsequences is defined by an input parameter, the embedded dimension $ m $.
Formally, the input time series under analysis is defined as a vector of $ N $ components $ \mathbf{x} = \left\{x_{0}, x_{1}, \ldots, x_{N-1}\right\} $. A generic subsequence extracted commencing at sample $ x_{j} $ of $ \mathbf{x} $ is defined as a vector of $ m $ components $ \mathbf{x}_j^{m} = \left\{x_{j}, x_{j+1}, \ldots, x_{j+m-1}\right\} $. In its original state, the samples in $ \mathbf{x}_j^{m} $ can be assigned a default growing set of indices given by $ \boldsymbol{\pi}^{m} = \left\{0, 1, \ldots, m-1\right\} $. The subsequence $ \mathbf{x}_j^{m} $ undergoes then an ascending sorting process, and the sample order changes in it, are mirrored in the vector of indices $ \boldsymbol{\pi}^{m} $. The resulting new version of this vector, $ \boldsymbol{\pi}_{j}^{m} = \left\{\pi_{0}, \pi_{1}, \ldots, \pi_{m-1}\right\} $, with $ x_{j+\pi_{0}}\leq x_{j+\pi_{1}}\leq x_{j+\pi_{2}} \ldots \leq x_{j+\pi_{m-1}} $, is compared, in principle, with all the possible $ m! $ ordinal patterns of length $ m $. When a coincidence is found, a specific associated counter to that pattern, $ c_{i} \in \mathbf{c} $, is increased. This process is repeated with all the possible $ N-(m-1) $ subsequences ($ 0\leq j < N-m+1 $) until the complete histogram is obtained. Each bin of the histogram is finally normalised by $ N-(m-1) $ in order to obtain an estimation of the probability of each ordinal pattern: $ \mathbf{p} = \left\{p_{0}, p_{1}, \ldots, p_{m!-1}\right\}\left|p_{i} = \frac{c_{i}}{N-(m-1)}\right. $. This vector of probabilities is used to calculate PE as (assuming log $ 0 = 0 $):
For example, let $ \mathbf{x} = \left\{-0.45, 1.9, 0.87, -0.91, 2.3, 1.1, 0.75, 1.3, -1.6, 0.47, -0.15, 0.65, 0.55, -1.1, 0.3\right\} $ be a time series of length 15 whose PE has to be calculated using $ m = 3 $. The procedure of subsequence extraction and sorting is illustrated in Table 1. Many other numerical examples of PE computation can be found in the literature. For example, in works such as [33,34].
2.2. Bubble Entropy
BE is a very recently proposed entropy measure [32] that has not received the attention it deserves yet, but it will surely become an indispensable tool in the field of non–linear dynamics analysis due to the possible improvements over PE it introduces.
The main objective of BE was to minimise the dependence of entropy measures on input parameters. In general, many of the most utilised measures require at least two for their computation, an embedded dimension $ m $, and a similarity threshold $ r $. Depending on the values of these parameters, the performance can vary significantly in terms of discriminating power, robustness to artifacts, or any other desirable feature. Along this line, the Rank–Entropy method (RankEn) described in [35] tried to reduce the dependence on $ r $ by calculating the amount of shuffling that the distances between two subsequences under comparison had to undergo to sort such distances in ascending order. In this case, the parameter $ r $ determines the maximum rank of the set of distances that contribute to the entropy measure, and therefore, the $ r $ value is less critical.
In [32], researchers went one step further in order to remove completely the $ r $ parameter from the entropy computation. Taking advantage of the PE method, already independent of $ r $, and the shuffling used for RankEn, the authors proposed first a new method, called Conditional Rényi Permutation Entropy, which combined Conditional Entropy (CE) [36], and Rényi Permutation Entropy (RPE) [37]. CE can be computed as CE$ (m) = $PE$ (m+1)- $PE$ (m) $. RPE achieved the best results when using a quadratic approach, as for Sample Entropy, and outperformed other entropy methods in terms of discriminating power [38]. Then, BE was finally defined by using two consecutive $ m $ values as CE, with a quadratic Rényi definition of entropy, and processing ordinal patterns, as PE. This way, BE does not need parameter $ r $, is less dependent on $ m $, or even independent for large $ m $ values, it gives more emphasis to peaks without neglecting lower values, the number of unique possible states is reduced (ties and amplitude influence are less critical since more matches to compute relative frequencies can be found), and converges faster than PE, with a higher discriminating power [32].
The core of the BE algorithm is that of PE, but instead of computing the relative frequency of the ordinal patterns, it computes the relative frequency of the necessary swaps to get an ordered subsequence. First, each subsequence $ \mathbf{x}_j^{m} $ is also sorted in ascending order using a bubble sort algorithm. The counter vector $ \mathbf{c} $ stores instead all the swaps necessary in each case, with a maximum given by $ \left[0, \frac{m(m-1)}{2}\right] $. Each bin is normalised by $ N-m+1 $ too. From all the resulting relative frequencies $ p_{i} $, accounting for how likely a number of swaps is [32], the Rényi entropy of order 2 is computed as:
The embedding dimension is then increased by 1, $ m \rightarrow m+1 $, and the procedure is repeated again to obtain a new entropy value from Eq. 2, $ H_{2}^{m+1} $. Finally, BE is obtained in a similar way as for Approximate Entropy, ApEn [39]:
The procedure of subsequence extraction, sorting, and swap computation, for the same input time series as for PE, is illustrated in Table 2. The maximum number of swaps in this case is 3.
From the results in Table 2, the counter vector components for the first iteration of the method are obtained as: $ c_0 = 0 $, $ c_1 = 7 $, $ c_2 = 3 $, and $ c_3 = 3 $. These values, once normalised, will become the probability vector $ p $ from which entropy $ H^{m} $ can be computed. The process is then repeated for $ m \rightarrow m+1 = 4 $ to obtain $ H^{m+1} $, with results: $ c_0 = 0 $, $ c_1 = 1 $, $ c_2 = 2 $, $ c_3 = 2 $, $ c_4 = 6 $, $ c_5 = 1 $, and $ c_6 = 0 $. Finally, applying Eq. 3, the value for BE obtained is 0.3115, with $ H^{4} = 1.1411 $, and $ H^{3} = 0.9252 $. An implementation of this method is detailed in Algorithm 1.
2.3. Performance analysis
The performance analysis of the methods under analysis will be assessed both in quantitative and qualitative terms. The classification accuracy will be quantified as the ratio of correctly assigned time series to classes. For example, a 0.80 classification accuracy will refer to the fact that 80% of the time series were labelled as their true class after the classification analysis has been completed. The remaining 20% has been incorrectly included in another class distinct to the true class to which they belong. The classification accuracy was quantified using the classical sensitivity, specificity and accuracy performance indicators. They were obtained using a threshold from the closest point in the ROC curve [40] to the (0, 1) point [41]. We first proceeded by computing the number of True Positives (TP), False Negatives (FN), True Negatives (TN), and False Positives (FP). Then, the classical performance metrics Sensitivity = TP / (TP+FN), Specificity = TN / (TN+FP), and Accuracy = (TN + TP) / (TN + TP + FN + FP) [42], were obtained.
However, the numerical result of the classification accuracy does not suffice to provide a complete picture of the discriminating power of the method. For example, a relatively high accuracy of 0.75 can be achieved for the classification of two size–balanced classes, but with a sensitivity close to 0.5, pure guess, and a specificity close to 1, a useless performance since there must be a trade–off between both parameters to avoid statistical uncertainty.
Therefore, in order to assess the statistical significance of the results quantified in terms of classification accuracy, we used a bootstrap version [43] of the equality of means (there is no difference between the classes under analysis according to the values of PE or BE obtained for classification) hypothesis testing. By using this bootstrap method, it is not necessary to assume any specific distribution of the data, and it can be applied even to small sizes of data.
Given two samples $ \mathbf{Y} = \left\{Y_{1}, \ldots, Y_{n_{Y}}\right\} $ and $ \mathbf{Z} = \left\{Z_{1}, \ldots, Z_{n_{Z}}\right\} $, the steps to carry out this test are:
1. Calculate the $ T $ statistic as in the standard t–Student test [44].
2. Resample the input data randomly with replacement to create bootstrapped versions of the data, $ \mathbf{Y}^{*} $ and $ \mathbf{Z}^{*} $.
3. Calculate a bootstrap statistic $ T^{*} $ as:
where $ \mu $ is the mean, and $ \sigma^{2} $ the variance of the data.
4. Repeat steps 2 and 3 several times ($ k = 200 $ in this case) to obtain the corresponding statistics $ T^{*}_{1}, T^{*}_{2}, \ldots, T^{*}_{k} $.
5. Sort the previous statistics in increasing order, $ T^{*}_{(1)}, T^{*}_{(2)}, \ldots, T^{*}_{(k)} $.
6. Reject the equal means hypothesis, $ H:\mu_{\mathbf{Y}} = \mu_{\mathbf{Z}} $, if $ T < T_{(q_{1})}^{*} $ or $ T > T_{(q_{2})}^{*} $, where $ q_{1} = \left\lfloor k\alpha/2 \right\rfloor $ and $ q_2 = k-q_{1}+1 $.
The null hypothesis of equal means of the classes in terms of PE or BE was assessed using this test. The acceptance threshold was set at $ \alpha = 0.05 $.
The possible synergy between PE and BE can be exploited in many ways. They can become independent variables of the same classification function, as in logistic regression applications [45,3], among many other similar methods. The input dataset can be split into training and test sets to obtain more complex polynomial classification functions, as is the case when using neural networks [46]. They can also conform the input feature vector for an unsupervised classification approach featured by a clustering algorithm [47].
We have chosen the clustering approach for its simplicity and good results in previous similar studies [48]. The specific method employed is the Max–Min algorithm [49]. The input number of clusters was set to 2, and therefore 2 centroids are selected, one from each experimental dataset. In order to further simplify the clustering method, since the goal was not to design a classification method but rather explore the possible synergy between PE and BE, the centroids are chosen from those time series with the maximum and minimum PE value, the furthest points in the PE feature space. Finally, each time series is assigned to the class of the closest centroid in a single iteration, quantified using a Euclidean distance. If the goal was to maximise the classification performance, a more evolved clustering algorithm could be chosen, such as a genetic method that converges to a global minimum cost [50], or a density–based method, that enables the use of highly complex partition regions [51]. Other distance metrics, or more iterations with centroid updating could also be used, such as in the $ k $–Means method or its variants [52,53].
3.
Experiments
3.1. Experimental dataset
The experimental dataset was composed of 7 biomedical records previously used in other studies. In addition, 4 out of the 7 datasets are publicly available at Physionet [54]. The information regarding the specific datasets employed is summarised in Table 3, for our proprietary data, and in Table 4, for the publicly available data at Physionet. Each row includes the dataset assigned name, a short description, and references to further studies or information about the specific dataset in each case. An example plot of one record is also included.
3.2. Results
The experiments were devised to assess the performance of BE and PE using a different and more varied dataset than in the seminal paper of BE [32], and also to explore the possible synergies between both measures. These experiments also included a variation of the parameter $ m $, from 3 to 8, since input parameter influence is another topic of intense debate and research in the scientific literature. All the experiments and algorithms were implemented in C++ programming language, using MinGW 4.9.2 32 bit compiler (www.mingw.org).
In this regard, Table 5 shows the classification performance (if statistically significant) of the results achieved by PE and BE using the TEMPERATURE dataset. In this case, PE exhibits a high classification accuracy, around 0.8 in some $ m $ cases. BE performance is not significant for any $ m $ value.
For the SURVIVAL dataset, the classification results achieved are shown in Table 6. The results for BE are not statistically significant for $ m = 8 $, being PE more stable with $ m $. The maximum performance achieved by both methods was 0.77.
For the last dataset in Table 3, GLUCOSE, the results are listed in Table 7. Both statistics yielded significant classification results in all $ m $ cases tested, but the performance of BE was slightly superior to that of PE, 0.80 vs. 0.79. This small difference is more significant if sensitivity is taken into account, since with PE it was 0.61, but with BE it was 0.66, a clear difference for a small class size of 18 records.
Table 8 shows the classification performance achieved by PE and BE using the BONN dataset. In this case, PE exhibits a very high classification accuracy, close to 0.9 in all $ m $ cases. BE performance is lower, 0.785 at most, and even with no significant results for $ m = 5, 6, 7 $.
In Table 9, the classification results for the three classes in the EMG database are shown (healthy, myopathy, neuropathy). PE was not able to achieve significant results for the second case (Healthy vs. Myopathy), whereas BE found differences in all cases for $ m = 3 $ and $ 5 $. Therefore, BE can be considered to outperform PE in this experiment.
Table 10 shows the results for the FANT database. In this case, BE was clearly better than PE, with significant results for $ m = 7, 8 $, and a maximum classification accuracy of 0.875. PE was not capable of achieving the significance threshold, probably because in many experiments either Sensitivity or Specificity were close to 0.5, despite a good accuracy in the other measure.
Finally, the results of the last dataset are shown in Table 11. The classification accuracy of PE was quite stable around 0.8, but BE clearly failed in this case.
A summary of the best statistically significant accuracy results achieved using the two measures assessed (PE, BE) is shown in Table 12. Of the 7 datasets, PE yielded a better accuracy in 3 cases, and BE in other 3. In 2 datasets each, PE and BE were not capable of finding significant differences. There was no dataset where none of the measures studied failed to find significant differences, but in 4 of the experiments, one of the measures achieved a good performance, whereas the other was unable to achieve statistically significant results. It is not possible to say what measure was better in this case. However, what became more apparent was the fact that there exists a clear complementarity between PE and BE, each one seems to look at different properties of the time series dynamics, and this should be exploited.
The second group of experiments were focused on exploring the possible synergy between PE and BE, used jointly for classification. Without any specific customisation, the clustering algorithm described in Section 2.3 was applied to some datasets in a completely unsupervised way. The quantitative results achieved are shown in Tables 13, 14 and 15 to provide an example of beneficial synergy or no synergy.
The results for the GLUCOSE dataset in Table 13 probably best illustrate the optimal synergy between BE and PE. The classification performance achieved combining these two measures is far higher than that achieved individually, which confirms the hypothesis that there exits at least some PE–BE complementarity. Moreover, it is independent of the $ m $ value, an almost ideal case.
However, one size does not fit all, and the method should be customised for each dataset. For example, what worked in Table 13, for the GLUCOSE dataset, did not work in other cases. Table 14 shows the classification accuracy achieved using the TEMPERATURE dataset, where the individual performance using PE is higher than using both measures. Since BE did not achieve any significant result, it seems it has a blurring effect on the differences between classes. The discerning method should be customised to automatically detect the measure that better features the differences, and therefore increase not only the accuracy, but also the robustness of the classification by reducing the number of datasets where no significance is achieved.
The results in Table 15 also correspond to a case where the possible synergy is not seamlessly exploited. The clustering method achieves a lower performance than the methods individually, but with a small difference for $ m < 6 $. As in the previous case, with clustering method optimisation and customisation, or using other more sophisticated pattern recognition methods, it can be hypothesised that there is room for performance improvement.
4.
Discussion
The experiments in Section 3 were first aimed at confirming the performance of the BE approach from a broader point of view than in [32], using a set of records with markedly different properties and behaviour: slow varying signals such as TEMPERATURE, SURVIVAL, and GLUCOSE datasets, faster varying signals such as the BONN dataset, spiky records in the EMG dataset, and a combination of probably all the previous, in the RR datasets.
According to the results, the performance of BE was, in general, similar but complementary to that of PE, in terms of classification accuracy. Namely, both statistics achieved similar performance, but on different datasets. Taking into account all the $ m $ values tested, PE seems to be more robust and stable with slow varying signals, and BE for spiky records (as theoretically stated in Section 2.2), with the rest of records in between. The dependence of both PE and BE on parameter $ m $ remains an unsolved problem, since there was a great accuracy variability depending on the specific $ m $ value chosen in many cases.
PE yielded a higher accuracy than BE for datasets TEMPERATURE (Table 5), BONN (Table 8), and PAF (Table 11), whereas BE outperformed PE when applied to GLUCOSE (Table 7), EMG (Table 9), and FANT (Table 10) time series. The performance was the same for the SURVIVAL dataset (Table 6). Obviously, a generalisation can not be made however representative the experimental dataset is, but it can arguably be stated that the combination of PE and BE is more likely to provide significant results than each measure isolatedly, mainly based on the fact that non–significance on one measure is often accompanied by high performance on the other (Table 12).
Along this line, we explored a potential synergy using a very simple approach based on a clustering algorithm, and PE and BE as the two extracted features. If the object distribution in the PE–BE plane matches the centroid computation and the clustering algorithm geometric properties, the possible synergy can be exploited successfully, as demonstrated in Table 13. However, this is not always the case, and the combination of PE and BE can also exert a blurring effect and have a detrimental impact on classification performance (Table 14 and Table 15). Therefore, whatever the discriminating function chosen is (linear, polynomial, logistic, etc.), or the classification algorithm (clustering, neural networks, random forest, etc.), it should be customised in each case to make the most of the information provided by PE and BE. Obviously, there will be cases where no synergy will be found, whatever the method is, but in some cases as in Table 13, combining more than a single method can make a significant difference.
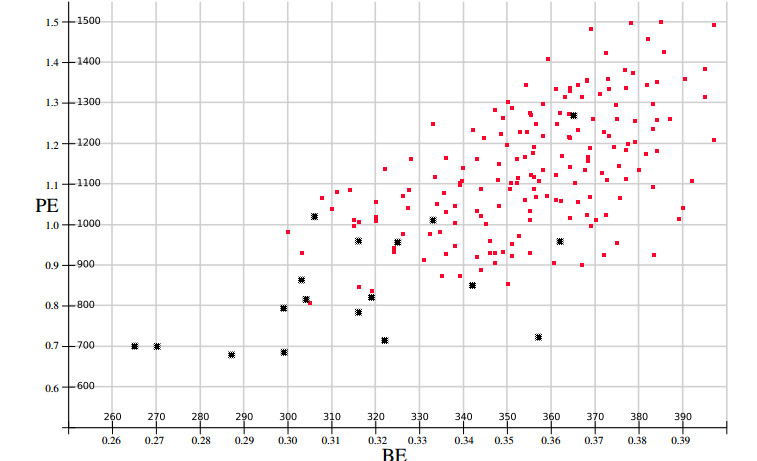
Fig. 1 depicts an example of the interaction between BE and PE for the dataset GLUCOSE, with $ m = 8 $. With a suitable computed class segmentation function, it is possible to increase the accuracy achieved by each method individually. As stated above, this is not always the case, and the possible synergy has to be assessed on a case–by–case basis. It will also depend on the complexity of the segmentation function employed, and on the match between the shape of the clusters and the clustering algorithm applied: spherical, linear, or other non–linear shapes. In a more general way, when one of the methods fails, either PE or BE, it is more likely the other yields a significantly better performance, since complementarity seems to be even more frequent than synergy (Tables 5, 8, 10 11).
5.
Conclusions
Every year quite many new tools to quantify the dynamical features of time series are described in the scientific literature. These new tools are claimed to be more efficient in algorithmic terms, more sensitive, more robust, or less dependent on input parameters, among many other possible benefits. In this regard, BE is a recently proposed measure that exploits the effort to sort subsequences instead of the ordinal patterns obtained [32].
BE was presented as an improvement over PE, less influenced by the time series length, the specific value of the input parameter $ m $, and with a better discriminating power [32]. The present study assessed this discriminant power using several different datasets, and we would conclude that the BE discriminating capability was not clearly better, but complementary, BE succeeded where PE failed, and the other way round. This led us to try to combine both measures in a single method to take advantage of BE and PE strengths and simultaneously minimise their weaknesses. The scheme used was based on a clustering algorithm, equivalent to a linear discriminant function.
According to the results obtained, the combination of methods can be considered a new strategy worth examining in the field of time series classification. It should not be claimed to be a cure–all method, but the classification performance confirmed the hypothesis in some cases, and it seems to be able to exploit the synergy between PE and BE provided there is some customisation to the problem at hand.
Moreover, classification performance should not be the only item to be maximised in quantitative terms. Since there are many datasets where only one measure is able to find significant differences, other customisations should be devised to increase the robustness of the classification. In other words, new algorithms able to automatically exploit the differences provided by a measure, and minimise the influence of the confounding measure, should be proposed. This way, it would be possible to have a method able to work with a wider input range of time series or properties, with, for example, statistically significant results in more datasets used in the present study.
There are many clustering algorithms described in the scientific literature, most of them more robust than the example used in this paper. In addition to implementation issues to save memory requirements or computational cost, the algorithms could be improved in terms of accuracy, unknown number of classes, optimality or convergence.
This approach will need further studies using other databases and other non–linear features. The direct combination of ordinal patterns and sorting relations in a single statistic should also be investigated, or the introduction of the BE information into PE computation as a some kind of histogram weighting. The influence of time series length [59], equal values in the subsequences [26], and time delay $ \tau $, could also be characterised. Further integration with other PE improvements could be worth exploring [30,23,20,4,11].
Acknowledgements
No funding was received to support this research work.
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: