Stochastic homogenization on perforated domains Ⅰ – Extension Operators

1.   Introduction

In 1979 Papanicolaou and Varadhan ^[22] and Kozlov ^[15] for the first time independently introduced concepts for the averaging of random elliptic operators. At that time, the periodic homogenization theory had already advanced to some extend (as can be seen in the book ^[23] that had appeared one year before) dealing also with non-uniformly elliptic operators ^[17] and domains with periodic holes ^[3]. The most recent and most complete work for extension operators on periodically perforated domains is ^[11].

In contrast, the homogenization on randomly perforated domains is still open to a large extend. Recent results focus on minimally smooth domains ^[9,24] or on decreasing size of the perforations when the smallness parameter tends to zero ^[8] (and references therein). The main issue in homogenization on perforated domains compared to classical homogenization problems is compactness. For elasticity, this is completely open.

The results presented below are meant for application in quenched homogenization, i.e. when one special but also typical realization of the random geometry is picked as a working model for the perforated domain. The presented estimates for the extension and trace operators strongly depend on this given realization of the geometry - thus on the random variable $\omega$. However, in order to have a law of large numbers, which allows us to consider ever larger domains (or arbitrary scaling ${\varepsilon} > 0$), we will assume that the geometry is stationary. This implies that even though the constant depends on the given realization, still such an estimate can be achieved for almost every $\omega$.

1.1.   The problem

In order to illustrate the issues in stochastic homogenization on perforated domains, we introduce the following example.

Let ${\bf{P}}(\omega)\subset{\mathbb{R}^{d}}$ be a stationary random open set and let ${\varepsilon} > 0$ be the smallness parameter and let $\tilde{{\bf{P}}}{\left({\omega}\right)}$ be an infinitely connected component (i.e., an unbounded connected domain) of ${\bf{P}}{\left({\omega}\right)}$. For a bounded open domain ${\bf{Q}}$, we consider ${\bf{Q}}_{\tilde{{\bf{P}}}}^{{\varepsilon}}(\omega): = {\bf{Q}}\cap{\varepsilon}\tilde{{\bf{P}}}(\omega)$ and $\Gamma^{{\varepsilon}}(\omega): = {\bf{Q}}\cap{\varepsilon}\partial\tilde{{\bf{P}}}(\omega)$ with outer normal $\nu_{\Gamma^{{\varepsilon}}(\omega)}$. For a sufficiently regular and ${\mathbb{R}^{d}}$-valued function $u$ we denote ${\nabla^{s}} u: = \frac{1}{2}\left(\nabla u+(\nabla u)^{\top}\right)$ the symmetric part of $\nabla u$. A typical homogenization problem then is the following:

Note that for simplicity of illustration, the only randomness that we consider in this problem is due to ${\bf{P}}(\omega)$.

One way to prove homogenization of Eq (1.1) is to prove $\Gamma$-convergence of

in a suitably chosen space where $G' = g$ and $F' = f$. Conceptually, this implies convergence of the minimizers ${u^{{\varepsilon}}}$ to a minimizer of a limit functional but if $G$ or $F$ are non-monotone, we need compactness. However, the minimizers are elements of ${\bf{W}}^{1, p}({\bf{Q}}_{\tilde{{\bf{P}}}}^{{\varepsilon}}): = W^{1, p}({\bf{Q}}_{\tilde{{\bf{P}}}}^{{\varepsilon}}; {\mathbb{R}^{d}})$ and since this space changes with ${\varepsilon}$, there is apriori no compactness of ${u^{{\varepsilon}}}$, even though we have uniform apriori estimates on the symmetric gradients.

One of the canonical paths to circumvent this issue in periodic homogenization–i.e., when ${\bf{P}}$ is a periodic set–is via uniformly bounded extension operators ${\mathcal{U}}_{{\varepsilon}}:\, W^{1, p}({\bf{Q}}_{\tilde{{\bf{P}}}}^{{\varepsilon}})\to W^{1, p}({\bf{Q}})$ that share the property that for some $C > 0$ independent from ${\varepsilon}$ it holds for all $u\in W^{1, p}({\bf{Q}}_{\tilde{{\bf{P}}}}^{{\varepsilon}})$ with $u|_{{\mathbb{R}^{d}}\backslash{\bf{Q}}}\equiv0$

see ^[11,12], combined with uniformly bounded trace operators, see ^[7,9]. Such operators have also been provided for elasticity problems ^{[11,21,30,31]}, i.e.,

The last estimate then allows to use Korn's inequality combined with Sobolev's embedding theorem to find ${\mathcal{U}}_{{\varepsilon}}{u^{{\varepsilon}}}{\rightharpoonup} u_{0}$ weakly in ${\bf{W}}^{1, p}({\bf{Q}})$.

What is the classical strategy? The existing results on extension and trace operators for random domains are focused on a.s. minimally smooth domains: A connected domain ${\bf{P}}\subset{\mathbb{R}^{d}}$ is minimally smooth ^[26] if there exist $(\delta, M)$ such that for every $x\in\partial{\bf{P}}$ the set $\partial{\bf{P}}\cap\mathbb{B}_{{\delta}}{\left(x\right)}$ is the graph of a Lipschitz continuous function with Lipschitz constant less than $M$. It is further assumed that the complement ${\mathbb{R}^{d}}\backslash{\bf{P}}$ consists of uniformly bounded sets. This concept leads to almost sure construction of uniformly bounded extension operators $W_{{\mathrm{loc}}}^{1, p}({\bf{P}})\to W^{1, p}({\mathbb{R}^{d}})$ ^[9] in the sense that for every bounded domain ${\bf{Q}}$ and every $u\in W^{1, p}({\mathbb{R}^{d}}\cap{\bf{P}})$ with $u|_{{\mathbb{R}^{d}}\backslash{\bf{Q}}}\equiv0$ holds

with $C$ independent from ${\bf{Q}}$. Similarly, one obtains for the trace ${\mathcal{T}}$ that ^[24]

Using a scaling argument to obtain e.g., Eq (1.2), such extension and trace operators are typically used in order to deal with nonlinearities in homogenization problems.

Why does this work? The theory cited above is directly connected to the theory of Jones ^[13] and Duran and Muschietti ^[5] on so-called John domains. These are precisely the bounded domains ${\bf{P}}$ that admit extension operators $W^{1, p}({\bf{P}})\to W^{1, p}({\mathbb{R}^{d}})$ satisfying

Definition (John domains). A bounded domain ${\bf{P}}\subset{\mathbb{R}^{d}}$ is a John domain (a.k.a $({\varepsilon}, \delta)$-domain) if there exists ${\varepsilon}, \delta > 0$ such that for every $x, y\in{\bf{P}}$ with $\left|x-y\right| < \delta$ there exists a rectifiable path $\gamma:\, [0, 1]\to{\bf{P}}$ from $x$ to $y$ such that

Because of the locality implied by $\delta$, it is possible to glue together local extension operators on John domains such as done in ^[11] for periodic or ^[9] for minimally smooth domains. In the stochastic case ^[9] one benefits a lot from the uniform boundedness of the components of ${\mathbb{R}^{d}}\backslash{\bf{P}}$, which allows to split the extension problem into independent extension problems on uniformly John-regular domains.

Why this is not enough for general random domains? As one could guess from the emphasis that is put on the above explanations, random geometries are merely minimally smooth or even John. On an unbounded random domain ${\bf{P}}$, the constant $M$ can locally become very large in points $x\in\partial{\bf{P}}$, while simultaneously, $\delta$ can become very small in the very same $x$. In fact, they are not even "uniformly John" as the following, yet deterministic example illustrates.

Example 1.1. Considering

the Lipschitz constant on $(2n, 2n+2)$ is $n$ and it is easy to figure out that this non-uniformly Lipschitz domain violates the John condition due to the cusps. Hence, a uniform estimate of the form Eq (1.3) cannot exist.

Therefore, an alternative concept to measure the large scale regularity of a random geometry is needed. Since the classical results do not exclude the existence of an estimate

or

where $1\leq r < p$ and $C$ is independent from ${\bf{Q}}$, such inequalities will be our goal.

Our results in a nutshell We will provide inequalities of the form Eqs (1.4) and (1.5) for a Voronoi-pipe model and for a Boolean model. On the way, we will provide several concepts and intermediate results that can be reused in further examples and general considerations such as in Part Ⅲ of this series. Scaled versions (replacing ${\varepsilon} = m^{-1}$ in Theorems 1.15 and 1.17) of Eqs (1.4) and (1.5) can be formulated for functions

and will be of the form

resp.

We will further show that there exists $\beta\in(0, 1)$ such that the support of ${\mathcal{U}}_{{\varepsilon}}u$ lies within $\mathbb{B}_{{{\varepsilon}^{\beta}}}{\left({{\bf{Q}}}\right)}$ for ${\varepsilon}$ small enough. This is a compensation for the property of periodic geometries, where the extended function has support within $\mathbb{B}_{{{\varepsilon}}}{\left({{\bf{Q}}}\right)}\subset\mathbb{B}_{{{\varepsilon}^{\beta}}}{\left({{\bf{Q}}}\right)}$ (for $0 < {\varepsilon}, \beta < 1$).

1.1.1.   Mathematical challenges

On the way to our final results, we will face the following problems that have to be overcome:

1. Quantifying local and global properties of the random geometry that are involved in the extension operator: These quantities are related to the local Lipschitz regularity, the mesoscopic distribution of mass and the connectivity of the perforated domain.

2. The "local" norm of the extension operator, i.e., when restricted to a given bounded domain, will be related to a polynomial expression on the above mentioned quantities. In order to find an upper bound for the local norms, i.e., one constant to bound the extension operator on all bounded domains, we need a law of large numbers for the involved geometric quantities. This law of large numbers will be provided by stationarity and ergodicity of the geometry.

3. In order to use the stationarity of the geometry, we are requested to show that they are Borel measurable. This allows one to consider them as stationary random variables and to apply the ergodic theorem.

While the author considers the first topic as the essential contribution of this article, the other two points are technically necessary to make the theory work. Many of the background provided below may sound very familiar to many readers, even if some details in the formulation are new. However, the author strongly suggest that the reader may have a detailed look at the following parts:

● Sections 2.8, 2.11 and Lemma 2.60

● Lemmas 2.60–3.9 and 3.17–3.18

● Lemmas 4.7 and 4.10

● This may be enough to develop a basic understanding how the concepts interact in the final proofs of Section 4.10.

1.1.2.   Quantifying properties of random geometries

As a replacement for periodicity, we introduce the concept of mesoscopic regularity of a stationary random open set:

Definition 1.2 (Mesoscopic regularity). Let ${\bf{P}}$ be a stationary ergodic random open set, let $\tilde{f}$ be a positive, monotonically decreasing function $\tilde{f}$ with $\tilde{f}(R)\to0$ as $R\to\infty$ and let ${\mathfrak{r}} > 0$ such that

Then ${\bf{P}}$ is called $({\mathfrak{r}}, \tilde{f})$-mesoscopic regular. ${\bf{P}}$ is called polynomially (exponentially) regular if $1/\tilde{f}$ grows polynomially (exponentially).

As a consequence of Lemmas 3.14, 3.16 and 3.17 we obtain the following.

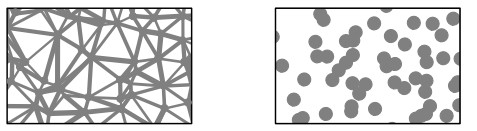
Corollary 1.3 (Stationary ergodic random open sets are mesoscopic regular, see Figure 1).

Let ${\bf{P}}(\omega)$ be a stationary ergodic random open set. Then there exists ${\mathfrak{r}} > 0$ and a monotonically decreasing function with $\tilde{f}(R)\to0$ as $R\to\infty$ such that ${\bf{P}}$ is $({\mathfrak{r}}, \tilde{f})$-mesoscopic regular.

Furthermore, there exists a jointly stationary random point process ${\mathbb{X}}_{{\mathfrak{r}}}(\omega) = \left(x_{a}\right)_{a\in{\mathbb{N}}}$ and for every $a\in{\mathbb{N}}$ it holds $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({x_{a}}\right)}\subset{\bf{P}}$ and for all $a, b\in{\mathbb{N}}$, $a\neq b$, it holds $\left|x_{a}-x_{b}\right| > 2{\mathfrak{r}}$.

Construct from ${\mathbb{X}}_{{\mathfrak{r}}}$ a Voronoi tessellation of cells $G_{a}$ with diameter $d_{a} = d(x_{a})$. Then for some constant $C > 0$ and some monotone decreasing $f:\, (0, \infty)\to{\mathbb{R}}$ and $C > 0$ with $f(R)\leq C\tilde{f}(C^{-1}R)$ it holds

The objects ${\mathfrak{r}}$, ${\mathbb{X}}_{{\mathfrak{r}}}$ and $f$ from Corollary 1.3 will play a central role in the analysis: They are connected to the stationarity of the geometry and will hence serve to construct a substitute for the periodic unit cell. We summarize some of their properties in the following.

Assumption 1.4. Let ${\bf{P}}$ be a Lipschitz domain and assume there exists a set of points ${\mathbb{X}}_{{\mathfrak{r}}} = \left(x_{a}\right)_{a\in{\mathbb{N}}}$ having mutual distance $\left|x_{a}-x_{b}\right| > 2{\mathfrak{r}}$ if $a\neq b$ and with $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({x_{a}}\right)}\subset{\bf{P}}$ for every $a\in{\mathbb{N}}$ (e.g., ${\mathbb{X}}_{{\mathfrak{r}}}({\bf{P}})$, see Eq (2.53)).

The second important concept to quantify in a stochastic manner is that of local Lipschitz regularity.

Definition 1.5 (Local $\left(\delta, M\right)$-Regularity). Let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be an open set. ${\bf{P}}$ is called $(\delta, M)$-regular in $p_{0}\in\partial{\bf{P}}$ if there exists an open set $U\subset{\mathbb{R}}^{d-1}$ and a Lipschitz continuous function $\phi:\, U\to{\mathbb{R}}$ with Lipschitz constant greater or equal to $M$ such that $\partial{\bf{P}}\cap\mathbb{B}_{{\delta}}{\left({p_{0}}\right)}$ is subset of the graph of the function $\varphi:\, U\to{\mathbb{R}^{d}}\, , \; \tilde{x}\mapsto\left(\tilde{x}, \phi{\left({\tilde{x}}\right)}\right)$ in some suitable coordinate system.

Every Lipschitz domain ${\bf{P}}$ is locally $(\delta, M)$-regular in every $p_{0}\in\partial{\bf{P}}$. In what follows, we bound $\delta$ from above by ${\mathfrak{r}}$ only for practical reasons in the proofs. The following quantities can be derived from local $(\delta, M)$-regularity.

Definition 1.6. For a Lipschitz domain ${\bf{P}}\subset{\mathbb{R}^{d}}$ and for every $p\in\partial{\bf{P}}$ and $n\in{\mathbb{N}}\cup\{0\}$

If no confusion occurs, we write $\delta = \delta_{\Delta}$. Furthermore, for $c\in(0, 1]$ let $\eta(p) = c\delta_{\Delta}(p)$ or $\eta(p) = c\rho_{n}(p)$, $n\in{\mathbb{N}}$ and $r\in C^{0, 1}(\partial{\bf{P}})$ and define

where $\inf\emptyset = \sup\emptyset: = 0$ for notational convenience. We also write $M_{[\eta], {\mathbb{R}^{d}}}(x): = M_{[\eta, \eta], {\mathbb{R}^{d}}}(x)$ and $\eta_{{\mathbb{R}^{d}}}{\left(x\right)}: = \eta_{[\eta], {\mathbb{R}^{d}}}{\left(x\right)}$. Of course, we can also consider $M_{[r], \partial{\bf{P}}}:\, p\mapsto M_{r(p)}(p)$ as a function on $\partial{\bf{P}}$, and we will do this once in Lemma 3.9.

When it comes to application of the abstract results found below, it is important to have in mind that $\eta$ and $M_{r}$ are quantities on $\partial{\bf{P}}$, while $\eta_{[r], {\mathbb{R}^{d}}}$ and $M_{[r, \eta], {\mathbb{R}^{d}}}$ are quantities on ${\mathbb{R}^{d}}$. Hence, while trivially

(and similarly for $M_{[r, \eta], {\mathbb{R}^{d}}}$) for every convex bounded open ${\bf{Q}}$, we have in mind

We will prove measurability of $\eta_{[r], {\mathbb{R}^{d}}}$ and $M_{[r, \eta], {\mathbb{R}^{d}}}$ in Lemma 3.11 and see how the weighted expectations of $\eta_{[r], {\mathbb{R}^{d}}}$ and $M_{[r, \eta], {\mathbb{R}^{d}}}$ can be estimated by weighted expectations of $M$ and $\eta$ in Lemma 3.12.

1.1.3.   Traces

The first important result is the boundedness of the trace operator.

Theorem 1.7. Let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be a Lipschitz domain, $\frac{1}{8} > {\mathfrak{r}} > 0$ and let ${\bf{Q}}\subset{\mathbb{R}^{d}}$ be a bounded open set and let $1\leq r < p_{0} < p$. Then the trace operator ${\mathcal{T}}$ satisfies for every $u\in W_{{\mathrm{loc}}}^{1, p}{\left({{\bf{P}}}\right)}$

where for some constant $C_{0}$ depending only on $p_{0}$, $p$ and $r$ and $d$ and for $\tilde{\rho} = 2^{-5}\rho_{1}$ one has

Proof. This is proved in Section 4.6. □

1.1.4.   Local covering of $\partial{\bf{P}}$

In view of Corollary 3.8 and recalling Eq (1.9), for every $n = 1$ or $n = 2$ there exist a complete covering of $\partial{\bf{P}}$ by balls $\mathbb{B}_{{\tilde{\rho}_{n}\left(p_{i}^{n}\right)}}{\left({p_{i}^{n}}\right)}$, $\left(p_{i}^{n}\right)_{i\in{\mathbb{N}}}$, where $\tilde{\rho}_{n}{\left(p\right)}: = 2^{-5}\rho_{n}{\left(p\right)}$. We write $\tilde{\rho}_{n, i}: = \tilde{\rho}_{n}(p_{i}^{n})$. The theory we develop is further using the following two quantities.

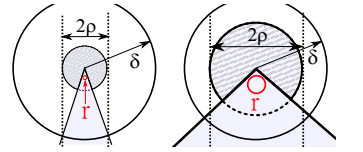
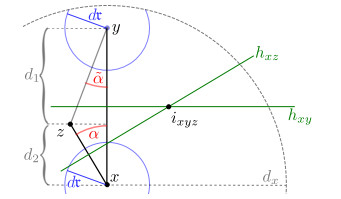
Definition 1.8 (Microscopic regularity (see also Figure 2)). The inner microscopic regularity $\alpha$ is

In Lemma 3.1 we will see that indeed $\alpha\leq1$.

Definition 1.9 (Extension order (see also Figure 2)). The geometry is of extension order $n\in{\mathbb{N}}\cup\{0\}$ if there exists $C > 0$ such that for almost every $p\in\partial{\bf{P}}$ there exists a local extension operator

The geometry is of symmetric extension order $n\in{\mathbb{N}}\cup\{0\}$ if there exists $C > 0$ such that for almost every $p\in\partial{\bf{P}}$ there exists a local extension operator

Corollary 3.7 shows that every locally Lipschitz geometry is of extension order $n = 1$ and every locally Lipschitz geometry is of symmetric extension order $n = 2$. However, for particular geometries better results for $n$ are possible, as we will see below.

1.1.5.   Global tessellation of ${\bf{P}}$

Let ${\mathbb{X}} = \left(x_{a}\right)_{a\in{\mathbb{N}}}$ be a jointly stationary point process with ${\bf{P}}$ such that $\mathbb{B}_{{{\mathfrak{r}}}}{\left({{\mathbb{X}}}\right)}\subset{\bf{P}}$. In this work, we will often assume that $\left|x_{a}-x_{b}\right| > 2{\mathfrak{r}}$ for all $a\neq b$ for simplicity in Sections 5 and 6. The existence of such a process is always guarantied by Lemmas 3.14 and 3.16. Its choice in a concrete example is, however, delicate. Worth mentioning, most of the theory developed until the end of Section 4 (Except for Lemmas 3.17 and 3.18 which are not used before Section 5), is completely independent from this mutual minimal distance assumption.

From ${\mathbb{X}}$ we construct a Voronoi tessellation with cells $\left(G_{a}\right)_{a\in{\mathbb{N}}}$ and we chose for each $x_{a}$ a radius ${\mathfrak{r}}_{a}\leq{\mathfrak{r}}$ with $\mathbb{B}_{{{\mathfrak{r}}_{a}}}{\left({x_{a}}\right)}\subset G_{a}\cap{\bf{P}}$. Again, using Corollary 1.3, we assume that ${\mathfrak{r}}_{a} = {\mathfrak{r}}$ is constant for simplicity.

1.1.6.   Extensions Ⅰ: Gradients

Notation. Given an extension order $n\in\{0, 1\}$ and microscopic regularity $\alpha\in[0, 1]$ we chose

and some $y_{n, \alpha, i}$ such that

For every $i$ and $a$, we define

local averages close to $\partial{\bf{P}}$ and in "bulk points" $x_{a}$. We say that $x_{a}\sim\sim x_{b}$ if $G_{a}\cap\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{b}}\right)}\neq\emptyset$ and we say $x_{a}\in{\mathbb{X}}_{{\mathfrak{r}}}({\bf{Q}})$ if $\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}\cap{\bf{Q}}\neq\emptyset$. Based on the explicit extension operator ${\mathcal{U}}$ given in (4.14) below we will obtain the following result.

Theorem 1.10. Let ${\mathfrak{r}} > 0$ and let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be a stationary ergodic random Lipschitz domain such that Assumption 1.4 holds for ${\mathbb{X}} = \left(x_{a}\right)_{a\in{\mathbb{N}}}$ and ${\bf{P}}$ has microscopic regularity $\alpha$ with extension order $n$. Let ${\bf{Q}}\subset{\mathbb{R}^{d}}$ be a bounded open set with $\mathbb{B}_{{\frac{1}{4}}}{\left(0\right)}\subset{\bf{Q}}$ and let $1\leq r < p$. Furthermore, let

then there exist $C > 0$ depending only on $d$, $r$ and $p$ such that for a.e. $\omega$ there exists an extension operator ${\mathcal{U}}_{\omega}:\, W_{{\mathrm{loc}}}^{1, p}({\bf{P}}(\omega))\to W_{{\mathrm{loc}}}^{1, p}({\mathbb{R}^{d}})$ and $C_{\omega} > 0$ such that for every $m\geq1$ and every $u\in W^{1, p}({\bf{P}}(\omega))$ with $u|_{{\bf{P}}(\omega)\backslash m{\bf{Q}}}\equiv0$ it holds

Proof. This is a consequence of Lemma 4.7. □

Imposing less restrictions on $\tilde{\rho}$ and $M$ leads to a weaker estimate on the extension operator.

Theorem 1.11. Under the assumptions of Theorem 1.10 let additionally

then there exists an extension operator ${\mathcal{U}}_{\omega}:\, W_{{\mathrm{loc}}}^{1, p}({\bf{P}}(\omega))\to W_{{\mathrm{loc}}}^{1, p}({\mathbb{R}^{d}})$ such that for every $m\geq1$ and every $u\in W^{1, p}({\bf{P}}(\omega))$ with $u|_{{\bf{P}}(\omega)\backslash m{\bf{Q}}}\equiv0$ it holds

Proof. This is a consequence of the proof of Lemma 4.7, replacing $M_{a}u$ in the definition of ${\mathcal{U}} u$ by $0$. □

1.1.7.   Percolation and connectivity

The terms depending on $\left|\tau_{n, \alpha, i}u-{\mathcal{M}}_{a}u\right|$ or $\left|{\mathcal{M}}_{a}u-{\mathcal{M}}_{a}u\right|$ appearing on the right-hand side in Theorem 1.10 need to be replaced by an integral over $\left|\nabla u\right|^{p}$. Here, the pathwise topology of the geometry comes into play. By this we mean that we have to integrate the gradient of $u$ over a path connecting e.g., $p_{i}$ and $x_{a}$. Here, the mesoscopic properties of the geometry will play a role. In particular, we need pathwise connectedness of the random domain, a phenomenon which is known as percolation in the theory of random sets. We will discuss two different examples to see that these terms can indeed be handled in application, but shift a general discussion of arbitrary geometries to a later publication.

1.1.8.   Extensions Ⅱ: Symmetric gradients

We now turn to the situation that $u$ is a ${\mathbb{R}^{d}}$-valued function and that the given PDE system yields only estimates for ${\nabla^{s}} u = \frac{1}{2}\left(\nabla u+(\nabla u)^{T}\right)$. We introduce the following quantities:

Definition 1.12. Given $n\in\{0, 1, 2\}$ and $\alpha\in[0, 1]$ such that (1.17) holds for ${\mathfrak{r}}_{i} = {\mathfrak{r}}_{n, \alpha, i}$ for every $i$ let for $i, a$

Using above introduced notation and the symbol ${\bf{W}}$ to denote ${\mathbb{R}^{d}}$-valued Sobolev spaces, we find the following.

Theorem 1.13. Let ${\mathfrak{r}} > 0$ and let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be a stationary ergodic random Lipschitz domain such that Assumption 1.4 holds for ${\mathbb{X}} = \left(x_{a}\right)_{a\in{\mathbb{N}}}$ and ${\bf{P}}$ has microscopic regularity $\alpha$ with symmetric extension order $n\leq2$. Let ${\bf{Q}}\subset{\mathbb{R}^{d}}$ be a bounded open set with $\mathbb{B}_{{\frac{1}{4}}}{\left(0\right)}\subset{\bf{Q}}$ and let $1\leq r < p_{0} < p$. Furthermore, let

Then there exist $C > 0$ depending only on $d$, $r$, $s$ and $p$ such that for a.e. $\omega$ there exists an extension operator ${\mathcal{U}}_{\omega}:\, {\bf{W}}_{{\mathrm{loc}}}^{1, p}({\bf{P}}(\omega))\to{\bf{W}}_{{\mathrm{loc}}}^{1, p}({\mathbb{R}^{d}})$ and $C_{\omega} > 0$ such that for every $m\geq1$ and every $u\in{\bf{W}}^{1, p}({\bf{P}}(\omega))$ with $u|_{{\bf{P}}(\omega)\backslash{\bf{Q}}}\equiv0$ it holds

Proof. This is a consequence of Lemma 4.10. □

Theorem 1.14. Under the assumptions of Theorem 1.13 let additionally

Then there exists an extension operator ${\mathcal{U}}_{\omega}:\, W_{{\mathrm{loc}}}^{1, p}({\bf{P}}(\omega))\to W_{{\mathrm{loc}}}^{1, p}({\mathbb{R}^{d}})$ such that for every $m\geq1$ and every $u\in W^{1, p}({\bf{P}}(\omega))$ with $u|_{{\bf{P}}(\omega)\backslash m{\bf{Q}}}\equiv0$ it holds

Proof. This is a consequence of the proof of Lemma 4.7, replacing $M_{a}^{{\mathfrak{s}}}u$ in the definition of ${\mathcal{U}} u$ by $0$. □

1.2.   Discussion: random geometries and applicability of the method

In Section 6 we discuss two standard models from the theory of stochastic geometries. The first one is a system of random pipes: Starting from a Poisson point process and deleting all points with nearest neighbor closer than $2{\mathfrak{r}}$ and introducing the Delaunay neighboring condition on the points, every two neighbors are connected through a pipe of random thickness $2\delta,$ where $\delta$ is distributed i.i.d among the pipes and we complete the geometry by adding a ball of radius $\frac{{\mathfrak{r}}}{2}$ around each point. Defining for bounded open domains ${\bf{Q}}\subset{\mathbb{R}^{d}}$ and $n\in{\mathbb{N}}$

and using again ${\bf{W}}$ instead of $W$ for ${\mathbb{R}^{d}}$-valued functions, we find our first result:

Theorem 1.15. In the pipe model of Section 6.1 let ${\mathbb{P}}(\delta(x, y) < \delta_{0})\leq C_{\delta}\delta_{0}^{\beta}$ and let $1\leq r < s < p$ be such that $\max\left\{ \frac{p\left(s+d\right)}{p-s}, \frac{p(2d-s-1)}{p-s}\right\} \leq\beta$ and $\frac{sr}{s-r}\leq\beta+d-1$. Then $\alpha = n = 0$ both for extension and symmetric extension order and there almost surely exists an extension operator ${\mathcal{U}}:\, W_{{\mathrm{loc}}}^{1, p}({\bf{P}})\to W_{{\mathrm{loc}}}^{1, p}({\mathbb{R}^{d}})$ and constants $C, R > 1$ such that for all $m\in{\mathbb{N}}$ and every $u\in W_{0, \partial(m{\bf{Q}})}^{1, p}({\bf{P}}\cap m{\bf{Q}})$ it holds

Furthermore there almost surely exists an extension operator ${\mathcal{U}}:\, {\bf{W}}_{{\mathrm{loc}}}^{1, p}({\bf{P}})\to{\bf{W}}_{{\mathrm{loc}}}^{1, p}({\mathbb{R}^{d}})$ and a constant $C > 0$ such that for all $m\in{\mathbb{N}}$ and every $u\in{\bf{W}}_{0, \partial(m{\bf{Q}})}^{1, p}({\bf{P}}\cap m{\bf{Q}})$

In both cases for every $\beta\in(0, 1)$ the following holds: for some $m_{0} > 1$ depending on $\omega$ and every $m > m_{0}$ the support of ${\mathcal{U}} u$ lies within $\mathbb{B}_{{m^{1-\beta}}}{\left({m{\bf{Q}}}\right)}$.

Proof. The proof is given at the very end of Section 6.1. □

Corollary 1.16. If ${\mathbb{P}}(\delta(x, y) < \delta_{0})\leq C_{\delta}e^{-\gamma\delta_{0}^{-1}}$ then the last theorem holds for every $1\leq r < p$.

In Section 6.2 we study the Boolean model based on a Poisson point process in the percolation case. Introduced in Example 2.49 we will consider a Poisson point process ${\mathbb{X}}_{{\mathrm{pois}}}(\omega) = \left(x_{i}(\omega)\right)_{i\in{\mathbb{N}}}$ with intensity $\lambda$ (recall Example 2.49). To each point $x_{i}$ a random ball $B_{i} = \mathbb{B}_{1}{\left({x_{i}}\right)}$ is assigned and the family ${\mathbb{B}}: = \left(B_{i}\right)_{i\in{\mathbb{N}}}$ is called the Poisson ball process. We say that $x_{i}\sim x_{j}$ if $\left|x_{i}-x_{j}\right| < 2$. In case $\lambda > \lambda_{c}$, where $\lambda_{c} > 0$ is the percolation threshold, the union of these balls has a unique infinite connected component (that means we have percolation) and we denote ${\mathbb{X}}_{{\mathrm{pois}}, \infty}$ the selection of all points that contribute to the infinite component and ${\bf{P}}_{\infty}\left(\omega\right): = \bigcup_{i\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}}B_{i}$ this infinite open set and seek for a corresponding uniform extension operator. The connectedness of ${\bf{P}}_{\infty}$ is hereby essential as we use results from percolation theory that otherwise would not hold.

Here we can show that the micro- and mesoscopic assumptions are fulfilled, at least in case ${\bf{P}}$ is given as the union of balls. If we choose ${\bf{P}}$ as the complement of the balls, the situation becomes more involved. On one hand, Theorem 6.8 shows that $\alpha$ and $n$ change in an unfortunate way. Furthermore, the connectivity estimate remains open. However, some of these problems might be overcome in the future using a Matern modification of the Poisson process. For the moment, we state the following.

Theorem 1.17. In the Boolean model of Section 6.2 it holds $\alpha = 0$ in case ${\bf{P}} = {\bf{P}}_{\infty}$ and both the extension order and the symmetric extension order are $n = 0$. If $d < p$ and

Then there almost surely exists an extension operator ${\mathcal{U}}:\, W_{{\mathrm{loc}}}^{1, p}({\bf{P}})\to W_{{\mathrm{loc}}}^{1, p}({\mathbb{R}^{d}})$ and a constant $C > 0$ such that for all $m\in{\mathbb{N}}$ and every $u\in W_{0, \partial{\bf{Q}}}^{1, p}({\bf{P}}\cap m{\bf{Q}})$

If furthermore

then there almost surely exists an extension operator ${\mathcal{U}}:\, {\bf{W}}_{{\mathrm{loc}}}^{1, p}({\bf{P}})\to{\bf{W}}_{{\mathrm{loc}}}^{1, p}({\mathbb{R}^{d}})$ and a constant $C > 0$ such that for all $m\in{\mathbb{N}}$ and every $u\in{\bf{W}}_{0, \partial{\bf{Q}}}^{1, p}({\bf{P}}\cap m{\bf{Q}})$

In both cases for every $\beta\in(0, 1)$ the following holds: for some $m_{0} > 1$ depending on $\omega$ and every $m > m_{0}$ the support of ${\mathcal{U}} u$ lies within $\mathbb{B}_{{m^{1-\beta}}}{\left({m{\bf{Q}}}\right)}$.

Proof. The proof is given at the very end of Section 6.2. □

1.3.   Notes

1.3.1.   Structure of the article

We close the introduction by providing an overview over the article and its main contributions. In Section 2 we collect some basic concepts and inequalities from the theory of Sobolev spaces, random geometries and discrete and continuous ergodic theory. We furthermore establish local regularity properties for what we call $\eta$-regular sets, as well as a related covering theorem in Section 2.8. In Section 2.13 we will demonstrate that stationary ergodic random open sets induce stationary processes on ${\mathbb{Z}^{d}}$, a fact which is used later in the construction of the mesoscopic Voronoi tessellation in Section 3.2.

In Section 3 we introduce the regularity concepts of this work. More precisely, in Section 3.1 we introduce the concept of local $\left(\delta, M\right)$-regularity and use the theory of Section 2.8 in order to establish a local covering result for $\partial{\bf{P}}$, which will allow us to infer most of our extension and trace results. In Section 3.2 we show how isotropic cone mixing geometries allow us to construct a stationary Voronoi tessellation of ${\mathbb{R}^{d}}$ such that all related quantities like "diameter" of the cells are stationary variables whose expectation can be expressed in terms of the isotropic cone mixing function $f$. Moreover we prove the important integration Lemma 3.18.

In Sections 4–5 we finally provide the aforementioned extension operators and prove estimates for these extension operators and for the trace operator. In Section 6 we study the sample geometries from Theorems 1.15 and 1.17.

1.3.2.   A Remark on notation

This article uses concepts from partial differential equations, measure theory, probability theory and random geometry. Additionally, we introduce concepts which we believe have not been introduced before. This makes it difficult to introduce readable self contained notation (the most important aspect being symbols used with different meaning in different disciplines) and enforces the use of various different mathematical fonts. Therefore, we provide an index of notation at the end of this work. As a rough orientation, the reader may keep the following in mind:

We use the standard notation ${\mathbb{N}}$, ${\mathbb{Q}}$, ${\mathbb{R}}$, ${\mathbb{Z}}$ for natural ($> 0$), rational, real and integer numbers. ${\mathbb{P}}$ denotes a probability measure, ${\mathbb{E}}$ the expectation. Furthermore, we use special notation for some geometrical objects, i.e., ${\mathbb{T}}^{d} = [0, 1)^{d}$ for the torus (${\mathbb{T}}$ equipped with the topology of the torus), ${\mathbb{I}}^{d} = (0, 1)^{d}$ the open interval as a subset of ${\mathbb{R}^{d}}$ (we often omit the index $d$), ${\mathbb{B}}$ a ball, ${\mathbb{C}}$ a cone and ${\mathbb{X}}$ a set of points. In the context of finite sets $A$, we write $\#A$ for the number of elements.

Bold large symbols (${\bf{U}}$, ${\bf{Q}}$, ${\bf{P}}$, $\dots$) refer to open subsets of ${\mathbb{R}^{d}}$ or to closed subsets with $\partial{\bf{P}} = \partial\mathring{{\bf{P}}}$. The Greek letter $\Gamma$ refers to a $d-1$ dimensional manifold.

Calligraphic symbols ($\mathcal{A}$, ${\mathcal{U}}$, $\dots$) usually refer to operators and large Gothic symbols (${\mathfrak{B}}, {\mathfrak{C}}, \dots$) indicate topological spaces, except for ${\mathfrak{A}}$.

1.4.   Outlook

This work is the first part of a trilogy. In part Ⅱ, we will see how to apply the extension and trace operators introduced above.

In part Ⅲ we will discuss general quantifiable properties of the geometry that are eventually accessible also to computer algorithms that will allow to predict homogenization behavior of random geometries.

2.   Preliminaries

We first collect some notation and mathematical concepts which will be frequently used throughout this paper. We first start with the standard geometric objects, which will be labeled by bold letters.

2.1.   Fundamental notation and Geometric objects

Throughout this work, we use $\left({\bf{e}}_{i}\right)_{i = 1, \dots d}$ for the Euclidean basis of ${\mathbb{R}^{d}}$. By $C > 0$ we denote any constant that depends on $p$ and $d$ but no further dependencies unless explicitly mentioned. Such mentioning may be expressed in some cases through the notation $C(a, b, \dots)$. Once the dependencies are made clear we may sometimes drop them for shortness of presentation. Furthermore, we use the following notation.

Unit cube The torus ${\mathbb{T}} = [0, 1)^{d}$ is equipped with the topology of the metric $d(x, y) = \min_{z\in{\mathbb{Z}^{d}}}\left|x-y+z\right|$. In contrast, the open interval ${\mathbb{I}}^{d}: = (0, 1)^{d}$ is considered as a subset of ${\mathbb{R}^{d}}$. We often omit the index $d$ if this does not provoke confusion.

Balls Given a metric space $\left(M, d\right)$ we denote $\mathbb{B}_{r}{\left(x\right)}$ the open ball around $x\in M$ with radius $r > 0$. The surface of the unit ball in ${\mathbb{R}^{d}}$ is ${\mathbb{S}}^{d-1}$. Furthermore, we denote for every $A\subset{\mathbb{R}^{d}}$ by $\mathbb{B}_{r}{\left(A\right)}: = \bigcup_{x\in A}\mathbb{B}_{r}{\left(x\right)}$.

Points A sequence of points will be labeled by ${\mathbb{X}}: = \left(x_{i}\right)_{i\in{\mathbb{N}}}$.

A cone in ${\mathbb{R}^{d}}$ is usually labeled by ${\mathbb{C}}$. In particular, we define for a vector $\nu$ of unit length, $0 < \alpha < \frac{\pi}{2}$ and $R > 0$ the cone

Inner and outer hull We use balls of radius $r > 0$ to define for a closed set ${\bf{P}}\subset{\mathbb{R}^{d}}$ the sets

One can consider these sets as inner and outer hulls of ${\bf{P}}$. The last definition resembles a concept of "negative distance" of $x\in{\bf{P}}$ to $\partial{\bf{P}}$ and "positive distance" of $x\not\in{\bf{P}}$ to $\partial{\bf{P}}$. For $A\subset{\mathbb{R}^{d}}$ we denote ${\mathrm{conv}}(A)$ the closed convex hull of $A$.

The natural geometric measures we use in this work are the Lebesgue measure on ${\mathbb{R}^{d}}$, written $\left|A\right|$ for $A\subset{\mathbb{R}^{d}}$, and the $k$-dimensional Hausdorff measure, denoted by ${\mathcal{H}}^{k}$ on $k$-dimensional sub-manifolds of ${\mathbb{R}^{d}}$ (for $k\leq d$).

2.2.   Simple local extensions and Traces

In the following, we formulate some extension and trace results. Although it is well known how such results are proved and the proofs are standard, we include them for completeness since we are interested in the dependence of the operator norm on the local Lipschitz regularity of the boundary.

The following is well known:

Lemma 2.1. For every $1\leq p\leq\infty$ there exists $C_{p} > 0$ such that for every $R > 0$ there exists an extension operator ${\mathcal{U}}:\, W^{1, p}(\mathbb{B}_{R}{\left(0\right)})\to W^{1, p}(\mathbb{B}_{{2R}}{\left(0\right)})$ such that

Let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be an open set and let $p\in\partial{\bf{P}}$ and $\delta > 0$ be a constant such that $\mathbb{B}_{{\delta}}{\left(p\right)}\cap\partial{\bf{P}}$ is graph of a Lipschitz function. We denote

Remark 2.2. For every $p$, the function $M(p, \cdot)$ is monotone increasing in $\delta$.

Lemma 2.3 (Uniform Extension for Balls). Let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be an open set, $0\in\partial{\bf{P}}$ and assume there exists $\delta > 0$, $M > 0$ and an open domain $U\subset\mathbb{B}_{{\delta}}{\left(0\right)}\subset{\mathbb{R}}^{d-1}$ such that $\partial{\bf{P}}\cap\mathbb{B}_{{\delta}}{\left(0\right)}$ is graph of a Lipschitz function $\varphi:\, U\subset{\mathbb{R}}^{d-1}\to{\mathbb{R}^{d}}$ of the form $\varphi(\tilde{x}) = (\tilde{x}, \phi(\tilde{x}))$ in $\mathbb{B}_{{\delta}}{\left(0\right)}$ with Lipschitz constant $M$ and $\varphi(0) = 0$. Writing $x = (\tilde{x}, x_{d})$ and defining $\rho = \delta\sqrt{4M^{2}+2}^{-1}$ there exist an extension operator

such that for

and for every $p\in[1, \infty]$ the operator

is continuous with

Remark 2.4. In case $\phi(\tilde{x})\geq0$ we find ${\mathcal{A}}\left(0, {\bf{P}}, \rho\right)\subset\mathbb{B}_{{\rho}}{\left(0\right)}$.

Proof of Lemma 2.3. In case $\phi(\tilde{x})\equiv0$ we consider the extension operator ${\mathcal{U}}_{+}:\, W^{1, p}({\mathbb{R}}^{d-1}\times({-}\infty, 0))\to W^{1, p}({\mathbb{R}^{d}})$ having the form (compare also [6, chapter 5], ^[1])

The general case follows from transformation. □

Lemma 2.5. Let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be an open set, $0\in\partial{\bf{P}}$ and assume there exists $\delta > 0$, $M > 0$ and an open domain $U\subset\mathbb{B}_{{\delta}}{\left(0\right)}\subset{\mathbb{R}}^{d-1}$ such that $\partial{\bf{P}}\cap\mathbb{B}_{{\delta}}{\left(0\right)}$ is graph of a Lipschitz function $\varphi:\, U\subset{\mathbb{R}}^{d-1}\to{\mathbb{R}^{d}}$ of the form $\varphi(\tilde{x}) = (\tilde{x}, \phi(\tilde{x}))$ in $\mathbb{B}_{{\delta}}{\left(0\right)}$ with Lipschitz constant $M$ and $\varphi(0) = 0$ and define $\rho = \delta\sqrt{4M^{2}+2}^{-1}$. Writing $x = (\tilde{x}, x_{d})$ we consider the trace operator ${\mathcal{T}}:\, C^{1}\left({\bf{P}}\cap\mathbb{B}_{{\delta}}{\left(0\right)}\right)\to C\left(\partial{\bf{P}}\cap\mathbb{B}_{{\rho}}{\left(0\right)}\right)$. For every $p\in[1, \infty]$ and every $r\geq1$ with $1-\frac{d}{p} > \frac{1-d}{r}$ the operator ${\mathcal{T}}$ can be continuously extended to

such that

Proof. We proceed similar to the proof of Lemma 2.3.

Step 1: Writing $B_{r} = \mathbb{B}_{r}{\left(0\right)}$ together with $B_{r}^{-} = \left\{ x\in B_{r}:\, x_{d} < 0\right\}$ and $\Sigma_{r}: = \left\{ x\in B_{r}:\, x_{d} = 0\right\}$ we recall the standard estimate

which leads to

Step 2: Using the transformation rule and the fact that $1\leq\left|\det D\varphi\right|\leq\sqrt{4M^{2}+2}$ we infer Eq (2.7) in the following way:

and from this we conclude the Lemma with $\varphi^{-1}(B_{\rho}^{-})\subset\mathbb{B}_{{\delta}}{\left(0\right)}$. □

2.3.   Local Nitsche-Extensions

We recall that we will use bold letters for ${\mathbb{R}^{d}}$-valued function spaces. In particular, we introduce for $1\leq p\leq\infty$

From ^[5] we know that on general Lipschitz domains an estimate like the following holds:

Lemma 2.6. For every $1\leq p\leq\infty$ there exists a constant $C > 0$ depending only on the dimension $d\geq2$ such that the following holds: For every radius $R > 0$ there exists an extension operator ${\mathcal{U}}_{R}:\, W^{1, p}{\left({\mathbb{B}_{R}{\left(0\right)}}\right)}\to W^{1, p}{\left({\mathbb{B}_{{2R}}{\left(0\right)}}\right)}$ such that

Again, we will need a refined estimate on extensions on Lipschitz domains which explicitly accounts for the local Lipschitz constant.

Lemma 2.7 (Uniform Nitsche-Extension for Balls). For every $d\geq2$ there exists a constant $C_{{\mathcal{N}}}$ depending only on the dimension $d$ such that the following holds: Let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be an open set, $0\in\partial{\bf{P}}$ and assume there exists $\delta > 0$, $M > 0$ and an open domain $U\subset\mathbb{B}_{{\delta}}{\left(0\right)}\subset{\mathbb{R}}^{d-1}$ such that $\partial{\bf{P}}\cap\mathbb{B}_{{\delta}}{\left(0\right)}$ is graph of a Lipschitz function $\varphi:\, U\subset{\mathbb{R}}^{d-1}\to{\mathbb{R}^{d}}$ of the form $\varphi(\tilde{x}) = (\tilde{x}, \phi(\tilde{x}))$ in $\mathbb{B}_{{\delta}}{\left(0\right)}$ with Lipschitz constant $M$ and $\varphi(0) = 0$. Writing $x = (\tilde{x}, x_{d})$ we define $\rho = \delta\sqrt{4M^{2}+2}^{-1}$ and

Then for every $p\in[1, \infty]$ there exists a continuous operator

such that for some constant $C$ independent from $\left(\delta, M\right)$ and ${\bf{P}}$ it holds

Remark 2.8. In case $\phi(\tilde{x})\geq0$ the proof reveals ${\mathcal{A}}\left(0, {\bf{P}}, \rho\right)\subset\mathbb{B}_{{c\rho}}{\left(0\right)}$ for some $c$ depending only on the dimension $d$.

In order to prove such a result we need the following lemma.

Lemma 2.9 (^[26] Chapter 6 Section 1 Theorem 2). There exist constants $c_{1}, c_{2}, c_{3} > 0$ such that for every open set ${\bf{P}}\subset{\mathbb{R}^{d}}$ with local Lipschitz boundary there exists a function $d_{{\bf{P}}}:\, {\mathbb{R}^{d}}\backslash\overline{{\bf{P}}^{\complement}}\to{\mathbb{R}}$ with

From the theory presented by Stein ^[26] we will not get an explicit form of $C_{{\mathcal{N}}}$ but only an upper bound that grows exponentially with dimension $d$.

Proof of Lemma 2.7. We use an idea by Nitsche ^[20], which we transfer from $p = 2$ to the general case, thereby explicitly quantifying the influence of $M$. For simplicity we write ${\bf{P}}_{\delta}: = {\bf{P}}\cap\mathbb{B}_{{\delta}}{\left(0\right)}$ and ${\bf{P}}_{\delta}^{\complement}: = \mathbb{B}_{{\delta}}{\left(0\right)}\backslash{\bf{P}}$ and assume that $x\in{\bf{P}}_{\delta}$ iff $x\in\mathbb{B}_{{\delta}}{\left(0\right)}$ and $x_{d} < \phi(\tilde{x})$.

As observed by Nitsche, it holds

and together with Lemma 2.9, we can define $d_{{\bf{P}}, M}(x): = 2c_{2}\left(1+M^{2}\right)^{\frac{1}{2}}d_{{\bf{P}}}(x)$ and find for $c > \max\left\{ \frac{2c_{2}}{c_{1}}, 4c_{2}c_{3}\right\}$ that

Using $\psi\in C([1, 2])$ satisfying

Nitsche introduced $x_{\lambda}: = (\tilde{x}, x_{d}-\lambda d_{{\bf{P}}, M}(x))$ and proposed the following extension on $x\in{\bf{P}}_{\delta}^{\complement}$:

One can quickly verify that this maps $C(\overline{{\bf{P}}_{\delta}})$ onto $C{\left({\overline{\mathbb{B}_{{\rho}}{\left(0\right)}}}\right)}$. In what follows, we write ${\varepsilon}[u](x): = \nabla^{s}u(x)$ and particularly ${\varepsilon}_{ij}[u](x): = \frac{1}{2}\left(\partial_{i}u_{j}+\partial_{j}u_{i}\right)$ as well as ${\varepsilon}_{ij}^{\lambda}[u](x) = {\varepsilon}_{ij}[u](x_{\lambda})$ for $x\in{\bf{P}}_{\delta}^{\complement}$. Then for $x\in{\bf{P}}_{\delta}^{\complement}\cap\mathbb{B}_{{\rho}}{\left(0\right)}$

From the fundamental theorem of calculus we find

which leads by Eq (2.10) to

We may now apply $\left|\, \cdot\, \right|^{p}$ on both sides of Eq (2.11), integrate over ${\bf{P}}_{\delta}^{\complement}\cap\mathbb{B}_{{\rho}}{\left(0\right)}$ and use the integral transformation theorem for each $\lambda$ to find

□

2.4.   Poincaré inequalities

We denote for bounded open $A\subset{\mathbb{R}^{d}}$

Note that this is not a linear vector space.

Lemma 2.10. For every $p\in[1, \infty)$ there exists $C_{p} > 0$ such that the following holds: Let $0 < r < R$ and $x\in\mathbb{B}_{R}{\left(0\right)}$ such that $\mathbb{B}_{r}{\left(x\right)}\subset\mathbb{B}_{R}{\left(0\right)}$ then for every $u\in W^{1, p}(\mathbb{B}_{R}{\left(0\right)})$

and for every $u\in W_{(0), r}^{1, p}((\mathbb{B}_{R}{\left(0\right)})$ it holds

Remark 2.11 In case $p\geq d$ we find that (2.14) holds iff $u(x) = 0$ for some $x\in\mathbb{B}_{1}{\left(0\right)}$.

Proof. In a first step, we assume $x = 0$ and $R = 1$. The underlying idea of the proof is to compare every $u(y)$, $y\in\mathbb{B}_{1}{\left(0\right)}\backslash\mathbb{B}_{r}{\left(0\right)}$ with $u(ry)$. In particular, we obtain for $y\in\mathbb{B}_{1}{\left(0\right)}\backslash\mathbb{B}_{r}{\left(0\right)}$ that

and hence by Jensen's inequality

We integrate the last expression over $\mathbb{B}_{1}{\left(0\right)}\backslash\mathbb{B}_{r}{\left(0\right)}$ and find

For general $x\in\mathbb{B}_{1}{\left(0\right)}$, use the extension operator ${\mathcal{U}}:\, W^{1, p}(\mathbb{B}_{1}{\left(0\right)})\to W^{1, p}(B_{4}(0))$ such that $\left\Vert {\mathcal{U}} u\right\Vert _{W^{1, p}(B_{4}(0))}\leq C\left\Vert u\right\Vert_{W^{1, p}(\mathbb{B}_{1}{\left(0\right)})}$ and

Since $\mathbb{B}_{1}{\left(0\right)}\subset B_{2}(x)\subset B_{4}(0)$ we infer

and hence Eq (2.13). Furthermore, since there holds $\left\Vert u\right\Vert _{L^{p}(\mathbb{B}_{1}{\left(0\right)})}^{p}\leq C\left\Vert \nabla u\right\Vert _{L^{p}(\mathbb{B}_{1}{\left(0\right)})}^{p}$ for every $u\in W_{(0)}^{1, p}(\mathbb{B}_{1}{\left(0\right)})$, a scaling argument shows $\left\Vert u\right\Vert _{L^{p}(\mathbb{B}_{r}{\left(0\right)})}^{p}\leq Cr^{p}\left\Vert \nabla u\right\Vert _{L^{p}(\mathbb{B}_{r}{\left(0\right)})}^{p}$ for every $u\in W_{(0), r}^{1, p}(\mathbb{B}_{1}{\left(0\right)})$ and hence Eq (2.14). For general $R > 0$ use a scaling argument. □

A similar argument leads to the following, where we remark that the difference in the appearing of $\frac{1}{r}$ is due to the fact, that integrating the cylinder needs no surface element $r^{d-1}$.

Corollary 2.12. For every $p\in[1, \infty)$ and $r > 0$ there exists $C_{p} > 0$ such that the following holds: Let $r < L$, $P_{L, r}: = \mathbb{B}_{\#2}^{\#1}(0)\times(0, L)$ and $x\in P_{L, r}$ such that $\mathbb{B}_{r}{\left(x\right)}\subset P_{L, r}$ then for every $u\in W^{1, p}(P_{L, r})$

and if additionally $\rlap{-} \smallint _{\mathbb{B}_{r}{\left(x\right)}}u = 0$ then

Let $y\in P_{L, r}$ such that $\mathbb{B}_{r}{\left(y\right)}\subset P_{L, r}$ then for every $u\in W^{1, p}(P_{L, r})$

2.5.   Korn inequalities

We introduce on open sets $A\subset{\mathbb{R}^{d}}$ the Sobolev space

To the authors best knowledge, the following is the most general Korn inequality in literature and it is formulated for John domains.

Theorem 2.13 (^[5] Theorem 2.7 and Corollary 2.8). Let $A$ be a John domain with constants ${\varepsilon}, \delta$. Let $1\leq p\leq\infty$ and $\tilde{\delta} > 0$ such that $\delta/{\mathrm{diam}} A\geq\tilde{\delta}$. Then there exists a constant $C_{p} > 0$ depending only on $d$, $p$, ${\varepsilon}$ and $\tilde{\delta}$ but not on $A$ such that it holds

Remark 2.14. In the original work the claimed dependence of $C_{p}$ was on $d$, $p$, ${\varepsilon}$, $\delta$ and $A$ with the observation that Eq (2.18) is invariant under scaling of $A$. However, this scale invariance results in the dependence on $d$, $p$, ${\varepsilon}$ and $\delta/{\mathrm{diam}} A$ since ${\varepsilon}$, $p$ and $d$ are not sensitive to scaling of $A$.

Corollary 2.15. For every $1\leq p\leq\infty$ there exists $C_{p}$ depending only on $d$ and $p$ such that for every bounded open convex set $A\subset{\mathbb{R}^{d}}$ the estimate (2.18) holds.

We furthermore introduce the set

which is not a vector space.

Lemma 2.16 (Mixed Korn inequality). Let $1\leq p\leq\infty$ and ${\varepsilon}, \delta\in(0, 1)$. Then there exists a constant $\tilde{C}_{p} > 0$ depending only on $d$, $p$, ${\varepsilon}$ and $\delta$ such that for every $({\varepsilon}, \delta)$-John domain $A\subset\mathbb{B}_{1}{\left(0\right)}$, for every $r\in(0, 1)$ and every $x\in A$ with $\mathbb{B}_{r}{\left(x\right)}\subset A$ it holds

Furthermore,

The difference to Theorem 2.13 is that $\int_{\mathbb{B}_{r}{\left(x\right)}}\partial_{i}u_{j}-\partial_{j}u_{i} = 0$ only holds on a subset of $A$. Unfortunately, we do not have a reference for a comparable Lemma in the literature except for ^[25] in case $p = 2$. The author strongly supposes a proof must exist somewhere, however, we provide it for completeness.

Proof. Let $C_{p}$ be the constant from Theorem 2.13 for domains with a diameter less than $2$ and suppose Eq (2.19) was wrong. Then there exists a sequence of $({\varepsilon}, \delta)$-John domains $A_{n}\subset\mathbb{B}_{1}{\left(0\right)}$ with $x_{n}\in A_{n}$, $r_{n}\in(0, 1)$ with $\mathbb{B}_{{r_{n}}}{\left({x_{n}}\right)}\subset A_{n}$ and functions $u_{n}\in{\bf{W}}^{1, p}{\left({A_{n}}\right)}$ such that

We define $\overline{\nabla_{n}^{\bot}}(u_{n}): = \rlap{-} \smallint _{A_{n}}\left(\nabla u_{n}-{\nabla^{s}} u_{n}\right)$ and $u_{n, \bot}(x): = u_{n}(x)-\overline{\nabla_{n}^{\bot}}(u_{n})\, x$ with $\nabla^{s}u_{n, \bot} = \nabla^{s}u_{n}$. Hence by Eq (2.18)

We directly infer with $C_{n}: = \frac{\left|A_{n}\right|}{\left|{\mathbb{S}}^{d-1}\right|r_{n}^{d}}$

Furthermore, we find

and hence $\left\Vert {\overline{\nabla_{n}^{\bot}}(u_{n})}\right\Vert_{L^{p}{\left({A_{n}}\right)}}\to1$ due to Eq (2.21). Since $\overline{\nabla_{n}^{\bot}}(u_{n})$ are constant, it holds

and we infer from a similar calculation

This implies $\left\Vert {\overline{\nabla_{n}^{\bot}}(u_{n})}\right\Vert_{L^{p}{\left({A_{n}}\right)}}\to0$ by Eq (2.21), a contradiction. Hence, Eq (2.19) holds with $\tilde{C}_{p} = nC_{p}$ for some $n\in{\mathbb{N}}$.

Estimate Eq (2.20) now follows from Eqs (2.19) and (2.18) (the latter applied to $A = \mathbb{B}_{r}{\left(x\right)}$ and the definition of ${\bf{W}}_{{\nabla^{\bot}}(0), r}^{1, p}(\mathbb{B}_{R}{\left(0\right)})$. □

2.6.   Korn-Poincaré inequalities

Generalizing the above Korn inequality to a Korn-Poincaré inequality, we define

Lemma 2.17 (Mixed Korn-Poincaré inequality on balls). For every $p\in[1, \infty)$ there exists $C_{p} > 0$ such that for every $R > 0$, $r\in(0, R)$, every $x\in\mathbb{B}_{R}{\left(0\right)}$ with $\mathbb{B}_{r}{\left(x\right)}\subset\mathbb{B}_{R}{\left(0\right)}$ and every $u\in{\bf{W}}_{(0), {\nabla^{\bot}}(0), r}^{1, p}{\left({\mathbb{B}_{R}{\left(0\right)}}\right)}$ it holds

Proof. Apply Eq (2.20) in Lemma 2.16 for $R = 1$ and use a simple scaling argument to obtain

Afterwards apply Lemma 2.10. □

Lemma 2.18 (Mixed Korn-Poincaré inequality on cylinders). For every $p\in[1, \infty)$ and $r > 0$ there exists $C_{p} > 0$ such that the following holds: Let $r < L$, $P_{L, r}: = (0, L)\times\mathbb{B}_{\#2}^{\#1}(0)$ and $x\in P_{L, r}$ such that $\mathbb{B}_{r}{\left(x\right)}\subset P_{L, r}$ then for every $u\in{\bf{W}}^{1, p}(P_{L, r})$

Furthermore,

and if additionally $u\in{\bf{W}}_{(0), \nabla^{\bot}(0), r}^{1, p}(P_{L, r})$ then

Defining $\overline{\nabla_{a, \delta}^{\bot}}u: = \rlap{-} \smallint _{\mathbb{B}_{{\delta}}{\left(a\right)}}\left(\nabla u-{\nabla^{s}} u\right)$ and

we find for $a, b$ with $\mathbb{B}_{{\delta}}{\left(a\right)}, \mathbb{B}_{{\delta}}{\left(b\right)}\subset P_{L, r}$ for every $u\in{\bf{W}}^{1, p}(P_{L, r})$ that

Furthermore, for every $\delta < r$ we find

Proof. Step1: We can assume $L\in{\mathbb{N}}$, $a = \frac{1}{2}{\bf{e}}_{1}$, $b = (L-\frac{1}{2}){\bf{e}}_{1}$, $r = \frac{1}{2}$ and define

Then we find by Lemma 2.16 for some $C > 0$ independent from $u$ or $K$

Since $\nabla\tau_{k}^{{\mathfrak{s}}}u$ are constant functions for every $k$, we find

Furthermore, we find

This implies by $\nabla\tau_{k+1}^{{\mathfrak{s}}}\left(u-\tau_{k}^{{\mathfrak{s}}}u\right) = \rlap{-} \smallint _{{\bf{B}}_{k+1}}\left(\nabla-{\nabla^{s}}\right)\left(u-\tau_{k}^{{\mathfrak{s}}}u\right)$ as a consequence of Eq (2.30) and Lemma 2.16 and Theorem 2.13

Since the last inequality implies

and since $\left\Vert {\nabla\tau_{0}^{{\mathfrak{s}}}u}\right\Vert_{L^{p}({\bf{P}}_{0})}^{p}\leq C\left(\left\Vert {{\nabla^{s}} u}\right\Vert_{L^{p}({\bf{P}}_{0})}^{p}+\left\Vert {\nabla u}\right\Vert_{L^{p}({\bf{B}}_{0})}^{p}\right)$ by Lemma 2.16 we find in total

Adding the last inequality from $K = 0$ to $K = L$ implies Eq (2.24) through scaling. Applying Corollary 2.12 we infer that Eqs (2.25) and (2.26).

Step 2: We observe that Step 1 also holds for $P_{L, r}$ being replaced by ${\mathrm{conv}}(\mathbb{B}_{{\delta}}{\left(a\right)}\cup\mathbb{B}_{{\delta}}{\left(b\right)})$. Writing $u_{b}: = u-{\mathcal{M}}_{b}^{{\mathfrak{s}}, \delta}u$ we find from the above calculations

Using that $u_{b}\in{\bf{W}}_{(0), \nabla^{\bot}(0), r}^{1, p}({\mathrm{conv}}(\mathbb{B}_{{\delta}}{\left(a\right)}\cup\mathbb{B}_{{\delta}}{\left(b\right)}))$, we find Eq (2.28) with help of Eq (2.26) and Lemma 2.17.

Step 3: We assume $a = 0$ for notational simplicity. Writing $\bar{u}(y): = u(y)-{\left({\overline{\nabla_{a, \delta}^{\bot}}u}\right)}\, y$ with $\rlap{-} \smallint _{\mathbb{B}_{r}{\left(0\right)}}u = \rlap{-} \smallint _{\mathbb{B}_{r}{\left(0\right)}}\overline{u}$ we infer Eq (2.29) from Lemmas 2.16 and 2.10 via

□

2.7.   Voronoi Tessellations and Delaunay Triangulation

Definition 2.19 (Voronoi Tessellation). Let ${\mathbb{X}} = \left(x_{i}\right)_{i\in{\mathbb{N}}}$ be a sequence of points in ${\mathbb{R}^{d}}$ with $x_{i}\neq x_{k}$ if $i\neq k$. For each $x\in{\mathbb{X}}$ let

Then $\left(G{\left({x_{i}}\right)}\right)_{i\in{\mathbb{N}}}$ is called the Voronoi tessellation of ${\mathbb{R}^{d}}$ with respect to ${\mathbb{X}}$. For each $x\in{\mathbb{X}}$ we define $d{\left(x\right)}: = {\mathrm{diam}} G{\left(x\right)}$ the diameter of $G(x)$.

We will need the following result on Voronoi tessellation of a minimal diameter.

Lemma 2.20. Let ${\mathfrak{r}} > 0$ and let ${\mathbb{X}} = \left(x_{i}\right)_{i\in{\mathbb{N}}}$ be a sequence of points in ${\mathbb{R}^{d}}$ with $\left|x_{i}-x_{k}\right| > 2{\mathfrak{r}}$ if $i\neq k$. For $x\in{\mathbb{X}}$ let ${\mathcal{I}}{\left(x\right)}: = \left\{ y\in{\mathbb{X}}\, :\; G{\left(y\right)}\cap\mathbb{B}_{{{\mathfrak{r}}}}{\left({G{\left(x\right)}}\right)}\not = \emptyset\right\}$. Then $y\in{\mathcal{I}}(x)$ implies $\left|x-y\right|\leq4d(x)$ and

Proof. Let ${\mathbb{X}}_{k} = \left\{ x_{j}\in{\mathbb{X}}\, :\; {\mathcal{H}}^{d-1}{\left({\partial G_{k}\cap\partial G_{j}}\right)}\geq0\right\}$ the neighbors of $x_{k}$ and $d_{k}: = d{\left({x_{k}}\right)}$. Then all $x_{j}\in{\mathbb{X}}$ satisfy $\left|x_{k}-x_{j}\right|\leq2d_{k}$. Moreover, every $\tilde{x}\in{\mathbb{X}}$ with $\left|{{\tilde{x}}}-x_{k}\right| > 4d_{k}$ has the property that ${\mathrm{dist}}{\left({\, \partial G\left(\tilde{x}\right), \, x_{k}\, }\right)} > 2d_{k} > d_{k}+{\mathfrak{r}}$ and $\tilde{x}\not\in{\mathcal{I}}_{k}$. Since every Voronoi cell contains a ball of radius ${\mathfrak{r}}$, this implies that $\#{\mathcal{I}}_{k}\leq\left|\mathbb{B}_{{4d_{k}}}{\left({x_{k}}\right)}\right|/\left|\mathbb{B}_{{{\mathfrak{r}}}}{\left(0\right)}\right| = \left(\frac{4d_{k}}{{\mathfrak{r}}}\right)^{d}$. □

Definition 2.21 (Delaunay Triangulation). Let ${\mathbb{X}} = \left(x_{i}\right)_{i\in{\mathbb{N}}}$ be a sequence of points in ${\mathbb{R}^{d}}$ with $x_{i}\neq x_{k}$ if $i\neq k$. The Delaunay triangulation is the dual unoriented graph of the Voronoi tessellation, i.e. we say ${\mathbb{D}}({\mathbb{X}}): = \left\{ (x, y):\; {\mathcal{H}}^{d-1}{\left({\partial G(x)\cap\partial G(y)}\right)}\neq0\right\}$.

2.8.   Local $\eta$-Regularity

Definition 2.22 ($\eta$- regularity). For a function $\eta:\, \partial{\bf{P}}\to(0, r]$ we call ${\bf{P}}$ $\eta$-regular if

Remark 2.23. This concept and its consequences from Lemma 2.24 and Theorem 2.25 will be extensively used later to cover $\partial{\bf{P}}$ by a suitable family of open balls.

Lemma 2.24. Let ${\bf{P}}$ be a locally $\eta$-regular set for $\eta:\partial{\bf{P}}\to(0, {\mathfrak{r}})$. Then $\eta:\, {\bf{P}}\to{\mathbb{R}}$ is locally Lipschitz continuous with Lipschitz constant $1$ and for every ${\varepsilon}\in\left(0, \frac{1}{2}\right)$ and $\tilde{p}\in\mathbb{B}_{{{\varepsilon}\eta}}{\left(p\right)}\cap{\bf{P}}$ it holds

Furthermore,

Proof. Let $p, \tilde{p}$ such that $\left|\tilde{p}-p\right| < \frac{1}{2}\eta(p)$ with ${\varepsilon}_{p, \tilde{p}}: = \inf\left\{ {\varepsilon}:\, \left|\tilde{p}-p\right| < {\varepsilon}\eta(p)\right\}$. This means ${\varepsilon}\in[{\varepsilon}_{p, \tilde{p}}, \frac{1}{2})$ iff $\eta{\left({\tilde{p}}\right)}\geq\left(1-{\varepsilon}\right)\eta(p)$ and we find

which implies $\left|\tilde{p}-p\right| < \frac{{\varepsilon}}{1-{\varepsilon}}\eta{\left({\tilde{p}}\right)}$ and the local Lipschitz continuity by a symmetry argument in $p$, $\tilde{p}$. Also this leads to $\left|p-\tilde{p}\right|\geq\eta{\left(p\right)}-\eta{\left({\tilde{p}}\right)}$ and $\eta{\left(p\right)} > \left(1-\frac{{\varepsilon}}{1-{\varepsilon}}\right)\eta{\left({\tilde{p}}\right)}$ or

implying Eq (2.33).

In order to prove Eq (2.34), assume $\eta{\left({\tilde{p}}\right)}\leq\eta{\left(p\right)}$. Then Eq (2.35)

□

Theorem 2.25. Let $\Gamma\subset{\mathbb{R}^{d}}$ be a closed set and let $\eta{\left({\cdot}\right)}\in C{\left({\Gamma}\right)}$ be bounded and satisfy for every ${\varepsilon}\in\left(0, \frac{1}{2}\right)$ and for $\left|p-\tilde{p}\right| < {\varepsilon}\eta{\left(p\right)}$

and define $\tilde{\eta}{\left(p\right)} = 2^{-K}\eta{\left(p\right)}$, $K\geq2$. Then for every $C\in(0, 1)$ there exists a locally finite covering of $\Gamma$ with balls $\mathbb{B}_{{\tilde{\eta}{\left({p_{k}}\right)}}}{\left({p_{k}}\right)}$ for a countable number of points ${\left({p_{k}}\right)}_{k\in{\mathbb{N}}}\subset\Gamma$ such that for every $i\neq k$ with $\mathbb{B}_{{\tilde{\eta}{\left({p_{i}}\right)}}}{\left({p_{i}}\right)}\cap\mathbb{B}_{{\tilde{\eta}{\left({p_{k}}\right)}}}{\left({p_{k}}\right)}\neq\emptyset$ it holds

Remark 2.26. The fact that Eq (2.37) can be satisfied for any given $C\in(0, 1)$ (even having in mind that the choice of points depends on $C$) is surprising. In fact, $\eta{\left(p\right)}-\left|p-\tilde{p}\right| > \left(1-{\varepsilon}\right)\eta{\left(p\right)}$ in Eq (2.36) seems to contradict (2.37). However, we have to keep in mind that Eq (2.37) holds for $\tilde{\eta} = 2^{-K}\eta$, $K\geq2$. Now suppose $\left|p-\tilde{p}\right| = 2^{-K}\eta{\left(p\right)}$ and $\eta{\left(p\right)} > \eta{\left({\tilde{p}}\right)}$. Since Eq (2.36) holds for every ${\varepsilon}\in(0, \frac{1}{2})$ we find for ${\varepsilon} = 2^{-K}$ that $\eta{\left({\tilde{p}}\right)} > (1-2^{-K})\eta{\left(p\right)}$ and hence

So the above calculation shows that the lemma to hold for every $C < 1$ is plausible. The major difficulty in the original proof is to provide an algorithm which provides the covering as claimed.

Proof. We chose $\delta > 0$, $n\in{\mathbb{N}}$ such that $\left(1-\frac{1}{n}\right)\left(1-\delta\right) > C$. Multiplying $\eta$ and $\Gamma$ by a factor $C > 0$ we can assume $\tilde{\eta} < (1-\delta)$. Consider $\tilde{Q}: = \left[0, \frac{1}{n}\right]^{d}$, let $q_{1, \dots, n^{d}}$ denote the $n^{d}$ elements of $[0, 1)^{d}\cap\frac{{\mathbb{Q}}^{d}}{n}$ and let $\tilde{Q}_{z, i} = \tilde{Q}+z+q_{i}$, $z\in{\mathbb{Z}^{d}}$. We set $B_{(0)}: = \emptyset$, $\Gamma_{1} = \Gamma$, $\eta_{k}: = \left(1-\delta\right)^{k}$ and for $k\geq1$ we construct the covering using inductively defined open sets $B_{(k)}$ and closed set $\Gamma_{k}$ as follows:

1. Define $\Gamma_{k, 1} = \Gamma_{k}$. For $i = 1, \dots, n^{d}$ do the following:

(a) For every $z\in{\mathbb{Z}^{d}}$ do

(b) $B_{(k), i}: = \bigcup_{z\in{\mathbb{Z}^{d}}}b_{z, i}$ and $\Gamma_{k, i+1} = \Gamma_{k, i}\backslash B_{(k), i}$ and ${\mathbb{X}}_{(k), i}: = \bigcup_{z\in{\mathbb{Z}^{d}}}{\mathbb{X}}_{z, i}$.

Observe: $p_{1}, p_{2}\in{\mathbb{X}}_{(k), i}$ implies $\left|p_{1}-p_{2}\right| > \left(1-\frac{1}{n}\right)\eta_{k}$ and $p_{3}\in{\mathbb{X}}_{(k), j}$, $j < i$ implies $p_{1}\not\in\mathbb{B}_{{\eta_{k}}}{\left({p_{3}}\right)}$ and hence $\left|p_{1}-p_{3}\right| > \eta_{k}$. Similar, $p_{3}\in{\mathbb{X}}_{l}$, $l < k$, implies $\left|p_{1}-p_{3}\right| > \eta_{l} > \eta_{k}$.

2. Define $\Gamma_{k+1}: = \Gamma_{k, n^{d}+1}$, ${\mathbb{X}}_{k}: = \bigcup_{i}{\mathbb{X}}_{(k), i}$.

The above covering of $\Gamma$ is complete in the sense that every $x\in\Gamma$ lies in one of the balls (by contradiction). We denote ${\mathbb{X}}: = \bigcup_{k}{\mathbb{X}}_{k} = \left(p_{i}\right)_{i\in{\mathbb{N}}}$ the family of centers of the above constructed covering of $\Gamma$ and find the following properties: Let $p_{1}, p_{2}\in{\mathbb{X}}$ be such that $\mathbb{B}_{{\tilde{\eta}{\left({p_{1}}\right)}}}{\left({p_{1}}\right)}\cap\mathbb{B}_{{\tilde{\eta}{\left({p_{2}}\right)}}}{\left({p_{2}}\right)}\neq\emptyset$. Assuming $\tilde{\eta}{\left({p_{1}}\right)}\geq\tilde{\eta}{\left({p_{2}}\right)}$ the following two properties are satisfied due to Eq (2.36)

1. It holds $\left|p_{1}-p_{2}\right|\leq2\tilde{\eta}{\left({p_{1}}\right)}\leq\frac{1}{2^{K-1}}\eta{\left({p_{1}}\right)}$ and hence $\mathbb{B}_{{\tilde{\eta}{\left({p_{2}}\right)}}}{\left({p_{2}}\right)}\subset\mathbb{B}_{{2^{2-K}\eta{\left({p_{1}}\right)}}}{\left({p_{1}}\right)}$ and $\eta{\left({p_{2}}\right)}\geq\frac{2^{K-1}-1}{2^{K-1}}\eta{\left({p_{1}}\right)}$. Furthermore $\tilde{\eta}{\left({p_{1}}\right)}\geq\tilde{\eta}{\left({p_{2}}\right)}\geq\frac{2^{K-1}-1}{2^{K-1}}\tilde{\eta}{\left({p_{1}}\right)}$.

2. Let $k$ such that $\tilde{\eta}{\left({p_{1}}\right)}\in\left(\eta_{k}, \eta_{k+1}\right]$. If also $\tilde{\eta}{\left({p_{2}}\right)}\in\left(\eta_{k}, \eta_{k+1}\right]$ then the observation in Step 1(b) implies

If $\tilde{\eta}{\left({p_{2}}\right)}\not\in\left[\eta_{k}, \eta_{k+1}\right)$ then $\tilde{\eta}{\left({p_{2}}\right)} < \eta_{k}$ and hence $p_{2}\not\in\mathbb{B}_{{\tilde{\eta}{\left({p_{1}}\right)}}}{\left({p_{1}}\right)}$, implying $\left|p_{1}-p_{2}\right| > \tilde{\eta}{\left({p_{1}}\right)}$.

Due to our choice of $n$ and $\delta$, this concludes the proof. □

2.9.   Dynamical systems, ergodicity and stationarity

The concept of stationarity provides us automatically with a law of large numbers (in space) when we average properties of random geometries over an ever growing large domain in space. The concept of ergodicity ensures that this law of large numbers in space holds independently from a given realization and thus it is equivalent with the law of large numbers for averaging over many samples in a given small region instead.

Assumption 2.27. Throughout this work we assume that $(\Omega, {\mathscr{F}}, {\mathbb{P}})$ is a probability space with countably generated $\sigma$-algebra ${\mathscr{F}}$.

Due to the insight in ^[10], shortly sketched in the next two subsections, after a measurable transformation the probability space $\Omega$ can be assumed to be metric and separable, which always ensures Assumption 2.27.

Definition 2.28 (Dynamical system). A dynamical system on $\Omega$ is a family $(\tau_{x})_{x\in{\mathbb{R}^{d}}}$ of measurable bijective mappings $\tau_{x}:\Omega\mapsto\Omega$ satisfying (ⅰ)–(ⅲ):

$({\rm{i}})$ $\tau_{x}\circ\tau_{y} = \tau_{x+y}$, $\tau_{0} = id$ (Group property)

$({\rm{ii}})$ ${\mathbb{P}}(\tau_{-x}B) = {\mathbb{P}}(B)\quad\forall x\in{\mathbb{R}^{d}}, \, \, B\in{\mathscr{F}}$ (Measure preserving)

$({\rm{iii}})$ $A:\, \, {\mathbb{R}^{d}}\times\Omega\rightarrow \Omega\qquad(x, \omega)\mapsto\tau_{x}\omega$ is measurable (Measurability of evaluation)

$A\subset\Omega$ is almost invariant if for every $x\in{\mathbb{R}^{d}}$ holds ${\mathbb{P}}\left(\left(A\cup\tau_{x}A\right)\backslash\left(A\cap\tau_{x}A\right)\right) = 0$. The family

of almost invariant sets is a $\sigma$-algebra and

A concept linked to dynamical systems is the concept of stationarity.

Definition 2.29 (Stationary). Let $X$ be a measurable space and let $f:\Omega\times{\mathbb{R}^{d}}\to X$. Then $f$ is called (weakly) stationary if $f(\omega, x) = f(\tau_{x}\omega, 0)$ for (almost) every $x$.

Definition 2.30. A family $\left(A_{n}\right)_{n\in{\mathbb{N}}}\subset{\mathbb{R}^{d}}$ is called convex averaging sequence if

$({\rm{i}})$ each $A_{n}$ is convex

$({\rm{ii}})$ for every $n\in{\mathbb{N}}$ holds $A_{n}\subset A_{n+1}$

$({\rm{iii}})$ there exists a sequence $r_{n}$ with $r_{n}\to\infty$ as $n\to\infty$ such that $B_{r_{n}}(0)\subseteq A_{n}$.

We sometimes may take the following stronger assumption.

Definition 2.31. A convex averaging sequence $A_{n}$ is called regular if

The latter condition is evidently fulfilled for sequences of cones or balls. Convex averaging sequences are important in the context of ergodic theorems.

Theorem 2.32 (Ergodic Theorem ^[4] Theorems 10.2.Ⅱ and also ^[27]).

Let $\left(A_{n}\right)_{n\in{\mathbb{N}}}\subset{\mathbb{R}^{d}}$ be a convex averaging sequence, let $(\tau_{x})_{x\in{\mathbb{R}^{d}}}$ be a dynamical system on $\Omega$ with invariant $\sigma$-algebra ${\mathscr{I}}$ and let $f:\, \Omega\to{\mathbb{R}}$ be measurable with $\left|{\mathbb{E}}(f)\right| < \infty$. Then for almost all $\omega\in\Omega$

For the calculations in this work, we will particularly focus on the case of trivial ${\mathscr{I}}$. This is called ergodicity, as we will explain in the following.

Definition 2.33 (Ergodicity and mixing). A dynamical system $(\tau_{x})_{x\in{\mathbb{R}^{d}}}$ on a probability space $(\Omega, {\mathscr{F}}, {\mathbb{P}})$ is called mixing if for every measurable $A, B\subset\Omega$ it holds

A dynamical system is called ergodic if

Remark 2.34. a) Let $\Omega = \left\{ \omega_{0} = 0\right\}$ with the trivial $\sigma$-algebra and $\tau_{x}\omega_{0} = \omega_{0}$. Then $\tau$ is evidently mixing. However, the realizations are constant functions $f_{\omega}(x) = c$ on ${\mathbb{R}^{d}}$ for some constant $c$.

b) A typical ergodic system is given by $\Omega = {\mathbb{T}} = [0, 1]^{d}$ with the Lebesgue $\sigma$-algebra and ${\mathbb{P}} = {\mathcal{L}}^{d}$ the Lebesgue measure in ${\mathbb{R}^{d}}$. The dynamical system is given by $\tau_{x}y: = \left(x+y\right)\!\mod{\mathbb{T}}$.

c) It is known that $(\tau_{x})_{x\in{\mathbb{R}^{d}}}$ is ergodic if and only if every almost invariant set $A\in{\mathscr{I}}$ has probability ${\mathbb{P}}(A)\in\left\{ 0, 1\right\}$ (see ^[4] Proposition 10.3.Ⅲ) i.e.,

d) It is sufficient to show Eq (2.41) or (2.42) for $A$ and $B$ in a ring that generates the $\sigma$-algebra ${\mathscr{F}}$. We refer to ^[4], Section 10.2.

A further useful property of ergodic dynamical systems, which we will use below, is the following:

Lemma 2.35 (Ergodic times mixing is ergodic). Let $(\tilde{\Omega}, \tilde{{\mathscr{F}}}, \tilde{{\mathbb{P}}})$ and $(\hat{\Omega}, \hat{{\mathscr{F}}}, \hat{{\mathbb{P}}})$ be probability spaces with dynamical systems $(\tilde{\tau}_{x})_{x\in{\mathbb{R}^{d}}}$ and $(\hat{\tau}_{x})_{x\in{\mathbb{R}^{d}}}$ respectively. Let $\Omega: = \tilde{\Omega}\times\hat{\Omega}$ be the usual product measure space with the notation $\omega = (\tilde{\omega}, \hat{\omega})\in\Omega$ for $\tilde{\omega}\in\tilde{\Omega}$ and $\hat{\omega}\in\hat{\Omega}$. If $\tilde{\tau}$ is ergodic and $\hat{\tau}$ is mixing, then $\tau_{x}(\tilde{\omega}, \hat{\omega}): = (\tilde{\tau}_{x}\tilde{\omega}, \hat{\tau}_{x}\hat{\omega})$ is ergodic.

Proof. Relying on Remark 2.34.c) we verify Eq (2.42) by proving it for sets $A = \tilde{A}\times\hat{A}$ and $B = \tilde{B}\times\hat{B}$ which generate ${\mathscr{F}}: = \tilde{{\mathscr{F}}}\otimes\hat{{\mathscr{F}}}$. We make use of $A\cap B = \left(\tilde{A}\cap\tilde{B}\right)\times\left(\hat{A}\cap\hat{B}\right)$ and observe that

Using ergodicity, we find that

Since $\hat{\tau}$ is mixing, we find for every ${\varepsilon} > 0$ some $R > 0$ such that $\left\Vert x\right\Vert > R$ implies $\left|\hat{{\mathbb{P}}}{\left({\hat{A}\cap\hat{\tau}_{x}\hat{B}}\right)}-\hat{{\mathbb{P}}}{\left({\hat{A}\cap\hat{B}}\right)}\right| < {\varepsilon}$. For $n > R$ we find

The last two limits Eqs (2.44) and (2.45) imply Eq (2.42). □

Remark 2.36. The above proof heavily relies on the mixing property of $\hat{\tau}$. Note that for $\hat{\tau}$ being only ergodic, the statement is wrong, as can be seen from the product of two periodic processes in ${\mathbb{T}}\times{\mathbb{T}}$ (see Remark 2.34). Here, the invariant sets are given by $I_{A}: = \left\{ \left(\left(y+x\right)\!\mod{\mathbb{T}}\, , \, x\right)\, :\; y\in A\right\}$ for arbitrary measurable $A\subset{\mathbb{T}}$.

2.10.   Random measures and palm theory

We recall some facts from random measure theory (see ^[4]) which will be needed for constructing ${\mathbb{X}}_{{\mathfrak{r}}}$ below. Let ${\mathfrak{M}}({\mathbb{R}^{d}})$ denote the space of locally bounded Borel measures on ${\mathbb{R}^{d}}$ (i.e., bounded on every bounded Borel-measurable set) equipped with the Vague topology, which is generated by the sets

This topology is metrizable, complete and countably generated. A random measure is a measurable mapping

which is equivalent to both of the following conditions

1. For every bounded Borel set $A\subset{\mathbb{R}^{d}}$ the map $\omega\mapsto\mu_{\omega}(A)$ is measurable

2. For every $f\in C_{c}({\mathbb{R}^{d}})$ the map $\omega\mapsto\int f\, {\mathrm{d}}\mu_{\omega}$ is measurable.

A random measure is stationary if the distribution of $\mu_{\omega}(A)$ is invariant under translations of $A$ that is $\mu_{\omega}(A)$ and $\mu_{\omega}(A+x)$ share the same distribution. From stationarity of $\mu_{\omega}$ one concludes the existence (^[10,22] and references therein) of a dynamical system $\left(\tau_{x}\right)_{x\in{\mathbb{R}^{d}}}$ on $\Omega$ such that $\mu_{\omega}\left(A+x\right) = \mu_{\tau_{x}\omega}\left(A\right)$. By a deep theorem due to Mecke (see ^[4,19]) the measure

can be defined on $\Omega$ for every positive $g\in L^{1}({\mathbb{R}^{d}})$ with $\left\Vert g\right\Vert_{L^{1}({\mathbb{R}^{d}})} = 1$ and with compact support. ${\mu_{\mathcal{P}}}$ is independent from $g$ and in case $\mu_{\omega} = {\mathcal{L}}$ we find ${\mu_{\mathcal{P}}} = {\mathbb{P}}$. Furthermore, for every ${\mathcal{B}}({\mathbb{R}^{d}})\times{\mathcal{B}}(\Omega)$-measurable non negative or ${\mu_{\mathcal{P}}}\times{\mathcal{L}}$- integrable functions $f$ the Campbell formula

holds. The measure $\mu_{\omega}$ has finite intensity if ${\mu_{\mathcal{P}}}(\Omega) < +\infty$.

We denote by

For random measures we find a more general version of Theorem 2.32.

Theorem 2.37 (Ergodic Theorem ^[4] 12.2.Ⅷ). Let $\left(\Omega, {\mathscr{F}}, {\mathbb{P}}\right)$ be a probability space, let $\left(A_{n}\right)_{n\in{\mathbb{N}}}\subset{\mathbb{R}^{d}}$ be a convex averaging sequence, let $(\tau_{x})_{x\in{\mathbb{R}^{d}}}$ be a dynamical system on $\Omega$ with invariant $\sigma$-algebra ${\mathscr{I}}$ and let $f:\, \Omega\to{\mathbb{R}}$ be measurable with $\int_{\Omega}\left|f\right|{\mathrm{d}}{\mu_{\mathcal{P}}} < \infty$. Then for ${\mathbb{P}}$-almost all $\omega\in\Omega$

Given a bounded open (and convex) set ${\bf{Q}}\subset\Omega$, it is not hard to see that the following generalization holds:

Theorem 2.38 (General Ergodic Theorem). Let $\left(\Omega, {\mathscr{F}}, {\mathbb{P}}\right)$ be a probability space, ${\bf{Q}}\subset{\mathbb{R}^{d}}$ be a bounded open set with $0\in{\bf{Q}}$, let $(\tau_{x})_{x\in{\mathbb{R}^{d}}}$ be a dynamical system on $\Omega$ with invariant $\sigma$-algebra ${\mathscr{I}}$ and let $f:\, \Omega\to{\mathbb{R}}$ be measurable with $\int_{\Omega}\left|f\right|{\mathrm{d}}{\mu_{\mathcal{P}}} < \infty$. Then for ${\mathbb{P}}$-almost all $\omega\in\Omega$ it holds

Sketch of proof. Chose a countable dense family of functions $\varphi\in C_{0}({\bf{Q}})$ that spans $L^{1}({\bf{Q}})$ and that have support on a ball. Use a Cantor argument and Theorem 2.37 to prove the statement for a countable dense family of $C_{0}({\bf{Q}})$. From here, we conclude by density. □ The last result can be used to prove the most general ergodic theorem which we will use in this work:

Theorem 2.39 (General Ergodic Theorem for the Lebesgue measure). Let $\left(\Omega, {\mathscr{F}}, {\mathbb{P}}\right)$ be a probability space, ${\bf{Q}}\subset{\mathbb{R}^{d}}$ be a bounded open set with $0\in{\bf{Q}}$, let $(\tau_{x})_{x\in{\mathbb{R}^{d}}}$ be a dynamical system on $\Omega$ with invariant $\sigma$-algebra ${\mathscr{I}}$ and let $f\in L^{p}(\Omega; {\mu_{\mathcal{P}}})$ and $\varphi\in L^{q}({\bf{Q}})$, where $1 < p, q < \infty$, $\frac{1}{p}+\frac{1}{q} = 1$. Then for ${\mathbb{P}}$-almost all $\omega\in\Omega$ it holds

Proof. Let $\varphi_{\delta}\in C(\overline{{\bf{Q}}})$ with $\left\Vert {\varphi-\varphi_{\delta}}\right\Vert_{L^{q}({\bf{Q}})} < \delta$. Then

which implies the claim. □

2.11.   Random sets

The theory of random measures and the theory of random geometry are closely related. In what follows, we recapitulate those results that are important in the context of the theory developed below and shed some light on the relations between random sets and random measures.

Let ${\mathfrak{F}}({\mathbb{R}^{d}})$ denote the set of all closed sets in ${\mathbb{R}^{d}}$. We write

The Fell-topology ${\mathscr{T}}_{F}$ is created by all sets ${\mathfrak{F}}_{V}$ and ${\mathfrak{F}}^{K}$ and the topological space $({\mathfrak{F}}({\mathbb{R}^{d}}), {\mathscr{T}}_{F})$ is compact, Hausdorff and separable ^[18].

Remark 2.40. We find for closed sets $F_{n}, F$ in ${\mathbb{R}^{d}}$ that $F_{n}\to F$ if and only if ^[18]

1. for every $x\in F$ there exists $x_{n}\in F_{n}$ such that $x = \lim_{n\to\infty}x_{n}$ and

2. if $F_{n_{k}}$ is a subsequence, then every convergent sequence $x_{n_{k}}$ with $x_{n_{k}}\in F_{n_{k}}$ satisfies $\lim_{k\to\infty}x_{n_{k}}\in F$.

If we restrict the Fell-topology to the compact sets $\mathfrak{K}({\mathbb{R}^{d}})$ it is equivalent with the Hausdorff topology given by the Hausdorff distance

Remark 2.41. For $A\subset{\mathbb{R}^{d}}$ closed, the set

is a closed subset of ${\mathfrak{F}}{\left({{\mathbb{R}^{d}}}\right)}$. This holds since

.

Lemma 2.42. (Continuity of geometric operations). The maps $\tau_{x}:\, A\mapsto A+x$ and $b_{\delta}:\, A\mapsto\overline{\mathbb{B}_{{\delta}}{\left(A\right)}}$ are continuous in ${\mathfrak{F}}\left({\mathbb{R}^{d}}\right)$.

Proof. We show that preimages of open sets are open. For open sets $V$ we find

The calculations for $\tau_{x}^{-1}{\left({{\mathfrak{F}}^{K}}\right)} = {\mathfrak{F}}^{\tau_{-x}K}$ and $b_{\delta}^{-1}{\left({{\mathfrak{F}}^{K}}\right)} = {\mathfrak{F}}^{b_{\delta}K}$ are analogue. □

Remark 2.43. The Matheron-$\sigma$-field $\sigma_{{\mathfrak{F}}}$ is the Borel-$\sigma$-algebra of the Fell-topology and is fully characterized either by the class ${\mathfrak{F}}_{V}$ of ${\mathfrak{F}}^{K}$.

Definition 2.44 (Random closed / open set according to Choquet (see ^[18] for more details)).

${\rm{a}})$ Let $(\Omega, \sigma, {\mathbb{P}})$ be a probability space. Then a Random Closed Set (RACS) is a measurable mapping

${\rm{b}})$ Let $\tau_{x}$ be a dynamical system on $\Omega$. A random closed set is called stationary if its characteristic functions $\chi_{A(\omega)}$ are stationary, i.e. they satisfy $\chi_{A(\omega)}(x) = \chi_{A(\tau_{x}\omega)}(0)$ for almost every $\omega\in\Omega$ for almost all $x\in{\mathbb{R}^{d}}$. Two random sets are jointly stationary if they can be parameterized by the same probability space such that they are both stationary.

${\rm{c}})$ A random closed set $\Gamma:(\Omega, \sigma, P)\longrightarrow({\mathfrak{F}}, \sigma_{{\mathfrak{F}}})\quad\omega\mapsto\Gamma(\omega)$ is called a Random closed $C^{k}$-Manifold if $\Gamma(\omega)$ is a piece-wise $C^{k}$-manifold for P almost every $\omega$.

${\rm{d}})$ A measurable mapping

is called Random Open Set (RAOS) if $\omega\mapsto{\mathbb{R}^{d}}\backslash A(\omega)$ is a RACS.

The importance of the concept of random geometries for stochastic homogenization stems from the following Lemma by Zähle. It states that every random closed set induces a random measure. Thus, every stationary RACS induces a stationary random measure.

Lemma 2.45 (^[32] Theorem 2.1.3 resp. Corollary 2.1.5). Let ${\mathfrak{F}}_{m}\subset{\mathfrak{F}}$ be the space of closed m-dimensional sub manifolds of ${\mathbb{R}^{d}}$ such that the corresponding Hausdorff measure is locally finite. Then, the $\sigma$-algebra $\sigma_{{\mathfrak{F}}}\cap{\mathfrak{F}}_{m}$ is the smallest such that

is measurable for every measurable and bounded $B\subset{\mathbb{R}^{d}}$.

This means that

is measurable with respect to the $\sigma$-algebra created by the Vague topology on ${\mathfrak{M}}({\mathbb{R}^{d}})$. Hence a random closed set always induces a random measure. Based on Lemma 2.45 and on Palm-theory, the following useful result was obtained in ^[10] (See Lemma 2.14 and Section 3.1 therein). We can thus assume in the following that $\Omega$ is a separable metric space.

Theorem 2.46 (See ^[10]). Let $(\Omega, \sigma, P)$ be a probability space with an ergodic dynamical system $\tau$. Let $A:(\Omega, \sigma, P)\longrightarrow({\mathfrak{F}}, \sigma_{{\mathfrak{F}}})$ be a stationary random closed $m$-dimensional $C^{k}$-Manifold.

There exists a separable metric space $\tilde{\Omega}\subset{\mathfrak{M}}{\left({{\mathbb{R}^{d}}}\right)}$ with an ergodic dynamical system $\tilde{\tau}$ and a mapping $\tilde{A}:\, (\tilde{\Omega}, {\mathcal{B}}_{\tilde{\Omega}}, {\mathbb{P}})\to({\mathfrak{F}}, \sigma_{{\mathfrak{F}}})$ such that $A$ and $\tilde{A}$ have the same law and such that $\tilde{A}$ still is stationary. Furthermore, $(x, \omega)\mapsto\tau_{x}\omega$ is continuous. We identify $\tilde{\Omega} = \Omega$, $\tilde{A} = A$ and $\tilde{\tau} = \tau$.

Also the following result will be useful below.

Lemma 2.47. Let $\mu$ be a Radon measure on ${\mathbb{R}^{d}}$ and let ${\bf{Q}}\subset{\mathbb{R}^{d}}$ be a bounded open set. Let ${\mathfrak{F}}_{0}\subset{\mathfrak{F}}\left(\overline{{\bf{Q}}}\right)$ be such that ${\mathfrak{F}}_{0}\to{\mathbb{R}}$, $A\mapsto\mu(A)$ is continuous. Then

is measurable.

Proof. For $f\in C_{c}({\mathbb{R}^{d}})$ we introduce $m_{f}$ through

and observe that $m$ is measurable if and only if for every $f\in C_{c}{\left({{\mathbb{R}^{d}}}\right)}$ the map $m_{f}$ is measurable (see Section 2.10). Hence, if we prove the latter property, the lemma is proved.

We assume $f\geq0$ and we show that the mapping $m_{f}$ is even upper continuous. In particular, let $(P_{n}, B_{n})\to(P, B)$ in ${\mathfrak{F}}\times{\mathfrak{F}}_{0}$ and assume that $B_{n}\subset P_{n}$ for all $n > N_{0}$. Since $\overline{{\bf{Q}}}$ is compact, Remark 2.40. 2. implies that $B\subset P\cap\overline{{\bf{Q}}}$. Furthermore, since $f$ has compact support and every Borel measure on ${\mathbb{R}^{d}}$ is regular, we find $\left|\int_{B_{n}}f\, {\mathrm{d}}\mu-\int_{B}f\, {\mathrm{d}}\mu\right|\leq\left\Vert f\right\Vert_{\infty}\left(\left|\mu{\left({B_{n}\setminus B}\right)}\right|+\left|\mu{\left({B\setminus B_{n}}\right)}\right|\right)\to0$. On the other hand, if there exists a subsequence such that $B_{n}\not\subset P_{n}$ for all $n$, then either $B\not\subset P$ and $m_{f}(P_{n}, B_{n}) = 0\to m_{f}(P, B) = 0$ or $B\subset P$ and $0 = \lim_{n\to\infty}m_{f}(P_{n}, B_{n})\leq\int_{B}f{\mathrm{d}}\mu = m_{f}(P, B)$. For $f\leq0$ we obtain lower semicontinuity and for general $f$ the map $m_{f}$ is the sum of an upper and a lower semicontinuous map, hence measurable. □

2.12.   Point processes

Definition 2.48 ((Simple) point processes). A ${\mathbb{Z}}$-valued random measure $\mu_{\omega}$ is called point process. In what follows, we consider the particular case that for almost every $\omega$ there exist points $\left(x_{k}(\omega)\right)_{k\in{\mathbb{N}}}$ and values $\left(a_{k}\left(\omega\right)\right)_{k\in{\mathbb{N}}}$ in ${\mathbb{Z}}$ such that

The point process $\mu_{\omega}$ is called simple if almost surely for all $k\in{\mathbb{N}}$ it holds $a_{k}\in\left\{ 0, 1\right\}$.

Example 2.49 (Poisson process). A particular example for a stationary point process is the Poisson point process $\mu_{\omega} = {\mathbb{X}}_{\omega}$ with intensity $\lambda$. Here, the probability ${\mathbb{P}}{\left({{\mathbb{X}}(A) = n}\right)}$ to find $n$ points in a Borel-set $A$ with finite measure is given by a Poisson distribution

with expectation ${\mathbb{E}}{\left({{\mathbb{X}}(A)}\right)} = \lambda\left|A\right|$. Shift-invariance of Eq (2.51) implies that the Poisson point process is stationary.

We can use a given random point process to construct further processes.

Example 2.50 (Hard core Matern process). The hard core Matern process is constructed from a given point process ${\mathbb{X}}_{\omega}$ by mutually erasing all points with the distance to the nearest neighbor smaller than a given constant $r$. If the original process ${\mathbb{X}}_{\omega}$ is stationary (ergodic), the resulting hard core process is stationary (ergodic) respectively.

Example 2.51 (Hard core Poisson–Matern process). If a Matern process is constructed from a Poisson point process, we call it a Poisson–Matern point process.

Lemma 2.52. Let $\mu_{\omega}$ be a simple point process with $a_{k} = 1$ almost surely for all $k\in{\mathbb{N}}$. Then ${\mathbb{X}}_{\omega} = \left(x_{k}(\omega)\right)_{k\in{\mathbb{N}}}$ is a random closed set of isolated points with no limit points. On the other hand, if ${\mathbb{X}}_{\omega} = \left(x_{k}(\omega)\right)_{k\in{\mathbb{N}}}$ is a random closed set that almost surely has no limit points then $\mu_{\omega}$ is a point process.

Proof. Let $\mu_{\omega}$ be a point process. For open $V\subset{\mathbb{R}^{d}}$ and compact $K\subset{\mathbb{R}^{d}}$ we will show that ${\mathbb{X}}^{-1}{\left({{\mathfrak{F}}_{V}}\right)}$ and ${\mathbb{X}}^{-1}{\left({{\mathfrak{F}}^{K}}\right)}$ are measurable. Since ${\mathfrak{F}}_{V}$ and ${\mathfrak{F}}^{K}$ generate the $\sigma$-algebra on ${\mathfrak{F}}\left({\mathbb{R}^{d}}\right)$, it then follows that $\omega\to{\mathbb{X}}_{\omega}$ is measurable. Now let

Then $f_{V, R}$ is Lipschitz with constant $1$ and $f_{\delta}^{K}$ is Lipschitz with constant $\frac{1}{\delta}$ and support in $\mathbb{B}_{{\delta}}{\left(K\right)}$. Moreover, since $\mu_{\omega}$ is locally bounded, the number of points $x_{k}$ that lie within $\mathbb{B}_{1}{\left(K\right)}$ is bounded. In particular, we obtain

are measurable.

In order to prove the opposite direction, let ${\mathbb{X}}_{\omega} = \left(x_{k}(\omega)\right)_{k\in{\mathbb{N}}}$ be a random closed set of points. Since ${\mathbb{X}}_{\omega}$ has almost surely no limit points the measure $\mu_{\omega}$ is locally bounded almost surely. We prove that $\mu_{\omega}$ is a random measure by showing that

For $\delta > 0$ let $\mu_{\omega}^{\delta}{\left(A\right)}: = \left(\left|{\mathbb{S}}^{d-1}\right|\delta^{d}\right)^{-1}{\mathcal{L}}{\left({A\cap\mathbb{B}_{{\delta}}{\left({{\mathbb{X}}_{\omega}}\right)}}\right)}$. By Lemmas 2.42 and 2.47 we obtain that $F_{\delta}:\, \omega\mapsto\int_{{\mathbb{R}^{d}}}f\, {\mathrm{d}}\mu_{\omega}^{\delta}$ are measurable. Moreover, for almost every $\omega$ we find $F_{\delta}\left(\omega\right)\to F\left(\omega\right)$ uniformly and hence $F$ is measurable. □

Corollary 2.53. A random simple point process $\mu_{\omega}$ is stationary iff ${\mathbb{X}}_{\omega}$ is stationary.

Hence we can provide the following definition based on Definition 2.44.

Definition 2.54. A point process $\mu_{\omega}$ and a random set ${\bf{P}}$ are jointly stationary if ${\bf{P}}$ and ${\mathbb{X}}$ are jointly stationary.

Lemma 2.55. Let ${\mathbb{X}}_{\omega} = \left(x_{i}\right)_{i\in{\mathbb{N}}}$ be a Matern point process from Example 2.50 with distance $r$ and let for $\delta < \frac{r}{2}$ be ${\bf{B}}(\omega): = \bigcup_{i}\overline{B_{\delta}(x_{i})}$. Then ${\bf{B}}(\omega)$ is a random closed set.

Proof. This follows from Lemma 2.42: ${\mathbb{X}}_{\omega}$ is measurable and ${\mathbb{X}}\mapsto\overline{B_{\delta}({\mathbb{X}})}$ is continuous. Hence ${\bf{B}}\left(\omega\right)$ is measurable. □

2.13.   Dynamical Systems on ${\mathbb{Z}^{d}}$

Definition 2.56. Let $\left(\hat{\Omega}, \hat{{\mathscr{F}}}, \hat{{\mathbb{P}}}\right)$ be a probability space and $r > 0$. A discrete dynamical system on $\hat{\Omega}$ is a family $(\hat{\tau}_{z})_{z\in r{\mathbb{Z}^{d}}}$ of measurable bijective mappings $\hat{\tau}_{z}:\hat{\Omega}\mapsto\hat{\Omega}$ satisfying (i)–(iii) of Definition 2.28 with ${\mathbb{R}^{d}}$ replaced by $r{\mathbb{Z}^{d}}$. A set $A\subset\hat{\Omega}$ is almost invariant if for every $z\in r{\mathbb{Z}^{d}}$ it holds ${\mathbb{P}}\left(\left(A\cup\hat{\tau}_{z}A\right)\backslash\left(A\cap\hat{\tau}_{z}A\right)\right) = 0$ and $\hat{\tau}$ is called ergodic with respect to $r{\mathbb{Z}^{d}}$ if every almost invariant set has measure $0$ or $1$.

Similar to the continuous dynamical systems, also in this discrete setting an ergodic theorem can be proved.

Theorem 2.57 (See Krengel and Tempel'man ^[16,27]). Let $\left(A_{n}\right)_{n\in{\mathbb{N}}}\subset{\mathbb{R}^{d}}$ be a convex averaging sequence, let $(\hat{\tau}_{z})_{z\in r{\mathbb{Z}^{d}}}$ be a dynamical system on $\hat{\Omega}$ with invariant $\sigma$-algebra ${\mathscr{I}}$ and let $f:\, \hat{\Omega}\to{\mathbb{R}}$ be measurable with $\left|{\mathbb{E}}(f)\right| < \infty$. Then for almost all $\hat{\omega}\in\hat{\Omega}$

In the following, we restrict to $r = 1$ for simplicity of notation.

Let $\Omega_{0}\subset{\mathbb{R}^{d}}$. We consider an enumeration $\left(\xi_{i}\right)_{i\in{\mathbb{N}}}$ of ${\mathbb{Z}^{d}}$ such that $\hat{\Omega}: = \Omega_{0}^{{\mathbb{Z}^{d}}} = \Omega_{0}^{{\mathbb{N}}}$ and write $\hat{\omega} = \left(\hat{\omega}_{\xi_{1}}, \hat{\omega}_{\xi_{2}}, \dots\right) = \left(\hat{\omega}_{1}, \hat{\omega}_{2}, \dots\right)$ for all $\hat{\omega}\in\hat{\Omega}$. We define a metric on $\hat{\Omega}$ through

We write $\Omega_{n}: = \Omega_{0}^{n}$ and ${\mathbb{N}}_{n}: = \left\{ k\in{\mathbb{N}}:\, k\geq n+1\right\}$. The topology of $\hat{\Omega}$ is generated by the open sets $A\times\Omega_{0}^{{\mathbb{N}}_{n}}$, where for some $n > 0$, $A\subset\Omega_{n}$ is an open set. In case $\Omega_{0}$ is compact, the space $\hat{\Omega}$ is compact. Further, $\hat{\Omega}$ is separable in any case since $\Omega_{0}$ is separable (see ^[14]).

Lemma 2.58. Suppose for every $n\in{\mathbb{N}}$ there exists a probability measure ${\mathbb{P}}_{n}$ on $\Omega_{n}$ such that for every measurable $A_{n}\subset\Omega_{n}$ it holds ${\mathbb{P}}_{n+k}{\left({A_{n}\times\Omega^{k}}\right)} = {\mathbb{P}}_{n}{\left({A_{n}}\right)}$. Then ${\mathbb{P}}$ defined as follows defines a probability measure on $\Omega$:

Proof. We consider the ring

and make the observation that ${\mathbb{P}}$ is additive and positive on ${\mathcal{R}}$ and ${\mathbb{P}}(\emptyset) = 0$. Next, let $\left(A_{j}\right)_{j\in{\mathbb{N}}}$ be an increasing sequence of sets in ${\mathcal{R}}$ such that $A: = \bigcup_{j}A_{j}\in{\mathcal{R}}$. Then, there exists $\tilde{A}_{1}\subset\Omega_{0}^{n}$ such that $A_{1} = \tilde{A}_{1}\times\Omega_{0}^{{\mathbb{N}}_{n}}$ and since $A_{1}\subset A_{2}\subset\dots\subset A$, for every $j > 1$, we conclude $A_{j} = \tilde{A_{j}}\times\Omega_{0}^{{\mathbb{N}}_{n}}$ for some $\tilde{A}_{j}\subset\Omega_{n}$. Therefore, ${\mathbb{P}}(A_{j}) = {\mathbb{P}}_{n}(\tilde{A}_{j})\to{\mathbb{P}}_{n}(\tilde{A}) = {\mathbb{P}}(A)$ where $A = \tilde{A}\times\Omega_{0}^{{\mathbb{N}}_{n}}$. We have thus proved that ${\mathbb{P}}:{\mathcal{R}}\to[0, 1]$ can be extended to a measure on the Borel-$\sigma$-Algebra on $\Omega$ (See [2, Theorem 6-2]). □

We define for $z\in{\mathbb{Z}^{d}}$ the mapping

Remark 2.59. In this paper, we consider particularly $\Omega_{0} = \left\{ 0, 1\right\}$. Then $\hat{\Omega}: = \Omega_{0}^{{\mathbb{Z}^{d}}}$ is equivalent to the power set of ${\mathbb{Z}^{d}}$ and every $\hat{\omega}\in\hat{\Omega}$ is a sequence of $0$ and $1$ corresponding to a subset of ${\mathbb{Z}^{d}}$. Shifting the set $\hat{\omega}\subset{\mathbb{Z}^{d}}$ by $z\in{\mathbb{Z}^{d}}$ corresponds to an application of $\hat{\tau}_{z}$ to $\hat{\omega}\in\hat{\Omega}$.

Now, let ${\bf{P}}(\omega)$ be a stationary ergodic random open set and let $r > 0$. Recalling Eq (2.2) the map $\omega\mapsto{\bf{P}}_{-r}(\omega)$ is measurable due to Lemma 2.42 and we can define ${\mathbb{X}}_{r}{\left({{\bf{P}}{\left({\omega}\right)}}\right)}: = 2r{\mathbb{Z}^{d}}\cap{\bf{P}}_{-\frac{r}{2}}{\left({\omega}\right)}$.

Lemma 2.60. If ${\bf{P}}$ is a stationary ergodic random open set then the set

is a stationary random point process with respect to $2r{\mathbb{Z}^{d}}$.

Remark 2.61. Note that ${\mathbb{X}}_{r}(\omega)$ is in general not ergodic since ${\bf{P}}\to{\mathbb{X}}$ is not necessarily injective.

Proof. By a simple scaling we can assume $2r = 1$ and write ${\mathbb{X}} = {\mathbb{X}}_{r}$. Evidently, ${\mathbb{X}}$ corresponds to a process on ${\mathbb{Z}^{d}}$ with values in $\Omega_{0} = \left\{ 0, 1\right\}$ writing ${\mathbb{X}}(z) = 1$ if $z\in{\mathbb{X}}$ and ${\mathbb{X}}(z) = 0$ if $z\not\in{\mathbb{X}}$. In particular, we write $\left(\omega, z\right)\mapsto{\mathbb{X}}{\left({\omega, z}\right)}$. This process is stationary as the shift invariance of ${\bf{P}}$ induces a shift-invariance of $\hat{{\mathbb{P}}}$ with respect to $\hat{\tau}_{z}$. It remains to observe that the probabilities ${\mathbb{P}}{\left({{\mathbb{X}}(z) = 1}\right)}$ and ${\mathbb{P}}{\left({{\mathbb{X}}(z) = 0}\right)}$ induce a random measure on $\hat{\Omega}$ in the way described in Remark 2.59. □

Remark 2.62. If ${\bf{P}}$ is mixing one can follow the lines of the proof of Lemma 2.35 to find that ${\mathbb{X}}_{r}{\left({{\bf{P}}{\left({\omega}\right)}}\right)}$ is ergodic. However, in the general case ${\mathbb{X}}_{r}{\left({{\bf{P}}{\left({\omega}\right)}}\right)}$ is not ergodic. This is due to the fact that by nature $\left(\tau_{z}\right)_{z\in{\mathbb{Z}^{d}}}$ on $\Omega$ has more invariant sets than$\left(\tau_{x}\right)_{x\in{\mathbb{R}^{d}}}$. For sufficiently complex geometries the map $\Omega\to\hat{\Omega}$ is onto.

Definition 2.63 (Jointly stationary). We call a point process ${\mathbb{X}}$ with values in $2r{\mathbb{Z}^{d}}$ to be strongly jointly stationary with a random set ${\bf{P}}$ if the functions $\chi_{{\bf{P}}(\omega)}$, $\chi_{{\mathbb{X}}(\omega)}$ are jointly stationary with respect to the dynamical system $\left(\tau_{2rx}\right)_{x\in{\mathbb{Z}^{d}}}$ on $\Omega$.

3.   Quantifying nonlocal regularity properties of the Geometry

3.1.   Microscopic regularity

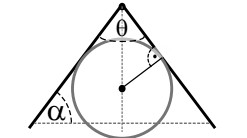
Lemma 3.1. Let ${\bf{P}}$ be a Lipschitz domain. Then for every $p_{0}\in\partial{\bf{P}}$ with $\delta(p_{0}) > 0$ the following holds: For every $\delta < \delta\left(p_{0}\right)$ and $M: = M_{\delta}(p_{0}) > 0$ there exists $y\in{\bf{P}}$ with $\left|p_{0}-y\right| = \frac{\delta}{4}$ such that with $r\left(p_{0}\right): = \frac{\delta}{4\left(1+M\right)}$ it holds $\mathbb{B}_{{r\left(p_{0}\right)}}{\left(y\right)}\subset\mathbb{B}_{{\delta/2}}{\left({p_{0}}\right)}\cap{\bf{P}}$.

Proof. We can assume that $\partial{\bf{P}}$ is locally a cone as in Figure 4. With regard to Figure 4, for $p_{0}\in\partial{\bf{P}}$ with $\delta$ and $M$ as in the statement we can place a right circular cone with vertex (apex) $p_{0}$ and axis $\nu$ and an aperture $\theta = \pi-2\arctan M$ inside $\mathbb{B}_{{\delta}}{\left({p_{0}}\right)}$, where $\alpha = \arctan M$. In other words, it holds $\tan\left(\alpha\right) = \tan\left(\frac{\pi-\theta}{2}\right) = M$. Along the axis we may select $y$ with $\left|p_{0}-y\right| = \frac{\delta}{4}$. Then the distance $R$ of $y$ to the cone is given through

In particular $r\left(p_{0}\right)$ as defined above satisfies the claim. □

Continuity properties of $\delta$, $M$ and $\varrho$

Lemma 3.2 ($\partial{\bf{P}}$ is $\delta_{\Delta}$-regular). Let ${\mathfrak{r}} > 0$, ${\bf{P}}$ be a Lipschitz domain and recall Eq (1.7). Then $\partial{\bf{P}}$ is $\delta_{\Delta}$-regular in the sense of Definition 2.22. In particular, $\delta_{\Delta}:\, \partial{\bf{P}}\to{\mathbb{R}}$ is locally Lipschitz continuous with Lipschitz constant $1$ and for every ${\varepsilon}\in\left(0, \frac{1}{2}\right)$ and $\tilde{p}\in\mathbb{B}_{{{\varepsilon}\delta}}{\left(p\right)}\cap\partial{\bf{P}}$ it holds

Remark 3.3. The latter lemma does not imply global Lipschitz regularity of $\delta_{\Delta}$.

Proof of Lemma 3.2. It is straightforward to verify that $\left|p-\tilde{p}\right| < {\varepsilon}\delta_{\Delta}(p)$ implies $\delta_{\Delta}(\tilde{p}) > (1-{\varepsilon})\delta_{\Delta}(p)$ and we conclude with Lemma 2.24. □

Corollary 3.4. For fixed $p\in\partial{\bf{P}}$ the function $r\mapsto M_{r}(p)$ is right continuous and monotone increasing (i.e. u.s.c.) on $[0, \delta_{\Delta}(p)]$.

Proof. This follows because $M$ being Lipschitz constant of $\partial{\bf{P}}$ in $\mathbb{B}_{R}{\left(p\right)}$ implies $M$ being Lipschitz constant of $\partial{\bf{P}}$ in $\mathbb{B}_{r}{\left(p\right)}$ for every $r\in(0, R]$. □

With regard to Lemma 2.3, the relevant quantity for local extension operators is related to $\delta{\left(p\right)}/\sqrt{4M{\left(p\right)}^{2}+2}$, where $M(p)$ is the related Lipschitz constant. While we can quantify $\delta{\left(p\right)}$ in terms of $\delta{\left({\tilde{p}}\right)}$ and $\left|p-\tilde{p}\right|$, this does not work for $M{\left(p\right)}$. Hence we cannot quantify $\delta{\left(p\right)}/\sqrt{4M{\left(p\right)}^{2}+2}$ in terms of its neighbors. This drawback is compensated by a variational trick in the following statement.

Lemma 3.5. Let ${\bf{P}}$ be a Lipschitz domain and let $\delta\leq\delta_{\Delta}$ satisfy Eq (3.1) such that $\partial{\bf{P}}$ is $\delta$-regular. For $p\in\partial{\bf{P}}$ and let $M_{r}{\left(p\right)}$ be given in Eq (1.8) and define for $n, K\in{\mathbb{N}}$

Then, $\rho_{n}$ is positive and locally Lipschitz continuous on $\partial{\bf{P}}$ with Lipschitz constant $1$ and $\partial{\bf{P}}$ is $\rho$-regular in the sense of Definition 2.22. In particular, for $\left|p-\tilde{p}\right| < {\varepsilon}\rho_{n}{\left(p\right)}$ it holds

Furthermore, $\hat{\rho}_{n, K}\leq\delta$ is well defined.

Remark 3.6. Like in Remark 3.3 this does not imply global Lipschitz regularity of $\rho_{n}$ or $\hat{\rho}_{n}$.

Corollary 3.7. Every Lipschitz domain ${\bf{P}}$ has extension order 1 and symmetric extension order 2.

Proof. This follows from $\hat{\rho}_{n, 3}\leq\delta$ and Lemmas 2.3 and 2.7 applied to $\mathbb{B}_{{\frac{1}{8}\hat{\rho}_{n, 3}}}{\left({p_{0}}\right)}$ and $\mathbb{B}_{{\frac{1}{8}\rho_{n}}}{\left({p_{0}}\right)}$. □

Proof of Lemma 3.5. Let $\left|p-\tilde{p}\right| < {\varepsilon}\rho{\left(p\right)} < {\varepsilon}\delta(p)$ with $\delta{\left(\tilde{p}\right)}\geq\left(1-{\varepsilon}\right)\delta{\left(p\right)}$ by Lemma 3.2. For every $\eta > 0$ let $r_{\eta}\in\left(\rho(p), \delta{\left(p\right)}\right)$ such that

Since $r_{\eta} > \rho{\left(p\right)}$ and $\left|p-\tilde{p}\right| < {\varepsilon}\rho{\left(p\right)}$ we find $\mathbb{B}_{{r_{\eta}}}{\left(p\right)}\supset\mathbb{B}_{{\left(1-{\varepsilon}\right)r_{\eta}}}{\left({\tilde{p}}\right)}$ and hence $M_{\left(1-{\varepsilon}\right)r_{\eta}}{\left(\tilde{p}\right)}\leq M_{r_{\eta}}{\left(p\right)}$. This implies at the same time that $\partial{\bf{P}}$ is $\rho$-regular and that

Since $\eta$ was arbitrary, we conclude $\rho{\left(\tilde{p}\right)}\geq\left(1-{\varepsilon}\right)\rho{\left(p\right)}$. Moreover, we find $\left|p-\tilde{p}\right| < \frac{{\varepsilon}}{1-{\varepsilon}}\rho{\left(\tilde{p}\right)}$. And we conclude the first part with Lemma 2.24.

Second, it holds for every $r < \delta$ and ${\varepsilon}\in(0, 1)$ that

and choosing ${\varepsilon} = 2^{-K}$ and taking the supremum on both sides, we infer that $\hat{\rho}_{n, K}$ is well defined. □

Corollary 3.8. Let ${\mathfrak{r}} > 0$ and let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be a locally $\left(\delta, M\right)$-regular open set, where we restrict $\delta$ by $\delta\left(\cdot\right)\leq\frac{{\mathfrak{r}}}{4}$. Then there exists a countable number of points $\left(p_{k}\right)_{k\in{\mathbb{N}}}\subset\partial{\bf{P}}$ such that $\partial{\bf{P}}$ is completely covered by balls $\mathbb{B}_{{\tilde{\rho}\left(p_{k}\right)}}{\left({p_{k}}\right)}$ where $\tilde{\rho}\left(p\right): = 2^{-5}\rho_{n}\left(p\right)$ for some $n\in{\mathbb{N}}$. Writing

For two such balls with $\mathbb{B}_{{\tilde{\rho}_{k}}}{\left({p_{k}}\right)}\cap\mathbb{B}_{{\tilde{\rho}_{i}}}{\left({p_{i}}\right)}\neq\emptyset$ it holds

Furthermore, there exists ${\mathfrak{r}}_{k}\geq\frac{\tilde{\rho}_{k}}{32\left(1+M_{\tilde{\rho}(p_{k})}{\left({p_{k}}\right)}\right)}$ and $y_{k}$ such that

$\mathbb{B}_{{{\mathfrak{r}}_{k}}}{\left({y_{k}}\right)}\subset\mathbb{B}_{{\tilde{\rho}_{k}/8}}{\left({p_{k}}\right)}\cap{\bf{P}}$ and $\mathbb{B}_{{2{\mathfrak{r}}_{k}}}{\left({y_{k}}\right)}\cap\mathbb{B}_{{2{\mathfrak{r}}_{j}}}{\left({y_{j}}\right)} = \emptyset$ for $k\neq j$.

Proof. The existence of the points and Balls satisfying Eq (3.5) follows from Theorem 2.25, in particular Eq (2.37). It holds for $\mathbb{B}_{{\tilde{\rho}_{k}}}{\left({p_{k}}\right)}\cap\mathbb{B}_{{\tilde{\rho}_{i}}}{\left({p_{i}}\right)}\neq\emptyset$

Lemma 3.1 yields existence of $y_{k}$ such that $\mathbb{B}_{{{\mathfrak{r}}_{k}}}{\left({y_{k}}\right)}\subset\mathbb{B}_{{\tilde{\rho}_{k}/8}}{\left({p_{k}}\right)}\cap{\bf{P}}$. By the mutual minimal distance the latter implies $\mathbb{B}_{{{\mathfrak{r}}_{k}}}{\left({y_{k}}\right)}\cap\mathbb{B}_{{{\mathfrak{r}}_{j}}}{\left({y_{j}}\right)} = \emptyset$ for $k\neq j$. □

Lemma 3.9. Let ${\mathfrak{r}} > 0$, ${\bf{P}}\subset{\mathbb{R}^{d}}$ be a locally $\left(\delta, M\right)$-regular open set and let $M_{0}\in(0, +\infty]$ such that for every $p\in\partial{\bf{P}}$ there exists $\delta > 0$, $M < M_{0}$ such that $\partial{\bf{P}}$ is $(\delta, M)$-regular in $p$. For $\alpha\in(0, 1]$ let $\eta(p) = \alpha\delta_{\Delta}(p)$ from Lemma 3.2 or $\eta(p) = \alpha\rho_{n}(p)$ from Lemma 3.5 and define

Then, for fixed $\xi$, ${\mathrm{M}}_{[\eta]}{\left({\cdot}\right)}:\; \partial{\bf{P}}\to{\mathbb{R}}$ is upper semicontinuous and on each bounded measurable set $A\subset{\mathbb{R}^{d}}$ the quantity

with ${\mathrm{M}}_{[\eta]}(A) = 0$ if $\overline{A}\cap\partial{\bf{P}} = \emptyset$ is well defined. The functions

are upper semicontinuous.

Remark 3.10. Note at this point that $M_{[\eta, r], {\mathbb{R}^{d}}}$ defined in Eq (1.11) is a function on ${\mathbb{R}^{d}}$ and different from $M_{[\eta]}$.

Notation. The infimum in Eq (3.6) is a $\liminf$ for $\delta\searrow\eta(p)$. We sometimes use the special notation

Proof of Lemma 3.9. Let $p, \tilde{p}\in\partial{\bf{P}}$ with $\left|p-\tilde{p}\right| < {\varepsilon}\eta(p)$. Writing $\tilde{{\varepsilon}}: = \frac{{\varepsilon}}{1-{\varepsilon}}$ and $r\left(p, {\varepsilon}\right): = \left(\frac{1}{1-2{\varepsilon}}+{\varepsilon}\right)\eta{\left(p\right)}$ and

we observe from $\eta$-regularity of $\partial{\bf{P}}$ (given by Lemma 3.5) that $\mathbb{B}_{{\eta\left(\tilde{p}\right)}}{\left({\tilde{p}}\right)}\subset\mathbb{B}_{{r\left(p, {\varepsilon}\right)}}{\left(p\right)}$ and $\mathbb{B}_{{\eta\left(p\right)}}{\left(p\right)}\subset\mathbb{B}_{{r\left(\tilde{p}, \tilde{{\varepsilon}}\right)}}{\left({\tilde{p}}\right)}$. Hence we find

Observing that $M_{r(p, {\varepsilon})}(p)\searrow{\mathrm{M}}_{\eta(p)}{\left(p\right)}$ as ${\varepsilon}\to0$ we find $\limsup_{\tilde{p}\to p}{\mathrm{M}}_{[\eta]}{\left({\tilde{p}}\right)}\leq{\mathrm{M}}_{[\eta]}{\left(p\right)}$ and ${\mathrm{M}}$ is u.s.c.

Let $x\to0$. First observe that ${\mathrm{M}}_{[\eta]}(A) = \max_{y\in\overline{A}}{\mathrm{M}}_{[\eta]}{\left(y\right)}$. The set $\overline{A}$ is compact and hence $\overline{A}+x\to\overline{A}$ in the Hausdorff metric as $x\to0$. Let $y_{x}\in\overline{A}+x$ such that ${\mathrm{M}}_{[\eta]}{\left({y_{x}}\right)} = {\mathrm{M}}_{[\eta]}\left(A, x\right)$. Since $\overline{A}+x\to\overline{A}$ we find $y_{x}\to y$ converges along a subsequence and $y\in\overline{A}$. Hence

In particular, $M_{[\eta], A}{\left({\cdot}\right)}$ is u.s.c. □

Measurability and Integrability of Extended Variables

Lemma 3.11. Let ${\mathfrak{r}} > 0$, let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be a Lipschitz domain, let $\eta, r:\, \partial{\bf{P}}\to{\mathbb{R}}$ be continuous such that $\eta\leq{\mathfrak{r}}$ and let ${\bf{P}}$ be $\eta$- and $r$-regular. For ${\varepsilon}\in(0, 1]$ let $\eta(p) = {\varepsilon}\delta(p)$ from Lemma 3.2 or $\eta(p) = {\varepsilon}\rho_{n}(p)$, $n\in{\mathbb{N}}$, from Lemma 3.5. Then $\eta_{[r], {\mathbb{R}^{d}}}$ from (1.10) is measurable and $M_{[\eta, r], {\mathbb{R}^{d}}}$ from (1.11) is upper semicontinuous.

In what follows, we write $A_{\eta, r, {\mathfrak{r}}}: = F_{\eta, r, {\mathfrak{r}}}^{-1}{\left({(0, \frac{3}{2}{\mathfrak{r}})}\right)}$ for

Proof. Step 1: We write $A = A_{\eta, \eta, {\mathfrak{r}}}$ for simplicity. Let $\left(p_{i}\right)_{i\in{\mathbb{N}}}\subset\partial{\bf{P}}$ be a dense subset. If $x\in\mathbb{B}_{{r{\left(p\right)}}}{\left(p\right)}$ for some $p\in\partial{\bf{P}}$ then also $x\in\mathbb{B}_{{r{\left({\tilde{p}}\right)}}}{\left({\tilde{p}}\right)}$ for $\left|p-\tilde{p}\right|$ sufficiently small, by continuity of $\eta$. Hence every $f_{p}$ is upper semicontinuous and it holds $F = \inf_{i\in{\mathbb{N}}}f_{p_{i}}$. In particular, $F$ is a measurable function and hence the set $A$ is measurable. This implies $\eta_{[r], {\mathbb{R}^{d}}} = \chi_{A}F$ is measurable.

Step 2: We show that for every $a\in{\mathbb{R}}$ the preimage $M_{[\eta, r], {\mathbb{R}^{d}}}^{-1}{\left({[a, +\infty)}\right)}$ is closed. Let $\left(x_{k}\right)_{k\in{\mathbb{N}}}$ be a sequence with $M_{[\eta, r], {\mathbb{R}^{d}}}{\left({x_{k}}\right)}\in[a, +\infty)$ and $x_{k}\to x\in{\mathbb{R}^{d}}$. Let $\left(p_{k}\right)\subset\partial{\bf{P}}$ be a sequence with $\left|x_{k}-p_{k}\right|\leq r{\left({p_{k}}\right)}$ where boundedness of $r$ implies $p_{k}\to p\in\partial{\bf{P}}$ along a subsequence. Since $r$ is continuous, it follows $\left|x-p\right|\leq r{\left(p\right)}$. On the other hand $M_{[\eta]}(p)\geq\limsup_{k\to\infty}M_{[\eta]}(p_{k})$ and thus $M_{[\eta, r], {\mathbb{R}^{d}}}{\left(x\right)}\geq M_{[\eta, r]}(p)\geq a$. □

Lemma 3.12. Under the assumptions of Lemma 3.11 let $\tilde{\eta}: = \eta_{[\frac{\eta}{8}], {\mathbb{R}^{d}}}$. Then there exists a constant $C > 0$ only depending on the dimension $d$ such that for every bounded open domain ${\bf{Q}}$ and $k\in[0, 4)$ it holds

Finally, it holds

Remark 3.13. Estimates Eqs (3.8) and (3.9) are only rough estimates and better results could be obtained via more sophisticated calculations that make use of particular features of given geometries.

Proof. Like in the previous proof we write $A = A_{\tilde{\eta}, \tilde{\eta}, {\mathfrak{r}}}$ for simplicity.

Step 1: Given $x\in{\mathbb{R}^{d}}$ with $\tilde{\eta}(x) > 0$ let

Such $p_{x}$ exists because $\partial{\bf{P}}$ is locally compact and $\eta$ is continuous. We observe with help of the definition of $p_{x}$, the triangle inequality and Eq (2.36)

The last line particularly implies Eq (3.10) and

Step 2: By Theorem 2.25 we can chose a countable number of points $\left(p_{k}\right)_{k\in{\mathbb{N}}}\subset\partial{\bf{P}}$ such that $\Gamma = \partial{\bf{P}}$ is completely covered by balls $B_{k}: = \mathbb{B}_{{\xi{\left({p_{k}}\right)}}}{\left({p_{k}}\right)}$ where $\xi{\left(p\right)}: = 2^{-4}\eta{\left(p\right)}$. For simplicity of notation we write $\eta_{k}: = \eta{\left({p_{k}}\right)}$ and $\xi_{k}: = \xi{\left({p_{k}}\right)}$. Assume $x\in A$ with $p_{x}\in\Gamma$ given by Eq (3.11). Since the balls $B_{k}$ cover $\Gamma$, there exists $p_{k}$ with $\left|p_{x}-p_{k}\right| < \xi_{k} = 2^{-4}\eta_{k}$, implying $\eta{\left({p_{x}}\right)} < \frac{2^{4}}{2^{4}-1}\eta_{k}$ and hence $\left|x-p_{k}\right|\leq\left(2^{-4}+\frac{2^{-3}2^{4}}{2^{4}-1}\right)\eta_{k} < \frac{3}{16}\eta_{k}$. Hence we find

Step 3: For $p\in\Gamma$ with $x\in\mathbb{B}_{{\frac{1}{4}\eta{\left(p\right)}}}{\left(p\right)}\cap\mathbb{B}_{{\frac{1}{8}\eta{\left({p_{x}}\right)}}}{\left({p_{x}}\right)}$ we can distinguish two cases:

1. $\eta{\left(p\right)}\geq\eta{\left({p_{x}}\right)}$: Then $p_{x}\in\mathbb{B}_{{\frac{3}{8}\eta{\left(p\right)}}}{\left(p\right)}$ and hence $\eta{\left({p_{x}}\right)}\ge\frac{5}{8}\eta{\left(p\right)}$ by Eq (2.36).

2. $\eta{\left(p\right)} < \eta{\left({p_{x}}\right)}$: Then $p\in\mathbb{B}_{{\frac{3}{8}\eta{\left({p_{x}}\right)}}}{\left({p_{x}}\right)}$ and hence$\eta{\left({p_{x}}\right)} > \frac{1-\frac{3}{8}}{1-\frac{6}{8}}\eta{\left(p\right)} = \frac{5}{2}\eta{\left(p\right)}$ by Eq (2.36).

and hence

Step 4: Let $k\in{\mathbb{N}}$ be fixed and define $B_{k} = \mathbb{B}_{{\frac{1}{4}\eta_{k}}}{\left({p_{k}}\right)}$, $M_{k}: = M_{\frac{1}{4}\eta_{k}}(p_{k})$. By construction, every $B_{j}$ with $B_{j}\cap B_{k}\neq\emptyset$ satisfies $\eta_{j}\geq\frac{1}{2}\eta_{k}$ and hence if $B_{j}\cap B_{k}\neq\emptyset$ and $B_{i}\cap B_{j}\neq\emptyset$ we find $\left|p_{j}-p_{i}\right|\geq\frac{1}{4}\eta_{k}$ and $\left|p_{j}-p_{k}\right|\leq3\eta_{k}$. This implies that

We further observe that the minimal surface of $B_{k}\cap\partial{\bf{P}}$ is given in case when $B_{k}\cap\partial{\bf{P}}$ is a cone with opening angle $\frac{\pi}{2}-\arctan M{\left({p_{k}}\right)}$. The surface area of $B_{k}\cap\partial{\bf{P}}$ in this case is bounded by $\frac{1}{d-1}\left|{\mathbb{S}}^{d-2}\right|\eta_{k}^{d-1}\left(M_{k}+1\right)^{2-d}$. This particularly implies up to a constant independent from $k$:

The second integral formula follows in a similar way. □

3.2.   Mesoscopic regularity and isotropic cone mixing

Lemma 3.14. Let ${\bf{P}}(\omega)$ be a stationary and ergodic random open set such that

Then there exists ${\mathfrak{r}} > 0$ and a positive, monotonically decreasing function $\tilde{f}$ such that almost surely ${\bf{P}}(\omega)$ is $({\mathfrak{r}}, \tilde{f})$-mesoscopic regular.

Proof. Step 1: For some ${\mathfrak{r}} > 0$ and with positive probability $p_{{\mathfrak{r}}} > 0$ the set $(0, 1)^{d}\cap{\bf{P}}$ contains a ball with radius $5\sqrt{d}{\mathfrak{r}}$: Otherwise, for every $r > 0$ the set $(0, 1)^{d}\cap{\bf{P}}$ almost surely would not contain an open ball with radius $r$. In particular with probability $1$ the set $(0, 1)^{d}\cap{\bf{P}}$ would not contain any ball. But then $(0, 1)^{d}\cap{\bf{P}} = \emptyset$ almost surely, contradicting the assumptions.

Step 2: We define

Due to Step 1 the stationary ergodic random measure $\tilde{\mu}_{\omega}(\, \cdot\, ): = {\mathcal{L}}{\left({\, \cdot\, \cap{\bf{P}}_{-4\sqrt{d}{\mathfrak{r}}}\left(\omega\right)}\right)}$ has positive intensity $\tilde{\lambda}_{0} > p_{{\mathfrak{r}}}\left|{\mathbb{S}}^{d-1}\left(\sqrt{d}{\mathfrak{r}}\right)^{d}\right|$. It holds further for $A\subset{\mathbb{R}^{d}}$ that $\tilde{\mu}_{\omega}(A)\neq0$ implies the existence of $\mathbb{B}_{{4\sqrt{d}{\mathfrak{r}}}}{\left(x\right)}\subset{\bf{P}}\cap\mathbb{B}_{{4\sqrt{d}{\mathfrak{r}}}}{\left(A\right)}$. We prove this using an indirect argument assuming that $\liminf_{R\to\infty}\tilde{f} > 0$. In particular, there exists for every $R > 0$ a set $\Omega_{R}\subset\Omega$ with $\tilde{\mu}_{\omega}{\left({\mathbb{B}_{R}{\left(0\right)}}\right)} = 0$ for every $\omega\in\Omega_{R}$ with $\Omega_{R+1}\subset\Omega_{R}$ and

But for almost every $\omega\in\Omega_{\infty}$ it holds by the ergodic theorem

which implies the existence of $\mathbb{B}_{{4\sqrt{d}{\mathfrak{r}}}}{\left(x\right)}\subset\mathbb{B}_{R}{\left(0\right)}\cap{\bf{P}}(\omega)$, a contradiction. □

Definition 3.15 (Isotropic cone mixing). A random set ${\bf{P}}(\omega)$ is isotropic cone mixing if there exists a jointly stationary point process ${\mathbb{X}}$ in ${\mathbb{R}^{d}}$ or in $2{\mathfrak{r}}{\mathbb{Z}^{d}}$, ${\mathfrak{r}} > 0$, such that almost surely two points $x, y\in{\mathbb{X}}$ have mutual minimal distance $2{\mathfrak{r}}$ and such that $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({{\mathbb{X}}(\omega)}\right)}\subset{\bf{P}}(\omega)$. Further there exists a function $f(R)$ with $f(R)\to0$ as ${\mathbb{R}}\to\infty$ and $\alpha\in\left(0, \frac{\pi}{2}\right)$ such that with ${\bf{E}}: = \left\{ e_{1}, \dots e_{d}\right\} \cup\left\{ -e_{1}, \dots-e_{d}\right\}$ ($\left\{ e_{1}, \dots e_{d}\right\}$ being the canonical basis of ${\mathbb{R}^{d}}$) and with the notation ${\mathbb{C}}_{e, \alpha, R}$ given in Eq (2.1)

Lemma 3.16 (A simple sufficient criterion for Eq (3.12)). Let ${\bf{P}}$ be stationary ergodic and $({\mathfrak{r}}, \tilde{f})$-regular. Then ${\bf{P}}$ is isotropic cone mixing with

and with

from Lemma 2.60. Vice versa, if ${\bf{P}}$ is isotropic cone mixing for $f$ then ${\bf{P}}$ satisfies Eq (1.6) with $\tilde{f} = f$.

Proof of Lemma 3.16. Because of ${\mathbb{P}}{\left({A\cup B}\right)}\leq{\mathbb{P}}{\left(A\right)}+{\mathbb{P}}{\left(B\right)}$ it holds for $a > 1$

The existence of $\mathbb{B}_{{4\sqrt{d}{\mathfrak{r}}}}{\left(x\right)}\subset\mathbb{B}_{R}{\left({aRe}\right)}\cap{\bf{P}}{\left({\omega}\right)}$ implies that there exists at least one $x\in{\mathbb{X}}_{{\mathfrak{r}}}\left({\bf{P}}\left(\omega\right)\right)$ such that $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left(x\right)}\subset\mathbb{B}_{R}{\left({aRe}\right)}\cap{\bf{P}}{\left({\omega}\right)}$ and we find

In particular, for $\alpha = \arctan a^{-1}$ and $R$ large enough we discover

The relation Eq (3.12) holds with $f(R) = 2d\tilde{f}{\left({\left(a+1\right)^{-1}R}\right)}$.

The other direction is evident. □

Properties of ${\mathbb{X}}$ from Lemma 3.16

The formulation of Definition 3.15 is particularly useful for the following statement.

Lemma 3.17 (Size distribution of cells). Let ${\bf{P}}(\omega)$ be a stationary and ergodic random open set that is isotropic cone mixing for ${\mathbb{X}}(\omega)$, ${\mathfrak{r}} > 0$, $f:\, (0, \infty)\to{\mathbb{R}}$ and $\alpha\in\left(0, \frac{\pi}{2}\right)$. Then ${\mathbb{X}}$ and its Voronoi tessellation have the following properties:

1. If $G(x)$ is the open Voronoi cell of $x\in{\mathbb{X}}(\omega)$ with diameter $d{\left(x\right)}$ then $d$ is jointly stationary with ${\mathbb{X}}$ and for some constant $C_{\alpha} > 0$ depending only on $\alpha$

2. For $x\in{\mathbb{X}}(\omega)$ let ${\mathcal{I}}{\left(x\right)}: = \left\{ y\in{\mathbb{X}}\, :\; G{\left(y\right)}\cap\mathbb{B}_{{{\mathfrak{r}}}}{\left({G{\left(x\right)}}\right)}\not = \emptyset\right\}$. Then

Proof. 1. For simplicity of notation let $x_{k} = 0$. The first part follows from the definition of isotropic cone mixing: We take arbitrary points $x_{\pm j}\in C_{\pm{\mathrm{e}}_{j}, \alpha, R}(0)\cap{\mathbb{X}}$. Then the planes given by the respective equations $\left(x-\frac{1}{2}x_{\pm j}\right)\cdot x_{\pm j} = 0$ define a bounded cell around $0$, with a maximal diameter $D(\alpha, R) = 2C_{\alpha}R$ which is proportional to $R$. The constant $C_{\alpha}$ depends nonlinearly on $\alpha$ with $C_{\alpha}\to\infty$ as $\alpha\to\frac{\pi}{2}$. Estimate Eq (3.14) can now be concluded from the relation between $R$ and $D(\alpha, R)$ and from Eq (3.12).

2. This follows from Lemma 2.31. □

Lemma 3.18. Let ${\mathbb{X}}_{{\mathfrak{r}}}$ be a stationary and ergodic random point process with minimal mutual distance $2{\mathfrak{r}}$ for ${\mathfrak{r}} > 0$ and let $f:\, (0, \infty)\to{\mathbb{R}}$ be such that the Voronoi tessellation of ${\mathbb{X}}$ has the property

Furthermore, let $n, s:\, {\mathbb{X}}_{{\mathfrak{r}}}\to[1, \infty)$ be measurable and i.i.d. among ${\mathbb{X}}_{{\mathfrak{r}}}$ and let $n, s, d$ be independent from each other. Let either

be the cell $G{\left(x\right)}$ enlarged by the factor $n(x)$ or a ball of radius $n(x)d(x)$ around $x$, let $d(x) = {\mathrm{diam}} G(x)$ and let

where $\eta, \xi, \zeta > 0$ are fixed a constant. Then ${\mathfrak{b}}_{n}$ is jointly stationary with ${\mathbb{X}}_{{\mathfrak{r}}}$ and for every $r > 1$ there exists $C\in(0, +\infty)$ such that

where

Corollary 3.19. Under the assumptions of Lemma 3.18 let additionally $n = const$, $s = const$. Then

Proof of Lemma 3.18. We write ${\mathbb{X}}_{{\mathfrak{r}}} = \left(x_{i}\right)_{i\in{\mathbb{N}}}$, $d_{i} = d(x_{i})$, $n_{i} = n(x_{i})$, $s_{i}: = s(x_{i})$. Let

We observe that the mutual minimal distance implies for every $x\in{\mathbb{R}^{d}}$

which follows from the uniform boundedness of cells $G_{n(x)}{\left(x\right)}$, $x\in X_{k, N}$ and the minimal distance of $\left|x_{i}-x_{j}\right| > 2{\mathfrak{r}}$. Then, writing $B_{R}: = \mathbb{B}_{R}{\left(0\right)}$ for every $y\in{\mathbb{R}^{d}}$ it holds by stationarity and the ergodic theorem

In the last inequality we made use of the fact that every cell $G_{n(x)}(x)$, $x\in X_{k, N}$, has volume smaller than ${\mathbb{S}}^{d-1}\left(N+1\right)^{d}\left(k+1\right)^{d}$. We note that for $\frac{1}{p}+\frac{1}{q} = 1$

Due to Eq (3.17) we find

and obtain for $q = \frac{p}{p-1}$ and $C_{q}: = \left(\sum_{k, N, S = 1}^{\infty}\alpha_{k, N, S}^{q}\right)^{\frac{p}{q}}\left|{\mathbb{S}}^{d-1}\right|^{p}$:

For the sum $\sum_{k, N, S = 1}^{\infty}\alpha_{k, N, S}^{q}$ to converge, it is sufficient that

for some $r > 1$. Hence, for such $r$ it holds

and thus Eq (3.16). □

4.   Extension and trace properties from $\left(\delta, M\right)$-Regularity

Remark 4.1. All calculations that follow in the present Section 4 equally work for arbitrarily distributed radii ${\mathfrak{r}}_{a}$ associated to $x_{a}$ and replacing the constant ${\mathfrak{r}}$, e.g., with

However, for simplicity of presentation, we chose to work with constant ${\mathfrak{r}}$ from the start.

4.1.   Preliminaries

For this whole section, let ${\bf{P}}$ be a Lipschitz domain which furthermore satisfies the following assumption.

Assumption 4.2. Let ${\bf{P}}$ be an open (unbounded) set and let ${\mathbb{X}}_{{\mathfrak{r}}} = \left(x_{a}\right)_{a\in{\mathbb{N}}}$ be a set of points having mutual distance $\left|x_{a}-x_{b}\right| > 2{\mathfrak{r}}$ if $a\neq b$ and with $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({x_{a}}\right)}\subset{\bf{P}}$ for every $a\in{\mathbb{N}}$ (e.g. ${\mathbb{X}}_{{\mathfrak{r}}}({\bf{P}})$, see Eq (2.53)). We construct from ${\mathbb{X}}_{{\mathfrak{r}}}$ a Voronoi tessellation and denote by $G_{a}: = G(x_{a})$ the Voronoi cell corresponding to $x_{a}$ with diameter $d_{a}$ with ${\mathfrak{A}}_{1, a}: = \mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({G_{a}}\right)}$. Let $\tilde{\Phi}_{0}\in C^{\infty}({\mathbb{R}}; [0, 1])$ be monotone decreasing with $\tilde{\Phi}_{0}' > -\frac{4}{{\mathfrak{r}}}$, $\tilde{\Phi}_{0}(x) = 1$ if $x\leq0$ and $\tilde{\Phi}_{0}(x) = 0$ for $x\geq\frac{{\mathfrak{r}}}{2}$. We define on ${\mathbb{R}^{d}}$ the Lipschitz functions

Lemma 2.20 implies

and thus Eq (4.1) yields for some $C$ depending only on $\tilde{\Phi}_{0}$, $d$ and ${\mathfrak{r}}$ that

Definition 4.3 (Weak Neighbors). Under the Assumption 4.2, two points $x_{a}, x_{b}\in{\mathbb{X}}_{{\mathfrak{r}}}$ are called to be weakly connected (or weak neighbors), written $a\sim\sim b$ or $x_{a}\sim\sim x_{b}$ if $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({G_{a}}\right)}\cap\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({G_{b}}\right)}\neq\emptyset$. For ${\bf{Q}}\subset{\mathbb{R}^{d}}$ open we say ${\mathfrak{A}}_{1, a}\sim\sim{\bf{Q}}$ if $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({{\mathfrak{A}}_{1, a}}\right)}\cap{\bf{Q}}\neq\emptyset$. We then define

In view of Assumption 4.2 we bound $\delta_{\Delta}$ by ${\mathfrak{r}} > 0$ and recall Eq (3.1). As announced in the introduction, we apply Corollary 3.8 for $n\in{\mathbb{N}}$ (we study mostly $n = 1$ and $n = 2$ in the following) to obtain a complete covering of $\partial{\bf{P}}$ by balls $\mathbb{B}_{{\tilde{\rho}_{n}\left(p_{i}^{n}\right)}}{\left({p_{i}^{n}}\right)}$, $\left(p_{i}^{n}\right)_{k\in{\mathbb{N}}}$, where $\tilde{\rho}_{n}{\left(p\right)}: = 2^{-5}\rho_{n}{\left(p\right)}$. Recalling Eqs (3.2) and (3.3) we define with $\tilde{\rho}_{n, i}: = \tilde{\rho}_{n}{\left({p_{i}^{n}}\right)}$ and $\hat{\rho}_{n, i}: = \hat{\rho}_{n, 3}{\left({p_{i}^{n}}\right)}$ with $\hat{\rho}_{n, 3}(p_{i}^{n})\leq\frac{\delta}{3}(p_{i}^{n})$ and define

where we recall the construction of ${\mathfrak{r}}_{n, \alpha, i}$ and $y_{n, \alpha, i}$ in Eqs (1.16) and (1.17) and note that $\mathbb{B}_{{\tilde{\rho}_{n, i}}}{\left({p_{i}^{n}}\right)}\supset\mathbb{B}_{{{\mathfrak{r}}_{n, \alpha, i}}}{\left({y_{n, \alpha, i}}\right)}$ independent from $\alpha$.

Lemma 4.4. For $n\in{\mathbb{N}}$, $\alpha\in[0, 1]$ and any two balls $A_{1, i}^{n}\cap A_{1, j}^{n}\neq\emptyset$ either $A_{1, i}^{n}\subset A_{2, j}^{n}$ or $A_{1, j}^{n}\subset A_{2, i}^{n}$ and

Furthermore, there exists a constant $C$ depending only on the dimension $d$ and some $\hat{d}\in[0, d]$ such that

Finally, there exist non-negative functions $\phi_{n, 0}$ and $\left(\phi_{n, i}\right)_{k\in{\mathbb{N}}}$ independent from $\alpha$ such that for $i\geq1$: ${\mathrm{supp}}\phi_{n, i}\subset A_{1, i}^{n}$, $\phi_{n, i}|_{B_{n, j}}\equiv0$ for $i\neq j$. Further, $\phi_{n, 0}\equiv0$ on all $B_{n, i}$ and on $\partial{\bf{P}}$ and $\sum_{k = 0}^{\infty}\phi_{n, i}\equiv1$ and there exists $C$ depending only on $d$ such that for all $i\in{\mathbb{N}}$ it holds

Remark 4.5. We often can improve $\hat{d}$ to at least $\hat{d} = d-1$. To see this assume $\partial{\bf{P}}$ is flat on the scale of $\delta$. Then all points $p_{i}$ lie on a $d-1$-dimensional plane and we can thus improve the argument in the following proof to $\hat{d} = d-1$.

Proof. Eq (4.6) follows from Eq (3.5). For improved readability we drop the indices $n$ and $\alpha$.

Let $k\in{\mathbb{N}}$ be fixed. By construction in Corollary 3.8, every $A_{1, j}$ with $A_{1, j}\cap A_{1, k}\neq\emptyset$ satisfies $\tilde{\rho}_{j}\geq\frac{1}{2}\tilde{\rho}_{k}$ and hence if $A_{1, j}^ {}\cap A_{1, k}\neq\emptyset$ and $A_{1, i}\cap A_{1, k}\neq\emptyset$ we find $\left|p_{j}-p_{i}\right|\geq\frac{1}{4}\tilde{\rho}_{k}$ and $\left|p_{j}-p_{k}\right|\leq3\tilde{\rho}_{k}$. This implies Eqs (4.7) and (4.8) for $A_{1, j}$ and the statement for $A_{2, j}$ follows analogously.

For two points $p_{i}$, $p_{j}$ such that $x\in A_{3, i}\cap A_{3, j}$ it holds due to the triangle inequality $\left|p_{i}-p_{j}\right|\leq\max\left\{ \frac{1}{4}\hat{\rho}_{i}, \frac{1}{4}\hat{\rho}_{j}\right\}$. Let ${\mathbb{X}}(x): = \left\{ p_{i}\in{\mathbb{X}}:\, x\in\overline{\mathbb{B}_{{\frac{1}{8}\hat{\rho}_{i}}}{\left({p_{i}}\right)}}\right\}$ and choose $\tilde{p}(x) = \tilde{p}\in{\mathbb{X}}(x)$ such that $\delta_{\text{m}}: = \delta{\left({\tilde{p}}\right)}$ is maximal. Then ${\mathbb{X}}(x)\subset\mathbb{B}_{{\frac{1}{4}\delta_{\text{m}}}}{\left({\tilde{p}}\right)}$ and every $p_{i}\in{\mathbb{X}}(x)$ satisfies $\delta_{\text{m}} > \delta_{i} > \frac{1}{3}\delta_{\text{m}}$. Correspondingly, $\tilde{\rho}_{i} > \frac{1}{3}\delta_{\text{m}}2^{-5}\tilde{M}_{\frac{\delta_{i}}{8}}^{-n} > \frac{1}{3}\delta_{\text{m}}2^{-5}\tilde{M}_{\frac{3\delta_{m}}{8}}^{-n}$ for all such $p_{i}$. In view of Eq (3.5) this lower local bound of $\tilde{\rho}_{i}$ implies a lower local bound on the mutual distance of the $p_{i}$. Since this distance is proportional to $\delta_{\text{m}}\tilde{M}_{\frac{3\delta_{m}}{8}}^{-n}$, this implies Eq (4.9) with $\hat{d} = d$. This is by the same time the upper estimate on $\hat{d}$.

Let $\phi:\, {\mathbb{R}}\to{\mathbb{R}}$ be symmetric, smooth, monotone on $(0, \infty)$ with $\phi'\leq2$ and $\phi = 0$ on $(1, \infty)$. For each $k$ we consider a radially symmetric smooth function $\hat{\phi}_{k}{\left(x\right)}: = \phi{\left({\frac{\left|x-p_{k}\right|^{2}}{\tilde{\rho}_{k}}}\right)}$ and an additional function $\tilde{\phi}_{0}\left(x\right) = {\mathrm{dist}}{\left({\, x, \, \partial{\bf{P}}\cup\bigcup_{k}B_{n, k}\, }\right)}$. In a similar way we may modify $\tilde{\phi}_{k}: = \hat{\phi}_{k}\, {\mathrm{dist}}{\left({x, \bigcup_{j\neq k}B_{n, j}}\right)}$ such that $\tilde{\phi}_{k}|_{B_{n, j}}\equiv0$ for $j\neq k$. Then we define $\phi_{k}: = \tilde{\phi}/\left(\tilde{\phi}_{0}+\sum_{j}\tilde{\phi}_{j}\right)$. Note that by construction of ${\mathfrak{r}}_{k}$ and $y_{k}$ we find $\phi_{k}|_{B_{k}}\equiv1$ and $\sum_{k\geq1}\phi_{k}\equiv1$ on $\partial{\bf{P}}$.

Estimate Eq (4.10) follows from Eq (4.7). □

4.2.   Extensions preserving the Gradient norm via $\left(\delta, M\right)$-Regularity of $\partial{\bf{P}}$

By Lemma 2.3 in case $n = 1$ there exist local extension operator

which is linear continuous with bounds

Of course, higher $n > 1$ are always valid, but the result becomes worse, as we will see.

Definition 4.6. Using Notation 1.1.6 for every ${\bf{Q}}\subset{\mathbb{R}^{d}}$ let

Due to the definitions, we find

Lemma 4.7. Let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be a Lipschitz domain (i.e. locally $\left(\delta, M\right)$-regular) with $\delta_{\Delta}$ bounded by ${\mathfrak{r}} > 0$ and let Assumption 1.8 hold and let $\hat{d}$ be the constant from (4.9). Then for every bounded open ${\bf{Q}}\subset{\mathbb{R}^{d}}$ with $\mathbb{B}_{{10{\mathfrak{r}}}}{\left(0\right)}\subset{\bf{Q}}$ and $1\leq r < p$ the linear operator

is continuous and writing

the operator ${\mathcal{U}}_{n, \alpha, {\bf{Q}}}$ satisfies for some $C$ not depending on ${\bf{P}}$

where

Remark 4.8. Since the covering $A_{1, i}$ is locally finite we find

4.3.   Extensions preserving the Symmetric Gradient norm via $\left(\delta, M\right)$–Regularity of $\partial{\bf{P}}$

By Lemmas 3.5 and 2.7 in case $n = 2$ the local extension operator

is linear continuous with bounds

Like in Section 4.2 lower values of $n$ are possible, acknowledged by Definition 1.9 of symmetric extension order.

Definition 4.9. Using the notation of Definition 1.12 let

where ${\mathcal{U}}_{n, k}$ are the extension operators on $A_{3, k}^{n}$ given by the symmetric extension order of ${\bf{P}}$.

By definition we verify ${\nabla^{s}}\left(u-\tau_{n, \alpha, i}^{{\mathfrak{s}}}u\right) = {\nabla^{s}} u$ as well as

and similarly for ${\mathcal{M}}_{a}^{{\mathfrak{s}}}u$. Furthermore, it holds

Lemma 4.10. Let ${\bf{P}}\subset{\mathbb{R}^{d}}$ be a locally $\left(\delta, M\right)$-regular open set with delta bounded by ${\mathfrak{r}} > 0$, let Assumption 1.8 hold and let $\hat{d}$ be the constant from Eq (4.9). Then for every bounded open ${\bf{Q}}\subset{\mathbb{R}^{d}}$, $1\leq r < p$ the operator

is linear, well defined and with

satisfies

where $D_{l+}^{\Phi}$ is given by Eq (4.18).

4.4.   Support

Due to Eq (4.14), even if $u\in W^{1, p}({\bf{P}}\cap\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({{\bf{Q}}}\right)}$ has boundary values $u = 0$ on $\partial{\bf{Q}}\cap{\bf{P}}$, the function ${\mathcal{U}}_{n, {\bf{Q}}}u$ can have values ${\mathcal{U}}_{n, {\bf{Q}}}u(x)$ for every $x\in\tilde{{\bf{Q}}}: = \bigcup_{x_{a}\in{\mathbb{X}}_{{\mathfrak{r}}}\cap{\bf{Q}}}\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}$, while it will be zero outside of $\tilde{{\bf{Q}}}$. For periodic geometries, however, we can assume without loss of generality that $\tilde{{\bf{Q}}}\subset\mathbb{B}_{{{\mathfrak{r}}}}{\left({{\bf{Q}}}\right)}$, while in the stochastic case the set $\tilde{{\bf{Q}}}$ can be arbitrary large, even though large $\tilde{{\bf{Q}}}$ might be unlikely. Fortunately, as the diameter of ${\bf{Q}}$ increases, the diameter of $\tilde{{\bf{Q}}}$ statistically approaches that of ${\bf{Q}}$. We can quantify this approaching via the following result.

Theorem 4.11. For $d > 1$ and for both operators given in Eqs (4.14) and (4.21) the following holds: For every bounded open set ${\bf{Q}}$ with $0\in{\bf{Q}}$ and $n_{0}, n_{1}\in{\mathbb{N}}$ let

If the mesoscopic regularity function $\tilde{f}$ of ${\bf{P}}$ satisfies $\tilde{f}(D)\leq CD^{-\frac{d-1}{\alpha}+\beta}$ for some $C > 0$, $\alpha\in(0, 1)$ and $\beta > 1$ then there exists almost surely $M_{0} > 1$ such that for every $M > M_{0}$ it holds $\tilde{{\bf{Q}}}_{M}\subset\mathbb{B}_{{M^{\alpha}}}{\left({M{\bf{Q}}}\right)}$.

Proof. We consider two balls $\mathbb{B}_{r}{\left(0\right)}\subset{\bf{Q}}\subset\mathbb{B}_{R}{\left(0\right)}$ with $r > 0$.

We write ${\bf{Q}}_{M}: = M{\bf{Q}}$ and ${\mathbb{B}}_{M, \alpha, {\bf{Q}}}: = \mathbb{B}_{{M^{\alpha}}}{\left({{\bf{Q}}_{M}}\right)}$ for $\alpha\in(0, 1)$ with ${\mathbb{B}}_{M, \alpha, {\bf{Q}}}^{\complement}: = {\mathbb{R}^{d}}\backslash{\mathbb{B}}_{M, \alpha, {\bf{Q}}}$. For $k\in{\mathbb{N}}$ we introduce

and find

On the other hand,

where $C$ depends only on the minimal mutual distance of the points, i.e. ${\mathfrak{r}}$, and the shape of ${\bf{Q}}$. Now, since $\beta > 1$ we can choose $\beta_{2} > 1$ and find

Since the right-hand side converges to $1$ as $M\to\infty$, we can conclude. □

4.5.   Proof of Lemmas 4.7 and 4.10

Lemma 4.12. Let $\alpha_{i}$, $u_{i}$, $i = 1\dots n$, be a family of real numbers such that $\sum_{i}\alpha_{i} = 0$ and let $\alpha_{+}: = \sum_{i:\, \alpha_{i} > 0}\alpha_{i}$. Then

Proof.

□

Proof of Lemma 4.7. For improved readability, we drop the indices $n$ and $\alpha$ in the following.

We prove Eq (4.16) of Lemma 4.7. Equation (4.7) can be derived in a similar but shorter way. Lemma 4.10 can be proved in a similar way with some inequalities used below being replaced by the "symmetrized" counterparts. We will make some comments towards this direction in Step 4 of this proof.

For shortness of notation (and by abuse of notation) we write

and similar for integrals over $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({{\bf{Q}}}\right)}\cap{\bf{P}}$ and $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({{\bf{Q}}}\right)}\backslash{\bf{P}}$. For simplicity of notation, we further drop the index $n = 1$ in the subsequent calculations.

We introduce the quantities

and note that $\tilde{\rho}_{i}\leq\hat{\rho}_{i}\leq\frac{1}{8}\delta_{i}$ as well as $\sqrt{4M_{i}^{2}+2}\leq2\tilde{M}_{i}$. Writing

the integral over $\nabla\left({\mathcal{U}}_{{\bf{Q}}}u\right)$ can be estimated via

Step 1: Using Eq (1.14) and $\nabla u_{i, a} = \nabla u_{i}$ as well as $\sum_{a}\Phi_{a} = 1$ we conclude

After a Hölder estimate and using $\tilde{M}_{\delta, 2, i}\leq1+M_{[\frac{1}{8}\delta], {\mathbb{R}^{d}}}$ on $A_{3, i}$, we obtain

and it only remains to estimate $\sum_{i}\chi_{A_{3, i}}(x)$.

Step 2: Concerning $I_{2}$, we first observe that for each $j\neq0$ it holds

We use $\sum_{j\in{\mathbb{N}}}\chi_{A_{1, j}}\geq1$ for every $i\in{\mathbb{N}}$ together with Eqs (4.29) and (4.7) to obtain

Note that

Furthermore $u_{i}$ and $u_{j}$ are defined on $A_{2, i}$ and $A_{2, j}$ respectively and $u_{i} = u_{j}$ on $\mathbb{B}_{{{\mathfrak{r}}_{j}}}{\left({p_{j}}\right)}$ and $\mathbb{B}_{{{\mathfrak{r}}_{i}}}{\left({p_{i}}\right)}$ because of Eq (4.6). Furthermore, both functions can be extended from $A_{2, i}$ and $A_{2, j}$ to $\tilde{u}_{i}$ and $\tilde{u}_{j}$ on $\mathbb{B}_{{4\tilde{\rho}_{i}}}{\left({p_{i}}\right)}$ and $\mathbb{B}_{{4\tilde{\rho}_{j}}}{\left({p_{j}}\right)}$ respectively using Lemma 2.1 such that for some $C$ independent from $i, j$

Since now $\tilde{u}_{i} = \tilde{u}_{j}$ on $\mathbb{B}_{{{\mathfrak{r}}_{j}}}{\left({p_{j}}\right)}$ and $\mathbb{B}_{{{\mathfrak{r}}_{i}}}{\left({p_{i}}\right)}$ we chose $k(i, j)$ such that for $\tilde{M}_{k(i, j)} = 1+\min\left\{ M_{\tilde{\rho}, i}, M_{\tilde{\rho}, j}\right\}$ and it holds by the Poincaré inequality (2.14), the microscopic regularity $\alpha$ and the estimate Eq (3.4)

We obtain with microscopic regularity $\alpha$, the finite covering Eq (4.8) and the proportionality (3.5) that

Next we estimate from Jensens inequality with $\sum_{a}\Phi_{a}, \sum_{j\neq0}\phi_{j}\leq1$ and Eq (4.10)

Using once more Assumption 1.8 as well as

and $\sum_{a}\Phi_{a} = 1$ we infer from Eq (2.14)

Now we make use of the extension estimate Eq (1.14) to find

which in total implies for $f_{12}(M) = \left(1+M_{[\frac{1}{8}\delta], {\mathbb{R}^{d}}}\right)^{\frac{rp}{p-r}}\left(1+M_{[\tilde{\rho}], {\mathbb{R}^{d}}}\right)^{\frac{p\alpha(d-1)}{p-r}}$

Making use of Eq (4.9) we find

and it only remains to estimate $I_{3}$.

Step 3: We observe with help of $\sum_{a}\nabla\Phi_{a} = 0$ and $\sum_{i\neq0}\phi_{i} = 1-\phi_{0}$ that

and Lemma 4.12 yields

Step 4: Concerning the proof of Lemma 4.10 we follow the above lines with the following modifications.

We use the Nitsche extension operators. Hence, instead of Eq (1.14) we use Eq (1.15). The local extended functions are called

and Eq (4.30) remains valid. We find it worth mentioning that ${\nabla^{s}}\left(\tau_{i}^{{\mathfrak{s}}}u-{\mathcal{M}}_{a}^{{\mathfrak{s}}}u\right) = 0$ and hence

We furthermore replace Lemma 2.1 by Lemma 2.6 and the Poincaré inequality (2.14) by (2.23). Finally we observe that Eq (4.31) is replaced by

□

4.6.   Traces on $\left(\delta, M\right)$-Regular Sets, Proof of Theorem 1.7

Proof. We use the covering of $\partial{\bf{P}}$ by $B_{i}: = A_{1, i}^{1}$ and set $\tilde{\rho}_{i}: = \tilde{\rho}_{1, i}$, $\hat{\rho}_{i}: = \hat{\rho}_{i, 5}(p_{i}^{1})$ and write $M_{i} = M_{\hat{\rho}_{i}}(p_{i}^{1})$, $\hat{B}_{i}: = \mathbb{B}_{{\hat{\rho}_{i}}}{\left({p_{i}^{1}}\right)}$. Due to Lemma 2.5 we find locally

We thus obtain

which yields by the uniform local bound of the covering, $\tilde{\eta}$ defined in Lemma 3.12, twice the application of Eqs (3.10) and (4.32)

With Hölders inequality and replacing $M_{k}$ by $M_{[\frac{1}{32}\delta], {\mathbb{R}^{d}}}$, the last estimate leads to Eq (1.12). The second estimate goes analogue since the local covering by $A_{2, k}$ is finite. □

5.   The issue of connectedness

Remark 5.1. The following Lemmas 5.2 and 5.3 also hold with $\tau_{i}$ and ${\mathcal{M}}_{a}$ replaced by $\tau_{i}^{{\mathfrak{s}}}$ and ${\mathcal{M}}_{a}^{{\mathfrak{s}}}$ respectively.

Lemma 5.2. Under Assumptions 1.8, 4.2 let $\left(f_{j}\right)_{j\in{\mathbb{N}}}$ be non-negative and have support ${\mathrm{supp}} f_{j}\supset\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({x_{j}}\right)}$ and let $\sum_{j\in{\mathbb{N}}}f_{j}\equiv1$.

Writing ${\mathbb{X}}({\bf{Q}}): = \left\{ x_{j}:\; {\mathrm{supp}} f_{j}\cap{\bf{Q}}\neq\emptyset\right\}$, and

for every $l = 1, \dots d$ and $r < \tilde{s} < s$ it holds

and

Proof. We find from Hölder's and Jensen's inequality

The second part follows accordingly. □

Lemma 5.3. Under Assumptions 1.8, 4.2 for every $l = 1, \dots d$ and $\tilde{\alpha} > 0$ it holds

with the similar formula holding for ${\mathcal{M}}_{\bullet}$ replaced by ${\mathcal{M}}_{\bullet}^{{\mathfrak{s}}}$.

Proof. We observe with help of Eq (4.3) and with Lemma 3.17.2)

We write

and find

Now we make use of Eq (5.1) and once more of Lemma 3.17.2) to obtain for the first bracket on the right-hand side an estimate of the form

which implies

where we used $\sum\left|\partial_{l}\Phi_{k}\right| = D_{l+}^{\Phi}$. From Hölder's inequality the Lemma follows. □

6.   Sample geometries

6.1.   Delaunay pipes for a matern process

For two points $x, y\in{\mathbb{R}^{d}}$, we denote

the cylinder (or pipe) around the straight line segment connecting $x$ and $y$ with radius $r > 0$.

Recalling Example 2.49 we consider a Poisson point process ${\mathbb{X}}_{{\mathrm{pois}}}(\omega) = \left(x_{i}(\omega)\right)_{i\in{\mathbb{N}}}$ with intensity $\lambda$ (recall Example 2.49) and construct a hard core Matern process ${\mathbb{X}}_{{\mathrm{mat}}}$ by deleting all points with a mutual distance smaller than $d{\mathfrak{r}}$ for some ${\mathfrak{r}} > 0$ (refer to Example 2.50). From the remaining point process ${\mathbb{X}}_{{\mathrm{mat}}}$ we construct the Delaunay triangulation ${\mathbb{D}}(\omega): = {\mathbb{D}}(X_{{\mathrm{mat}}}(\omega))$ and assign to each $(x, y)\in{\mathbb{D}}$ a random number $\delta(x, y)$ in $(0, {\mathfrak{r}})$ in an i.i.d. manner from some probability distribution $\delta(\omega)$. We finally define

the family of all pipes generated by the Delaunay grid "smoothed" by balls with the fix radius ${\mathfrak{r}}$ around each point of the generating Matern process.

Since the Matern process is mixing and $\delta$ is mixing, Lemma 2.35 yields that the whole process is still ergodic. We start with a trivial observation.

Corollary 6.1. The microscopic regularity of ${\bf{P}}$ is $\alpha = 0$ (Def. 1.8) and it holds $\hat{d} = d-1$ in Lemma 4.4. Furthermore both the extension order and the symmetric extension order are $n = 0$. In particular, it holds

with $C$ independent from $i$.

Proof. This follows from the fact that $\partial{\bf{P}}$ can be locally represented as a graph in the upper half space with ${\bf{P}}$ filling the lower half space. □

Lemma 6.2. For the Voronoi tessellation $\left(G_{a}\right)_{a\in{\mathbb{N}}}$ corresponding to ${\mathbb{X}}_{{\mathrm{mat}}}$ holds

Proof. For the underlying Poisson point process ${\mathbb{X}}_{{\mathrm{pois}}}$ it holds for the void probability inside a ball $\mathbb{B}_{R}{\left(x\right)}$

The probability for a point $x\in{\mathbb{X}}_{{\mathrm{pois}}}$ to be removed is thus $1-{\mathbb{P}}_{d{\mathfrak{r}}, 0}$ and is i.i.d distributed among points of ${\mathbb{X}}_{{\mathrm{pois}}}$. The total probability to not find any point of ${\mathbb{X}}_{{\mathrm{mat}}}$ in $\mathbb{B}_{R}{\left(x\right)}$ is thus given by not finding a point of ${\mathbb{X}}_{{\mathrm{pois}}}$ plus the probability that all points of ${\mathbb{X}}_{{\mathrm{pois}}}$ are removed, i.e.

From here one concludes. □

Remark 6.3. The family of balls $\mathbb{B}_{{{\mathfrak{r}}/2}}{\left(x\right)}$ can also be dropped from the model ${\bf{P}}$. However, this would imply ${\mathbb{X}}_{{\mathfrak{r}}}\not = {\mathbb{X}}_{{\mathrm{mat}}}$ and would cause technical difficulties which would not change much in the result, as the probability for the size of Voronoi cells would still decrease exponentially.

Lemma 6.4. ${\mathbb{X}}_{{\mathrm{mat}}}$ is a point process for ${\bf{P}}(\omega)$ that satisfies Assumption 4.2 and ${\bf{P}}$ is isotropic cone mixing for ${\mathbb{X}}_{{\mathrm{mat}}}$ with exponentially decreasing $f(R)\leq Ce^{-R^{d}}$ and it holds $n = 0$ and $\alpha = 0$. Furthermore, assume there exists $C_{\delta}, a_{\delta} > 0$ such that ${\mathbb{P}}(\delta(x, y) < \delta_{0})\leq C_{\delta}e^{-a_{\delta}\frac{1}{\delta_{0}}}$, then ${\mathbb{P}}(\tilde{M} > M_{0})\leq Ce^{-aM_{0}}$ for some $C, a > 0$. If ${\mathbb{P}}(\delta(x, y) < \delta_{0})\leq C_{\delta}\delta_{0}^{\beta}$ then for every $R\in(0, \infty)$ it holds

where ${\mathbb{E}}{\left({\left|x-y\right|}\right)}$ is the expectation of the length of pipes.

Proof. Isotropic cone mixing: For $x, y\in2d{\mathfrak{r}}{\mathbb{Z}^{d}}$ the events $\left(x+[0, 1]^{d}\right)\cap{\mathbb{X}}_{{\mathrm{mat}}}$ and $\left(y+[0, 1]^{d}\right)\cap{\mathbb{X}}_{{\mathrm{mat}}}$ are mutually independent, implying

Hence the open set ${\bf{P}}$ is isotropic cone mixing for ${\mathbb{X}} = {\mathbb{X}}_{{\mathrm{mat}}}$ with exponentially decaying $f(R)\leq Ce^{-R^{d}}$.

Estimate on the distribution of $M$: By definition of the Delaunay triangulation, two pipes intersect only if they share one common point $x\in{\mathbb{X}}_{{\mathrm{mat}}}$.

Given three points $x, y, z\in{\mathbb{X}}_{{\mathrm{mat}}}$ with $x\sim y$ and $x\sim z$, the highest local Lipschitz constant on $\partial\left(P_{\delta(x, y)}(x, y)\cup P_{\delta(x, z)}(x, z)\right)$ is attained in

It is bounded by

where $\alpha: = \sphericalangle\left((x, y), (x, z)\right)$ in the following denotes the angle between $(x, y)$ and $(x, z)$, see Figure 7. If $d_{x}$ is the diameter of the Voronoi cell of $x$, we show that a necessary (but not sufficient) condition that the angle $\alpha$ can be smaller than some $\alpha_{0}$ is given by

where $C > 0$ is a constant depending only on the dimension $d$. Since for small $\alpha$ we find $M\approx\frac{1}{\sin\alpha}$, and since the distribution for $d_{x}$ decays sub-exponentially, also the distribution for $M$ at the junctions of two pipes decays sub-exponentially. However, inside the pipes, we find $\delta_{\Delta}(p) = \delta(x, y)$. Due to the cylindrical structure, we furthermore find essential boundedness of $M$. This also implies $\alpha = n = 0$ inside the pipes. At the junction of Balls and pipes we find $\partial{\bf{P}}$ to be in the upper half of the local plane approximation and hence also here $\alpha = n = 0$ can be chosen (see also Remarks 2.4 and 2.8).

Concerning the expectation of $M_{[\frac{\delta}{2}], {\mathbb{R}^{d}}}$ and $\delta_{{\mathbb{R}^{d}}}$, we only have to account for the pipes by the above argumentation since the contribution to $M$ by the balls is exponentially distributed. In particular, we find for one single pipe $P_{\delta(x, y)}(x, y)$ that

and hence Eq (6.3) due to the mutual independence of $\left|x-y\right|$ and diameter $\delta(x, y)$. It thus remains to proof Eq (6.4).

Proof of Eq (6.4): Given an angle $\alpha > 0$ and $x\in{\mathbb{X}}_{{\mathrm{mat}}}$ we derive a lower bound for the diameter of $G(x)$ such that for two neighbors $y, z$ of $x$ it can hold $\sphericalangle\left((x, y), (x, z)\right)\leq\alpha$. With regard to Figure 7, we assume $\left|x-y\right|\geq\left|x-z\right|$.

Writing $d_{x}: = d(x)$ the diameter of $G(x)$ and $\tilde{\alpha} = \sphericalangle\left((x, z), (z, y)\right)$, let $y = (d_{1}+d_{2}, 0, \dots, 0)$, where $d_{1}+d_{2} < d_{x}$ and $d_{1} = \left|y-z\right|\cos\tilde{\alpha}$, $d_{2} = \left|y-z\right|\cos\alpha$. Hence we can assume $z = (d_{2}, -\left|y-z\right|\sin\tilde{\alpha}, 0, \dots, 0)$ and in what follows, we focus on the first two coordinates only. The boundaries between the cells $x$ and $z$ and $x$ and $y$ lie on the planes

respectively. The intersection of these planes has the first two coordinates

Using the explicit form of $d_{2}$, the latter point has the distance

to the origin $x = 0$. Using $\left|y-z\right|\sin\tilde{\alpha} = \left|z\right|\sin\alpha$ and $d_{2} = \left|y\right|-\left|z\right|\cos\alpha$ we obtain

Given $y$, the latter expression becomes small for $\left|y-z\right|$ small, with the smallest value being $\left|y-z\right| = d{\mathfrak{r}}$. But then

and hence the distance becomes

We finally use $\left|y\right| = \left|z\right|\cos\alpha-\sqrt{\left(d{\mathfrak{r}}\right)^{2}-\left|z\right|^{2}\sin^{2}\alpha}$ and obtain

The latter expression now needs to be smaller than $d_{x}$. We observe that the expression on the right-hand side decreases for fixed $\alpha$ if $\left|z\right|$ increases.

On the other hand, we can resolve $\left|z\right|(y) = \left|y\right|\cos\alpha-\sqrt{\left|y\right|^{2}\sin^{2}\alpha+\left(d{\mathfrak{r}}\right)^{2}}$. From the conditions $\left|y\right|\leq d_{x}$ and $\left|i_{xyz}\right|\leq d_{x}$, we then infer Eq (6.4). □

Theorem 6.5. Assuming ${\mathbb{E}}{\left({\delta^{-s-d}+\delta^{1+s-2d}}\right)}^{\frac{p}{p-s}} < \infty$ and using the notation of Lemma 5.2 ${\bf{P}}$ from 6.1 has the property that for $1\leq r < s < p$ there almost surely exists $C > 0$ such that for every $n\in{\mathbb{N}}$ and every $u\in W_{0, \partial(n{\bf{Q}})}^{1, p}({\bf{P}}\cap n{\bf{Q}})$

and for every $u\in{\bf{W}}_{0, \partial(n{\bf{Q}})}^{1, p}({\bf{P}}\cap n{\bf{Q}})$

Lemma 6.6. For every bounded open set ${\bf{Q}}$ with $0\in{\bf{Q}}$ and $n_{0} < n_{1}\in{\mathbb{N}}$ let

Then for fixed $n_{0}$ and $n_{1}$ there almost surely exists $r > 0$ such that for every $M > 1$ it holds $\tilde{{\bf{Q}}}_{M, n_{0}, n_{1}}\subset Mr{\bf{Q}}$

Proof. There exists $r_{0} < R$ such that $\mathbb{B}_{{r_{0}}}{\left(0\right)}\subset{\bf{Q}}\subset\mathbb{B}_{R}{\left(0\right)}$ and we assume without loss of generality that ${\bf{Q}} = \mathbb{B}_{R}{\left(0\right)}$. We denote ${\bf{Q}}_{M}: = M{\bf{Q}}$ and observe that $\frac{\left|\partial{\bf{Q}}_{M}\right|}{\left|{\bf{Q}}_{M}\right|}\leq C\, M^{-1}$ where $\left|\partial{\bf{Q}}_{M}\right|: = {\mathcal{H}}^{d-1}(\partial{\bf{Q}}_{M})$. For

we observe that $\#{\left({{\bf{Q}}_{M, a, b}\cap{\mathbb{X}}_{{\mathrm{mat}}}}\right)}\leq CM^{d-1}(b-a)$ due to the minimal mutual distance. The probability that at least one $x\in{\bf{Q}}_{M, a, b}\cap{\mathbb{X}}_{{\mathrm{mat}}}$ satisfies $\mathbb{B}_{{n_{0}d(x)}}{\left(x\right)}\cap{\bf{Q}}_{M}\neq\emptyset$ is given by

Now let $r > 0$ and observe $\left|{\bf{Q}}_{M, a, b}\right|\leq C\, (b-a)\, \left(b+MR\right)^{d-1}$ while ${\mathbb{P}}{\left({d > \frac{a}{n_{0}}}\right)}\leq Ce^{-\alpha\, a^{d}}$. Then the probability that there exists $x\in{\mathbb{X}}_{{\mathrm{mat}}}\backslash{\bf{Q}}_{rM}$ such that $\mathbb{B}_{{n_{0}d(x)}}{\left(x\right)}\cap{\bf{Q}}_{M}\neq\emptyset$ is smaller than

and the right-hand side tends uniformly to $0$ as $r\to\infty$. □

Proof of Theorem 6.5. In what follows, we will mostly perform the calculations for $\tau_{i}^{{\mathfrak{s}}}$ and ${\mathcal{M}}_{a}^{{\mathfrak{s}}}$ since these calculations are more involved and drop the index $n$ in the definition except for the last Step 5.

We first estimate the difference $\left|{\mathcal{M}}_{a}^{{\mathfrak{s}}}u-{\mathcal{M}}_{b}^{{\mathfrak{s}}}u\right|$ for two directly neighbored points $x_{a}\sim x_{b}$ of the Delaunay grid. These are connected through a cylindrical pipe

with round ends and of thickness $\delta(a, b)$ and total length $\left|x_{a}-x_{b}\right|+2\delta(a, b) < 2\left|x_{a}-x_{b}\right|$ and we first introduce the new averages in the spirit of Eq (2.27)

As for Eqs (4.15) and (4.22) we obtain

For every $i, a\in{\mathbb{N}}$ with $p_{i}\in\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}$ there exists almost surely $a_{i}\in{\mathbb{N}}$ such that $p_{i}$ and $x_{a_{i}}$ are connected in ${\bf{P}}$ through a straight line segment (i.e. $p_{i}$ lies on the boundary of one of the pipes emerging at $x_{a_{i}}$ or in $\mathbb{B}_{{{\mathfrak{r}}}}{\left({x_{a_{i}}}\right)}$) and

The second terms on the right-hand sides are of "mesoscopic type", while the first terms are of local type. We will study both separately in Steps 1 and 2.

Step 1: Using Eqs (2.28) and (2.29), we observe for neighbors $a\sim b$

where

Step 2: For reasons that we will encounter below, we define

Recalling the notations of Section 4.1 we assume $\chi_{\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}}\chi_{A_{1, i}}\not\equiv0$. Then it holds $p_{i}\in\mathbb{B}_{{2d_{a_{i}}}}{\left({x_{a_{i}}}\right)}$ which implies for $f_{a}$ from Lemma 5.2

Hence, for $a, b$ making a non-zero contribution to Eq (6.8), we encounter the conditions $\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}\cap{\bf{Q}}\neq\emptyset$ and $\mathbb{B}_{{2d_{b}}}{\left({x_{b}}\right)}\cap\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}\neq\emptyset$ as well as

In particular, this is covered by the more general and symmetric condition

and with respect to Eq (6.7)

Similarly

Step 3: We now derive an estimate for $I_{\alpha}$. For pairs $(a, b)$ with $d_{b}\leq d_{a}, \, \left|x_{a}-x_{b}\right|\leq3d_{a}$ let $y_{a, b}: = \left(y_{1}, \dots, y_{n(a, b)}\right)$ be a discrete path on the Delaunay grid of ${\mathbb{X}}_{{\mathrm{mat}}}$ with length smaller than $2\left|x_{a}-x_{b}\right|$ (this exists due to ^[28]) that connects $x_{a}$ and $x_{b}$. By the minimal mutual distance of points, this particularly implies that $n(a, b)\leq6d_{a}/2{\mathfrak{r}}$ and the path lies completely within $\mathbb{B}_{{4.5\, d_{a}}}{\left({x_{a}}\right)}$. Because

it holds with Eq (6.5)

We make use of $\left|x-x_{e}\right|^{s}\leq2^{s}\left(\left|x-x_{a}\right|^{s}+\left|x_{a}-x_{e}\right|^{s}\right)\leq2^{s}\left(\left|x-x_{a}\right|^{s}+d_{a}^{s}\right)$ and $\left|x_{e}-x_{f}\right|^{2s}\leq Cd_{a}^{2s}$ and $B_{e, f}: = \mathbb{B}_{{\frac{{\mathfrak{r}}}{16}}}{\left({\{x_{e}, x_{f}\}}\right)}\cup P_{\delta, e, f}$ to find

In the integrals $I_{\alpha}$, any of the integrals $\int\chi_{\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}}\left|{\mathcal{M}}_{a}^{{\mathfrak{s}}}u-{\mathcal{M}}_{b}^{{\mathfrak{s}}}u\right|^{s}{\mathrm{d}} x$ has $\left|x-x_{a}\right| < 2d_{a}$ and we have an estimate of the form

With this estimate, and using

the integral $I_{\alpha}$ can be controlled through

Denoting

and using $u\equiv0$ outside ${\bf{Q}}$, we observe

Step 4: We observe

and for every fixed $x$ (and using that $x\in\mathbb{B}_{{2d_{a_{i}}}}{\left({x_{a_{i}}}\right)}$) using again Jensens inequality

Having this in mind and using Eq (6.2), we may sum over all $y_{i}$ to find

With the splitting $u-{\mathcal{M}}_{a}^{{\mathfrak{s}}}u = u-{\mathcal{M}}_{a}^{{\mathfrak{s}}, \delta(a, b)}u+{\mathcal{M}}_{a}^{{\mathfrak{s}}, \delta(a, b)}u-{\mathcal{M}}_{a}^{{\mathfrak{s}}}u$ and Lemmas 2.18 and 2.17 it follows with $F_{s}^{{\mathfrak{s}}, 1}$ from Eq (6.6)

Restructuring the right-hand side similar to (6.11)$\Rightarrow$(6.12), the right-hand side is bounded by

where

Step 5: We can replace in the above calculations ${\bf{Q}}$ by $n{\bf{Q}}$. By Lemma 6.6 we can extend $f(\omega, n{\bf{Q}})$ to $f(\omega)|_{Rn{\bf{Q}}}$ for some fixed $R > 1$ and on $R{\bf{Q}}$ we can use standard ergodic theory. Hence, the expressions in $\delta$ and $d_{a}$ converge to a constant as $n\to\infty$ provided

However, $f$, $f_{1}$ and $g$ are stationary by definition and $f$ and $g$ or $f_{1}$ and $g$ are independent. Since $f$ and $f_{1}$ clearly have finite expectation by the exponential distribution of $d_{a}$ and Lemma 3.18, we only mention that due to the strong mixing of $\delta$ and its independence from the distribution of connections

and thus Eq (6.13) holds. □

The work ^[28] which we used in the last proof also opens the door to demonstrate the following result which will be used in part Ⅲ of this series to prove regularity properties of the homogenized equation.

Theorem 6.7. For fixed $y_{0}\in{\mathbb{X}}_{{\mathrm{mat}}}$ and every $\tilde{y}\in{\mathbb{X}}_{{\mathrm{mat}}}$ let

with $y_{N}(\tilde{y}) = \tilde{y}$ be the shortest path of points in ${\mathbb{X}}_{{\mathrm{mat}}}$ connecting $y_{0}$ and $\tilde{y}$ in ${\bf{P}}$ and having length $L(y_{0}, \tilde{y})$. Then there exists

such that $\gamma_{y_{0, }\tilde{y}}(t, \cdot)$ is invertible for every $t$ and $\left\Vert {\partial_{t}\gamma_{y_{0, }\tilde{y}}}\right\Vert_{\infty}\leq2$. For $R > 1$ let

Then there exists $C > 0$ such that for every $y_{0}$ it holds

Proof. The function $\gamma_{y_{0, }\tilde{y}}$ consists basically of pipes connecting $y_{i}(\tilde{y})$ with $y_{i+1}(\tilde{y})$ that conically become smaller within the ball $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({y_{i}(\tilde{y})}\right)}$ before entering the pipe and vice versa in $\mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({y_{i+1}(\tilde{y})}\right)}$. Defining

^[28] implies $N_{y_{0}, r, R}(x) = 0$ for all $\left|x-y_{0}\right| > 2R$ but also due to the minimal mutual distance $N_{y_{0}, r, R}(x)\leq CR^{d-1}(R-r)$, where $C$ depends only on ${\mathfrak{r}}$ and $d$. Hence writing $\left\lfloor x\right\rfloor : = \min\left\{ n\in{\mathbb{N}}:\, n+1 > x\right\}$ we can estimate for every $K\in{\mathbb{N}}$

□

We close this section by proving Theorem 1.15.

Proof of Theorem 1.15. The statement on the support is provided by Theorem 4.11 and the fact that we restrict to functions with support in $m{\bf{Q}}$. Hence in the following we can apply all cited results to $\mathbb{B}_{{m^{1-\beta}}}{\left({m{\bf{Q}}}\right)}$ instead of $m{\bf{Q}}$. According to Lemmas 4.7 and 5.2, 5.3 and to Theorem 6.5 we need only need to ensure

since $d_{a}$ is distributed exponentially and the corresponding terms are bounded as long as $r\neq s\neq p$. We note that the exponential distribution of $M$ allows us to restrict to the study of $\delta$ and $\tilde{\rho}$.

According to Lemma 6.4 it is sufficient that $\max\left\{ \frac{p\left(s+d\right)}{p-s}, \frac{p(2d-s-1)}{p-s}\right\} \leq\beta$ and $\frac{sr}{s-r}\leq\beta+d-1$. □

6.2.   Boolean Model for the Poisson Ball Process

The following argumentation will be strongly based on the so called void probability. This is the probability ${\mathbb{P}}_{0}(A)$ to not find any point of the point process in a given open set $A$ and is given by Eq (2.51) i.e., ${\mathbb{P}}_{0}(A): = e^{-\lambda\left|A\right|}$. The void probability (which we recall to be the probability that no ball intersects with $A\subset{\mathbb{R}^{d}}$) for the ball process is given accordingly by

Theorem 6.8. Let ${\bf{P}}\left(\omega\right): = \bigcup_{i}B_{i}(\omega)$ (or ${\bf{P}}\left(\omega\right): = {\mathbb{R}^{d}}\backslash\bigcup_{i}B_{i}(\omega)$). Then $\partial{\bf{P}}$ is almost surely locally $\left(\delta, M\right)$ regular and we can define

where $\min\emptyset: = 0$ for convenience. For every $\gamma < 1$, $\beta < d+2$ it holds

Furthermore, it holds $\hat{d}\le d-1$ and $\alpha = 0$ in inequalities (4.9) and (4.4). Furthermore the extension order and symmetric extension order are both $n = 0$. If ${\bf{P}}\left(\omega\right): = {\mathbb{R}^{d}}\backslash\overline{\bigcup_{i}B_{i}}(\omega)$ the above holds with $\alpha$ replaced by $1$ and with extension order $n = 1$ and symmetric extension order $n = 2$.

Remark 6.9. In view of the influence of $\alpha$ and $n$ on the $r$-$p$-ratio given by Lemmas 4.7 4.10 we observe that the union of balls has better properties than the complement.

Proof. We study only ${\bf{P}}\left(\omega\right): = \bigcup_{i}B_{i}(\omega)$ since ${\mathbb{R}^{d}}\backslash\overline{\bigcup_{i}B_{i}}(\omega)$ is the complement sharing the same boundary. Hence, in case ${\bf{P}}(\omega) = {\mathbb{R}^{d}}\backslash\overline{\bigcup_{i}B_{i}}(\omega)$, all calculations remain basically the same. However, in the first case, it is evident that $\alpha = 0$ and $n = 0$ because the geometry has only cusps and no dendrites and we refer to Remarks 2.4 and 2.8.

In what follows, we use that the distribution of balls is mutually independent. That means, given a ball around $x_{i}\in{\mathbb{X}}_{{\mathrm{pois}}}$, the set ${\mathbb{X}}_{{\mathrm{pois}}}\backslash\left\{ x_{i}\right\}$ is also a Poisson process. By translation invariance, we assume $x_{i} = x_{0} = 0$ with $B_{0}: = \mathbb{B}_{1}{\left(0\right)}$. First we note that $p\in\partial B_{0}\cap\partial{\bf{P}}$ if and only if $p\in\partial B_{0}\backslash{\bf{P}}$, which holds with probability ${\mathbb{P}}_{0}{\left({\mathbb{B}_{1}{\left(p\right)}}\right)} = {\mathbb{P}}_{0}{\left({B_{0}}\right)}$. This is a fixed quantity, independent from $p$.

Now assuming $p\in\partial B_{0}\backslash{\bf{P}}$, the distance to the closest ball besides $B_{0}$ is denoted

with a conditioned probability distribution

It is important to observe that $\partial B_{0}$ is $r$-regular in the sense of Lemma 2.24. Another important feature in view of Lemma 3.2 is $r(p) < 2\delta(p)$. In particular, $\delta^{-1}(p) < 2r^{-1}(p)$ and $\partial B_{0}$ is $(\delta, 1)$-regular in case $\delta < \sqrt{\frac{1}{2}}$. Hence, in what follows, we will derive estimates on $r^{-\gamma}$, which immediately imply estimates on $\delta^{-\gamma}$.

Estimate on $\gamma$: A lower estimate for the distribution of $r(p)$ is given by

This implies that almost surely for $\gamma < 1$

i.e., ${\mathbb{E}}{\left({\delta^{-\gamma}}\right)} < \infty$.

Intersecting balls: Now assume there exists $x_{i}$, $i\neq0$ such that $p\in\partial B_{i}\cap\partial B_{0}$ and for readability assume $x_{i} = x_{1}: = (2x, 0, \dots, 0)$ and $p = \left(x, \sqrt{1-x^{2}}, 0, \dots, 0\right)$. Then

and $p$ is at least $M(p) = \frac{x}{\sqrt{1-x^{2}}}$-regular. Again, a lower estimate for the probability of $r$ is given by Eq (6.14) on the interval $(0, \delta_{0})$. Above this value, the probability is approximately given by $\lambda\left|{\mathbb{S}}^{d-1}\right|\delta_{0}$ (for small $\delta_{0}$ i.e., $x\approx1$). We introduce as a new variable $\xi = 1-x$ and obtain from $1-x^{2} = \xi(1+x)$ that

No touching: Assume now that two balls "touch" each other, i.e., we would have $x = 1$ in the previous step and for every ${\varepsilon} > 0$ we had $x_{1}\in\mathbb{B}_{{2+{\varepsilon}}}{\left({x_{0}}\right)}\backslash\mathbb{B}_{{2-{\varepsilon}}}{\left({x_{0}}\right)}$. But

Therefore, the probability that two balls "touch" (i.e., that $x = 1$) is zero. The almost sure local boundedness of $M$ now follows from the countable number of balls.

Estimate on $\tilde{\delta}$: We again study each ball separately. Let $p\in\partial B_{0}\backslash\overline{{\bf{P}}}$ with tangent space $T_{p}$ and normal space $N_{p}$. Let $x\in N_{p}$ and $\tilde{p}\in\partial B_{0}$ such that $x\in\mathbb{B}_{{\frac{1}{8}\delta(\tilde{p})}}{\left({\tilde{p}}\right)}$, then also $p\in\mathbb{B}_{{\frac{1}{8}\delta(\tilde{p})}}{\left({\tilde{p}}\right)}$ and $\delta(p)\in(\frac{7}{8}, \frac{7}{6})\delta(\tilde{p})$ and $\delta(\tilde{p})\in(\frac{7}{8}, \frac{7}{6})\delta(p)$ by Lemma 2.24. Defining

we find

Studying $\delta_{0}$ on $\partial B_{0}$ we can assume $M\leq M_{0}$ in Eq (3.8) and we find

Hence we find

Estimate on $\beta$: For two points $x_{i}, x_{j}\in{\mathbb{X}}_{{\mathrm{pois}}}$ let $\mathrm{Circ}_{ij}: = \partial B_{i}\cap\partial B_{j}$ and $\mathbb{B}_{{\frac{1}{8}\tilde{\delta}}}{\left({\mathrm{Circ}_{ij}}\right)}: = \bigcup_{p\in\mathrm{Circ}_{ij}}\mathbb{B}_{{\frac{1}{8}\tilde{\delta}(p)}}{\left(p\right)}$. For the fixed ball $B_{i} = B_{0}$ we write $\mathrm{Circ}_{0j}$ and obtain $\left|\mathrm{Circ}_{0j}\right|\leq C\delta_{0}^{d}$ with $\delta_{0}$ from Eq (6.15). Therefore, we find

We now derive an estimate for ${\mathbb{E}}{\left({\int_{\mathbb{B}_{{1+{\mathfrak{r}}}}{\left(0\right)}}\tilde{M}^{\beta}}\right)}.$ To this aim, let $q\in(0, 1)$. Then $x\in\mathbb{B}_{{2-q^{k+1}}}{\left(0\right)}\backslash\mathbb{B}_{{2-q^{k}}}{\left(0\right)}$ implies $\xi\geq q^{k+1}$ and

The only random quantity in the latter expression is $\#\left\{ x_{j}\in\mathbb{B}_{{2-q^{k+1}}}{\left(0\right)}\backslash\mathbb{B}_{{2-q^{k}}}{\left(0\right)}\right\}$. Therefore, we obtain with ${\mathbb{E}}{\left({{\mathbb{X}}(A)}\right)} = \lambda\left|A\right|$ that

Since the point process has finite intensity, this property carries over to the whole ball process and we obtain the condition $\beta < d+2$ in order for the right-hand side to remain bounded.

Estimate on $\hat{d}$: We have to estimate the local maximum number of $A_{3, k}$ overlapping in a single point in terms of $\tilde{M}$. We first recall that $\hat{\rho}(p)\approx8\tilde{M}(p)\tilde{\rho}(p)$. Thus large discrepancy between $\hat{\rho}$ and $\tilde{\rho}$ occurs in points where $\tilde{M}$ is large. This is at the intersection of at least two balls. Despite these "cusps", the set $\partial{\bf{P}}$ consists locally on the order of $\hat{\rho}$ of almost flat parts. Arguing like in Lemma 4.4 resp. Remark 4.5 this yields $\hat{d}\leq d-1$. □

It remains to verify bounded average connectivity of the Boolean set ${\bf{P}}_{\infty}$ or its complement. Associated with the connected component ${\mathbb{X}}_{{\mathrm{pois}}, \infty}$ there is a graph distance

Using this distance, we shall rely on the following concept.

Definition 6.10 (Statistical Stretch Factor). For $x\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}$ and $R > {\mathfrak{r}}$ we denote

the statistical local stretch factor $S(x, R)$ and statistical (global) stretch factor $S(x)$.

Lemma 6.11. There exists $S_{0} > 1$ depending only on $d$ and $\lambda$ such that for $x\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}$ it holds

where $\nu, \mu > 0$ are the constants from the following Theorem 6.12.

In order to prove this, we will need the following large deviation result.

Theorem 6.12. (Shape Theorem [29, Thm 2.2]). Let $\lambda > \lambda_{c}$. Then there exist positive constants $\mu$, $\nu$ and $k_{0}$ such that the following holds: For every $k > k_{0}$

Proof of Lemma 6.11. We have for $\alpha\geq1$

i.e.

One quickly verifies for $k\in{\mathbb{N}}$ that $S(0, k)\leq S$ and $S(0, k+1)\leq S$ implies $S(0, k+r)\leq2S$ for all $r\in(0, 1)$. Hence we find

□

While the choice of the points $\left(p_{i}\right)_{i\in{\mathbb{N}}}\subset\partial{\bf{P}}$ is clearly specified in Section 4.1, there is lots of room in the choice and construction of ${\mathbb{X}}_{{\mathfrak{r}}}$. In what follows, we choose ${\mathbb{X}}_{{\mathfrak{r}}}$ in the form Eq (2.53). Then we find the following:

Theorem 6.13. Under the above assumptions on the construction of ${\bf{P}}_{\infty}$, as well as $p > d$ and using the notation of Lemma 5.2, for every $1\leq r < s < p$ there almost surely exists $C > 0$ such that for every $n\in{\mathbb{N}}$ and every $u\in W_{0, \partial(n{\bf{Q}})}^{1, p}({\bf{P}}_{\infty}\cap n{\bf{Q}})$

and for every $u\in{\bf{W}}_{0, \partial(n{\bf{Q}})}^{1, p}(\tilde{{\bf{P}}}\cap n{\bf{Q}})$

We will prove Theorem 6.13 in a moment, but we first need to provide two more lemmas.

Lemma 6.14. Let ${\mathbb{X}}_{{\mathrm{pois}}}$ be a Poisson point process with finite intensity. Generate a Voronoi tessellation from ${\mathbb{X}}_{{\mathrm{pois}}}$ and for each $x_{a}\in{\mathbb{X}}_{{\mathrm{pois}}}$ let $d_{a}$ be the diameter of the corresponding Voronoi cell. Then for each $n\in{\mathbb{N}}$ the following function has finite expectation

Note that this statement is not covered by Lemma 3.18 due to the lack of a minimal distance between the points.

Proof. Given the condition $0\in{\mathbb{X}}_{{\mathrm{pois}}}$ we observe

Since ${\mathbb{P}}{\left({nd_{0}\in[k, k+1)}\right)}\leq Ce^{-\alpha k}$ for some $\alpha, C > 0$, we infer

From here, we conclude with the exponentially in $N$ decreasing probability to find more than $N$ points within $[0, 1]^{d}$:

for some $\beta > 0$. Summing up over all cubes we infer

□ Similar to the proof of Theorem 6.5 it will be necessary to introduce the following quantity for $y\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}$ based on Eq (2.27):

An important property of ${\mathcal{M}}_{y}^{{\mathfrak{s}}}$ is the following.

Lemma 6.15. Let $y_{1}, y_{2}\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}$ with $\left|y_{1}-y_{2}\right| < 2$ and

Then there exists $f:\, \mathbb{B}_{1}{\left({\left\{ y_{1}, y_{2}\right\} }\right)}\to{\mathbb{R}}$ such that

and

Furthermore for some fixed $C > 0$ and for every $y\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}$

Proof. We only treat the vector valued case, the other is proved similarly using results from Section 2.4.

Without loss of generality $n = \min\left\{ n\in{\mathbb{N}}:\, \mathbb{B}_{{2^{-n}{\mathfrak{r}}}}{\left(0\right)}\subset\tilde{{\bf{P}}}\right\}$, $\delta\in(2^{-n-1}{\mathfrak{r}}, 2^{-n}{\mathfrak{r}})$ and let $y_{1} = y{\bf{e}}_{1}$ and $y_{2} = -y{\bf{e}}_{1}$. Furthermore, let $\alpha_{k}: = 2{\mathfrak{r}}\sum_{j = 1}^{k}2^{-(n-j)}$ for $k = 1, \dots, n$ and $\alpha_{-k} = -\alpha_{k}$ with $\alpha_{0} = 0$. Using (2.27), for every number $j = -n, \dots, n$ let further

Then for $j\geq0$ we find from Lemma 2.18

Defining

and using local finiteness of the covering as well as

we find with $\frac{\left(s-d\right)p}{p-s}+d = \frac{s(p-d)}{p-s}-1 = \frac{s(1-d)-p+s}{p-s} = \frac{2s-d-p}{p-s}$ $\delta$

From here we conclude the first part. Inequality (6.17) follows from the fact that $\tilde{\rho}_{i}\propto{\mathfrak{r}}_{i}$ and the disjointedness of the balls $\mathbb{B}_{{\frac{{\mathfrak{r}}}{16}}}{\left({x_{a}}\right)}$ with $\mathbb{B}_{{{\mathfrak{r}}_{i}}}{\left({p_{i}}\right)}$ and Lemma 2.17 with ${\mathfrak{r}} = const$. □

Proof of Theorem 6.13. We work with the enumeration $\left(p_{i}\right)_{i\in{\mathbb{N}}}$ and ${\mathbb{X}}_{{\mathfrak{r}}} = \left(x_{a}\right)_{a\in{\mathbb{N}}}$ and make use of the underlying point process ${\mathbb{X}}_{{\mathrm{pois}}}$: For every $a\in{\mathbb{N}}$ there exists $y_{x_{a}}\in{\mathbb{X}}_{{\mathrm{pois}}}$ such that $x_{a}\in\mathbb{B}_{1}{\left({y_{x_{a}}}\right)}$ for every $p_{i}$ there almost surely exists a unique $y_{p_{i}}\in{\mathbb{X}}_{{\mathrm{pois}}}$ such that $p_{i}\in\mathbb{B}_{1}{\left({y_{p_{i}}}\right)}$. Due to the minimal mutual distance of points in ${\mathbb{X}}_{{\mathfrak{r}}}$, we can conclude the following: Since $p_{i}\in\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}$, $\mathbb{B}_{{{\mathfrak{r}}}}{\left({x_{a}}\right)}\subset\tilde{P}\cap G_{a}$ there exists a constant $C$ depending only on ${\mathfrak{r}}$ and $d$ such that always

Since

we find after multiplying with $f_{a}\frac{\left|\partial_{l}\Phi_{i}\right|}{D_{l+}^{\Phi}}$, with $\Phi_{i}$ corresponding to $y_{p_{i}}$, then summing over $i$ and $a$ and integrating over ${\bf{Q}}_{{\mathfrak{r}}}\cap{\bf{P}}$:

where we provide and estimate $I_{1}$, $I_{2}$ and $I_{3}$ in the following. For the moment, let us observe that an estimate on $I_{1}+I_{2}+I_{3}$ implies an estimate on $F_{s}^{3, {\mathfrak{s}}}({\bf{Q}}, u)$ from Lemma 5.2 when we choose the present $f_{a}$ to coincide with the $f_{a}$ there. To simplify further notation, we will do so. Further, we will estimate a more general term than $I_{3}$, which allows us to immediately apply Lemma 5.3.

Step 1: First, we observe there exists $n_{0}$ such that $n_{0}{\mathfrak{r}} > 1$. Then with help of Eq (6.17) and $\sum_{a}f_{a}\leq1$ as well as $\sum_{i}\frac{\left|\partial_{l}\Phi_{i}\right|}{D_{l+}^{\Phi}}\leq2$

Because of Lemmas 3.18 and 6.14 and the exponential decay of probabilities of $d_{a}$ the first integral on the right-hand side is always bounded.

Step 2. Note that (6.17) also implies by the boundedness of $\frac{\left|\partial_{l}\Phi_{i}\right|}{D_{l+}^{\Phi}}$ that

Again, the first integral on the right-hand side is bounded.

Step 3: Last but not least, the term

is the most tricky part. The value of the integral will only grow if we assume $f_{a}\equiv1$.

We find a path $Y(y_{x_{a}}, y_{p_{i}}) = (y_{1}, \dots, y_{n(x_{a}, p_{i})})$ such that $y_{1} = y_{x_{a}}$, $y_{n(x_{a}, p_{i})} = y_{p_{i}}$ such that $y_{j}$, $y_{j+1}$ are neighbors. By our assumptions, for every two points $y, \tilde{y}\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}$ with $y-\tilde{y} < 2{\mathfrak{r}}$, the convex hull of $\mathbb{B}_{{{\mathfrak{r}}}}{\left({\left\{ y, \tilde{y}\right\} }\right)}$ lies in ${\bf{P}}_{\infty}$. Hence we iteratively replace sequences $(\dots y_{i}, y_{i+1}, y_{i+2}, \dots)$ in the path $Y$ by $(\dots y_{i}, y_{i+2}, \dots)$ if $\left|y_{i+2}-y_{i}\right| < 2{\mathfrak{r}}$. Hence, we obtain from Eq (6.19) and the definition of the statistical stretch factor

Therefore, for $y\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}$ with $\chi_{\mathbb{B}_{1}{\left(y\right)}}\chi_{G_{a}}\neq0$ we observe and the shortest path $Y(x_{a}, y_{p_{i}})$ and with Lemma 6.15

Now all points $y_{i}\in Y(x_{a}, y_{p_{i}})$ lie within a radius of $2Cd_{a}S(y_{x_{a}})$ around $x_{a}$, which implies

Now, by independence of the respective variables, the constant in front converges to

The first term in the product can be estimated with help of Lemma 3.18 and is bounded for every $p$ and $s$ by the exponential distribution of $d_{a}$ and $S$. The second term can be estimated similarly.

Step 4: The term

can be estimated in the same way as in Step 3. Together this yields the claim. □

A further important property which we will not use in this work, but which is central for part Ⅲ of this series is the following result.

Theorem 6.16. Let ${\mathbb{X}}_{{\mathrm{pois}}, \infty, {\mathfrak{r}}}: = \left\{ x\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}:\, \, \forall y\in{\mathbb{X}}_{{\mathrm{pois}}, \infty}\backslash\{x\}\, , \, \left|x-y\right| > \frac{{\mathfrak{r}}}{8}\right\}$ be a Matern reduction of the infinite component. For fixed $y_{0}\in{\mathbb{X}}_{{\mathrm{pois}}, \infty, {\mathfrak{r}}}$ and every $\tilde{y}\in{\mathbb{X}}_{{\mathrm{pois}}, \infty, {\mathfrak{r}}}$ let $P(y_{0}, \tilde{y}) = \left(y_{0}, y_{1}(\tilde{y}), \dots, y_{N}(\tilde{y})\right)_{N\in{\mathbb{N}}}$ with $y_{N}(\tilde{y}) = \tilde{y}$ be the shortest path of points in ${\mathbb{X}}_{{\mathrm{pois}}, \infty, {\mathfrak{r}}}$ connecting $y_{0}$ and $\tilde{y}$ in ${\bf{P}}$ and having length $L(y_{0}, \tilde{y})$. Then there exists

such that $\gamma_{y_{0, }\tilde{y}}(t, \cdot)$ is invertible for every $t$ and $\left\Vert {\partial_{t}\gamma_{y_{0, }\tilde{y}}}\right\Vert_{\infty}\leq2$. For $R > 1$ let

Then for every $y_{0}$ there exists almost surely $C > 0$, $S > 0$ such that it holds

Proof. The function $\gamma_{y_{0, }\tilde{y}}$ consists basically of pipes connecting $y_{i}(\tilde{y})$ with $y_{i+1}(\tilde{y})$ that conically become smaller within the ball $\mathbb{B}_{{\frac{1}{2}}}{\left({y_{i}(\tilde{y})}\right)}$ to fit through the connection between two neighboring balls. Defining

we apply Lemma 6.11 instead of ^[28] implies $N_{y_{0}, r, R}(x) = 0$ for all $\left|x-y_{0}\right| > SR$ but also due to the minimal mutual distance $N_{y_{0}, r, R}(x)\leq CR^{d-1}(SR-r)$, where $C$ depends only on ${\mathfrak{r}}$ and $d$. From here we follow the proof of Theorem 6.7. □

We close this section and this work by proving Theorem 1.17.

Proof of Theorem 1.17. The statement on the support is provided by Theorem 4.11 and the fact that we restrict to functions with support in $m{\bf{Q}}$. Hence in the following we can apply all cited results to $\mathbb{B}_{{m^{1-\beta}}}{\left({m{\bf{Q}}}\right)}$ instead of $m{\bf{Q}}$. According to Lemmas 4.7 and 5.2–5.3 and to Theorem 6.13 we need only need to ensure $p > d$ as well as

where $k = 1$ for the simple extension case and $k = 2$ for the symmetric extension case. Since $d_{a}$ is distributed exponentially and the corresponding terms are bounded as long as $r\neq s\neq p$, we observe that we do not have to care about the involved polynomial terms.

According to Theorem 6.8 it is sufficient that $\frac{sr}{s-r} < 2$ (i.e., $\frac{pr}{p-r} < 2$) and $kr < d+2$. □

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work was financed by DFG through the SPP2256 VariationalMethods for Predicting Complex Phenomena in Engineering Structuresand Materials, project HE 8716/1-1 project ID: 441154659.

Conflict of interest

The authors declare that there is no conflict of interest.