Influence maximization in social networks using role-based embedding

1.   Introduction

This paper concerns inverse problems for differential equations on quantum graphs. Under quantum graphs or differential equation networks (DENs) we understand differential operators on geometric graphs coupled by certain vertex matching conditions. Network-like structures play a fundamental role in many problems of science and engineering. The range for the applications of DENs is enormous. Here is a list of a few.

–Structural Health Monitoring. {DENs, classically, arise in the study of stability, health, and oscillations of flexible structures that are made of strings, beams, cables}, and struts. Analysis of these networks involve DENs associated with heat, wave, or beam equations whose parameters inform the state of the structure, see, e.g., [44].

–Water, Electricity, Gas, and Traffic Networks. An important example of DENs is the Saint-Venant system of equations, which model hydraulic networks for water supply and irrigation, see, e.g., [33]. Other important examples of DENs include the telegrapher equation for modeling electric networks, see, e.g., [3], the isothermal Euler equations for describing the gas flow through pipelines, see, e.g., [21], and the Aw-Rascle equations for describing road traffic dynamics, see e.g., [29].

–Nanoelectronics and Quantum Computing. Mesoscopic quasi-one-dimensional structures such as quantum, atomic, and molecular wires are the subject of extensive experimental and theoretical studies, see, e.g., [37], the collection of papers in [38,39,40]. The simplest model describing conduction in quantum wires is the Schrödinger operator on a planar graph. For similar models appear in nanoelectronics, high-temperature superconductors, quantum computing, and studies of quantum chaos, see, e.g., [42,41,45].

–Material Science. DENs arise in analyzing hierarchical materials like ceramic and metallic foams, percolation networks, carbon and graphene nano-tubes, and gra-phene ribbons, see, e.g., [1,46,47].

–Biology. Challenging problems involving ordinary and partial differential equations on graphs arise in signal propagation in dendritic trees, particle dispersal in respiratory systems, species persistence, and biochemical diffusion in delta river systems, see, e.g., [7,24,48].

Quantum graph theory gives rise to numerous challenging problems related to many areas of mathematics from combinatoric graph theory to PDE and spectral theories. A number of surveys and collections of papers on quantum graphs appeared in previous years; we refer to the monograph by Berkolaiko and Kuchment, [25], for a complete reference list. The inverse theory of network-like structures is an important part of a rapidly developing area of applied mathematics---analysis on graphs. Being tremendously important for all aforementioned applications these theories have not been, however, sufficiently developed. To date, there are relatively few results related to inverse problems on graphs, and almost exclusively they concern trees, i.e. graphs without cycles.

The first question to be asked when studying inverse problems is how to establish the uniqueness result, i.e. to characterize spectral, or scattering, or dynamical data ensuring uniques solution of the inverse problem. It was shown that inverse boundary spectral and scattering problems for differential equations on graphs with cycles do not have in general a unique solution [41,34,43]. The results on stable identification are known only for trees, and only for the case of boundary inputs (controls) and observations. It was proved that a DEN is identifiable if the actuators and sensors are placed at all or all but one boundary vertices.

There are two groups of uniqueness results in this direction: for trees with a priori known topology and lengths of the edges [28,49,32] and for trees with unknown topology [22,23,11,13]. The most significant result of the last two cited papers is developing a constructive and robust procedure for the recovery tree's parameters, which became known as the leaf peeling method. This method was extended to boundary inverse problems for various types of PDEs on trees in a series of our subsequent papers [7,15,20].

The boundary control method in inverse theory demonstrates [11,23] that inverse (identification) problems for DENs are closely related to control and observation problems for PDEs on graphs. The latter problems were studied in numerous papers, see, e.g. [5,16,30,35,44,50] and references therein.

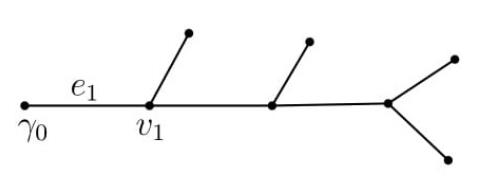
In this paper, we solve a non-standard dynamical inverse problem for the wave equation on a metric tree graph. Let $\Omega = \{V, \, E\}$ be a finite compact and connected metric tree (i.e. graph without cycles), where $V$ is a set of vertices and $E$ is a set of edges. We recall that a graph is called a metric graph if every edge $e_j \in E, \, j = 1, \ldots, N,$ is identified with an interval $(a_{2j-1}, a_{2j})$ of the real line with a positive length $\ell_j.$ We denote the set of boundary vertices (i.e. vertices of degree one) by $\Gamma = \{ \gamma_0,..., \gamma_m\}$, and the set of interior vertices (whose degree is at least two) by $\{ v_{m+1},...., v_N\}$. The vertices can be regarded as equivalence classes of the edge end points $a_j$. For each vertex $v_k$, denote its degree by $\Upsilon_k$. We write $j \in J(v)$ if $e_{j} \in E(v),$ where $E(v)$ is the set of edges incident to $v.$

The graph $\Omega$ determines naturally the Hilbert space of square integrable functions $\mathcal{H} = L^2 (\Omega).$ We define its subspace $\mathcal{H}^1$ as the space of continuous functions $y$ on $\Omega$ such that $y|_e \in H^1(e)$ for every $e \in E$ and $y|_{\Gamma} = 0,$ and let $\mathcal{H}^{-1}$ be the dual space to $\mathcal{H}^1$. When convenient, we will denote the restriction of a function $y$ on $\Omega$ to $e_j$ by $y_j$. For any vertex $v_k$ and function $y(x)$ on the graph, we denote by $\partial y_j(v_k)$ the derivative of $y_j$ at $v_k$ in the direction pointing away from the vertex.

We will assume that for each internal vertex $v_k$, a mass $M_k \geq 0$ is placed at $v_k$. Our system is described by the following initial boundary value problem (IBVP):

Here $T$ is an arbitrary positive number, $q_j\in C^N([a_{2j-1}, a_{2j}])$ for all $j$, and $f\in L^2(0,T)$. In what follows, we will refer to $\gamma_0$ as the root of $\Omega$ and $f$ as the control. The well-posedness of this system is discussed in Section 2, see Theorem 2.8, where it is proved that $u^f \in C([0,T];{\mathcal H}) \cap C([0,T];{\mathcal H}^{-1}) .$ In the absence of any masses, and for sufficiently regular $q$, it was discussed in several papers, see, e.g. [44,19,15,16]. In the presence of masses, the function $u$ will have more regularity properties, see Section 2 and [2,36].

Inverse Problem 1. Assume an observer knows the topology of the tree, i.e. the number of boundary vertices and interior vertices, the adjacency relations for this tree, i.e. for each pair of vertices, whether or not there is an edge joining them. Assume the observer also knows the boundary condition (5), and that (6) holds at the other boundary vertices. The unknowns are the lengths $\{ \ell_j\}$, the masses $M_k$, and the function $q$. We wish to determine these quantities with a set of measurements that we describe now.

Let $v_{1}$ be the interior vertex adjacent to $\gamma_0$ and let $e_{1}$ be the edge joining the two, see Figure 1. Our first measurement is then the following measurement at $\gamma_0$:

Physically, this corresponds to applying a Dirichlet control and placing a tension sensor, both at $\gamma_0$. In what follows, we will refer to $R_{01}$ as the "root response operator".

Theorem 1.1. From operator $R_{01}$ one can recover the following data: $\ell_1,q_1$, $\Upsilon_{1}$, and $M_{1}$.

The proof of this, appearing in Section 2, is an adaptation of an argument well known for the massless case, $M_{1} = 0$, see [11].

We now define the other measurements required for the inverse problem. For interior vertex $v_{k}$ we list the incident edges by $\{ e_{kj}: \ j = 1,..., \Upsilon_{k}\}$. Here $e_{k1}$ is chosen to be the edge lying on the unique path from $\gamma_0$ to $v_k$, and the remaining edges are labeled randomly, see Figure 2. Then the tension sensors, represented by arrows in Figure 2, measure

We remark in passing that because the control and sensors are at different places, Theorem 1.1 does not apply. We will show that it is not required to measure $\partial u^f_j(v_{k},t)$ for $j = 1$ or $\Upsilon_{k}.$ Thus for the whole graph, the total number of sensors needed is $1+\sum_{k = 1}^{N-m-1}(\Upsilon_k-2)$. It is easy to check that this number is equal to $|\Gamma | -1.$ We denote by $R^T$, which we call the "total response operator", the $(|\Gamma|-1)$-tuple $(R_{01},R_{12},R_{13},....)$ acting on $L^2(0,T).$

Let $\ell$ be equal to the maximum distance between $\gamma_0$ and any other boundary vertex. In our first main result, we solve Inverse Problem 1.

Theorem 1.2. Assume $q_j \in C^N([a_{2j-1}, a_{2j}])$ for all $j.$ Suppose $T>2\ell$. Then from $R^T$ one can determine $q$, the point masses and the lengths of the edges.

Placement of internal sensors has been considered in the engineering and computer science literature, see, e.g. [26,27]. We are unaware of any mathematical works treating the inverse problem on general tree graphs with measurements at the internal vertices, except for [8] where the interior vertices are assumed to satisfy delta-prime matching conditions instead of (3), (4). Internal measurements might have advantages in situations where some boundary vertices are inaccessible. In future work, we will study inverse problems of graphs with cycles, in which case both boundary and internal observations appear to be necessary. For a discussion on inverse problems for graphs with cycles see [4] and references therein.

We briefly mention some of the ideas used in the proof of Theorem 1.2. Denote by $\Omega_{kj}$ the unique subtree of $\Omega$ having $v_{k}$ as root with incident edge $e_{kj}$, see Figure 3. In Section 3, we will define the operator $\tilde{R}_{kj}$, analogously to our definition of $R_{01}$, as the root response operator associated to $\Omega_{kj}$. Assume for now $k = 1$ and fix $j>1$. We will show that $\tilde{R}_{1j}$ can be determined by using our knowledge of $R_{01}$ and $R_{1j}$. This will be achieved using two ingredients. The first ingredient is an identity relating the Schwartz kernels of $\tilde{R}_{1j}$ and ${R}_{1j}$, using general properties of wave propagation on graphs. The second is our knowledge of the data associated with the edge $e_1$. Having determined $\tilde{R}_{1j}$, we apply Theorem 1.1 to determine the data associated to $e_{1j}$. Similarly we will determine the data associated to all edges incident to $v_1$. Then using this newly determined data together with the appropriate components of $R^T$, we then determine the data for all edges incident to the neighbors of $v_1$. The argument can then be iterated until the data associated with each edge are determined.

The iterative nature of our solution actually allows us to solve what at first glance seems to be a much harder inverse problem.

Inverse Problem 2. Assume an observer knows $\Omega$ is a tree, that the boundary condition (5) holds, and that (6) holds at the other boundary vertices. All other data are unknowns. The problem then is to use $R^T$ to determine the topology, the lengths $\{ \ell_j\}$, the masses $M_k$, and the function $q$.

To solve this inverse problem, for $P\in \Bbb N$, define $\Omega_P$ to be the subgraph of $\Omega$ covered by paths in $\Omega$ starting at $\gamma_0$ and containing $(P+1)$ vertices. Define $R_P^T$ to be the vector consisting of elements $R_{kj}$ of $R^T$ such that $v_k\in \Omega_P$. Then we have the following refinement of Theorem 1.2.

Theorem 1.3. Assume $q_j \in C^N([a_{2j-1}, a_{2j}])$ for all $j.$ Suppose $T>2\ell$. Then for any $P\in \Bbb N$, one can determine from $R_{(P-1)}^T$ the following: a) the topology of $\Omega_P$, b) $M_k, \ \Upsilon_k$ for all $v_k\in \Omega_P$, and c) for each $e_j\in \Omega_P$, the length of $e_j$ and $q_j$.

We remark that in the theorem, $\Upsilon_k$ should be interpreted as the degree of $v_k$ as an element of $\Omega$. Evidently, this theorem will allow one to solve Inverse Problem 2 by choosing $P$ large enough. It will be clear that the proof of Theorem 1.2 actually proves Theorem 1.3.

In an engineering setting, Inverse Problem 2 could be solved using the following process. One begins with only the control and sensor at $\gamma_0$. Once these are used to determine $\Upsilon_1$, one transports $(\Upsilon_1 -2)$ sensors to edges incident to $v_1$, perhaps by robots along $e_1$. Then the arguments of this paper allow one to determine $\tilde{R}_{1j}$, and thus the data associated with those edges including the degrees of the vertices adjacent to $v_1$. Mathematically, this will be equivalent to having derived the conclusions of Theorem 1.3 for $\Omega_1$. Then more sensors would be transported to those vertices, enabling the next steps in our iterative process to proceed to solve for $\Omega_2$. Clearly this process could be continued until the graph is exhausted. It will be clear that our proof of Theorem 1.2 actually tracks this process.

We now compare our paper with the literature. All papers referred to in this paragraph assume all controls and measurements take place at boundary vertices. In [11], the authors consider trees with no masses, and assume that controls and measurements are placed at $(|\Gamma|-1)$ boundary vertices. The authors use an iterative method called "leaf peeling'', where the response operator on $\Omega$ is used first to determine the data on the edges adjacent to the boundary, and then to determine the response operator associated to a proper subgraph. The leaf peeling argument includes spectral methods that require knowing $R^T$ for all $T$. The tools used in our paper mostly closely resemble those in [20,17], where an iterative dynamical argument, called "dynamical leaf peeling", is developed for a tree with no masses and with response operators at all but one boundary vertices, allowing for the solution of the inverse problem for finite $T$ sufficiently large. The arguments in the present paper differ from those papers in two main ways: (a) the presence of masses in our paper complicates the underlying analysis, and (b) our use of interior measurements makes the proofs somewhat simpler. In [2], the methods of [11] are extended to the case where masses are placed at internal vertices, see also [6]; however these methods still require knowledge of $R^T$ for all $T$. Also in [2], it is proven that that for a single string of length $\ell$ with $N$ attached masses and $T>2\ell$, $R_{01}^T$ is sufficient to solve the inverse problem.

In the present paper we develop a new version of the dynamical leaf peeling method. A special feature of our paper is that we use only one control together internal observations. This may be useful in some physical settings where some or most boundary points are inaccessible, or where use of more than one control might be difficult. The extension of dynamical leafing peeling to systems with attached masses, for which the underlying analysis is more complicated than in the mass-free setting, should also be of interest. Another potential advantage of the method presented here is that we recover all parameters of the graphs, including its topology, from the $(|\Gamma|-1)$-tuple response operator acting on $L^2(0,T).$ In previous papers, the authors recovered the graph topology from a larger number of measurements: the $(|\Gamma|-1)\times (|\Gamma|-1)$ matrix (boundary) response operator or, equivalently, from $(|\Gamma|-1)\times (|\Gamma|-1)$ Titchmarsh–Weyl matrix function. In [12], the inverse problems on a star graph for the wave equation with general self-adjoint matching conditions was solved by the $(|\Gamma|-1)\times (|\Gamma|-1)$ matrix boundary response operator.

2.   Representation of solution and the response function for star graph

In this section, we prove well-posedness of our IBVP for a star shape graph. We also derive representations of both the solution and the Schwartz kernel of the components of the response operator. The representations will be used in Section 3 to solve the inverse problem. We then indicate how these results can be extended from star graphs to arbitrary trees.

2.1.   Preliminaries

In what follows, it will convenient to denote

where ${\mathcal H}^n( { \mathbb R })$ are the standard Sobolev spaces. We define the Heaviside function by $H(t) = 1$ for $t>0$, and $H(t) = 0$ for $t<0$. Then define $H_n\in \mathcal{F}^n$ as the unique solution to

at times we will use $H_{-1}(t),$ resp. $H_{-2}(t)$ for $\delta (t),$ resp. $\delta' (t).$ In this section and those that follow, we will drop the superscript $T$ from $R^T$ when convenient.

Consider a star shaped graph with edges $e_1,...,e_N$. For each $j$, we identify $e_j$ with the interval $(0,\ell_j)$ and the central vertex with $x = 0$, see Figure 4.

Recall the notation $q_j = q|_{e_j}$, and $u_j(\cdot,t) = u(\cdot,t)|_{e_j}$. We consider the case where a point mass $M\geq 0$ is attached at the central vertex. Thus we consider the system

Let $u^f$ solve (9)-(14), and set

For (10), it is standard that the waves have unit speed of propagation on the interval, so $g(t) = 0$ for $t<\ell_1$. It will be useful first to consider the vibrating string on an interval.

2.2.   Representation of solution on an interval and reduced response operator

We will use a representation of $u^f(x,t)$ developed in [16]. For the reader's convenience, we recall facts proven in that work. Fix $j\in \{ 1,...,N\}$. We extend $q_j$ to $(0,\infty)$ as follows: first evenly with respect to $x = \ell_j$, and then periodically. Thus $q_j(2n\ell_j \pm x) = q_j(x)$ for all positive integers $n$.

Define $w_j$ to be the solution to the Goursat problem

A proof of solvability of the Goursat problem can be found in [14].

Consider the IBVP on the interval $(0,\ell_j )$:

Then the solution to (16)-(17) on $e_j$ can be written as

Setting $h(t) = g(t)$, with $g$ given by (15), we get a representation of the solution $u^f$ to (9)-(14) on $e_2,...,e_N$.

Define the "reduced response operator" on $e_j$, with $j\geq 2$, by

associated to the IBVP (16)-(17). From (18) we immediately obtain:

Lemma 2.1. For $j = 2,..., N$, and any $h\in C_0^{\infty}( { \mathbb R }^+)$, we have

with

and $\tilde{r}_{0j} = \partial w_j(0,s)+2\sum_{n\geq 1}H(s-2n\ell_j)\partial w_j(2n\ell_j,s)$. If $T$ is finite, the sums above are finite.

In what follows we will refer to $\tilde{R}_{0j}(s)$ as the "response function".

It will be useful also to represent the solution of a wave equation on an interval when the control is on the right end. Thus consider the IBVP:

Set $\tilde{q}_1(x) = q_1(\ell_1-x)$, and extend $\tilde{q}_1$ to $[0,\infty )$ by $\tilde{q}_1(2n\ell_1\pm x) = \tilde{q}_1(x)$. Define $\omega_j$ to be the solution to the Goursat problem

By changing coordinates in (18), we get

2.3.   Representation of $R_{01}$ for $M>0$ for star graph

We begin section by proving an analog of Lemma 2.1 for $R_{01}(t)$, and also $R_{1j}(t)$ in the case of a positive mass at the central vertex. As a corollary, we recover the data associated to the edge $e_1$. The case of a massless central vertex requires a modified analysis, and will be covered in the next subsection.

Lemma 2.2. The response function for $R_{01}^T$ has the form

Here $r_{01}$ is a piecewise continuous function, $a_n$ and $b_n$ are real constants,

If $T$ is finite, then the sum is finite.

Proof. We see that on $e_1$, the solution to (9)-(14) is given by

Thus by (18) with $h = g$ and (20),

Next, we study the structure of $g$. Using the equation $u^f(0,t) = g(t)$, along with (12), (18) with $h = g$, and (20), we have

In what follows, we will assume $t<T$ for some positive $T$, so the sums above are all finite. Adapting the argument in [11], we let $f(t) = \delta (t)$. In what follows, it will be useful to note that by the uniqueness of the solution of the wave equation, we have for $p = p(t)$

As a consequence, $(R_{01}p)(t) = (p*u^{\delta}_x)(\ell_1,t),$ so $R_{01}(s) = u^{\delta}_x(\ell_1,s)$.

For $g(t) = u^{\delta}(0,t)$, we claim $g$ will have the structure:

Here $\tilde{a}\in \mathcal{F}^2$, $\{ \beta_n\}$ is a discrete, increasing set of positive constants with $\beta_0 = \ell_1$, and $c_n$ and $t_n$ are constants. In what follows, we will solve for these various unknowns, thereby justifying the claim. Assuming the claim for the moment and inserting $f(t) = \delta (t)$ and (25) into (23), the lemma follows except (21) which we will prove below.

We will now justify the claim. Substituting (25) into (24), and matching the $\delta'$ terms, we get

We conclude that $c_m = 2/M$ for all $m$. This equation together with (25) and (23) imply the equalities in (21). In what follows we denote $c_m$ as $c$. Matching the $\delta$ terms in (25) and (24),

We can solve for $\{\beta_m\}$ by matching $\beta_0< \beta_1<\beta_2<...$ with the set

Next, for any given $m$, we solve for $t_m$ as follows. First, inspection of (27) gives

For larger $m$, inspection of (27) gives three cases.

Case 1. $\beta_m = (2n+1)\ell_1$ and $\beta_m\neq 2n_0\ell_j+(2m_0+1)\ell_1$ for any $m_0,n_0,j\in \Bbb N$. Then $t_m = \frac{1}{M}(-Nc+2 \omega_1((2n+1)\ell_1,(2n+1)\ell_1))$.

Case 2. For some positive integer $L$ and any $l = 1,...,L$, we have $\beta_m \neq (2n+1)\ell_1$ and $\beta_m = 2n_{l}\ell_{j_l}+(2m_{l}+1)\ell_1$. Then $t_m = \frac{1}{M}(-2Lc)$.

Case 3. For some positive integer $L$ and any $l = 1,...,L$, we have $\beta_m = (2n+1)\ell_1 = 2n_{l}\ell_{j_l}+(2m_{l}+1)\ell_1$. Then

Accounting for these cases, we thus solve for $t_m$ of each $m$.

Next, we solve for $\tilde{a}$, which by (24) and (25) satisfies:

where $\tilde{b}_0\in L^2$. We will assume $\tilde{a}\in \mathcal{F}^2$ (an assumption later justified). Since $\tilde{a}'(0) = 0$, integrating the equation above gives

with $\tilde{b}_1\in \mathcal{F}^1$. We solve for $\tilde{a}$ by an iterative argument. For simplicity of presentation, assume $\beta_1 = \ell_1+2\ell_2,\ \beta_2 = \ell_1+2\ell_3$, and $\ell_3<\min (\ell_1,\ell_j:\ j>3)$; the other cases can be treated similarly. Then for $t<\beta_1$ we have $\tilde{a}(t-2n\ell_j-\ell_1) = 0$ for all $j$, so (29) simplifies to an equation that we can integrate to

with $\tilde{b}_2\in \mathcal{F}^2$. It is not hard to show that this is a Volterra equation of the second kind, and we can thus uniquely solve for $\tilde{a}(t)\in \mathcal{F}^1$ for for $t<2\ell_2$. Next, we consider the interval $t\in [\beta_1,\beta_2] = [\ell_1+2\ell_2,\ell_1+2\ell_3]$, so $\tilde{a}(t-2\ell_j-\ell_1) = 0$ for $j\neq 2$. We claim the term $\tilde{a}(t-2\ell_2-\ell_1)$ has already been determined. To see this, note that by the construction of the set $\{ \beta_n\}$ together with our assumption for $\beta_2$, we have $2\ell_3 <4\ell_2$. Hence for $t< 2\ell_3+\ell_1$, we have $t-2\ell_2-\ell_1<2\ell_2$, so $\tilde{a}(t-2\ell_2-\ell_1)$ has been determined as claimed. We can absorb this known term into $\tilde{b}_2$ in the right hand side of (29). We then integrate (29) to get

Again we solve this Volterra equation to determine $\tilde{a}(t)\in \mathcal{F}^1$ for $t<2\ell_3$. Iterating this procedure, we can solve for $\tilde{a}(t)$ for any large $t$. Since the right hand side of (29) is in $\mathcal{F}^1$, it follows that $\tilde{a}\in \mathcal{F}^2$. This completes the proof of the lemma.

Lemma 2.3. Let $g(t)$ be given by (24). Then

where

Furthermore, $\tilde{a}\in \mathcal{F}^2,$ $a_m = 2/M$ for all $m$, and $\nu_0 = \ell_1$, and $a_m,t_m$ are constants.

Proof. Since $g (t) = u^f(0,t) = (f*u^{\delta})(0,t)$, we have $a(t) = u^{\delta}(0,t)$. The formula (31) follows from (25).

Proposition 1. Let $T>2\ell_1$ and $M>0$. From $R_{01}^T$ one can determine $M,N, q_1,$ and $\ell_1$.

Proof. One can determine $\ell_1$ immediately from Lemma 2.2 because $\alpha_1 \neq 0$. Then a well known argument (see, eg. [11]) shows that one can recover $q_1$ from $R_{01}^T$. Having determined $q_1$ one can solve the Goursat problem to determine $\omega_1$, and then one gets $M$ from (21). To find $N$ we observe that near $t = 2\ell_1$, setting $f(t) = \delta (t)$, we can extract from (23)

where $c_1,c_2$ are constants, $F(t)$ is a function that has been explicitly determined, and $G(t)$ is continuous. Thus we can distinguish the coefficient $(t_0+w_1(\ell_1,\ell_1)\psi )$. Also, $w_1$ can be determined from $q_1$, and so we solve for $t_0$ hence $N$ (see (28)).

Lemma 2.4. Label the central vertex $v_1$, and let $e_j$ be an incident edge other than $e_1$. Assume $M_1>0$. Let $T>0$, and let $R^T_{1j}$ be associated with (9)-(14), defined by $(R^T_{1j}f)(t) = \partial u_j^f(v_1,t)$. The response function for $R_{1j}^T$ has the form

Here $r_{1j}\in \mathcal{F}^1$, and the sequence $\{ \beta_n \}$ is positive and strictly increasing, and $b_n,r_n$ are constants.. If $T$ is finite then the sums are finite.

Proof. the lemma follows immediately from Lemmas 2.2 and 2.3; the details are left to the reader.

2.4.   Adaptation when $M=0$

We can adapt the methods of the previous subsection to the case the internal vertex is massless (also see [11] for a proof of the results below). Here we will only mention the modifications necessary. In Subsection 2.3, the argument carries through word for word until (24), which becomes a first order integral-differential equation, since $M = 0$. As a consequence, the function $g(t) = u^{\delta}(0,t)$ will be less regular, because its singularities are not mollified when transmitted across vertices. Instead of(25) and Lemma 2.3 we have:

Lemma 2.5. Let $g(t)$ be given by (24) with $M = 0$. Then

where

Here $\{ \xi_k\}$ is a increasing positive sequence, and $a_k,b_k$ are constants. Furthermore, $\tilde{a}\in \mathcal{F}^1$, and $\xi_0 = \ell_1$.

Inserting $f(t) = \delta (t)$ and (32) into (23), we obtain the following analog of Lemma 2.2:

Lemma 2.6. The response function for $R_{01}^T$ has the form

Here $\{ \zeta_n\}$ is a increasing positive sequence with $\zeta_0 = 0$, $\zeta_1 = 2\ell_1$, and $z_n,y_n$ are constants. Function $r_{01}$ is piecewise continuous. If $T$ is finite, then the sum is finite.

Proposition 2. Let $T>2\ell_1$. From $R_{01}^T$ one can determine $M = 0,N, q_1,$ and $\ell_1$.

The reader is referred to [11] for a proof of this.

We conclude this section with the following lemma, whose proof is similar to that of Lemma 2.4 and is left to the reader.

Lemma 2.7. Label the central vertex $v_1$, and let $e_j$ be an incident edge other than $e_1$. Assume $M_1 = 0$. Let $T>0$, and let $R^T_{1j}$ be associated with (9)-(14), The response function for $R_{1j}^T$ has the form

Here $r_{1j}\in L^2$, and the sequence $\{ \beta_n \}$ is positive and strictly increasing, and $a_n,b_n$ are constants. If $T$ is finite then the sums are finite.

This lemma should be compared with Lemma 2.4. For this lemma, the lead singularity is of the form $\delta'$, compared with $\delta$ in the case $M_1>0$; this reflects the mollifying effect of the mass.

2.5.   Extension to trees

In this subsection, we extend some of the previous results to trees. The extensions will be used in Section 3 in solving the inverse problem on trees.

We begin by discussing the wellposed of the system (1)-(6). Let $d_{j}$ be the minimum number of nonzero masses on the path from edge $e_j$ to the boundary vertex $\gamma_0$.

Theorem 2.8. If $f \in L^2(0,T)$ then $u^f \in C([0,T];{\mathcal H})\cap C^1([0,T];{\mathcal H}^{-1}).$ Furthermore, for each $e_j \in \Omega,$ $u^f|_{e_j} \in C([0,T];H^{d_j}(e_j)).$

The proof of the theorem is based on the analysis of the waves incoming to, transmitted through and reflected from an interior vertex, and the waves reflected from the boundary vertices. The details are left to the reader; also see [6].

Theorem 2.9. Let $u$ solve the system (1)-(6), and define $R_{01}$ by (7). Let $v_{1}$ be the vertex adjacent to $\gamma_0$, with connecting edge labeled $e_1$, as in Figure 5. Then

a) The response function for $R_{01}^T$ has the form

Here $r_{01}\in L^2$, and the sequence $\{ \zeta_n \}$ is positive and strictly increasing, and $a_n,b_n$ are constants. If $T$ is finite then the sums are finite, and

b) from ${R}_{01}$ one can determine $M_{1},\Upsilon_{1}, q_1,$ and $\ell_1$.

Proof. We sketch this proof, leaving the details to the reader. The key point is the waves propagate at unit speed. Hence for $T>2\ell_1+\epsilon$ and $\epsilon>0$ sufficiently small, the response operator ${R}_{01}$ will not "feel'' the vertices $v_{m}$ for $m>1$, regardless of whether they are boundary or interior vertices. Thus by Propositions 1 and 2, $l_1$, $\Upsilon_{1}$ and $M_{1}$ can be determined. Having established $l_1$, one determines $q_1$ as in the proof of 1.

For an internal vertex $v_{k}$, let $K = K(k)$ be the number of positive masses on the path from $\gamma_0$ to $v_{k}$, including $v_{k}$. We have the following generalization to a tree of Lemmas 2.4 and 2.7.

Lemma 2.10. Let $T>0$, and let $R^T_{kj}$ be defined by (3)-(6) and (8). The response function for $R_{kj}^T$ has the form

Here $r_{kj}\in \mathcal{F}^K$, and the sequence $\{ \beta_n \}$ is positive and strictly increasing, and $b_n,r_n$ are constants. If $T$ is finite then the sums are finite.

Proof. The proof follows from the proof of Lemma 2.2, together with the transmission and reflection properties of waves at interior vertices, and reflection properties at boundary vertices. The details are left to the reader; see also [11]- where, however, the formula analogous to Lemma 2.2 should have the terms of the form $\rho_n\delta (s-\beta_n)$.

3.   Solving the inverse problem for the tree

In this section we prove Theorem 1.2. In the first subsection, we establish some notation, and give an outline of the solution method, Steps 1-3. Then in Subsection 3.2, we present the technical heart of our argument, using the equation

and the expansions for $\tilde{R}_{12}(s),\ A(s)$ and $R_{12}(s)$ derived in the previous section to solve for $\tilde{R}_{12}(s)$. Then, in Subsection 3.3, we show how to compute $\tilde{R}_{22}(s)$. From the proof there, it will be evident that we can compute $\tilde{R}_{kj}(s)$ for general $k,j$.

3.1.   Reduced response operators

We begin by establishing some notation. Let $v_k$ be some fixed interior vertex. We list the incident edges by $\{ e_{kj}: \ j = 1,..., \Upsilon_{k}\}$. Denote $\ell_{kj}: = |e_{kj}|$. Let $j$ satisfy $1<j\leq \Upsilon_{k}$. Denote by $\Omega_{kj}$ as in the introduction, see Figure 3, and let the vertices of $\Omega_{kj}$ be denoted $V_{kj}$.

We will define an associated response operator as follows. Suppose $w = w^p$ solves the following IBVP: for $t\in [0,T]$,

and initial conditions

Then we define an associated reduced response operator

with associated response function $\tilde{R}_{kj}(s)$.

We have the following important result is essentially a restatement of Theorem 2.9.

Theorem 3.1. For vertex $v_k$ and incident edge $e_{kj}$, suppose $v_{k'}$ is the other vertex on $e_{kj}$. Then from $\tilde{R}_{kj}$ one can determine the data: $q_{kj}, \ell_{kj}, M_{k'},$ and $\Upsilon_{k'}.$

In this section we will present an iterative method to determine the operator $\tilde{R}_{kj}$ from the $(|\Gamma |-1)$-tuple of operators, $R^T$, for arbitrary $k,j$. By Theorem 3.1, this allows us to solve the inverse problem. We now sketch our method for solving for $\tilde{R}_{kj}$. Fix $T>2\ell$. In what follows, we will repeatedly refer to Figure 6.

Step 1. Let $v_{1}$ be the vertex adjacent to the root $\gamma_0$, with connecting edge labeled $e_1$. By Theorem 3.1, we can use $R_{01}^T$ to recover $\Upsilon_{1}$, $\ell_1$, $q_1$, and $M_{1}$.

Step 2. Consider $e_{12}$. In the next subsection, we will show how to solve for $\tilde{R}_{12}$ given our knowledge of $R_{01}$ and $R_{12}$. Thus applying Theorem 3.1, we can solve for the data $\Upsilon_{2}$, $|e_{12}|$, $q_2$, and $M_{2}$. Because $R_{1j}$ for $j = 2,..., \Upsilon_{1}-1$ are known $by \ assumption$, the data associated to these edges can be solved for in the same way. We now consider the edge $e_{{1},\Upsilon_{1}}$. In the next subsection, we will also show that $\partial u_1^{f}(v_{1},t)$ is also determined. Furthermore, by assumption we know $\partial u_j^{f}(v_{1},t)$ for $j = 2,..., \Upsilon_{1}-1$. Hence by (4), $R_{1\Upsilon_{1}} = \partial u_{\Upsilon_{1}}^{f}(v_{1},t)$ is also determined, with it the data associated to that edge.

Step 3. In Subsection 3.3, we will solve for determine $\tilde{R}_{2j}$ for all $j$. It will be clear at that point that the same argument can be used to solve for all $\tilde{R}_{kj}$.

3.2.   Solving for $\tilde{R}_{12}$

Proposition 3. The function $\tilde{R}_{12}(s)$ can be determined from $R_{01}(s)$ and $R_{12}(s)$.

The rest of this subsection will be devoted to proving this proposition.

Let $f\in L^2(0,T)$, and let $u^f$ be the solution of (1)-(6). Since we know $\ell_1$ and $q_1$, we can solve the wave equation on $e_1$ with known boundary data. We identify $e_1$ as the interval $(0,\ell_1)$ with $v_{k_1}$ corresponding to $x = 0$. Then $u^{f}$, restricted to $e_1$, solves the following Cauchy problem, where we view $x$ as the "time" variable:

Since the operator $R_{01}$ is known, we can thus uniquely determine $u^{f}(0,t) = u^{f}(v_{1},t)$ and $\partial u_1^{f}(v_{1},t)$. Since $u^f(0,t) = (u^{\delta}(0,\cdot)*f)(t)$, it follows that $A(t) = u^{\delta}(v_{1},t)$ is a known quantity. We now show how $A$ and $R_{12}$ can be used to determine $\tilde{R}_{12}(s)$. A key ingredient is the following equation, which relates ${R}_{12}(s)$ with $\tilde{R}_{12}(s)$.

This follows from the definition of the response operators for any $f\in L^2$, in particular $(R_{12}*f)(t) = \partial u^f_2 (v_{1},t).$ We rewrite this equation:

Below, we will use (40) to determine $\tilde{R}_{12}(s).$ To this end, we now insert representations of $\tilde{R}_{12}(s),\ {R}_{12}(s),$ and $A$ that were derived in the previous section.

Since $v_{1}$ is the root of $\Omega_{12}$, the following equation is essentially an restatement Theorem 3.1.

Here $0 = \zeta_0<\zeta_1<...$, and $0 = \eta_0<\eta_1<...$, and $\tilde{r}_{12}(s)$ is piecewise continuous and vanishes for $s<0$. In what follows, we will for readability rewrite $\tilde{r}_{12}$ as $\tilde{r}$.

We now must separately consider the cases $M_{1}>0$ and $M_{1} = 0$.

Case A. $M_{1}>0$

In what follows, it will be convenient to extend $f(t)\in L^2(0,T)$ as zero for $t<0$. By Lemma 2.10 and by an adaptation of Lemma 2.3 to general trees, we have the following expansions:

Here $r_{12}\in \mathcal{F}^1$ and $\tilde{a}(s)\in \mathcal{F}^2$, and $\{ \alpha_k\}$ and $\{ \beta_n\}$ are positive and increasing. Clearly $\tilde{a}(s) ,r_{12}(s), \{ a_k\},$ $\{ t_k\},$ $\{ \alpha_k\},$ $\{ \nu_k\}$, $\{ b_n\},$ $\{ \beta_n\}, \{ r_n\}$ are known because we assume knowledge of $R_{01}$ and $R_{12}$, whereas for now $\tilde{r}$ and the sets $\{ \zeta_p \} ,\{ z_p\}$, $\{ y_j\}$, $\{ \eta_j\}$ are unknown. In what follows, we mimick an iterative argument in [20]. Both sides of (40) are a linear combination of $\delta$, Heavyside, and continuous functions. We will split the rather intricate argument solving for the unknowns in (40) into three lemmas. In the first, we match the delta functions on each side of (40).

Lemma 3.2. The sets $\{ \zeta_p \} ,\{ z_p\}$, can be determined by $R_{01}$ and $R_{12}$.

Proof. By (40), (41), (42), and (43), we get by matching delta functions:

Step 1. We solve for $z_1,\zeta_1$. Since the sequences $\{\beta_n\},\{ \zeta_p\},\{ \alpha_k\}$ are all strictly increasing, clearly we have $\beta_1 = \zeta_1+ \alpha_1$, so that $b_1 = z_1a_1$, and so $\zeta_1 = \beta_1 - \alpha_1$ and $z_1 = b_1/a_1$. We represent that the set $\{ b_1, \beta_1\}, \ \{ a_1, \alpha_1 \}$ determines the set $\{ z_1,\zeta_1 \}$ by

Step 2. We solve for $z_2,\zeta_2$. We match the term $\delta(t-\beta_2 )$ with its counterpart on the right hand side of (44). There are three possible cases.

Case 1. $\beta_2 \neq \zeta_1+ \alpha_2$.

In this case, we must have $\beta_2 = \zeta_2+ \alpha_1$, hence

Case 2a. $\beta_2 = \zeta_1+ \alpha_2$ and $b_2\neq a_2z_1.$ Note that the last inequality can be verified by an observer at this stage, because we have determined $b_2,a_2, z_1$. We conclude $\beta_2 = \zeta_2+ \alpha_1$ and $b_2 = a_1z_2+a_2z_1,$ and hence

Case 2b. $\beta_2 = \zeta_1+ \alpha_2$ and $b_2 = a_2z_1.$ Then $\beta_2< \zeta_2+ \alpha_1$. Note we have not yet solved for $\{ \zeta_2, z_2\}$. In this case, we now repeat the matching coefficient argument just used with $\delta(t-\beta_3 )$.

Again there are three cases:

Case 2bⅰ. $\beta_{3}\neq \zeta_1+ \alpha_3$. Note all of these terms are known, so this inequality can be verified. In this case, $\beta_3 = \zeta_2+ \alpha_1$, so $\zeta_2 = \beta_3- \alpha_1$ and $z_2 = b_3/a_1$.

Case 2bⅱ. $\beta_{3} = \zeta_1+ \alpha_3$ and $b_3\neq z_1a_3$. Then $\beta_{3} = \zeta_2+ \alpha_1$, and $b_3 = z_1a_3+z_2a_1$. Thus $\zeta_2 = \beta_3- \alpha_1$ and $z_2 = (b_3- z_1a_3)/a_1$.

Case 2bⅲ. $\beta_{3} = \zeta_1+ \alpha_3$ and $b_3 = z_1a_3$. Then $\beta_{3}< \zeta_2+ \alpha_1$, and we will need to continue our procedure with $\beta_4$.

Repeating this procedure as necessary, say for a total of $N_2$ times, we solve for $\{ \zeta_2, z_2\}$. We represent this process as

We must have $N_2$ finite by (44) and the finiteness of the graph.

Step $(p+1)$. we solve for $z_{p+1}, \zeta_{p+1}$

Iterating the procedure above, suppose for $p\in \Bbb N$ we have

Here $N_p$ is chosen to be minimal, and so $\beta_{N_p} = \zeta_p+ \alpha_1$. We wish to solve for $\{ z_{p+1},\zeta_{p+1} \}$.

We can again distinguish three cases:

Case 1. $\beta_{(N_p+1)}\neq \zeta_j+ \alpha_k,\ \forall j\leq p, \ \forall k.$ Note that we know $\{ \zeta_j\}_1^p$ and $\{ \alpha_k\}$, so these inequalities are verifiable. In this case, we must have $\beta_{(N_p+1)} = \zeta_{p+1}+ \alpha_1$ and $a_1z_{p+1} = b_{(N_p+1)}$, so we have determined $z_{p+1}$ and $\zeta_{p+1}$ in this case.

Case 2. There exists an integer $Q$ and pairs $\{ \zeta_{j_n}, \alpha_{j_n}\}_{n = 1}^Q$, with $j_n\leq p$, such that

Note that all the numbers $\{ \zeta_{j_n}, \alpha_{j_n}\}$ have been determined, so these equations can be all verified. In this case, we have either

Case 2ⅰ. $b_{(N_p+1)}\neq z_{j_1}a_{j_1}+...+z_{j_Q}a_{j_Q}.$ It follows then that $\beta_{(N_p+1)} = \zeta_{p+1}+ \alpha_{1}$, and

We thus solve for $z_{p+1},\zeta_{p+1}$.

Case 2ⅱ. $b_{(N_p+1)} = z_{j_1}a_{j_1}+...+z_{j_Q}a_{j_Q}.$ It follows then that $\beta_{(N_p+1)}\neq \zeta_{p+1}+ \alpha_{1}$, and we have to repeat this process with $\beta_{(N_p+2)}$.

Repeating the reasoning in Case 2ii as often as necessary, we will eventually solve for $\{ z_{p+1},\zeta_{p+1}\}$. Thus,

Hence we can solve for $\{ \zeta_p: p\leq L \} ,\{ z_p: p\leq L\}$ for any positive integer $L$ given knowledge of $R_{01}^T,R_{12}^T$ for $T = T(L)$ sufficiently large.

Lemma 3.3. The sets $\{ \chi_j\}$, $\{ y_j\}$ can be determined by $R_{01}$ and $R_{12}$.

Proof. We identify the Heavyside functions in (40). By (41), (42), and (43), we get

Since the left hand side is known, we can argue as in Lemma 3.2 to solve for $\{ y_j,\ \eta_j \}$. The details are left to the reader.

Lemma 3.4. The function $\tilde{r}$ can be determined by $R_{01}$ and $R_{12}$.

Proof. We solve for $\tilde{r}$ with an iterative integral equation argument. By (40), we have

Hence by (41), (42), and (43), we calculate

We set $z: = t- \alpha_1 = t-\nu_1 = t-\ell_1$ and use that $\tilde{a}(s) = 0$ for $s<0$ to obtain

Setting $\alpha_0 = \nu_0 = 0$ for convenience, we introduce the number

Since we will be choosing finite $T$ and $t<T$, we have $\alpha >0$. The integral equation for $\tilde{r}$ can be solved by an iterative argument with a finite number of steps.

1) For $z<0$, we have $\tilde{r}(z) = 0$.

2) Suppose we have solved for $\tilde{r}(z)$ for $z<(n-1)\alpha$, $n\geq 1$. We will now suppose

and identify terms in (45) that we already know. We have for $k\geq 2$

For $s \geq (n-1)\alpha$ and $z<n\alpha$ we have

so

Similarly, for $k\geq 2$ we have $z+ \alpha_1- \alpha_k<(n-1)\alpha$, so

Combining (46) and (47) with (45), we get

This is a Volterra equation of the second kind, and thus we solve for $\tilde{r}(z)$ for $z$ in

Iterating this argument finitely many times, we will have solved for $\tilde{r} = \tilde{r}_{12}$, and hence $\tilde{R}^T_{12}$, on the interval $[0,T]$ for any $T>0$.

Case B: $M_{1} = 0$.

In this case, we must replace (42), (43) by

with piecewise continuous $r_{12}$ and continuous, piecewise $C^1$ function $\tilde{a}$. The argument is then a straightforward adaptation of Case A; the details are left to the reader.

Careful reading of Steps 2, 3 shows that we can choose any $T>2(\ell_1+\ell_{1j})$.

3.3.   Solving for $\tilde{R}_{22}$

The purpose of this subsection is to determine $\tilde{R}_{22}$. Mimicking the previous subsection, let $u^\delta$ solve (1)-(6), let $B(t) = u^\delta(v_{2},t)$ and let $f\in L^2(0,T)$. We have the following formula holding by the definition of response operators:

Of course $R_{22}(s)$ is assumed to be known. We determine $B$ as follows. We have from Step 2 that $A(t) = u^{\delta}(v_{1},t)$ is known. We identify $e_{12}$ as the interval $(0,\ell_2)$ with $v_{2}$ corresponding to $x = 0$. Then $B(t) = u^{f}(v_{2},t)$ arises as a solution to the following Cauchy problem on $e_2$, where we view $x$ as the "time" variable:

Since $q_2,\ell_2,$ and $R_{12}$ are all known, we can thus determine $B(t) = y(0,t)$.

The rest of the argument here is a straightforward adaptation of the previous subsection. The details are left to the reader.

Acknowledgments

We would like to thank the referee for his many suggestions that improved the exposition in this paper.