Irrigable measures for weighted irrigation plans

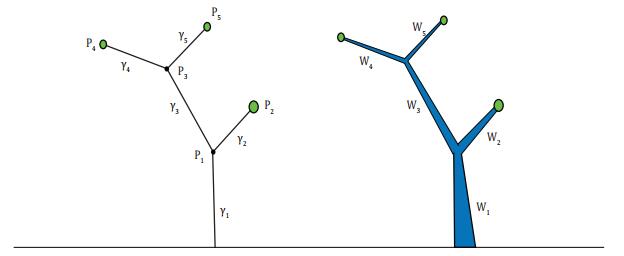
Left: A free standing tree with 5 branches. In this example, $ \mathcal{O}(1) = \{2,3 \},\mathcal{O}(3) = \{4,5\}, \mathcal{O}(2) = \mathcal{O}(4) = \mathcal{O}(5) = \emptyset $. Right: On each branch, the weight decreases as one moves from the lower portion to the tip

Left: Two finite truncation plans, showing three maximal $ \varepsilon $-good paths (thick lines) and six maximal $ \varepsilon' $-good paths (thin lines), for $ 0<\varepsilon'<\varepsilon $. Right: The three maximal $ \varepsilon $-good paths can be partitioned into five elementary branches, by the Path Splitting Algorithm

Left: The dyadic approxmiated measure $ \mu_1 $ is supported on the four centers $ x_1^1,\ldots,x^1_4 $ of small cubes. Right: Dyadic approximated measures corresponding to a family of partitions into dyadic cubes in $ \bf{R}^2 $

The dyadic irrigation plans in $ \bf{R}^2 $. Left: The dyadic irrigation plan $ \chi_1 $. The multiplicity on each branch equals to the mass on the terminal point. Right: The dyadic irrigation plan $ \chi_2 $. The particles are first transported to the 4 centers in $ \mathcal{P}_1 $, then on each center in $ \mathcal{P}_1 $, the particles are transported to the neighboring 4 centers in $ \mathcal{P}_2 $