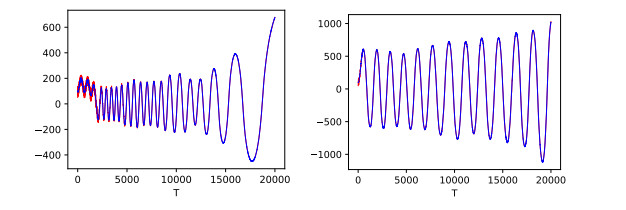
1.0, 5.0 ratios: 10/50 buyers (red) and 10/10 sellers (blue), mean price sequences; blue line hides in large part the red one
.This paper presents a development of the mathematical theory of swarms towards a systems approach to behavioral dynamics of social and economical systems. The modeling approach accounts for the ability of social entities are to develop a specific strategy which is heterogeneously distributed by interactions which are nonlinearly additive. A detailed application to the modeling of the dynamics of prices in the interaction between buyers and sellers is developed to describe the predictive ability of the model.
Citation: Nicola Bellomo, Sarah De Nigris, Damián Knopoff, Matteo Morini, Pietro Terna. Swarms dynamics approach to behavioral economy: Theoretical tools and price sequences[J]. Networks and Heterogeneous Media, 2020, 15(3): 353-368. doi: 10.3934/nhm.2020022
| [1] | Nicola Bellomo, Sarah De Nigris, Damián Knopoff, Matteo Morini, Pietro Terna . Swarms dynamics approach to behavioral economy: Theoretical tools and price sequences. Networks and Heterogeneous Media, 2020, 15(3): 353-368. doi: 10.3934/nhm.2020022 |
| [2] | Nicola Bellomo, Francesca Colasuonno, Damián Knopoff, Juan Soler . From a systems theory of sociology to modeling the onset and evolution of criminality. Networks and Heterogeneous Media, 2015, 10(3): 421-441. doi: 10.3934/nhm.2015.10.421 |
| [3] | Marina Dolfin, Mirosław Lachowicz . Modeling opinion dynamics: How the network enhances consensus. Networks and Heterogeneous Media, 2015, 10(4): 877-896. doi: 10.3934/nhm.2015.10.877 |
| [4] | Fabio Camilli, Italo Capuzzo Dolcetta, Maurizio Falcone . Preface. Networks and Heterogeneous Media, 2012, 7(2): i-ii. doi: 10.3934/nhm.2012.7.2i |
| [5] | Michele Gianfelice, Enza Orlandi . Dynamics and kinetic limit for a system of noiseless $d$-dimensional Vicsek-type particles. Networks and Heterogeneous Media, 2014, 9(2): 269-297. doi: 10.3934/nhm.2014.9.269 |
| [6] | A.C. Rocha, L.H.A. Monteiro . On the spread of charitable behavior in a social network: a model based on game theory. Networks and Heterogeneous Media, 2023, 18(2): 842-854. doi: 10.3934/nhm.2023036 |
| [7] | Rossella Della Marca, Nadia Loy, Andrea Tosin . An SIR–like kinetic model tracking individuals' viral load. Networks and Heterogeneous Media, 2022, 17(3): 467-494. doi: 10.3934/nhm.2022017 |
| [8] | Carlo Brugna, Giuseppe Toscani . Boltzmann-type models for price formation in the presence of behavioral aspects. Networks and Heterogeneous Media, 2015, 10(3): 543-557. doi: 10.3934/nhm.2015.10.543 |
| [9] | Qinglan Xia, Shaofeng Xu . On the ramified optimal allocation problem. Networks and Heterogeneous Media, 2013, 8(2): 591-624. doi: 10.3934/nhm.2013.8.591 |
| [10] | Sabrina Bonandin, Mattia Zanella . Effects of heterogeneous opinion interactions in many-agent systems for epidemic dynamics. Networks and Heterogeneous Media, 2024, 19(1): 235-261. doi: 10.3934/nhm.2024011 |
This paper presents a development of the mathematical theory of swarms towards a systems approach to behavioral dynamics of social and economical systems. The modeling approach accounts for the ability of social entities are to develop a specific strategy which is heterogeneously distributed by interactions which are nonlinearly additive. A detailed application to the modeling of the dynamics of prices in the interaction between buyers and sellers is developed to describe the predictive ability of the model.
A recent literature has shown a rapidly growing interest towards a systems approach to social dynamics and behavioral economy, where mathematical sciences are deemed to capture the complexity features of these systems under the influence of individual and collective human behaviors. As observed in [4], the emerging point of view is the interaction between economics, psychology, and sociology, which is no longer grounded on the traditional assumption of rational behaviors. Indeed, the scientific community supports the assumption that economics can be highly affected by rational or even irrational behaviors [1,10,41,55,56].
The general framework of behavioral economy is delivered in the books [58,59] by Richard Thaler, Nobel laureate. Additional hints suggest to go beyond the concept of rationality and to explore the role of ethical and unethical behaviors [34,36,52,53] which might lead to important social injustice, even in the wealth distribution. According to Angus Deaton [28], the dynamics of economy should not hide the important role of welfare distribution and social inequalities. In some cases, mathematical models might contribute to anticipate the discovery of rare events, say black swans [57], which might be induced by several concomitant and interactive causes [16].
A recent approach refers to developments of the mathematical tools of the kinetic theory and statistical mechanics towards the study of behavioral systems, social and economical. The development is achieved by taking mathematical models, for instance Fokker-Planck or Boltzmann equation [33], of the classical kinetic theory in the case of space homogeneity and replacing the velocity variable by new variables deemed to model social or economical expressions. This approach is documented in the book [49], where this topic has been developed from the modeling issues to computational tools.
We have selected, out of the recent literature, five interesting papers as examples of applications on opinion formation [6,22], on the interaction between wealth distribution and the dynamics of collective knowledge [50] and on price and good exchange dynamics in financial markets [23,24], where the last two papers chase objectives analogous to those of our paper. In detail, a deep analysis of stock prices, considering the role of opinions mainly in the behavior of the chartist agents is developed in [23], while a structure incorporating the Edgeworth box tool, which the authors employ in the presence of an agent-based system, characterizes [24]. In both cases, an appropriate set of hypotheses coming from the literature in strictly related to the results.
A parallel alternative appears to be the so-called kinetic theory of active particles, where the common feature with respect to [49] is that the dependent variable, deemed to model the state of the overall system, is a probability distribution function over the state of the interacting entities viewed as active (living) agents (particles). A systematic use of theoretical tools of stochastic, evolutionary game theory is applied to model interactions. This multiscale vision leads to differential structures suitable to capture the complexity features of living entities.
The aforementioned theoretical approach has been focused in [3] to the study of the dynamics of systems within the framework of behavioral economy. Detailed hints have been given in [3] to indicate how the overall systems can be subdivided into groups of interest, called functional subsystems, each of them expressing a specific social and/or economical strategy, and subsequently how these groups interact at various levels. This article refers to a general conceptual framework [17], where mathematics interacts with the so-called soft sciences. More recent developments are available in the surveys [4,25,31] as well as in the book [12], which combines tools of the mathematical kinetic theory with theoretical tools of behavioral game theory [37,40,48].
Mathematical models derived by the kinetic theory approach [12,17] refer to opinion formation on networks [30], to the role of nonlinear interactions in wealth dynamics[29], and to a mathematical interpretation of Acemoglu's trapping dynamics [32]. Additional literature has been developed to show how interactions between welfare policy and spread of political opinions might lead to radicalization [16], evolutionary economy [14], as well as to the interactions between welfare policy and onset and propagation of criminality [13,26]. The role of exogenous networks has been studied in [43,44]. An important feature of the mathematical theory is that interactions are nonlinearly additive and are allowed to depend on the probability distribution function, namely on the dependent variable. This specific feature generates conceptual difficulties which challenge mathematical sciences.
The mathematical approaches which have been outlined above have marched in parallel to classical agents methods [19,35,38,39,41,42], and nonlinear dynamical systems [9,18,20]. All different approaches present advantages as well as drawbacks so that it is worth developing scientific investigation to discover possible alternatives to the mathematical tools that have been briefly presented above.
Our paper is devoted to develop an approach based on a suitable development of the theory of swarms arguably initiated by the celebrated paper by Cucker and Smale [27] with the aim of developing a systems approach to behavioral dynamics of social and economical systems. The contents of our paper also accounts for some pioneer articles that have already introduced a swarm approach to model financial markets [2,7,8] as well as to the derivation of kinetic type models from the underlying description of interactions by individual based models [15]. In more detail, our paper is mainly focused on modeling and simulations with application to the study of price sequences, while the contents are presented throughout three more sections.
Section 2 presents our main theoretical result, namely the development of a systems approach based on the differential structures, derived by mathematical structures of the swarms theory, suitable to describe the dynamics of models of socio-economical systems inspired by the visionary Cucker-Smale theory of swarms [27].
Section 3 deals with a well defined case study, selected as a possible benchmark to test the approach proposed in this paper in view of further applications. In more detail, a model of price dynamics accounting for heterogeneous individual behaviors. Some sample simulations are developed to test the predictive ability of the model. It is shown that the approach leads to a consistent descriptive ability by employing a very parsimonious set of economic bases.
Section 4 looks at research perspectives focusing both on possible applications in behavioral economy, specifically the dynamics on networks and on space in general, modeling external actions, and on the interaction of price dynamics and other social-economical dynamics.
This section is devoted to the derivation of a differential system, inspired by the theory of swarms, to model a broad variety of social-economical systems. As it is known, modeling and simulations of real systems are developed, with predictive purposes or with explorative aims, to investigate the scenario of the possible trends of socio-economical systems depending on the parameters of models.
As mentioned in Section 1, we refer to the mathematical structures of swarm theory. Let us consider the dynamics of a swarm of
The scientific literature on swarms has been arguably initiated by physicists, while the interest of mathematicians has been boosted by the visionary paper [27]. An overview of the vast literature on this topic is far beyond the aims of our paper which consists in understanding how the structure delivered by the classical mathematical theory of swarms [6] can be modified towards the modeling of social and economical systems. Of course, the first step consists in setting the variables that can describe the individual state of the interacting entities. If particles are viewed as agents which carry a certain social variable, for instance a social or political opinion, an analogous structure has been used to study and control the dynamics of the collective behavior of one or more populations [46,51]. The concept of topological interactions in swarms has been introduced in [11], by which interactions occur with a fixed number of individuals rather than with those included in an influence domain.
Our approach refers to a large system of interacting individual living entities, called active particles, in short a-particles, subdivided into different groups of interest which, according to [4], can be called functional subsystems, in short FSs. This subdivision accounts for different objectives in each FS or for a different strategy to pursue them. This objective-strategy can be called activity which corresponds to the individual state of each individual entity.
The kinetic theory approach, briefly mentioned in Section 1, presents a number of advantages, but also some withdraws. For instance, the derivation of models requires the assumption of continuity of the dependent variable, which is the probability distribution function over the activity variable, can be admissible only for very many active particles. The dynamics is studied under the assumption that a-particles can communicate independently of their localization, hence space dynamics is not accounted for. Interactions occur either within each functional subsystem or across them. Proliferative/destructive events are not taken into account, hence the total number of a-particles is constant in time within each functional subsystem.
Firstly, a general mathematical structure is derived with the aim of providing the conceptual basis for the derivation of models, subsequently some constructive concepts are given as a first step towards the derivation of specific models, as the derivation of models can be achieved by a detailed modeling of interactions to be inserted into the aforementioned structure, and finally some hints towards the modeling of interactions are brought to the attention of the interested reader in view of the next section where a specific application is studied. This new conceptual approach leading should account, at least, of the following features:
- Social entities are able to develop a specific strategy which is heterogeneously distributed.
- Interactions are nonlinearly additive, can modify the activity in each FS.
- Asymmetric interactions can be taken into account.
The search for a general framework suitable to provide the conceptual basis to derive models of social/economical behavioral systems. We refer to a system constituted by
The rationale towards the derivation of models is proposed as follows:
1. A-particles are grouped into
2. The intensity by which each
3. Each particle feels the individual actions, corresponding both to micro-micro (individual based) interactions, from the other particles and the actions of each functional subsystem viewed as a whole, corresponding to micro-macro (mean field) interactions. In the general case both actions can occur across FSs.
4. Both micro-micro and micro-macro interactions depend nonlinearly on the microscopic state of the interacting pairs and on the mean value of the activity of the interacting micro and macro systems, respectively. Interactions can cause modification of the activity, while since proliferative and destructive events are not taken into account, the total number of a-particles
5. The derivation of specific models is in two steps, firstly a mathematical structure is derived accounting, still at a formal level, the interaction dynamics described in the above items, and subsequently by a detailed modeling of interactions referring to the specific system object of the modeling approach.
According to this representation
| Emi=1NiNi∑j=1umijwithN=n∑i=1Ni,andEm={Emi}, | (1) |
where first and second order moments provide the expected (or mean) activity and variance, respectively, while higher order moments give an information on the distortion.
Let us now introduce the following quantities deemed to model, still at a formal level, interactions:
The mathematical structure is obtained modeling the action given by the product
| {duijdt=vij,dvijdt=n∑p=1Np∑q=1ηpqij(u,v)φpqij(u,v)+n∑p=1μpij(u,Ep)ψpij(u,Ep), | (2) |
where
The mathematical structure (2), as mentioned, can be viewed as a formal framework towards the derivation of specific models by specializing the said structure by a detailed modeling of interactions. The derivation can be developed only referring to well defined case studies which might invoke as simplification of (2). Two different cases, among various possible ones, are reported below having in mind the dynamics of price formation.
Case 1. The following types of interactions are significant: micro-micro only across FSs and micro-macro only within the same FS. The mathematical structure can be particularized as follows:
| {duijdt=vij,dvijdt=n∑p=1Np∑q=1ηpqij(u,v)φpqij(u,v)+μiij(u,Ei)ψiij(u,Ei). | (3) |
Case 2. The following types of interactions are significant: micro-micro only within the same FS and micro-macro only across FSs. The mathematical structures is as follows:
| {duijdt=vij,dvijdt=Ni∑q=1ηiqij(u,v)φiqij(u,v)+n∑p=1μipij(u,Ep)ψipij(u,Ep). | (4) |
Some additional technical indications, somehow inspired to the rationale which guides the kinetic theory of active particles [12], can be given towards this aim.
Selection of the functional subsystems: The overall system is subdivided into groups, called i-functional subsystem, in short i-FS, within which individual entities, called ij-particles, share the same objective and the strategy to achieve it.
Interaction domain: Each ij-particle has an interaction domain
Sensitivity: Each ij-particle has a sensitivity domain
Interaction rates: The micro-micro interaction rate decays with a distance between the state of the ij-particle and the iq-particles in the sensitivity domain, while the macro-micro interaction rate decays with a distance between the state of the ij-particle and the first order moment of the iq-particles in the sensitivity domain.
Actions: All actions act in the sensitivity domain. The micro-micro action over the ij-particle is applied by all iq-particles, namely by particles of the same FS, while the macro-micro action over the ij-particle is applied by all p-FSs, with
The choice of the issue of price formation as a starting application for our methodological framework has two pillars: the possibility of creating clear boundaries to our search path; the significativeness of the results also in the presence of those boundaries.
Synthetically, the price formation in the real world—with both heterogeneity and realistic person to person interactions—is a puzzle. In an orthodox way, the explanation that the price theory suggests that the price formation is a classic microeconomic concept that uses the abstraction of supply and demand functions. The intersection of the two functions determines the appropriate price for a good or service. This construction allows for price adjustments as market conditions change, modifying the functions.
Using such mechanical aggregate explanation, what is missing is the role of individual agents, as buyers and sellers, in bargaining. The Appendix A of a recent book [45] is dedicated precisely to this problem, developing an agent-based model in the perspective of a simplified Hayekian market. This market structure is necessary for the macro model of the book [45], where agents' interaction is strategic for the construction of the simulation model, focusing correctly on the agents. The model, in this way, produces complex price sequences. A very interesting analysis of the so-called Hayek's market algorithm is in Bowles, Kirman, and Sethi [21].
A step ahead is in Nieddu [47], where the framework of the agents' behavior is sounder, following the Brownian Motion model to define agents' behavior [54], again generating an interesting price path over time.
Here, with the mathematical swarm particle perspective—with a rigorous formal background—we look for a further step in the fundamental analysis of price formation.
Is this step worth to be done? Recent literature ([60], [61]) demonstrates the centrality of price theory in the development of economic modeling.
Let us consider, as a simple - it might be the simplest - case study to show how the theory of active particle swarms, proposed in Section 2, can be applied and tested for a dynamics of a market where
We consider two populations, sellers and buyers, viewed as functional subsystems with
| u=(u1,…,us,…,uN)andw=(w1,…,w2b,…,wM), |
while the corresponding speeds are
| v=(v1,…,vs,…,vN)andz=(z1,…,zb,…,zM), |
where if both prices and related speeds are normalized with respect to their highest value at initial time
The mathematical structure corresponding to the setting given in the preceding subsection is a particularization of the general structure of Eq. (2) as follows:
| {dusdt=vs,dwbdt=zb,dvsdt=1MM∑q=1ηqs(us,w2q)φqs(us,wq,vs,zq)+μs(us,E1)ψs(us,E1),dzbdt=1NN∑q=1ηqb(wb,uq)φqb(wb,uq,zb,vq)+μb(wb,E2)ψb(ub,E2), | (5) |
for
Remark 1. The system presents asymmetry features which arise as the sellers' prices are public (one could think of price tags), while buyers' prices are unknown to the sellers. Therefore, the modeling of the interaction rates for the sellers should not include any attenuation related to the distance with respect to the buyers' prices, as these are inaccessible to them. On the other hand the interaction rates for the buyers should include some attenuation related to the distance with respect to the sellers' prices, as these are accessible to them.
The following assumptions, which take into account Remark 3.1, are proposed towards a minimal model to describe interactions:
1. The interaction rates for both micro-micro and macro-micro interactions asymmetrically decay with increasing metrics modeling the distance between the interacting entities starting from the same rates
| {ηbs≅η0,ηsb≅η0exp(−1ε|us−wb|wb), | (6) |
and
| {μs≅μ0μb≅μ0exp(−1ε|wb−E2|wb). | (7) |
2. The actions
| {φbs≅αussign(wb−us),φsb≅β(us−wb), | (8) |
and
| {ψs≅γ(E1−us),ψb≅δ(E2−ub). | (9) |
Replacing the description of interactions delivered in (6)–(9) into the general structure (structure-model) yields:
| {dusdt=vs,dwbdt=zb,dvsdt=αMM∑q=1ussign(wb−us)+ϵ1(E1−us),dzbdt=βNN∑q=1exp(−1ε|us−wb|wb)(us−wb)+ϵ2exp(−1ε|wb−E2|wb)(E2−ub), | (10) |
where time has been scaled with respect to
Remark 2. The sticking effect denotes that, as in the macro-offer curve analysis, the underlying difficulty to move prices, not only decreasing them by the so-called "menu costs". The action is equal to zero when extreme values are assigned to the prices, while if the price is higher than zero and lower than one, then a consensus dynamics occur, for instance if the buyer with price
Some essential premises to read the simulation results:
(i) we have no accounting effects on households' and firms' economy, so we consider price levels only as ordered numbers, accepting them also to be negative;
(ii) we are operating in a short term perspective as defined in economics: NB, what is relevant is not the length of the period under analysis, but the hypothesis that the productive factors are not changing (capital and labor, here represented by the number of sellers);
(iii) consistently with the (ii) statement, we do not consider new sellers' entries or existent sellers' exits in or from the market;
(iv) the statements (ii) and (iii) consequence is that any automatic price control mechanism is missing; instead, allowing the entry and exit mechanism, if prices go too high new sellers (firms) enter in the market increasing the offer side and lowering the prices, and vice versa;
(v) both in our construction and in reality—when price are exposed by the sellers (e.g., in the mall)—, buyers coordination is easier than that of the sellers, which ignore the reservation prices of the buyers (the max price that a buyer accepts to pay); sellers blindly react step by step to their successes (made a sale) or failures (no sale) in dealing;
(vi) consistently with (v), buyers very well coordinate their reservation prices because they see all the set of the sellers, which on turn receive the reactions of all the other buyers; sellers instead have to act on the basis of information collected observing buyers' decision without seeing their internal reservation prices; certainly, they have micro-macro (mean field) interactions with the other sellers;
(vii) observing the price standard-deviation within buyers and within sellers—relatively to different ratios buyers to sellers (in increasing order)—we can find a proxy of the market power of the buyers. As the ratio increases, the power of the buyers is imposing the sellers to differentiate their price proposals, while buyers' results are quite compact.
Figure 1 reports, in order of increasing ratios between buyers to sellers, the mean prices of the buyers (their reservation prices) and of the sellers (the exposed prices) in two simulation runs. In both cases, a realistic cyclical market emerges, with a more regular behavior in the second case, where we have a higher ratio buyers/sellers.
Figure 2 reports zoom on the final part of the two runs, showing how sellers fail to coordinate while buyers have very close prices, consistently with (vi) above.
We examine now how prices are differentiating within agents in each time step. In Figure 3, we follow the increasing ratios buyers to sellers. The two plots show that the standard deviation, measuring price differentiation within the agents' groups, is low and stable for the buyers and more relevant and quickly increasing for the sellers' group. Then it decreases if the ratio is
The graphs appearing in Figures 4 and 5 are meant to offer, for buyers and sellers respectively, a visual representation of the degree of coordination (either in- or counterphase) between agents belonging to the same
Formally, the graphs are heatmaps based on the correlation coefficient between individual time series of the prices. Blue tiles and red tiles show coordination and counter-coordination, respectively, for pairs of agents1. Washed out colors appear in the case of non-coordinated pairs, white representing perfect absence of correlation.
1 Diagonals are filled with ones by construction.
Each row represents a different scenario in terms of buyers-to-sellers ratio: top to bottom, 10 buyers / 10 sellers, 50 buyers / 10 sellers.
Each column, left to right, captures a different moment in the simulation, each one comprising a 500-steps long window: the beginning, a middle point, the end (steps [0-500], [9750-10250], [19500-20000]).
Buyers appear to be systematically well-coordinated (featuring a slight de-coherence in the final period for the 10 buyers / 10 sellers scenario).
Sellers appear to start moving in sync and end up losing synchronization along the way (even quicker for the 50:10 scenario).
A new mathematical approach, based on theoretical tools of swarms' theory, has been proposed in this paper and applied to modeling the dynamics of prices induced by the interactions between buyers and firms. Simulations have shown the ability to capture interesting features of the dynamics. Our approach goes beyond the continuity assumptions needed by the kinetic theory methods.
The flexibility of the proposed method to capture specific features of economical systems, motivates to develop further applications and economical studies. Bearing this perspective in mind, let us remain at a methodological level and let us outline some technical developments somewhat related to the application studied in our paper. The following specific hints are selected according to the authors' bias among various possible ones.
1. Modeling external effects by adding functional subsystem actions with the ability to modify price dynamics, from advertising by firms to political-economical control. Asymmetric actions should be taken into account also in this case.
2. Modeling the interaction of price dynamics with additional dynamics such as wealth distribution which definitely has a significant influence on the heterogeneous distribution of buyers followed with a feedback to seller firms.
3. Dynamics over networks to describe how the dynamics develop in nodes, and how it propagates on the network, being in turn modified by collective effects emerging from individual behaviors.
4. The mathematical structures proposed in our approach go beyond the celebrated Cucker-Smale approach, reviewed in [5]. Therefore a qualitative analysis of models appears to be an challenging objective worth to be developed accounting for the additional nonlinearities included in our paper to account for the attraction of individuals towards the mean value of the collectivity.
| [1] |
Emergence and persistence of inefficient states. Journal of European Economic Association (2011) 9: 177-208. 
|
| [2] |
Application of flocking mechanisms to the modeling of stochastic volatily. Math. Models Methods Appl. Sci. (2013) 23: 1603-1628. 
|
| [3] |
Towards a mathematical theory of complex socio-economical systems by functional subsystems representation. Kinetic & Related Models (2008) 1: 249-278. 
|
| [4] |
Stochastic evolutionary differential games toward a systems theory of behavioral social dynamics. Math. Models Methods Appl. Sci. (2016) 26: 1051-1093. 
|
| [5] |
Traffic, crowds, and swarms: From kinetic theory and multiscale methods to applications and research perspectives. Math. Models Methods Appl. Sci. (2019) 29: 1901-2005. 
|
| [6] | Recent advances in opinion modeling: Control and social influence. Active Particles, Advances in Theory, Models, and Applications, Model. Simul. Sci. Eng. Technol., Birkhäuser/Springer, Cham (2017) 1: 49-98. |
| [7] |
A particle model for herding phenomena induced by dynamic market signals. Journal of Statistical Physics (2019) 177: 365-398. 
|
| [8] |
A kinetic description for the herding behavior in financial market. Journal of Statistical Physics (2019) 176: 398-424. 
|
| [9] | (1994) Sociology and New Systems Theory - Toward a Theoretical Syntesis.Suny Press. |
| [10] |
P. Ball, Why Society is a Complex Matter, Springer-Verlag, 2012. |
| [11] |
Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proceedings of the Natural Academy of Sciences USA (2008) 105: 1232-1237. 
|
| [12] |
N. Bellomo, A. Bellouquid, L. Gibelli and N. Outada, A Quest Towards a Mathematical Theory of Living Systems, Modeling and Simulation in Science, Engineering and Technology, Birkhäuser/Springer, Cham, 2017. |
| [13] |
From a systems theory of sociology to modeling the onset and evolution of criminality. Netw. Heterog. Media (2015) 10: 421-441. 
|
| [14] |
From particles to firms: on the kinetic theory of climbing up evolutionary landscapes. Math. Models Methods Appl. Sci. (2020) 30: 1441-14060. 
|
| [15] |
A quest toward a mathematical theory of the dynamics of swarms. Math. Models Methods Appl. Sci. (2017) 27: 745-770. 
|
| [16] |
On the dynamics of social conflicts: Looking for the black swan. Kinet. Relat. Models (2013) 6: 459-479. 
|
| [17] |
On the difficult interplay between life "complexity" and mathematical sciences. Math. Models Methods Appl. Sci. (2013) 23: 1861-1913. 
|
| [18] |
J. Bissell, C. C. S. Caiado, M. Goldstein and B. Straughan, Tipping Points: Modelling Social Problems and Health, Wiley, London, 2015. |
| [19] |
R. Boero, M. Morini, M. Sonnessa and P. Terna, Agent-based Models of the Economy From Theories to Applications, Palgrave Macmillan, 2015. |
| [20] |
P. Bonacich and P. Lu, Introduction to Mathematical Sociology Princeton University Press, Princeton, NJ, 2012. |
| [21] |
Retrospectives: Friedrich hayek and the market algorithm. Journal of Economic Perspectives (2017) 31: 215-230. 
|
| [22] |
C. Brugna and G. Toscani, Kinetic models of opinion formation in the presence of personal conviction, Physical Review E, 92 (2015), 052818. |
| [23] |
Boltzmann-type models for price formation in the presence of behavioral aspects. Netw. Heterog. Media (2015) 10: 543-557. 
|
| [24] |
Kinetic models for goods exchange in a multi-agent market. Physica A (2018) 499: 362-375. 
|
| [25] | Stochastic differential "nonlinear" games modeling collective learning dynamics. Physics of Life Reviews (2016) 16: 123-139. |
| [26] | A kinetic theory approach to the modeling of complex living systems. Active Particles, Advances in Theory, Models, and Applications, Model. Simul. Sci. Eng. Technol., Birkhäuser/Springer, Cham (2017) 1: 229-258. |
| [27] |
Emergent behavior in flocks. IEEE Transactions on Automatic Control (2007) 52: 853-862. 
|
| [28] |
Measuring and understanding behavior, welfare, and poverty. American Economic Review (2016) 106: 1221-1243. 
|
| [29] |
Modeling altruism and selfishness in welfare dynamics: The role of nonlinear interactions. Mathematical Models and Methods in Applied Sciences (2014) 24: 2361-2381. 
|
| [30] |
Modeling opinion dynamics: How the network enhances consensus. Netw. Heterog. Media (2015) 10: 877-896. 
|
| [31] | Modeling human behaviour in economics and social science. Physics of Life Reviews (2017) 22: 1-21. |
| [32] |
Escaping the trap of 'blocking': A kinetic model linking economic development and political competition. Kinet. Relat. Models (2017) 10: 423-443. 
|
| [33] |
Fokker-Planck equations in the modeling of socio-economic phenomena. Math. Models Methods Appl. Sci. (2017) 27: 115-158. 
|
| [34] | Intrinsic honesty and the prevalence of rule violations across societies. Nature (2017) 531(7595): 496-499. |
| [35] |
S. Galam, Sociophysics. A Physicist's Modeling of Psycho-Political Phenomena, Understanding Complex Systems, Springer, New York, 2012. |
| [36] | The abundance effect: Unethical behavior in the presence of wealth. Organizational Behavior and Human Decision Processes (2009) 109: 142-155. |
| [37] |
H. Gintis, Game Theory Evolving, Second edition, Princeton University Press, Princeton NJ, 2009. |
| [38] |
R. Hegselmann, Thomas C. Shelling and James M. Sakoda: The intellectual, technical and social history of a model, Journal of Artificial Societies and Social Simulation, 20 (2017). |
| [39] |
Opinion dynamics under the influence of radical groups, charismatic and leaders, and other constant signals: A simple unifying model. Netw. Heterog. Media (2015) 10: 477-509. 
|
| [40] |
Evolutionary game dynamics. Bull. Amer. Math. Soc. (N.S.) (2003) 40: 479-519. 
|
| [41] |
A. Kirman, Complex Economics: Individual and Collective Rationality, Routledge, London, 2011. |
| [42] |
A. P. Kirman and J. B. Zimmermann, Economics with Heterogeneous Interacting Agents, Lecture Notes in Economics and Mathematical Systems, 503. Springer-Verlag, Berlin, 2001. |
| [43] |
On the modeling of migration phenomena on small networks. Math. Models Methods Appl. Sci. (2013) 23: 541-563. 
|
| [44] |
On a mathematical theory of complex systems on networks with application to opinion formation. Math. Models Methods Appl. Sci. (2014) 24: 405-426. 
|
| [45] |
(2019) Rethinking Macroeconomics with Endogenous Market Structure.Cambridge University Press. 
|
| [46] |
Social dynamics models with time-varying influence. Math. Models Methods Appl. Sci. (2019) 29: 681-716. 
|
| [47] |
M. Nieddu, Brownian and More Complex Agents to Explain Markets Behavior, Master's thesis, University of Torino, 2018, https://terna.to.it/tesi/nieddu.pdf. |
| [48] |
M. A. Nowak, Evolutionary Dynamics. Exploring the Equations of Life, The Belknap Press of Harvard University Press, Cambridge, MA, 2006. |
| [49] |
L. Pareschi and G. Toscani, Interacting Multiagent Systems: Kinetic Equations and Monte Carlo Methods, Oxford University Press, Oxford, 2013. |
| [50] |
L. Pareschi and G. Toscani, Wealth distribution and collective knowledge: A Boltzmann approach, Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci., 372 (2014), 20130396, 15 pp. |
| [51] |
Sparse control of Hegselmann-Krause models: Black hole and declustering. SIAM Journal on Control and Optimization (2019) 57: 2628-2659. 
|
| [52] |
Higher social class predicts increased unethical behavior. Proceedings of the Natural Academy of Sciences USA (2014) 109: 4086-4091. 
|
| [53] | Corruption corrupts: Society-level rule violations affect individuals' intrinsic honesty. Nature (2016) 53: 456-457. |
| [54] |
F. Schweitzer, Brownian Agents and Active Particles: Collective Dynamics in the Natural and Social Sciences, Springer Series in Synergetics, Springer-Verlag, Berlin, 2003. |
| [55] |
K. Sigmund, The Calculus of Selfishness, Princeton Series in Theoretical and Computational Biology, Princeton University Press, Princeton, NJ, 2010. |
| [56] |
Information and the change in the paradigm in economics. The American Economic Review (2009) 92: 460-501. 
|
| [57] |
N. N. Taleb, The Black Swan: The Impact of the Highly Improbable, Random House, New York City, 2007. |
| [58] |
R. H. Thaler, Misbehaving: The Making of Behavioral Economics, W. W. Norton & Company, New York, 2015. |
| [59] | Behavioral economics: Past, present, and future. The American Economic Review (2016) 106: 1577-1600. |
| [60] |
T. A. Weber, Price theory in economics, in Ö. Özer, and R. Phillips, The Oxford Handbook of Pricing Management, (2012), 281–340. |
| [61] |
Price theory. Journal of Economic Literature (2019) 57: 329-384. 
|
| 1. | Nicola Bellomo, Damián A. Knopoff, Pietro Terna, Special Issue “Kinetic Theory and Swarming Tools to Modeling Complex Systems—Symmetry problems in the Science of Living Systems”—Editorial and Research Perspectives, 2020, 12, 2073-8994, 456, 10.3390/sym12030456 | |
| 2. | Damian Knopoff, Valeria Secchini, Pietro Terna, Cherry Picking: Consumer Choices in Swarm Dynamics, Considering Price and Quality of Goods, 2020, 12, 2073-8994, 1912, 10.3390/sym12111912 | |
| 3. | Mirosław Lachowicz, Mateusz Dȩbowski, Diauxic Growth at the Mesoscopic Scale, 2020, 22, 1099-4300, 1280, 10.3390/e22111280 | |
| 4. | Nicola Bellomo, Seung-Yeal Ha, Nisrine Outada, G. Buttazzo, E. Casas, L. de Teresa, R. Glowinsk, G. Leugering, E. Trélat, X. Zhang, Towards a mathematical theory of behavioral swarms, 2020, 26, 1292-8119, 125, 10.1051/cocv/2020071 | |
| 5. | Nicola Bellomo, Diletta Burini, Giovanni Dosi, Livio Gibelli, Damian Knopoff, Nisrine Outada, Pietro Terna, Maria Enrica Virgillito, What is life? A perspective of the mathematical kinetic theory of active particles, 2021, 31, 0218-2025, 1821, 10.1142/S0218202521500408 | |
| 6. | N. Bellomo, M. Esfahanian, V. Secchini, P. Terna, What is life? Active particles tools towards behavioral dynamics in social-biology and economics, 2022, 43, 15710645, 189, 10.1016/j.plrev.2022.10.001 | |
| 7. | Dongnam Ko, Seung-Yeal Ha, Euntaek Lee, Woojoo Shim, Collective behaviors of stochastic agent-based models and applications to finance and optimization, 2023, 33, 0218-2025, 1373, 10.1142/S021820252350032X | |
| 8. | Nicola Bellomo, Diletta Burini, Valeria Secchini, Pietro Terna, 2024, 9781009548755, 10.1017/9781009548755 |
1.0, 5.0 ratios: 10/50 buyers (red) and 10/10 sellers (blue), mean price sequences; blue line hides in large part the red one
1.0, 5.0 ratio: 10/50 buyers (red) and 10/10 sellers (blue), zoom on individual price sequences. Y axes do not share the same scale
1.0, 5.0 ratio: 10/50 buyers (red) and 10/10 sellers (blue), standard deviation of mean prices within buyers and within sellers over time
Buyers
Sellers