1. Introduction

Our fundamental understanding of brain (dys)functions is today at a cross-road. While decades of concerted research led to immense progresses in the field, understanding, repairing, or enhancing the brain still represent the greatest challenges in science and engineering. Recently, advances in nanotechnologies paved the way to a potential revolution in Neuroscience, inspiring many investigators and offering novel tools for studying the brain at the nanoscale [1]. Progresses in material science in particular offered novel perspectives for identifying new ways of repairing and interfacing the brain at the cellular and molecular levels. In fact, micro- and nanostructured materials display intriguing geometrical similarities with the (sub)cellular organization of brain, and have been repeatedly considered as a potential new substrate for engineering future neuroprosthetics [2,3] and novel electrodics. Ultimately, the goal is developing micro- and nanosized sensors and actuators, capable of functional interfacing with the biological tissue and with individual nerve cells at mechanical, chemical, and electrical levels. At the same time, interest for overcoming existing limitations of microfabrication technologies and conventional in vitro interfacing techniques [4,5], inherently leading to 2-dimensional neuronal networks, increasingly became widespread. Thus, active research started on 3-dimensional scaffolding for the formation of functional neuronal networks [6] and of brain-like layered tissue [7,8].

Along these lines, Graphene [9,10] as well as other Carbon-based nanomaterials such as Carbon nanotubes became extremely interesting for Neuroscientists, who started numerous studies on their exploitation as nanoscale electrodes, hybrid devices, or nanostructured substrates for neuronal growth and regeneration [2,3,11], investing on their unrivalled electrochemical properties [12,13,14,15,16,17,18,19]. Graphene in particular, a 2D monoatomic layer of C atoms arranged in a honeycomb lattice, is the youngest member of Carbon-based nanomaterials family. Its existence has been first reported in 2004 [13], and rapidly attracted huge attention, as proved by the more than 10’000 papers published on this topic.

Existing biological investigations of Graphene Oxide (GO) and reduced Graphene Oxide (rGO) are becoming increasingly common and today they range from drug delivery and gene therapy [20] to biosensors [21], as well as from electrodes for electrical extracellular stimulation of excitable cells [22] to photothermal tumour ablation therapy [23] and tissue scaffolding [24]. In Neuroscience, GO and rGO have been so far considered as substrates for the growth of neurons [25,26] and for the differentiation of stem cells [27,28], as well as employed as 3-dimensional scaffolds for neural stem cells [29]. Furthermore, Graphene has also recently been exploited in the fabrication of transparent neural electrode arrays [30,31] for both in vivo and ex vivo electrophysiological and neuroimaging applications. As these applications could lead to long-term, or even chronic, Graphene electrodes implants, we feel that investigations of the elementary properties of GO and rGO in terms of cytotoxicity as well as alteration of the electrical phenotype of cells and networks as observed with other nanostructured materials [2,11], deserves more attention. Particularly the use of primary mammalian neurons instead of pluripotent or immortalised cell lines is of great importance for future preclinical translation studies.

In this brief contribution, we compare the properties of GO and rGO, obtained by spin coating onto conventional glass coverslips, as substrates for neuronal growth, studying their biocompatibility and whether the electrical properties of neurons and networks are altered.

2. Materials and Methods

2.1. GO and rGO substrates preparation and characterization

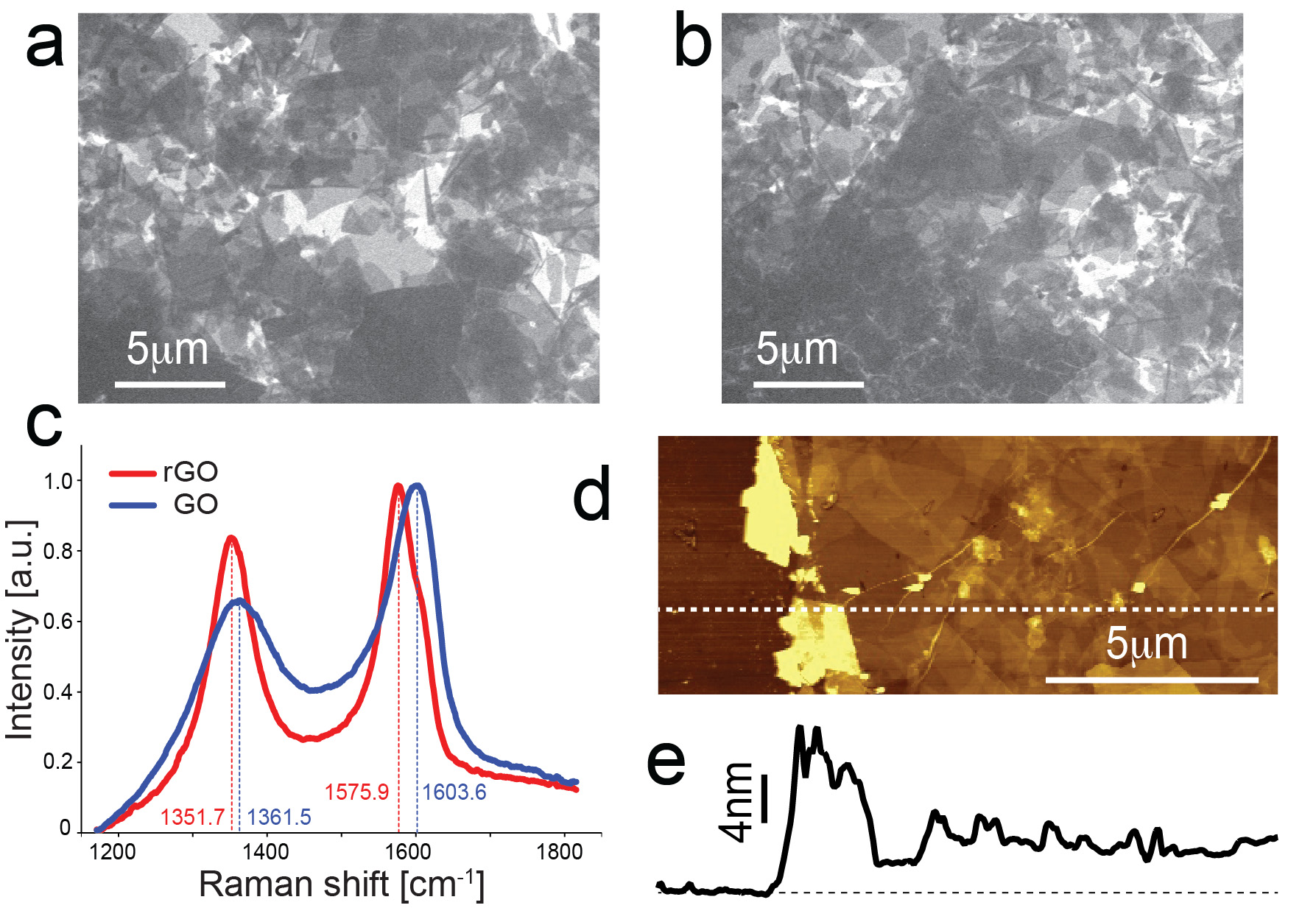
GO substrates were prepared by spin coating (2000 rpm, 30 s) GO solution (2mg/ml; Graphene Supermarket, USA) over glass coverslips.

Reduction of GO into rGO was carried electrochemically (Autolab Potentiostat, Metrohm, Singapore), upon immersing GO/glass substrates into a Sodium Phosphate buffer solution (pH = 4.5). The substrates were connected to a working electrode, while an Ag/AgCl electrode and a Pt mesh were used as reference and counter electrodes, respectively. Chronoamperometry was used holding GO/glass substrates at −0.9 V for 1 min. Substrates were then rinsed with deionized water and dried on a heater at 100 °C for 2 min. The morphology of GO and rGO flakes was characterised by Scanning Electron Microscopy (Figure 1a-b) (SEM; FEGSEM JSM 7600F, Jeol, USA), while Atomic Force Microscopy (AFM, ICON-PKG, Bruker, USA) was employed to determine the thickness of GO and rGO layers (Figure 1d-e) by characterising the boundary of the GO/rGO layer and the glass, after exposing by localised minimal scratching the underlying glass layer (Figure 1d). Raman spectra of GO and rGO substrates were finally acquired with a spectrometer (excitation wavelength: 488 nm; Jobin Yvon T64000, Horiba, Japan) at backscattering configuration (Figure 1c).

Figure 1. Characterization of the rGO/GO substrates. Images of GO (a) and rGO (b) spin-coated on glass, obtained by scanning electron microscopy with a 5000 times magnification, reveal an even distribution of the flakes on the entire glass substrate. Spectra of rGO/GO (c) show peaks at characteristic Raman shifts typical of Graphene, while Atomic Force Microscopy shows a 4 nm high step profile (e) at the boundary between rGO/GO and the underlying glass substrate, exposed upon scratching (d).

DownLoad: Full-Size ImgPowerPoint

2.2. Culturing of mammalian primary cortical neurons

GO/rGO were employed as substrate for neuronal culturing and compared to control conditions, represented by the use of standard glass coverslips. To ensure microbiological sterility, all GO/rGO and control substrates were first autoclaved, upon high-pressure saturated steam at 121 °C for 30 min (SA-260FA, Sturdy Industrial Co., LTD, Taiwan). All substrates were then coated with Polyethyleneimine (PEI, Sigma-Aldrich, Belgium) [32], by soaking their surface in a 0.1% PEI solution (w/v) overnight, and afterwards rinsed in deionized water and left drying at room temperature, prior to cell seeding. No adequate cell adhesion was ever observed in the lack of PEI treatment (not shown).

Rat primary neuronal cultures were obtained by standard methods and in accordance with national and institutional guidelines on animal experimentation. Briefly, cortices were dissected from newborn (i.e., postnatal day 0) Wistar rats (Charles River, France), sliced, digested in a trypsin solution (0.025%), and then mechanically dissociated, using repeated passage through the tip of a small glass pipette. Prior to seeding, cells were centrifuged and suspended in Modified Essential Medium supplemented with 50µg/mL gentamycin, 2M glucose, 5% horse serum, and 200mM l-glutamine (Sigma-Aldrich, Belgium). Cells were seeded at a density of ~1000 mm⁻², ensuring rapid maturation of fully functional neuronal networks ex vivo [33].

2.3. Cell viability

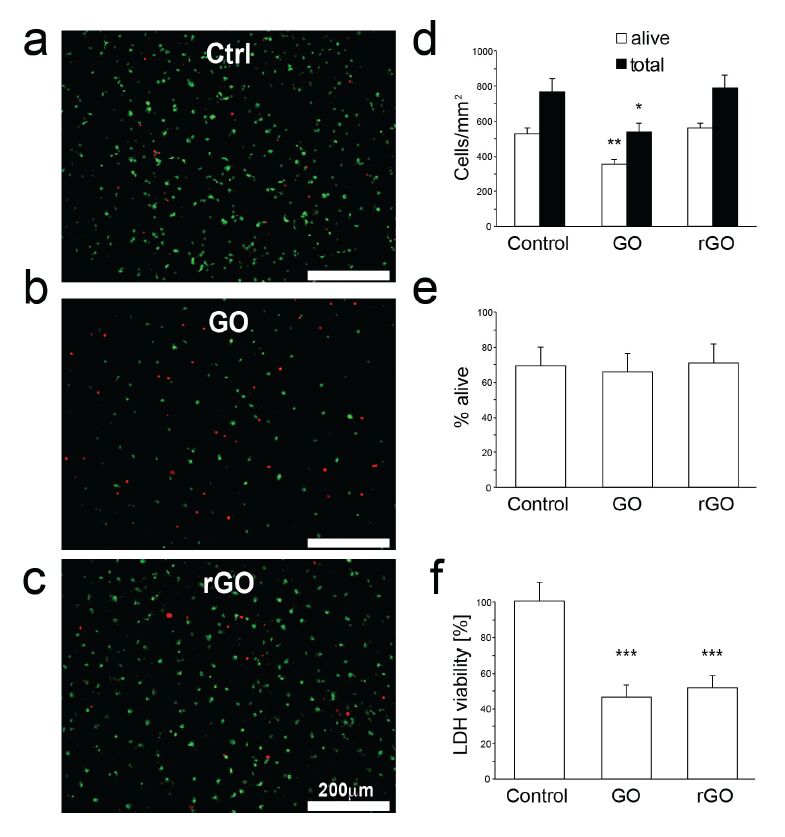
To assess GO/rGO substrates biocompatibility in terms of cell adhesion and viability, the Live/Dead Cell double staining assay kit (Sigma-Aldrich, Belgium) was performed in neuronal cultures 9 days in vitro (DIVs) after plating. Four coverslips for each of the three conditions (i.e., control, GO and rGO), obtained over two distinct culture preparations, were stained. Digital photos from six distinct fields of view for each sample (Figure 2a-c) were acquired using a fluorescence microscope (BX51, Olympus Life Sciences, Belgium) with green (U-MWIBA3, 460-495 nm) and red (U-MWIGA3, 530-550nm) filters, equipped with a digital camera (DP71, Olympus Life Sciences, Belgium). The CellSens software (Olympus Life Sciences, Belgium) was used for image acquisition. Cells were counted using the Cell Counter plugin of ImageJ 1.47v analysis system [34], and densities of alive cells were computed as the average across 24 different images (Figure 2d-e).

Figure 2. Viability and cytotoxicity of culture substrates. Fluorescence microscopy images (a-c) show living (green) and dead (red) cells. Cell densities (d) and their fraction (e) are quantified by automated cell count and referred to individual substrates. Further cytotoxicity tests revealed potential suboptimal Graphene surface treatment, when compared to control conditions.

DownLoad: Full-Size ImgPowerPoint

To indirectly quantify cell plasma membrane damage or rupture, and thus evaluate cytotoxicity of GO and rGO, the lactate dehydrogenase (LDH) assay test (Sigma Aldrich, Belgium) was used at 9 DIVs. Cell viability was calculated (Figure 2f) as reported in literature [35,36].

2.4. Cellular electrophysiology

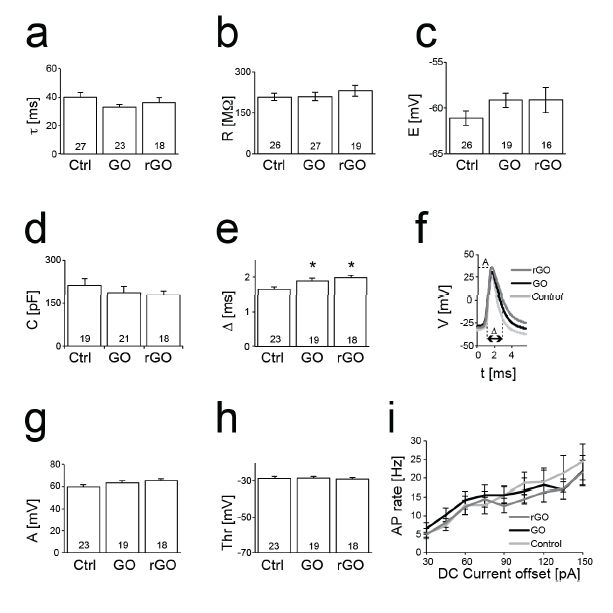
Whole-cell patch-clamp electrophysiological recordings were carried out at 34°C from the soma of neurons, at 9-13 DIVs. Intracellular electrical signals were amplified by an Axon Multiclamp 700B Amplifier (Molecular Devices, USA), under voltage- or current-clamp, controlled by the LCG software [37]. Patch pipettes were pulled from standard borosilicate glass (1B150F-4, World Precision Instruments, USA) and filled with solution containing (in mM): 135 K-gluconate, 4 NaCl, 10 HEPES, 10 PC-Na₂, 0.2 EGTA, 4 ATP-Mg²⁺, and 0.3 GTP-Na₂; pH 7.3 titrated with KOH, resulting in an electrical impedance of 6-8 MΩ. The extracellular solution contained (in mM): 145 NaCl, 4 KCl, 2 Na-pyruvate, 5 Hepes, 5 glucose, 2 CaCl₂, and 1 MgCl₂; pH adjusted to 7.4 with NaOH. In order to assess passive and excitable electrical properties of single neurons, ad hoc current stimulation step-waveforms were injected to estimate the effective membrane time constant and the apparent input resistance (Figure 3a-d). Estimates of the resting membrane potential, as well as the spontaneous emission of action potential were obtained without injecting any stimulus (Figure 4). All recordings were analysed using custom MATLAB scripts (The Mathworks, Natik, USA).

Figure 3. Single-cell passive and excitable electrical phenotype is largely unaffected by the growth substrate. No differences were observed for membrane time constant τ, input resistance R, resting potential E, and membrane capacitance C (a-d). Similarly, active excitable electrical properties (e-h; f, Control: n = 23, GO: n = 19, rGO: n = 18; i, Control: n = 16, GO: n = 14, rGO: n = 16) were unaltered, with the minor yet significant exception of the AP peak amplitude (e). Values inside histograms indicate the number of patched neurons (a-e, g-h).

DownLoad: Full-Size ImgPowerPoint

Figure 4. Network-level electrical phenotype is largely unaffected by the growth substrate. No major differences were observed for the rate of spontaneous occurrence of APs (a) and of bursts of APs (b), as also demonstrated by representative raw intracellular voltage recordings (c-d). Values above box-and-whisker plots (a) and inside histograms (b) indicate the number of patched neurons.

DownLoad: Full-Size ImgPowerPoint

2.5. Statistical analysis

The normality of each data set was tested by the Lilliefors test and subsequent statistical analysis was performed accordingly. For non-normal distributions, Wilcoxon rank sum test was used, while Student’s t-test was employed otherwise. Statistical significance has been reported in the figures as p < 0.05 (*), p < 0.005 (**), and p < 0.0005 (***). Data are presented as percentage ± ratio error, as mean ± standard error of the mean (SEM) for normal distributions, and as median and interquartile range otherwise.

3. Results and Discussion

3.1. Characterization of the rGO/GO substrates

Substrates were characterized using Scanning Electron Microscopy (SEM, Figure 1a-b), Atomic Force Microscopy (AFM, Figure 1d-e), and Raman spectroscopy (Figure 1c). SEM revealed an excellent coverage of GO and rGO flakes, over the entire surface of the glass substrates (Figure 1a-b).

The Raman spectra of GO and rGO samples reveal two of dominant peaks, D and G, present in Graphene [38,39,40], centered at 1361 and 1603 cm⁻¹ for GO, and at 1351 and 1575 cm⁻¹ for rGO (Figure 1c). As expected, the ratio of the amplitude of those peaks increases, confirming the successful GO reduction [41,42].

The height profile of deposited Graphene was obtained by AFM at the boundary between rGO/GO and the underlying glass, and revealed a 4 nm thick layer for both samples, with a root mean square value of 2.4 nm (Figure 1d-e).

3.2. Cell viability

A standard assay for cell viability, based on bath application of calcein AM and ethidium homodimer-1 solutions and their read out by epifluorescence, was employed to perform a quantitative analysis of cell viability upon measurements of (live) cell density (Figure 2a-c). The quantification of microscopy images revealed as expected that the total cell density after 9 DIVs decreased to ~50% of the initial seeding density, for both control and rGO. However, the cell density decreased to ~35% of the initial seeding density, for GO substrates (Figure 2d). Interestingly however, the percentage of living cells of out the total calculated for each condition was not significantly different across the conditions, including GO and rGO. Although GO substrates are atomically rougher than rGO [43,44] and thus in principle more likely to promote neuronal adhesion, its superficial charge is known to be more negative than rGO [45,46]. We speculate that the last property might have been then predominant, under our culture conditions, and determining a lower cell adhesion performance in GO compared to rGO and control conditions [47].

We also assessed cytotoxicity of GO and rGO by the lactate dehydrogenase assay (LDH, Sigma Aldrich, Belgium) and observed generally higher membrane damage for neurons grown on GO and rGO, with respect to control conditions (Figure 2f). While this is partly at odd with the clear results of overall cell viability and cellular electrophysiology (Figure 3-4), incongruity might be attributed to suboptimal properties of the Graphene surface coating, prior to cell seeding (i.e., by PEI), or to incompatibility of the LDH assay with the Graphene substrate.

3.3. Cellular Electrophysiology

To investigate the electrical phenotype of neuronal cells growing and establishing functional neuronal networks on GO and rGO substrates, patch-clamp recordings were performed. Live neurons, identified under differential interference contrast videomicroscopy by their morphology and their ability to respond with a sustained train of action potential upon external electrical stimulation, were recorded in whole-cell configuration, after establishing a giga-ohm seal from the cell somata. A variety of current-clamp stimulation waveforms were injected somatically, in order to infer the passive and excitable electrical properties of neuronal membranes (Figure 3). These were the membrane time constant (τ, Figure 3a), the apparent input resistance (R, Figure 3b), the resting membrane potential (E, Figure 3c), the cell capacitance (C, Figure 3d), the width of action potentials (APs) at half-amplitude (Δ, Figure 3e-d), the peak AP amplitude (Figure 3g), the AP threshold (Figure 3h), and the rate of AP emission evoked by external DC current pulses (Figure 3i). Passive properties (R, E, C, τ) did not significantly differed for neurons grown on GO and rGO, compared to control conditions, and also active membrane properties were comparable, with the exception of the peak AP amplitude that was slightly, but significantly larger on GO and rGO, compared to control. Importantly, the functional relationships between the output AP rate and the input injected current amplitude (Figure 3i) of neurons growing on GO and rGO were undistinguishable, upon removing to each neuron its own rheobase current, for the sake of comparison. Small but significant differences were instead observed solely on the peak AP amplitude (Figure 3e), potentially attributed to marginal hete rogeneity of ionic channels expression, (e.g., K_V) whose density and membrane distribution is known to affect AP shape [48].

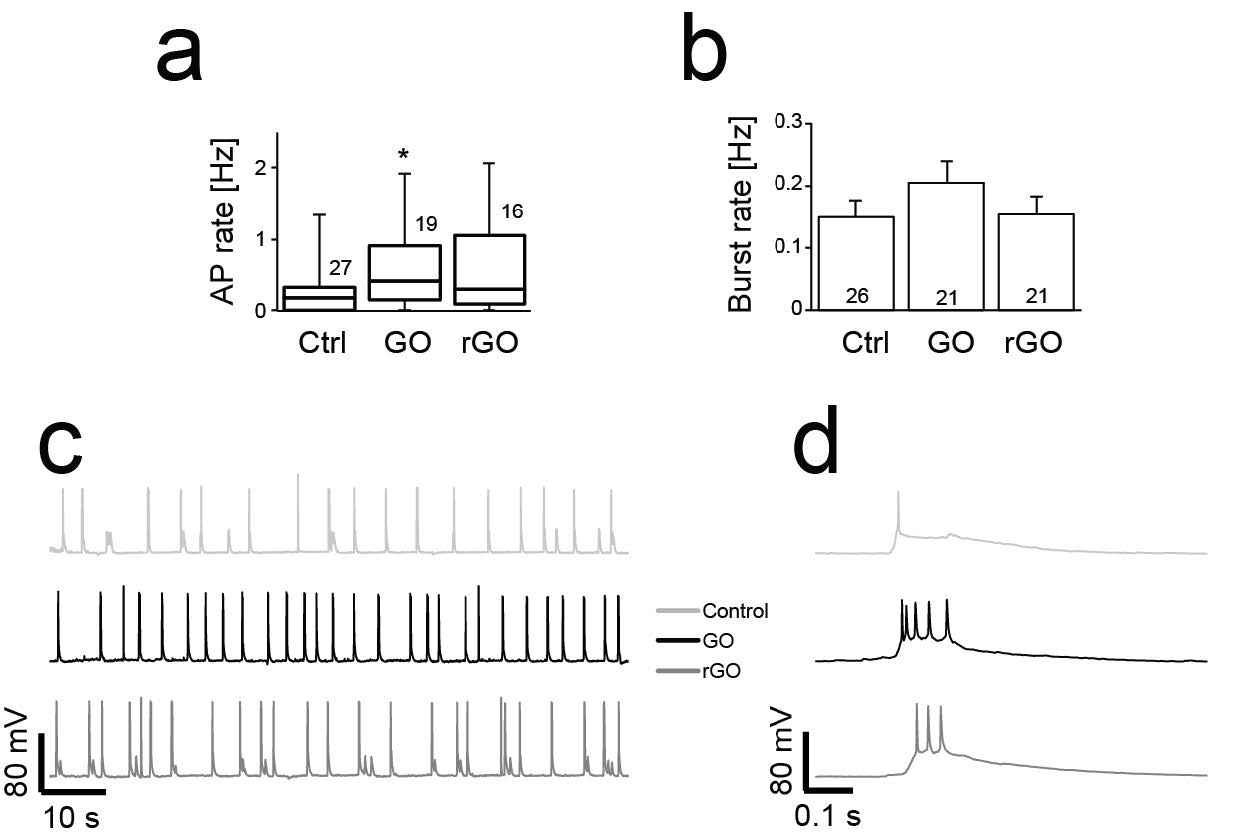
The same recording technique, enable us to indirectly infer network properties, by monitoring the spontaneous AP firing rate and frequency of AP burst discharges (Figure 4). When compared to control conditions, neuronal networks formed on GO and rGO had slightly higher spontaneous activity (Figure 4a-b), significant for GO only, suggesting an earlier formation of synaptic connections or marginally stronger synaptic connectivity than control. Representative intracellular recordings of spontaneous activity are shown in Figure 4c-d.

A corresponding increase in spontaneous postsynaptic currents amplitudes, measured with GO under voltage-clamp conditions, was also observed (not shown).

While distinct network-level electrical phenotype have been reported for neurons coupled to conductive thin-films of carbon nanotubes [11,49], and attributed to specific electrical properties of the substrate [2], GO and rGO seem to largely leave neuronal network formation ex vivo unaltered.

Nonetheless, neurons and neural stem cells growing on Graphene [25] and surface-modified GO [47] have increased length and number of neurites [50], which might account for enhanced network connectivity and thus explain the observed increased network activity, despite the reduction in absolute number of neurons. Indeed, number of neurons, efficacy of excitatory synaptic connections or their overall number all influences the rate of spontaneous electrical activity in vitro [51]. We hypothesize therefore that the slightly increased spontaneous AP firing, observed for neurons grown on GO, is the result of an increased number or efficacy of excitatory synaptic connections rather than a consequence of the absolute number of viable cells. This is supported by the well-known homeostatic scaling of synaptic efficacy [55] and by the variation in the ration of synapses-per-neuron during neuronal maturation [56].

On the other side, it has been demonstrated that firing frequency depends on neuronal density [52,53,54]: very dense cultures or very sparse display lower levels of spontaneous AP firing, than medium dense cultures. Here, we observed generally both a decreased total number of adhered cells and an increased spontaneous activity on GO, confirming the relationship between density and activity, while excluding a direct alteration of network formation by GO.

Similarly, no significant differences were observed also in the rate of occurrence of bursts of APs (Figure 4b), further indicating that recurrent excitatory connections were not altered by GO or rGO [51].

4. Conclusions

In this brief report we presented, to the best of our knowledge, a first quantitative comparison between GO and rGO as substrates for neuronal growth, employing mammalian primary cortical neurons. We found that GO and rGO are suitable candidates for neuronal interfacing, though rGO displayed better performances than GO, and that both allow the formation of a fully developed and active neuronal network. The electrical phenotype of individual neurons did not appeared altered by the choice of the substrate, while small but significant differences were found in the spontaneous rate of AP firing, greater for neurons grown on GO with respect to both control and rGO conditions.

Acknowledgement

We are grateful to Drs. P. De Marco and G. Panuccio for discussions, and to Mr. D. Van Dyck and M. Wijnants for excellent technical assistance. Financial support from the European Commission (FP7-PEOPLE-IEF “INCA-NANEP”, contract n. 328214; FP7-NMP “MERIDIAN”, contract n. 280778-02; FP7-“BrainLeap”, contract n. 306502), the Flanders Research Foundation (FWO, contract no. G088812N), and the Belgian Science Policy Office (BELSPO) is kindly acknowledged. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Contributions

AMM and AM performed electrophysiological experiments, analysed data and wrote the paper. JM performed the viability studies and earlier electrophysiological experiments. FV characterized GO and rGO substrates. AMHN prepared and characterized GO and rGO substrates. LKP, MN, and MG designed and supervised the research. All authors read and approved the final manuscript.

Conflict of Interest

All authors declare no conflict of interest in this paper.