The band-gap structure of the spectrum in a periodic medium of masonry type

1.   Introduction

1.1.   Statement of the problem

Let $\Omega^0 = (-l_1, l_1)\times (-l_2, l_2)$ be a rectangle containing another, deformed rectangle $\Omega^h$ with curved sides, Fig. 1, a,

where $h>0$ is a small parameter and $H^\pm_j$ are positive profile functions, which are smooth in the variable $x_{3-j}\in [-l_j, l_j]$. We will treat the plane ${\mathbb R}^2$ as paved by the shifts

of the periodicity cell $\Omega^0$. In the plane, we consider the spectral problem for an elliptic system of second-order differential equations

and its variational form

Let us explain the notation. The number $\lambda^h$ is a spectral parameter and $u^h = (u^h_1, \dots, u^h_J)^\top$ is a column of functions so that $\top$ stands for the transposition. In (3), $L^h(x, \nabla)$ is a $J\times J$-matrix of differential operators,

where $D(\nabla)$ is a $N\times J$-matrix of first-order homogeneous differential operators with constant (complex) coefficients and $D(\nabla)^\ast = \overline{D(-\nabla)}^\top$ is the adjoint of $D(\nabla)$, while $A^h$ and $B^h$ are Hermitian matrix functions of sizes $N\times N$ and $J\times J$, respectively. These matrices are assumed piecewise constant and of high contrast, depending on the small parameter $h$ and the subdomain $\Omega^h$,

where $A^\bullet$, $A^\circ$ and $B^\bullet$, $B^\circ$ are positive definite, constant matrices. Moreover, $A^h$ and $B^h$ are extended periodically to the plane $\mathbb{R}^2$:

for all $x \in \Omega^0$ and $\theta \in \mathbb{Z}^2$.

Furthermore, in (4) $a^h$ and $b^h$ are Hermitian sesquilinear forms,

where $(\, , )_\Xi$ is the natural scalar product in the Lebesgue space $L^2(\Xi)^m$, which is either scalar $(m = 1)$, or vectorial $(m>1)$. In (4), $H^1(\Xi^h)$ stands for the standard Sobolev space, while the superscript $J$ indicates the number of the components of the test vector functions $v^h$; this superscript is omitted in the notation of norms and scalar products.

As a consequence of our assumptions, the operator (5) is formally self-adjoint and the forms (7) are positive.

The main goal of our paper is to describe the asymptotic behavior of the spectrum of the problem (4) when $h\rightarrow+0$. For the formal asymptotic procedure, we assume that the exponents in (6) satisfy

In the framework of elastic materials, see Example 1.2, this means that the material in $\Omega^h$ is much harder and much heavier than in $\Gamma^h$, provided $\alpha_B\in(-1, 0)$. This kind of structure appears in many natural and man-made elastic composites, e.g. quartzite and brick masonry.

We restrict ourselves to treating only the main asymptotic term in the expansion of eigenvalues. Thus, the formal asymptotic structures, which are derived in Section 2, are sufficient for the justification of the asymptotics only under the additional assumptions

These will be accepted in Section 3 in order to avoid the construction of higher order asymptotic terms and to simplify the proofs (see Section 2.4 for a generalization of the presented results).

1.2.   Spectrum

We assume that the matrix $D(\xi)$ is algebraically complete [24]: there exists a positive integer $\rho_D\in{\mathbb N} = \{1, 2, 3, \dots\}$ such that, for any row $p(\xi) = (p_1(\xi), \dots, p_J(\xi))$ of homogeneous polynomials of degree $\rho\geq\rho_D$, one can find a row $q(\xi) = (q_1(\xi), \dots, q_N(\xi))$ of polynomials satisfying

Furthermore, the form $a^h$ in (7) possesses the polynomial property [17], namely, there exists a finite dimensional space ${\mathcal{P}}$ of polynomials in $x$ such that for any domain $\Xi\subset{\mathbb R}^2$ there holds the equivalence

In other words, the quadratic energy form $a^h$ degenerates only for some polynomials. From (10) it follows that all polynomials in ${\mathcal{P}}$ are of degree at most $\rho_D-1$.

As proved in [24,Thm 3.7.7], the property (10) assures the Korn inequality

where the constant $c_D$ is independent of $u\in H^1(\Omega^0)$, so that the sum

is a scalar product in the Hilbert space ${\mathcal{H}} = H^1({\mathbb R}^2)^J$. We introduce the positive definite, symmetric and continuous, therefore, self-adjoint, operator ${\mathcal{T}}^h$ by the identity

which reduces the problem (4) to the abstract equation

with the new spectral parameter

The spectrum ${\mathcal{S}}^h$ of the operator ${\mathcal{T}}^h$ is contained to the segment $[0, 1]$ where $t^h = 1$ is the norm of ${\mathcal{T}}^h$, see [20,Remark 1]. The set

is regarded as the spectrum of the problem (4).

The structure of the spectrum (16) is described by the Floquet–Bloch–Gelfand- (FBG-) theory, see, e.g. [11,25,12], which yields for it the band-gap structure

Here, the bands

are formed by the eigenvalue sequence

of the model problem in the periodicity cell

depending on the Floquet parameter $\eta = (\eta_1, \eta_2)$, which is the Gelfand dual variable belonging to the rectangle

In (20), $H^1_\eta(\Omega^0)$ is the subspace of functions $U^h\in H^1(\Omega^0)$ subject to the quasi-periodicity conditions

Using an argument similar to (13)–(15) and recalling the compactness of the embedding $H^1(\Omega^0)\subset L^2(\Omega^0)$, we conclude that the spectrum of the model problem (20) is discrete and consists of the positive monotone unbounded sequence (19), cf. [3,Thm 10.1.5,10.2.2], while the corresponding eigenvectors $U^h_{(m)}(\cdot;\eta)\in {\mathcal{H}}(\eta)$ can be subject to the normalization and orthogonality conditions

where $\delta_{m, n}$ is the Kroneker symbol. Moreover, the functions ${\mathbb Y}\ni\eta\mapsto\Lambda^h_m(\eta)$ are continuous and periodic with the periods $1/l_j$ in $\eta_j$ so that the bands (18) indeed are compact intervals.

The variational problem (20) is obtained from (4) by the FBG-transform [5]. All objects related to the model problem are denoted by capital letters; in particular, $\{\Lambda^h(\eta), U^h(x;\eta)\}$ is a new notation for eigenpairs.

The spectral bands (18) may overlap, but between them there can also exist gaps, i.e., nonempty open intervals $\gamma^h_m = ] \beta^h_m, \beta^h_{m+1}[$ which are free of the spectrum. In the paper [20] it was proved that the spectrum of the problem (4) has at least one open gap of width $O(1)$. In what follows, we will describe the asymptotic structure of the low-frequency range $\{\lambda^h\in\sigma^h:\, \lambda^h\leq const\}$ of the spectrum (17). The results imply the existence of a large number of open gaps, the geometric characteristics of which will also be described asymptotically.

1.3.   Special cases

Let us list some concrete problems in mathematical physics which have the properties assumed above. Other important examples will be discussed in Sections 4.4 and 4.5.

Example 1.1. Let $J = 1$ and $N = 2$. Then $D(\nabla) = \nabla$ and (5) is a scalar elliptic second-order differential operator in the divergence form. Clearly, ${\mathcal{P} } = {\mathbb R}$ in (11). The problem (3) describes e.g. a heterogeneous acoustic medium with thin high-conductive streaks.

Example 1.2. Let $J = 2$, $N = 3$ and

It is known that in this case $\rho_D = 2$ in the property (10), cf. [24,§3.7], [17,Example 1.12]. In the Voigt–Mandel notation of elasticity, $u = (u_1, u_2)^\top$ is the displacement vector, $D(\nabla )u$ and $AD(\nabla )u$ are the strain and stress columns and $A$ is a real, symmetric and positive definite $3\times3$-matrix of elastic moduli. Furthermore, $B = \mbox{diag}\{b, b\}$ and $b>0$ is the mass density of the elastic material. The space of polynomials (11)

consists of rigid motions.

The problem (3) describes elastic composites, some of which were already mentioned in Section 1.1.

1.4.   State of the art and the architecture of the paper

The band-gap structure of the spectrum of an elliptic equation

with highly contrasting coefficients

which are $1$-periodic in all coordinates $x_j$, was first investigated in the paper [6], where the existence of a non-empty spectral gap was proved; see also [7]. Notice that the coefficients of $d\times d$-matrix (25) become large in an interior subdomain $\omega$ of the unit open cube $\Omega$, $\overline{\omega}\subset\Omega$ ($\varepsilon>0$ is a small parameter). A similar problem was considered in [28], and there it was in addition shown that the number of open gaps grows unboundedly when $\varepsilon\rightarrow+0$.

The subdomain $\omega$ is fixed in the definition (25), but the papers [20,1] deal with the situation described in Section 1.1: the subdomain (1) of the high contrast covers the whole periodicity cell $\Omega^h$ in the limit $h\rightarrow+0$.

In the present paper we employ an asymptotic method which differs quite significantly from the analysis used in [6,7,28,22,2] and [20,1].

2.   Formal asymptotic analysis

2.1.   The limit problem

First of all, we rewrite the problem (20) in differential form. In view of (5) and (6), it consists of two systems

coupled by the transmission conditions

where $U^{\bullet\, h}$ and $U^{\circ\, h}$ are the restrictions of $U^h$ onto $\Omega^h$ and $\Gamma^h$, respectively, and $\nu^h(x)$ is the exterior normal unit vector on the boundary $\Sigma^h$ of $\Omega^h$, i.e. the interface. The sides of the rectangle $\Omega^0$ are supplied, in the terminology of [14], with the stable quasi-periodicity conditions (21) as well as the intrinsic conditions

where $\partial_j = \partial/\partial x_j$, $j = 1, 2$.

Since the right-hand-side of (29) includes the small coefficient $h^{\alpha_A}$, the passing to the limit $h\rightarrow0$ turns $\Sigma^h$ into $\Sigma^0 = \partial\Omega^0$ (see (1)) and leads to the limit problem

Notice that the Floquet parameter $\eta$ does not appear in this problem because the quasi-periodicity conditions (21), (30) are isolated from the interior part $\Omega^h$ by a thin "shim" $\Gamma^h$. The variational formulation of this problem is written as the integral identity [14]

The spectrum of the problem (31), (32) or (33) is discrete, as it consists of the eigenvalues

while the corresponding vector eigenfunctions $U^0_{(m)}\in H^1(\Omega^0)^J$ can be subject to the orthogonality and normalization conditions

We emphasize that the multiplicity of the null eigenvalue in (34) equals $\dim{\mathcal{P}}$, by (11).

2.2.   Formal asymptotics of eigenvalues

Let $\{\Lambda^0, U^0\}$ be an eigenpair of the limit problem (31), (32). Due to the boundary condition (32), the eigenfunction $U^0$ leaves only a small discrepancy in the intrinsic transmission conditions (29), but the discrepancy in the stable transmission condition (28) is of order $1 = h^0$. To compensate the latter, we need to construct a boundary layer $W$ in the thin bordering $\Gamma^h$. We consider two vertical curved strips

and denote by $W^1$ the restriction of $W$ onto $\Gamma^h_1 = \Gamma_{1-}^h \cup\Gamma_{1+}^h$. Notice that due to the periodicity, the set $\Gamma^h_1$ can be identified with

As always in the asymptotic theory of elliptic problems in thin domains, we introduce the rapid variable

so that, according to (1) and (36),

while $y = x_2$ is still a slow variable. The boundary layer term $W^1$ depends on the coordinate couple $(\zeta, y)$. Inside the set $\Gamma_2^h = \Gamma_{2-}^h\cup \Gamma_{2+}^h$ we define the corresponding coordinates and the boundary layer term $W^2$ analogously.

We have

Thus, the left-hand side of (27) takes the form

where dots stand for higher-order terms that are inessential in our asymptotic analysis, and the right-hand side is

In other words, by (8), the expression (39) is much smaller than (38). Thus, the boundary layer term $W^1$ satisfies the problem

together with the following transmission conditions at the point $\zeta = 0$

coming from (30) and (37).

It follows from (40)–(42) that

where the coefficient columns $C^0(y)$ and $C^1(y)$ can be found from the linear system

Thus,

where

We will not need an explicit expression for the coefficient $C^0(y)$.

Let us return to the transmission conditions. By (1), the normal vector on $\Sigma^h_{1\pm}$ equals

hence, the main asymptotic term of the right-hand side of (29), calculated for the boundary layer term $W^1(\zeta, x_2)$, reads as

where $\Sigma^h_{j\pm} = \Sigma^h\cap \partial \Gamma^h_{j\pm}$ and $A^\circ_{(1)}$ is a Hermitian and positive definite $J\times J$- matrix; we denote

The coefficient $h^{\alpha_A-1}$ is small, since its exponent is positive in view of our assumption (8). We thus readily accept the asymptotic ansätze

The correction term satisfies the problem

where the data of the boundary conditions is taken from (47) and a similar formula for $j = 2$ so that

The variational formulation of the problem (49), (52) reads as

where $\Sigma^0_{j\pm}$ denote the sides of the rectangle $\Omega^0$.

First, we assume that $\Lambda^0 = \Lambda^0_m$ is a simple eigenvalue of the problem (31) and hence, by the Fredholm alternative, the problem (51), (52) gets one compatibility condition, namely

and, therefore,

where the Hermitian sesquilinear form ${\mathcal{J}}$ is defined by

see the notation in (45).

Second, if $\Lambda^0 = \Lambda^0_m$ is an eigenvalue of multiplicity $\varkappa_m$ and $U^0_{(m)}, \dots, U^0_{(m+\varkappa_m-1)}$ are the related, orthonormalized eigenfunctions, similar calculations show that the correction terms in the ansatz (50) for the eigenvalues $\Lambda^0_{m}(\eta), \dots, \Lambda^0_{m+\varkappa_m-1}(\eta)$ are nothing but eigenvalues of the Hermitian $\varkappa_m\times \varkappa_m$-matrix $M^m$ with entries

Moreover, the eigenvectors $U^0_{(m)}, \dots, U^0_{(m+\varkappa_m-1)}$ can be fixed such that the matrix $M(\eta)$ with the entries (56) becomes diagonal with eigenvalues

2.3.   Theorem on asymptotics and its consequences

In Section 3, we will prove the following error estimates for the asymptotics constructed above. However, one additional albeit reasonable assumption, (68), on the eigenfunction $U^0_{(m)}\in H^2(\Omega^0)$ has to be made; see Section 3.1 for details.

Theorem 2.1. Let the assumptions (8), (9) and (68) hold true. Then, for any eigenvalue $\Lambda^0_m$ of multiplicity $\varkappa_m$ of the limit problem (33),

there exist positive $h_m$ and $c_m$ such that, for $h\in(0, h_m]$, the sequence (19) contains the eigenvalues $\Lambda^h_n(\eta), \dots, \Lambda^h_{n+\varkappa_m-1}(\eta)$ of the problem (20) satisfying the estimates

where

and $\Lambda^\prime_{m+l}(\eta)$ are the corrections terms constructed in Section 2.4, see (54) and (57). Moreover, $n = m$, i.e. formula (59) includes the asymptotic relationship between the corresponding entries of the eigenvalue sequencies (19) and (34).

The number (60) is positive because of the restrictions (8) and (9) so that Theorem 2.1 indeed confirms the asymptotic form (50) of the eigenvalues, including the formulas (54)–(57) for the correction term.

Since the $J\times J$-matrix (48) is positive definite, the matrix $M^m$ is positive. The latter means that the numbers (54) and (57) are non-negative. Thus, formulas (50) and (59) imply that, for a small $h>0$, the inequalities

are valid. In other words, the appearence of the flexible thin frame $\Gamma^h$ shifts the dispersion surfaces upwards.

The following description of the spectral bands is an important consequence of Theorem 2.1, and it will have further applications in Section 4.

Theorem 2.2. If the hypotheses of Theorem 2.1 are true, then the endpoints of the spectral band (18) have the asymptotic form

where $h\in(0, h_m]$,

and the correction terms in (61) come from the formulas (54), (55) and (57).

Relation (61) shows in particular that in the situation (58) there appears an open spectral gap of width

between the bands $\beta^h_{m-1}$ and $\beta^h_m$. To make conclusions on gaps between the bands $\beta^h_m, \dots,$ $\beta^h_{m+\varkappa-1}$ we need to put the formulas (56)–(57) into a more conrete form, see Section 3.3.

3.   Justification of the asymptotics

3.1.   Additional assumptions on singularities at the corners

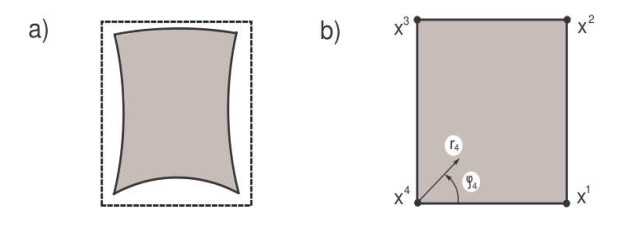
The Kondratiev theory of elliptic problems in domains with corners and conical points of the boundary (see the key works [8,15,16,17] and, e.g., the monographs [21,10]) shows that the solution of the problem (31), (32) is of the form

where $P^{jk}$ are some vector polynomials, $(r_j, \varphi_j)$ are polar coordinates centered at the corner points $x^j$ (see Fig. 1.b), $\varphi_{j}\in(0, \pi/2)$ in $\Omega^0$,

and $\chi_j$ is a smooth cut-off function supported and equal to $1$ in a small neighborhood of $x^j$. Moreover, $C_{kj}$ is a constant coefficient and $\Psi^{kj}$ is a power-logarithmic solution,

where $\psi^{kj}$ is a polynomial of degree deg $\psi^{kj}$ in $\ln r_j$ with coefficients, which are smooth functions in the angular variable $\varphi_j\in[0, \pi/2]$. The number $K^j$ in (62) can be fixed such that $\widetilde{U}^0\in H^2(\Omega^0)^J$ and in this way the exponents of power-law solutions (64) satisfy the inequalities

In view of (65), the polynomials $P^j$ can be reduced to linear vector functions, i.e. (64) with $\mu_{kj} = 1$ and deg $\psi^{kj} = 0$

Lemma 3.1. In (62) we have

Proof. By the above conclusion, we can write

and here the constant term $P^j_{(0)}$ satisfies (66). The boundary conditions (32) on the sides of the rectangle $\Omega^0$ imply

and, hence,

We obtain the formula (66), since $A^\bullet$ is Hermitian and positive definite.

To simplify the justification scheme, which would otherwise become too cumbersome, we assume that for some $\delta_0>0$ we have in (62)

In other words, non-constant and non-linear power-logarithmic terms (64) are assumed not to exist in the representation (62). Consequently, we have $U^0\in H^2(\Omega^0)^J$. Moreover, Hölder estimates in domains with corner and conical points on the boundary (see the original paper [16] and also the monographs [21,10]) yield the bounds

where $r = \min\{r_j\, |\, j = 1, \dots, 4\}$ is the distance of the rectangle $\Omega^0$ to the vertices and $\delta_0>0$ is the number in (65).

In Section 4.2, we will consider examples of scalar equations and elasticity systems which meet all the assumptions made above.

Let us then turn to the equations for the correction term $U'$. The right-hand side of the system (51) is sufficiently smooth but the data (53) of the Neumann conditions (52) does not vanish at the corner points (63) of $\Omega^0$. Again, the Kondratiev theory provides for the solution $U'$ the decomposition

where $\widetilde{U}^\prime\in H^2(\Omega^2)^J$, the term $P^{j\prime}$ is a linear vector function in $x$, and $\Psi^j$ is of the form (64), where $\mu_j = 1$ and $\psi^j$ is a linear function of $\ln r_j$. Therefore, $\chi_j\Psi^j\not\in H^2(\Omega^2)^J$, if a logarithmic term exists. Furthermore, $\Psi^j (r_j, \varphi_j)$ is a polynomial in $x$ if and only if, in the Neumann conditions (52), the data (53) frozen at sides of the rectangle $\Omega^0$ in the corner point $x^j$ can be compensated by a linear vector function (67). This remark allows us to verify the following property.

Lemma 3.2. The terms $\Psi^j(r_j, \varphi_j)$ are always of the form (67) with some $P^j_{(k)}</italic> <italic>\in{\mathbb C}^j$, $k = 0, 1, 2$. Moreover, $P^j_{(0)} = 0$ if and only if ${\mathcal{P}} = {\mathbb C}^J$.

Proof. Considering the vertex $x^1$ and searching for the linear vector (67), we need to solve the system of $2J$ algebraic equations

The $(2J\times2J)$-matrix of this system is Hermitian and, therefore, the system is uniquely solvable provided the homogeneous system (71) has only the trivial solution. According to Lemma 3.1, the latter is true provided the polynomial subspace $\mathcal{P}$ in (11) does not contain a non-trivial linear vector function. This completes the proof, since $\mathcal{P}$ is invariant with respect to the coordinate translation $x\mapsto x+x^0$.

Using the notation of (69), we derive the following estimates for the decomposion (70) :

In spite of the singularities these will be sufficient to justify our asymptotic formulas for the eigenvalues (19).

3.2.   The operator formulation of the model problem in the periodicity cell

Similarly to (12), we introduce the scalar product

in the space

and define the self-adjoint and positive operator $\mathcal{T}^h(\eta)$ in ${\mathcal{H}}(\eta)$ by the identity

In this way, the variational formulation

of the problem (26)–(30), (21) turns into the abstract equation in ${\mathcal{H}}(\eta)$,

where

The operator ${\mathcal{T}}^h(\eta)$ is compact because of the compact embedding $H^1(\Omega^0)\subset L^2(\Omega^0)$ in the bounded domain $\Omega^0$, and its spectrum forms the monotone positive sequence (see, e.g., [3,Theorem 10.1.5,10.2.2])

which turns into the sequence (19) by the formula $\Lambda^h(\eta) = \tau^h(\eta)^{-1}-1$, cf. (74).

The following assertion is known as lemma on "near eigenvalues and eigenvectors", cf. [27], and it follows immediately from the spectral decomposition of resolvent, see [3,Ch.6].

Lemma 3.3. Let ${\mathcal{U}}^h(\eta)\in{\mathcal{H}}(\eta)$ and $t^h(\eta)\in(0, +\infty)$ be such that

Then at least one eigenvalue $\tau^h_n(\eta)$ of the operator $\mathcal{T}^h(\eta)$ satisfies the inequality

Moreover, for every $\epsilon_\ast\in(\epsilon, t^h(\eta))$ one can find coefficients $a^h_M(\eta), \dots, a^h_{M+X-1}(\eta)$ such that

where $\tau^h_M(\eta), \dots, \tau^h_{M+X-1}(\eta)$ are all the eigenvalues of ${\mathcal{T}}^h(\eta)$ contained in the interval $[t^h(\eta)-\epsilon_\ast, t^h(\eta)+\epsilon_\ast]$ (the numbers $M$ and $X$ may dependent on $h$), and $U^h_{(M)}(\eta), \dots, U^h_{(M+X-1)}(\eta)\in \mathcal{H}(\eta)$ are the corresponding eigenvectors subject to the orthogonality and normalization conditions

Naturally, our next task is the construction of a proper approximate eigenpair $\{t^h(\eta), {\mathcal{U}}^h(\eta)\}$. This will be based on the formal asymptotic analysis in Section 2.

3.3.   The global approximation of an eigenpair

Let $\Lambda^0_m$ be an eigenvalue of the limit problem (31), (32) with multiplicity $\varkappa = \varkappa_m$ and let the corresponding eigenvectors $U^0_{(m)}, \dots,$ $U^0_{(m+\varkappa-1)}$ be subject to the normalization and orthogonality conditions (35). We take

as an approximate eigenvalue of the operator ${\mathcal{T}}^h(\eta)$ in (74). Here, $\ell = m, \dots, m+\varkappa-1$ and $\Lambda^\prime_\ell(\eta)$ is the correction term constructed in Section 2.1.

The approximate eigenvectors are defined in $\Omega^h$ as

However, the definition becomes much more complicated inside the thin frame $\Gamma^h$ and it involves several smooth cut-off functions. First of all, we select a cut-off function whose support covers almost the whole cell:

Then, the function $\chi^h_{j\pm}\in C^\infty(\overline{\Omega^0})$ is defined such that the support is contained in $\overline{\Gamma^h_{j\pm}}$ and

where $\varrho>0$ is chosen such that $\mbox{supp}\chi^h_{j\pm}\cap (\Gamma^h_{3-j-}\cup\Gamma^h_{3-j+}) = \varnothing$. Finally, ${\mathcal{X}}^h_1$ is supported in a small neighborhood ${\mathcal{V}}_1$ of the corner point $x^1$ of the rectangle $\Omega^0$, vanishes in the vicinity of $\Sigma^0$ and equals $1-\chi^h_{2-} -\chi^h_{2+}$ near the curve $\Sigma^h\cap{\mathcal{V}}_1$. The relations (81) hold true for all these cut-off-functions.

Completing the definition (78) of $u^h_{(\ell)}$, we set in $\Gamma^h_{1+}$

where $U^\prime_{(\ell)}$ is the correction term in the ansatz (49), i.e. the solution of the problem (51), (52) with data (53). The definitions (82) can clearly be extended to $\Gamma^h_{1-}$, $\Gamma^h_{2\pm}$ and thus to the whole frame $\Gamma^h$.

Owing to the boundary conditions (41), relations (42) and the definitions of the cut-off functions, we conclude that (82) satisfies the quasi-periodicity conditions (21) and has the same trace on $\Sigma^h = \partial\Omega^h$ as the approximate solution (79).

We proceed to evaluate the scalar product $\langle u^h_{(\ell)}, u^h_{(n)}\rangle_{h, \eta}$, see (73). The inequality

follows from the formulas (79) for $u^{h\bullet}_{(\ell)}$, (35), (33) and (69) for the eigenfunction $U^0_{(\ell)}$ and (72) for the correction term $U^\prime_{(\ell)}$ as well as the fact that area of $\Gamma^h$ is of order $h$.

Now, to derive the formulas

we recall (6) and write the estimate

Here, in the central expression, the factor $h^{-1}$ comes from the differentiation of the cut-off functions and the boundary layer term (cf. (81) and (37)). The factor $h^1$ is the order of the area of $\Gamma^h$ and $h^{\alpha_A-1}|\ln h|$ results from the gradient estimate (72) of $h^{\alpha_A-1}U^\prime_{(\ell)}$. Notice that the exponent of $h$ in the bound (84) equals $\alpha_A-1$, owing to (9).

Let us estimate the value $\epsilon = \epsilon_\ell$ in (75) for the number (78) and the vector

We have

where the supremum is calculated over the unit ball in ${\mathcal{H}}(\eta)$. Since the first two factors on the right-hand side of (86) are uniformly bounded in $h$, see (68) and (84), it suffices to consider the expression

where

For the first term $I^h_\bullet$ we have, according to (31) and (52),

We will need some additional inequalities for the processing of the other terms in (88). To this end, we introduce eight geometric figures depicted in Fig. 3, namely four squares $\square^h_k$ attached to the vertices $x^k$ ($k = 1, \dots, 4$) having side lengths $\varrho h$, and four rectangles $\Pi^h_{j\pm}$ with short and long sides of lengths $\rho h$ and $l_{3-j}-2\varrho h$, respectively. Here, the coefficient $\varrho>0$ of the parameter $h$ is chosen such that the union of the eight sets contains $\Gamma^h$ and a $ch$-neighborhood of $\Sigma^h = \partial\Omega^h$ for some $c>0$ which we fix now. In the following we will use the symmetry to replace some estimates over the set $\Gamma^h$ by corresponding estimates only over the rectangle $\Pi^h_{1+}$ and the squares $\square^h_1$ and $\square^h_2$. We denote $\square^h_{1, 2} = \Pi^h_{1+} \cup \square^h_1 \cup \square^h_2$.

Lemma 3.4. If $v^h\in{\mathcal{H}}(\eta)$, then there holds the inequalities

where $c$ is independent of $v^h$ and $h\in(0, h_\circ]$.

Proof. Let $\sphericalangle^h_1 = \{x:\, {\bf r}\in(0, d_1), \phi\in(0, \phi_1)\}\subset \Omega^h$ be the sector which is shown in Fig. 2.a and which contains the small triangle $\blacktriangle^h_1$ (marked with black in Fig. 3.a) inside the square $\square^h_1$. The estimate

is a consequence of the classical one-dimensional Hardy inequality

integrated in the angular variable $\phi$. Taking into account the weight factor on the left-hand side of (92), we can write

Then, we apply the Poincaré ineqality

which can be easily derived by a coordinate dilation, and obtain the desired inequality (90) as follows:

To derive (91), we employ the Newton–Leibnitz formula and write

We estimate

It suffices to integrate $x_2$ over the interval $(-l_2+\varrho h, l_2-\varrho h)$ and to apply the standard trace inequality.

Since $\|v^h;{\mathcal{H}}(\eta)\| = 1$ in (86), we can use in the following calculations the fact that the left-hand sides of (90) and (91) are uniformly bounded in $h$. Moreover, we denote by $I_A^h (\Box)$ and $I_B^h (\Box)$ the quantities where the inner products of the expressions $I_A^h$ and $I_B^h$, respectively, are taken over the set $\Box_{1, 2}^h \cap \Gamma^h$ instead of $\Gamma^h$. For $I^h_A (\Box)$ we obtain the bound

Here, the norms $h^{2-p}\|\nabla^p U^0_{(m)};L^2(\square^h_{1, 2})\|$, $p = 0, 1, 2$, came from the differentiation of the product $\mathcal{X}^h_kU^0_{(\ell)}$ and (81); they were estimated by using (69) and taking into account the area $O(h^2)$ of $\square^h_k$. In a similar way we used (40) and (43), (44), (69) to get

Finally, inequalities (90) and (91) for $v^h$ together with bounds for the areas of the above-mentioned supports were used to complete the estimate (93). A much simpler consideration yields the estimate

Notice that the exponents of the bounds in (93) and (94) are included in the formula (60).

In view of symmetry, the same estimates hold when $\Box_{1, 2}^h$ is replaced by the unions of the other rectangles $\Box_k^h$ and $\Pi_{j\pm}^h$ (see the explanation above Lemma 3.4). Since the frame $\Gamma^h$ is covered by these sets, we obtain

To treat the fourth and fifth terms $I^{h\prime}_A$ and $I^{h\prime}_B$ on the right-hand side of (87), we apply formulas (72) and the basic estimates following directly from definitions (73) and (6),

Accordingly, we obtain

Exponents in both bounds are included in (60).

Let us consider the last term $I^h_\Sigma$ in (88). Here, our assumption on the smoothness properties in Section 3.1 plays an important role. Since the vector function $U^0_{(\ell)}\in C^2(\Omega^0)$ satisfies the homogeneous Neumann conditions (32), we have

Furthermore, the boundary condition (52), (53), formula (46) for the normal vector $\nu^h$ and the relations (72) for $U^\prime_{(\ell)}$ imply that, for $x\in \Sigma^h$,

where the last singular factor $r^{-1}$ is caused by the second derivatives of $U^\prime_{(\ell)}$. Now we use the known weighted trace inequality

cf. (92) and (97), (98), to obtain

where we also applied the inequalities $r\geq {\bf r} +ch$, $c>0$ on $\Sigma^h$, see Fig. 2.a, and $h|\ln h|\leq c h^{(\alpha_A-1)/2}$, due to (9).

Combining the estimates (89), (95), (96), (99) and recalling the definition (60) yield for the number (86) the estimates

which according to Lemma 3.3 means that the operator $\mathcal{T}^h(\eta)$ has an eigenvalue $\tau^h_{n(\ell)}(\eta)$ related to the "almost eigenvalues" (78) by

If all eigenvalues (57) of the matrix $M^n(\eta)$ are simple, in particular, $\Lambda^0_m$ is a simple eigenvalue in the sequence (34), then the distance of any two points $t^h_m(\eta), \dots, t^h_{m+\varkappa_m-1}(\eta)$ is at least $Ch^{\alpha_A-1+\delta_{AB}}$, and thus there exist $\varkappa_m$ different eigenvalues $\tau^h_{n(m)}(\eta), \dots, \tau^h_{n(m+\varkappa_m-1)}(\eta)$. However, in the case

with ${\bf x}>1$, Lemma 3.3 would not prevent that some of the eigenvalues $\tau^h_{n({\bf m})}(\eta), \dots,$ $\tau^h_{n({\bf m}+{\bf x}-1)}(\eta)$ might coincide. We show that they can be chosen to be different from each other.

Taking into account the second assertion in Lemma 3.3, we set $\epsilon = \max\{\epsilon_{\bf m}, \dots, \epsilon_{{\bf m}+{\bf x}-1}\}$ and

where $T$ is fixed to be large enough, and denote by $\tau^h_M, \dots, \tau^h_{M+X-1}$ all eigenvalues of the operator ${\mathcal{T}}^h$ in the interval

For each $\ell = {\bf m}, \dots, {\bf m}+{\bf x}-1$, Lemma 3.3 gives a column of coefficients $a^h_{(\ell)} = (a^h_{M\ell}, \dots,$ $a^h_{M+X-1\ell} )$ such that the relations (76) are valid for the vector function (85). We denote by ${\mathcal{S}}^h_\ell$ the linear combination

and write

Inequalities (84), (76), (100) and conditions (77) yield

In other words, the columns $a^h_{\bf m}, \dots, a^h_{{\bf m}+{\bf x}-1}\in{\mathbb C}^X$ are almost orthonormalized for small $h$ and big $T$. The latter situation can only happen in the case $X\geq {\bf x}$, when the interval (102) contains at least $\bf x$ eigenvalues of the operator ${\mathcal{T}}^h(\eta)$ which meet the estimate

see (101), (102), (100). Definition (78) and relation (74) between the spectral parameters, turn formula (103) into the desired inequality (59).

Finally, the assertion on the equality of $n$ and $m$ in Theorem 2.1 follows from a standard convergence theorem which we formulate as the next lemma and prove in the next section.

Lemma 3.5. The entries of the eigenvalue sequencies (19) and (34) are related by $\Lambda^h_m\rightarrow\Lambda^0_m$, as $h\rightarrow+0$.

3.4.   Completion of the proof of Theorem 2.1: The convergence result

To prove Lemma 3.5, let $\{\Lambda^h_m(\eta), U^h_m(\cdot;\eta)\}$ be an eigenpair of the problem (20) for some $\eta\in{\mathbb Y}$. We fix this Floquet parameter and suppress it in the notation from now on. In Section 3.3 it was proved that in the vicinity of each eigenvalue $\Lambda^0_p$, $p = 1, \dots, m$, of the limit problem (33) there exists an eigenvalue $\Lambda^h_{n(p)}$ of the problem (20) and $n(p_1)\not = n(p_2)$ for $p_1\not = p_2$, and we have

We normalize the eigenvector $U^h_{(m)}$ by

The integral identity (20) and formulas (6), (7) yield the implication

where the number $\varrho>0$ is chosen such that the rectangular domain

is contained in the domain $\Omega^h.$

According to (104), the vector function

has a uniformly bounded $H^1(\Omega^0)$-norm and, hence, there exists a positive sequence $\{h_n\}_{n\in{\mathbb N}}$ tending to 0 such that

We take an arbitrary test function ${\bf V}\in C^\infty(\overline{\Omega^0})$, extend it smoothly outside the square $\Omega^0$ and insert into the integral identity (20) the function

where ${\bf V}^h(x) = {\bf V}((1-\varrho h)^{-1}x)$. Notice that the function (107) vanishes in the vicinity of $\partial\Omega^0$, cf. (80), and therefore it belongs to ${\mathcal{H}}(\eta)$.

We have

Using (105) and (107), (80) we observe that

To process the remaining terms in (108) we write

Thus, passing to the limit $h_n\rightarrow+0$ yields the integral identity for the limit problem,

By a completion argument, the test function space can be changed here to be $H^1(\Omega)^J$.

Hence, to conclude that $\{\Lambda^0, {\bf U}^0\}$ is an eigenpair of the problem (31), (32), it is sufficient to verify that ${\bf U}^0$ is non-zero. To this end we write

Lemma 3.4 gives estimates for the last two terms:

These the upper bounds tend to 0 as $h\rightarrow+0$, see (9). Recalling (105) yields

and we thus obtain $b^\bullet({\bf U}^0, {\bf U}^0;\Omega^0) = 1$ by passing to the limit $h\rightarrow+0$ in (109).

Now Lemma 3.5 can be proved in a standard way. Namely, if $U^h$ and $U^h_\ast$ are two different eigenvectors of the problem (20) and they are orthogonal in the sense that $b^h(U^h, U^h_\ast) = 0$, see (22), then the orthogonality $b^\bullet({\bf U}^0, {\bf U}^0_\ast) = 0$ follows from the above calculations. In this way, supposing $n>m$ would contradict our way to compose the eigenvalue sequences (19) and (34). But we recall that the inequality $n\geq m$ was already verified in Section 3.3. Thus, the identity $n = m$ holds, and this completes the proofs of Lemma 3.5 as well as Theorem 2.1.

4.   Some examples and generalizations

4.1.   Concrete formulas

Let us derive exactly the correction terms in the eigenvalue asymptotics (59) for the problems mentioned in Examples 1.1 and 1.2.

Example 4.1. Let $L^\bullet = -\Delta$ and $L^\circ = -\Delta$, cf. Example 1.1, and let $1/2 = l_1>l_2$. Then

The asymptotic formulas (59), (54) and the definitions (55), (45) show that

Example 4.2. Assuming that the frame $\Gamma^h$ is made of a homogeneous isotropic material, we have the following $3\times3$-matrix

where $\lambda_\circ \geq0$ and $\mu_\circ>0$ are the Lamé constants, cf. Example 1.2. We choose the orthonormalized basis

in the polynomial space $\mathcal{P}$ of rigid motions.

We have

4.2.   Singularities at corner points

The next two examples show that the restrictions introduced in Section 3.1 are relevant in certain problems of mathematical physics.

Example 4.3. An appropriate affine transform converts the problem (31), (32) into the spectral Neumann problem for the Laplace operator in a parallelogram $\lozenge$ with angles $\phi\in(0, \pi/2]$ and $\pi-\phi\in[\pi/2, \pi)$. As known for example by [21,Ch. 2], the worst singularity of an eigenfunction of this problem in $\lozenge$ is

Example 4.4. According to [13], an affine transform can be used to reduce the stationary elasticity problem (31), (32) with $\Lambda^0 = 0$, in $\Omega^0$, to the particular case of an orthotropic elastic parallelogram with the elastic symmetry axis of rank 4. This means that the rigidity matrix $A$ is of the form

Singularities at corner points for such orthotropic materials have been computed in, e.g., [26]. However, the inequality $\mu>1$ for the positive singularity exponents in (69) at the tops of the convex angles of the parallelogram has been proved in [9] so that the elasticity problem in Example 1.2 also satisfies our assumption (68).

4.3.   Possible geometric generalizations

Until now we have restricted ourselves to two-dimensional problems, in order to simplify formulas and the justification scheme in Section 3. However, our formal asymptotic analysis would apply also in the multi-dimensional cases without notable changes. Namely, the periodicity cell $\Omega^0 = \{x\in{\mathbb R}^d:\, |x_j|<l_j, j = 1, \dots, d\}$, $d\geq3$, can composed of the curved parallelepiped

and the surrounding box-shaped frame $\Gamma^h = \Omega^0\setminus\Omega^h$. Here, the notation is similar to that in (1) except that $x^\prime_{(j)} = (x_1, \dots, x_{j-1}, x_{j+1}, \dots, x_d)$. On the other hand, stating smoothness properties of the eigenvectors, which we used in Section 3, would become much more complicated in higher dimensions, due to the many edges and corners of the boundary of the curved parallelepiped (110). Thus, the justification of the asymptotics might require some additional assumptions.

Other shapes of the periodicity cells like the honeycomb structure in Fig. 3.a, can be used to cover the plane, and they can be treated with the same asymptotic tools. Another example of a non-rectangular tiling with the periodicity cell in Fig. 3.b requires a modification of our asymptotic procedure, because of the inward obtuse angle. However, the main difficulty is caused in formulas (43)–(45) by the strong corner singularities on the short sides of the curved rectangle $\Gamma^{h+}_1$. The resulting strengthening of the singularities of the solutions may seriously reduce the accuracy of our asymptotic formulas (cf. Section 3.1 and the error estimates in Theorems 2.1 and 2.2).

The influence of these corner singularities may be compensated by constructing two-dimensional boundary layers (cf. [4,18] for the Poisson equation and [19] for general elliptic problems and the elasticity system). It should be mentioned that using the same scheme as in Section 2.2 one can up to some extend find higher order asymptotic terms in $\Omega^h$ and in $\Gamma^h_{j\pm}$ outside small neighborhoods of the vertices of $\Omega^0$, but it is not possible to specify them completely without the two-dimensional boundary layers. This was the very reason for introducing the assumption (9) which helps to avoid the problem.

It looks that near concave corner points the required, acceptable approximation can be achieved by constructing two dimensional boundary layers (cf. [19]).

There is no obstacle to treat strongly curved thin frames in the geometric situation of Fig. 3.c.

4.4.   Periodic piezoelectric composites

Example 4.5. Let $J = 3$, $N = 5$ and

where $D^{{\mathsf{M}}}(\nabla)^\top$ is the matrix (23) and $\mathbb{O}_{m\times n }$ is the null matrix of size $m \times n$. Furthermore, let

Here, $A^{{{\mathsf{M}}} {{\mathsf{M}}}}$ and $A^{{{\mathsf{E}}} {{\mathsf{E}}}}$ are symmetric and positive definite matrices of elastic and di-electric moduli, respectively, while there is no restriction on the piezoelectric matrix $A^{{{\mathsf{M}}} {{\mathsf{E}}}} = \big( A^{{{\mathsf{E}}} {{\mathsf{M}}}}\big)^\top$ of size $3 \times 2$. Finally, $u = (u^{{\mathsf{M}}}, u^{{\mathsf{E}}})$, $u^{{\mathsf{M}}} = (u_1, u_2)$ is the displacement vector and $u^{{\mathsf{E}}}$ is the electric potential.

Due to the minus sign of $A^{{{\mathsf{E}}} {{\mathsf{E}}}}$, the symmetric matrix $A^\bullet$ is not positive definite and therefore the Hermitian sesquilinear form $A^h$ in (7) does not satisfy condition (11). However, thanks to the right lower null entry of the matrix $B^\bullet$, (112), and the Dirichlet condition

on the insulator surface, all necessary conditions are actually satisfied and we conclude in particular that the space of polynomials $\mathcal{P}$ can be chosen to be

where $\mathcal{P}^{{\mathsf{M}}}$ is the space (24) of mechanical rigid motions.

We consider the composite plane $\Omega_\infty^h \cup \Gamma_\infty^h$, where $\Omega_\infty^h$ is the union over $\theta \in \mathbb{Z}^2$ of the identical piezoelectric inclusions $\Omega^h(\theta)$ (cf. (2)), which are connected by thin paddings of pure elastic solid insulator $\Gamma_\infty^h$. The boundary value problem consists of the system of differential equations

the transmission conditions

and the Dirichlet condition (113) on the union $\Sigma_\infty^h$ of the contours $\Sigma^h(\theta) = \partial \Omega^h(\theta)$, $\theta \in \mathbb{Z}^2$. The notation in (116) and on the right-hand side of (117) is the same as in Example 1.2. We emphasize that condition (117) means that the traction is continuous on the contact surface. Moreover, (113) describes the fact that the electric potential is constant on the surface of the insulator, and this constant can be set to zero because the set $\overline{ \Gamma_\infty^h} = \cup_{\theta \in \mathbb{Z}^2} \overline{\Gamma^h (\theta)}$ is connected.

The limit problem in the rectangle $\Omega^\circ = ( -\ell_1, \ell_1) \times (- \ell_2 , \ell_2)$ consists of the system (31) including the matrices (111) and (112), the quasiperiodicity condition (21), (30) and the boundary conditions, cf. (32) and (117), (113), and

Although the matrix $A^\bullet$ in (112) is not positive definite, the spectrum of the problem is discrete and consists of the monotone non-negative unbounded sequence (34). For example in the paper [23] one can find a procedure for reducing the weak formulation of this piezoelectricity problem to a problem with a positive self-adjoint operator in $H^1(\Omega^\circ) \ni U^{ {{\mathsf{M}}} \circ}$; the reduction uses the specific structure of the matrix $B^\bullet$ in (112). The corresponding eigenfunctions $U_{(1)}^\circ, U_{(2)}^\circ, \ldots \in H^1(\Omega)^\circ)^3$ can be subject to the normalization and orthogonality conditions (35), which read as

with the positive constant $b^\bullet$ of (112).

Since the material in $\Gamma^h$ is purely elastic, the forms of the second limit problem (40)–(42) and its solution (43) are kept unchanged. Thus, our calculation of the correction term in the eigenvalue ansatz (45) does not need modifications, and also the final formulas (56), (57) remain unchanged, if the formulas (48) and (55) are understood as

with the notation (45) preserved as such.