Homogenization of Bingham flow in thin porous media

1.   Introduction

In this paper we study the asymptotic behavior of the flow of a viscoplastic Bingham fluid in a thin porous medium which contains an array of bodies modelized as vertical cylindrical obstacles (the pores). We refer the reader to the very recent paper [8] and the references therein for the application of our study to problems issued from the real life applications. As a first example one can mention the flow of the volcanic lava through dense forests (see [30]). Another important application is the flow of fresh concrete spreading through networks of steel bars (see [33]).

The model of thin porous medium of thickness much smaller than the distance between the pores was introduced in [34], where a stationary incompressible Navier-Stokes flow was studied. Recently, the model of thin porous medium under consideration in this paper was introduced in [20], where the flow of an incompressible viscous fluid described by the stationary Navier-Stokes equations was studied by the multiscale expansion method, which is a formal but powerful tool to analyse homogenization problems. These results were rigorously proved in [5] using an adaptation introduced in [4] of the periodic unfolding method from [16] and [17]. This adaptation consists of a combination of the unfolding method with a rescaling in the height variable, in order to work with a domain of fixed height, and to use monotonicity arguments to pass to the limit. In [4], in particular, the flow of an incompressible stationary Stokes system with a nonlinear viscosity, being a power law, was studied. For non-stationary incompressible viscous flow in a thin porous medium see [1], where a non-stationary Stokes system is considered, and [2], where a non-stationary non-newtonian Stokes system, where the viscosity obeyed the power law, is studied. For the periodic unfolding method applied to the study of problems stated in other type of thin periodic domains we refer for instance to [23] for crane type structures and to [24], [25] for thin layers with thin beams structures, where elasticity problems are considered. In [32], the homogenization of elasticity problems in thin periodic domains of planar grids type is studied. For problems involving arrays of bodies in high-contrast materials we refer the reader to [6], Chapter 2.

If $\Pi$ is a three-dimensional domain with smooth boundary $\partial \Pi$ and $f = (f_1,f_2,f_3)$ are external given forces defined on $\Pi$, then the velocity $u = (u_1,u_2,u_3)$ of a fluid and its pressure $p$ satisfy the equations of motion

completed with fluid's incompressibility condition ${ \rm{div}}\, u = \sum _{i = 1}^{3}\partial_{x_i}{u_i} = 0 \hbox { in } \Pi$, and the no-slip boundary condition $u = 0$ on the boundary $\partial\Pi$. What distinguishes different fluids is the expression of the stress tensor $\sigma$. Newtonian fluids are the most encountered ones in real life and as typical examples one can mention the water and the air. For a newtonian fluid, the entries of the stress tensor $\sigma(p,u)$ are given by

where $\delta_{ij}$ is the Kronecker symbol, the real positive $\mu$ is the viscosity of the fluid and the entries of the strain tensor are $(D(u))_{ij} = (\partial_{x_j} u_{i} + \partial_{x_i} u_{j})/2.$ If $f$ belongs to $(L^2(\Pi))^3$ and the space $V$ is defined by $V \,\, = \,\, \{ v \in (H_0^1(\Pi))^3 \,\, | \,\, \mbox{div}\, v = 0 \},$ then $u$ and $p$ satisfying (1) with (2) are such that (see for instance [22]):

(Stokes) There is a unique $u \in V$ and a unique (up to an additive real constant) $p \in L^2(\Pi)$ such that (if $<\cdot, \cdot >$ is the dual pairing between $(H^{-1}(\Pi))^3$ and $(H_0^1(\Pi))^3$)

with $a(u,v) = 2 \mu\int_{\Pi}\hbox {D(u)} \colon \hbox {D(v)} dx$ and $l(v) = \int_{\Pi} f \cdot v dx$.

A fluid whose stress is not defined by relation (2) is called a non-newtonian fluid. There are several classes of non-newtonian fluids, as the power law, Carreau, Cross, Bingham fluids. It is on the study of the last type of fluid that we are interested in this paper. We refer to [18] for a review on non-newtonian fluids. For a Bingham fluid, the nonlinear stress tensor is defined by (see [19])

where $\vert D (u) \vert ^2 = D(u) \colon D(u) \neq 0$ and the positive number $g$ represents the yield stress of the fluid. If $g = 0$, then (4) becomes (2). Viscoplastic Bingham fluids are quite often encountered in real life. As examples one can mention volcanic lava, fresh concrete, the drilling mud, oils, clays and some paintings. For $u_g$ and $p_g$ satisfying (1) with (4), according to [19], one has the following result:

(Bingham) There is a unique $u_g \in V$ and a (non-unique) $p_g \in L^2(\Pi)/\mathbb{R}$ such that

Here $a, l, <\cdot, \cdot >$ are as before and

If the yield stress of the Bingham fluid is of the form $g(\varepsilon)$, with $\varepsilon \in ]0,1[$ and such that $g (\varepsilon)$ tends to zero when $\varepsilon$ tends to zero, then, according to [[19], Chapter 6, Théorème 5.1.], the following result holds

When $\varepsilon$ tends to zero, one has for the solution $u_\varepsilon$ of problem (5) corresponding to $g(\varepsilon)$ the following convergence

where $u$ is the solution of problem (3).

This means that, in a fixed domain, the nonlinear character of the Bingham flow is lost in the limit when the yield stress tends to zero, as it is expected. A natural question that arises is the following: If the yield stress $g(\varepsilon)$ is as before and, moreover, the domain $\Pi$ itself depends on the small parameter $\varepsilon$, what happens when $\varepsilon$ tends to zero? The answer is that, in the limit, the nonlinear character of the flow may be preserved. For instance, if $\Pi_\varepsilon$ is a classical rigid porous medium, it was proven in [29] with the asymptotic expansion method that, in a range of parameters, the nonlinear character of the Bingham flow is preserved in the homogenized problem, which is a nonlinear Darcy equation. The convergence corresponding to the above mentioned result was proven in [10] with the two-scale convergence method and then recovered in [12] with the periodic unfolding method. The case of a doubly periodic rigid porous medium was studied in [11], where a more involved nonlinear Darcy equation is derived. Another class of domains for which the nonlinear character of the flow may be preserved in the limit is those of thin domains. The case of a domain $\Pi_\varepsilon$ which is thin in one direction was addressed in [14] and [15]. We refer to [13] for the asymptotic analysis of a Bingham fluid in a thin T-like shaped domain. In all these cases, a lower-dimensional Bingham-like law was exhibited in the limit. This law was already encountered in engineering (see [31]), but no rigurous mathematical justification was previously known. A first mathematical result combining both periodic and thin domains for the Bingham flow was announced in [3]. For the shallow flow of a viscoplastic fluid we refer the reader to [21], [9], [26], [27] and [28]. For a homogenized non-newtonian viscoelastic model we refer to [7].

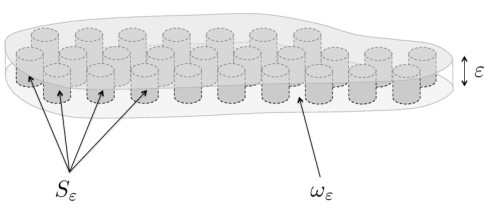
The paper is organized as follows. In Section 2. we state the problem: we define in (6) the thin porous medium $\Omega_\varepsilon$ (see also Figure 1), of height $\varepsilon$ and relative dimension $a_\varepsilon$ of its periodically distributed pores. In $\Omega_\varepsilon$ we consider the flow of a viscoplastic Bingham fluid with velocity $u_\varepsilon$ and pressure $p_\varepsilon$ verifying the nonlinear variational inequality (9). In Section 3. we give some a priori estimates for the velocity and for the pressure obtained after the change of variables (10) and verifying (12), and then for the velocity and for the pressure defined in (21). In Section 4. by passing to the limit $\varepsilon \rightarrow 0$, we prove the main convergence results of our paper, stated in Theorems 4.2, 4.4 and 4.6, respectively. Up to our knowledge, problems (37), (59) and (81) are new in the mathematical literature. We conclude in Section 5. with the interpretation of these limit problems, which all three preserve the nonlinear character of the flow; both effects of a nonlinear Darcy equation and a lower dimensional Bingham-like law appear. The paper ends with a list of References.

2.   Statement of the problem

A periodic porous medium is defined by a domain $\omega$ and an associated microstructure, or periodic cell $Y^{\prime} = [-1/2,1/2]^2$, which is made of two complementary parts: the fluid part $Y^{\prime}_{f}$, and the solid part $Y^{\prime}_{s}$ ($Y^{\prime}_f \bigcup Y^{\prime}_s = Y^\prime$ and $Y^{\prime}_f \bigcap Y^{\prime}_s = \varnothing$). More precisely, we assume that $\omega$ is a smooth, bounded, connected set in $\mathbb{R}^2$, and that $Y_s^{\prime}$ is an open connected subset of $Y^\prime$ with a smooth boundary $\partial Y_s^\prime$, such that $\overline Y_s^\prime$ is strictly included in $Y^\prime$.

The microscale of a porous medium is a small positive number $a_{\varepsilon}$. The domain $\omega$ is covered by a regular mesh of size $a_{\varepsilon}$: for $k^{\prime}\in \mathbb{Z}^2$, each cell $Y^{\prime}_{k^{\prime},a_{\varepsilon}} = a_{\varepsilon}k^{\prime}+a_{\varepsilon}Y^{\prime}$ is divided in a fluid part $Y^{\prime}_{f_{k^{\prime}},a_{\varepsilon}}$ and a solid part $Y^{\prime}_{s_{k^{\prime}},a_{\varepsilon}}$, i.e. is similar to the unit cell $Y^{\prime}$ rescaled to size $a_{\varepsilon}$. We define $Y = Y^{\prime}\times (0,1)\subset \mathbb{R}^3$, which is divided in a fluid part $Y_{f}$ and a solid part $Y_{s}$, and consequently $Y_{k^{\prime},a_{\varepsilon}} = Y^{\prime}_{k^{\prime},a_{\varepsilon}}\times (0,1)\subset \mathbb{R}^3$, which is also divided in a fluid part $Y_{f_{k^{\prime}},a_{\varepsilon}}$ and a solid part $Y_{s_{k^{\prime}},a_{\varepsilon}}$.

We denote by $\tau(\overline Y'_{s_{k'},a_\varepsilon})$ the set of all translated images of $\overline Y'_{s_{k'},a_\varepsilon}$. The set $\tau(\overline Y'_{s_{k'},a_\varepsilon})$ represents the solids in $\mathbb{R}^2$. The fluid part of the bottom $\omega_{\varepsilon}\subset \mathbb{R}^2$ of the porous medium is defined by $\omega_{\varepsilon} = \omega\backslash\bigcup_{k^{\prime}\in \mathcal{K}_{\varepsilon}} \overline Y^{\prime}_{s_{k^{\prime}}, {a_\varepsilon}}$, where $\mathcal{K}_{\varepsilon} = \{k^{\prime}\in \mathbb{Z}^2: Y^{\prime}_{k^{\prime}, {a_\varepsilon}} \cap \omega \neq \emptyset \}$. The whole fluid part $\Omega_{\varepsilon}\subset \mathbb{R}^3$ in the thin porous medium is defined by

We make the assumption that the solids $\tau(\overline Y'_{s_{k'},a_\varepsilon})$ do not intersect the boundary $\partial \omega$. We define $Y^\varepsilon_{s_{k'},a_\varepsilon} = Y'_{s_{k'},a_\varepsilon}\times (0,\varepsilon)$. Denote by $S_\varepsilon$ the set of the solids contained in $\Omega_\varepsilon$. Then, $S_\varepsilon$ is a finite union of solids, i.e. $S_\varepsilon = \bigcup_{k^{\prime}\in \mathcal{K}_{\varepsilon}} \overline Y^\varepsilon_{s_{k'},a_\varepsilon}.$

We define $\widetilde{\Omega}_{\varepsilon} = \omega_{\varepsilon}\times (0,1),$ $\Omega = \omega\times (0,1),$ and $Q_\varepsilon = \omega\times (0,\varepsilon).$ We observe that $\widetilde{\Omega}_{\varepsilon} = \Omega\backslash \bigcup_{k^{\prime}\in \mathcal{K}_{\varepsilon}} \overline Y_{s_{k^{\prime}}, {a_\varepsilon}},$ and we define $T_\varepsilon = \bigcup_{k^{\prime}\in \mathcal{K}_{\varepsilon}} \overline Y_{s_{k^\prime}, a_\varepsilon}$ as the set of the solids contained in $\widetilde \Omega_\varepsilon$.

We denote by $:$ the full contraction of two matrices; for $A = (a_{i,j})_{1\leq i,j\leq 3}$ and $B = (b_{i,j})_{1\leq i,j\leq 3}$, we have $A:B = \sum_{i,j = 1}^3 a_{ij}b_{ij}$.

In order to apply the unfolding method, we will need the following notation. For $k'\in \mathbb{Z}^2$, we define $\kappa:\mathbb{R}^2\to \mathbb{Z}^2$ by

Remark that $\kappa$ is well defined up to a set of zero measure in $\mathbb{R}^2$ (the set $\cup_{k^\prime\in \mathbb{Z}^2}\partial Y^{\prime}_{k^{\prime},1}$). Moreover, for every $a_\varepsilon>0$, we have

We denote by $C$ a generic positive constant which can change from line to line.

The points $x\in\mathbb{R}^3$ will be decomposed as $x = (x^{\prime},x_3)$ with $x^{\prime} = (x_1,x_2)\in \mathbb{R}^2$, $x_3\in \mathbb{R}$. We also use the notation $x^{\prime}$ to denote a generic vector of $\mathbb{R}^2$.

In $\Omega_\varepsilon$ we consider the stationary flow of an incompressible Bingham fluid. As already seen in the Introduction, following Duvaut and Lions [19], the problem is formulated in terms of a variational inequality.

For a vectorial function $v = (v',v_3)$, we define

We introduce the following spaces

For $u,v\in (H_0^1(\Omega_\varepsilon))^3$, we introduce

where the yield stress $g(\varepsilon)$ will be made precise in Section 3.1. Let $f\in (L^2(\Omega))^3$ be given such that $f = (f',0)$. Let $f_\varepsilon\in (L^2(\Omega_\varepsilon))^3$ be defined by

The model of the flow is described by the following variational inequality:

Find $u_\varepsilon \in V(\Omega_\varepsilon)$ such that

From Duvaut and Lions [19], we know that there exists a unique $u_\varepsilon\in V(\Omega_\varepsilon)$ solution of problem (8). Moreover, from Bourgeat and Mikelić [10], we know that if $p_\varepsilon$ is the pressure of the fluid in $\Omega_\varepsilon$, then problem (8) is equivalent to the following one: Find $u_\varepsilon \in V(\Omega_\varepsilon)$ and $p_\varepsilon \in L_0^2(\Omega_\varepsilon)$ such that

Problem (9) admits a unique solution $u_\varepsilon \in V(\Omega_\varepsilon)$ and a (non) unique solution $p_\varepsilon \in L_0^2(\Omega_\varepsilon)$, where $L_0^2(\Omega_\varepsilon)$ denotes the space of functions belonging to $L^2(\Omega_\varepsilon)$ and of mean value zero.

Our aim is to study the asymptotic behavior of $u_{\varepsilon}$ and $p_\varepsilon$ when $\varepsilon$ tends to zero. For this purpose, we first use the dilatation of the domain $\Omega_\varepsilon$ in the variable $x_3$, namely

in order to have the functions defined in an open set with fixed height, denoted $\widetilde{\Omega}_{\varepsilon}$.

Namely, we define $\tilde{u}_{\varepsilon}\in (H_0^{1}(\widetilde{\Omega}_{\varepsilon}))^3$, $\tilde p_\varepsilon \in L^2_0(\widetilde\Omega_\varepsilon)$ by

Let us introduce some notation which will be useful in the following. For a vectorial function $v = (v',v_3)$ and a scalar function $w$, we will denote $\mathbb{D}_{x^\prime}\left[v\right] = \frac{1}{2}(D_{x^\prime}v+D_{x^\prime}^t v)$ and $\partial_{y_3}\left[v\right] = \frac{1}{2}(\partial_{y_3}v+\partial_{y_3}^t v)$, where we denote $\partial_{y_3} = (0,0,\frac{\partial}{\partial y_3})^t$. Moreover, associated to the change of variables (10), we introduce the operators: $D_{\varepsilon}$, $\mathbb{D}_\varepsilon$, ${\rm div}_{\varepsilon}$ and $\nabla_\varepsilon$, defined by

We introduce the following spaces

For $\tilde u,\tilde v\in V(\widetilde\Omega_\varepsilon)$, we introduce

and

Using the transformation (10), the variational inequality (8) can be rewritten as:

Find $\tilde u_\varepsilon \in V(\widetilde\Omega_\varepsilon)$ such that

and (9) can be rewritten as:

Find $\tilde u_\varepsilon \in V(\widetilde \Omega_\varepsilon)$ and $\tilde p_\varepsilon \in L_0^2(\widetilde \Omega_\varepsilon)$ such that

Our goal now is to describe the asymptotic behavior of this new sequence $(\tilde{u}_{\varepsilon}$, $\tilde{p}_{\varepsilon})$.

3.   A priori estimates

We start by obtaining some a priori estimates for $\tilde{u}_{\varepsilon}$.

Lemma 3.1. There exists a constant $C$ independent of $\varepsilon$, such that if $\tilde{u}_{\varepsilon}\in (H_0^{1}(\widetilde{\Omega}_{\varepsilon}))^3$ is the solution of problem (11), one has

$i)$ if $a_{\varepsilon}\approx \varepsilon$, with $a_\varepsilon/\varepsilon\to \lambda$, $0<\lambda<+\infty$, or $a_\varepsilon\ll \varepsilon$, then

$ii)$ if $a_\varepsilon\gg \varepsilon$, then

Proof. Setting successively $\tilde v = 2\tilde u_\varepsilon$ and $\tilde v = 0$ in (11), we have

Using Cauchy-Schwarz's inequality and the assumption of $f$, we obtain that

and taking into account that $\int_{\widetilde{\Omega}_{\varepsilon}}|\mathbb{D}_{\varepsilon}[\tilde u_\varepsilon]|dx'dy_3\ge 0,$ by (15), we have

For the cases $a_\varepsilon \approx \varepsilon$ or $a_\varepsilon \ll \varepsilon$, taking into account Remark 4.3(ⅰ) in [4], we obtain the second estimate in (13), and, consequently, from classical Korn's inequality we obtain the last estimate in (13). Now, from the second estimate in (13) and Remark 4.3(ⅰ) in [4], we deduce the first estimate in (13). For the case $a_\varepsilon \gg \varepsilon$, proceeding similarly with Remark 4.3(ⅱ) in [4], we obtain the desired result.

3.1.   The extension of $(\tilde u_\varepsilon,\tilde p_\varepsilon)$ to the whole domain $\Omega$

We extend the velocity $\tilde u_\varepsilon$ by zero to the $\Omega\backslash \widetilde \Omega_\varepsilon$ and denote the extension by the same symbol. Obviously, estimates (13)-(14) remain valid and the extension is divergence free too.

We study in the sequel the following cases for the value of the yield stress $g (\varepsilon)$:

ⅰ) if $a_{\varepsilon}\approx \varepsilon$, with $a_\varepsilon/\varepsilon\to \lambda$, $0<\lambda<+\infty$, or $a_\varepsilon\ll \varepsilon$, then $g(\varepsilon) = g\,a_\varepsilon,$

ⅱ) if $a_\varepsilon\gg \varepsilon$, then $g (\varepsilon) = g\,\varepsilon,$

where $g$ is a positive number. These choices are the most challenging ones and they answer to the question adressed in the paper, namely they all preserve in the limit the nonlinear character of the flow.

In order to extend the pressure to the whole domain $\Omega$, the mapping $R^\varepsilon$ (defined in Lemma 4.5 in [4] as $R_2^\varepsilon$) allows us to extend the pressure $p_\varepsilon$ to $Q_\varepsilon$ by introducing $F_\varepsilon$ in $(H^{-1}(Q_\varepsilon))^3$:

Setting succesively $v = u_\varepsilon + R^{\varepsilon} w$ and $v = u_\varepsilon - R^{\varepsilon} w$ in (9) we get the inequality

Moreover, if ${\rm div}\,w = 0$ then $\left\langle F_{\varepsilon}, w\right\rangle_{Q_\varepsilon} = 0,$ and the DeRham Theorem gives the existence of $P_\varepsilon$ in $L_0^2(Q_\varepsilon)$ with $F_\varepsilon = \nabla P_\varepsilon$.

Using the change of variables (10), we get for any $\tilde w\in (H_0^1(\Omega))^3$ where $\tilde w(x',y_3) = w(x',\varepsilon y_3)$,

Then, using the identification (16) of $F_\varepsilon$ and the inequality (17),

and applying the change of variables (10),

where $\tilde R^{\varepsilon}\tilde w = R^\varepsilon w$ for any $\tilde w\in (H_0^1(\Omega))^3$.

Now, we estimate the right-hand side of (18) using the estimates given in Lemma 4.6 in [4].

Lemma 3.2. There exists a constant $C$ independent of $\varepsilon$, such that the extension $\tilde{P}_{\varepsilon}\in L_0^{2}(\Omega)$ of the pressure $\tilde{p}_{\varepsilon}$ satisfies

Proof. Let us estimate $\nabla_{\varepsilon} \tilde{P}_{\varepsilon}$ in the cases $a_{\varepsilon}\approx \varepsilon$ or $a_\varepsilon\ll \varepsilon$. We estimate the right-hand side of (18). Using Cauchy-Schwarz's inequality and from the second estimate in (13) we have

Using the assumption made on the function $f$, we obtain

and by Cauchy-Schwarz's inequality and taking into account that $|\widetilde{\Omega}_{\varepsilon}|\leq |\Omega|$, we obtain

Then, from (18), we deduce

Taking into account the third point in Lemma 4.6 in [4], we have

If $a_{\varepsilon}\approx \varepsilon$ we take into account that $a_{\varepsilon}\ll1$, and if $a_\varepsilon\ll \varepsilon$ we take into account that $a_\varepsilon/\varepsilon\ll 1$ and $a_{\varepsilon}\ll1$, and we see that there exists a positive constant $C$ such that

and consequently

It follows that (see for instance Girault and Raviart [22], Chapter I, Corollary 2.1) there exists a representative of $\tilde P_\varepsilon\in L^2_0(\Omega)$ such that

Finally, let us estimate $\nabla_{\varepsilon} \tilde{P}_{\varepsilon}$ in the case $a_\varepsilon\gg \varepsilon$. Similarly to the previous case, we estimate the right side of (18) by using Cauchy-Schwarz's inequality and from the second estimate in (14), and we have

Taking into account the proof in Lemma 4.5 in [4], the change of variables (10) and that $a_\varepsilon\gg \varepsilon$, we can deduce

and using that $a_{\varepsilon}\ll1$, we see that there exists a positive constant $C$ such that

and reasing as the previous case, we have the estimate (19).

According to these extensions, problem (12) can be written as:

for every $\tilde v$ that is the extension by zero to the whole $\Omega$ of a function in $(H_0^1(\widetilde \Omega_\varepsilon))^3$.

3.2.   Adaptation of the unfolding method

The change of variable (10) does not provide the information we need about the behavior of $\tilde{u}_{\varepsilon}$ in the microstructure associated to $\widetilde{\Omega}_{\varepsilon}$. To solve this difficulty, we use an adaptation introduced in [4] of the unfolding method from [16] and [17].

Let us recall this adaptation of the unfolding method in which we divide the domain $\Omega$ in cubes of lateral length $a_\varepsilon$ and vertical length $1$. For this purpose, given $(\tilde{u}_{\varepsilon}, \tilde{P}_{\varepsilon})\in (H_0^{1}(\Omega))^3\times L^{2}_0(\Omega)$, we define $(\hat{u}_{\varepsilon}, \hat{P}_{\varepsilon})$ by

a.e. $(x^{\prime},y)\in \omega\times Y$, where the function $\kappa$ is defined in (7).

Remark 1. For $k^{\prime}\in \mathcal{K}_{\varepsilon}$, the restriction of $(\hat{u}_{\varepsilon}, \hat{P}_{\varepsilon})$ to $Y^{\prime}_{k^{\prime},a_{\varepsilon}}\times Y$ does not depend on $x^{\prime}$, whereas as a function of $y$ it is obtained from $(\tilde{u}_{\varepsilon}, \tilde{P}_{\varepsilon})$ by using the change of variables $y^{\prime} = \frac{x^{\prime}-a_{\varepsilon}k^{\prime}}{a_{\varepsilon}},$ which transforms $Y_{k^{\prime},a_{\varepsilon}}$ into $Y$.

We are now in position to obtain estimates for the sequences $(\hat{u}_{\varepsilon}, \hat{P}_{\varepsilon})$, as in the proof of Lemma 4.9 in [4].

Lemma 3.3. There exists a constant $C$ independent of $\varepsilon$, such that the couple $(\hat{u}_{\varepsilon}, \hat{P}_{\varepsilon})$ defined by (21) satisfies

$i)$ if $a_{\varepsilon}\approx \varepsilon$, with $a_\varepsilon/\varepsilon\to \lambda$, $0<\lambda<+\infty$, or $a_\varepsilon\ll \varepsilon$,

$ii)$ if $a_\varepsilon\gg \varepsilon$,

and, moreover, in every cases,

4.   Main convergence results

When $\varepsilon$ tends to zero, we obtain for problem (20) different behaviors, depending on the magnitude of $a_\varepsilon$ with respect to $\varepsilon$. We will analyze them in the next sections.

4.1.   Critical case $a_{\varepsilon}\approx \varepsilon$, with $a_\varepsilon/\varepsilon\to \lambda$, $0<\lambda<+\infty$

First, we obtain some compactness results about the behavior of the sequences $(\tilde u_\varepsilon, \tilde P_\varepsilon)$ and $(\hat u_\varepsilon, \hat P_\varepsilon)$ satisfying the a priori estimates given in Lemmas 3.1-ⅰ) and 3.3-ⅰ), respectively.

Lemma 4.1 (Critical case). For a subsequence of $\varepsilon$ still denote by $\varepsilon$, there exist $\tilde{u}\in H^1(0,1;L^2(\omega)^3)$, where $\tilde u_3 = 0$ and $\tilde{u} = 0$ on $y_3 = \{0,1\}$, $\hat{u}\in L^2(\omega;H^1_{\sharp}(Y)^3)$ ("$\sharp$" denotes $Y'$-periodicity), with $\hat{u} = 0$ on $\omega\times Y_s$ and $\hat u = 0$ on $y_3 = \{0,1\}$ such that $\int_{Y}\hat u(x',y)dy = \int_0^1 \tilde u(x',y_3)dy_3$ with $\int_Y \hat u_3dy = 0$, and $\hat{P}\in L^{2}_0(\omega \times Y)$, independent of $y$, such that

where ${\rm div}_{\lambda} = {\rm div}_{y^\prime}+\lambda \partial_{y_3}$.

Proof. We refer the reader to Lemmas 5.2, 5.3 and 5.4 in [4] for the proof of (22)-(26). Here, we prove that $\hat P$ does not depend on the microscopic variable $y$. To do this, we choose as test function $\tilde v(x^{\prime},y)\in \mathcal{D}(\omega;C_{\sharp}^{\infty}(Y)^3)$ with $\tilde v(x^{\prime},y) = 0\in \omega \times Y_s$ (thus, $\tilde v(x^{\prime},x^{\prime}/a_{\varepsilon},y_3)\in (H_0^{1}(\widetilde{\Omega}_{\varepsilon}))^3$). Setting $a_\varepsilon\tilde v(x',x'/a_\varepsilon, y_3)$ in (20) (we recall that $g(\varepsilon) = g\, a_\varepsilon)$) and using that ${\rm div}_\varepsilon \tilde u_\varepsilon = 0$, we have

By the change of variables given in Remark 1 and by Lemma 3.3, we get for the first term in relation (27)

and for the second term in relation (27)

Moreover, applying the change of variables given in Remark 1 to the fourth term in relation (27), we have

Therefore, applying the change of variables given in Remark 1 to relation (27), we obtain

According with (23), the first term in relation (31) can be written by the following way

In order to pass to the limit in the first nonlinear term, we have

Now, in order to pass the limit in the second nonlinear term, we are taking into account that

and using (23) and the fact that the function $E(\varphi) = |\varphi|$ is proper convex continuous, we can deduce that

Moreover, using (23) the two first terms in the right hand side of (31) can be written by

We consider now the terms which involve the pressure. Taking into account the convergence of the pressure (23), passing to the limit when $\varepsilon$ tends to zero, we have

Therefore, taking into account (32)-(36), when we pass to the limit in (31) when $\varepsilon$ tends to zero, we have $0\ge\int_{\omega\times Y} \hat{P}\, {\rm div}_{\lambda} \tilde v\,dx^{\prime}dy.$ Now, if we choose as test function $-a_\varepsilon\tilde v(x',x'/a_\varepsilon, y_3)$ in (20) and we argue similarly, we obtain $\int_{\omega\times Y} \hat{P}\, {\rm div}_{\lambda} \tilde v\,dx^{\prime}dy\ge0.$ Thus, we can deduce that $\int_{\omega\times Y} \hat{P}\, {\rm div}_{\lambda} \tilde v\,dx^{\prime}dy = 0,$ which shows that $\hat P$ does not depend on $y$.

Theorem 4.2 (Critical case). If $a_{\varepsilon}\approx \varepsilon$, with $a_\varepsilon/\varepsilon\to \lambda$, $0<\lambda<+\infty$, then $(\hat u_\varepsilon/a_\varepsilon^2,\hat P_\varepsilon)$ converges to $(\hat u,\hat P)$ in $L^2(\omega;H^1(Y)^3)\times L^{2}_0(\omega \times Y)$, which satisfies the following variational inequality

where $\mathbb{D}_\lambda[\cdot] = \mathbb{D}_{y^\prime}[\cdot]+\lambda\partial_{y_3}[\cdot]$ and for every $\tilde v\in L^2(\omega;H^1(Y)^3)$ such that

Proof. We choose a test function $\tilde v(x^{\prime},y)\in \mathcal{D}(\omega;C_{\sharp}^{\infty}(Y)^3)$ with $\tilde v(x^{\prime},y) = 0\in \omega \times Y_s$ (thus, we have that $\tilde v(x^{\prime},x^{\prime}/a_{\varepsilon},y_3)\in (H_0^{1}(\widetilde{\Omega}_{\varepsilon}))^3$). We first multiply (20) by $a_\varepsilon^{-2}$ and we use that ${\rm div}_\varepsilon \tilde u_\varepsilon = 0$. Then, we take as test function $a_\varepsilon^{2}\tilde v_\varepsilon = a_\varepsilon^{2} (\tilde v'(x',x'/a_\varepsilon, y_3), \lambda \varepsilon/a_\varepsilon v_3(x',x'/a_\varepsilon, y_3))$, with $\tilde v(x',y) = 0$ in $\omega\times Y_s$ and satisfying the incompressibility conditions (25)-(26), that is, ${\rm div}_{\lambda}\tilde v = 0$ in $\omega\times Y$ and $\left( \int_Y \tilde v^{\prime}(x^{\prime},y)dy \right)\cdot n = 0$ on $\partial \omega$, and we have

By the change of variables given in Remark 1 and by Lemma 3.3, we have (28) for the first term in relation (38), and for the second term in relation (38) we obtain

Moreover, applying the change of variables given in Remark 1 to the fourth term in relation (38), we have (30). Therefore, applying the change of variables given in Remark 1 to relation (38), we obtain

According with (23), the first term in relation (40) can be written

and, taking into account that $\lambda\,\varepsilon/a_\varepsilon\to 1$, this term tends to the following limit

The second term in relation (40) writes

and, taking into account that the function $B(\varphi) = | \varphi |$ is proper convex continuous and $\lambda\,\varepsilon/a_\varepsilon\to 1$, we get that the $\liminf_{\varepsilon \to 0}$ of this second is greater or equal than

In order to pass to the limit in the first nonlinear term, we have

and we can deduce that the first nonlinear term tends to the following limit

Now, in order to pass the limit in the second nonlinear term, we are taking into account that

and using (23) and the fact that the function $E(\varphi) = |\varphi|$ is proper convex continuous, we can deduce that

Moreover, using (23) the two first terms in the right hand side of (40) tend to the following limit

We consider now the terms which involve the pressure. Taking into account the convergence of the pressure (23) the first term of the pressure tends to the following limit $\int_{\omega\times Y} \hat{P}\, {\rm div}_{x^\prime} \tilde v^\prime\,dx^{\prime}dy,$ and using (25) and taking into account that $\hat P$ does not depend on $y$, we have

Finally, using that ${\rm div}_{\lambda}\tilde v = 0$, we have

Therefore, taking into account (41)-(47), we have (37).

4.2.   Subcritical case $a_{\varepsilon}\ll \varepsilon$ ($\lambda=0$)

We obtain some compactness results about the behavior of the sequences $(\tilde u_\varepsilon, \tilde P_\varepsilon)$ and $(\hat u_\varepsilon, \hat P_\varepsilon)$ satisfying the a priori estimates given in Lemmas 3.1-ⅰ) and 3.3-ⅰ), respectively.

Lemma 4.3 (Subcritical case). For a subsequence of $\varepsilon$ still denoted by $\varepsilon$, there exist $\tilde{u}\in (L^2(\Omega))^3$, where $\tilde u_3 = 0$ and $\tilde{u} = 0$ on $y_3 = \{0,1\}$, $\hat{u}\in L^2(\Omega;H^1_{\sharp}(Y')^3)$ ("$\sharp$" denotes $Y'$-periodicity), with $\hat{u} = 0$ in $\omega\times Y_s$ and $\hat u = 0$ on $y_3 = \{0,1\}$ such that $\int_{Y}\hat u(x',y)dy = \int_0^1 \tilde u(x',y_3)dy_3$ with $\int_Y \hat u_3dy = 0$ and $\hat u_3$ independent of $y_3$, and $\hat{P}\in L^{2}_0(\omega \times Y)$, independent of $y$, such that

Proof. See Lemmas 5.2, 5.3 and 5.4 in [4] for the proof of (48)-(52). In order to prove that $\hat P$ does not depend on $y'$ we argue as in the proof of Lemma 4.1 using that $a_{\varepsilon}\ll \varepsilon$, and we obtain $\int_{\omega\times Y} \hat{P}\, {\rm div}_{y'} \tilde v'\,dx^{\prime}dy = 0,$ which shows that $\hat P$ does not depend on $y'$. Now, in order to prove that $\hat P$ does not depend on $y_3$, setting $\varepsilon \tilde v = \varepsilon(0, \tilde v_3(x',x'/a_\varepsilon,y_3))$ in (20) (we recall that $g(\varepsilon) = g\, a_\varepsilon)$) and using that ${\rm div}_\varepsilon \tilde u_\varepsilon = 0$, we have

Applying the change of variables given in Remark 1 to relation (53) and taking into account (28)-(30), we obtain

According with (49) and using that $a_{\varepsilon}\ll \varepsilon$, the first term in relation (54) can be written by the following way

In order to pass to the limit in the first nonlinear term, we have

In order to pass to the limit in the second nonlinear term, we proceed as in Lemma 4.1. Moreover, using (49) the first term in the right hand side of (54) can be written by

We consider now the term which involves the pressure. Taking into account the convergence of the pressure (49), passing to the limit when $\varepsilon$ tends to zero, we have

Therefore, taking into account (34) and (55)-(58), when we pass to the limit in (54) when $\varepsilon$ tends to zero, we have $0\ge\int_{\omega\times Y} \hat{P}\, \partial_{y_3} \tilde v_3\,dx^{\prime}dy.$ Now, if we choose as test function $-\varepsilon \tilde v = -\varepsilon(0, \tilde v_3(x',x'/a_\varepsilon,y_3))$ in (20) and we argue similarly, we can deduce that $\hat P$ does not depend on $y_3$, so $\hat P$ does not depend on $y$.

Theorem 4.4 (Subcritical case). If $a_{\varepsilon}\ll \varepsilon$, then $(\hat u_\varepsilon/a_\varepsilon^2,\hat P_\varepsilon)$ converges to $(\hat u,\hat P)$ in $L^2(\Omega;H^1(Y')^3)\times L^{2}_0(\omega \times Y)$, which satisfies the following variational inequality

for every $\tilde v\in L^2(\Omega;H^1(Y')^3)$ such that

Proof. We choose a test function $\tilde v(x^{\prime},y)\in \mathcal{D}(\omega;C_{\sharp}^{\infty}(Y)^3)$ with $\tilde v(x^{\prime},y) = 0\in \omega \times Y_s$ (thus, we have that $\tilde v(x^{\prime},x^{\prime}/a_{\varepsilon},y_3)\in (H_0^{1}(\widetilde{\Omega}_{\varepsilon}))^3$). We first multiply (20) by $a_\varepsilon^{-2}$ and we use that ${\rm div}_\varepsilon \tilde u_\varepsilon = 0$. Then, we take a test function $a_\varepsilon^{2} \tilde v(x',x'/a_\varepsilon, y_3)$, with $\tilde v_3$ independent of $y_3$ and with $\tilde v(x',y) = 0$ in $\omega\times Y_s$ and satisfying the incompressibility conditions (51)-(52), that is, ${\rm div}_{y'}\tilde v' = 0$ in $\omega\times Y$ and $\left( \int_Y \tilde v^{\prime}(x^{\prime},y)dy \right)\cdot n = 0$ on $\partial \omega$, and we have

Applying the change of variables given in Remark 1 to relation (60) and taking into account (28), (30) and (39), we obtain

In the left-hand side, we only give the details of convergence for the first nonlinear term, the most challenging one.

Using (49) the two first terms in the right hand side of (61) tend to the following limit

We consider now the terms which involve the pressure. Taking into account the convergence of the pressure (49) the first term of the pressure tends to the following limit $\int_{\omega\times Y} \hat{P}\, {\rm div}_{x^\prime} \tilde v^\prime\,dx^{\prime}dy,$ and using (51) and taking into account that $\hat P$ does not depend on $y$, we have (46). Finally, using that ${\rm div}_{y'}\tilde v' = 0$, we have

It is straightforward to obtain that $\hat u_3 = 0$ and therefore we get (59).

4.3.   Supercritical case $a_{\varepsilon}\gg \varepsilon$ ($\lambda=+\infty$)

We obtain some compactness results about the behavior of the sequences $(\tilde u_\varepsilon, \tilde P_\varepsilon)$ and $(\hat u_\varepsilon, \hat P_\varepsilon)$ satisfying the a priori estimates given in Lemmas 3.1-ⅱ) and 3.3-ⅱ), respectively.

Lemma 4.5 (Supercritical case). For a subsequence of $\varepsilon$ still denote by $\varepsilon$, there exist $\tilde{u}\in H^1(0,1;L^2(\omega)^3)$, where $\tilde u_3 = 0$ and $\tilde{u} = 0$ on $y_3 = \{0,1\}$, $\hat{u}\in H^1(0,1;L^2_{\sharp}(\omega\times Y')^3)$ (" $\sharp$" denotes $Y'$-periodicity), with $\hat{u} = 0$ in $\omega\times Y_s$, $\hat u = 0$ on $y_3 = \{0,1\}$ such that $\int_{Y}\hat u(x',y)dy = \int_0^1 \tilde u(x',y_3)dy_3$ with $\int_Y \hat u_3dy = 0$ and $\hat u_3$ independent of $y_3$, and $\hat{P}\in L^{2}_0(\omega \times Y)$, independent of $y$, such that

Proof. See Lemmas 5.2, 5.3 and 5.4 in [4] for the proof of (63)-(67). Here, we prove that $\hat P$ does not depend on the microscopic variable $y$. To do this, we choose as test function $\tilde v(x^{\prime},y)\in \mathcal{D}(\omega;C_{\sharp}^{\infty}(Y)^3)$ with $\tilde v(x^{\prime},y) = 0\in \omega \times Y_s$ (thus, $\tilde v(x^{\prime},x^{\prime}/a_{\varepsilon},y_3)\in (H_0^{1}(\widetilde{\Omega}_{\varepsilon}))^3$). In order to prove that $\hat P$ does not depend on $y_3$, we set $\varepsilon\tilde v(x',x'/a_\varepsilon, y_3)$ in (20) (we recall that $g(\varepsilon) = g\,\varepsilon)$)and using that ${\rm div}_\varepsilon \tilde u_\varepsilon = 0$, we have

Applying the change of variables given in Remark 1 to relation (68) and taking into account (28)-(30), we obtain

According with (64) and using that $a_{\varepsilon}\gg \varepsilon$, one has for the first term in relation (69)

We pass to the limit in the first nonlinear term and we have

In order to pass the limit in the second nonlinear term, we taking into account that

and using (64), with $a_{\varepsilon}\gg \varepsilon$, and the fact that the function $E(\varphi) = |\varphi|$ is proper convex continuous, we can deduce that

Moreover, using (64) the two first terms in the right hand side of (69) can be written by

We consider now the terms which involve the pressure. Taking into account the convergence of the pressure (64) and $a_{\varepsilon}\gg \varepsilon$, passing to the limit when $\varepsilon$ tends to zero, we have

Therefore, taking into account (70)-(74), when we pass to the limit in (69) when $\varepsilon$ tends to zero, we have $0\ge\int_{\omega\times Y} \hat{P}\, \partial_{y_3} \tilde v_3\,dx^{\prime}dy.$ Now, if we choose as test function $-\varepsilon\tilde v(x',x'/a_\varepsilon, y_3)$ in (20) and we argue similarly, we can deduce that $\hat P$ does not depend on $y_3$. Now, in order to prove that $\hat P$ does not depend on $y'$, we set $a_\varepsilon \tilde v = a_\varepsilon(\tilde v'(x',x'/a_\varepsilon, y_3),0)$ in (20) and using that ${\rm div}_\varepsilon \tilde u_\varepsilon = 0$, we have

Applying the change of variables given in Remark 1 to relation (75) and taking into account (28)-(30), we obtain

According with (64) and using that $a_{\varepsilon}\gg \varepsilon$, the first term in relation (76) can be written by the following way

In order to pass to the limit in the first nonlinear term, we have

Moreover, using (64) the two first terms in the right hand side of (76) can be written by

We consider now the terms which involve the pressure. Taking into account the convergence of the pressure (64), passing to the limit when $\varepsilon$ tends to zero, we have

Therefore, taking into account (72) and (77)-(80), when we pass to the limit in (76) when $\varepsilon$ tends to zero, we have $0\ge\int_{\omega\times Y} \hat{P}\, {\rm div}_{y'} \tilde v'\,dx^{\prime}dy.$ Now, if we choose as test function $-a_\varepsilon \tilde v = -a_\varepsilon(\tilde v'(x',x'/a_\varepsilon, y_3),0)$ in (20) and we argue similarly, we can deduce that $\hat P$ does not depend on $y'$, so $\hat P$ does not depend on $y$.

Theorem 4.6 (Supercritical case). If $a_{\varepsilon}\gg \varepsilon$, then $(\hat u_\varepsilon/\varepsilon^2,\hat P_\varepsilon)$ converges to $(\hat u,\hat P)$ in $H^1(0,1;L^2(\omega \times Y')^3)\times L^{2}_0(\omega \times Y)$, which satisfies the following variational equality

for every $\tilde v\in H^1(0,1;L^2(\omega\times Y')^3)$ such that

Proof. We choose a test function $\tilde v(x^{\prime},y)\in \mathcal{D}(\omega;C_{\sharp}^{\infty}(Y)^3)$ with $\tilde v(x^{\prime},y) = 0\in \omega \times Y_s$ (thus, $\tilde v(x^{\prime},x^{\prime}/a_{\varepsilon},y_3)\in (H_0^{1}(\widetilde{\Omega}_{\varepsilon}))^3$). We first multiply (20) by $\varepsilon^{-2}$ and we use that ${\rm div}_\varepsilon \tilde u_\varepsilon = 0$. Then, we take a test function $\varepsilon^{2} \tilde v(x',x'/a_\varepsilon, y_3)$, with $\tilde v_3$ independent of $y_3$ and with $\tilde v(x',y) = 0$ in $\omega\times Y_s$ and satisfying the incompressibility conditions (66)-(67), that is, ${\rm div}_{y'}\tilde v' = 0$ in $\omega\times Y$ and $\left( \int_Y \tilde v^{\prime}(x^{\prime},y)dy \right)\cdot n = 0$ on $\partial \omega$, and we have

Applying the change of variables given in Remark 1 to relation (82), arguing as in the critical case, we obtain

According with (64), the first term in relation (83) can be written by the following way

and, taking into account that $a_\varepsilon\gg \varepsilon$, this term tends to the following limit

The second term in relation (83) writes

and, taking into account that the function $B(\varphi) = | \varphi |$ is proper convex continuous and $a_\varepsilon\gg \varepsilon$, we get that the $\liminf_{\varepsilon \to 0}$ of this second is greater or equal than

In order to pass to the limit in the first nonlinear term, using that $a_\varepsilon\gg \varepsilon$, we have

Now, in order to pass the limit in the second nonlinear term, taking into account that

and using (64) and the fact that the function $E(\varphi) = |\varphi|$ is proper convex continuous and $a_\varepsilon\gg \varepsilon$, we can deduce that

Moreover, using (64) the two first terms in the right hand side of (83) tend to the following limit

We consider now the terms which involve the pressure. Taking into account the convergence of the pressure (64) the first term of the pressure tends to the following limit $\int_{\omega\times Y} \hat{P}\, {\rm div}_{x^\prime} \tilde v^\prime\,dx^{\prime}dy,$ and using (66) and taking into account that $\hat P$ does not depend on $y$, we have (46). Finally using that ${\rm div}_{y'}\tilde v' = 0$, we have (62). Therefore, taking into account (46), (62) and (84)-(87), we get (81).

5.   Conclusions

By using dimension reduction and homogenization techniques, we studied the limiting behavior of the velocity and of the pressure for a nonlinear viscoplastic Bingham flow with small yield stress, in a thin porous medium of small height $\varepsilon$ and for which the relative dimension of the pores is $a_\varepsilon$. Three cases are studied following the value of $\lambda = \lim_{\varepsilon \rightarrow 0} {a_\varepsilon}/{\varepsilon}$ and, at the limit, they all preserve the nonlinear character of the flow. More precisely, according to [29], each of the limit problems (37), (59) and (81), is written as a nonlinear Darcy equation:

The velocity of filtration $\tilde{U}(x') = \left(\tilde{U'}(x'), \tilde{U}_3 (x') \right)$ is defined by

We remark that in all three cases, the vertical component $\tilde{U}_3$ of the velocity of filtration equals zero and this result is in accordance with the previous mathematical studies of the flow in this thin porous medium, for newtonian fluids (Stokes and Navier-Stokes equations) and for power law fluids (see [20], [1], [2], [4], [5]). Moreover, despite the fact that the limit pressure is not unique, the velocity of filtration is uniquely determined (see Section 4.3 in [29]). In (88), the function $K^{\lambda}:{\mathbb R}^2 \longrightarrow {\mathbb R}^2$ is nonlinear and its expression can not be made explicit for the Bingham flow (see [29]). Nevertheless, in each case, for a given $\xi \in {\mathbb R}^2$, one has $K^{\lambda}(\xi) = \int \limits_{Y}\chi_{\lambda}^{\xi}(y)dy$, with $\chi_{\lambda}^{\xi}$ solution of a local problem stated in the cell $Y$. If $0<\lambda<+\infty$, the local problem is a 3-D Bingham problem. If $\lambda = 0$, the local problem is a 2-D Bingham problem (defined for each $y_3 \in]0,1[)$, while if $\lambda = +\infty$ the 1-D local problem (defined for each $y' \in Y'$) corresponds to a lower-dimensional Bingham-like law (see [15]).

We end with the remark that if in the initial problem (9) we take $g = 0$, then the problem under study becomes the Stokes problem. We refer to [4] (case $p = 2$) for the asymptotic analysis of the Stokes problem. If we set $g = 0$ in the limit problems (37), (59) and (81), they become exactly the ones in [4], Theorem 6.1 (case $p = 2$), corresponding to the Stokes case.

Acknowledgments

We are grateful to the anonymous referee whose suggestions and questions were very valuable.