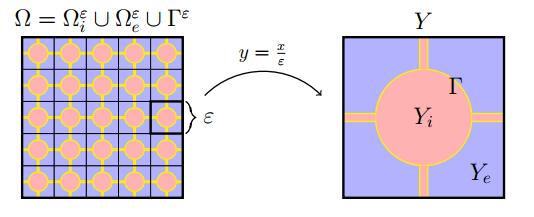
The rescaled sets
We provide a rather simple proof of a homogenization result for the bidomain model of cardiac electrophysiology. Departing from a microscopic cellular model, we apply the theory of two-scale convergence to derive the bidomain model. To allow for some relevant nonlinear membrane models, we make essential use of the boundary unfolding operator. There are several complications preventing the application of standard homogenization results, including the degenerate temporal structure of the bidomain equations and a nonlinear dynamic boundary condition on an oscillating surface.
Citation: Erik Grandelius, Kenneth H. Karlsen. The cardiac bidomain model and homogenization[J]. Networks and Heterogeneous Media, 2019, 14(1): 173-204. doi: 10.3934/nhm.2019009
| [1] | Erik Grandelius, Kenneth H. Karlsen . The cardiac bidomain model and homogenization. Networks and Heterogeneous Media, 2019, 14(1): 173-204. doi: 10.3934/nhm.2019009 |
| [2] | Mostafa Bendahmane, Kenneth H. Karlsen . Analysis of a class of degenerate reaction-diffusion systems and the bidomain model of cardiac tissue. Networks and Heterogeneous Media, 2006, 1(1): 185-218. doi: 10.3934/nhm.2006.1.185 |
| [3] | Alexander Mielke, Sina Reichelt, Marita Thomas . Two-scale homogenization of nonlinear reaction-diffusion systems with slow diffusion. Networks and Heterogeneous Media, 2014, 9(2): 353-382. doi: 10.3934/nhm.2014.9.353 |
| [4] | Brahim Amaziane, Leonid Pankratov, Andrey Piatnitski . An improved homogenization result for immiscible compressible two-phase flow in porous media. Networks and Heterogeneous Media, 2017, 12(1): 147-171. doi: 10.3934/nhm.2017006 |
| [5] | Boris Andreianov, Mostafa Bendahmane, Kenneth H. Karlsen, Charles Pierre . Convergence of discrete duality finite volume schemes for the cardiac bidomain model. Networks and Heterogeneous Media, 2011, 6(2): 195-240. doi: 10.3934/nhm.2011.6.195 |
| [6] | Catherine Choquet, Ali Sili . Homogenization of a model of displacement with unbounded viscosity. Networks and Heterogeneous Media, 2009, 4(4): 649-666. doi: 10.3934/nhm.2009.4.649 |
| [7] | Gaziz F. Azhmoldaev, Kuanysh A. Bekmaganbetov, Gregory A. Chechkin, Vladimir V. Chepyzhov . Homogenization of attractors to reaction–diffusion equations in domains with rapidly oscillating boundary: Critical case. Networks and Heterogeneous Media, 2024, 19(3): 1381-1401. doi: 10.3934/nhm.2024059 |
| [8] | Oleh Krehel, Toyohiko Aiki, Adrian Muntean . Homogenization of a thermo-diffusion system with Smoluchowski interactions. Networks and Heterogeneous Media, 2014, 9(4): 739-762. doi: 10.3934/nhm.2014.9.739 |
| [9] | Markus Gahn, Maria Neuss-Radu, Peter Knabner . Effective interface conditions for processes through thin heterogeneous layers with nonlinear transmission at the microscopic bulk-layer interface. Networks and Heterogeneous Media, 2018, 13(4): 609-640. doi: 10.3934/nhm.2018028 |
| [10] | Hakima Bessaih, Yalchin Efendiev, Florin Maris . Homogenization of the evolution Stokes equation in a perforated domain with a stochastic Fourier boundary condition. Networks and Heterogeneous Media, 2015, 10(2): 343-367. doi: 10.3934/nhm.2015.10.343 |
We provide a rather simple proof of a homogenization result for the bidomain model of cardiac electrophysiology. Departing from a microscopic cellular model, we apply the theory of two-scale convergence to derive the bidomain model. To allow for some relevant nonlinear membrane models, we make essential use of the boundary unfolding operator. There are several complications preventing the application of standard homogenization results, including the degenerate temporal structure of the bidomain equations and a nonlinear dynamic boundary condition on an oscillating surface.
The bidomain model [39,13,38] is widely used as a quantitative description of the electric activity in cardiac tissue. The relevant unknowns are the intracellular (
The bidomain model can be viewed as a PDE system consisting of two degenerate reaction-diffusion equations involving the unknowns
Starting from a more accurate microscopic (cell-level) model of cardiac tissue, with the heterogeneity of the underlying cellular geometry represented in great detail, it is possible to heuristically derive the bidomain model (tissue-level) using the multiple scales method of homogenization. This derivation was first carried out in [31]. It should be noted that the microscopic model is in general too complex to allow for full organ simulations, although there have been some very recent efforts in that direction [40]. The complexity of cell-level models, which themselves can be heuristically derived from the Poisson-Nernst-Planck equations [35], motivates the search for simpler homogenized (macroscopic) models. The work [31] assumes, as we do herein, that cardiac tissue can be viewed as a uniformly oriented periodic assembly of cells (see also [14,22]). There have been some attempts to remove this assumption. We refer to [26,25,36] for extensions to somewhat more realistic tissue geometries.
Despite the widespread use of the bidomain model, there are few mathematical rigorous derivations of the model from a microscopic description of cardiac tissue. From a mathematical point of view, rigorous homogenization is often linked to the study of the asymptotic behavior (convergence) of solutions to PDEs with oscillating coefficients. In the literature several approaches have been developed to handle this type of problem, like Tartar's method of oscillating test functions,
We are aware of two earlier works [4,34] containing rigorous homogenization results for the bidomain model (but see [16,15,43] for examples of elliptic and parabolic equations on"two-component" domains). With a fairly advanced proof involving
We mention that there are several complications preventing the application of standard homogenization results (for elliptic/parabolic equations) to the bidomain equations, including its degenerate structure (seen at the tissue-level), resulting from differing anisotropies of the intra- and extracellular spaces, and the highly nonlinear, oscillating dynamic boundary condition (seen at the cell-level).
The main contribution of our paper is to provide a simple homogenization proof that can handle some relevant nonlinear membrane models (the generalized FitzHugh-Nagumo model), relying only on basic two-scale convergence techniques. We now explain our contribution in more detail. The point of departure is the following microscopic model [13,14,22,41] for the electric activity in cardiac tissue:
|
$ −div(σεi∇uεi)=sεiin(0,T)×Ωεi,−div(σεe∇uεe)=sεein(0,T)×Ωεe,ε(∂tvε+I(vε,wε))=−ν⋅σεi∇uεion(0,T)×Γε,ε(∂tvε+I(vε,wε))=−ν⋅σεe∇uεeon(0,T)×Γε,∂twε=H(vε,wε)on(0,T)×Γε, $
|
(1.1) |
where
|
$ Ω=(0,1)×(0,1)×(0,1). $
|
(1.2) |
In (1.1),
| $ \sigma_j^ \varepsilon (x) = \sigma_j\left(x,\frac{x}{ \varepsilon }\right), \qquad j = i,e, $ |
where
We denote by
For each fixed
|
$ vε|t=0=vε0in Ω,wε|t=0=wε0in Ω,n⋅σj∇uεj=0on (0,T)×(∂Ω∩∂Ωεj),j=i,e, $
|
(1.3) |
where
The dimensionless number
|
$ uεj(t,x,y)=uj(t,x,y)+εu(1)j(t,x,y)+ε2u(2)j(t,x,y)+⋯(j=i,e),vε(t,x,y)=v(t,x,y)+εv(1)(t,x,y)+ε2v(2)(t,x,y)+⋯,wε(t,x,y)=w(t,x,y)+εw(1)(t,x,y)+ε2w(2)(t,x,y)+⋯, $
|
where
|
$ {|Γ|∂tv−div(Mi∇ui)+|Γ|I(v,w)=|Yi|si,in (0,T)×Ω,|Γ|∂tv+div(Me∇ue)+|Γ|I(v,w)=−|Ye|se,in (0,T)×Ω,∂tw=H(v,w),in (0,T)×Ω, $
|
(1.4) |
where the homogenized conductivity tensors
|
$ Mj(x)=∫Yjσj(x,y)(I+∇yχj(x,y))dy,j=i,e, $
|
(1.5) |
and the
|
$ {−divy(σj∇yχj)=−divyσj,in Ω×Yj,ν⋅σj∇yχj=ν⋅σj,on Ω×Γ. $
|
(1.6) |
Note that the effective potentials
Regarding the existence and uniqueness of properly defined solutions, standard theory for parabolic-elliptic systems does not apply naturally to the bidomain model (1.4). A number of works [6,7,8,14,42] have recently provided well-posedness results for (1.4), applying differing solution concepts and technical frameworks.
As alluded to earlier, we will provide a rigorous derivation of the homogenized system (1.4), (1.5), (1.6) based on the theory of two-scale convergence (see [33] and [1,2,28]). This result is not covered by standard parabolic homogenization theory. A complication is the nonlinear dynamic boundary condition (posed on an underlying oscillating surface), which makes it difficult to pass to the limit in (1.1) as
Unfolding operators, presented and carefully analyzed in [11,10], facilitate elementary proofs of classical homogenization results on fixed as well as perforated domains/surfaces. An unfolding operator
For somewhat similar unfolding of "two-component" domains separated by a periodic boundary, see [16,15,43]. For other relevant works that combine two-scale convergence and unfolding methods, we refer to [19,18,20,29,32]. Among these, our work borrows ideas mostly from [19,18,32].
The remaining part of the paper is organized as follows: In Section 2, we collect relevant functional spaces and analysis results. Moreover, we gather definitions and tools linked to two-scale convergence and unfolding operators. In Section 3, we define precisely what is meant by a weak solution of the microscopic problem (1.1), state a well-posedness result, and establish several "
For a general review of integer and fractional order Sobolev spaces (on Lipschitz domains) and relevant analysis tools, see [9,Chaps. 2 & 3] and [30,Chap. 3]. For relevant background material on mathematical homogenization, we refer to [12].
Let
We make use of Sobolev spaces on surfaces, as defined for example in [27,p. 34] and [30,p. 96]. Specifically, we use the (Hilbert) space
|
$ ‖u‖2H1/2(Γ)=‖u‖2L2(Γ)+|u|2H1/20(Γ), $
|
where
| $ \left|u\right|_{H_0^{1/2}}^2 = \int_{ \Gamma }\int_{ \Gamma } \frac{|u(x)-u(x')|^2}{|x-x'|^3}\, dS(x)\, dS(x'), $ |
and
| $ \left\|u\right\|_{H^{-1/2}( \Gamma )} : = \underset{\left\|\phi\right\|_{H^{1/2}( \Gamma )} = 1}{\sup\limits_{\phi\in H^{1/2}( \Gamma )}} \left \langle u, \phi \right\rangle_{H^{-1/2}( \Gamma ),H^{1/2}( \Gamma )}. $ |
The following trace inequality holds:
|
$ ‖u|Γ‖H1/2(Γ)≤C‖u‖H1(Ω),u∈H1(Ω). $
|
(2.1) |
Any function in
|
$ ‖I(u)‖H1(Ω)≤C‖u‖H1/2(Γ),∀u∈H1/2(Γ), $
|
(2.2) |
where the constant
|
$ ‖u‖L4(Γ)≤C‖u‖H1/2(Γ). $
|
(2.3) |
Indeed,
Let
Recall that
|
$ VΓ,T={u∈L2(0,T;H1/2(Γ))∩L4((0,T)×Γ)|∂tu∈L2(0,T;H−1/2(Γ))+L4/3((0,T)×Γ)}, $
|
equipped with the norm
| $ \left\|u\right\|_{\mathcal{V}_{ \Gamma ,T}} = \left\|u\right\|_{L^2(0,T;H^{1/2}( \Gamma ))\cap L^4((0,T)\times \Gamma )} +\left\| \,{\partial _t}u\right\|_{L^2(0,T;H^{-1/2}( \Gamma ))+L^{4/3}((0,T)\times \Gamma )}, $ |
where
|
$ ∫t2t1⟨∂tu1,u2⟩dt+∫t2t1⟨∂tu2,u1⟩dt=(u1(t2),u2(t2))L2(Γ)−(u1(t1),u2(t1))L2(Γ), $
|
(2.4) |
for all
Taking
|
$ ∫t2t1⟨∂tu,u⟩dt=12‖u(t2)‖2L2(Γ)−12‖u(u1)‖2L2(Γ). $
|
(2.5) |
Adapting standard arguments (see e.g. [9,p. 101]), the embedding
|
$ VΓ,T↪C(0,T;L2(Γ)) $
|
(2.6) |
is continuous. Indeed, this result follows from the continuity of the squared norm
Let us dwell a bit further on the time continuity of functions in
|
$ L2(0,T;H−1/2(Γ))+L4/3((0,T)×Γ)⊂L4/3(0,T;H−1/2(Γ)). $
|
With
|
$ (u(t2)−u(t1),ϕ)L2(Γ)=∫t2t1⟨∂tu,ϕ⟩dt≤‖ϕ‖H1/2(Γ)∫t2t1‖∂tu‖H−1/2(Γ)dt≤‖ϕ‖H1/2(Γ)‖∂tu‖L4/3(t1,t2;H−1/2(Γ))(t2−t1)1/4. $
|
Fix a small shift
|
$ ‖u(t+Δt,⋅)−u(t,⋅)‖2L2(Γ)≤‖u(t+Δt,⋅)−u(t,⋅)‖H1/2(Γ)‖∂tu‖L4/3(0,T;H−1/2(Γ))Δ1/4t. $
|
Integrating this inequality over
|
$ ‖u(⋅+Δt,⋅)−u(⋅,⋅)‖L2(0,T−Δt;L2(Γ))≤CT‖u‖1/2L2(0,T;H1/2(Γ))‖∂tu‖1/2L4/3(0,T;H−1/2(Γ))Δ1/8t,u∈VΓ,T, $
|
where
There is a compact embedding of
We need a generalization of this result due to Simon [37]. Given two Banach spaces
| $ \left\|u(\cdot+\Delta_t)-u\right\|_{L^p(0,T-\Delta_t;X_0)}\to 0 \quad \text{as $\Delta_t\to 0$, uniformly for $u\in \mathcal{K}$}, $ |
cf. [37,Theorem 3]. We apply this result with
Recall that
Let
| $ \overline{Y_i} \cup \overline{Y_e} = Y, \quad \Gamma = \partial Y_i \setminus \partial Y. $ |
Denote by
|
$ Ωεj=⋃k∈Kεε(k+Yj),j=i,e,Γε=⋃k∈Kεε(k+Γ). $
|
(2.7) |
Both sets
To derive estimates for the microscopic model, we employ the following trace inequality for
|
$ ε‖u|Γε‖2L2(Γε)≤C(‖u‖2L2(Ωεj)+ε2‖∇u‖2L2(Ωεj)),u∈H1(Ωεj),j=i,e, $
|
(2.8) |
for some constant
We need a uniform Poincaré inequality for perforated domains [10].
Lemma 2.1. There exists a constant
|
$ ‖u−1|Ωεj|∫Ωεjudx‖L2(Ωεj)≤C‖∇u‖L2(Ωεj), $
|
(2.9) |
for all
Estimate (2.9) holds under mild regularity assumptions on the perforated domains; a Lipschitz boundary is more than sufficient (but connectedness is essential).
Recall that a sequence
|
$ ∫T0∫Ωuε(t,x)φ(t,x,xε)dxdtε→0→∫T0∫Ω∫Yu(t,x,y)φ(t,x,y)dydxdt, $
|
(2.10) |
for all
| $ u^{ \varepsilon }\overset{2}{\rightharpoonup} u. $ |
By density properties, the convergence (2.10) also holds for test functions
The two-scale compactness theorem [1,12] is of fundamental importance.
Theorem 2.2 (two-scale compactness). Let
Consider a sequence
|
$ ~uεj(t,x):={uεj(t,x)if(t,x)∈(0,T)×Ωεj,0if(t,x)∈(0,T)×(Ω∖Ωεj). $
|
By Theorem
Lemma 2.3. Fix
|
$ ~uεn2⇀1Yj(y)u(t,x)inL2((0,T)×Ω;L2per(Y)),~∇uεn2⇀1Yj(y)(∇xu(t,x)+∇yu1(t,x,y))inL2((0,T)×Ω;L2per(Y)). $
|
Here,
|
$ 1j(y)={1ify∈Yj,0ify∉Yj. $
|
For a proof of this lemma in the time independent case, see [1,Theorem 2.9]. The extension to time dependent functions is straightforward.
There is an extension of two-scale convergence to periodic surfaces [2]. Recall that a periodic surface
|
$ Γε:={x∈Ω|xε∈k+Γfor some k∈Z3}, $
|
where
A sequence
| $ v^{ \varepsilon }\overset{2-{\rm{S}}}{\rightharpoonup} v, $ |
if, for all
|
$ limε→0ε∫T0∫Γεvε(t,x)φ(t,x,xε)dS(x)dt=∫T0∫Ω∫Γv(t,x,y)φ(t,x,y)dS(y)dxdt. $
|
As with (2.10), this convergence continues to hold for test functions
There is a version of Theorem 2.2 for functions on periodic surfaces [2].
Theorem 2.4 (two-scale compactness on surfaces). Suppose
|
$ ε∫T0∫Γε|vε|2dSdt≤C, $
|
(2.11) |
for some function
| $ v^{ \varepsilon _n}\overset{2-{\rm{S}}}{\rightharpoonup} v. $ |
One can characterize the two-scale limit of traces of bounded sequences in
Lemma 2.5. Fix
| $ g^{ \varepsilon }: = u^{ \varepsilon }\big|_{ \Gamma^{\varepsilon} } \in L^2((0,T)\times \Gamma^{\varepsilon} ) $ |
be the trace of
| $ g^{ \varepsilon } \overset{2-{\rm{S}}}{\rightharpoonup} g : = {1}_{\Gamma}(y)u(t,x). $ |
Remark 2.6 In view of Lemma 2.5, we have (in the sense of measures)
| $ \varepsilon \, u^{ \varepsilon }\big|_{ \Gamma^{\varepsilon} } \,dS\, dt \overset{\star}\rightharpoonup \left| \Gamma \right|\, u\, dx\, dt, \qquad \widetilde{u^{ \varepsilon }}\,dx\, dt \overset{\star}\rightharpoonup \left|Y_j\right|\, u \,dx\, dt. $ |
An alternative approach to studying convergence on oscillating surfaces
| $ \lfloor x+n\rfloor = \lfloor x \rfloor+n, \quad \{ x+n\} = \{ x\}, \quad \lfloor x+\bar x\rfloor\le \lfloor x\rfloor +\lfloor \bar x\rfloor+(1,1,1). $ |
Applying the above decomposition to
| $ x = \varepsilon \left( \lfloor x/ \varepsilon \rfloor +\{ x / \varepsilon \}\right), $ |
where
The boundary unfolding operator
|
$ Tbε:L2(0,T;L2(Γε))→L2(0,T;L2(Ω×Γ)),Tbε(v)(t,x,y)=v(t,ε⌊xε⌋+εy),(t,x,y)∈(0,T)×Ω×Γ. $
|
(2.12) |
The advantage of the unfolding operator is that we can formulate questions of convergence in a fixed space
The boundary unfolding operator
|
$ Tbε(v1v2)=Tbε(v1)Tbε(v2),v1,v2∈L2(0,T;L2(Γε)). $
|
(2.13) |
For any
|
$ Tbε(ψε)(x,y)=ψ(y),x∈Ω,y∈Γ. $
|
For
|
$ ε∫Γεv(t,x)dS(x)=∫Ω∫ΓTbε(v)(t,x,y)dS(y)dx, $
|
(2.14) |
for a.e.
|
$ ‖Tbε(v)‖L2(Ω×Γ)=ε1/2‖v‖L2(Γε), $
|
(2.15) |
for a.e.
|
$ Tbε(v)ε↓0→vin L2(Ω×Γ), $
|
(2.16) |
for a.e.
|
$ vε2−S⇀v⟺Tbε(vε)⇀vin L2((0,T)×Ω×Γ). $
|
(2.17) |
We need also the unfolding operators linked to the domains
|
$ Tjε:L2((0,T)×Ωεj)→L2(0,T;L2(Ω×Yj)),j=i,e,Tjε(u)(t,x,y)=u(t,ε⌊xε⌋+εy),(t,x,y)∈(0,T)×Ω×Yj. $
|
The unfolding operator
|
$ Tjε(uv)=Tjε(u)Tjε(v),u,v∈L2((0,T)×Ωεj). $
|
For any
|
$ Tjε(ψε)(x,y)=ψ(y),x∈Ω,y∈Yj. $
|
For
|
$ ∫Ωεju(t,x)dxdt=∫Ω∫YjTjε(u)(t,x,y)dydxdt, $
|
for a.e.
|
$ ‖Tjε(u)‖L2(Ω×Yj)=‖u‖L2(Ωεj), $
|
(2.18) |
for a.e.
|
$ ∇yTjε(u)=εTjε(∇u),a.e. in (0,T)×Ω×Yj, $
|
and hence
|
$ ‖∇yTjε(u)‖L2(Ω×Yj))=ε‖∇u‖L2(Ωεj). $
|
(2.19) |
The unfolding operators
|
$ Tbε(u|Γε)=Tjε(u)|Γ,u∈L2(0,T;H1(Ωεj)),j=i,e, $
|
(2.20) |
for a.e.
|
$ ‖Tbε(u|Γε)‖2L2(Ω;H1/2(Γ))≤C(‖Tjε(u)‖2L2(Ω;L2(Yj))+‖∇yTjε(u)‖2L2(Ω;L2(Yj)))=C(‖u‖2L2(Ωεj)+ε2‖∇u‖2L2(Ωεj)),j=i,e, $
|
(2.21) |
for a.e.
Next, we consider the local average (mean in the cells) operator
|
$ Mjε(u)(t,x)=∫YjTjε(u)(t,x,y)dy,(t,x)∈(0,T)×Ω,j=i,e, $
|
and the piecewise linear interpolation operator [10,Definition 2.5]
|
$ Qjε:L2(0,T;H1(Ωεj))→L2(0,T;H1(Ω)),j=i,e,Qjε(u)is the Q1-interpolation (in x) of Mjε(u). $
|
(2.22) |
Given the Lipschitz regularity of
|
$ ‖Qjε(u)−u‖L2((0,T)×Ωεj)≤Cε‖∇u‖L2((0,T)×Ωεj),‖∇Qjε(u)‖L2((0,T)×Ωεj)≤C‖∇u‖L2((0,T)×Ωεj), $
|
(2.23) |
where
In this section we present a relevant notion of (weak) solution for the microscopic problem (1.1), (1.3), along with an accompanying existence theorem. We also derive some "
We impose the following set of assumptions on the "membrane" functions
● Generalized FitzHugh-Nagumo model: For
|
$ I(v,w)=I1(v)+I2(v)w,H(v,w)=h(v)+cH,1w,where I1,I2,h∈C1(R),cH,1∈R, and|I1(v)|≤cI,1(1+|v|3),I1(v)v≥cI|v|4−cI,2|v|2,I2(v)=cI,3+cI,4v,|h(v)|≤cH,2(1+|v|2), (GFHN) $
|
for some constants
The classical FitzHugh-Nagumo model corresponds to
|
$ I(v,w)=v(v−a)(v−1)+w,H(v,w)=ϵ(kv−w), $
|
(3.1) |
where
Repeated applications of Cauchy's inequality yields
|
$ vI(v,w)−wH(v,w)≥γ|v|4−β(|v|2+|w|2), $
|
(3.2) |
for some constants
Consider a quadratic matrix
| $ \lambda_{\text{min}} \left|z\right|^2\le Az\cdot z \le \lambda_{\text{max}} \left|z\right|^2, \qquad \forall z. $ |
For
|
$ F^\mu(z) = (μI(z)−H(z)) . $
|
Denote by
|
$ λμmin(z)≥λ,∀z∈R2. $
|
(3.3) |
One can verify that the FitzHugh-Nagumo model (3.1) obeys (3.3) (with
A consequence of (3.3) is that
| $ F^\mu(z_2)-F^\mu(z_1) = \int_0^1 \nabla F^\mu(\theta z_2+(1-\theta)z_1)(z_2-z_1)\,d\theta, $ |
it follows that
| $ \left(F^\mu(z_2)-F^\mu(z_1)\right) \cdot (z_2-z_1)\geq -\lambda\left|z_2-z_1\right|^2. $ |
More explicitly, assumption (3.3) implies the following "dissipative structure" on a suitable linear combination of
|
$ μ(I(v2,w2)−I(v1,w2))(v2−v1)−(H(v2,w2)−H(v1,w1))(w2−w1)≥−λ(|v2−v1|2+|w2−w1|2),∀v1,v2,w1,w2∈R. $
|
This inequality implies the
Remark 3.1. There are many membrane models of cardiac cells [13,38]. We utilize the FitzHugh-Nagumo model [17], which is a simplification of the Hodgin-Huxley model of voltage-gated ion channels. It is possible to treat other membrane models by blending the arguments used herein with those found in [7,8,13,38,41,42].
As a natural assumption for homogenization, we assume that the
|
$ σεj(x)=σj(x,xε),sεj(x)=sj(x,xε),vε0(x)=v0(x,xε),wε0(x)=w0(x,xε), $
|
(3.4) |
for some fixed functions
The conductivity tensors are assumed to be bounded and continuous,
|
$ σj(x,y)∈L∞(Ω×Yj)∩C(Ω;Cper(Yj)), $
|
(3.5) |
and satisfy the usual ellipticity condition, i.e., there exists
|
$ η⋅σj(x,y)η≥α|η|2,∀η∈R3,∀(x,y)∈Ω×Yj, $
|
(3.6) |
for
The regularity assumption (35) implies that
| $ \lim\limits_{ \varepsilon \rightarrow 0}\int_{ \Omega_j^{\varepsilon} } \sigma^{ \varepsilon }_j(x) \varphi ^{ \varepsilon }(x) \, dx = \int_{ \Omega \times Y_j} \sigma(x,y) \varphi (x,y) \, dx\, dy, \qquad j = i,e, $ |
for every two-scale convergent sequence
For the stimulation currents we assume the compatibility condition
|
$ ∑j=i,e∫Ωεjsεjdx=0, $
|
(3.7) |
and the boundedness in
|
$ ‖sεj‖L2((0,T)×Ωεj)≤C,j=i,e, $
|
(3.8) |
which, in view of (3.4), is guaranteed if we take [12,p. 174]
|
$ sj∈L2(Ω;Cper(Yj)). $
|
(3.9) |
Similarly, we assume that
|
$ v0,w0∈L2(Ω;Cper(Γ)). $
|
(3.10) |
Throughout this paper we denote by
Testing (1.1) against appropriate functions
Definition 3.2 (weak formulation of microscopic system). A weak solution to (1.1), (1.3) is a collection
ⅰ (algebraic relation).
|
$ vε=uεi|Γε−uεe|Γεa.e. on (0,T)×Γε. $
|
(3.11) |
ⅱ (regularity).
|
$ uεj∈L2(0,T;H1(Ωεj)),j=i,e,∫Ωεeuεe(t,x)dx=0,t∈(0,T),vε∈L2(0,T;H1/2(Γε))∩L4((0,T)×Γε),∂tv∈L2(0,T;H−1/2(Γε))+L4/3((0,T)×Γε),wε∈H1(0,T;L2(Γε)). $
|
ⅲ (initial conditions).
|
$ vε(0)=vε0,wε(0)=wε0. $
|
(3.12) |
ⅳ (differential equations).
|
$ ε∫T0⟨∂tvε,φi⟩dt+∫T0∫Ωεiσεi∇uεi⋅∇φidxdt+ε∫T0∫ΓεI(vε,wε)φidSdt=∫T0∫Ωεisεiφidxdt, $
|
(3.13) |
|
$ ε∫T0⟨∂tvε,φe⟩dt−∫T0∫Ωεeσεe∇uεe⋅∇φedxdt+ε∫T0∫ΓεI(vε,wε)φedSdt=−∫T0∫Ωεesεeφedxdt, $
|
(3.14) |
|
$ ∫Γε∂twεφwdx=∫ΓεH(vε,wε)φwdS, $
|
(3.15) |
for all
Remark 3.3. In (3.13), (3.14) we use
By the embedding (2.6),
| $ \varepsilon \int_0^T \left\langle \,{\partial _t}v^{ \varepsilon }, \varphi _j\right\rangle \, dt, \quad j = i,e, $ |
in (3.13) and (3.14) by
|
$ −ε∫T0∫Γεvε∂tφjdS(x)dt−ε∫Γεvε0φj(0)dS(x)dt, $
|
(3.16) |
for all test functions
Remark 3.4. Consider a weak solution
Indeed,
|
$ J:=|∫T0∫ΓεI(vε,wε)φjdSdt|≤‖I(vε,wε)‖L4/3((0,T)×Γε)‖φj‖L4((0,T)×Γε). $
|
For the membrane model (GFHN), the growth condition on
|
$ |I(v,w)|43≤CI(1+|v|4+|w|2), $
|
(3.17) |
and therefore
We actually have a more precise bound. As
| $ \left\|I(v^{ \varepsilon },w^{ \varepsilon })\right\|_{H^{-1/2}( \Gamma^{\varepsilon} )}^{4/3} \le \tilde C \left\|I(v^{ \varepsilon },w^{ \varepsilon })\right\|_{L^{4/3}( \Gamma^{\varepsilon} )}^{4/3} \le C \left(1+\left\|v^{ \varepsilon }\right\|_{L^4( \Gamma^{\varepsilon} )}^4 +\left\|w^{ \varepsilon }\right\|_{L^2( \Gamma^{\varepsilon} )}^2\right). $ |
Integrating this over
The integral on the right-hand side of (3.15) can be treated similarly, since
Existence and uniqueness results for certain classes of membrane models have been established in [14,41]. These works employ the variable
The following theorem can be proved by adapting arguments found in [14,41] (see also [21]), or those utilized in [8,6,5] for the (macroscopic) bidomain model.
Theorem 3.5 (existence of weak solution for microscopic system). Fix any
Remark 3.6. The unknowns
The next lemma, which is utilized below to derive some a priori estimates, is a consequence of the uniform Poincaré inequality (2.9) and the trace inequality for
Lemma 3.7. Let
|
$ ‖ui‖2L2(Ωεi)≤C(ε‖v‖2L2(Γε)+∑j=i,e∫Ωεj|∇uj|2dx). $
|
Proof. First, since
|
$ ‖ue‖2L2(Ωεe)(2.9)≤C1∫Ωεe|∇ue|2dx. $
|
(3.18) |
To estimate the
| $ \left\|u_i\right\|_{L^2( \Omega_j^{\varepsilon} )}^2 = \left\|\bar{u}_i\right\|_{L^2( \Omega_i^{\varepsilon} )}^2 +\left\|\tilde{u}_i\right\|_{L^2( \Omega_i^{\varepsilon} )}^2. $ |
In view of the Poincaré inequality (2.9),
|
$ ‖˜ui‖2L2(Ωεi)≤˜C1∫Ωεi|∇˜ui|2dx=˜C1∫Ωεi|∇ui|2dx. $
|
(3.19) |
Let us bound
| $ \left\|\bar{u}_i\right\|_{L^2( \Omega_i^{\varepsilon} )}^2 \le \bar C_1 \varepsilon \left\|\bar{u}_i\right\|_{L^2( \Gamma^{\varepsilon} )}^2. $ |
Noting that
| $ \left|\bar{u}_i\right|^2 \le \bar C_2\left(\left|u_i - u_e\right|^2 + \left|\tilde u_i\right|^2 + \left|u_e\right|^2\right), $ |
we obtain
|
$ ‖ˉui‖2L2(Ωεi)≤ˉC3(ε‖v‖2L2(Γε)+ε‖˜ui‖2L2(Γε)+ε‖ue‖2L2(Γε))(2.8)≤ˉC3ε‖v‖2L2(Γε)+ˉC4(‖˜ui‖2L2(Ωεi)+ε2‖∇˜ui‖2L2(Ωεi))+ˉC4(‖ue‖2L2(Ωεe)+ε2‖∇ue‖2L2(Ωεe))≤ˉC3ε‖v‖2L2(Γε)+ˉC5‖∇ui‖2L2(Ωεi)+ˉC5‖∇ue‖2L2(Ωεe), $
|
where the final inequality is a result of (3.18) and (3.19).
For the sake of the upcoming homogenization result, we now list some precise (
Lemma 3.8 (basic estimates for microscopic system). Referring Theorem 3.5, the weak solution
|
$ (a)‖∇uεj‖L2((0,T)×Ωεj)≤C,j=i,e,(b)‖uεj‖L2((0,T)×Ωεj)≤C,j=i,e,(c)ε1/2‖vε‖L∞(0,T;L2(Γε))≤C,(d)ε1/4‖vε‖L4((0,T)×Γε)≤C,(e)ε1/2‖wε‖L∞(0,T;L2(Γε))≤C,(f)ε1/2∂twε∈L2(0,T;L2(Γε)), $
|
(3.20) |
where
Proof. We only outline a proof of these (mostly standard) estimates.
Specifying
|
$ ε2ddt(‖vε‖2L2(Γε)+‖wε‖2L2(Γε))+α∑j=i,e∫Ωεj|∇uεj|2dx,+ε∫Γε(I(vε,wε)vε−H(vε,wε)wε)dS≤∑j=i,e∫Ωεjsεjuεjdx. $
|
(3.21) |
Thanks to (3.2),
|
$ ∫Γε(I(vε,wε)vε−H(vε,wε)wε)dS≥γ‖vε‖4L4(Γε)−β(‖vε‖2L2(Γε)+‖wε‖2L2(Γε)), $
|
(3.22) |
for some
Using Cauchy's inequality ("with
|
$ |∑j=i,e∫Ωεjsεjuεjdx|≤∑j=i,e(‖uεj‖L2(Ωεj)‖sεj‖L2(Ωεj))≤δ∑j=i,e‖uεj‖2L2(Ωεj)+Cδ∑j=i,e‖sεj‖2L2(Ωεj), $
|
(3.23) |
with
|
$ ∑j=i,e‖uεj‖2L2(Ωεj)≤C1(ε‖vε‖2L2(Γε)+∑j=i,e∫Ωεj|∇uεj|2dx). $
|
(3.24) |
Insert (3.22), (3.23), (3.24) into (3.21), use (3.6), and choose
|
$ ε(‖vε(τ)‖2L2(Γε)+‖wε(τ)‖2L2(Γε))+α2∑j=i,e∫τ0‖∇uεj‖2L2(Ωεj)dt $
|
|
$ +γε∫τ0‖vε(t)‖4L4(Ω)dt≤ε(‖vε(0)‖2L2(Γε)+‖wε(0)‖2L2(Γε))+C2ε∫τ0(‖vε(t)‖2L2(Γε)+‖wε(t)‖2L2(Γε))dt+Cδ∑j=i,e‖sεj‖2L2((0,τ)×Ωεj), $
|
for some positive constant
| $ \left| \,{\partial _t}w^ \varepsilon \right|^2 \le C \left(1+\left|v^ \varepsilon \right|^4 + \left|v^ \varepsilon \right|^2\right). $ |
Estimate (f) follows by integrating this over
Remark 3.9. Let us motivate the regularity requirements in Definition 3.2 that are not covered by Lemma 3.8. First, due to (3.11), (2.1) and (3.20),
| $ \left\|v^{ \varepsilon }\right\|_{L^2(0,T;H^{1/2}( \Gamma^{\varepsilon} ))} \leq \tilde C_{ \varepsilon } \sum\limits_{j = i,e}\left\|u_j^{ \varepsilon }\right\|_{L^2(0,T;H^1( \Omega_j^{\varepsilon} ))} \le C_ \varepsilon , $ |
where the constants
Next, we claim that
| $ \varepsilon \left\| \,{\partial _t}v^ \varepsilon \right\|_{L^2(0,T;H^{-1/2}( \Gamma^{\varepsilon} ))+L^4((0,T)\times \Gamma^{\varepsilon} )}\le C_ \varepsilon , $ |
for some constant that may depend on
| $ \varepsilon \left\langle \,{\partial _t}v^ \varepsilon , \psi\right\rangle_{H^{-1/2}( \Gamma^{\varepsilon} ),H^{1/2}( \Gamma^{\varepsilon} )} = J_1(\psi) +J_2(\psi)+J_3(\psi), $ |
for a.e.
|
$ |J1(ψ)|=|∫Ωεjσεj∇uεj⋅∇Ij(ψ)dx|,|J2(ψ)|=|∫ΩεjsεjIj(ψ)dx|,|J3(ψ)|=|ε∫ΓεI(vε,wε)ψdS|, $
|
and
|
$ |J1(ψ)|≤˜C1‖∇uεj‖L2(Ωεj)‖ψ‖H1/2(Γε),|J2(ψ)|≤˜C2‖sεj‖L2(Ωεj)‖ψ‖H1/2(Γε),and|J3(ψ)|≤ε‖I(vε,wε)‖H−1/2(Γε)‖ψ‖H1/2(Γε), $
|
where the constants
| $ \left\|J_1\right\|_{H^{-1/2}( \Gamma^{\varepsilon} )}^2 \le \tilde C_1^2\left\|\nabla u_j^{ \varepsilon }\right\|_{L^2( \Omega_j^{\varepsilon} )}^2, \quad \left\|J_2\right\|_{H^{-1/2}( \Gamma^{\varepsilon} )}^2 \le \tilde C_2^2\left\|s_j^{ \varepsilon }\right\|_{L^2( \Omega_j^{\varepsilon} )}^2. $ |
Integrating this over
| $ \left\|J_1\right\|_{L^2(0,T;H^{-1/2}( \Gamma^{\varepsilon} ))}\le C_1, \qquad \left\|J_2\right\|_{L^2(0,T;H^{-1/2}( \Gamma^{\varepsilon} ))}\le C_2, $ |
for some constants
As in Remark 3.4,
| $ \left\|I(v^{ \varepsilon },w^{ \varepsilon })\right\|_{H^{-1/2}( \Gamma^{\varepsilon} )} \le C_I \left(1+\left\|v^{ \varepsilon }\right\|_{L^4( \Gamma^{\varepsilon} )}^4 +\left\|w^{ \varepsilon }\right\|_{L^2( \Gamma^{\varepsilon} )}^2\right)^{3/4}, $ |
and hence, for a.e.
| $ \left\|J_3\right\|_{H^{-1/2}( \Gamma^{\varepsilon} )}^{4/3} \le \tilde C_3 \varepsilon ^{4/3}\left(1+\left\|v^{ \varepsilon }\right\|_{L^4( \Gamma^{\varepsilon} )}^4 +\left\|w^{ \varepsilon }\right\|_{L^2( \Gamma^{\varepsilon} )}^2\right). $ |
Integrating over
| $ \left\|J_3\right\|_{L^{4/3}(0,T;H^{-1/2}( \Gamma^{\varepsilon} ))}\le C_3, $ |
for some constant
For the upcoming convergence analysis, we need a temporal translation estimate for the membrane potential
Lemma 3.10 (temporal translation estimate in
|
$ ε∫T−Δt0∫Γε|vε(t+Δt,x)−vε(t,x)|2dxdt≤CΔt. $
|
(3.25) |
Proof. The translated functions
|
$ −ε∫T−Δt0∫Γε(vε(t+Δt)−vε(t))∂t(φi−φe)dSdt+ε∫Γε(vε(T)−vε(T−Δt))(φi(T−Δt)−φe(T−Δt))dS−ε∫Γε(vε(Δt)−vε0)(φi(0)−φe(0))dS+∑j=i,e∫T−Δt0∫Ωεjσεj∇(uεj(t+Δt)−uεj(t))⋅∇φjdxdt+ε∫T−Δt0∫Γε(I(vε(t+Δt),wε(t+Δt)−I(vε(t),wε(t))(φi−φe)dSdt−ε∫T−Δt0∫Γε(H(vε(t+Δt),wε(t+Δt))−H(vε(t),wε(t))φwdSdt=∑j=i,e∫T−Δt0∫Ωεj(sεj(t+Δt)−sε(t))φjdxdt. $
|
Specifying the test functions
| $ \varphi _j(t) = -\int_t^{t+\Delta_t} u_j^ \varepsilon (s) \,ds, \quad j = i,e, \qquad \varphi _w(t) = -\int_t^{t+\Delta_t} w_j^ \varepsilon (s) \,ds, $ |
we obtain
|
$ ε∫T−Δt0∫Γε|vε(t+Δt)−vε(t)|2dSdt+ε∫Γε(vε(T)−vε(T−Δt))(−∫TT−Δtv(s)ds)dS−ε∫Γε(vε(Δt)−vε0)(−∫Δt0v(s)ds)dS+∑j=i,e∫T−Δt0∫Ωεjσεj∇(uεj(t+Δt)−uεj(t))⋅∇(−∫t+Δttuεj(s)ds)dxdt+ε∫T−Δt0∫Γε(I(vε(t+Δt),wε(t+Δt))−I(vε(t),wε(t)))×(−∫t+Δttvε(s)ds)dSdt+ε∫T−Δt0∫Γε(H(vε(t+Δt),wε(t+Δt))−H(vε(t),wε(t)))×(∫t+Δttwε(s)ds)dSdt=∑j=i,e∫T−Δt0∫Ωεjsεj(−∫t+Δttuεj(s)ds)dxdt. $
|
Let us write this equation as
| $ \varepsilon \int_0^{T-\Delta_t} \int_{ \Gamma^{\varepsilon} } \left|v^{ \varepsilon }(t+\Delta_t)-v^{ \varepsilon }(t)\right|^2\, dS\, dt +J_1+J_2+J_3+J_4+J_5 = J_6. $ |
By the Cauchy-Schwarz and Minkowski integral inequalities,
|
$ |J1|≤ε‖vε(T)−vε(T−Δt)‖L2(Γε)‖∫TT−Δtvε(s)ds‖L2(Γε)≤2ε‖vε‖L∞(0,T;L2(Γε))∫TT−Δt‖vε‖L2(Γε)ds≤2ε‖vε‖2L∞(0,T;L2(Γε))Δt(3.20)−(c)≤C1Δt. $
|
Similarly,
We need the following facts involving a real-valued function
|
$ ∫t+Δttf(s)ds=(1[0,Δt]⋆f)(t),‖1[0,Δt]⋆f‖Lp≤‖1[0,Δt]‖L1‖f‖Lp=Δt‖f‖Lp, $
|
(3.26) |
where the second line follows from Young's convolution inequality.
By (3.5) and the Cauchy-Schwarz inequality,
|
$ |J3|≤∑j=i,e2‖σεj‖L∞‖∇uεj‖L2((0,T)×Ωεj)‖∫t+Δtt∇uεj(s)ds‖L2((0,T−Δt)×Ωεj). $
|
As a result of Minkowski integral inequality,
|
$ ‖∫t+Δtt∇uεj(s)ds‖2L2((0,T−Δt)×Ωεj)=∫T−Δt0∫Ωεj|∫t+Δtt∇uεj(s)ds|2dxdt≤∫T−Δt0(∫t+Δtt(∫Ωεj|∇uεj(s)|2dx)1/2ds)2dt=∫T−Δt0(∫t+Δtt‖∇uεj(s)‖L2(Ωεj)ds)2dt(3.26)≤Δ2t∫T−Δt0‖∇uεj‖2L2(Ωεj)dt≤Δ2t‖∇uεj‖2L2((0,T)×Ωεj). $
|
Therefore,
| $ \left|J_3\right|\le \sum\limits_{j = i,e} 2 \left\|\sigma_j^ \varepsilon \right\|_{L^\infty} \left\|\nabla u_j^ \varepsilon (t)\right\|_{L^2((0,T)\times \Omega_j^{\varepsilon} )}^2\Delta_t \overset{ (3.20)-(a)}{\le} C_3\Delta_t. $ |
An application of Hölder's inequality yields
|
$ |J4|≤2ε‖Iε‖L4/3((0,T)×Γε)‖∫t+Δttvε(s)ds‖L4((0,T−Δt)×Γε)(3.17)≤C4ε(‖vε‖4L4((0,T)×Γε)+‖wε‖2L2((0,T)×Γε))3/4Δt‖vε‖L4((0,T)×Γε)≤C5Δtε(‖vε‖4L4((0,T)×Γε)+‖wε‖2L2((0,T)×Γε))(3.20)−(d,e)≤C6Δt, $
|
where we have repeated the argument for
Similarly,
|
$ |J5|(GFHN)≤C7Δtε(‖vε‖4L4((0,T)×Γε)+‖wε‖2L2((0,T)×Γε))1/2‖vε‖L2((0,T)×Γε)(3.20)−(d,e)≤C8Δt, $
|
and
|
$ |J6|≤2Δt∑j=i,e‖sεj‖L2((0,T)×Ωεj)‖uεj‖L2((0,T)×Ωεj)(3.8),(3.20)−(b)≤C9Δt. $
|
Summarizing our findings, we conclude that (3.25) holds.
Remark 3.11. Due to the degenerate structure of the microscopic system (2), temporal estimates are not available for the intra- and extracellular potentials
This section contains the main result of the paper. We start by recalling the weak formulation of the macroscopic bidomain system (1.4), which is augmented with the following initial and boundary conditions:
|
$ v|t=0=v0in Ω,w|t=0=w0,in Ω.n⋅σ∇uj=0on (0,T)×∂Ω, j=i,e. $
|
(4.1) |
Definition 4.1 (weak formulation of bidomain system). A weak solution to (1.4),
(4.1) is a collection
ⅰ (algebraic relation).
| $ v = u_i - u_e \quad \text{a.e. in $(0,T)\times \Omega $}. $ |
ⅱ (regularity).
|
$ uj∈L2(0,T;H1(Ω)),j=i,e,∫Ωuεe(t,x)dx=0,t∈(0,T),v∈L2(0,T;H1(Ω))∩L4((0,T)×Ω),∂tv∈L2(0,T;H−1(Ω))+L4/3((0,T)×Ω),w∈H1(0,T;L2(Ω)). $
|
ⅲ (initial conditions).
|
$ v(0)=v0,w(0)=w0. $
|
ⅳ (differential equations).
|
$ |Γ|∫T0⟨∂tv,φi⟩dt+∫T0∫ΩMi∇ui⋅∇φidxdt+|Γ|∫T0∫ΩI(v,w)φidxdt=|Yi|∫T0∫Ωsiφidxdt, $
|
|
$ |Γ|∫T0⟨∂tv,φe⟩dt−∫T0∫ΩMe∇ue⋅∇φedxdt+|Γ|∫T0∫ΩI(v,w)φedxdt=−|Ye|∫T0∫Ωseφedxdt, $
|
|
$ ∫T0∫Ω∂twφwdxdt=∫T0∫ΩH(v,w)φwdxdt, $
|
(4.2) |
for all test functions
The macroscopic bidomain system is well studied for a variety of cellular models [5,6,7,8,14,42]. For the following result, see [5,6,7].
Theorem 4.2 (well-posedness of bidomain system). Suppose (1.2) holds,
We are now in a position to state the main result, which should be compared to Theorem 1.3 in [34].
Theorem 4.3 (convergence to the bidomain system). Suppose conditions (GFHN), (1.2), (3.3), (3.4), (3.5), (3.6), (3.7), (3.9), and (3.10) hold. Let
|
$ ε1/2‖vε−v‖L2(Γε)→0,as ε→0. $
|
(4.3) |
Remark 4.4. The strong convergence (4.3) is a corrector-type result. In the current setting it allows us to pass to the limit in the nonlinear ionic terms. By employing standard techniques [12] one can also show that the energies
| $ \left\{\int_0^T\int_{ \Omega_j^{\varepsilon} } \sigma_j^{ \varepsilon } \nabla u_i^{ \varepsilon } \cdot \nabla u_j^{ \varepsilon } \, dx \, dt\right\}_{ \varepsilon > 0} $ |
converge to the homogenized energy
| $ \int_0^T\int_{ \Omega } M_j \nabla u_i \cdot \nabla u_j \, dx \, dt, $ |
where
The rest of this section is devoted to the proof of Theorem 4.3. Homogenization of the linear terms in (1.1) is handled with standard techniques, cf. Subsection 4.1.
Passing to the limit in the nonlinear terms
Wild oscillations of the underlying domain do however pose difficulties. For this reason, we use the boundary unfolding operator
Recall that
|
$ ~uεj2⇀1Yj(y)uj(t,x),j=i,e~∇uεj2⇀1Yj(y)(∇xuj(t,x)+∇yu1j(t,x,y)),j=i,e,vε2−S⇀v=ui−ue,wε2−S⇀w,∂twε2−S⇀∂tw,I(vε,wε)2−S⇀¯I,H(vε,wε)2−S⇀¯H, $
|
(4.4) |
for some limits
Nonlinear functions are not continuous with respect to weak convergence, which prevents us from immediately making the identifications
| $ \overline{I} = I(v,w), \qquad \overline{H} = H(v,w). $ |
Using the two-scale convergences in (4.4), Remark 3.3, the choice of test function
|
$ φ(t,x)+εφ1(t,x,xε),withφ∈C∞0((0,T)×Ω),φ1∈C∞0((0,T)×Ω;C∞per(Y)), $
|
in (3.13), (3.14), and (3.15), standard manipulations [12,2] will reveal that the two-scale limit
|
$ |Γ|∫T0∫Ω⟨∂tv,φ⟩dxdt+limε→0ε∫T0∫ΓεI(vε,wε)φdSdt+∫T0∫ΩMi∇ui⋅∇φdxdt=|Yi|∫T0∫Ωsiφdxdt, $
|
(4.5) |
|
$ |Γ|∫T0∫Ω⟨∂tv,φ⟩dxdt+limε→0ε∫T0∫ΓεI(vε,wε)φdSdt+∫T0∫ΩMe∇ue⋅∇φdxdt=|Ye|∫T0∫Ωseφdxdt, $
|
(4.6) |
and
|
$ |Γ|∫T0∫Ω∂twφdxdt=limε→0ε∫T0∫ΓεH(vε,wε)φdSdt, $
|
(4.7) |
for all
In (4.5) and (4.6),
| $ \Phi(t,x,y) : = \sigma_j(x,y)\nabla_y \varphi _1(t,x,y) $ |
as a test function for two-scale convergence, we have by (4.4) that
|
$ limε→0∫T0∫ΩεjΦ(t,x,xε)⋅∇uεjdxdt=∫T0∫Ω∫Yjσj[∇xuj+∇yu1j]⋅∇yφ1dxdydt. $
|
Note that the oscillating
| $ \int_0^T \int_{ \Omega }\int_{Y_j} \sigma_j \left[ \nabla_x u_j + \nabla_y u^1_j \right] \cdot \nabla_y \varphi _1 \,dx \, dy\,dt = 0, $ |
for all
|
$ 0=∫T0∫Ω∫Yjσj[∇xuj+∇yu1j]⋅∇xψdxdydt=∫T0∫Ω(∫Yjσj+∇yχjdy)∇xuj⋅∇xψdxdydt, $
|
so (1.5) is indeed the homogenized conductivity tensor.
Up to the convergences of the nonlinear terms, it is now clear that (4.5), (4.6), and (4.7) constitute the weak formulation of the bidomain system (1.4), (4.1) (in the sense of Definition 4.1).
To finalize the proof of Theorem 4.3, it remains to identify the limits
|
$ limε→0ε∫T0∫ΓεI(vε,wε)φdSdt=|Γ|∫T0∫ΩI(v,w)φdxdt,limε→0ε∫T0∫ΓεH(vε,wε)φdSdt=|Γ|∫T0∫ΩH(v,w)φdxdt, $
|
(4.8) |
for all
| $ \varepsilon \int_0^T \int_{ \Gamma^{\varepsilon} } I(v^{ \varepsilon },w^{ \varepsilon }) \varphi _i \,dS \, dt $ |
into
| $ \int_0^T \int_{\Omega}\int_{ \Gamma } I\left( \mathcal{T} _{ \varepsilon }^b(v^{ \varepsilon }), \mathcal{T} _{ \varepsilon }^b(w^{ \varepsilon })\right) \mathcal{T} _{ \varepsilon }^b( \varphi _i) \,dS(y) \, dx\, dt, $ |
coming from the integration formula (2.14) for
| $ I\left( \mathcal{T} _{ \varepsilon }^b(v^{ \varepsilon }), \mathcal{T} _{ \varepsilon }^b(w^{ \varepsilon })\right) \to I(v,w), \quad \text{weakly in $L^2((0,T)\times \Omega \times \Gamma )$}, $ |
where
As a step towards verifying the required strong convergence, we need to show that
The rest of this section is devoted to the detailed proof that
Lemma 4.5. There exists a constant
|
$ ‖Tbε(vε)‖L2(0,T;L2(Ω;H1/2(Γ))≤C $
|
(4.9) |
and
|
$ ‖Tbε(vε)(⋅+Δt,⋅,⋅)−Tbε(vε)(⋅,⋅,⋅)‖L2(0,T−Δt;L2(Ω×Γ))≤CΔ12t, $
|
(4.10) |
for sufficiently small temporal shifts
Proof. By (3.11) and the linearity of
|
$ ∫T−Δt0∫Ω∫Γ|Tbε(vε)(t+Δt,x,y)−Tbε(vε)(⋅,⋅,⋅)|2dS(y)dxdt=ε∫T−Δt0∫Γε|vε(t+Δt,x)−vε(t,x)|2dS(x)dt≤CΔt. $
|
Let us think of
For
|
$ Q=⋃σ∈ΣQξσ,for any ξ∈Rn such that Qξ≠∅. $
|
(4.11) |
Let
| $ \tau_\Delta f(x) = f(x+\Delta). $ |
The following theorem, due to Gahn and Neuss-Radu [19], is a multi-dimensional generalization of Simon's main result [37,Theorem 1].
Theorem 4.6 ([19]). Let
i.
ii. for each
|
$ supf∈F‖τzf−f‖Lp(Qz;B)→0,as z→0. $
|
(4.12) |
Recall (4.11), this time specifying
|
$ supf∈F‖τzσf−f‖Lp(Qξσ;B)z→0→0,z∈Rn, z≥0, ∀σ∈Σ. $
|
(4.13) |
The difference between (4.12) and (4.13) is the fixed domain that is utilized in the latter (it does not depend on the shift
We now verify that the sequence
Lemma 4.7 (verification of
| $ v^{ \varepsilon }_A(t,y) = \int_A \mathcal{T} _{ \varepsilon }^b(v^ \varepsilon )(t,x,y)\,dx, \qquad (t,x)\in (0,T)\times \Gamma . $ |
Then the sequence
Proof. In view of Jensen's inequality, it follows that
|
$ ‖vεA‖2L2(0,T;H1/2(Γ))=∫T0‖∫ATbε(vε)(t,x,⋅)dx‖2H1/2(Γ)dt≤|A|∫T0∫A‖Tbε(vε)(t,x,⋅)‖2H1/2(Γ)dxdt≤|A|‖Tbε(vε)‖2L2(0,T;L2(Ω;H1/2(Γε))(4.9)≤C. $
|
Let
|
$ ‖vεA(⋅+Δt,⋅)−vεA(⋅,⋅‖2L2(0,T−ΔT;L2(Γ))≤|A|∫T−Δt0∫A‖Tbε(vε)(t+Δt,x,⋅)−Tbε(vε)(t,x,⋅)‖2L2(Γ)dxdt≤|A|‖Tbε(vε)(⋅+Δt,⋅,⋅)−Tbε(vε)(⋅,⋅,⋅)‖2L2(0,T−Δt,L2(Ω×Γ))(4.10)≤CΔt. $
|
Summarizing, there exists an
| $ \left\|v_A^{ \varepsilon }\right\|_{L^2(0,T;H^{1/2}( \Gamma ))}\le C, \quad \left\|v_A^{ \varepsilon }(\cdot+\Delta_t,\cdot) -v_A^{ \varepsilon }(\cdot,\cdot\right\|_{L^2(0,T-\Delta_T;L^2( \Gamma ))} \le C \Delta_t^{1/2}. $ |
The lemma follows from these estimates and Simon's compactness criterion.
In the next lemma we verify (4.13) with
Lemma 4.8 (verification of
|
$ ‖Tbε(vε)(⋅,⋅+(Δx)σ,⋅)−Tbε(vε)(⋅,⋅,⋅)‖L2(Ωξσ;L2((0,T)×Γ))<δ,∀σ∈Σ. $
|
(4.14) |
Proof. We wish to estimate the quantity
|
$ J(Δx;ε):=‖Tbε(vε)(⋅,⋅+(Δx)σ,⋅)−Tbε(vε)(⋅,⋅,⋅)‖2L2(Ωξσ;L2((0,T)×Γ))=∫T0∫Ωξσ∫Γ|vε(t,ε⌊x+(Δx)σε⌋+εy)−vε(t,ε⌊xε⌋+εy)|2dS(y)dxdt. $
|
Recall that
Choose
| $ \sum\limits_{k\in K^ \varepsilon _{\xi_\sigma}} \int_0^T\!\!\int_{ \varepsilon Y^k}\int_ \Gamma \left|v^ \varepsilon \left(t, \varepsilon \left\lfloor \frac{x+(\Delta_x)_\sigma}{ \varepsilon } \right\rfloor + \varepsilon y\right) -v^ \varepsilon \left(t, \varepsilon \left\lfloor \frac{x}{ \varepsilon } \right\rfloor + \varepsilon y\right)\right|^2 \, dS(y)\, dx\, dt. $ |
If
We decompose each cell
| $ \varepsilon Y^k = \bigcup\limits_{m\in \left\{0,1\right\}^3} \varepsilon Y^{k,m}_\sigma, \quad \varepsilon Y^{k,m}_\sigma : = \left\{x\in \varepsilon Y^k: \varepsilon \left\lfloor \frac{x+ \varepsilon \left\{\frac{(\Delta_x)_\sigma}{ \varepsilon }\right\}}{ \varepsilon }\right\rfloor = \varepsilon (k+m_\sigma)\right\}, $ |
for
|
$ ε⌊x+(Δx)σε⌋=ε⌊x+ε{(Δx)σε}ε+⌊(Δx)σε⌋⌋=ε⌊x+ε{(Δx)σε}ε⌋+ε⌊(Δx)σε⌋=ε(k+mσ)+ε⌊(Δx)σε⌋. $
|
As a result of this,
|
$ J=∑k∈Kεξσ∑m∈{0,1}3∫T0∫εYk,mσ∫Γ×|vε(t,εk+εmσ+ε⌊(Δx)σε⌋+εy)−vε(t,εk+εy)|2dS(y)dxdt(x:=εk+εydS(x)=ε2dS(y))≤ε∑k∈Kεξσ∑m∈{0,1}3∫T0∫ε(k+Γ)×|vε(t,x+ε(mσ+⌊(Δx)σε⌋))−vε(t,x)|2dS(x)dt, $
|
where we have also used
| $ J\le \varepsilon \sum\limits_{m\in \left\{0,1\right\}^3}\int_0^T\int_{( \Gamma^{\varepsilon} )_{\xi_\sigma}} \left|v^ \varepsilon (t,x+z)-v^ \varepsilon (t,x\right|^2 \, dS(x) \, dt, $ |
where the shift
|
$ ε∫T0∫(Γε)ξσ|vε(t,x+z)−vε(t,x|2dS(x)dt≤C∑j=i,e∫T0∫(Ωεj)ξσ|uεj(t,x+z)−uεj(t,x)|2dxdt+Cε2∑j=i,e∫T0∫(Ωεj)ξσ|∇uεj(t,x+z)−∇uεj(t,x)|2dxdt, $
|
where the last term is bounded by a constant times
It remains to estimate the term on the second line, which will be done utilizing the well-known characterization of Sobolev spaces by means of translation (difference) operators. Recalling the standard proof of this characterization, a problem that arises (due to the geometry of
Using the triangle inequality and recalling the estimates (2.23), we obtain
|
$ ∫T0∫(Ωεj)ξσ|uεj(t,x+z)−uεj(t,x)|2dxdt≤∫T0∫(Ωεj)ξσ|uεj(t,x+z)−Qjε(uεj)(t,x+z)|2dxdt+∫T0∫(Ωεj)ξσ|Qjε(uεj)(t,x+z)−Qjε(uεj)(t,x)|2dxdt+∫T0∫(Ωεj)ξσ|Qjε(uεj)(t,x)−uεj(t,x)|2dxdt≤C1ε∫T0∫(Ωεj)ξσ|∇uεj|2dxdt+C2|z|∫T0∫(Ωεj)ξσ|∇Qjε(uεj)|2dxdt≤C3(ε+|z|)‖∇uεj‖2L2(0,T;L2(Ωεj))(3.20)−(a)≤C4(ε+|z|). $
|
Hence,
| $ J \le C_5 \varepsilon + C_6 \left|\Delta_x\right|, $ |
where the constants
Summarizing, we know that
| $ \mathcal{T} _{ \varepsilon }^b(w^{ \varepsilon })\overset{ \varepsilon \downarrow 0}{ \rightharpoonup } w \quad \text{in $L^2((0,T)\times \Omega \times \Gamma )$}, $ |
because
| $ \left\| \mathcal{T} _{ \varepsilon }^b (v^{ \varepsilon })\right\|_{L^4((0,T)\times \Omega \times \Gamma )} = \varepsilon ^{1/4}\left\|v^{ \varepsilon }\right\|_{L^4((0,T)\times \Gamma^{\varepsilon} )}\le C, $ |
where
| 1. | Brodie A.J. Lawson, Rodrigo Weber dos Santos, Ian W. Turner, Alfonso Bueno-Orovio, Pamela Burrage, Kevin Burrage, Homogenisation for the monodomain model in the presence of microscopic fibrotic structures, 2023, 116, 10075704, 106794, 10.1016/j.cnsns.2022.106794 | |
| 2. | Carlos Jerez-Hanckes, Isabel A. Martínez Ávila, Irina Pettersson, Volodymyr Rybalko, Derivation of a bidomain model for bundles of myelinated axons, 2023, 70, 14681218, 103789, 10.1016/j.nonrwa.2022.103789 | |
| 3. | Micol Amar, Daniele Andreucci, Claudia Timofte, Homogenization of a modified bidomain model involving imperfect transmission, 2021, 20, 1553-5258, 1755, 10.3934/cpaa.2021040 | |
| 4. | Fakhrielddine Bader, Mostafa Bendahmane, Mazen Saad, Raafat Talhouk, Microscopic Tridomain Model of Electrical Activity in the Heart with Dynamical Gap Junctions. Part 1 – Modeling and Well-Posedness, 2022, 179, 0167-8019, 10.1007/s10440-022-00498-7 | |
| 5. | Fakhrielddine Bader, Mostafa Bendahmane, Mazen Saad, Raafat Talhouk, Derivation of a new macroscopic bidomain model including three scales for the electrical activity of cardiac tissue, 2021, 131, 0022-0833, 10.1007/s10665-021-10174-8 | |
| 6. | M. Amar, D. Andreucci, C. Timofte, Well-Posedness for a Modified Bidomain Model Describing Bioelectric Activity in Damaged Heart Tissues, 2021, 18, 1660-5446, 10.1007/s00009-021-01839-w | |
| 7. | Vitaly Kalinin, Alexander Shlapunov, Konstantin Ushenin, On uniqueness theorems for the inverse problem of electrocardiography in the Sobolev spaces, 2023, 103, 0044-2267, 10.1002/zamm.202100217 | |
| 8. | Megan E. Farquhar, Kevin Burrage, Rodrigo Weber Dos Santos, Alfonso Bueno-Orovio, Brodie A.J. Lawson, Graph-based homogenisation for modelling cardiac fibrosis, 2022, 459, 00219991, 111126, 10.1016/j.jcp.2022.111126 | |
| 9. | Matthias Hieber, Amru Hussein, Martin Saal, Global Strong Well-Posedness of the Stochastic Bidomain Equations with FitzHugh–Nagumo Transport, 2023, 55, 0036-1410, 4140, 10.1137/22M1478008 | |
| 10. | M Bendahmane, K H Karlsen, F Mroué, Stochastic electromechanical bidomain model * , 2024, 37, 0951-7715, 075023, 10.1088/1361-6544/ad5132 | |
| 11. | Irina Pettersson, Antonina Rybalko, Volodymyr Rybalko, 2023, Chapter 6, 978-3-031-35870-8, 93, 10.1007/978-3-031-35871-5_6 |
The rescaled sets