Asymptotic problems and numerical schemes for traffic flows with unilateral constraints describing the formation of jams

1.   Introduction

In order to describe traffic flows and to reproduce the formation of congestions, several models based either on Ordinary Differential Equations (ODE) or Partial Differential Equations (PDE) have been proposed. Starting from individual-based "Follow-the-Leader" models [20], a very active stream in the traffic community considers now PDE models. A first example dates back to Lighthill and Whitham in the 50's [25]: the evolution of the density of cars is described by means of a mass conservation equation, where the flux is defined by a prescribed function of the density. In these so-called first-order models, the relation between flux and density is referred to as the fundamental diagram in the traffic flows community. A more accurate description can be expected by considering second-order models where a system of PDE governs the evolution of the density and the speed of cars. A first attempt in this direction is due to Payne [31], strongly inspired by the principles of fluid mechanics. However, Daganzo [15] pointed out the drawbacks of this approach: the Payne-Whitham model may lead to inconsistent behaviors for the flow, such as vehicles going backwards. The model introduced independently by Aw and Rascle [2] and by Zhang [37], which still has the form of a $2\times 2$ system of conservation laws, is intended to correct these inconsistencies. In [1], a derivation of the system is proposed from a Follow-the-Leader model. We can also mention that some kinetic models [3,29,30,33,36] are under consideration, after the pioneering work [32]. Further details and references can be found in the survey~[4].

This work is concerned with the numerical simulation of certain variants of the Aw-Rascle-Zhang model. Let $\rho(x,t)$ and $v(x,t)$ be the density and the velocity of cars at position $x \in \mathbb{R}$ and time $t>0$, respectively. The Aw-Rascle-Zhang model writes

where $\rho\mapsto p(\rho)$ plays the role of the pressure in the gas dynamic equations. In fact, the quantity $w=v+p(\rho)$ describes the desired velocity of the drivers, whereas $v$ corresponds to the actual velocity of the cars. Therefore, the term $p(\rho)$, the velocity offset, stands for the difference between these two velocities, reflecting the fact that the drivers slow down because of the density of cars. It is convenient to rewrite the equations in the form of a conservative system; namely (1) is, at least formally, equivalent to

Of course, a crucial modeling issue relies on the expression of the velocity offset $p(\rho)$. At first glance, again inspired from gas dynamics, we can set $p(\rho)=\rho^\gamma$ for some $\gamma> 1$. However, such a model does not permit to impose a priori a limitation to the cars density. Consequently, Berthelin, Degond, Delitala and Rascle proposed in [8] to define the velocity offset as follows: given $0<\rho_\star<\infty$,

which can be rewritten, for $\rho \neq 0$, by $p(\rho)=\left(\frac{1}{\rho}-\frac{1}{\rho_\star}\right)^{-\gamma}$, where $\rho_{\star}$ denotes a maximal value for the density. The velocity offset tends to infinity when $\rho \to \rho_{\star}$ while we get the classical expression $p(\rho) \sim \rho^\gamma$ when $\rho \to 0$. Such a pressure law also arises in gas dynamics, where it is referred to as the Bethe-Weyl law [5]; for instance it is used to model close-packing effects in multi-fluid flows, see [7] and the references therein. This expression for $p$ has the role of enforcing that $\rho$ satisfies the constraint $0 \leq \rho(x,t) \leq \rho_\star$ for all $x \in \mathbb{R}$ and $t>0$, as it can be seen from the bounds on the Riemann invariants of the system [8]. Moreover, [8] points out that drivers do not reduce significantly their speed unless they reach a congested region. Accordingly the velocity offset is appropriately rescaled with a small parameter $0<\varepsilon \ll 1$, and we use

in the Aw-Rascle-Zhang model. We are thus led to the Rescaled Modified Aw-Rascle (RMAR) system

In this model, the velocity offset is small unless the density is getting close to the threshold $\rho_\star$. Finally, [8] studies the limit when $\varepsilon \to 0$ in (3). In this regime we obtain (at least formally) the constrained system

In (4), the limit "pressure" $\pi=\lim_{\varepsilon \to 0 } p^\varepsilon (\rho^{\varepsilon })$ appears as the Lagrange multiplier associated to the unilateral constraint $0 \leq \rho \leq \rho_{\star}$. In particular, $\pi$ becomes active only in the congested regions, where the density reaches the threshold $\rho_\star$. Otherwise, in absence of congestion, the system is reduced to the pressure-less gas dynamic model [11,22]

The asymptotic model is further investigated in [8], exhibiting the formation of clusters, and proving the existence of weak solutions to the system (4) through the stability analysis of "sticky blocks" dynamics. It is also worth pointing out the original numerical approach developed in [28] for (4) which uses ideas from the modelling of crowd motion and includes a fine description of the non elastic collision processes.

The asymptotic system (4) is thus specifically intended to describe the formation and the dynamics of jams. In this paper, we are interested in the numerical simulations of the system (4), and in the asymptotic regime $\varepsilon \to 0$ in (3). The difficulty is two-fold. On the one hand, in the free flow case, it is well-known that the pressureless gas dynamics system (5) can lead to delta-shocks formation, which makes it difficult to treat numerically [10]. On the other hand, with the formation of a congestion, there is no direct access to the limit velocity offset $\pi$ which is defined in a quite abstract way. Therefore, in order to go beyond the simple particulate approach in [8], we wish to develop numerical simulations of the RMAR model (3) with the velocity offset (VO1) for small values of $\varepsilon$. We are still facing several numerical challenges. Firstly, the model prohibits that the density exceeds the threshold $\rho_\star$. Secondly, (one of) the characteristic speeds of the system become very large in congested region, which makes the time step shrink: the smaller $\varepsilon$, the more severe the stability constraint. Therefore, we need to design a scheme which can preserve the natural estimates of the problem, in particular the density limitation. As already observed in [12,13] standard schemes may fail this objective due to the very specific structure of the PDE system. We also refer the reader to [23] for further examples related to fluid mixtures. Moreover, we would like to relax the stability constraints on the time step. To this end, a first attempt would be to adapt the explicit-implicit method proposed in [19] for the Euler system with congestion constraint. However, this method applied to (3) is not satisfactory: it produces excessively smoothed density profiles and it overestimates the velocity in congested regions. Thus we design a different splitting strategy, partly inspired from [17]. Beyond the conception of a numerical scheme able to handle the stiffness of the problem, we will also discuss different asymptotic approaches of the constrained problem (4), based on different definitions of the scaled offset velocity in (3) which all lead asymptotically to (4). It is interesting to study how the shape of the pseudo-pressure affects the intermediate states (for not so extreme values of the scaling parameter), and the numerical costs.

The outline of this article is the following. In Section 2, we go back to some properties of the Aw-Rascle-Zhang system and we detail the numerical difficulties we face. Additionally, we propose different velocity offsets and scaling that can be used to recover asymptotically the constrained system (4). Then, in Section 3, we propose a new explicit-implicit scheme based on a splitting strategy. The splitting is constructed to reduce the characteristic speeds in the explicit part so that we can expect to use larger time steps. Finally, in Section 4, we display some numerical simulations in order to prove the efficiency of the scheme and to compare the behavior of the system when using different velocity offsets.

2.   Properties of the Aw-Rascle-Zhang model and numerical difficulties

We will describe in this Section the main numerical difficulties we have to deal with, when computing solutions of system (3).

2.1.   Different velocity offsets

With the velocity offset (VO1), it is forbidden to produce numerical densities larger than the threshold $\rho_\star$: if, due to any numerical error, the code returns a density larger than $\rho_\star$, we cannot update further the system and the simulation breakdowns. To cope with this difficulty, we propose to slightly modify the law, replacing (VO1) by a function $\rho\mapsto \tilde p^{\varepsilon }(\rho)$ which is defined for any positive entry, which behaves like $p^{\varepsilon }$ for $\rho<\rho_\star$, and which blows up as $\varepsilon\to 0$ for $\rho\geq \rho_\star$. For instance, we set

In this formula, $\rho_{trans}^{\varepsilon }$ is a transition density, which has a modeling nature; it should satisfy $\rho_{trans}^{\varepsilon } \to \rho_\star$ as $\varepsilon$ tends to 0. Beyond the transition, $\tilde p^{\varepsilon }$ is a second order polynomial, computed so that $\tilde p^{\varepsilon }$ remains a $\mathcal C^2$ function. We thus set

The expected behavior holds for instance with $h(\varepsilon )=\varepsilon$, since it satisfies the two following properties when $\varepsilon \to 0$: $h(\varepsilon ) \to 0$ and $c^0_{\varepsilon } \to +\infty$. We point out that $\rho_{trans}^{\varepsilon }$ is purely a modeling parameter and the model (VO2) leads us to the same difficulties as (VO1) in terms of stability issues, as we will see in the next Section.

Another option is to use the following velocity offset

for large values of the exponent $\gamma$. In this formula $V_{\mathrm{ref}}>0$ is a reference velocity, to bear in mind the physical meaning of $p$ (in the numerical simulations below we will simply set $V_{\mathrm{ref}}=1$). This approach is used in fluid mechanics, for modeling certain free boundary problems where bubbles are immersed in a gas [26]. This function is defined on $[0,\infty)$, it behaves proportionally to the gas-law $\rho^\gamma$ for $\rho \to 0$ and it blows up as $\gamma\to +\infty$ for $\rho\geq \rho_\star$. Using (VO3) and the regime of large $\gamma$'s in traffic flows modeling is quite new; we shall see that this simple law has certain advantages in the numerical simulations of congested situations.

In what follows, $p$ refers to (VO1), (VO2) or (VO3). We will see that similar behaviors, corresponding to what can be expected for (4), are captured asymptotically (namely as $\varepsilon \to 0$ or $\gamma\to \infty$) by these velocity offsets. However, the intermediate behaviors can significantly differ and the definition of the velocity offset seriously impacts the numerical costs.

2.2.   Stability issues

As long as the functions $\rho$ and $v$ are smooth enough, we can rewrite system (1) in the fully non-conservative form

The two eigenvalues of the system are therefore equal to

with related eigenvectors

The system is strictly hyperbolic, away from the regions where $\rho=0$. The largest eigenvalue $\lambda_{2}$ is always linearly degenerate, leading to contact discontinuities, while $\lambda_{1}$ is genuinely non-linear, except for certain forms of the velocity offset we are not considering here, and it thus admits shocks or rarefaction waves. The information does not travel faster than the actual cars speed $v$, and the system preserves the natural properties $\rho\geq 0$, $v\geq 0$. One of the difficulties of the computations is that vacuum regions may appear.

We are considering here Finite Volume (FV) schemes in order to compute the solutions of system (1). Let us denote by $\Delta t$ and $\Delta x$ the time step and the space step of the method, respectively. We consider the discrete times $t_{n}=n \Delta t$, for $n \in \mathbb{N}$ and the discretization cells $\mathcal{C}_{j}=[x_{j-1/2},x_{j+1/2}]$, $j \in \mathbb{Z}$ (neglecting for the time being the issue of the boundary conditions) where $x_{j+1/2}=(j+1/2) \Delta x$. We go back to the conservative form (2) and we denote

the conservative variables. In terms of the conservative variables $\rho$ and $y$, we simply have

which recasts as follows, using only the variables $\rho$ and $y$,

The numerical unknown $U^n_j=(\rho_{j}^n, y_{j}^n)$ is thought of as an approximation of the mean value of $U(x,t)$ on the cell $\mathcal{C}_{j}$ at time $t_{n}$. The FV scheme has the following general form

which mimics what we obtain by integrating the continuous equation (7) over $\left[ {{t}^{n}},{{t}^{n+1}} \right]\times {{\mathcal{C}}_{j}}$. For the simple schemes we wish to deal with, the numerical flux at the interface $x_{j+1/2}$ is a function of the neighbouring cells $F_{j+1/2}^{n}=\mathbb{F}\left( U_{j+1}^{n},U_{j}^{n} \right)$. Without entering into the details of the schemes, the numerical stability of such a method relies (at least) on the following inequality, see for example [9,Sect. 2.3.3] or [35],

where $\lambda_{1}$ and $\lambda_{2}$ are the two eigenvalues given by (6). It imposes that the state $U({x_{j+1/2},t^{n+1}})$ on the interface $x_{j+1/2}$ at time $t^{n+1}=t^n+\Delta t$ only depends on the states of the unknown at time $t^n$ on the neighbouring cells $\mathcal C_j$ and $\mathcal C_{j+1}$. It can thus be obtained by solving the corresponding Riemann problem with data $U^n_j$ and $U^n_{j+1}$.

Let us first consider the case of the pressure (VO1). In case of a congestion formation, $\rho^{\varepsilon } \to\rho_{\star}$ but we expect that $p^{\varepsilon }(\rho^{\varepsilon })$ remains bounded and admits the limit $\pi$ as $\varepsilon \to 0$; it leads to the ansatz

Accordingly the behavior of the characteristic speeds is given by

since $v^{\varepsilon }$ should remain bounded when $\varepsilon \to 0$. Hence, as $\varepsilon$ goes to zero, the time step $\Delta t$ shrinks due to the condition (8). The same remarks apply to the velocity offset (VO2), which essentially behaves like (VO1) when $\varepsilon \to 0$. For the velocity offset (VO3), we find

which again imposes tiny time steps. This observation motivates the design of a scheme based on splitting strategy so that the fast waves can be treated implicitly.

2.3.   Invariant regions

Let us detail another difficulty which is very specific to the traffic flow system (1). The Riemann invariants for the system (1) are given by, see [2],

Therefore, the domain

is an invariant region for (1): if the initial datum lies in such a region, the solution will still be contained in the same region for all times. However, numerical difficulties arise due to the fact that such domains are non-convex for the conserved quantities $\rho, y$. This point has been observed in [12] for the traffic flows model, see also [13,23] for similar problems. At first sight, it would be tempting to define the numerical fluxes by using the Godunov scheme, which is a standard for systems of conservation laws. It works into two steps. Owing to the stability condition (8), we solve a set of uncoupled Riemann problems, centered at the interfaces $x_{j+1/2}$ with data $U_j^n,U^{n}_{j+1}$. Then, we project the obtained piecewise constant solution to construct the updated numerical unknown, constant on the cells $\mathcal C_j$. This projection step does not preserve the invariant region, since the latter is non-convex (for the role of the convexity of the invariant domain we refer the reader to [24] for gas dynamics equations, and more generally to the textbook [9,Prop. 2.11]). A counter-example is detailed in [12] to explain why the Godunov scheme fails to satisfy the maximum principle for the Riemann invariants of (1), and especially for $v$. To solve this difficulty, [12] proposes a hybrid scheme which mixes the Glimm scheme to compute the contact discontinuities, and the Godunov procedure to compute 1-shock or 1-rarefaction wave. This hybrid method is well-adapted to handle the specific velocity offsets dealt with in [12,13], see Remark 2 below, which differ from the models we wish to consider here.

We bear in mind that, instead of using the mean of the solutions of the Riemann problems over the cells, the Glimm scheme uses a random sampling strategy in the reconstruction procedure. Hence, by construction, the Glimm scheme preserves the invariant regions, despite the defect of convexity. It is thus well adapted to the simulation of the system (1). Note however the final scheme is non conservative.

Remark 1. Note that, depending on the definition of the numerical fluxes, the stability condition can be even more constrained than (8), for instance in order to fulfill the bound from above on the density with the "close-packing-like" velocity offset (VO1), see e.g. [7].

Remark 2. In [12,13], the discussion focuses on the velocity offset

which has some very specific features:

● First of all, $\rho\mapsto p(\rho)$ is defined on $(0,\infty)$ and non decreasing. The model cannot treat vacuum regions since the velocity offset is not defined for $\rho=0$. With this model, the velocity offset is well-defined beyond $\rho_\star$, and we note that $p(\rho)<0$ for $0<\rho<\rho_\star$, which might be physically questionable.

● Second of all, we have $\rho p'(\rho)= V_{\mathrm{ref}}$. In particular, we get $\lambda_1=v- V_{\mathrm{ref}}$ so that the CFL condition depends only on $v$ and it does not shrink as the density approaches $\rho_\star$.

3.   Description of the scheme

Let us now explain in more details the construction of the scheme that we wish to use for the simulation of (1), with a velocity offset $\rho\mapsto p(\rho)$ that introduces some stiffness in order to reproduce the expected behavior of the constrained system (4). In what follows, $p$ thus refers to $p^{\varepsilon }$ in (VO1), to $\tilde p^{\varepsilon }$ in (VO2) or to $p^{\gamma}$ in (VO3).

In order to get rid of the large characteristic speeds, the idea consists in splitting the velocity offset into two parts

so that the system with $p_{exp}$ has a stability CFL condition (8) of order 1 with respect to the scaling parameters. Namely, the eigenvalue $\lambda_{exp,1}^{(\varepsilon )}$ (resp. $\lambda_{exp,1}^{(\gamma)}$) is bounded with respect to $0<\varepsilon \ll 1$ (resp. $\gamma\gg 1$). The corresponding system can thus be treated explicitly by means of the Glimm scheme, which preserves the invariant domains. Next, only the stiff part that involves $p_{imp}$ is treated implicitly. We expect also that the implicit part has a simple structure that can be handled with a not too complicated scheme. Such splitting approach appeared in [18,19,17] for more standard fluid mechanics systems, for instance as an efficient strategy to handle low Mach number regimes. However, as explained above, the structure of the PDE system (1) significantly differs from the Euler equations, in particular with the lack of convexity of the invariant domains and these methods cannot be directly applied to (1).

3.1.   Definition of the explicit velocity offset

In the first step of the splitting, we consider the system

It has the same structure as the Aw-Rascle-Zhang system (2), just replacing the full velocity offset $p$, that can be (VO1), (VO2) or (VO3), by $p_{exp}$. The characteristic speeds are

In order to relax the stability constraint, we define $p_{exp}$ so that the characteristic speed does not blow up as the scaling parameters $\varepsilon$ goes to 0 or $\gamma$ goes to $\infty$. It leads to require that $p'_{exp}(\rho)$ is bounded uniformly with respect to $\varepsilon$ (resp. $\gamma$ for the law (VO3)), when $\rho$ lies in a compact set of $(0,\infty)$. The definition depends on a truncation parameter $0<\rho_{num}<\rho_\star$. Following an idea of [18,19], we set

We use a second order polynomial for $\rho>\rho_{num}$ to ensure that $p_{exp}$ is a $\mathcal{C}^2$ function. We will see below that it is important to reach such a regularity. The transition density $\rho_{num}$ is chosen so that $p_{exp}'(\rho_{num})$ is bounded when $\varepsilon \to 0$ (resp. $\gamma \to +\infty$). If such a condition is satisfied, then the two eigenvalues are bounded with respect to $\varepsilon$ (resp. $\gamma$) and therefore the stability condition (8) is independent of $\varepsilon$ (resp. $\gamma$). Let us now explain how to choose $\rho_{num}$ for the velocity offsets under consideration.

a) For the laws (VO1) and (VO2), when $\varepsilon \to 0$ and $\rho^{\varepsilon }\to \rho_{\star}$, we expect that $\rho^{\varepsilon }=\rho_{\star} - O(\varepsilon ^{1/\gamma})$, since $p^\varepsilon (\rho^{\varepsilon })$ remains finite. We set $\rho_{num}=\rho_{\star}(1-\delta \rho)$ with $\delta \rho>0$. A simple computation shows that

which leads us to set

For the velocity offset (VO2), we point out that $\rho_{num}$ is a truncation parameter of numerical nature, designed to ensure a certain stability property of the scheme, while $\rho_{trans}$ relies on modeling consideration and does not prevent the blow up of the velocity offset. In any case, we have $0<\rho_{num}<\rho_{trans}<\rho_\star$.

b) For the law (VO3), we require that $p_{exp}'(\rho_{num})$ remains bounded when $\gamma \to +\infty$. Denoting again $\rho_{num}=\rho_{\star}(1-\delta \rho)$, a simple computation leads to

So, we are looking for $\delta \rho$ such that $\delta \rho \to 0$ and both terms in this sum are $O(1)$ when $\gamma \to +\infty$. A simple study of the two sequences of functions $\left( \gamma \exp\left( -\gamma x\right) \right)_{\gamma \in \mathbb{N}}$ and $\left( \gamma^2 x \exp\left( -\gamma x\right) \right)_{\gamma \in \mathbb{N}}$ shows that we should have $\delta \rho=O(\gamma^{-\alpha})$ with $\alpha \in (0,1)$ in order to satisfy the required properties.

In [17] the pressure term is split as $p=p_{exp}+p_{imp}$ with $p_{exp}=\alpha p$ and $p_{imp}=(1-\alpha)p.$ Here, due to the singularity of $p$ at $\rho_{\star}$, this approach does not permit to keep $p'_{exp}$ bounded and we have to define $p_{exp}$ and $p_{imp}$ as explained above.

3.2.   A time-splitting scheme

As said above, it is convenient to work on the conservative form (7) of the system (1), dealing with the unknowns $U=\big(\rho,y\big)$ where $y=\rho(v+p(\rho))$. With $p=p_{exp}+p_{imp}$, we arrive at

We use now a time-splitting scheme. Knowing some approximate values $U^n=(\rho^n,y^n)$ at time $t_{n}$, we proceed as follows.

● Step 1: Solve with an explicit scheme the system of conservation laws

As said above, this system has the same structure as the original problem (7). In particular the invariant domains are non-convex. It can be solved with the Glimm scheme adapted for the pressure $p_{exp}$. More details will be given in Section 3.3. It defines some intermediate values $(\rho^{n+1/2}, y^{n+1/2})$.

● Step 2: Solve implicitly the system

Note that the system has a simple structure and the two equations decouple. The first equation is a non linear scalar conservation law for the density $\rho$, the second is a linear transport equation for $y$ where the velocity $-p_{imp}(\rho)$ can be considered as given. The numerical method to solve the system (12) is thus not that complicated. More details will be given in Section 3.4.

3.3.   A few words about the Glimm scheme for (1)

In order to use a Glimm scheme, we need to know the Riemann solutions of the problem. This computation has already been done in [2] and in [8,Section~6] where all the details can be found. We refer the reader to some classical books [34,35] for general discussions about the role of Riemann problems in the theory of conservation laws and to [2,8] for the specific case of the traffic flow system. We recap here only the Riemann solutions, omitting the details on the elementary waves and on the admissibility of solutions.

3.3.1.   A brief overview on the Riemann problem for (1)

The Riemann solution of (1), with an initial datum

can be computed according to the five following cases:

● if $\rho^L>0,\;\rho^R>0$ and $0\leq v^R\leq v^L$, the solution consists of a 1-shock that connects $({\rho^L,v^L})$ to the intermediate state $(\rho^*,v^*)$ and a contact discontinuity between $(\rho^*,v^*)$ and $({\rho^R,v^R})$;

● if $\rho^L>0,\;\rho^R>0$ and $v^L< v^R\leq v^L+ p(\rho^L)$, the solution consists of a 1-rarefaction wave that connects $({\rho^L,v^L})$ to $(\rho^*,v^*)$ and a contact discontinuity between $(\rho^*,v^*)$ and $({\rho^R,v^R})$;

● if $\rho^L>0,\;\rho^R>0$ and $v^L+ p({\rho^L})< v^R$, a vacuum region appears; the solution consists of a 1-rarefaction wave that connects $({\rho^L,v^L})$ to $(0,v^*)$, then a vacuum region between $(0,v^*)$ and $(0,v^R)$ and a contact discontinuity between $({0,v^R})$ and $({\rho^R,v^R})$;

● if $\rho^L>0,\; \rho^R=0$, the solution is only a 1-rarefaction wave connecting $({\rho^L,v^L})$ and $({0,v^R})$;

● if $\rho^L=0,\; \rho^R>0$, the solution is only a 2-contact discontinuity connecting $({0,v^L})$ and $({\rho^R,v^R})$.

The intermediate state $(\rho^*,v^*)$ of the Riemann solution is computed with the Riemann invariants, that is to say

In the case of a shock, the speed of the shock between $(\rho^*,v^*)$ and $({\rho^L,v^L})$ is given by

In the case of a rarefaction wave, the self-similar solution $(\rho,v)(\xi)$ with $\xi=x/t$ is given by the following formulae

which apply for $\xi \in \left[ {{\lambda }_{1}}({{\rho }^{L}},{{v}^{L}}),{{\lambda }_{1}}({{\rho }^{R}},{{v}^{R}}) \right]$.

Remark 3. In practice, we compute the self-similar solutions of equation (13), by using the Newton algorithm. The method requires that $p$ has the $\mathcal{C}^2$ regularity. This remark explains the construction of the explicit part of the velocity offset (11) (we have observed bad behaviors of the scheme when $p"$ has jumps).

3.3.2.   Glimm scheme

Hence, we have at hand formula to compute the solution of the Riemann problems, which are the elementary bricks of the Glimm's scheme (like for Godunov's scheme). This scheme has been introduced for theoretical purposes [21], and its implementation for hyperbolic systems is further discussed in [12,14,27]. Let $U^n_j= ({\rho_{j}^n, y_{j}^n})$ be the approximated mean value on the cell $\mathcal{C}_{j}$ of $U=(\rho,y)$ at time $t_{n}$. We proceed as follows to update the numerical unknown:

● We solve the associated Riemann problem at each interface $x_{j+1/2}$, namely all the Riemann problems with $U_L=U^n_j$, $U_R=U^n_{j+1}$.

● We pick a random number $a_n$ in $[0,1]$. We define the value $U^{n+1}_j$ of the numerical unknown in the cell $\mathcal C_j$ at time $t^{n+1}$ as to be the solution of the Riemann problem evaluated at $x_{j-\frac{1}{2}}+a_n\Delta x \in \mathcal{C}_{j}.$ The scheme does not use any averaging or projection procedure and the obtained solution, by construction, remains in the invariant region of the PDE system. In practice, we use the Van Der Corput quasi-random sequence $(a_n)_{n\in\mathbb{N}}$ (see [14]) defined by

where $n=\sum_{k=0}^m i_k2^k$, with $i_k\in\{0,1\}$, denotes the binary expansion of the integer $n$.

3.4.   Treatment of the implicit part

Let us now discuss how we handle the system (12) where we remind the reader that $p_{imp}$ contains the stiff part of the velocity offset. As said above, the system decouples and it has a very simple structure. Let us set $\Phi:\rho \in [0,\infty)\mapsto - \rho p_{imp}(\rho)\in (-\infty,0]$. We solve the scalar conservation law for $\rho$ with the classical Engquist-Osher scheme. Other schemes are likely possible, but this one leads to simple and natural formula. The Engquist-Osher flux is defined by

where $[X]_{+}=\max(X,0)$ and $[X]_{-}=\min(X,0)$. The implicit scheme takes the following form

where $\rho^{n+1/2}_j$ is the result from the first (explicit) step of the scheme.

Here, the velocity field $\Phi'(\rho)=-\frac{\text{d} }{\text{d} \rho}\big(\rho p_{imp}(\rho)\big) = -p_{imp}(\rho) - \rho p_{imp}'(\rho)$ of this scalar equation is always non positive. Accordingly, the numerical flux reduces to a mere function of the right density

Consequently, the non-linear equation (14) becomes

It forms a triangular system of non linear scalar equations. If $J$ stands for the number of grid points, we have to solve $J$ non linear scalar equations, which means $J$ executions of the scalar Newton algorithm to update the density. In practice we start the Newton algorithm by using the available value $\rho^{n+1/2}_j$ as initial guess. Then a mere linear system defines the updated $y$. Indeed, once $\rho^{n+1}$ is determined, we solve the transport equation for updating $y$. To this end, we use the standard implicit upwind scheme

with

The specific case $p_{imp}\geq 0$, yields

It forms a triangular linear system of equations that can be solved by backward substitution, leading to the straightforward formula

4.   Simulations

As indicated in the introduction, it is far from clear how to design a "natural" scheme for a direct simulation of the constrained model (4). We can only mention the recent approach for crowd dynamics proposed in [28]; here we are rather motivated by the asymptotic issues. Our aim is two-fold. On the one hand we wish to discuss the asymptotic behavior of the different models (VO1), (VO2) and (VO3) for the velocity offset, which are all expected to capture asymptotically (for $\varepsilon \to 0$ or $\gamma\to \infty$) the features of the limit system (4). On the other hand, we shall discuss the numerical difficulties and the ability of the time-splitting strategy, which will be compared to the standard Glimm scheme with a small enough time step, in handling the asymptotic behaviour.

The simulations presented below are thought of as Riemann problems and we impose boundary conditions that maintain constant the inflow conditions. Of course, the method can be adapted to treat further boundary conditions. In particular imposing zero-influx produces vacuum regions, a numerical difficulty that our method is able to handle, as shown with the decongestion case below.

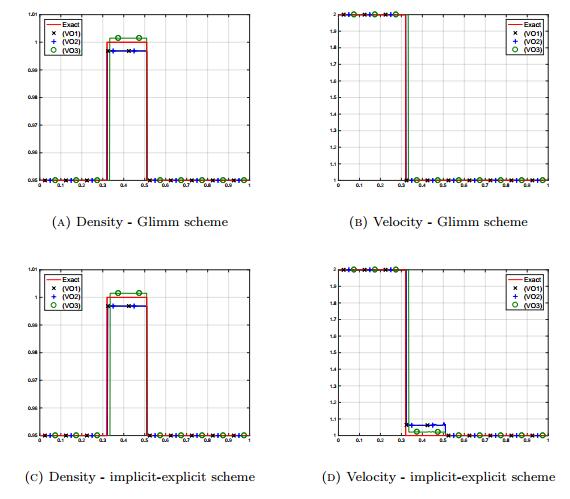
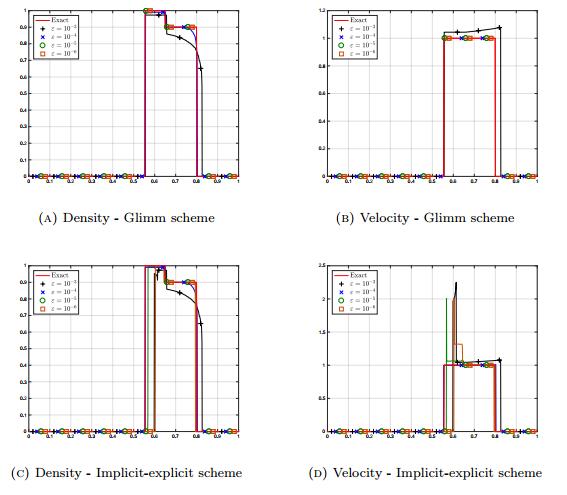
4.1.   Case of simple transport

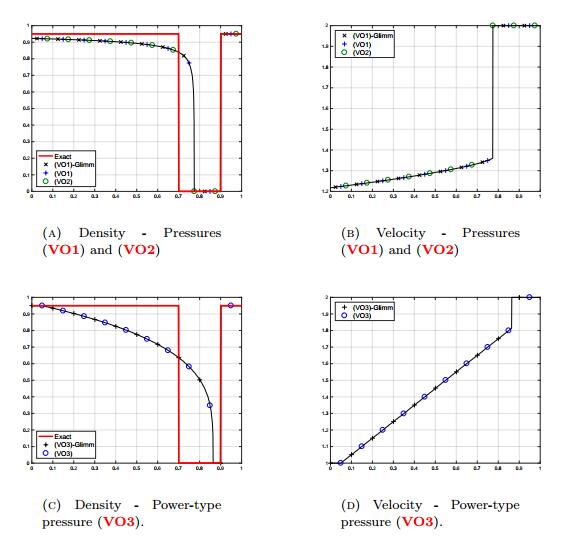
To begin with, we test the case of a simple transport: the computational domain is the interval $[0,1]$ and for the initial data we set

We compare the six following situations:

● system (1) with pressure (VO1), using the Glimm scheme,

● system (1) with pressure (VO1), using the scheme presented in Section 3,

● system (1) with pressure (VO2), using the Glimm scheme,

● system (1) with pressure (VO2), using the scheme presented in Section 3,

● system (1) with pressure (VO3), using the Glimm scheme,

● system (1) with pressure (VO3), using the scheme presented in Section 3.

The solution at $T=0.4$ should be

The space step is equal to $\Delta x=10^{-3}$ and the time step is computed in order to satisfy the stability condition (evaluated with the full $p$ for the Glimm scheme, and with $p_{\exp}$ for the implicit-explicit method). The parameters are taken as follows:

● Pressure (VO1) with $\gamma=2$, $\varepsilon=10^{-3}$, $\rho_{\star}=1$. For the explicit-implicit scheme, the numerical threshold is chosen as $\rho_{num}=\rho_{\star}\left(1-\frac 1 5\varepsilon ^{1/(\gamma+1)}\right).$

● Pressure (VO2) with $\gamma=2$, $\varepsilon=10^{-3}$, $\rho_{\star}=1$ and $\rho_{trans}^{\varepsilon}=\rho_{\star}-\varepsilon$. For the explicit-implicit scheme, the numerical threshold is chosen as $\rho_{num}=\rho_{\star}\left(1-\frac 1 5 \varepsilon ^{1/(\gamma+1)}\right).$

● Pressure (VO3) with $\gamma=4$. For the explicit-implicit scheme, the numerical threshold is chosen as $\rho_{num}=\rho_{\star}\left(1-10^{-2}\right).$

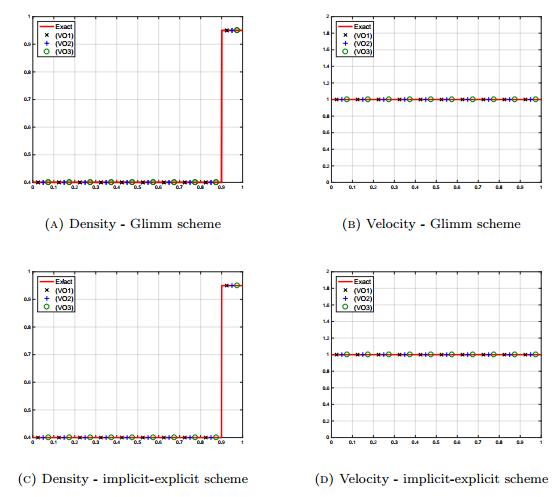
The results of the numerical simulations for the three different pressures performed with the Glimm scheme are displayed at Figure 1a-Figure 1b, whereas the same simulations using the scheme constructed in Section 3 are exhibited at Figures Figure 1c-Figure 1d. All the results are equivalent and agree with the exact solution.

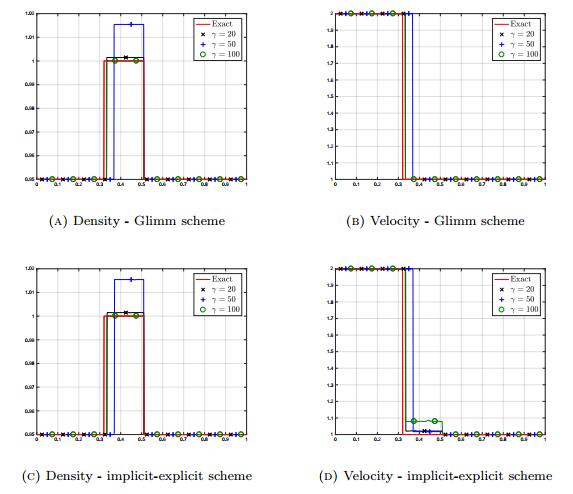
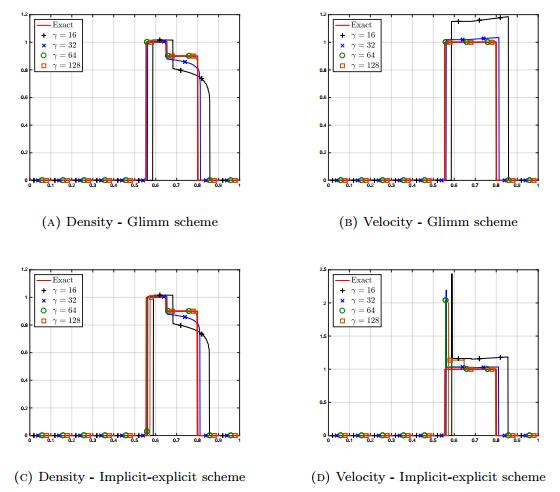
4.2.   Case of decongestion

Next, we study the case of a decongestion in the traffic. The data are defined by

The initial density is close to the threshold. Since the vehicles ahead are going faster, a decongestion occurs. The expected solution at $T=0.2$ should be equal to

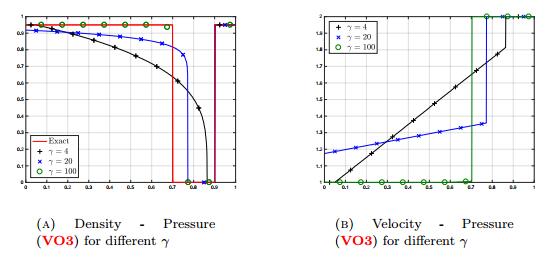
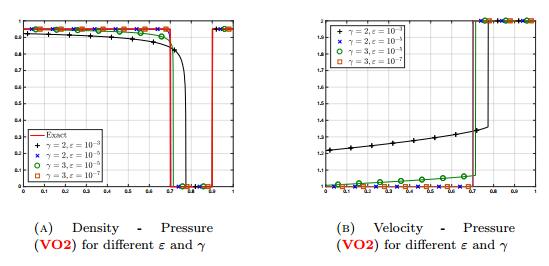
Note the formation of a vacuum region, where $v$ does not make sense. It is indeed particularly interesting and relevant to check the ability of the models and of the numerical methods to handle the formation of vacuum regions, where the density vanishes. The velocity offsets are defined as in the previous Section and we work with the same numerical parameters. The results can be found in Figure 2. The Glimm scheme and the explicit-implicit scheme give the same results for all three pressures (VO1), (VO2) and (VO3). Note that the density and velocity are the same for (VO1) and (VO2), while, for the considered parameters, (VO3) provides significantly different profiles. We observe that pressures (VO1) and (VO2) on the one hand and pressure (VO3) on the other hand give different results, especially in the vacuum region, none of them being totally in agreement with the "expected" result. This can be explained by the moderate value of the parameters $\varepsilon$ or $\gamma$. Indeed, the constrained behavior (18) can be obtained by changing the parameters, see Figure 3, where we test (VO3) for different values of $\gamma \to +\infty$ and Figure 4, where we make $\varepsilon \to 0$ vary for (VO2). In the former case, the limit behavior is captured with $\gamma=100$ and for the latter, we get a satisfactory result with $\varepsilon =10^{-5}$ if $\gamma=2$, and $\varepsilon =10^{-7}$ if $\gamma=3$. We notice also at Figure 4 that if we take $\gamma=3$ for pressure (VO2) instead of $\gamma=2$, we need to take a smaller value of $\varepsilon$, namely $\varepsilon =10^{-7}$ instead of $\varepsilon =10^{-5}$. Note that the results for the original model (VO1) and for the modified model (VO2) are totally equivalent.

4.3.   Case of congestion

4.3.1.   A jump of velocity creating a congestion

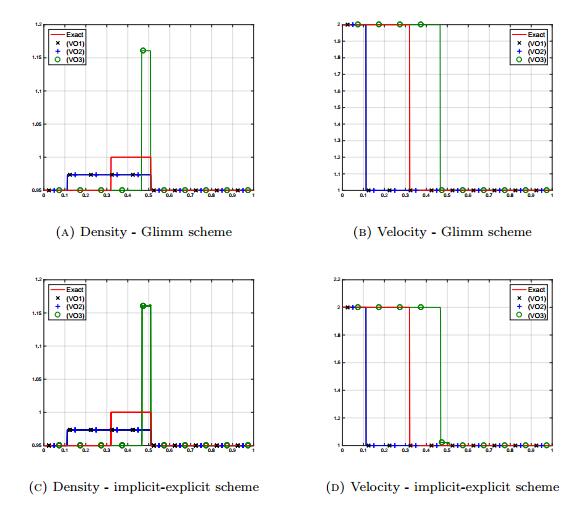
Finally, we turn to the simulation of a congestion in the traffic. The initial conditions are given by

The density is initially close to the threshold; since the cars ahead are slower, a congestion might occur and the Lagrange multiplier becomes active to prevent an excess of vehicle density.

Indeed, discontinuous solutions are characterized by the Rankine-Hugoniot conditions: with $t\mapsto s(t)$ the speed of the discontinuity curve, we have

and

We can check that

with

and a Lagrange multiplier active only in the congestion domain

is solution of (4). The presence of slow vehicles ahead of the fast ones instantaneously creates a congestion behind the velocity jump: the slow vehicles ahead make the faster ones behind brake. This is typical of the Follow-the-Leader approach, which has led to a derivation of the Aw-Rascle-Zhang system [1,20]. However, it is likely that solutions of the constrained model (4) are not uniquely defined for such data; we refer the reader to [6] for such considerations.

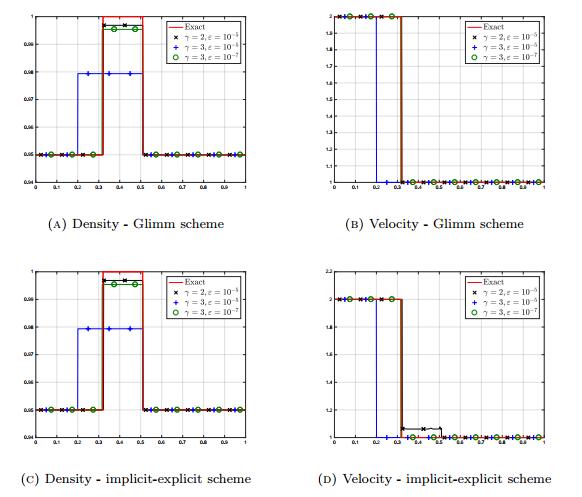
The parameters are defined as in Section 4.1 and we show the solutions obtained at the final time $T=0.01$ in Figure 5. We observe exactly the same behaviors between the Glimm scheme and the implicit-explicit scheme with (VO1) or (VO2). We observe that with these parameters, the three models do not find the solution (18). The time steps for the Glimm scheme are smaller than with the explicit-implicit scheme, but, quite surprisingly, by a factor 3 or 4 only.

Regarding the velocity offsets, (VO3) overshoots the maximal value of the density, equal to $1$, whereas the two other pressures (VO1) and (VO2) underestimate it. This is not surprising since (VO3) allows values larger than the threshold, but it contrasts with the behavior of the model (VO2) which has the same feature. In Figure 6, we make the parameters vary as follows:

● Pressure (VO1) with $\gamma=2$, $\varepsilon=10^{-5}$,

● Pressure (VO2) with $\gamma=2$, $\varepsilon=10^{-5}$,

● Pressure (VO3) with $\gamma=50$.

We observe that these parameters provide a result closer to the explicit solution $(\rho_1,v_1)$. The results for (VO3) with different values of $\gamma$ are given at Figure 7 and for (VO2) with different values of $\gamma$ and $\varepsilon$ at Figure 8. The two schemes behave equivalently in that case, with some advantage in terms of time step for the implicit-explicit method, see Table 1 (the smaller $\varepsilon$, resp. the larger $\gamma$, the more important the gain). Note that in the case when $\gamma=3$, the results are exactly the same because the density is below the numerical threshold; consequently, the implicit part of the scheme is not used and the final result is the same as the one given by the explicit step, that is to say the final result is the same as the one given by the Glimm scheme. As expected, making $\varepsilon \to 0$ for (VO2) or $\gamma \to +\infty$ for (VO3) allows us to obtain a result compatible with $(\rho_1,v_1)$. In particular, we point out that the approach of (4) as an asymptotic model from (3) provides the solution where the fastest cars should brake behind the slow vehicles, independently of the density of slow vehicles ahead. This behavior corresponds to the derivation originally introduced in [2].

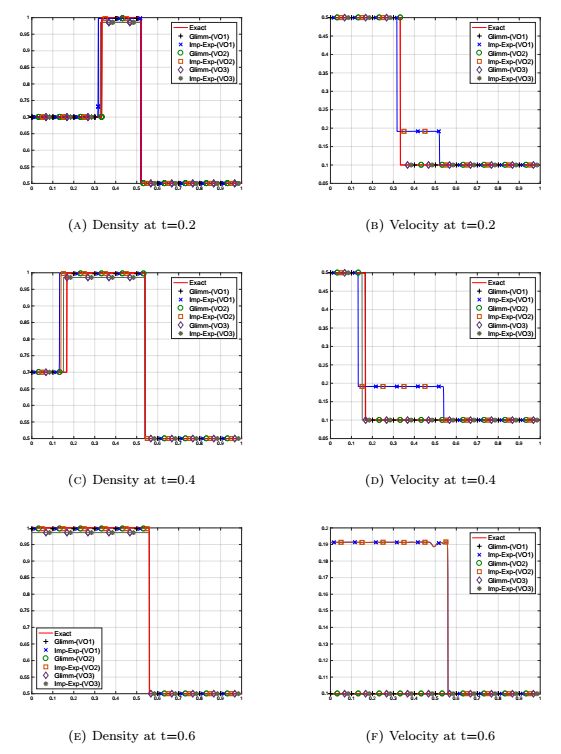
4.3.2.   A fast cluster reaching a slower one

We now consider the situation of a slow car cluster reached by a faster cluster of vehicles. The initial conditions are

and the expected solution at $T=0.3$ is

Again, this solution presents a vacuum region. The results for the different velocity offsets are represented in Figures 9, 10 and 11 for the scheme presented in Section 3 and the Glimm scheme.

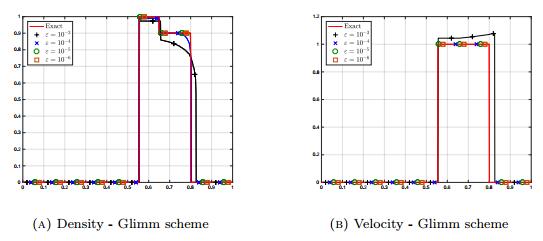
When using the Glimm scheme, we obtain the expected limit solution as we make the parameters vary: for (VO1) as $\varepsilon$ goes to 0, see Figure 9, for (VO2) as $\varepsilon$ goes to 0, see Figure 10, and for (VO3) as $\gamma$ goes to infinity, see Figures 11c and Figures 11d. The explicit-implicit scheme is able to compute precisely the car density with the velocity offset (VO3), see Figure 11a. However, difficulties arise for the computation of the velocity, especially in the back of the jam, see Figure 11b: the velocity of the last cars in the congestion (coordinate $x=0.555$) is over estimated. Moreover, we observe in the case when $\gamma=128$ a loss of the quantity of cars between initial and final times of around $9 \%$. This behavior is even worse with (VO2), see Figures 10c and Figures 10d. Here again, the quantity of mass is not conserved: the difference between the initial density and the final one is around $23\%$. We point out that this simulation is quite tough; the results obtained with the Glimm scheme are neater but at the price of a significative numerical cost.

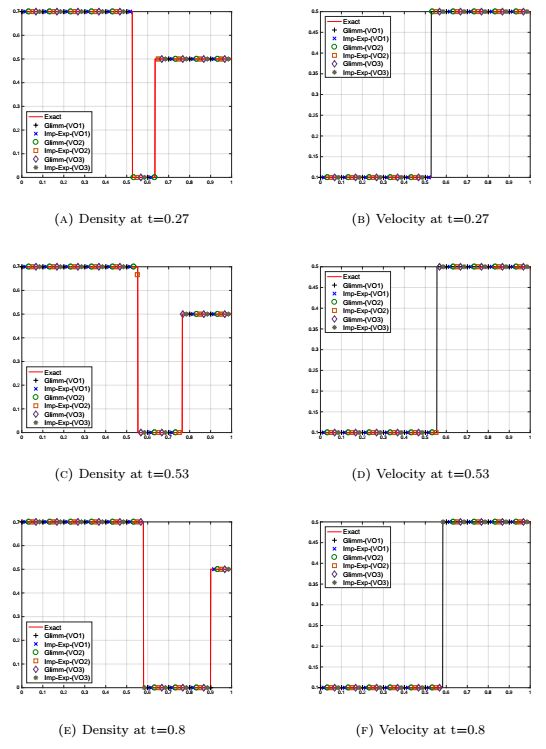
4.3.3.   Riemann problems: Comparison with [16]

In this section we present the numerical results obtained with the Glimm scheme and the implicit-explicit schemes of Section 3 for the sub-cases AI and AⅢ of [8,16]. So we consider in the following a road $[{0,1}]$ with the initial data

and

where we use the same labels as in [8,16]. A solution for (AⅠ) is

and

is a solution for (AⅢ) (note that $v$ does not make sense in the vacuum region $x\in [{0.5+0.1t,0.5+0.5t}]$). In order to compare our scheme with the results of [16] we take the same parameters, namely for the velocity offset (VO1) and (VO2) we use $\gamma=1$ and $\varepsilon =10^{-3}$. For the velocity offset (VO3) we use $\gamma=64$.

Figure 12 represents the results for the sub-case (AI) computed with the three velocity offsets and with the Glimm scheme or the explicit-implicit scheme, at time $t=0.2$, $t=0.4$ and $t=0.6$. According to Figures 12a, 12c and e, the explicit-implicit scheme for the velocity offset (VO2) overestimates the length of the congestion. For example at $t=0.4$ using (21), the tail of the congestion should be at $x=0.166$ instead of $x=0.13$. Moreover, the velocity in the congested area is over estimated, see Figures 12b, Figures 12d and Figures 12f.

Figure 13 represents the results for the sub-case (AⅢ) for the three velocity offsets and for different times. In order to ease the comparison between the Glimm scheme and explicit-implicit scheme presented in Section 3, the results for the two numerical approaches are displayed simultaneously. According to Figure 13, all the different numerical approaches give similar results which coincide with the solution given by (22).

5.   Conclusion

The model (4) is intended to describe the formation and the dynamics of traffic jams, through a Lagrange multiplier that accounts for a density threshold. This model can be motivated, at least formally, through asymptotic arguments from the Aw-Rascle-Zhang system with a rescaled velocity-offset. It raises the question of simulating efficiently the Aw-Rascle-Zhang system with potentially stiff velocity offsets. Depending on the values of the parameters it can be seen either as the simulation of a model for traffic flows with stiff parameters or as a way to access the limiting behavior described by (4), alternative for instance to the approach of [28]. However the scaling induces fast propagation waves and, in turn, severe stability conditions. In this paper, we propose several approaches to obtain asymptotically (4) and we introduce an implicit-explicit method in order to cope with the large characteristic speeds of the system.

This study exhibits numerical difficulties, related to both the lack of convexity of the invariant domains of (1) and the large characteristic speeds. We have proposed a time-splitting method, based on a decomposition of the velocity-offset and the use of the Glimm scheme which avoids the non admissible solutions produced by schemes based on a projection step. Our findings bring out that the behavior of the system (4) can be obtained asymptotically, but the shape of the solution for intermediate values of the scaling parameters highly depends on the expression of the penalized velocity offset. It means that a serious modeling work should decide what is the most appropriate model.

Acknowledgments

We thank Frédéric Coquel for friendly advices and warm encouragements during the preparation of this work.