Hydroxyurea and pyridostigmine repurposed for treating Covid-19 multi-systems dysfunctions

1.   Introduction

In the present paper we study the effective conductivity of an $n$-dimensional periodic two-phase composite, with $n \in \{2, 3\}$ which from now on we assume fixed. The composite is obtained by introducing into a homogeneous matrix a periodic set of inclusions of a large class of sufficiently smooth shapes. Both the matrix and the set of inclusions are filled with two different homogeneous and isotropic heat conductor materials of conductivity $\lambda^-$ and $\lambda^+$, respectively, with

We note that the limit case of zero conductivity corresponds to a thermal insulator. On the other hand, if the conductivity tends to $+\infty$, the material is a perfect conductor. The inclusions' shape is determined by the image of a fixed domain through a diffeomorphism $\phi$, and the periodicity cell is a 'box' of edges of lengths $q_{11}, \ldots, q_{nn}$. As it is known, it is possible to define the composite's effective conductivity matrix $\lambda^{\mathrm{eff}}$ by means of the solution of a transmission problem for the Laplace equation (see Definition 1.1, cf. Mityushev, Obnosov, Pesetskaya, and Rogosin [43,§5]). The effective conductivity can be thought as the conductivity of a homogeneous material whose global behavior as a conductor is 'equivalent' to the composite. Our aim is to study the dependence of $\lambda^{\mathrm{eff}}$ upon the 'triple' $((q_{11}, \ldots, q_{nn}), \phi, (\lambda^+, \lambda^-))$, i.e., upon the perturbation of the periodicity structure of the composite, of the inclusions' shape, and of the conductivity parameters of each material. A perturbation analysis of the properties of composite materials has been carried out by several authors with different techniques. For example, in Ammari, Kang, and Touibi [5] the authors have exploited a potential theoretic approach in order to investigate the asymptotic behavior of the effective properties of a periodic dilute composite. Then Ammari, Kang, and Kim [3] and Ammari, Kang, and Lim [4] have studied anisotropic composite materials and elastic composites, respectively. The method of Functional Equations has been used to study the dependence on the radius of the inclusions for a wide class of 2D composites. For ideal composites, we mention here, for example, the works of Mityushev, Obnosov, Pesetskaya, and Rogosin [43], Gryshchuk and Rogosin [26], Kapanadze, Mishuris, and Pesetskaya [28]. Contributions to composites with different contact conditions are, for example, Drygaś and Mityushev [20] and Castro, Kapanadze, and Pesetskaya [9,10] (non-ideal composites), Castro and Pesetskaya [11] (composites with inextensible-membrane-type interface). The effect of shapes on the properties of composites has been studied under several different points of view by many authors. For example, Berlyand, Golovaty, Movchan, and Phillips [7] have analyzed the transport properties of fluid/solid and solid/solid composites and have investigated how the curvature of the inclusions affects such properties. Berlyand and Mityushev [8] have studied the dependence of the effective conductivity of two-phase composites upon the polydispersivity parameter. Gorb and Berlyand [25] considered the asymptotic behavior of the effective properties of composites with close inclusions of optimal shape. For 2D composites, we also mention the recent work by Mityushev, Nawalaniec, Nosov, and Pesetskaya [42], where the authors have applied the generalized alternating method of Schwarz in order to study the effective conductivity of two-phase random composites with non-overlapping inclusions whose boundaries are arbitrary Lyapunov's curves. In Lee and Lee [37], the authors have studied how the effective elasticity of dilute periodic elastic composites is affected by its periodic structure. Finally, Pukhtaievych [48] has explicitly computed the effective conductivity of a periodic dilute composite with perfect contact as a power series in the size of the inclusions. In the present paper we perform a regularity analysis of the behavior of the effective conductivity upon joint perturbation of periodicity structure of the composite, of the inclusions' shape, and of the conductivity parameters. Moreover, in contrast with previous contributions we do not confine our attention just to specific shapes.

We now introduce the geometry of the problem. If $q_{11}, \ldots, q_{nn}\in ]0, +\infty[$, we will use the following notation:

and

The set $Q$ plays the role of the periodicity cell and the diagonal matrix $q$ plays the role of the periodicity matrix. Clearly $|Q|_n \equiv \prod_{j = 1}^n q_{jj}$ is the measure of the fundamental cell $Q$ and $q\mathbb{Z}^n\equiv \{qz:z\in \mathbb{Z}^n\}$ is the set of vertices of a periodic subdivision of $\mathbb{R}^n$ corresponding to the fundamental cell $Q$. We denote by $q^{-1}$ the inverse matrix of $q$. We denote by ${\mathbb{D}}_{n}({\mathbb{R}})$ the space of $n\times n$ diagonal matrices with real entries and by ${\mathbb{D}}_{n}^{+}({\mathbb{R}})$ the set of elements of ${\mathbb{D}}_{n}({\mathbb{R}})$ with diagonal entries in $]0, +\infty[$. Moreover, we find it convenient to set

Then we take

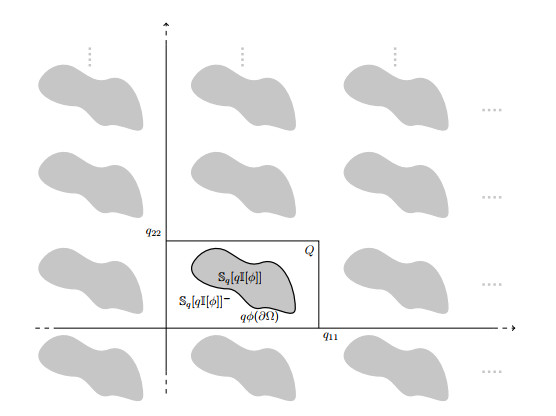
The symbol '$\overline{\cdot}$' denotes the closure of a set. For the definition of sets and functions of the Schauder class $C^{k, \alpha}$ ($k \in \mathbb{N}$) we refer, e.g., to Gilbarg and Trudinger [23]. Then we consider a class of diffeomorphisms ${\mathcal{A}}_{ \partial\Omega }^{\widetilde{Q}}$ from $\partial\Omega$ into their images contained in the unitary cell $\widetilde{Q}$ (see (14)). If $\phi\in {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}$, the Jordan-Leray separation theorem ensures that ${\mathbb{R}}^{n}\setminus\phi (\partial\Omega)$ has exactly two open connected components (see, e.g, Deimling [18,Thm. 5.2,p. 26]), and we denote by ${\mathbb{I}}[\phi]$ the bounded open connected component of ${\mathbb{R}}^{n}\setminus\phi (\partial\Omega)$. Since $\phi (\partial\Omega)\subseteq \widetilde{Q}$, a simple topological argument shows that $\widetilde{Q}\setminus\overline{\mathbb{I}[\phi]}$ is also connected. If $q \in \mathbb{D}_n^+(\mathbb{R})$, we consider the following two periodic domains (see Figure 1):

The set $\mathbb{S}_{q}[q\mathbb{I}[\phi]]^-$ represents the homogeneous matrix made of a material with conductivity $\lambda^-$ where the periodic set of inclusions $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]}$ with conductivity $\lambda^+$ is inserted. Globally, the union of the matrix and the inclusions represents the two-phase composite material we consider.

With the aim of introducing the definition of the effective conductivity, we first have to introduce a boundary value problem for the Laplace equation. If $q \in \mathbb{D}_n^+(\mathbb{R})$, $\phi \in C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}$, and $(\lambda^+, \lambda^-) \in [0, +\infty[^2_\ast$, for each $j \in \{1, \ldots, n\}$ we consider the following transmission problem for a pair of functions $(u_j^+, u_j^-)\in C^{1, \alpha}_{\mathrm{loc}}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]})\times C^{1, \alpha}_{\mathrm{loc}}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^{-}})$:

where $\nu_{ q\mathbb{I}[\phi]}$ is the outward unit normal to $\partial q\mathbb{I}[\phi]$ and $\{e_{1}, \dots, e_{n}\}$ is the canonical basis of ${\mathbb{R}}^{n}$. We observe that for $C^{1, \alpha}$ functions, the Laplace equations of problem (4) have to be considered in the sense of distributions. Then, by elliptic regularity theory (see for instance Friedman [21,Thm. 1.2,p. 205]), if the Laplace equation is satisfied by a function in the sense of distributions, we know that such a function is of class $C^\infty$ in the interior, and that accordingly the Laplace equation is satisfied in the classical sense. As we will see, problem (4) admits a unique solution $(u_j^+, u_j^-)$ in $C^{1, \alpha}_{\mathrm{loc}}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]})\times C^{1, \alpha}_{\mathrm{loc}}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^{-}})$, which we denote by $(u_j^+[q, \phi, (\lambda^+, \lambda^-)], u_j^-[q, \phi, (\lambda^+, \lambda^-)])$. Such family of solutions is needed in order to define the effective conductivity as follows (cf., e.g., Mityushev, Obnosov, Pesetskaya, and Rogosin [43,§5]).

Definition 1.1. Let $q \in \mathbb{D}_n^+(\mathbb{R})$, $\phi \in C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}$, and $(\lambda^+, \lambda^-) \in [0, +\infty[^2_\ast$. Then the effective conductivity

is the $n\times n$ matrix with $(i, j)$-entry defined by

Remark 1.2. Under the assumptions of Definition 1.1, by applying the divergence theorem, one can verify that

Indeed, if we set

then

Therefore, in order to conclude that the two definitions are equivalent, we need to show that

By an application of the divergence theorem for $C^1$ functions (cf. Ziemer [50,Thm. 5.8.2,Rmk. 5.8.3]), we have

and

By the periodicity of $\tilde u_i^-[q, \phi, (\lambda^+, \lambda^-)]$ and of $\tilde u_j^-[q, \phi, (\lambda^+, \lambda^-)]$, we have

since contributions on opposite sides of $\partial Q$ cancel each other. Thus by (6)–(8) we obtain

Since the validity of (4) implies that

and that

we then deduce by (9) that (5) holds true.

As a consequence, the effective conductivity matrix of Definition 1.1 coincides with the one analyzed by Ammari, Kang, and Touibi [5,p. 121] for a periodic two-phase composite and which can be deduced by classical homogenization theory (see, e.g., Allaire [1], Bensoussan, Lions, and Papanicolaou [6], Jikov, Kozlov, and Oleĭnik [27], Milton [41]). We emphasize that the justification of the expression of the effective conductivity via homogenization theory holds for 'small' values of the periodicity parameters. For further remarks on the definition of effective conductivity we refer to Gluzman, Mityushev, and Nawalaniec [24,§2.2].

The main goal of our paper is to give an answer to the following question:

We answer to the above question by proving that for all $i, j \in \{1, \ldots, n\}$ there exist $\varepsilon \in ]0, 1[$ and a real analytic map

such that

for all $(q, \phi, (\lambda^+, \lambda^-))\in \mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times [0, +\infty [^2_\ast$ (see formula (25) of Theorem 5.1 below). The approach we use was introduced by Lanza de Cristoforis in [31] and then exploited to analyze a large variety of singular and regular perturbation problems (cf., e.g., Lanza de Cristoforis [32], Dalla Riva and Lanza de Cristoforis [15], Dalla Riva [14]).

In particular, in the present paper we follow the strategy of [39] where we have studied the behavior of the longitudinal flow along a periodic array of cylinders upon perturbations of the shape of the cross section of the cylinders and the periodicity structure, when a Newtonian fluid is flowing at low Reynolds numbers around the cylinders. More precisely, we transform the problem into a set of integral equations defined on a fixed domain and depending on the set of variables $(q, \phi, (\lambda^+, \lambda^-))$. We study the dependence of the solution of the integral equation upon $(q, \phi, (\lambda^+, \lambda^-))$ and then we deduce the result on the behavior of $\lambda^{\mathrm{eff}}_{ij}[q, \phi, (\lambda^+, \lambda^-)]$.

Formula (11) implies that the effective conductivity $\lambda^{\mathrm{eff}}[q, \phi, (\lambda^+, \lambda^-)]$ can be expressed in terms of the conductivity $\lambda^-$ of the matrix, of the conductivity $\lambda^+$ of the inclusions, and of a real analytic function of the periodicity parameters $q_{11}, \dots, q_{nn}$, of the shape $\phi$ and of the contrast parameter $\frac{\lambda^+-\lambda^-}{\lambda^++\lambda^-}$. In particular, by the real analyticity of $\Lambda_{ij}$, the expression $\Lambda_{ij}\left[q, \phi, \frac{\lambda^+-\lambda^-}{\lambda^++\lambda^-}\right]$ can be written as a convergent power series of $q, \phi, \frac{\lambda^+-\lambda^-}{\lambda^++\lambda^-}$ in a suitable Banach space. Also, formula (11) immediately implies that the map

from $\mathbb{D}_n^+(\mathbb{R}) \times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right) \times [0, +\infty [^2_\ast$ to $\mathbb{R}$ admits a real analytic extension around every point $(q, \phi, (\lambda^+, \lambda^-)) \in \mathbb{D}_n^+(\mathbb{R}) \times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right) \times [0, +\infty [^2_\ast$. Such a result implies that if $\delta_0>0$ and we have a family of triples $\{(q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta))\}_{\delta \in ]-\delta_0, \delta_0[}$ in $\mathbb{D}_n^+(\mathbb{R}) \times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right) \times [0, +\infty [^2_\ast$ such that the map $\delta \mapsto (q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta))$ is real analytic, then we can deduce the possibility to expand $\lambda^{\mathrm{eff}}_{ij}[q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta)]$ as a power series in $\delta$, i.e.,

for $\delta$ close to zero. Moreover, the coefficients $(c_{k} )_{{k} \in \mathbb{N}}$ in (13) can be constructively determined by computing the differentials of $\lambda^{\mathrm{eff}}_{ij}$.

Furthermore, such a high regularity result can be seen as a theoretical justification which guarantees that differential calculus may be used in order to characterize critical periodicity-shape-conductivity triples $(q, \phi, (\lambda^+, \lambda^-))$ as a first step to find optimal configurations, under specific constraints. Indeed, if one is interested in finding a triple $(q, \phi, (\lambda^+, \lambda^-))$ that maximizes (or minimizes) the effective conductivity $\lambda^{\mathrm{eff}}_{ij}[q, \phi, (\lambda^+, \lambda^-)]$ under given constraints on $(q, \phi, (\lambda^+, \lambda^-))$, then, since the map in (12) is analytic, one can try to apply differential calculus to characterize critical configurations. In the present paper, by critical we mean critical points of the effective conductivity functional, that we think as a map defined on a suitable function space. In this sense, finding a critical point could be a first step to search for (local) maximum or minimum points under suitable restrictions. If, for example, we have a family $\{(q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta))\}_{\delta \in ]-\delta_0, \delta_0[}$ in $\mathbb{D}_n^+(\mathbb{R}) \times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right) \times [0, +\infty [^2_\ast$, for some $\delta_0>0$, which depends smoothly on $\delta$, then we can apply differential calculus to the map $\delta \mapsto \lambda^{\mathrm{eff}}_{ij}[q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta)]$ to find, for example, local minimizers or maximizers. Similar considerations can be done if, more in general, $(q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta))$ depends smoothly on a parameter $\delta$ which belongs to a differentiable manifold. Moreover, we note that, in contrast with other approaches that can be applied only to particular shapes as circles or ellipses, our method permits to consider inclusions of a large class of sufficiently smooth shapes.

As already mentioned, our method is based on integral equations, that are derived by potential theory. However, integral equations could also be deduced by the generalized alternating method of Schwarz (cf. Gluzman, Mityushev, and Nawalaniec [24] and Drygaś, Gluzman, Mityushev, and Nawalaniec [19]), which also allows to produce expansions in the concentration.

Incidentally, we observe that the are several contributions concerning optimization of effective parameters from many different points of view. For example, one can look for optimal lattices without confining to rectangular distributions. In this direction, Kozlov [29] and Mityushev and Rylko [44] have discussed extremal properties of hexagonal lattices of disks. On the other hand, even if, in wide generality, the optimal composite does not exist (cf. Cherkaev [13]), one can discuss the dependence on the shape under some specific restrictions. For example, one could build composites with prescribed effective conductivity as described in Lurie and Cherkaev [38] (see also Gibiansky and Cherkaev [22]). In Rylko [49], the author has studied the influence of perturbations of the shape of the circular inclusion on the macroscopic conductivity properties of 2D dilute composites. Inverse problems concerning the determination of the shape of equally strong holes in elastic structures were considered by Cherepanov [12]. For an experimental work concerning the analysis of particle reinforced composites we mention Kurtyka and Rylko [30]. Also, we mention that one could apply the topological derivative method as in Novotny and Sokołowski [46] for the optimal design of microstructures.

2.   Preliminaries and notation

Let $\alpha$, $\Omega$ be as in (3). We denote by $\nu_{\Omega}$ the outward unit normal to $\partial\Omega$ and by $d\sigma$ the area element on $\partial\Omega$. We retain the standard notation for the Lebesgue space $L^{1}(\partial\Omega)$ of Lebesgue integrable functions. We denote by $|\partial \Omega|_{n-1}$ the $(n-1)$-dimensional measure of $\partial \Omega$. To shorten our notation, we denote by ${\rlap{-} \smallint } _{\partial\Omega}f\, d\sigma$ the integral mean $\frac{1}{|\partial \Omega|_{n-1}}\int_{\partial\Omega} f\, d\sigma$ for all $f\in L^{1}(\partial\Omega)$. Also, if ${\mathcal{X}}$ is a vector subspace of $L^{1}(\partial\Omega)$ then we set ${\mathcal{X}}_{0}\equiv\left\{f\in{\mathcal{X}}:\, \int_{\partial\Omega}f\, d\sigma = 0 \right\}.$ Moreover, we note that throughout the paper 'analytic' always means 'real analytic'. For the definition and properties of analytic operators, we refer to Deimling [18,§15].

Let $q, Q$ be as in (1) and (2). If $\Omega_{Q}$ is a subset of $\mathbb{R}^n$ such that $\overline{\Omega_{Q}} \subseteq Q$, we define the following two periodic domains

If $u$ is a real valued function defined on $\mathbb{S}_q[\Omega_{Q}]$ or $\mathbb{S}_q[\Omega_{Q}]^-$, we say that $u$ is $q$-periodic provided that $u(x+qz) = u(x)$ for all $z \in \mathbb{Z}^{n}$ and for all $x$ in the domain of definition of $u$. If $k\in {\mathbb{N}}$, we set

and we endow $C^{k}_{b}(\overline{ \mathbb{S}_q[\Omega_{Q}]^-})$ with its usual norm

where $|\gamma|\equiv \sum_{i = 1}^n\gamma_i$ denotes the length of the multi-index $\gamma \equiv (\gamma_1, \ldots, \gamma_n) \in \mathbb{N}^n$. Moreover, if we further take $\beta\in]0, 1]$, then we set

and we endow $C^{k, \beta}_{b}(\overline{ \mathbb{S}_q[\Omega_{Q}]^- })$ with its usual norm

where $|D^{\gamma}u: \overline{ \mathbb{S}_q[\Omega_{Q}]^- } |_{\beta}$ denotes the $\beta$-Hölder constant of $D^{\gamma}u$. Similarly, we set

which we regard as a Banach subspace of $C^{k}_{b}(\overline{\mathbb{S}_q[\Omega_Q]^-} )$, and

which we regard as a Banach subspace of $C^{k, \beta}_{b}(\overline{\mathbb{S}_q[\Omega_Q]^-} )$. The spaces $C^{k}_{b}(\overline{\mathbb{S}_q[\Omega_Q]})$, $C^{k, \beta}_{b}(\overline{\mathbb{S}_q[\Omega_Q]})$, $C^{k}_{q}(\overline{\mathbb{S}_q[\Omega_Q]})$, and $C^{k, \beta}_{q}(\overline{\mathbb{S}_q[\Omega_Q]})$ can be defined similarly.

Our method is based on a periodic version of classical potential theory. In order to construct periodic layer potentials, we replace the fundamental solution of the Laplace operator by a $q$-periodic tempered distribution $S_{q, n}$ such that

where $\delta_{qz}$ denotes the Dirac measure with mass in $qz$ (see e.g., [34,p. 84]). The distribution $S_{q, n}$ is determined up to an additive constant, and we can take

in the sense of distributions in ${\mathbb{R}}^{n}$ (see e.g., Ammari and Kang [2,p. 53], [34,§3]). Moreover, $S_{q, n}$ is real analytic in ${\mathbb{R}}^{n}\setminus q{\mathbb{Z}}^{n}$ and locally integrable in ${\mathbb{R}}^{n}$ (see e.g., [34,§3]).

We now introduce periodic layer potentials. Let $\Omega_Q$ be a bounded open subset of ${\mathbb{R}}^{n}$ of class $C^{1, \alpha}$ for some $\alpha\in]0, 1[$ such that $\overline{\Omega_Q}\subseteq Q$. We set

for all $\mu\in C^0(\partial\Omega_Q)$. Here above, $DS_{q, n}(\xi)$ denotes the gradient of $S_{q, n}$ computed at the point $\xi \in \mathbb{R}^n \setminus q\mathbb{Z}^n$. The function $v_q[\partial\Omega_Q, \mu]$ is called the $q$-periodic single layer potential, and $w_{q, *}[\partial\Omega_Q, \mu]$ is a function related to the normal derivative of the single layer potential. As is well known, if $\mu\in C^{0}(\partial\Omega_Q)$, then $v_q[\partial\Omega_Q, \mu]$ is continuous in ${\mathbb{R}}^{n}$ and $q$-periodic, and we set

We collect in the following theorem some properties of $v^{\pm}_q[\partial\Omega_Q, \cdot]$ and $w_{q, *}[\partial\Omega_Q, \cdot]$. For a proof of statements (ⅰ)–(ⅲ) we refer to [34,Thm. 3.7] and to [16,Lem. 4.2]. For a proof of statements (ⅳ) we refer to [16,Lem. 4.2 (ⅰ),(ⅲ)].

Theorem 2.1. Let $q, Q$ be as in (1) and (2). Let $\alpha \in ]0, 1[$. Let $\Omega_Q$ be a bounded open subset of ${\mathbb{R}}^{n}$ of class $C^{1, \alpha}$ such that $\overline{\Omega_Q}\subseteq Q$. Then the following statements hold.

(i) The map from $C^{0, \alpha}(\partial\Omega_Q)$ to $C^{1, \alpha}_q(\overline{{\mathbb{S}}_q[\Omega_Q]})$ which takes $\mu$ to $v^{+}_q[\partial\Omega_Q, \mu]$ is linear and continuous. The map from $C^{0, \alpha}(\partial\Omega_Q)$ to $C^{1, \alpha}_q(\overline{{\mathbb{S}}_q[\Omega_Q]^-})$ which takes $\mu$ to $v^{-}_q[\partial\Omega_Q, \mu]$ is linear and continuous.

(ii) Let $\mu \in C^{0, \alpha}(\partial\Omega_Q)$. Then

Moreover,

(iii) Let $\mu \in C^{0, \alpha}(\partial\Omega_Q)_0$. Then

(iv) The operator $w_{q, *}[\partial \Omega_Q, \cdot]$ is compact in $C^{0, \alpha}(\partial\Omega_Q)$ and in $C^{0, \alpha}(\partial\Omega_Q)_0$.

In order to consider shape perturbations of the inclusions of the composite, we introduce a class of diffeomorphisms. Let $\Omega$ be as in (3) and let $\Omega'$ be a bounded open connected subset of $\mathbb{R}^n$ of class $C^{1, \alpha}$. We denote by $\mathcal{A}_{\partial \Omega}$ and by $\mathcal{A}_{\overline{\Omega'}}$ the sets of functions of class $C^1(\partial\Omega, \mathbb{R}^{n})$ and of class $C^1(\overline{\Omega'}, \mathbb{R}^n)$ which are injective and whose differential is injective at all points of $\partial\Omega$ and of ${\overline{\Omega'}}$, respectively. One can verify that $\mathcal{A}_{\partial \Omega}$ and $\mathcal{A}_{\overline{\Omega'}}$ are open in $C^1(\partial\Omega, \mathbb{R}^{n})$ and $C^1({\overline{\Omega'}, \mathbb{R}^ n})$, respectively (see, e.g., Lanza de Cristoforis and Rossi [36,Lem. 2.2,p. 197] and [35,Lem. 2.5,p. 143]). Then we find it convenient to set

If $\phi \in \mathcal{A}_{\partial \Omega}$, the Jordan-Leray separation theorem ensures that $\mathbb{R}^n\setminus \phi(\partial \Omega)$ has exactly two open connected components, and we denote by $\mathbb{I}[\phi]$ the bounded open connected component of $\mathbb{R}^n\setminus\phi(\partial \Omega)$ (see, e.g, Deimling [18,Thm. 5.2,p. 26]).

We conclude this section of preliminaries with some results on problem (4). By means of the following proposition, whose proof is of immediate verification, we can transform problem (4) into a $q$-periodic transmission problem for the Laplace equation.

Proposition 2.2. Let $q, Q$ be as in (1) and (2) and $\alpha$, $\Omega$ be as in (3). Let $(\lambda^+, \lambda^-) \in [0, +\infty[^2_\ast$. Let $\phi \in C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}$. Let $j \in \{1, \ldots, n\}$. A pair

solves problem (4) if and only if the pair

delivered by

solves

Next, we show that problems (4) and (15) admit at most one solution.

Proposition 2.3. Let $q, Q$ be as in (1) and (2) and $\alpha$, $\Omega$ be as in (3). Let $(\lambda^+, \lambda^-) \in [0, +\infty[^2_\ast$. Let $\phi \in C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}$. Let $j \in \{1, \ldots, n\}$. Then the following statements hold.

(i) Problem (4) has at most one solution in $C^{1, \alpha}_{\mathrm{loc}}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]})\times C^{1, \alpha}_{\mathrm{loc}}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^{-}})$.

(ii) Problem (15) has at most one solution in $C^{1, \alpha}_{q}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]})\times C^{1, \alpha}_{q}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^{-}})$.

Proof. By the equivalence of problems (4) and (15) of Proposition 2.2, it suffices to prove statement (ⅱ), which we now consider. By the linearity of the problem, it clearly suffices to show that if $(\tilde u_j^+, \tilde u_j^-)\in C^{1, \alpha}_{q}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]})\times C^{1, \alpha}_{q}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^{-}})$ solves

then $(\tilde u_j^+, \tilde u_j^-) = (0, 0)$. The case $(\lambda^+, \lambda^-) \in ]0, +\infty[^2$ was proved in Pukhtaievych [47,Prop. 1]. Accordingly it suffices to consider the limiting cases $\lambda^+ = 0, \lambda^- \neq 0$ and $\lambda^- = 0, \lambda^+ \neq 0$.

Let $\lambda^+ = 0, \lambda^- \neq 0$. The fifth equation in (16) implies that

Accordingly, the divergence theorem implies that

Indeed, by the $q$-periodicity of $\tilde u_j^-$ one has that

Then, there exists $c \in \mathbb{R}$ such that $\tilde{u}_j^- = c$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^-}$. The sixth equation in (16) and the maximum principle for harmonic functions imply that also $\tilde{u}_j^+ = c$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]}$. Finally, the seventh equation in (16) implies that $c = 0$, i.e., $\tilde{u}_j^+ = 0$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]}$ and $\tilde{u}_j^- = 0$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^-}$.

Next we consider the case $\lambda^- = 0, \lambda^+ \neq 0$. The fifth equation in (16) implies that

By the uniqueness of the solution of the interior Neumann problem up to constants, there exists $c \in \mathbb{R}$ such that $\tilde{u}_j^+ = c$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]}$. The sixth equation in (16) and the periodic analog of the maximum principle for harmonic functions imply that also $\tilde{u}_j^- = c$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^-}$ (see e.g., [45,Prop. A.1]). Finally, the seventh equation in (16) implies that $c = 0$, i.e., $\tilde{u}_j^+ = 0$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]}$ and $\tilde{u}_j^- = 0$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^-}$.

3.   An integral equation formulation of problem (4)

In this section, we convert problem (4) into an equivalent integral equation. As done in [39] for the longitudinal flow along a periodic array of cylinders, we do so by representing the solution in terms of single layer potentials, whose densities solve certain integral equations. Therefore, we first start with the following proposition regarding the invertibility of an integral operator that will appear in such integral formulation of problem (4).

Proposition 3.1. Let $q, Q$ be as in (1) and (2) and $\alpha$, $\Omega$ be as in (3). Let $\phi \in C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}$. Let $\gamma \in [-1, 1]$. Let $K_\gamma$ be the operator defined by

Then the following statements hold.

(i) $K_\gamma$ is a linear homeomorphism from $C^{0, \alpha}(\partial q\mathbb{I}[\phi])_0$ to itself.

(ii) $K_\gamma$ is a linear homeomorphism from $C^{0, \alpha}(\partial q\mathbb{I}[\phi])$ to itself.

Proof. We first consider statement (ⅰ). If $\gamma \in ]-1, 1[$, then statement (ⅰ) follows from Pukhtaievych [47,Prop. 2] by noting that there exists a pair $(\gamma^+, \gamma^-) \in ]0, +\infty[^2$ such that

Accordingly, we have to consider only the limit cases $\gamma \in \{-1, 1\}$. We start with the case $\gamma = 1$. Since by Theorem 2.1 (ⅳ) the operator $w_{q, *}[\partial q\mathbb{I}[\phi], \cdot]$ is compact in $C^{0, \alpha}(\partial q\mathbb{I}[\phi])_0$, the Fredholm alternative theorem implies that it suffices to show that $K_{1}[\cdot]$ is injective. Accordingly let $\mu \in C^{0, \alpha}(\partial q\mathbb{I}[\phi])_0$ be such that

The jump formula for the normal derivative of the single layer potential of Theorem 2.1 (ⅱ) implies that $\frac{\partial}{\partial \nu_{q\mathbb{I}[\phi]}} v^+_q[ \partial q\mathbb{I}[\phi], \mu] = 0$ on $\partial q\mathbb{I}[\phi]$. Then, the properties of the single layer potential and the proof of Theorem 2.3 imply that there exists $c \in \mathbb{R}$ such that $v^+_q[ \partial q\mathbb{I}[\phi], \mu] = c$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]}$ and $v^-_q[ \partial q\mathbb{I}[\phi], \mu] = c$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^{-}}$. Finally by the jump formula for the normal derivative of the single layer potential of Theorem 2.1 (ⅱ) we have that

Next, we consider the case $\gamma = -1$. As before, it suffices to show that $K_{-1}[\cdot]$ is injective. Accordingly let $\mu \in C^{0, \alpha}(\partial q\mathbb{I}[\phi])_0$ be such that

The jump formula for the normal derivative of the single layer potential of Theorem 2.1 (ⅱ) implies that $\frac{\partial}{\partial \nu_{q\mathbb{I}[\phi]}} v^-_q[ \partial q\mathbb{I}[\phi], \mu] = 0$ on $\partial q\mathbb{I}[\phi]$. Then, the properties of the single layer potential and the proof of Theorem 2.3 imply that there exists $c \in \mathbb{R}$ such that $v^+_q[ \partial q\mathbb{I}[\phi], \mu] = c$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]}$ and $v^-_q[ \partial q\mathbb{I}[\phi], \mu] = c$ in $\overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^{-}}$. Finally by the jump formula for the normal derivative of the single layer potential of Theorem 2.1 (ⅱ) we have that

Next, we consider statement (ⅱ). The Fredholm alternative theorem and the compactness of $w_{q, *}[\partial q\mathbb{I}[\phi], \cdot]$ in $C^{0, \alpha}(\partial q\mathbb{I}[\phi])$ imply that it suffices to show that $K_{\gamma}$ is injective in $C^{0, \alpha}(\partial q\mathbb{I}[\phi])$. To this aim, we show that if $\mu \in C^{0, \alpha}(\partial q\mathbb{I}[\phi])$ is such that

then $\mu \in C^{0, \alpha}(\partial q\mathbb{I}[\phi])_0$, i.e., $\int_{\partial q\mathbb{I}[\phi]}\mu\, d\sigma = 0$. Then statement (ⅰ) would imply that $\mu = 0$. So let $\mu \in C^{0, \alpha}(\partial q\mathbb{I}[\phi])$ be such that (17) holds. Theorem 2.1 (ⅱ) implies

A straightforward computation shows that $\frac{1}{2}-\gamma \left(\frac{1}{2}-\frac{|q\mathbb{I}[\phi]|}{|Q|}\right) = 0$ if and only if $\frac{|q\mathbb{I}[\phi]|}{|Q|} \neq\frac{1}{2}$ and $\gamma = \frac{1}{1-2\frac{|q\mathbb{I}[\phi]|}{|Q|}}$. Since $\frac{|q\mathbb{I}[\phi]|}{|Q|} \in ]0, 1[$ one can easily realize that $\frac{1}{1-2\frac{|q\mathbb{I}[\phi]|}{|Q|}} \notin [-1, 1]$. Thus $\frac{1}{2}-\gamma\left(\frac{1}{2}-\frac{|q\mathbb{I}[\phi]|}{|Q|}\right) \neq 0$ for all $\gamma \in [-1, 1]$ and then $\int_{\partial q\mathbb{I}[\phi]}\mu\, d\sigma = 0$.

We are now ready to show that problem (4) can be reformulated in terms of an integral equation which admits a unique solution.

Theorem 3.2. Let $q, Q$ be as in (1) and (2) and $\alpha$, $\Omega$ be as in (3). Let $(\lambda^+, \lambda^-) \in [0, +\infty[^2_\ast$. Let $\phi \in C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}$. Let $j \in \{1, \ldots, n\}$. Then problem (4) has a unique solution

Moreover

where $\mu_j$ is the unique solution in $C^{0, \alpha}(\partial q\mathbb{I}[\phi])_0$ of the integral equation

Proof. We first note that, by Proposition 2.3 (ⅱ), problem (4) has at most one solution in $C^{1, \alpha}_{\mathrm{loc}}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]})\times C^{1, \alpha}_{\mathrm{loc}}( \overline{\mathbb{S}_{q}[q\mathbb{I}[\phi]]^{-}})$. As a consequence, we only need to prove that the pair of functions defined by (18) solves problem (4). Since

Proposition 3.1 (ⅰ) implies that there exists a unique solution $\mu_j \in C^{0, \alpha}(\partial q\mathbb{I}[\phi])_0$ of the integral equation (19). A straightforward computation and the continuity of the single layer potential imply that

Accordingly, the properties of the single layer potential (see Theorem 2.1) together with Proposition 2.2 imply that the pair of functions defined by (18) solves problem (4).

The previous theorem provides an integral equation formulation of problem (4) and a representation formula for its solution. We conclude this section by writing the effective conductivity in a form which makes use of the density $\mu_j$ solving equation (19). To do that, we exploit the representation formula given by the previous theorem. Let the assumptions of Theorem 3.2 hold and let $u_j^+[q, \phi, (\lambda^+, \lambda^-)]$, $u_j^-[q, \phi, (\lambda^+, \lambda^-)]$ and $\mu_j$ be as in Theorem 3.2. Then by the divergence theorem we have

Similarly, we have

Indeed

Moreover, by the divergence theorem, we have

Accordingly, by the continuity of the single layer potential, we have that

4.   Analyticity of the solution of the integral equation

Thanks to Theorem 3.2, the study of problem (4) can be reduced to the study of the boundary integral equation (19). Therefore, our first step in order to study the dependence of the solution of problem (4) upon the triple $(q, \phi, (\lambda^+, \lambda^-))$ is to analyze the dependence of the solution $\mu_j$ of equation (19). Since in equation (19) the conductivity parameters $\lambda^+$ and $\lambda^-$ enter only in the quotient $\frac{\lambda^+-\lambda^-}{\lambda^++\lambda^-}$, we will study the dependence of $\mu_j$ upon the periodicity $q$, the shape $\phi$, and a parameter $\gamma$ that will play the role of the contrast parameter $\frac{\lambda^+-\lambda^-}{\lambda^++\lambda^-}$.

Before starting with this plan, we note that equation (19) is defined on the $(q, \phi)$-dependent domain $\partial q\mathbb{I}[\phi]$. Thus, in order to bypass this problem, we first need to provide a reformulation on a fixed domain. More precisely, we have the following lemma.

Lemma 4.1. Let $q, Q$ be as in (1) and (2) and $\alpha$, $\Omega$ be as in (3). Let $(\lambda^+, \lambda^-) \in [0, +\infty[^2_\ast$. Let $\phi \in C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}$. Let $j \in \{1, \ldots, n\}$. Then the function $\theta_j\in C^{0, \alpha}(\partial\Omega)$ solves the equation

if and only if the function $\mu_j\in C^{0, \alpha}(\partial q \mathbb{I}[\phi])_0$, with $\mu_j$ delivered by

solves equation (19). Moreover, equation (21) has a unique solution in $C^{0, \alpha}(\partial\Omega)$.

Proof. The equivalence of equation (21) in the unknown $\theta_j$ and equation (19) in the unknown $\mu_j$, with $\mu_j$ delivered by (22), is a straightforward consequence of a change of variables. Then, the existence and uniqueness of a solution of equation (21) in $C^{0, \alpha}(\partial\Omega)$ follows from Theorem 3.2 and from the equivalence of equations (19) and (21).

Inspired by Lemma 4.1, for all $j \in \{1, \ldots, n\}$ we introduce the map

by setting

for all $(q, \phi, \gamma, \theta)\in\mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times ]-2, 2 [\times C^{0, \alpha}(\partial\Omega)$. As one can readily verify, under the assumptions of Lemma 4.1, equation (21) can be rewritten as

Our aim is to recover the regularity of the solution $\theta$ of the above equation upon the periodicity $q$, the shape $\phi$, and the contrast parameter $\frac{\lambda^+-\lambda^-}{\lambda^++\lambda^-}$. Our strategy is based on the implicit function theorem for real analytic maps in Banach spaces applied to equation (24). As a first step, we need to prove that $M_j$ is real analytic. In order to do that, we need the following result of [40], where we show that some integral operators associated with the single layer potential and its normal derivative depend analytically upon the periodicity $q$ and the shape $\phi$.

Lemma 4.2. Let $\alpha$, $\Omega$ be as in (3). Then the following statements hold.

(i) The map from $\mathbb{D}_n^+(\mathbb{R})\times\left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n)\cap\mathcal{A}^{\widetilde Q}_{\partial\Omega}\right)\times C^{0, \alpha}(\partial\Omega)$ to $C^{1, \alpha}(\partial\Omega)$ which takes a triple $(q, \phi, \theta)$ to the function $V[q, \phi, \theta]$ defined by

is real analytic.

(ii) The map from $\mathbb{D}_n^+(\mathbb{R})\times\left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n)\cap\mathcal{A}^{\widetilde Q}_{\partial\Omega}\right)\times C^{0, \alpha}(\partial\Omega)$ to $C^{0, \alpha}(\partial\Omega)$ which takes a triple $(q, \phi, \theta)$ to the function $W_*[q, \phi, \theta]$ defined by

is real analytic.

Next, we state the following technical lemma about the real analyticity upon the diffeomorphism $\phi$ of some maps related to the change of variables in integrals and to the outer normal field (for a proof we refer to Lanza de Cristoforis and Rossi [35,p. 166] and to Lanza de Cristoforis [33,Prop. 1]).

Lemma 4.3. Let $\alpha$, $\Omega$ be as in (3). Then the following statements hold.

(i) For each $\phi \in C^{1, \alpha}(\partial\Omega, \mathbb{R}^{n})\cap\mathcal{A}_{\partial \Omega}$, there exists a unique $\tilde \sigma[\phi] \in C^{0, \alpha}(\partial\Omega)$ such that $\tilde \sigma[\phi] > 0$ and

Moreover, the map $\tilde \sigma[\cdot]$ from $C^{1, \alpha}(\partial\Omega, \mathbb{R}^n)\cap\mathcal{A}_{\partial \Omega}$ to $C^{0, \alpha}(\partial\Omega)$ is real analytic.

(ii) The map from $C^{1, \alpha}(\partial\Omega, \mathbb{R}^n)\cap\mathcal{A}_{\partial \Omega}$ to $C^{0, \alpha}(\partial\Omega, \mathbb{R}^{n})$ which takes $\phi$ to $\nu_{\mathbb{I}[\phi]} \circ \phi$ is real analytic.

We are now ready to prove that the solutions of (24) depend real analytically upon the triple 'periodicity-shape-contrast'. We do so by means of the following.

Proposition 4.4. Let $\alpha$, $\Omega$ be as in (3). Let $j \in \{1, \ldots, n\}$. Then the following statements hold.

(i) For each $(q, \phi, \gamma) \in \mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times [-1, 1]$, there exists a unique $\theta_j$ in $C^{0, \alpha}(\partial\Omega)$ such that

and we denote such a function by $\theta_j[q, \phi, \gamma]$.

(ii) There exist $\varepsilon \in ]0, 1[$ and a real analytic map $\Theta_j[\cdot, \cdot, \cdot]$ from

to $C^{0, \alpha}(\partial\Omega)$ such that

Proof. The proof of statement (ⅰ) is a straightforward modification of the proof of Lemma 4.1. Indeed, it suffices to replace $\frac{\lambda^+-\lambda^-}{\lambda^++\lambda^-}$ by $\gamma$ in the proof of Lemma 4.1.

Next we turn to consider statement (ⅱ). As a first step we have to study the regularity of the map $M_j$. The analyticity in the domain of definition of $M_j$ of the second term in the right hand side of (23) follows from Lemma 4.2 (ⅱ). Moreover, the analyticity in the domain of definition of $M_j$ of the third term in the right hand side of (23) follows from Lemma 4.3 (ⅱ) and from the analyticity of the map from $\mathbb{D}_n^+(\mathbb{R}) \times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n)\cap \mathcal{A}^{\widetilde Q}_{\partial\Omega}\right)$ to $C^{1, \alpha}(\partial\Omega, \mathbb{R}^n)\cap \mathcal{A}_{\partial\Omega}$ which takes $(q, \phi)$ to $q\phi$. Accordingly, $M_j$ is real analytic from $\mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times ]-2, 2 [\times C^{0, \alpha}(\partial\Omega)$ to $C^{0, \alpha}(\partial\Omega)$. By standard calculus in normed spaces, for all $(q, \phi, \gamma) \in \mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times [-1, 1]$, the partial differential $\partial_{\theta}M_j[q, \phi, \gamma, \theta_j[q, \phi, \gamma]]$ of $M_j$ at $(q, \phi, \gamma, \theta_j[q, \phi, \gamma])$ with respect to the variable $\theta$ is delivered by

for all $\psi \in C^{0, \alpha}(\partial\Omega)$. By Lemma 3.1 (ⅱ) and by changing the variable as in the proof of Lemma 4.1, we deduce that $\partial_{\theta}M_j[q, \phi, \gamma, \theta_j[q, \phi, \gamma]]$ is a linear homeomorphism from $C^{0, \alpha}(\partial\Omega)$ onto $C^{0, \alpha}(\partial\Omega)$. Accordingly, we can apply the implicit function theorem for real analytic maps in Banach spaces (see, e.g., Deimling [18,Thm. 15.3]), and we deduce the existence of $\varepsilon$ and of $\Theta_j[\cdot, \cdot, \cdot]$ as in the statement.

5.   Analyticity of the effective conductivity

In this section we prove our main result that answers to question (10) on the behavior of the effective conductivity upon the triple 'periodicity-shape-conductivity'. To this aim, we exploit the representation formula in (20) of the effective conductivity and the analyticity result of Proposition 4.4.

Theorem 5.1. Let $\alpha$, $\Omega$ be as in (3). Let $i, j \in \{1, \ldots, n\}$. Let $\varepsilon$ be as in Proposition 4.4. Then there exists a real analytic map $\Lambda_{ij}$ from the space $\mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times ]-1-\varepsilon, 1+\varepsilon[$ to $\mathbb{R}$ such that

for all $(q, \phi, (\lambda^+, \lambda^-))\in \mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times [0, +\infty [^2_\ast$.

Proof. Let $\varepsilon \in ]0, +\infty[$ and $\Theta_j[\cdot, \cdot, \cdot]$ be as in Proposition 4.4. Then, we set $\Lambda_{ij}$ to be the map from the space $\mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times ]-1-\varepsilon, 1+\varepsilon[$ to $\mathbb{R}$ defined by

for all $(q, \phi, \gamma) \in \mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times ]-1-\varepsilon, 1+\varepsilon[$. By formula (20) for the effective conductivity, by Proposition 4.4, by Lemma 4.1 and by Theorem 3.2, the only thing that remains in order to complete the proof is to show that the map $\Lambda_{ij}$ is real analytic. Lemma 4.3 implies that

for all $(q, \phi, \gamma) \in \mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times ]-1-\varepsilon, 1+\varepsilon[$. Since

clearly $|Q|_n$ depends analytically on $q \in \mathbb{D}_n^+(\mathbb{R})$. Moreover, by the divergence theorem and by Lemma 4.3

Then, by taking into account that the pointwise product in Schauder spaces is bilinear and continuous, and that the integral in Schauder spaces is linear and continuous, Lemma 4.3 implies that the map from $\mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)$ to $\mathbb{R}$ which takes $(q, \phi)$ to $|q\mathbb{I}[\phi]|_{n}$ is real analytic. Now, by Proposition 4.4, by Lemma 4.2 (ⅰ), by Lemma 4.3, together again with the above considerations, we can conclude that the map $\Lambda_{ij}$ is real analytic from $\mathbb{D}_n^+(\mathbb{R})\times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right)\times ]-1-\varepsilon, 1+\varepsilon[$ to $\mathbb{R}$ and accordingly the statement holds.

6.   Conclusions

In the present paper we considered the effective conductivity of a two or three dimensional periodic two-phase composite material. The composite is obtained by introducing into a homogeneous matrix a periodic set of inclusions of a large class of sufficiently smooth shapes. We proved a regularity result for the effective conductivity of such a composite upon perturbations of the periodicity structure, of the shape of the inclusions, and of the conductivities of each material. Namely, we showed the real analytic dependence of the effective conductivity as a functional acting between suitable Banach spaces.

The consequences of our result are twofold. First, this high regularity result represents a theoretical justification to guarante that differential calculus may be used in order to characterize critical periodicity-shape-conductivity triples $(q, \phi, (\lambda^+, \lambda^-))$ as a first step to find optimal configurations, under specific constraints for the triple $(q, \phi, (\lambda^+, \lambda^-))$ (cf. Section 1). Second, if $\delta_0>0$ and we have a family $\{(q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta))\}_{\delta \in ]-\delta_0, \delta_0[}$ in $\mathbb{D}_n^+(\mathbb{R}) \times \left(C^{1, \alpha}(\partial\Omega, \mathbb{R}^n) \cap {\mathcal{A}}_{\partial\Omega}^{\widetilde{Q}}\right) \times [0, +\infty [^2_\ast$ such that the map $\delta \mapsto (q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta))$ is real analytic, then we can deduce the possibility to expand $\lambda^{\mathrm{eff}}_{ij}[q_\delta, \phi_\delta, (\lambda^+_\delta, \lambda^-_\delta)]$ as a power series in $\delta$, i.e.,

for $\delta$ close to zero. Our result implies the possibility of an expansion of this type; then one can apply the method developed in [17] to determine the coefficients $\{c_j\}_{j\in\mathbb{N}}$, by computing the differentials of $\lambda^{\mathrm{eff}}_{ij}$.

Acknowledgments

Both the authors are members of the 'Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni' (GNAMPA) of the 'Istituto Nazionale di Alta Matematica' (INdAM) and acknowledge the support of the Project BIRD191739/19 'Sensitivity analysis of partial differential equations in the mathematical theory of electromagnetism' of the University of Padova. P.M. acknowledges the support of the grant 'Challenges in Asymptotic and Shape Analysis - CASA' of the Ca' Foscari University of Venice. The authors wish to thank the anonymous referees for many valuable comments that have improved the presentation of the paper.