1.
Introduction
Granular computing (GrC) is a procedure that throws light on complicated problems using different granular structures. This concept is utilized in various fields, including interval analysis, artificial intelligence, quantization, cluster analysis and fuzzy set theory. The subject of GrC was first introduced by Lin [1] and it involves the idea of classes, groups or collection of elements having similar properties, which are called granules. Broadly speaking, granulation decomposes the whole universe into parts, or more generally, into granules. Thereby the basic purpose of GrC is the construction of granules and their manipulation through mathematical computations. The formation of granules includes the details of their representation and interpretation, whereas their mathematical computations allow us to make practical use of these granular structures in problem solving. In particular, elements having some similarity, or related by indiscernibility or indistinguishability, are grouped together in a granule. It is mandatory to illustrate the criteria for keeping more than one element in the same group while constructing a granule. The idea of GrC exploits some useful structures, namely, the granular structures which are characterized by multi-levels. A granular structure consists of different integrated levels with different granularities.
1.1. Related work
In this subsection, we review some remarkable works in the field of GrC and present the advantages and limitations of each method. As said above, granular computing was commenced by Lin [1]. It gradually achieved the interest of many researchers owing to its remarkable applications coupled with theoretical appeal. On the account of the efforts of numerous scholars, more concrete and efficient models of GrC have been presented. Hierarchical granular structures are developed to provide a multi-view representation of the problem. Yao and Zhong [2] suggested that information tables can generate a simple and more physical framework of granular computing. They proposed a model where every element of the universal set was described through a finite collection of attributes. The fundamental principles and basic issues of granulation were examined by Yao [3]. He discussed the formation, description, and representation of granules from algorithmic as well as semantic perspectives, and proposed a partition model of granular computing using set-theoretic notions. Yao and Yao [4] reconstructed the classification and consistent problems in granular computing frameworks of data mining. They defined certain novel concepts to suggest a more generalized tool for classification. The same authors presented the classification problems in the view of granular computing [5]. They discussed the ID3 and PRISM algorithms and generalized them to granular computing. Chiaselotti et al. [6] studied the lattice of all indiscernibility partitions induced from the collection of attributes of information tables. They named the corresponding lattice as "granulation partition lattice" and provided several isomorphic properties for this lattice. Wong and Wu [7] introduced an algorithm for automated mining of granular database schemes. Certain models of granular computing (such as micro and macro models using the equivalence and indiscernibility relations) were proposed by Bisi et al. [8].
Graph theory is a most effective framework in order to analyze the elements that are linked in a network [9]. The study of pairwise relations between objects is very useful in mathematical structures. Stell [10] first studied the design of granular structures with simple graphs. He investigated various types of granulation for simple crisp graphs, as well as the relation of vague graphs and granulations. Two graph embedded models were proposed by Bianchi et al. [11] that were based on the principles of granular computing. They conducted tests relying on synthetic as well as real data to obtain competitive results. Chen and Zhong [12] studied the granulation of simple graphs and introduced the extraction of granular structures using graphs. They focused on multiview understanding of problems through granules. The same authors also studied three models of granulation corresponding to three types of elements in a graph [13]. Chiaselotti et al. [14] studied the correspondence between the information tables and the adjacency matrices of simple graphs. They introduced novel concepts such as topological descriptions of graphs and extended core. Chen et al. [15] proposed a hypergraph model describing granular structures by representing an element through a vertex and a hyperedge corresponding to a granule. In their model a family of granules was presented through a hypergraph, and a set of hypergraphs was utilized to represent the hierarchical structures. Stell [16] discussed the relational granularity of hypergraphs, plus applications of those relations to the theory of granularity.
Zadeh [17,18] pioneered the research on information granulation using fuzzy sets. In his model, fuzzy sets and fuzzy graphs capture the relationships between granules, groups or clusters. Fuzzy information granulation improves the understanding of indeterminate or uncertain behaviors of granules. Yang et al. [19] studied a hypergraph clustering model that was based on fuzzy frequent item sets, and with this tool they evaluated the quality of agricultural land. Wang and Gong [20] proposed an application of fuzzy hypergraphs in granular computing. The same authors also discussed the fuzzy classification through the equivalence relation between fuzzy hypergraphs, fuzzy information systems, and fuzzy formal concept lattices [21]. Singh et al. [22] proposed a model to generate the interval-valued fuzzy formal concepts. They utilized the Shannon entropy method to measure the weights of fuzzy concepts. ˇSeˇselja and Tepavˇseviˊc [23] established the links among reflexive, transitive, and antisymmetric lattice valued fuzzy relations. Pedrycz et al. [24] introduced the granulation of the membership function of fuzzy sets. They formulated the concepts of consistency of granular structures. Akram et al. [25] proposed two modified techniques, named as Pythagorean fuzzy hybrid TOPSIS and ELECTRE I methods, to measure the risk rankings in FMEA (failure modes and effects analysis). Luqman et al. [26] proposed the digraph and matrix approach for risk evaluation under Pythagorean fuzzy information. They studied the example of a steam valve system for the description of the proposed model. Akram et al. [27] set up the foundations for a novel concept, the complex spherical fuzzy model, to express the two-dimensional uncertain information.
From another perspective, Pawlak's [28,29] rough sets deal with the approximate features of granulation information more effectively. An extended technique of pattern matching for classification through fuzzy analytical hierarchy procedures was proposed by Kaur and Kumar [30]. William-West and Singh [31] provided an extended model to formulate the approximations of rough sets for information granulation. They developed generalized operators to account for various combinations of data and knowledge in granules. Yao [32] examined the granular structures using rough set theory and reviewed the corresponding structures of approximations. He also studied the structures of approximations and hierarchical granulation. The same author [33] proposed the formation of two granular structures, i.e., the classification induced by an equivalence relation and the covering constructed through the reflexive relation. He established a strong foundation for rough sets and provided a systematic method to determine the parameters which are required in defining approximation operators. Moreover, Luqman et al. [34] defined m−polar fuzzy hierarchical quotient space structures through the series of level hypergraphs. The same authors defined the q−rung picture fuzzy hypergraphs and illustrated the construction of granular structures through level hypergraphs [35]. They also presented a numerical example and a comparative analysis to guarantee the validity of their model. Akram et al. [36] applied the combined theories of rough fuzzy sets and rough fuzzy digraphs for the extraction of granular structures. Further, they discussed the granulation of social networks using rough fuzzy digraphs. The extraction of granular structures using fuzzy soft graphs was presented by Akram and Luqman [37]. They proposed two degree based models for the abstraction of granular structures and granulated the various relations between different species in ecological systems.
To summarize, a brief comparison of previous research works is presented in Table 1.
1.2. Motivation and contribution
In this research article, fuzzy models of granular computing based on fuzzy relation and fuzzy indiscernibility relation are presented. We are motivated by the belief that fuzzy information granulation yields a better setting for the investigation of uncertain or indeterminate behaviors of granules. The main goal of the research presented in this article is to formulate the granular structure associated with any information table on the set of all the indiscernibility partitions under fuzzy information. The formation of granules or granular structures, and the representation of their relationships through fuzzy set theory, produce an effective mathematical framework for the discussion of multilevels of granularity. Moreover, this approach happens to produce a nice connection between the modelization of granular structures and fuzzy graph theory. It is efficient to represent the granulation of networks and hypernetworks with the help of fuzzy information, and it is an effective method for the representation of granules using hybrid models of fuzzy theory. In this way, the applicability and effectiveness of granular structures is enhanced through fuzzy information tables. Another important inspiration for the proposed study is the construction of different granulation levels considering different procedures of granulation.
To summarize, the main goals of our research work are as follows:
1. To build a lattice structure for any information table on the set of all the indiscernibility partitions under a fuzzy environment.
2. To construct fuzzy indistinguishability granules based on fuzzy indistinguishability relations in order to describe the micro granular inclusions between the members of fuzzy equivalence classes.
3. To enhance the applicability and effectiveness of granular structures through fuzzy information tables.
4. To construct different granulation levels considering different procedures of granulation, for example, the fact that distinct levels might possess different granularities.
Fuzzy graphs amalgamate the advantages of fuzzy sets with crisp graphs in a way that achieves the multi visualization of granularities. By applying fuzzy sets to develop granular structures, the multilevels of granularity can be obtained. Thus certain families of granular structures sharing some imprecise relations between them can be constructed by virtue of the flexible model of fuzzy graphs. The hybrid models of GrC proposed in this study are more practical and applicable for the granulation of network models having vagueness and impreciseness. Indiscernible relations can be determined more effectively through the representation of information tables in the form of the adjacency matrices of fuzzy graphs.
The main contributions of this article are as follows:
1. We extend the use of information tables in granular structures to fuzzy information tables.
2. We construct certain models, i.e., micro, macro, reduct, etc, of granular structures using fuzzy indistinguishability relations.
3. We extend the formation of granules using simple graphs, to the formation of granules under fuzzy graphs.
4. We elaborate the construction of the model developed in this paper with the assistance of an algorithm, and then this algorithm is related to a real life application.
This paper is organized in six sections. In Section 2, some preliminary ideas of fuzzy sets and fuzzy relations are reviewed. Certain basic concepts which are useful for further consideration, including fuzzy partition lattice, fuzzy meet and fuzzy join, are defined. Section 3 deals with a fuzzy indiscernibility and fuzzy knowledge representation system I. We define the fuzzy indiscernibility relation, and various indiscernibility structures induced by this relation. In the same section we also define the fuzzy discernibility hypergraph, fuzzy reduct as well as core hypergraph and fuzzy essential hypergraph. We explain the role of these structures in GrC through some concrete examples. In Section 4, we develop granular structures based on fuzzy graphs. Fuzzy levels and fuzzy granules are defined and a degree based model of granulation using fuzzy graphs is constructed. We discuss the granularities for different values of the parameter belonging to the unit closed interval [0,1], and concluded that decreasing values of this parameter lead to finer granularities. The construction of this model is illustrated with an algorithm, and this algorithm is then applied to a real life case study. In Section 5, we present a comprehensive comparative analysis of our models with existing techniques. The last section gives some concluding remarks and discusses future research directions.
2.
Review of fuzzy concepts
Definition 2.1. [9] A hypergraph is a pair H = (U,E), where U={u1,u2,⋯,un} is a finite set and E={Y1,Y2,⋯,Ym} is a non-empty family of subsets of U. The elements u1,⋯,un are the vertices of H and Y1,⋯,Ym are called hyperedges of H.
Definition 2.2. [23] A partially ordered set (poset) is defined as a pair P = (U,≤), where ≤ is reflexive, antisymmetric and transitive relation on U.
Let P = (U,≤) and L = (U,∧,∨) be a poset and a complete lattice, respectively, then a fuzzy poset is defined as a fuzzy set μ:P→L corresponding to the given crisp relation ≤.
Definition 2.3. [40,41] A fuzzy set μ on a non-empty set U is a mapping μ:U→[0,1]. A fuzzy relation λ is a fuzzy set on U×U.
Let μ and λ be fuzzy sets on U and U×U, respectively, such that λ(uw)≤min{μ(u),μ(w)}, for all u,w∈U, then λ is a fuzzy relation on U.
Definition 2.4. [42] Let U be a finite universal set and λ be a fuzzy relation on U. λ is called a fuzzy equivalence relation on U, if:
(i) λ is reflexive, i.e., λ(u,u) = 1,
(ii) λ is symmetric, i.e., λ(u,w) = λ(w,u),
(iii) λ is transitive, i.e., λ(u,v) = supw∈Uinf{λ(u,w),λ(w,v)}, for u,v,w∈U.
Definition 2.5. [43] A fuzzy hypergraph on U is a pair H=(A,B), where A={A1,A2,⋯,Ak} are fuzzy subsets of U such that ⋃supp(Ai)=U and B is a fuzzy relation on Ai such that B(Ei)≤min{Ai(u1),Ai(u2),⋯,Ai(ul)}, i=1,2,⋯,k.
Definition 2.6. A collection of non-trivial fuzzy subsets S={P1,P2,⋯,Pk} of U is called a fuzzy partition if it satisfies:
(i) ⋃isupp(Pi)=U,
(ii) ⋂isupp(Pi)=∅,
(iii) Σki=1μPi(u)=1, for all u∈U.
Note that, supp(Pi)={u|μPi(u)>0}.
Definition 2.7. Let u∈U, then the cover set of u, denoted by [u|→P], is defined as the collection of elements of U such that [u|→P]={v∈U|μ(u)<μ(v)}.
The co-covers of u, denoted by [u|←P], are defined as the collection of elements of U such that [u|←P]={z∈U|μ(z)>μ(u)}.
Definition 2.8. Let S={Pi|i∈N} be a fuzzy partition of U, where {Pi|i∈N} denotes the block family of S. Then, S(w) represents that fuzzy block of P in which the element w is contained.
If W⊆U and W⊆Pi, for some i, then W is a fuzzy sub-block.
If U is a finite set of universe, then S=P1|P2|⋯|P|S|, where the number of distinct fuzzy blocks of S are denoted by |S|. The set S(U) represents all the fuzzy partitions of U. A partial order relation ≤ can be defined on the set of fuzzy partitions S(U) of U as: if S1,S2∈S(U), then S1≤S2⇔ for all P1i∈S1, there exists P2j∈S1, such that P1i⊆P2j.
The pair FP(U)=(S(U),≤) is called the fuzzy partition lattice of U.
Definition 2.9. Let S1=P1|P2|⋯|Pr and S2=P1|P2|⋯|Ps be two fuzzy partitions of U. A collection of fuzzy subsets B on U can be settled as π(S1,S2)={B⊆U,ifu∈B,thenS1(u)⊆BandS2(u)⊆B}. The membership degrees of elements of π(S1,S2) are defined as:
The fuzzy join of S1 and S2, denoted by S1∧μS2, is defined as S1∧μS2={Pi∩Qj|i=1,2,⋯,randj=1,2,⋯,s}, where Pi and Qj are fuzzy blocks of S1 and S2, respectively.
Note that,
The fuzzy meet of S1 and S2, denoted by S1∨μS2, is defined as S1∨μS2={Pi∪Qj|i=1,2,⋯,randj=1,2,⋯,s}, where Pi and Qj are fuzzy blocks of S1 and S2, respectively.
Here,
A more generic way to describe the fuzzy join of S1 and S2 is as follows: S1∧μS2=B1|B2|⋯|Bl, where B1,B2,⋯,Bl are the minimal elements of π(S1,S2).
3.
Fuzzy information system
Definition 3.1. [42] A knowledge representation system is given as I=(U,˜A,g,Val), i.e., a mathematical structure, where U is non trivial set, ˜A={ai|i∈N} is a collection of attributes and ai:U→Val. The information mapping g:UטA→Val of I is given as g(u,ai)=ai(u).
A fuzzy knowledge representation system or fuzzy information system, in case of finite set, is a structure I=(U, A, ϕ, [0,1]), where A is the collection of fuzzy attributes and ϕk(u,ak)=μk(u)∈Valk.
Definition 3.2. Let I=(U,A,ϕ,[0,1]) be a fuzzy information system and A1⊆A. Then, ≡A1 on U, i.e., a binary relation, is defined as: if u,w∈U then u≡A1w⇔ϕk(u,ak)=ϕk(w,ak), i.e., μk(u)=μk(w), for all ak∈A1. The degrees of this binary relation are inclined as:
(i) λ≡A1(u,u) = 1, for all u∈U,
(ii) λ≡A1(u,w)=λ≡A1(w,u), for u,w∈U,
(iii) λ≡A1(u,v)=supw∈Uinf{λ≡A1(u,w),λ≡A1(w,v)}, for u,v,w∈U.
Note that, the binary relation ≡A1 is fuzzy equivalence relation and is called a fuzzy A1−indiscernibility relation on I. If z∈U, then the fuzzy equivalence class of z w.r.t ≡A1 is denoted by [z]A1 and S(A1)={[z]A1|z∈U} is defined as the A1-indiscernibility fuzzy partition of I.
Although, the fuzzy relation and fuzzy indiscernibility relation have been discussed by many researchers. The Novelty of the proposed work is that we have discussed the fuzzy equivalence relation and fuzzy indiscernibility relation as well as these relations have been utilized for the construction of granular structures. That is, fuzzy indiscernibility relation has also been introduced corresponding to a certain subset of attributes and distinct partitions of the universal set are obtained with respect to the different subsets of attributes. In previous researching results, the indiscernibility relations have been discussed considering the crisp information tables. Whereas, the indiscernibility relations have been discussed considering the fuzzy information tables and fuzzy attributes in the proposed work as described through the following example.
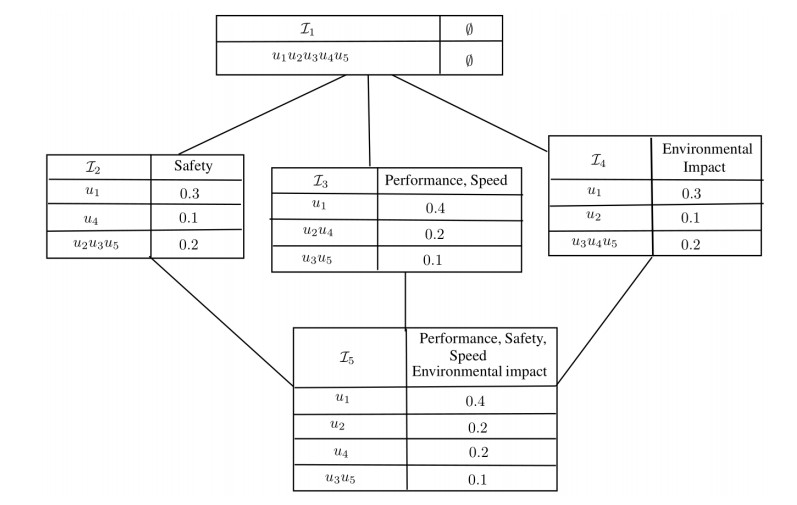
Example 3.1. Let us consider that a person wants to buy a car and has five possible choices, u1,u2,u3,u4,u5. Suppose that he considers the following properties: performance, safety, speed and environmental impact. Thus, the set of attributes be A={a1,a2,a3,a4}. The fuzzy information table I=(U,A,ϕ,[0,1]) is given in Table 2, where U={u1,u2,u3,u4,u5} is the collection of cars and A={a1,a2,a3,a4} is the set of attributes. Note that, a1 represents the performance of the car, a2 shows the safety, a3 determines the speed and a4 finds the environmental impact of corresponding car.
The function ϕk(u,ak)=μk(u)∈Valk indicates that the object u possesses the kth attribute, i.e., ϕ(u1,a1)=0.4 shows that u1 choice fulfills 40% the customer requirement of performance and so on. Then, the fuzzy indiscernibility partition of all cars corresponding to their attributes is given as follows:
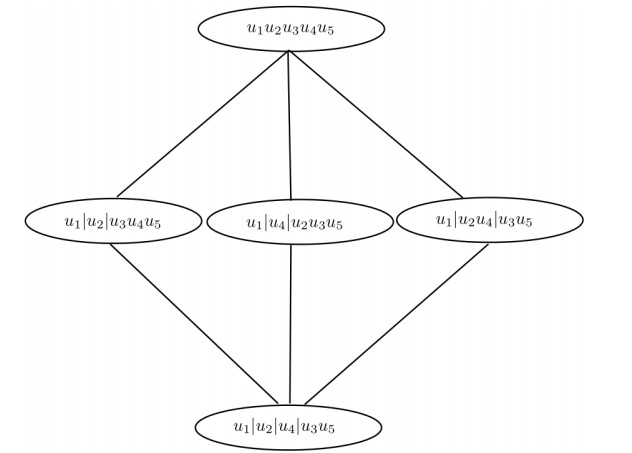
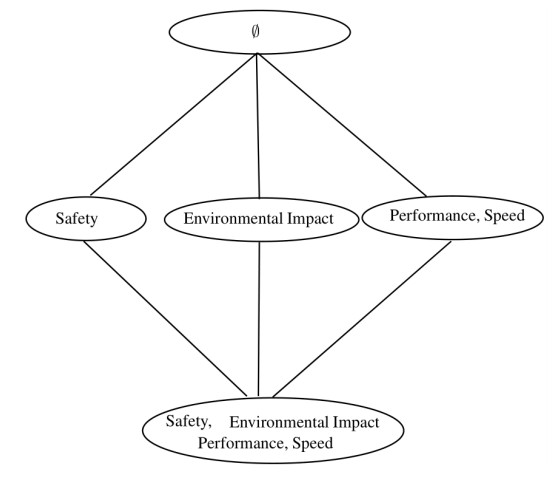
The above fuzzy indiscernibility partitions can induce the fuzzy information sub tables I1, I2, I3, I4 and I5, where UI1={u1u2u3u4u5}, AI1={∅}, UI2={u1,u2u3u5,u4}, AI2 = {Safety}, UI3={u1,u2u4,u3u5}, AI3 = {Performance, Speed}, UI4={u1,u2,u3u4u5}, AI4 = {Environmental impact}, UI5={u1,u2,u4,u3u5}, AI5 = {Performance, Speed, Safety, Environmental impact}. These tables are called fuzzy indiscernibility sub tables of I and are given in Tables 3 and 4, respectively.
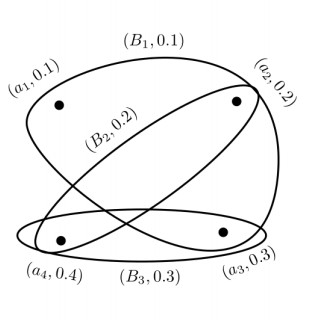
The lattice and complete lattice structures of these fuzzy indiscernibility partitions L(I) are shown in Figures 1 and 2, respectively.
Note that, in all above structures one may lose the information relevant to the value set of I. It is clear that all lattices induce a structure which is order isomorphic O(I) on the set {I1, I2, I3, I4, I5} with the following order:
The order isomorphic lattice structure O(I) of I is shown in Figure 3.
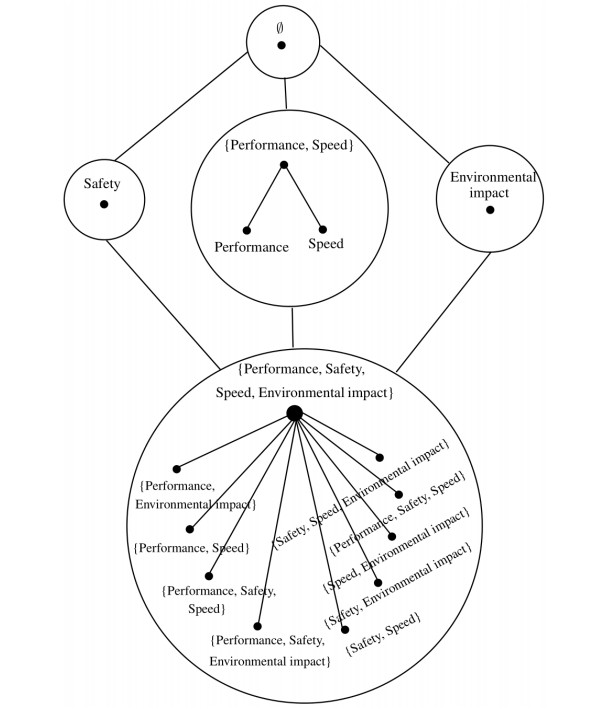
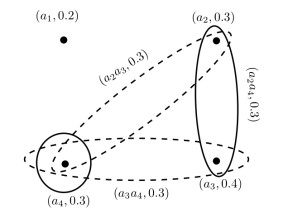
Definition 3.3. Let A1, A2⊆A and S(A1), S(A2) be their fuzzy indiscernibility partitions then we define A1≈A2⇔S(A1)=S(A2). Let [A]≈ be the fuzzy equivalence class of A w.r.t. ≈. Then, ≈ is the fuzzy indistinguishability relation and [A]≈ is the fuzzy indistinguishability granule of I. Furthermore, [A]≈ is considered as a kind of macro granule in which we can also describe the micro granular inclusions between the elements of [A]≈. This lattice is called the fuzzy indistinguishability granular lattice of I and is denoted by Ind(I). A representation of Ind(I) is shown in Figure 4.
We now define certain set operating notions that extends the core concept of discernibility matrix for a fuzzy information system.
Definition 3.4. Let I=(U,A,ϕ,[0,1]) be the fuzzy information system and W⊆U, A1⊆A. A mapping △(W,A1):W×W→P(A1) is defined as follows:
for some u1,u2∈W.
In particular, △A = △(U,A) and △A1 = △(U,A1), then we have △(W,A1)(u1,u2)=△(W,A)(u1,u2)∩A.
Definition 3.5. Let A⊆A and W⊆U. Then, a fuzzy (W,A)−discernibility hypergraph is an ordered pair H=(A,B), where A is the fuzzy vertex set of H and fuzzy hyperedges set B is defined as follows:
for all bk∈Bi and for some u1,u2∈W. The membership degrees of fuzzy vertex set A and fuzzy hyperedge set B are defined as follows:
● A(ai)=min{μi(u1),⋯,μi(uk)},
● B(Bi)=B({a1,⋯,ak})≤min{A(a1),⋯,A(ak)},
● ⋃isupp(μ(ai))=A, for all ai∈A.
In particular, if we have Dis(I)=Dis(U,A) and Dis(A)=Dis(U,A), then D(I)=(A,Dis(I)) is called the fuzzy discernibility hypergraph of I.
Example 3.2. Let I=(U,A,ϕ,[0,1]) be a fuzzy information system as given in Table 5.
Then, the fuzzy discernibility hypergraph H is given in Figure 5.
The fuzzy discernibility based hypergraph has been used to represent the fuzzy information system. There are several examples of social, biological, ecological and technological systems where the use of complex networks gives very limited information about the structure of the system. In such cases, hypergraphs are used to represent these systems by introducing the concept of the complex hyper-network. The hypergraphs that represent a complex system are known as complex hyper-networks. Moreover, if the volume of the data is bigger, then the structure of hypergraph may be complex. To represent the bigger volume of data, it is more convenient to represent a hypergraph by an incidence matrix in which each of the rows is associated with a vertex and each of the columns is associated with a hyper-edge. Thus, any Boolean matrix may be considered as the incidence matrix of a crisp hypergraph. Furthermore, a fuzzy information table is considered as the incidence matrix of a fuzzy discernibility based hypergraph. For instance, the corresponding incidence matrix of fuzzy discernibility hypergraph H as shown in Figure 5 is given in Table 6.
Proposition 3.1. Let Z⊆A1 and u,w∈W, then we have:
(i) Z=△(W,A1)(u,w)⟹u≡A1 Zw,
(ii) u≡A1 Zw⟹△(W,A1)(u,w)⊆Z,
(iii) for D⊆A1, △(W,A1)(u,w)∩D=∅⟺u≡Dw.
Proof. (i) Let Z=△(W,A1)(u,w) and assume that a1∈A1∖Z. Then, the definition of △(W,A1)(u,w) implies that μ(a1,u)≠μ(a1,w). Thus, u≡A1∖Zw.
(ii) Let u≡A1∖Zw and a1∈A1∖Z. The definition of ≡A1∖Z implies that ϕ(a1,u)=ϕ(a1,u), i.e., μ(a1,u)=μ(a1,w), so a1∉△(W,A1)(u,w). It follows that A1∖Z⊆A1∖△(W,A1)(u,w) and △(W,A1)(u,w)⊆Z.
(iii) Let D⊆A1. Assume that △(W,A1)(u,w)∩D=∅ and let d∈D, then d∉△(W,A1)(u,w) implies that ϕ(u,d)=ϕ(w,d). This shows that u≡Dw. We now suppose that u≡Dw, then the definition of ≡D implies that △(W,A1)(u,w)∩D=∅. Hence, the proposition is proved.
Definition 3.6. Let A⊆A. An element a∈A is called a fuzzy indispensable if S(A)≠S(A∖a). The collection of all attributes of A that are fuzzy indispensable is known as the fuzzy core set of A, signified by Cor(A). In particular, we have Cor(A)=Cor(I).
Definition 3.7. A fuzzy reduct of A is defined as a subset D⊆A, if it satisfies:
● S(A)=S(D),
● S(A)≠S(B), for all B⫋D.
The family of all fuzzy reducts of A is given as Red(A) and Red(A)=Red(I).
A fuzzy reduct hypergraph of A is an ordered pair R(A)=(A,Red(A)) and R(A)=(A, Red(A))=R(I) is the fuzzy reduct hypergraph of I.
Definition 3.8. Let A⊆A. A subset A1⊆A is said to be A−essential, if it satisfies:
● S(A∖A1)≠S(A),
● S(A∖C)=S(A), for all C⫋A1.
The collection of all A−essential subsets of A is identified by Ess(A). The essential hypergraph of A is an ordered pair E(A)=(A,Ess(A)). In particular, E(A)=E(I).
Remark 3.1. (i) Ess(A)=minDis(A).
(ii) Tr(Dis(A))=Tr(Ess(A)).
(iii) D(I), R(I) and E(I) are called the indiscernibility structures of I.
In order to better illustrate the all above defined concepts, we consider the following example.
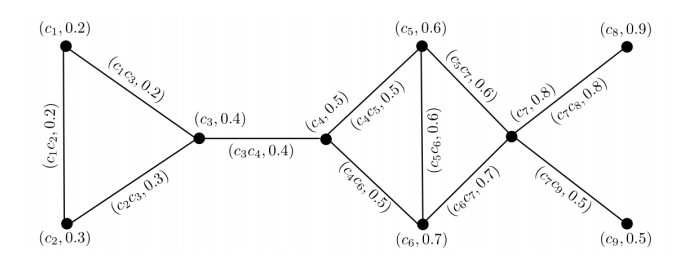
Example 3.3. Assume that a person wants to purchase a laptop. He is considering the following attributes: Memory, RAM, Battery life and Portability. He can select between five models u1,u2,u3,u4 and u5. Thus, the occurring situation can be modeled through fuzzy information table as given in Table 7.
Note that, U={u1,u2,u3,u4,u5} is the collection of considered laptops and A={a1,a2,a3,a4} is the family of characteristics or attributes. The discernibility matrix △(I) of I is given in Table 8.
Hence, we have
The fuzzy reduct R(I) and fuzzy essential E(I) hypergraphs of I are shown by dashed lines and simple lines, respectively, in Figure 6.
Let us suppose that A1={a1,a2,a3}. The discernibility matrix △A1 of I restricted to A1 is given in Table 9.
Note that, Dis(A1)={(a1,0.2),(a2a3,0.4),(a1a2a3,0.6)}, Ess(A1)={(a1,0.2),(a2a3,0.4)}, Red(A1)={(a1a3,0.4),(a1a2,0.4)} and Cor(A1)={(a1,0.2)}.
This shows that the subsets of attributes {a1,a3} and {a1,a2} give the same information as provided by {a1,a2,a3}. More generally, by considering {a1,a2}, the attribute a3 is not considered to distinguish two laptop models. The procedure of above discussed example is illustrated through Algorithm 1.
The indiscernibility structure and the granular structure both are formed by the consequence of the information granulation. Here, the term "indiscernibility structure" is utilized to describe those structures that are obtained through fuzzy indiscernibility relation, including fuzzy reducts, fuzzy core set, essential subsets, etc. On the other hand, the term "granular structures" is used in case of granulation of fuzzy graphs. That is, both structures are the results of information granulation of universal set and information granulation of fuzzy graphs, respectively.
4.
Granular structures under fuzzy graphs
Definition 4.1. [44] A fuzzy graph is defined as an algebraic structure FG=(U,α,β) of non trivial universe U along with a pair of mappings α:U→[0,1] and β:U×U→[0,1] such that β(u,v)≤min{α(u),α(v)}, for all u,v∈U.
Here, α is called the fuzzy set of vertices and β is called the fuzzy set of edges of FG.
Definition 4.2. Let FG=(U,α,β) be a fuzzy graph. A fuzzy granule αi is given as a fuzzy subset αi⊆α of fuzzy vertex set α, i.e, αi(u)≤α(u), for all u∈U.
The power set 2|U| contains all possible fuzzy granules of U.
A partial ordering is defined on 2|U| by using the set inclusion relation ⊆, which determines the sub-super relationships between granules.
Definition 4.3. Let α1⊆α2, i.e., α1(w)≤α2(w), for all w∈U, then α1 is called the fuzzy sub granule of α2 and α2 is known as the fuzzy super granule of α1.
A granule may be a part of another granule and is considered to be a component to construct another granule. It may also be a family of granules and may be considered as a single granule. Under the set inclusion relation ⊆, ∅ is the smallest possible granule and α(U) is known as the largest granule.
Definition 4.4. A fuzzy level is a fuzzy graph FG=(U,α,β), whose all vertices are granulated, i.e., when all the vertices of a fuzzy graph are integrated to granules then the process of granulation is completed and the fuzzy graph is granulated to a fuzzy level.
Different granulation levels can be constructed by considering different procedures of granulation. Every distinct level may possess a different granularity.
Definition 4.5. Let L1 and L2 be two fuzzy levels. If for each fuzzy granule α1i in L1, there exists a fuzzy super granule α2j in L2 such that α1i⊆α2j. Then, we say that L1 owns the finer granularity than L2. Equivalently, L2 owns the coarser granularity than L1.
The concrete view of the problem is represented by the finer level and that of abstract view through the coarser level. These levels can be interchanged by using the transformations or mappings between the concrete and abstract representations.
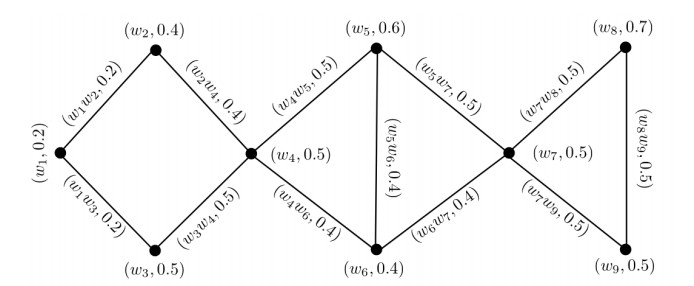
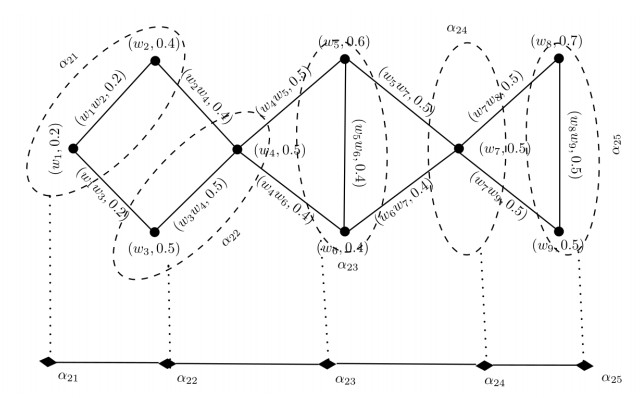
Example 4.1. Let FG=(U,α,β) be a fuzzy graph, where U={w1,w2,w3,w4,w5,w6,w7,w8,w9}, α is a fuzzy set and β is a fuzzy relation on U. The corresponding fuzzy graph is shown in Figure 7.
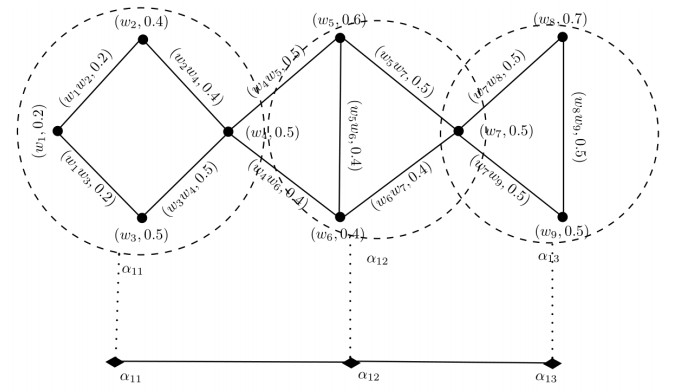
The coarser granulation of this fuzzy graph is shown in Figure 8. Note that, the fuzzy graph is granulated in three fuzzy granules α11, α12 and α13 in this level, where
The finer granulation of the above shown fuzzy graph is shown in Figure 9. Note that, the fuzzy graph is granulated in five fuzzy granules α21, α22, α23, α24 and α25 in this level, where
The distribution of vertices and the structure of a fuzzy graph can be visualized clearly through granulated fuzzy graphs.
Definition 4.6. Let G∗ be a non-empty family of fuzzy granules of some level, i.e., G∗⊆2|U|. A granular structure is defined as the poset (G∗,⊆), where ⊆ is considered as the set inclusion operator.
By considering the partial order relation ⊆, a hierarchical structure can be constructed through the integration of distinct levels. Each distinct level owns a different granularity and various descriptions of a fuzzy graph can be represented using these distinct levels. These granularities can be switched among different levels using specific mappings and functions.
Definition 4.7. Let L1 and L2 be two fuzzy levels of a granular structure. By considering the set inclusion relation ⊆, a mapping σ:L1→L2 maps a granule of L1 to a granule in L2, i.e., σ(α1i)=α2j⟺α2j⊆α1i.
A mapping σ−1:L2→L1 maps a granule of L2 to a granule in L1, i.e., σ−1(α2i)=α1j⟺α2i⊆α1j.
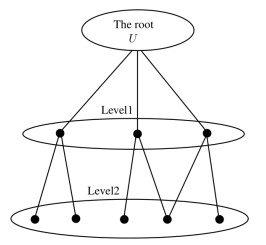
Example 4.2. Consider a fuzzy graph FG=(U,α,β) as shown in Figure 7. The whole universe is assumed as the root. Then, the granular structure of this fuzzy graph, as shown in Figure 10, integrates three levels of FG=(U,α,β).
We divide the root into three granularities and then further subdivide into five granularities. This formation can be visualized as a consecutive bottom-up or top-down analysis of the universe according to the mappings.
We now discuss degree based model of fuzzy granular structures.
Definition 4.8. [45] The degree of a fuzzy vertex u in FG is defined as the sum of membership degrees of all fuzzy edges incident to u, i.e., deg(u)=∑u≠vβ(uv), for all uv∈β.
Definition 4.9. Let FG=(U,α,β) be a connected fuzzy graph. The length l(P) of a path P(u,w)=u,β1,u1,⋯,βn−1,w, from u to w, is defined as the sum of membership degrees of arcs βi in P.
The distance between two vertices u and w is defined as the minimum length of paths between u and w, i.e., dis(u,w)=min{l(Pi)|Pi∈P}.
Definition 4.10. The central vertex or center of a fuzzy granule, denoted by cent(αi), is defined as the vertex having maximum degree among all the vertices of this granule.
Definition 4.11. The distance between two fuzzy granules is defined as the distance between their central vertices, i.e., dis(α1,α2)=dis(cent(α1),cent(α2)).
The procedure to construct the degree based model of fuzzy granular structures is explained in Algorithm 2.
By following the Algorithm 2, we get a new graph, which is considered as the summary of the original graph. A real life application of the degree based model of fuzzy granules is illustrated in Section 4.1.
4.1. Application
Granular computing can be used to build an effective mathematical model to handle the large amount of information or data. The whole universe is divided into granules or granular structures and the complicated computations are then simplified. By applying fuzzy graph theory to granular computing, we can overcome the problems of uncertain relation among the elements of universe or between the granules. In this section, we illustrate that how a degree based model of fuzzy granules can be applied to real World problems.
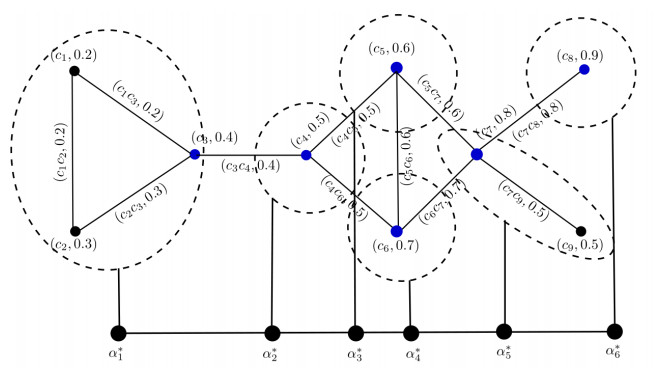
Consider a fuzzy graph FG=(U,α,β), where U={c1,c2,c3,⋯,c9} is the set of universe, α is the fuzzy set and β is the fuzzy relation on U, respectively. The set U indicates the different companies that want to join some business association. The fuzzy membership degrees of vertices describe the positive impacts of corresponding company. These companies are linked together through edges of FG. The membership degree of each edge describes the strength of relationship between the corresponding vertices. A fuzzy graph FG=(U,α,β) depicting the graphical view of these companies is shown in Figure 11.
Step 1: Now, to find the central elements of above graph, we calculate the degree of all the vertices. By direct calculations, we have the degrees of all vertices as given in Table 12.
Step 2: Here, we fix a parameter θ∈[0,1], such that the vertices having the degrees greater that θ will be the central vertices of the graph. Let θ=1.0, then it can be noted clearly from Table 12 that c5, c6 and c7 are the central vertices. These vertices are considered as the centers of three fuzzy granules.
Step 3: To group the vertices into a fuzzy granule, we calculate the distances of all vertices, except of centers, from he central vertices. The corresponding distances are given in Table 13.
Step 4: The vertices having minimum distances form centers are grouped into one fuzzy granule. From Table 13, it can be seen that
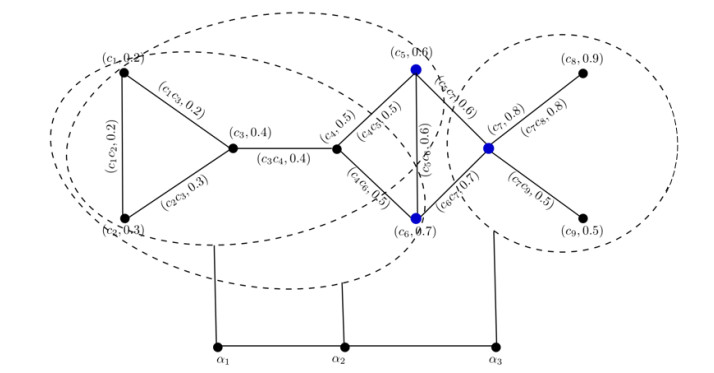
Note that, cent(α1)=c5, cent(α2)=c6 and cent(α3)=c7. These central vertices represent those companies, which have most powerful positive impacts to business networks as compared to other companies. The fuzzy granules represent the business associations and the vertices contained in these granules show the companies, which become the part of that association. The degree based constructed model of FG is shown in Figure 12.
Here, the colored vertices represent the central elements or centers of the granules and dashed lines represent the granules α1, α2 and α3. These granules are the business associations or networks that will consider the companies contained in them. The central vertex of a network represents the strongest member of that network as it tightly close the other members of that network. These associations possess different attributes and objectives and are connected to each other to enhance their business activities. These linked networks can also share their ideas, members and goals for more profits and benefits.
Construction of another level: We now change the value of parameter θ to construct another level of granular structures. Let θ=0.5, then Table 12 shows that c3, c4, c5, c6, c7 and c8 are the central vertices. These vertices are considered as the centers of six fuzzy granules.
To group the vertices into a fuzzy granule, we calculate the distances of all vertices, except of centers, from he central vertices. The corresponding distances are given in Table 14.
The vertices having minimum distances form centers are grouped into one fuzzy granule. From Table 14, it can be seen that
Note that, cent(α∗1)=c3, cent(α∗2)=c4, cent(α∗3)=c5, cent(α∗4)=c6, cent(α∗5)=c7 and cent(α∗6)=c8. These central vertices represent those companies, which have most powerful positive impacts to business networks as compared to other companies. The degree based constructed model of FG at this level is given in Figure 13.
The Figure 13 shows that by changing the value of parameter θ∈[0,1], we can construct different levels having distinct granularities. Note that, when the value of parameter θ is decreased, we obtain a finer level of granularity. Thus, by taking the decreasing values of parameters, we move towards the finer granularities of our model. Every distinct level is then mapped to the upcoming level through mappings σ or σ−1. In this way, we obtain a hierarchical structure, which gives the better understanding of our problem. Thus, a huge amount of uncertain data can be easily manipulated through degree based models of fuzzy granular structures.
5.
Comparative analysis with existing techniques
Here, we demonstrate the advantages of formation of granular structures or granules using fuzzy graphs. Bisi et al. [8] studied the mathematical structures of indistinguishability relation based on crisp information tables. Here, we discuss the applicability of our proposed models through an example. Suppose that a person wants to buy a car and avails four choices, a1,a2,a3,a4. To meet his requirements, he considers the following characteristics: color, speed and roadH. The information table corresponding to above data is given in Table 15.
In this case, the indiscernibility partitions are formed considering the crisp attributes. In many real life situations, crisp partitions may not provide complete information about attributes. That is, crisp information granulation does not reflect those phenomena of concept formation and human reasoning in which the fuzzy granules or fuzzy attributes appear. For example, the attribute "color" is fuzzy in the sense that the "Green" color does not have sharp boundaries, i.e., it may have different shades such as dark green, light green, parrot green, etc. In such cases, to represent information using crisp tables may not be appropriate and may lack some knowledge. To handle such type of shortcomings of crisp information tables, we present the construction of granules or granular structures considering fuzzy information tables. The information table given in 15 can be described in terms of fuzzy information as given in Table 16.
Table 16 shows that a1 choice fulfils 50% the speed requirements, 60% the color requirements and 50% the roadH specifications of the purchaser. similarly, the remaining choices can be evaluated according to their fuzzy values. Thus, the relationships between clusters, groups or granules are presented using FSs and FGs in fuzzy granulation and this granulation provides a better way of studying the uncertain or indeterminate behaviors of granules.
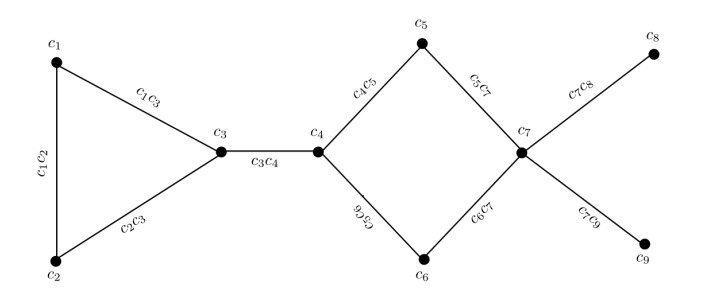
On the other hand, Chen and Zhong [12] combined the notions of granules and graphs. They studied the granulation of a crisp graph and extraction of the granular structures in graphs. In the proposed model, we studied the extraction of the granular structures using fuzzy graphs to handle the uncertainties in graphical representations. The graphical representation of the problem given in Application 4.1 using crisp graph is shown in Figure 14.
Note that, the crisp model just depicts the relations between companies but fails to illustrate the strength of relationships among them or the impacts of companies on each other. The granular structures extracted from this graph cannot deal with uncertain information. Whereas, the fuzzy graph model as given in Figure 11 fully explains the strength of relations as well as the positive impacts of companies to be the part of certain business associations. Based upon above discussion, we conclude that the proposed granulation has the following advantages:
1. The visual representation of the fuzzy graph provides a better way of problem solving using fuzzy granules.
2. The multi levels and multi views of granular structures having uncertainties are examined through fuzzy graphs.
3. We can obtain a well explained understanding of a fuzzy graph by granular structures.
4. Fuzzy information tables provide more accurate and effective description of granules or attributes occurring in human reasoning problems.
5. It is more applicable and practical to consider fuzzy granules in modeling of real life situations rather than the crisp granules.
6. Fuzzy information granulation provides a better way of studying the uncertain or indeterminate behaviors of granules.
To be more precise, we have established new formal properties of the hypergraph. Furthermore, the family of maximum partitions enables us to define several new attribute subset families, that we called indiscernibility hypergraphic structures of fuzzy knowledge representation systems. Our basic aim is to strengthen a granular interpretation in the investigation of any knowledge representation system. In fact, as the indiscernibility hypergraphs lead to the construction and the interaction of macro-granular and micro-granular structures, we proved that both of them are strongly related to many classical notions of GrC. We have also discussed the basic properties of the above structures on two concrete cases, in order to provide a basis for the better interpretation of these hypergraphs. Thus, the proposed work could play a key role both in all applications based on data and in the development of new mathematical theories.
6.
Conclusions
The multi-level visualization of questions endowed with uncertain information can be achieved by fuzzy granulation. This research article has provided a formal approach to GrC based on fuzzy indiscernibility, fuzzy graphs and fuzzy hypergraphs. This approach has ensured interesting links between the modelization of granular structures and fuzzy graph theory. Thus, fuzzy granulation plays a significant part in all problems based on indeterminate data as well as in developing novel mathematical frameworks. The construction of granules and granular structures using fuzzy graphs and hypergraphs has shown that this way of granulation is more effective than its crisp graph theoretic counterpart. We have investigated the basis of indistinguishability relation by introducing two new frameworks, namely, a fuzzy complete lattice and a fuzzy simplicial complex. We have proved that the fuzzy indiscernibility relation enables us to define the indiscernibility hypergraphic structures of I, and in turn, these structures led us towards the construction of granular structures. Granular structures using graphs allow us to solve problems with two advantages: visual description of the graph, and multi-view of these granular structures. Thus we have defined the granular structures in fuzzy graphs to combine the advantages of both theories. We have constructed a degree based model of fuzzy granules. We have discussed the granularities for different values of the parameter within unit closed interval [0,1]. Decreasing values of this parameter produces finer granularities. Further, we have developed an algorithm for the construction of this model and implemented it in a real life application. Based on [47,48,49,50], we aim to extend our study to include the following topics:
1. Fuzzy rough and rough fuzzy hypergraph models of granular computing.
2. Models of granular structures based on m−polar fuzzy graphs.
3. Fuzzy rough models of granular computing.
4. Hesitant fuzzy hypergraphs in granular computing.
5. Relational granularity of fuzzy hypergraphs.
Acknowledgments
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (DF-146-130-1441). The authors, therefore, gratefully acknowledge DSR technical and financial support.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: