Figure 1.
The structure of CNN.
The survival rate of cervical cancer can be improved by the early screening. However, the screening is a heavy task for pathologists. Thus, automatic cervical cell classification model is proposed to assist pathologists in screening. In cervical cell classification, the number of abnormal cells is small, meanwhile, the ratio between the number of abnormal cells and the number of normal cells is small too. In order to deal with the small sample and class imbalance problem, a generative adversarial network (GAN) trained by images of abnormal cells is proposed to obtain the generated images of abnormal cells. Using both generated images and real images, a convolutional neural network (CNN) is trained. We design four experiments, including 1) training the CNN by under-sampled images of normal cells and the real images of abnormal cells, 2) pre-training the CNN by other dataset and fine-tuning it by real images of cells, 3) training the CNN by generated images of abnormal cells and the real images, 4) pre-training the CNN by generated images of abnormal cells and fine-tuning it by real images of cells. Comparing these experimental results, we find that 1) GAN generated images of abnormal cells can effectively solve the problem of small sample and class imbalance in cervical cell classification; 2) CNN model pre-trained by generated images and fine-tuned by real images achieves the best performance whose AUC value is 0.984.
Citation: Suxiang Yu, Shuai Zhang, Bin Wang, Hua Dun, Long Xu, Xin Huang, Ermin Shi, Xinxing Feng. Generative adversarial network based data augmentation to improve cervical cell classification model[J]. Mathematical Biosciences and Engineering, 2021, 18(2): 1740-1752. doi: 10.3934/mbe.2021090
| [1] | Xin Liu, Chen Zhao, Bin Zheng, Qinwei Guo, Yuanyuan Yu, Dezheng Zhang, Aziguli Wulamu . Spatiotemporal and kinematic characteristics augmentation using Dual-GAN for ankle instability detection. Mathematical Biosciences and Engineering, 2022, 19(10): 10037-10059. doi: 10.3934/mbe.2022469 |
| [2] | Binjie Hou, Gang Chen . A new imbalanced data oversampling method based on Bootstrap method and Wasserstein Generative Adversarial Network. Mathematical Biosciences and Engineering, 2024, 21(3): 4309-4327. doi: 10.3934/mbe.2024190 |
| [3] | Luqi Li, Yunkai Zhai, Jinghong Gao, Linlin Wang, Li Hou, Jie Zhao . Stacking-BERT model for Chinese medical procedure entity normalization. Mathematical Biosciences and Engineering, 2023, 20(1): 1018-1036. doi: 10.3934/mbe.2023047 |
| [4] | Hui Yao, Yuhan Wu, Shuo Liu, Yanhao Liu, Hua Xie . A pavement crack synthesis method based on conditional generative adversarial networks. Mathematical Biosciences and Engineering, 2024, 21(1): 903-923. doi: 10.3934/mbe.2024038 |
| [5] | Xin Shu, Xin Cheng, Shubin Xu, Yunfang Chen, Tinghuai Ma, Wei Zhang . How to construct low-altitude aerial image datasets for deep learning. Mathematical Biosciences and Engineering, 2021, 18(2): 986-999. doi: 10.3934/mbe.2021053 |
| [6] | Qi Cui, Ruohan Meng, Zhili Zhou, Xingming Sun, Kaiwen Zhu . An anti-forensic scheme on computer graphic images and natural images using generative adversarial networks. Mathematical Biosciences and Engineering, 2019, 16(5): 4923-4935. doi: 10.3934/mbe.2019248 |
| [7] | Bingyu Liu, Jiani Hu, Weihong Deng . Attention distraction with gradient sharpening for multi-task adversarial attack. Mathematical Biosciences and Engineering, 2023, 20(8): 13562-13580. doi: 10.3934/mbe.2023605 |
| [8] | Jia Yu, Huiling Peng, Guoqiang Wang, Nianfeng Shi . A topical VAEGAN-IHMM approach for automatic story segmentation. Mathematical Biosciences and Engineering, 2024, 21(7): 6608-6630. doi: 10.3934/mbe.2024289 |
| [9] | Xingyu Gong, Ling Jia, Na Li . Research on mobile traffic data augmentation methods based on SA-ACGAN-GN. Mathematical Biosciences and Engineering, 2022, 19(11): 11512-11532. doi: 10.3934/mbe.2022536 |
| [10] | Wenli Cheng, Jiajia Jiao . An adversarially consensus model of augmented unlabeled data for cardiac image segmentation (CAU+). Mathematical Biosciences and Engineering, 2023, 20(8): 13521-13541. doi: 10.3934/mbe.2023603 |
The survival rate of cervical cancer can be improved by the early screening. However, the screening is a heavy task for pathologists. Thus, automatic cervical cell classification model is proposed to assist pathologists in screening. In cervical cell classification, the number of abnormal cells is small, meanwhile, the ratio between the number of abnormal cells and the number of normal cells is small too. In order to deal with the small sample and class imbalance problem, a generative adversarial network (GAN) trained by images of abnormal cells is proposed to obtain the generated images of abnormal cells. Using both generated images and real images, a convolutional neural network (CNN) is trained. We design four experiments, including 1) training the CNN by under-sampled images of normal cells and the real images of abnormal cells, 2) pre-training the CNN by other dataset and fine-tuning it by real images of cells, 3) training the CNN by generated images of abnormal cells and the real images, 4) pre-training the CNN by generated images of abnormal cells and fine-tuning it by real images of cells. Comparing these experimental results, we find that 1) GAN generated images of abnormal cells can effectively solve the problem of small sample and class imbalance in cervical cell classification; 2) CNN model pre-trained by generated images and fine-tuned by real images achieves the best performance whose AUC value is 0.984.
Cervical cancer, in which the cells of the cervix become abnormal, is the fourth most common cancer for women in the worldwide [1]. However, cervical cancer can be prevented by the early screening. In a Pap test, pathologist checks the cells of the cervix to judge if they look abnormal under a microscope. It's time-consuming and even error prone. Hence computer assisted cervical cancer screening has been widely studied [2,3,4,5,6,7,8,9,10,11,12]. An automatic screening system includes image segmentation model, which is used to extract cells from the background, and cell classification model, which is applied to distinguish abnormal cells from normal cells.
In order to build automatic cell classification model, traditional machine learning methods and deep learning methods are proposed. In traditional machine learning methods, features are extracted from the cell images [13], and these features are fed to classify the normal and abnormal cells. In deep learning methods, the cell images are directly fed into the model to distinguish abnormal cells from normal cells [4]. Compared with the traditional machine learning model, the performance of the deep learning based classification model has been greatly improved.
The deep learning method learns multi-level features of cervical cells for the classification task. A large amount of data is required to support the learning process, and performance of the model can be improved as the scale of data increases. In the cervical cell classification, most of the cells are normal, therefore, the classification data of cervical cells is essentially unbalanced data in which the number of abnormal cells is much less than the number of normal cells. In machine learning community, it is called the class imbalance problem that the number of one class is far less than the number of another class. The classification model learned from the imbalanced data tends to classify abnormal cells as normal cells. This kind of model is useless in practical application. Hence most machine learning algorithms should work on the balanced training set in which the number of samples of each class is roughly equal.
In order to get the balanced training set, sampling based approaches are usually applied, including the under-sampling method [14,15,16,17,18], the over-sampling method [19,20,21,22,23,24] and the hybrid method [25]. The under-sampling method removes some samples with the majority class, the over-sampling method add some samples with the minority class, and the hybrid method combines the under-sampling method and the over-sampling method together. The basic algorithms of sampling are random undersampling [14] and random oversampling [19], however, these two strategies are not stable, and always not good enough. In [15], two popular undersampling algorithms, EasyEnsemble and BalanceCascade, were proposed. In these two algorithms, the performances of models were improved with less time consuming. In [16], NearMiss algorithm was proposed, which chose some of the representative data to build the model. In [17,18], Tomek et.al removed the similar data in different classes to improve the result. Some oversampling algorithms such as Generative Oversampling, Synthetic Minority Oversampling Technique (SMOTE), KM-SMOTE and Random Forest, Borderline-SMOTE, Adaptive Synthetic Sampling (ADASYN) were proposed in [20,21,22,23,24]. The generated new data increased the number of minority class. In [25], Batista et al. proposed the combination of undersampling algorithms and oversampling algorithms. Besides sampling techniques, cost-sensitive learning is also a good way to deal with the class-imbalance problem. By changing the weight of learning process of different class, the results are improved. Fan et al. stated an algorithm named AdaCost [26], which can automatically adjust the cost of learning process.
In the cervical cell classification, the number of abnormal cells is small. In deep learning community, it is called the small sample problem. One of the important factors in building a deep learning model with high performance is to collect the amount of data. However, it is difficult to collect large amounts of data in medical diagnosis, for example, the abnormal cells in cervical cell classification. To deal with small sample problem, data augmentation strategy is proposed, including basic image manipulation strategy [27,28,29,30,31], for example, image flipping, image cropping, image rotation, and noise injection; image generation strategy [32], for example, GAN based data augmentation; pretraining strategy with the help of existing image dataset, for example, deep learning model can be pre-trained on existing large dataset, and then, finetuning on specific small data. To increase the number of data, geometric transformation is a basic algorithm. It includes rotation, flipping, filtering, color adjustment and so on. Besides these, some algorithms such as Grid Mask, CutMix, Mixup, Pairing Samples, Smart Augmentation are also proposed to augment data [27,28,29,30,31]. Li et al. augmented data on feature space [33]. GAN [32] is a famous generative deep learning model. It has many variations, such as DCGAN, CGAN, CycleGAN, CoGAN, ProGAN and so on. It can generate synthesized data as real as possible to compensate short of training data. Cubuk et al. presented an Autoaugment algorithm [34], automatically choosing the best data augmentation algorithm; however, it costs too much time and resource. In recent years, deep learning methods were widely applied to build cytological classification model. On the one hand, they provided data augmentation strategies; on the other hand, they built classification models. In [2], Chen et al. used RCGAN to generate data, improving the test accuracy from 84.25 to 95.18%. In [7], Shanthi et al. used 5 different ways of data augmentation to improve model performance.
Motivated by the sampling based approach for class imbalance problem and the data augmentation strategy for small sample problem, we propose to apply GAN to generate images of abnormal cells. The generated images of abnormal cells are merged into the real data to form a new dataset with balanced samples. Based on this new dataset, a deep learning model is built for the cervical cell classification.
The key contribution of this paper is that GAN based data augmentation strategy and pre-trained strategy are combined for the first time to deal with class imbalance problem and small sample problem in cervical cell classification model.
The structure of this paper is as follows. The modeling methods are specified in Section 2. The experimental results and comparisons are shown in Section 3. Finally, the discussions and the conclusions are given in Sections 4 and 5, respectively.
The dataset, collected from the fourth central hospital of Baoding city, China, consists of 22,124 cell samples including 1202 abnormal samples and 20,922 normal samples. The pathologists manually cutout the single cells from the whole images of thin prep cytologic test by the digital camera with microscope, and then partition the single cells into normal or abnormal category. All the cells are double checked by pathologists. The dataset is randomly divided into training set and testing set. The resolution of sample image is 0.2 μm per pixel. In our dataset, image size is from 482 × 577 to 34 × 68 pixels. We revise all images into 227 × 227 pixels for the inputs of our model.
The aim of this work is to use GAN augmented data to improve classification of deep learning models, specifically, distinguishing abnormal cells from normal cells in this work.
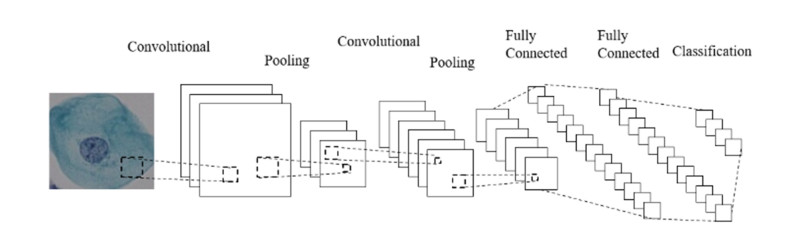
We apply convolutional neural networks (CNN) to learn cervical cell classification model from the provided data. CNN is most popular for image processing tasks. It consists of convolutional (conv), non-linearity and pooling (pool) layers, followed by more conv and fully connected (FC) layers. Figure 1 shows a general structure of CNN.
CNN extracts the features of input images by many convolutional layers. The convolutional layer can include several filters. The input images will be processed by every filter. The result is the inner product of two matrixes, one is a part of input images and the other is the filter. Pooling layers compress the information of input images. Max pooling is usually used. The result is the maximum of each matrix. It can remove some redundant information and prevent overfitting. Fully connected layers integrate the features formal layers extracted. The final output layer can be used for classification.
Here, Alex-net is selected to build the cervical cell classification model. It is a famous deep learning model that has achieved 2012 ImageNet champion [35]. It uses tricks such as ReLU, Dropout, and Local Response Normalization (LRN). ReLU is a kind of activation function that can strongly increase the speed of training. Dropout is a strategy that the network will randomly delete some neurons. It can avoid overfitting. And the LRN is a kind of normalization method. It enlarges the neurons which are more active (the values are bigger). It can improve the generalization ability of models.
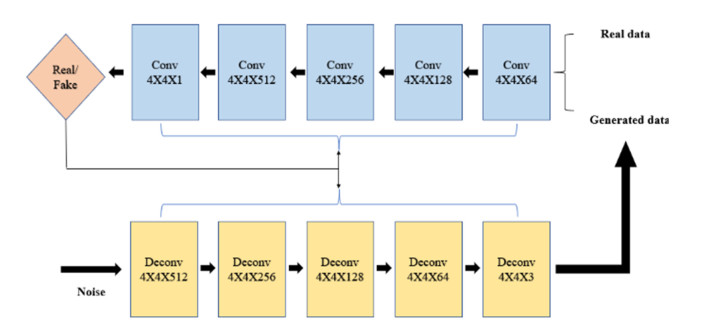
Since the numbers of normal samples and abnormal samples are imbalanced, we generate some abnormal samples by Generative Adversarial Networks (GAN). GAN is a kind of deep learning models [33]. It has at least 2 modules: Generative Model (G-model) and Discriminative Model (D-model). The G-model accepts a random noise (z) and generate an image G(z). The D-model accepts an image and outputs its probability of being a real image. By training the GAN with real images, these two models will affect each other.
| minGmaxDV(D,G)=EX pdata(x)[logD(x)]+Ez pz(z)[log(1−D(G(z)))] | (1) |
Equation (1) shows the process that optimizer finds the Nash equilibrium between G-model and D-model. pz(z) means the distribution of the noise z. E(·) means the empirical estimation of the joint probability distribution. x means real samples received by discriminator. In the training process, the generator and discriminator are optimized in an alternative way. D is optimized by maximizing EX pdata(x)[logD(x)]+Ez pz(z)[log(1−D(G(z)))] and G is optimized by minimizing Ez pz(z)[log(1−D(G(z)))]. Finally, after many iterations, the G-model will create images that the D-model cannot determine whether it is real or not.
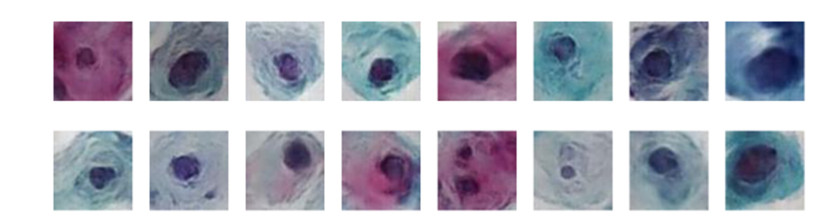
Figure 2 illustrates our employed GAN model, where 5-layers CNN model is used for composing both generator and discriminator. The real data includes 1202 abnormal samples. We train the model until the discriminator is confused by generated image and real image, reaching a balance of zero-sum game, satisfactory result. Then, employing the generator, we generate augmented images for our concerned cervical cell classification task. Some examples of generated images are shown in Figure 3.
We implement the algorithm in Python and perform all the experiments using NVIDIA GeForce RTX 2070 8G, Windows operating system, Intel(R) Core(TM) i7-9700K CPU @ 3.60 GHz and 16 GB RAM.
In this study, we summarize the performance of our model with respect to precision, sensitivity, specificity, accuracy, F1 score, and Area Under Curve (AUC) which are defined as follows.
| precision=TPTP+FP | (2) |
| sensitivity=TPTP+FN | (3) |
| specificity=TNTN+FP | (4) |
| accuracy=TP+TNTP+TN+FP+FN | (5) |
| F1score=2∗TP2∗TP+FP+FN | (6) |
| Hmean=2∗sensitivity∗specificitysensitivity+specificity | (7) |
Precision represents the exactness of classifiers, whereas sensitivity shows the completeness of classifiers. Specificity shows that a classifier can correctly classify normal data as normal. Using both recall and precision, the F1 score is used to evaluate the detection results. Accuracy shows that a classifier can correctly categorize the two-class task. And the AUC is a figure to compare different models.
There are 4 different strategies of using real data, GAN augmented data and other data (ImageNet) in our experiments, including 1) only real data, 2) pretraining over other data, 3) mixed real data and GAN augmented data, and 4) pretraining over GAN augmented data. The whole process of our concerned task is shown in Figure 4.
We firstly divide the 1202 abnormal samples into training set and testing set with the ratio of 4:1. Then, we adjust the number of normal samples in each strategy for class balance. In Task 1, real data only strategy, we train the Alex-net by a small number of balanced real samples. Since we have only 961 real abnormal samples for training, the number of normal samples should be around 961. In this task, we evaluate the ability of Alex-net trained by a small real dataset. In Task 2, the Alex-net model is firstly pretrained over ImageNet, and then finetuned by the same balanced real samples as in the Task 1. In Task 3, mixing real data and GAN augmented data, we train the Alex-net on a larger dataset mixed with GAN augmented data and real data. The number of abnormal samples and normal samples are both 16,961 (16,000 generated data and 961 real data). In this task, the generated data and real data are mixed together and randomly shuffled. In Task 4, pretraining on GAN augmented data strategy, we pretrain the Alex-net by 16,000 generated data as abnormal samples and 16,000 real normal samples. And then, we finetune the best model by 961 real abnormal samples and 961 real normal samples as Task 1. Since our generated data are not perfect, we only use them for pretrain. And, the real data will improve the model in the finetuning process.
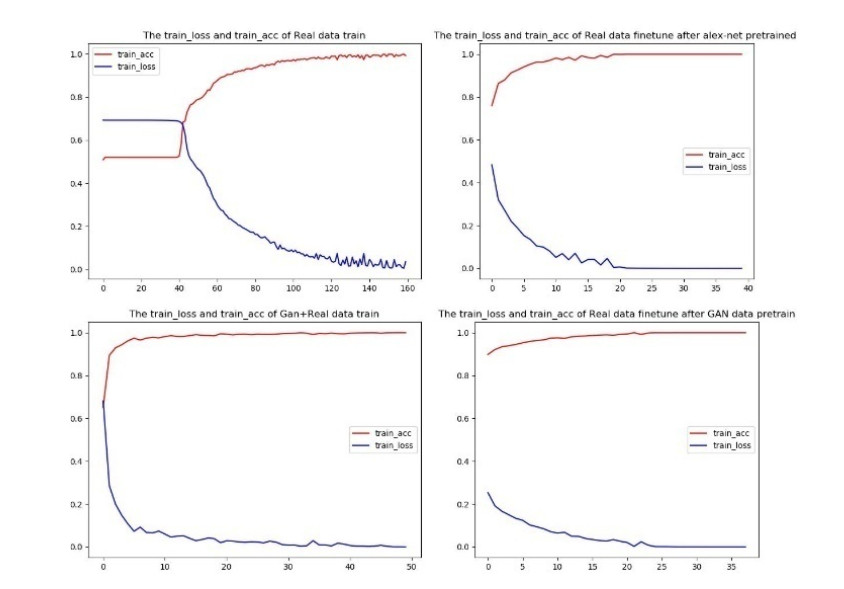
The testing set includes 241 real abnormal samples and 3961 real normal samples. The unbalanced testing set is more likely to the real situation (even the proportion of normal samples should be larger). In task 1, we train the models for 160 epochs using a learning momentum of 0.9, a learning rate of 0.0001, batch size of 1. Task 2 for 40 epochs, Task 3 for 50 epochs and Task 4 for 38 epochs using same parameters. Figure 5 shows the train accuracy and train loss of Tasks 1–4.
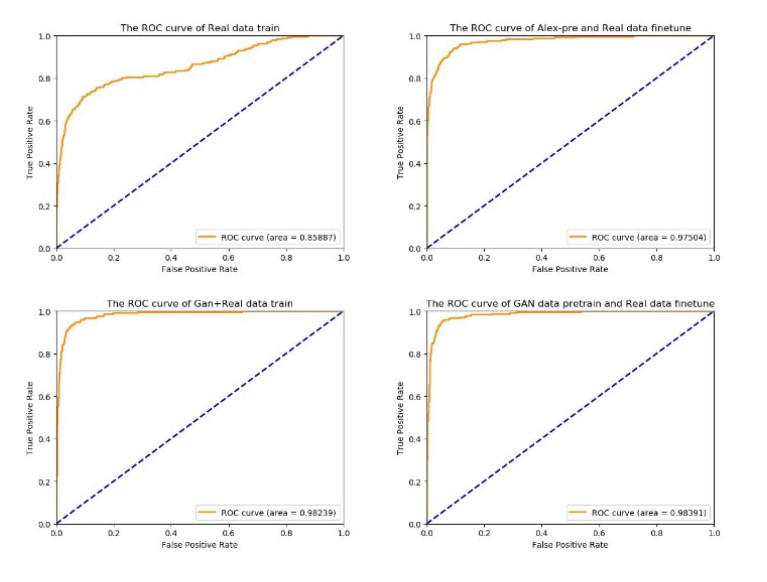
Figure 6 shows the ROC of Model in Tasks 1–4. In Task 1, the AUC is unsatisfied. And the AUC of Tasks 3 and 4 are bigger than Task 2. It means GAN augmented data really makes sense.
Table 1 lists the detail statistics of all evaluation metrics over the 4 tasks on testing set. The Task 1 yields a precision score of 28.9%, which is markedly inferior to Tasks 3 and 4 with GAN augmented data strategy. The same conclusions are to the other two popular metrics, accuracy and AUC. Comparing Task 1 and 2, achievement of precision and accuracy is significant, indicating that a small sample problem can be improved a bit by pretraining over other large dataset. Comparing Task 1 with Tasks 3 and 4, achievement of precision and accuracy is more remarkable, which proving the big success of our designed GAN based data augmentation strategy. Comparing Tasks 3 and 4, the former is more competitive relative to precision and accuracy metrics. It indicates that mixed synthesized and real data together may achieve more than only synthesized data during training process.
| Task | precision (%) | sensitivity (%) | specificity (%) | accuracy (%) | F1 score (%) | H-mean (%) | AUC |
| 1 | 28.9 | 73.4 | 89.0 | 88.1 | 41.5 | 80.5 | 0.859 |
| 2 | 38.3 | 93.8 | 90.8 | 91.0 | 54.4 | 92.3 | 0.975 |
| 3 | 54.5 | 92.5 | 95.3 | 95.1 | 68.6 | 93.9 | 0.982 |
| 4 | 47.8 | 95.9 | 93.6 | 93.8 | 63.8 | 94.7 | 0.984 |
DownLoad:
CSV
In Task 1, all of the measure values are quite low. It performs very unsatisfied in precision, sensitivity. It means the Alex-net cannot deal with the imbalanced dataset directly. Although the accuracy achieves 88.1% which seems not too bad, it is not enough to represent the true performance. In Task 2, we use transfer learning to improve the model. The sensitivity is much better than Task 1, however, the precision is still not good enough. In Tasks 3 and 4, we apply the generated data by GAN to deal with the imbalanced problem. The different uses of generated data both make sense. Pretrain with generated data and finetune with original data, or mix original data with generated data both works well. To find a better strategy, we consider more about the data imbalance [36,37,38,39].
Since the testing set is imbalanced, the AUC is the most powerful scores to measure the models. The Task 4 has the best AUC of all 4 tasks. And the Task 3's AUC is only a little lower than it. It means training with GAN data improves the performance of the model.
Figure 7 shows the original image and some feature maps after the first convolutional layer of Tasks 2 and 4. As we can see, in Task 2, models focus more on the cell nucleus. Most of the features extract the features of the cell nucleus and the edge of it. Besides this, the extracted features are discontinuous. Since this model is pretrained by ImageNet, a dataset of macroscopic objects, it may create some obstacles to get the features of microcosmic cell. Compared with Task 2, Task 4 can focus more purely on each part of cell in each feature map. It means that the model extracts the features from only part of the cell every time, such as cell nucleus, cytoplasm, the edge of cell nucleus and the edge of cytoplasm. These four parts are always the crucial parts in traditional method. Moreover, the features are more continuous, we can find the boundary of each part clearly. This model is pretrained by GAN samples, which are more likely to the real cell samples, may be more closed to the perfect pretrained model. Since the performance of Task 4 model are better, we guess in this classification, extracting features of each part of cell and getting continuous features are more helpful. The GAN samples make sense.
In this paper, a cell dataset of normal samples and abnormal samples is collected. Since the numbers of each samples is imbalanced, we generate a large number of abnormal samples by GAN. On the basis of this mixed dataset, Alex-net are trained by 4 different ways and tested. By comparing the performances of these tasks, the best training way is determined. Training the model with GAN data is an available way to improve the performance. Pretraining the model with the GAN data, then finetuning the model with the real data is better. Its AUC value is 0.984, which is the highest within the 4 Tasks. We draw the following main conclusions:
1) In cervical cell classification, the number of abnormal cells is limited, far less than the number of normal cells. This situation belongs to imbalanced class problem and small samples problem. And traditional undersampling strategies are not able to achieve a satisfactory result.
2) Generating abnormal samples by GAN is an effective way to solve imbalanced class problem and small samples problem simultaneously. The result of our experiment shows that training with samples generated by GAN improve the performance of our models.
3) Comparing the feature maps of models pretrained by GAN samples and other data (ImageNet), we find that pretraining model with GAN samples are more helpful to the classification. The model is more likely to extract the features of each part of cell, and the extracted features are more continuously.
4) Comparing the different training strategies of GAN samples, we find that pretraining by GAN samples and finetuning by real samples is the best training strategy.
In conclusion, the abnormal samples of medical data are always limited and hard to collect. It is an essential problem of medical classification. We can generate abnormal samples by GAN and pretrain models with them, then finetune the model by real samples.
In the future, we need to build a multi-classification model to classify the cells more carefully since abnormal samples of cervical cell still have many subclasses. In addition, since the abnormal samples can be divided into subclasses, generating samples by GAN should be update simultaneously.
The authors declare that they have no conflicts of interest.
| [1] | L. Torre, F. Bray, R. L. Siegel, J. Ferlay, J. Lortet-Tieulent, A. Jemal, Global cancer statistics, 2012, CA Cancer J. Clin., 65 (2015), 87–108. |
| [2] | S. Chen, D. Gao, L. Wang, Y. Zhang, Cervical Cancer Single Cell Image Data Augmentation Using Residual Condition Generative Adversarial Networks, 2020 3rd International Conference on Artificial Intelligence and Big Data (ICAIBD), 2020. |
| [3] |
D. Xue, X. Zhou, C. Li, Y. Yao, M. M. Rahaman, J. Zhang. et al., An Application of Transfer Learning and Ensemble Learning Techniques for Cervical Histopathology Image Classification, IEEE Access, 8 (2020), 104603–104618. doi: 10.1109/ACCESS.2020.2999816
|
| [4] | N. Sompawong, J. Mopan, P. Pooprasert, W. Himakhun, K. Suwannarurk, J. Ngamvirojcharoen, et al., Automated pap smear cervical cancer screening using deep learning, 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2019. |
| [5] | M. Wu, C. Yan, H. Liu, Q. Liu, Y. Yin, Automatic classification of cervical cancer from cytological images by using convolutional neural network, Biosci. Rep., 6 (2018), 38. |
| [6] | O. E. Aina, S. A. Adeshina, A. M. Aibinu, Classification of Cervix types using Convolution Neural Network (CNN), 15th International Conference on Electronics, Computer and Computation (ICECCO), 2019. |
| [7] |
P. B. Shanthi, F. Faruqi, K. S. Hareesha, K. Ranjini, Deep convolution neural network for malignancy detection and classification in microscopic uterine cervix cell images, Asian Pac. J. Cancer Prev., 20 (2019), 3447–3456. doi: 10.31557/APJCP.2019.20.11.3447
|
| [8] |
H. Lin, Y. Hu, S. Chen, J. Yao, L. Zhang, Fine-grained classification of cervical cells using morphological and appearance based convolutional neural networks, IEEE Access, 7 (2019), 71541–71549. doi: 10.1109/ACCESS.2019.2919390
|
| [9] | J. Payette, J. Rachleff, C. V. Graaf, Intel and MobileODT Cervical Cancer Screening Kaggle Competition: cervix type classification using Deep Learning and image classification, 2017. Available from: http://cs231n.stanford.edu/reports/2017/pdfs/923.pdf. |
| [10] | M. Kwon, M. Kuko, M. Pourhomayoun, V. Martin, T. H. Kim, S. E. Martin, Multi-label classification of single and clustered cervical cells using deep convolutional networks, California State University, Los Angeles, 2018. |
| [11] |
Kurnianingsih, K. H. S. Allehaibi, L. E. Nugroho, Widyawan, L. Lazuardi, A. S. Prabuwono, et al., Segmentation and classification of cervical cells using deep learning, IEEE Access, 7 (2019), 116925–116941. doi: 10.1109/ACCESS.2019.2936017
|
| [12] | Y. Xue, Q. Zhou, J. Ye, L. R. Long, S. Antani, C. Cornwell, et al., Synthetic augmentation and feature-based filtering for improved cervical histopathology image classification, International conference on medical image computing and computer-assisted intervention. Springer, Cham, 2019. |
| [13] | W. William, A. Ware, A. H. Basaza-Ejiri, J. Obungoloch, A review of image analysis and machine learning techniques for automated cervical cancer screening from pap-smear images, Comput. Methods Programs Biomed., 164 (2018), 15–22. |
| [14] | N. V. Chawla, Data mining for imbalanced datasets: An overview, in Data Mining and Knowledge Discovery Handbook, Springer, Boston, MA, 2009,875–886. |
| [15] |
X. Y. Liu, J. Wu, Z. H. Zhou, Exploratory undersampling for class-imbalance learning, IEEE Trans. Syst. Man Cybern. Part B, 39 (2009), 539–550. doi: 10.1109/TSMCB.2008.2007853
|
| [16] | I. Mani, I. Zhang, kNN approach to unbalanced data distributions: a case study involving information extraction, Proceedings of workshop on learning from imbalanced datasets, 2003. |
| [17] | I. Tomek, Two Modifications of CNN, IEEE Trans. Syst. Man Cybern., 11 (1976), 769–772. |
| [18] | I. Tomek, An Experiment with the Edited Nearest-Neighbor Rule, IEEE Trans. Syst. Man Cybern., 6 (1976), 448–452. |
| [19] | C. X. Ling, C. Li, Data mining for direct marketing: Problems and solutions, Plenary Presentation, 98 (1998), 73–79. |
| [20] |
N. V. Chawla, K. W. Bowyer, L. O. Hall, W. P. Kegelmeyer, SMOTE: Synthetic Minority Over-sampling Technique, J. Artif. Intell. Res., 16 (2002), 321–357. doi: 10.1613/jair.953
|
| [21] | H. Han, W. Y. Wang, B. H. Mao, Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning, International conference on intelligent computing. Springer, Berlin, Heidelberg, 2005. |
| [22] |
X. Li, L. Wang, E. Sung, AdaBoost with SVM-based component classifiers, Eng. Appl. Artif. Intell., 21 (2008), 785–795. doi: 10.1016/j.engappai.2007.07.001
|
| [23] | A. Liu, J. Ghosh, C. E. Martin, Generative Oversampling for Mining Imbalanced Datasets, DMIN, 2007, 66–72. |
| [24] | B. Chen, Y. D. Su, S. Huang, Classification of imbalance data based on KM-SMOTE algorithm and random forest, Comput. Technol. Dev., 5 (2015), 17–21. |
| [25] |
G. E. Batista, R. C. Prati, M. C. Monard, A study of the behavior of several methods for balancing machine learning training data, ACM SIGKDD Explor. Newsl., 6 (2004), 20–29. doi: 10.1145/1007730.1007735
|
| [26] | W. Fan, S. J. Stolfo, J. Zhang, P. K. Chan, AdaCost: misclassification cost-sensitive boosting, ICML, 1999. |
| [27] | P. Chen, S. Liu, H. Zhao, J. Jia, Grid Mask data augmentation, preprint, arXiv: 2001.04086. |
| [28] | S. Yun, D. Han, S. J. Oh, S. Chun, J. Choe, Y. Yoo, Cutmix: Regularization strategy to train strong classifiers with localizable features, Proceedings of the IEEE International Conference on Computer Vision, 2019. |
| [29] | H. Zhang, M. Cisse, Y. N. Dauphin, D. Lopez-Paz, Mixup: Beyond empirical risk minimization, preprint, arXiv: 1710.09412. |
| [30] | H. Inoue, Data augmentation by pairing samples for images classification, preprint, arXiv: 1801.02929. |
| [31] |
J. Lemley, S. Bazrafkan, P. Corcoran, Smart augmentation learning an optimal data augmentation strategy, IEEE Access, 5 (2017), 5858–5869. doi: 10.1109/ACCESS.2017.2696121
|
| [32] | I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, et al., Generative adversarial nets, Advances in neural information processing systems, 2014. |
| [33] | B. Li, F. Wu, S. N. Lim, S. Belongie, K. Q. Weinberger, On Feature Normalization and Data Augmentation, preprint, arXiv: 2002.11102. |
| [34] | E. D. Cubuk, B. Zoph, D. Mane, V. Vasudevan, Q. V. Le, Autoaugment: Learning augmentation strategies from data, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019. |
| [35] | A. Krizhevsky, I. Sutskever, G. E. Hinton, Imagenet classification with deep convolutional neural networks, Adv. Neural Inf. Proc. Syst., 25 (2012), 1097–1105. |
| [36] |
M. Frid-Adar, I. Diamant, E. Klang, M. Amitai, J. Goldberger, H. Greenspan, GAN-based Synthetic Medical Image Augmentation for increased CNN Performance in Liver Lesion Classification, Neurocomputing, 321 (2018), 321–331. doi: 10.1016/j.neucom.2018.09.013
|
| [37] | M. Frid-Adar, E. Klang, M. Amitai, J. Goldberger, H. Greenspan, Synthetic data augmentation using GAN for improved liver lesion classification, Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging, Washington, DC, 2018. |
| [38] | Y. Onishi, A. Teramoto, M. Tsujimoto, T. Tsukamoto, K. Saito, H. Toyama, et al., Automated Pulmonary Nodule Classification in Computed Tomography Images Using a Deep Convolutional Neural Network Trained by Generative Adversarial Networks, BioMed Res. Int., 2019 (2019), 6051939. |
| [39] |
Y. Onishi, A. Teramoto, M. Tsujimoto, T. Tsukamoto, K. Saito, H. Toyama, et al., Investigation of pulmonary nodule classification using multi-scale residual network enhanced with 3DGAN-synthesized volumes, Radiol. Phys. Technol., 13 (2020), 160–169. doi: 10.1007/s12194-020-00564-5
|
| 1. | T. P. Deepa, A. Nagaraja Rao, Classification of normal and abnormal overlapped squamous cells in pap smear image, 2023, 0975-6809, 10.1007/s13198-022-01805-z | |
| 2. | Xingyu Gong, Ling Jia, Na Li, Research on mobile traffic data augmentation methods based on SA-ACGAN-GN, 2022, 19, 1551-0018, 11512, 10.3934/mbe.2022536 | |
| 3. | Jianguo Xu, Cheng Wan, Weihua Yang, Bo Zheng, Zhipeng Yan, Jianxin Shen, A novel multi-modal fundus image fusion method for guiding the laser surgery of central serous chorioretinopathy, 2021, 18, 1551-0018, 4797, 10.3934/mbe.2021244 | |
| 4. | Hao Jiang, Yanning Zhou, Yi Lin, Ronald C.K. Chan, Jiang Liu, Hao Chen, Deep learning for computational cytology: A survey, 2023, 84, 13618415, 102691, 10.1016/j.media.2022.102691 | |
| 5. | Chuanyun Xu, Mengwei Li, Gang Li, Yang Zhang, Chengjie Sun, Nanlan Bai, Cervical Cell/Clumps Detection in Cytology Images Using Transfer Learning, 2022, 12, 2075-4418, 2477, 10.3390/diagnostics12102477 | |
| 6. | Laixiang Xu, Fuhong Cai, Yanhu Fu, Qian Liu, Cervical cell classification with deep-learning algorithms, 2023, 61, 0140-0118, 821, 10.1007/s11517-022-02745-3 | |
| 7. | Yasunari Matsuzaka, Shinji Kusakawa, Yoshihiro Uesawa, Yoji Sato, Mitsutoshi Satoh, Deep Learning-Based In Vitro Detection Method for Cellular Impurities in Human Cell-Processed Therapeutic Products, 2021, 11, 2076-3417, 9755, 10.3390/app11209755 | |
| 8. | Faiza Jibril, Steve A. Adeshina, Agwu A. Nnanna, 2021, A Deep Learning Based Covid-19 Detection Framework, 978-1-6654-3493-5, 1, 10.1109/ICMEAS52683.2021.9739806 | |
| 9. | Krishna Kant Dixit, Upendra Singh Aswal, V. Saravanan, Manishn Sararswat, N Shalini, Amit Srivastava, 2023, Data Augmentation with Generative Adversarial Networks for Deep Learning in Healthcare, 979-8-3503-3091-5, 1, 10.1109/ICAIIHI57871.2023.10489462 | |
| 10. | Ruinan Jin, Xiaoxiao Li, Backdoor attack and defense in federated generative adversarial network-based medical image synthesis, 2023, 90, 13618415, 102965, 10.1016/j.media.2023.102965 | |
| 11. | Ming Fang, Bo Liao, Xiujuan Lei, Fang-Xiang Wu, A systematic review on deep learning based methods for cervical cell image analysis, 2024, 610, 09252312, 128630, 10.1016/j.neucom.2024.128630 | |
| 12. | Youyi Song, Jing Zou, Kup-Sze Choi, Baiying Lei, Jing Qin, Cell classification with worse-case boosting for intelligent cervical cancer screening, 2024, 91, 13618415, 103014, 10.1016/j.media.2023.103014 | |
| 13. | Betelhem Zewdu Wubineh, Andrzej Rusiecki, Krzysztof Halawa, Classification of cervical cells from the Pap smear image using the RES_DCGAN data augmentation and ResNet50V2 with self-attention architecture, 2024, 0941-0643, 10.1007/s00521-024-10404-x | |
| 14. | Ziqian Wu, Jiyoon Park, Paul R. Steiner, Bo Zhu, John X. J. Zhang, Generative adversarial network model to classify human induced pluripotent stem cell-cardiomyocytes based on maturation level, 2024, 14, 2045-2322, 10.1038/s41598-024-77943-0 | |
| 15. | Debabrata Ghosh, Kuntal Chowdhury, Samya Muhuri, Finding correlation between diabetic retinopathy and diabetes during pregnancy based on computer-aided diagnosis: a review, 2023, 83, 1573-7721, 27037, 10.1007/s11042-023-16449-9 | |
| 16. | Manjit Kaur, Dilbag Singh, Vijay Kumar, Heung-No Lee, MLNet: Metaheuristics-Based Lightweight Deep Learning Network for Cervical Cancer Diagnosis, 2023, 27, 2168-2194, 5004, 10.1109/JBHI.2022.3223127 | |
| 17. | Peng Jiang, Xuekong Li, Hui Shen, Yuqi Chen, Lang Wang, Hua Chen, Jing Feng, Juan Liu, A systematic review of deep learning-based cervical cytology screening: from cell identification to whole slide image analysis, 2023, 56, 0269-2821, 2687, 10.1007/s10462-023-10588-z | |
| 18. | Chongzhe Tian, Xiuli Liu, Shenghua Cheng, Jiaxin Bai, Li Chen, Shaoqun Zeng, Disentanglement of content and style features in multi-center cytology images via contrastive self-supervised learning, 2024, 95, 17468094, 106395, 10.1016/j.bspc.2024.106395 | |
| 19. | Betelhem Zewdu Wubineh, Andrzej Rusiecki, Krzysztof Halawa, 2024, Chapter 32, 978-3-031-61856-7, 325, 10.1007/978-3-031-61857-4_32 | |
| 20. | Hua Chen, Juan Liu, Peng Jiang, Yu Jin, Jing Feng, Baochuan Pang, Dehua Cao, Cheng Li, 2023, MSCCNet: Multi-Scale Convolution-Capsule Network for Cervical Cell Classification, 979-8-3503-3748-8, 1842, 10.1109/BIBM58861.2023.10385911 | |
| 21. | Yunhao Chen, Zihui Yan, Yunjie Zhu, A comprehensive survey for generative data augmentation, 2024, 600, 09252312, 128167, 10.1016/j.neucom.2024.128167 | |
| 22. | Hannah Ahmadzadeh Sarhangi, Dorsa Beigifard, Elahe Farmani, Hamidreza Bolhasani, Deep learning techniques for cervical cancer diagnosis based on pathology and colposcopy images, 2024, 47, 23529148, 101503, 10.1016/j.imu.2024.101503 | |
| 23. | Vitória Maria S. Bispo, Natália Fernanda de C. Meira, Ricardo A. R. Campos, Andrea G. Campos Bianchi, 2024, Explorando DCGANs na geração de imagens citológicas para diagnóstico assistido por computador, 53, 10.5753/ercas.2024.238706 | |
| 24. | Betelhem Zewdu Wubineh, Łukasz Jeleń, Andrzej Rusiecki, DCGAN-based Cytology Image Augmentation for Cervical Cancer Cell Classification Using Transfer Learning, 2025, 256, 18770509, 1003, 10.1016/j.procs.2025.02.206 |
Suxiang Yu, Shuai Zhang, Bin Wang, Hua Dun, Long Xu, Xin Huang, Ermin Shi, Xinxing Feng. Generative adversarial network based data augmentation to improve cervical cell classification model[J]. Mathematical Biosciences and Engineering, 2021, 18(2): 1740-1752. doi: 10.3934/mbe.2021090
| Task | precision (%) | sensitivity (%) | specificity (%) | accuracy (%) | F1 score (%) | H-mean (%) | AUC |
| 1 | 28.9 | 73.4 | 89.0 | 88.1 | 41.5 | 80.5 | 0.859 |
| 2 | 38.3 | 93.8 | 90.8 | 91.0 | 54.4 | 92.3 | 0.975 |
| 3 | 54.5 | 92.5 | 95.3 | 95.1 | 68.6 | 93.9 | 0.982 |
| 4 | 47.8 | 95.9 | 93.6 | 93.8 | 63.8 | 94.7 | 0.984 |
DownLoad:
CSV
