A topical VAEGAN-IHMM approach for automatic story segmentation

1.   Introduction

The development of multimedia and networking technology has led to an exponential increase in multimedia data, such as broadcast news, lectures, and conference records. With the emergence of such large amounts of content, there is a growing demand for multimedia information processing techniques, such as topic detection and tracking ^[1,2], document summarization ^[3], content indexing and retrieval ^[4,5], and information extraction ^[6,7]. Story segmentation ^[8,9,10,11] divides video, audio, or text streams into a series of independent segments with distinct themes, each with a specific topic. Story segmentation is one of the important preprocessing operations in multimedia information processing.

Story segmentation allows us to retrieve and analyze media documents from the level of chapters to the level of semantic paragraphs precisely. Without story segmentation, the content returned by a user search might consist of an entire document, speech, or video, requiring users to browse through the entire file to find what they need, thus reducing the efficiency of information retrieval. Pre-cutting multimedia data streams into thematic segments manually, although it can more accurately return the desired information, requires a significant amount of time and manpower. By utilizing automatic story segmentation technology to divide documents into independently themed segments, refining the smallest unit of retrieval from the chapter level to the level of semantic paragraphs, users can conveniently locate the desired information quickly, saving time and enhancing the user experience. Story segmentation is an important part of a news broadcast story retrieval system. The story segmentation module identifies theme transitions in the program, detects theme boundaries, and thus segments a video, audio, or text stream into stories with independent themes. By segmenting the entire news program into stories with independent themes, and by classifying, summarizing, and indexing them, a news broadcast story retrieval system can be constructed. When users search, the system presents relevant stories rather than the entire news program containing irrelevant content.

Story segmentation technology is also an important foundation for automatic text summarization. Story segmentation pre-divides documents into smaller units with different themes, breaking down the automatic summarization of the entire document into summaries of smaller thematic segments, greatly reducing the difficulty and complexity of automatic summarization, and improving the accuracy of this task. Specifically, for extractive-based automatic summarization methods, it is necessary to identify themes to determine the framework for summarizing documents in that domain, making automatic story segmentation an indispensable and important component.

Story segmentation methods can be classified based on audio ^[12], video ^[13], and text ^[1], depending on the medium of the input stream. They can also be categorized based on the type of document, such as broadcast news ^[13], conference records ^[14], and lectures ^{[12,13,14,15]}. In recent years, deep neural networks (DNNs) have achieved significant success in the field of large vocabulary continuous speech recognition (LVCSR) ^{[14,15,16,17]}, making it easier for people to obtain large amounts of accurate transcripts of broadcast news. Compared to abstract speech signals, text transcripts have meaningful hierarchical units such as words and sentences, along with explicit syntactic structures, making them more conducive to analyzing semantic information. Moreover, many traditional text segmentation methods can be directly applied to transcripts. Therefore, we focus on story segmentation technology for English broadcast news speech recognition transcripts.

2.   Related work

Story segmentation involves two steps: Feature representation and segmentation algorithm. Word or sentence features that contain prominent themes or semantic information significantly impact on the effectiveness of story segmentation. The bag-of-words (BOW) ^{[18,19,20,21,22,23]} model and term frequency-inverse document frequency (TF-IDF) are simple and effective text feature representation methods commonly used in story segmentation methods such as TextTiling and dynamic programming (DP) ^[14,24,25]. However, TF-IDF and BOW calculate only the frequency of word occurrence in each sentence, ignoring the semantic relationships between words. Probabilistic topic models model topics by calculating the probability distribution of words on the topic, revealing the inherent connection between word frequency and semantic information. Common feature representation methods based on probabilistic topic models include probabilistic latent semantic analysis (PLSA) ^[23], latent Dirichlet allocation (LDA) ^[26], and LapPLSA ^[27]. Using a topic probability model, the BOW feature vector is transformed into a feature vector in the topic domain, and this feature containing rich semantic information significantly improves the performance of story segmentation ^[28]. In addition, artificial neural networks (ANN) can also be used for topic modelling, and ANN-based topic models have achieved good experimental results in tasks such as document classification and retrieval and topic detection ^[29,30,31].

Story segmentation algorithms can be built based on the word or sentence vectors mentioned above. Story segmentation algorithms can be divided into two categories: those based on semantic detection and those based on probabilistic models. Detection-based segmentation methods optimize local objectives ^[14] or global objectives ^[27,32] to find the optimal partition of word sequences on the topic. Probability model-based methods calculate the probability relationship between words or sentences and latent topic variables, and the position where the latent variable topic changes is the story boundary. Common probability models include PLSA, BayesSeg, and DDCRP.

HMM is a powerful probabilistic sequence labeling tool ^[33] that was successfully applied to story segmentation tasks in 1998 ^[34]. In traditional HMM-based story segmentation tasks, the hidden states of the HMM are regarded as latent topics, and words are generated from a topic-related probability distribution. The transition of hidden states in the HMM indicates a change of topic, and the transition position is the story boundary. The transition probability matrix and the emission probability matrix in the HMM can be computed from the training dataset. A state's emission probability matrix is calculated using a topic-related language model (LM) ^[35]. For a given input text, the trained HMM model is used along with the Viterbi algorithm to decode the hidden topic information of the text and obtain the corresponding topic sequence. The transition positions of topics indicate the story boundaries.

However, in traditional HMM-based approaches, a limitation arises where the precise count of topics (hidden states) necessitates manual configuration, which becomes particularly challenging when the actual number of topics in a document remains unknown, as is often the case in practical scenarios. The resource-intensive process of manually determining topic counts, akin to directly identifying all story boundaries, proves unfeasible. Additionally, an erroneously selected topic count can detrimentally impact story segmentation outcomes. Therefore, the ability to automatically deduce topic counts from documents is of paramount importance. To address this, the integration of a hierarchical Dirichlet process (HDP) within the HMM framework (IHMM) is adopted, enabling topic count inference through clustering. This obviates the need for predefining the number of hidden states. The primary contributions of this study chiefly emanate from these two practical quandaries.

Our previous work focuses on the modelling process of IHMM, ignoring exploring the topic information from text which is crucial to the story segmentation task. In ^[36], we utilized a Sentence to Vector (Sen2Vec) model to convert entire sentences into fixed-length vector representations. Although Sen2Vec can learn the semantics of words through context, it contains few obvious topic information that is helpful to improve the performance of story segmentation systems. Thus, this paper uses a topical supervised VAEGAN to generate feature representation in the topic domain, on which each topic can be modelled accurately.

In this paper, we propose a story segmentation method based on a variational autoencoder generative adversarial network-infinite hidden Markov model (VAEGAN-IHMM). Unlike the traditional HMM method that the number of hidden states have to be preset, IHMM can infer the number of topics from data automatically. Besides, VAEGAN can capture intricate data representations through VAE's probabilistic encoding and decoding mechanism and enhance feature diversity and quality via GAN's adversarial training. Thus, we use VAEGAN to generate topical domain feature representation.

Our main contributions are described as follows:

1)   Powerful Feature Generation: by leveraging the robust feature generation capabilities of VAEGAN, VAEGAN-IHMM creates domain-specific features for story segmentation tasks under the guidance of topic labels. This enhances the relevance and quality of the generated features.

2)   Automatic topic number inference: to address the practical issue of unavailability of topic labels, VAEGAN-IHMM employs IHMM to automatically infer the number of topics. This approach eliminates the need for manually counting label categories or incorrectly presetting the number of labels, thereby preventing potential negative impacts on system performance.

3)   Improved segmentation accuracy: VAEGAN-IHMM achieves superior segmentation accuracy compared to other methods. This higher precision ensures more reliable and effective segmentation results in practical applications.

3.   The architecture of VAEGAN-IHMM

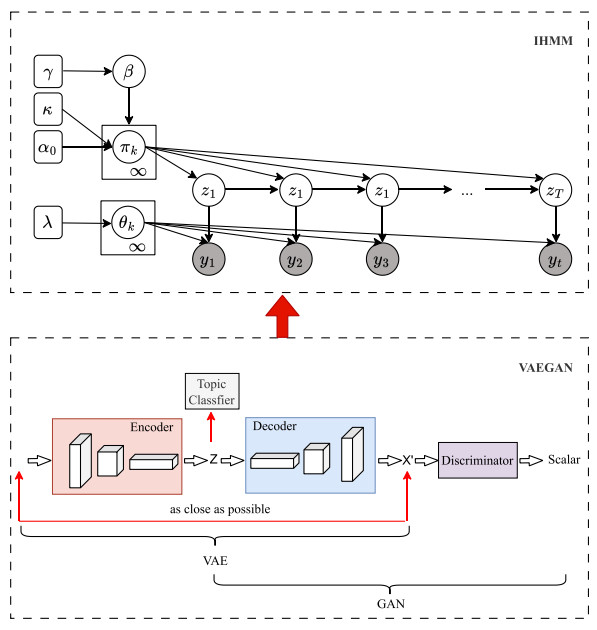
Figure 1 is the proposed VAEGAN-IHMM architecture. The lower part is a VAEGAN, and the upper part is an IHMM. The VAEGAN model is composed of four main components: 1) An encoder, 2) a decoder/generator, 3) a discriminator, and 4) a topical classifier layer. The encoder's function is to capture meaningful features within a latent topical space. The decoder, also serving as the generator, produces pseudo-documents from these latent representations. Concurrently, the discriminator assesses whether a document originates from the generator or the actual database. The objective of the generator is to create documents that closely mimic real ones, thereby complicating the task for the classifier in differentiating them from genuine database documents. Additionally, a topical classifier layer is connected to the generator to enhance the learning of topical information from the data. The classifier's role is to precisely identify whether documents are synthetically generated by the generator or are original to the database. Both the generator and the classifier undergo training through an adversarial process, continually improving their respective abilities to generate and evaluate documents.

In the described model, the lower section represents an IHMM. In traditional HMM, each hidden state is indicative of a specific topic, and transitions between these states are governed by a transition matrix 𝐴 of dimension 𝑁×𝑁, which models the probability of transitioning between states. Associated with each state is an emission probability distribution function (PDF), typically derived from an n-gram distribution related to the topic.

For the IHMM, the concept is expanded by transitioning the number of states to infinity. This is achieved by introducing a HDP prior distribution on the transition matrices, accommodating countably infinite state spaces as illustrated in the upper part of Figure 1. Within this framework, 𝜃 signifies the distribution of topics across an infinite dimensional space, while 𝜋 extends the HMM state transition matrix 𝐴 from a finite size 𝑁 to an infinite dimension. The parameters ${\alpha }_{0}$ and κ are key to our model. ${\alpha }_{0}$ measures how widely the base distribution varies, while κ shows how often the same state occurs consecutively. The parameter ${\alpha }_{0}$ is crucial for deciding how likely we are to create new clusters, with higher values of ${\alpha }_{0}$ leading to more topics. On the other hand, κ helps determine how long a topic remains relevant over time.

During the model's inference phase, the IHMM leverages the training data to automatically infer the number of topics from this infinite state space, allowing for a dynamically scalable model that adjusts to the complexity and breadth of the data it processes.

4.   VAEGAN based generative model

Given the powerful feature processing ability of neural networks, this paper uses the VAEGAN adversarial learning to model the probability distribution of the text stream in the topic space. VAEs are known for their ability to create a continuous and interpretable latent space representation. By combining VAE and GAN, we can potentially obtain both the power of GANs to generate realistic data and the interpretability of VAEs in the feature learning process. Besides, we use topic categories to guide model training. Then we use IHMM to model the document topic which can infer the number of topics from data automatically.

The lower part of Figure 1 shows the basic structure of VAEGAN. In this figure, the encoder is to learn a meaningful feature representation in the latent topical space. The Generator generates pseudo-documents based on their corresponding latent representation, while the discriminator distinguishes whether a document comes from the Generator or the real database. The goal of the Generator is to produce documents that are as realistic as possible, thus increasing the difficulty of the Classifier in distinguishing them from the original documents in the database. Besides, a topical classifier layer is linked to generator to learning the topical information from data. The purpose of the Classifier is to accurately distinguish the documents generated by the Generator from the original documents in the database. The Generator and the Classifier are trained by playing against each other.

4.1.   The joint generative model

A VAE involves training a neural network model to encode input data into a lower-dimensional latent space representation using an encoder network. The encoder generates mean $\left(\mu \right)$ and standard deviation ($\delta$) vectors to parameterize a multivariate Gaussian distribution, enabling the reparameterization trick for differentiable sampling. The decoder network then reconstructs the input data from the sampled latent vectors, minimizing the reconstruction loss (e.g., MSE or binary cross-entropy) during training. Additionally, a KL divergence loss regularizes the latent space, promoting a structured and interpretable representation. Given a running text, we elaborate the training process from Eqs (1) to (5). To better utilize contextual information, we adopt a fixed window length strategy to compute the BOW vector representation of the current word ${\mathrm{w}}_{\mathrm{t}}$:

where ${T}^{\mathrm{\text{'}}}+1$represents the window length of the text, ${\stackrel{~}{w}}_{t}$ represents the one-hot encoding of the word ${w}_{t}$, and ${x}_{t}$is the BOW vector representation of the current word. It is obtained by taking the mean of the words within the window, and its dimensionality is the same as the vocabulary size. At the beginning and end of a sentence, we represent the window length ${T}^{\mathrm{\text{'}}}$+1 by the actual number of words used in sum. In this way, we normalize ${x}_{t}$ independent of its position in the input sequence. The BOW vector ${x}_{t}$ has the dimension equal to the size of the vocabulary $\left|V\right|$, and captures the context where topical information derived from.

The encoder encodes real samples ${x}_{t}$ to obtain the mean $\left(\mu \right)$ and standard deviation ($\sigma$) of the latent space: $\mu$, $\sigma = Encoder\left({x}_{t}\right)$, and then sample a latent vector $z$ from the distribution $N\left(\mu, \sigma \right)$ using the reparameterization trick:

In the decoding process, the decoder decodes the latent vector $z$ to obtain the reconstructed samples$\widehat{{x}_{t}} = Decoder\left({z}_{t}\right),$and then calculate the reconstruction $loss\left({L}_{rec}\right)$ by computing the squared Euclidean distance between the input samples ${x}_{t}$ and the reconstructed samples:

The regularization loss (KL Divergence) is calculated between the approximated posterior distribution ${q}_{\varphi }\left(z\right|x$) and its corresponding true posterior distribution ${p}_{\theta }$($z\left|x\right)$:

In Eq (4), ${q}_{\varphi }\left(z\right|x$) is the function to approximate the posterior distribution ${p}_{\theta }\left(z\right|x)$. $z$ is the prior and follows normal distribution. KL loss is measured by computing the difference between the approximated posterior distribution and its corresponding true posterior distribution. To better learning topical domain feature representation, we use class labels to jointly train the VAE. The classifier loss is denoted as ${L}_{class}$. The loss of VAE is computed by combining the reconstruction loss and the regularization term:

By optimizing Eq (5), the encoder can capture the inherent structure of real features, which helps generator synthesize features with a similar distribution as the real ones.

4.2.   Adversarial categorization network

Given the inherent limitations of the element-wise similarity metric in adequately encapsulating intricate high-level global structures, our approach extends its capabilities by incorporating a conditional generative adversarial network (GAN) framework. This augmentation facilitates the simultaneous acquisition of feature distributions. Through a strategic interplay characterized by a two-player minimax competition, the generator, denoted as G, collaborates with the discriminator, denoted as D, to iteratively apprehend and refine the encompassing feature distribution landscape.

where G aims to minimize the loss ${L}_{GD}$:

where $z$ signifies an arbitrary representation sampled from a Gaussian distribution. This representation serves as the input to the GAN, in conjunction with the associated semantic embedding.

The discriminator (D) endeavors to minimize the ensuing loss function, articulated as follows:

Given the input elements $z, \widehat{z}$, and the semantic embedding, the primary objective of the generator resides in the synthesis of features akin to those extracted from authentic instances. Correspondingly, the discriminator's pivotal role entails the demarcation between genuine features and those artificially generated. It is worth noting that our amalgamated model seamlessly intertwines both GANs and VAEs. As such, both $\widehat{z}$ and $z$ are used to generate features based on the semantic embedding $s$. The generators in VAE and GAN are combined so that the joint generative model can capture both detailed and global information at the same time.

The stochastic gradient descent (SGD) is used to minimize the discriminator loss. From Eqs (1) and (8), we iteratively perform VAE training and GAN training steps to update the corresponding parameters in each step.

4.3.   Visualization of VAEGAN generated features

We extract the topic posterior vectors from a news segment in the TDT2 database using different network structures. Then, we use the t-SNE algorithm to map the high-dimensional vectors to a two-dimensional space for visualization. Figures 2(a)−(c) are the visualization results based on the DNN, LSTM, and VAEGAN models, respectively. Each point in the figure represents the topic posterior vector of a sentence, with different colors indicating different topic categories. The more compact the clusters in the figure, and the more uniform the color of the points within the clusters, the stronger the distinction of the vectors they represent in the topic space. Compared with Figures 2(a), (b), the clusters in Figure 2(c) are more compact, the colors of the points within the same cluster are more uniform, and the distance between clusters is greater. Besides, we utilized the silhouette coefficient (SC) to quantitatively analyze the classification performance of predictions made by DNN, LSTM networks, and VAEGAN. The Silhouette Coefficient assesses how closely a data point lies to others within its cluster (cohesion) and how far it is from points in other clusters (separation). The SC scores were 0.712 for DNN, 0.746 for LSTM, and 0.753 for VAEGAN, indicating that the VAEGAN model outperformed the others in distinguishing between different topics. We calculated these scores using the Euclidean distance. For the DNN and LSTM models, we set the number of topics at 170. In the VAEGAN-IHMM setup, we configured the parameters ${\alpha }_{0}$and $\kappa$ to 1. These results suggest that VAEGAN generates vectors with superior separation in the topic space.

5.   IHMM based story segmentation

5.1.   HMM based story segmentation

HMM is a typical generative model, and it was first applied to the story segmentation task by Yamron et al. in 1998 ^[34]. In HMM, each hidden state represents a topic. An N × N transition matrix describes the transitions between hidden states, which can be inferred from training data. Each hidden state in HMM is associated with a probability distribution function (emission probability), and each observed value (word) in the data stream is generated iteratively according to this probability distribution. The probability distribution function can be computed using an N-gram language model related to the hidden states. Given an observed word sequence and an HMM, the topic category can be inferred through the following process:

$\mathrm{z} = \left[{\mathrm{z}}_{1}, {\mathrm{z}}_{2}, \dots, {\mathrm{z}}_{\mathrm{T}}\right]$ represents topic sequences, $\mathrm{w} = \left[{\mathrm{w}}_{1}, {\mathrm{w}}_{2}, \dots, {\mathrm{w}}_{\mathrm{T}}\right]$ are observations, $\mathrm{\theta }$ represents HMM parameters, including transition probability and emission probability. According to Bayes' theorem, the optimization problem mentioned above can be transformed into:

p(w) is independent of the hidden state z in probability and can be ignored. The transition probability between states, p(z), is calculated using the following formula:

$\mathrm{p}\left({\mathrm{z}}_{\mathrm{t}}|{\mathrm{z}}_{\mathrm{t}-1}\right)$ is the transition probability from state ${\mathrm{z}}_{\mathrm{t}-1}$ to state${\mathrm{z}}_{\mathrm{t}}$. Assuming the conditional probabilities of words under a specific topic are independent of each other, it can be derived that:

The conditional probability of a word given a topic, $\mathrm{p}\left({\mathrm{w}}_{\mathrm{t}}|{\mathrm{z}}_{\mathrm{t}}\right)$, is computed using a language model that is related to the hidden state (topic). The topic transition probability and the topic-based language model can be obtained from a training set that includes boundary information and topic labels. From Eqs (9) to (13), we can effectively find the best topic sequence for test data using the Viterbi algorithm.

The segmentation based on HMMs constitutes a generative methodology. This approach encapsulates the generative progression governing both individual words and stories during the training phase. In the subsequent testing phase, the generative process is reversed to deduce the corresponding topic labels. The allocation of states within the HMM necessitates careful consideration, and the states number should be set in advance. Nonetheless, situations frequently arise where the topic number cannot be pre-set. Inspired by the recent success of HMM in the domain of speaker recognition ^[37], we introduce an HDP prior distribution governing transition matrices across infinite state spaces. This incorporation imparts the HMM with the intrinsic capability to autonomously infer the latent number of concealed states from the provided data, obviating the need for a priori knowledge. Consequently, the number of topics in a text does not need to be known in advance and can be derived from an inferring process.

5.2.   HDP for topic distribution description

5.2.1.   Dirichlet process

The Dirichlet process (DP) ^{[37,38,39,40]} serves as a stochastic process utilized for characterizing probability distributions within a measurable function space. Each instance drawn from a DP represents a distinct distribution. In a comprehensible context, the DP can be elucidated as an extension of the Dirichlet distribution to an infinite-dimensional setting. The formal specification of the DP is established through a base distribution denoted as $H$, alongside a concentration parameter denoted as ${\alpha }_{0}$, delineated as follows:

Consider H as a distribution defined over a parameter space denoted as $\theta$, with ${\alpha }_{0}$ representing a positive real value. Let ${A}_{1}, {A}_{2}, \mathrm{ }\dots, {A}_{r}$ constitute an arbitrary finite measurable partition of the parameter space $\theta$:

In the context of a stochastic probability measure $G$, if its distribution with respect to each finite partition adheres to a Dirichlet distribution:

We denote the assertion that G is sampled from a DP as $G\sim DP\left({\alpha }_{0}, H\right)$. The stochastic probability distribution $G$ is colloquially described as a partition derived from the underlying base distribution $H$. Consequently, $G$ is a discrete distribution sampled from the DP. The base distribution $H$ effectively represents the average of the DP. The concentration parameter, denoted as ${\alpha }_{0}$, quantifies the extent of dispersion in the $G$ distribution. A smaller value of α corresponds to heightened dispersion, while a larger value yields the opposite effect.

The stick-breaking construction ^[40] elucidates the generative procedure underlying the creation of a distribution $G$, which constitutes a realization of a DP. Precisely, $G$ is composed through a weighted aggregation of impulse functions, characterized by two crucial parameters: The positions of these impulse functions and their corresponding weights. These impulse functions, also referred to as atoms, collectively contribute to a sum of weights that is constrained to unity. Consequently, the formal representation of $G$ is as follows:

Here, ${\delta }_{\theta }$ represents a probability measure at$\theta,$ and ${\pi }_{k}$ denotes the associated weight, which is amenable to generation through a stick-breaking process as expounded in reference ^[41]:

With the introduction of a stick of unit length, the recursive procedure commences by drawing a sample ${\beta }^{1}$ from a Beta distribution characterized by the concentration parameter $\alpha$. The length of the initial broken portion is designated as ${\pi }^{1}$. Subsequently, the remaining portion of the stick, with a length of$1\mathrm{ }–{\beta }^{1}$, is divided once more using ${\beta }^{2}$, with the resulting segment representing ${\pi }^{2}$. Through this iterative process, an infinite sequence of weights, denoted as $\pi \mathrm{ₖ}$, is derived, signifying the weights assigned to new atoms, satisfying the condition ${\sum }_{k = 1}^{\mathrm{\infty }}{\pi }_{k} = 1$he concentration parameter $\alpha$ exerts an influence on the decay rate of $\pi$, implying that a smaller $\alpha$ leads to higher average values for lower-order $\pi \mathrm{ₖ}$ compared to those of higher-order terms. This construction, known as the Griffiths, Engen, and McCloskey (GEM) model, is commonly symbolized as $\pi \sim GEM\left({\alpha }_{0}\right)$ ^[40].

The DP is commonly employed as a prior distribution for the constituents of a mixture model, leading to what is known as the Dirichlet process mixture model (DPMM), as Figure 3 shows. A DPMM is characterized by a variable count of atoms, each accompanied by its respective weight. For instance, in the context of story segmentation, a DP can be applied to represent an individual topic (or state) along with its associated set of features. This parallel is reminiscent of how a standard Gaussian mixture model (GMM) is utilized to represent a distinct phonetic unit in speech recognition. The primary divergence between employing a DPMM and a GMM lies in the expansion of the number of mixture components from a finite to an infinite continuum. Furthermore, the incorporation of a DP prior over the transition matrix of topics (states) facilitates the modeling of documents as DPMMs. Within this construct, the number of topics can be inferred directly from the training data without necessitating predetermined specifications.

One intuitive way to understand how the DP allows for an infinite number of components is through the stick-breaking process. Imagine a stick of unit length. We break this stick at a point determined by a Beta distribution (parametrized by 1 and 𝛼), which gives us the size of the first piece (or the weight of the first cluster). We continue breaking the remaining part of the stick to determine the sizes of subsequent clusters. Theoretically, this process can continue infinitely, though in practice, the sizes of the pieces become increasingly small as the process continues. Figure 4 presents the graphical representation of the stick-breaking process, with the ensuing generative procedure articulated as follows:

Here, the subscript index of $\theta$ is denoted as ${z}_{i}$, while ${x}_{i}$ represents the observation.

5.2.2.   Hierarchical Dirichlet process

In the context of the DP, the conventional treatment involves data being modeled independently, precluding the sharing of elements, or atoms, between data groups. However, real-world scenarios frequently involve interconnected data groups that warrant the establishment of associations. An illustrative example is the aspiration to interlink topics across numerous documents, each modeled by their respective Dirichlet processes. To enable such element-sharing, a stratagem involves employing a common DP as the foundational distribution, followed by modeling each document using a DP that shares elements with other instances. This foundation dictates that topics adhere to a uniform set. This configuration, termed the HDP, facilitates the sharing of elements, though their associated weights are recalculated. Importantly, within the HDP construct, element-sharing is exclusive to atoms, while the reevaluation of their associated weights is a requisite undertaking. The procedural generation of the ${i}^{th}$observation within the ${j}^{th}$ group adheres to the ensuing description:

The above equations can be written as follows if we use ${z}_{jt} = k$ to represent ${\varphi }_{jt} = {\theta }_{k}$. The generative process is depicted by Figure 4.

5.2.3.   IHMM with HDP prior

The IHMM leverages the HDP to allow a HMM to support an infinite number of states, adapting its complexity to fit the data. In traditional HMMs, the number of hidden states is predefined and fixed, limiting the model's flexibility. IHMM addresses this by using a two-level DP: the first level, a global base distribution ${G}_{0}$, is drawn from a DP parameterized by a base distribution 𝐻 and a concentration parameter 𝛾. This global distribution acts as the prior for the second level, where each state-specific transition distribution ${\pi }_{i}$ is drawn from another DP that uses ${G}_{0}$ as its base, with its own concentration parameter 𝛼. This hierarchical structure allows each state to have its own set of transition probabilities while sharing statistical strengths through the global base distribution, enabling the model to potentially use an infinite number of states as needed.

An infinite IHMM encompasses a boundless count of concealed states. It can be viewed as a traditional HMM where the number of hidden states, denoted as $k$, extends indefinitely. As previously mentioned, within the context of conventional HMM-based story segmentation, let ${\pi }_{j}$ signify the distribution of words specific to a particular topic (also serving as the distribution for state transitions). Furthermore, ${z}_{t}$ represents a distinct topic (the state of a Markov chain) at time $t$, with its evolution governed by the equation ${z}_{t}\sim {{\pi }_{z}}_{t}-1$. The HDP, expounded in the preceding section, engenders an HMM endowed with an infinite topic space, termed the IHMM. Notably, the IHMM incorporates a doubly-infinite transition matrix where columns correspond to an endless array of topics, and each row, denoted as ${\pi }_{j}$, characterizes the associated word distribution specific to the respective topic. In this context, each row's constituents align with a group within the HDP structure.

The upper part of Figure 1 is the graphical model of IHMM and its corresponding generative process:

The notation GEM represents the stick-breaking construction. Notably, the prior distribution DP (α₀, β) serves as a foundational distribution that generates common topics for every topic-specific distribution ${\pi }_{j}$. In other words, this means that the set of topics is shared across all states.

5.3.   Inference

In terms of inference, determining the underlying structure and parameters of an IHMM from observed data typically involves Bayesian computational techniques such as Markov Chain Monte Carlo (MCMC). In the proposed approach, we utilized blocked sampling, a kind of MCMC, to inference the number of hidden states from data.

Given a sequence of observations represented as $X = {x}_{1}, {x}_{2}, \dots, {x}_{T}$, the task aims at inferring hidden states $Z,$the self-transition matrix $\pi$, the base distribution $\beta$, and emission probabilities $\theta$. Various inference algorithms are available, such as direct assignments ^[41,42,43] and blocked sampling ^[44]. The fundamental concept behind direct assignments is to marginalize state-specific transitions ${\pi }_{k}$, ${\theta }_{k}$ and sequentially sample the state ${z}_{t}$ based on state assignments ${z}_{\backslash t}$, the observation ${x}_{1:T}$, and the transition distribution $\beta$. Subsequently, the posterior probability of the global transition distribution $\beta$ can be sampled. However, direct assignment suffers from low efficiency due to certain limitations. The efficiency of direct assignment is compromised by its low mixing rate, a result of the global state sequence changing strategy applied coordinate by coordinate. In contrast, the blocked sampler ^[44] employs a modified forward-backward procedure to address the sluggish mixing rate inherent in direct assignment sampling. Thus, we use blocked sampling to infer the parameters of IHMM. The detailed information is depicted in Algorithms 1 and 2.

6.   Experiments

6.1.   Experimental setting

We use a F1-measure (the weighted average of precision and recall) to validate the story segmentation results. We compare the topic boundaries found by the algorithm with the manually annotated topic boundaries. According to the TDT2 ^[45] international evaluation standard ^[38], if the boundary position error is within 50 words, it is considered that the algorithm has successfully found a story boundary. Precision represents the percentage of correctly discovered boundaries in the total number of boundaries. Recall represents the percentage of correctly discovered boundaries in the actual number of boundaries. The specific definition of F1-measure is as follows:

6.2.   Results of IHMM on synthetic data

Within this section, an in-depth analysis is conducted on the efficacy of the Infinite IHMM framework through the utilization of synthetic data. The dataset encompasses a total of 288 samples, each exhibiting 3 dimensions. The IHMM model is employed for the purpose of deducing the probability distributions inherent to the data, and this inferred distribution is juxtaposed against the actual distribution of the data. It is presumed that the data conforms to a Gaussian distribution, with the hyperparameters ${\alpha }_{0}$, $\kappa$, and $\gamma$ set to specific values of 1.

Figure 5 illustrates the outcomes following 2361 iterations of IHMM sampling. In Figure 5(a), the three-dimensional values of the synthetic data are graphically portrayed. The x-axis corresponds to time, while the y-axis denotes data values across three dimensions, color-coded in red, blue, and green. Concurrently, the adjacent portion portrays the corresponding probability distribution of the data values within these dimensions. Moving to Figure 5(b), the distribution inferred by IHMM is depicted, with the background showcasing the probability distribution of the synthetic data for comparative evaluation. The similarity observed in the shapes of corresponding curves between Figure 5(a), (b) suggests a consistent alignment between the probability distribution deduced by IHMM and that of the training data, providing initial evidence of the framework's efficacy. Figure 5(c) offers a visual representation of the transition matrix within IHMM. Notably, the yellow-colored dot along the diagonal signifies a substantial self-transition probability, indicating the successful in enhancing state persistence.

6.3.   Experimental results and analysis

6.3.1.   Results of TextTiling and DP approaches on VAEGAN generated features

The VAEGAN generated features can be used directly for the story segmentation algorithm. To preliminarily verify the effectiveness of the VAEGAN feature, we used it in two traditional story segmentation algorithms, TextTiling and Dynamic Programming (DP), and compares it with the story segmentation results obtained using TF-IDF and LDA feature representations. The experimental results are shown in Table 1. Through parameter tuning, this paper sets the sliding window length of the VAEGAN input words to 60 and the number of topics to 150. The experimental results show that we have obtained story segmentation results superior to those of TF-IDF and LDA topic features using the topic posterior feature. VAEGAN achieved the best story segmentation results.

6.3.2.   F1-measure with different value of ${\alpha }_{0}and\kappa$

As detailed in Section 3.2, the parameters ${\alpha }_{0}$ and $\kappa$ bear significance in representing the extent of dispersion in the base distribution and the likelihood of self-transitions within states, respectively. Parameter $\alpha$ plays a pivotal role in determining the likelihood of introducing new clusters, thereby favoring a higher count of topics with larger $\alpha$ values. Moreover, parameter $\kappa$ contributes to modeling the temporal duration of a topic's persistence. To scrutinize the impact of ${\alpha }_{0}$ and $\kappa$ on segmentation performance, these parameters are treated as tunable variables. With reference to ^[46], we set γ to 1, and designate the freedom parameter $v$ as 52. In Figure 6, diverse values of ${\alpha }_{0}$ are examined, while maintaining $\kappa$at 1. The x-axis denotes ${\alpha }_{0}$ values, whereas the y-axis on both sides of the figure signifies the topic count and the F1-measure. Across the ${\alpha }_{0}$ range of 0.01 to 100, the F1-measure ranges from 0.770 to 0.781, while the topic count fluctuates within a small interval of 153 to 172. The optimal segmentation outcome of 0.781 is achieved at ${\alpha }_{0}$ = 1, corresponding to a topic count of 172. Moving to Figure 7, the impact of varying $\kappa$ values on segmentation outcomes and topic counts is depicted. Evidently, across different combinations of ${\alpha }_{0}$ and $\kappa$, the topic count hovers around the actual value of 170, underscoring the minor influence of these parameters on segmentation results. The highest F1-measure of 0.781 is realized when both ${\alpha }_{0}$ and $\kappa$ are set to 1.

6.3.3.   The influence of the number of topics on the results of story segmentation

Figure 8 elucidates the impact of topic numbers on the segmentation outcomes within both the VAEGAN-IHMM and the conventional HMM approach. In the traditional HMM framework, a sentence vector of dimensionality 50 is utilized, the same as that in VAEGAN-IHMM. The solid and dashed lines correspondingly represent the F1-measure values for the traditional HMM and VAEGAN-HMM. A salient observation emerges, wherein the segmentation performance of the conventional HMM is notably contingent on the selected topic count, and an ill-suited predefined topic count leads to suboptimal segmentation outcomes. In contrast, the IHMM exhibits a comparatively stable topic count inferred from the dataset, consistently aligning within a restricted range (153 to 172) around the accurate topic number (170), across diverse hyperparameter settings. Consequently, IHMM proves to be considerably more effective when dealing with documents of an unknown topic count, circumventing the subpar segmentation performance stemming from the conventional HMM's reliance on an improperly specified topic number.

Table 2 highlights how the F1-measure is significantly impacted by the number of topics in the conventional HMM approach. Conversely, our IHMM is capable of automatically inferring the number of topics from the text, thus circumventing the performance degradation typically associated with incorrectly preset topic numbers in traditional HMMs. Table 2 clearly demonstrates that an inappropriate preset number of topics can severely affect the F1-measure, leading to suboptimal performance.

6.3.4.   Comparison with different methods

We conducted a comprehensive comparison of the proposed approach against various approaches, with the summarized results presented in Table 3. In the PLSA-DP-CE approach, the dimensionality of LE projection is set at 50. For Lap-PLSA, convergence is achieved at a threshold of 1.0 × 10⁻⁴, and the latent topic count is established at 50 to match the dimensionality of the sentence vector in the VAEGAN-IHMM approach, ensuring a fair assessment. It is worth noting that all these approaches were meticulously executed on the TDT2 corpus to facilitate an equitable evaluation. To account for potential variability, each combination of hyperparameters and features underwent 10 trial runs, yielding reported mean and standard deviation values for F1-measure alongside corresponding precision and recall scores. It is observed that all approaches yield higher recall scores than their corresponding precision scores, indicative of the propensity to uncover false positive boundaries. Among these, the proposed VAEGAN-IHMM approach emerges as the superior performer, signifying the effectiveness of both VAEGAN-generated features and the segmentor IHMM. This approach not only demonstrates a higher F1 score in comparison to traditional methodologies but also highlights a significant advantage: Its ability to operate without prior knowledge of the number of topics, a pivotal asset in real-world scenarios. Additionally, VAEGAN-IHMM attains a heightened recall score compared to conventional methods, implying the discovery of more authentic story boundaries.

Comparing to the nonparametric Bayesian DD-CRP approach, which can also function without prior topic count knowledge, VAEGAN-IHMM excels in terms of achieving a superior F1-measure. However, it's acknowledged that VAEGAN-IHMM does involve a more substantial computational cost than DD-CRP due to the utilization of Gibbs sampling and EM algorithms in its inference process. While one iteration of Gibbs sampling is computationally similar to an iteration of EM, the former undergoes more iterations, consequently incurring a greater computational expense.

Comparing to our previous work ^[48], the F1-measure of this study is 3.9% higher than SHDP-HMM (from 0.752 to 0.781), which can be attributed to the topical domain representation generated by topical VAEGAN.

Furthermore, the proposed approach is evaluated against prominent state-of-the-art techniques, namely DNN-HMM and LSTM-HMM. These methodologies utilize neural networks for estimating the emission probability of hidden states, thus achieving commendable F1-measure results attributed to their robust feature extraction capabilities. Nonetheless, these approaches necessitate a predefined topic count, rendering them impractical for real-world scenarios, as previously discussed. Notably, the results show that the proposed VAEGAN-IHMM approach, LapPLSA, and the neural network-based approaches are relatively stable, as indicated by small standard deviations all below 0.010.

7.   Conclusions

We propose a VAEGAN-IHMM method for story segmentation, an innovative approach that integrates VAEGAN with an Infinite Hidden Markov Model to advance feature learning and segmentation accuracy. By harnessing VAEGAN, which utilizes both the VAE and GAN, adapting these frameworks to capture the probabilistic distributions of text in hidden topic spaces. VAE excels in learning features in the latent space, while GAN is renowned for its generative capabilities, which may enhance the model's ability to manage sequence context information. Additionally, the inclusion of topic labels aids the model in extracting topic-relevant information from the context. This adaptation is crucial for transforming bag-of-words vectors into meaningful topical domain embeddings, a step forward in text analysis that responds to the need for deeper semantic understanding.

Our IHMM extends traditional HMM approaches by incorporating HDP which enables our model to autonomously infer the number of topics (hidden states) within a document, addressing a common limitation in traditional text segmentation methodologies, which often require predetermined parameters. By using an HDP, our approach aligns with recent shifts towards more flexible, data-driven models that can adapt to the complexities and variabilities of real-world data.

Experiments on the TDT2 database showed that the method proposed in this paper achieved the state-of-the-art story segmentation results compared with other segmentation approaches.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the China Scholarship Council (Grant No. 202008410014) and the Science and Technology Breakthrough Project of Henan Science and Technology Department (232102210065). Conception of the study: Jia Yu, Nianfeng Shi; Analysis and preprocessing of data: Jia Yu, Huiling Peng; Algorithm design: Huiling Peng, Guoqiang Wang, Jia Yu; Experiment performing: Jia Yu; Drafting the manuscript: Jia Yu; Revising the manuscript: Nianfeng Shi.

Conflicts of interest

The authors declare that they have no conflicts of interest to report regarding the present study.

Availability of data and materials

The TDT2 corpus is available on: https://catalog.ldc.upenn.edu/LDC2001T57.