Stability of an adaptive immunity delayed HIV infection model with active and silent cell-to-cell spread

1.   Introduction

During the last decades, mathematical modeling and analysis of within-host human immunodeficiency virus (HIV) infection have become important and helpful tools for better understanding of HIV dynamics ^[1]. HIV is the causative agent of acquired immunodeficiency syndrome (AIDS). The main target cells of HIV is the healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells which play an important role in the immune system. The basic HIV dynamics model has been formulated by Nowak and Bangham ^[1], which describes the interaction between ${\rm{CD}}{4^ + }{\rm{T}}$ cells ($S$), infected cells ($I$), and free HIV particles ($V$). The incidence rate of infection has been given by bilinear form $\eta SV$. This form has been generalized by considering saturation incidence ^[2,3], Beddington-DeAngelis incidence ^[4,5], general incidence ^[6,7,8,9]. The basic model has also been extended by including time delay ^{[10,11,12,13]}.

An adaptive immunity after viral infection plays a fundamental role in controlling the disease progression for long period up to 10 years. The adaptive immune response has two main arms, cell-mediated immunity which based on the Cytotoxic T lymphocytes (CTLs) that kill the HIV-infected cells, and humoral immunity which based on the B cells that produce antibodies to neutralize the HIV particles. In the literature, many works have been published which are devoted to address the effect of CTL-mediated immune response on the HIV infection (see e.g. ^[1] and ^[14,15]). Moreover, antibody immune response has been considered into mathematical models of viral infection in several works (see e.g. ^[16,17,18]). In 2003, Wodarz ^[19] has presented a virus dynamics model which incorporates the effect of both antibody and CTL-mediated immune responses. Dubey et al. ^[20] have extended the model in ^[19] by adding a logistic growth term which represents the proliferation of healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells. Moreover, the model in ^[20] incorporates a combination of two classes of antiviral treatment, protease inhibitor and reverse transcriptase. Su et al. ^[21] have developed the model presented in ^[19] by considering Beddington-DeAngelis incidence rate to replace the mass-action incidence rate. Yousfi et al. ^[22] have suggested a model to describe the dynamics of hepatitis B virus. In ^[20,21,22], it has been assumed that the infection processes are instantaneous. However, it has been estimated that the time between the HIV enters a target cell until producing new HIV particlesis about 0.9 day ^[23]. Therefore, more realistic virus dynamics models are obtained when time delay is incorporated. Yan and Wang ^[24] have extended the model of Wodarz ^[19] by incorporating a discrete-time delay for production of active infected cells. The model of Yan and Wang ^[24] has been extended by Wang and Liu ^[25] and Wang et al. ^[26] to include; saturated incidence rate and two types of distributed delays, respectively. Elaiw and AlShamrani ^[27] have studied an adaptive immunity viral infection model with distributed time delays and general incidence rate.

In ^{[19,20,21,22,23,24,25,26,27]}, it has been assumed that the infection occurs due to virus-to-cell transmission (VTC). It has been reported in several works that the healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells can also be infected due to cell-cell contact known as cell-to-cell transmission (CTC) (see e.g. ^[28,29,30]). Therefore, CTC transmission plays an important role in the HIV infection process even during the antiviral treatment ^[31]. Guo et al. ^[32] incorporated the CTC transmission and two discrete-time delays to the same model of Yan and Wang ^[24]. Lin et al. ^[33] have replaced the VTC bilinear incidence rate by a saturated incidence one. Adaptive immunity HIV dynamics model with two distributed-time delays and both VTC and CTC transmission has been studied in ^[34].

Highly active anti-retroviral therapy is very effective in controlling HIV replication and reducing disease progression, however, it can not completely remove the HIV from the body. The major barrier to HIV clearance is the silent (latent) ${\rm{CD}}{4^ + }{\rm{T}}$ infected cells ^[35]. Silent ${\rm{CD}}{4^ + }{\rm{T}}$ infected cells are considered as viral reservoirs for long time until they are activated to produce new HIV particles. Mathematical models of HIV with silent infected cells have been considered in several works (see e.g. ^{[36,37,38,39,40]}). Recently, Agosto et al. ^[41] have shown that both silent and active infected ${\rm{CD}}{4^ + }{\rm{T}}$ cells can infect the healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells through CTC mechanism. Silent HIV-infected cells have been included in the virus dynamics models with both VTC and CTC transmissions in ^{[42,43,44,45]}, however, the contribution of silent infected cells in the CTC transmission has been neglected. In ^[46,47] a class of viral infection models have been formulated by assuming that both silent and active infected cells can participate in cell-to-cell infection, however, the immune response has been neglected. In a very recent work, Elaiw and Alshamrani ^[48] have investigated an HIV dynamics model with silent and active CTC transmissions and CTL immune response. In ^[48] the antibody immune response has not been included.

In this present paper, we extend on the research done in the above mentioned works by including three distributed time delays and both VTC and CTC transmissions. The CTC mechanism consists of silent HIV-infected CTC and active HIV-infected CTC transmissions. The incidence rates of the healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells with free HIV particles, silent HIV-infected cells, and active HIV-infected cells are given by general functions. Moreover, the production/proliferation and removal/death rates of all compartments are represented by general functions.

The rest of the paper is organized as follows: In Section 2, we formulate an HIV dynamics model. In Section 3, we prove the nonnegativity and boundedness of solutions of the proposed model. Then we study the existence of all possible equilibria of the model in Section 4, which depend on five threshold parameters. In Section 5, we investigate the global stability of the five equilibria by constructing suitable Lyapunov functionals. These results are supported with numerical simulations in Section 6. The paper ends with a conclusion.

2.   Model formulation

We formulate an adaptive immunity HIV infection model by assuming that the HIV virions can replicate by two mechanisms, VTC and CTC transmissions. The CTC infection has two sources, (i) the contact between healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells and silent HIV-infected cells, and (ii) the contact between healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells and active HIV-infected cells. Under these assumptions we propose a model that contains six compartments: healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells, silent HIV-infected ${\rm{CD}}{4^ + }{\rm{T}}$ cells, active HIV-infected ${\rm{CD}}{4^ + }{\rm{T}}$ cells, free HIV particles, HIV-specific CTLs and HIV-specific antibodies.

where $S(t),$ $L(t),$ $I(t),$ $V(t),$ $C(t)$ and $A(t)$ are the concentrations of healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells, silent HIV-infected cells, active HIV-infected cells, free HIV particles, HIV-specific CTLs and HIV-specific antibodies at time $t$, respectively. Function $\yen (S)$ refers to the intrinsic growth rate of healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells accounting for both production and natural mortality. The virus-cell, silent infected cell-cell and active infected cell-cell incidence rates are given by general nonlinear functions $\aleph_{1}(S, V),$ $\aleph_{2}(S, L)$ and $\aleph_{3}(S, I)$, respectively. The terms $\lambda \mathcal{J}_{1}(L)$ and $\gamma \mathcal{J} _{1}(L)$ are the rates of silent HIV-infected cells that become active and the natural death of the silent HIV-infected cells, respectively. The term $\mu \mathcal{J}_{4}(C)\mathcal{J}_{2}(I)$ is the killing rate of active HIV-infected cells due to their specific CTL-mediated immunity. The proliferation rates for effective HIV-specific CTLs is given by $\sigma \mathcal{J}_{4}(C)\mathcal{J}_{2}(I)$. The proliferation rate for HIV-specific antibodies is given by $\tau \mathcal{J}_{5}(A)\mathcal{J}_{3}(V)$. The integral $\int \limits_{0}^{\kappa_{3}}\Lambda_{3}(\theta)e^{-\hslash_{3} \theta}\mathcal{J}_{2}(I(t-\theta))d\theta$ describes the mature viral particles produced at time $t$. The mature HIV particles die at rate $\varepsilon \mathcal{J}_{3}(V)$ and neutralized from the plasma due to HIV-specific antibodies at rate $\varpi \mathcal{J}_{5}(A)\mathcal{J}_{3}(V)$. In this proposed model, we assume the following:

● The virus or silent HIV-infected cells or active HIV-infected cells contacts a healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cell at time $t-\theta$, and the cell becomes silent HIV-infected cells at time $t$, where $\theta$ is a random variable taken from a probability distribution $\Lambda_{i}(\theta)$ over the time interval $\left[0, \kappa_{1}\right],$ where $\kappa_{1}$ is the limit superior of this delay period. The term $e^{-\hslash_{1}\theta}$ represents the probability of surviving from time $t-\theta$ to time $\theta$ ^[37].

● The silent HIV-infected cell takes $\theta$ time units to transmit to active HIV-infected cell, where $\theta$ is a random variable taken from a probability distribution $\Lambda_{2}(\theta)$ over the time interval $\left[0, \kappa_{2}\right],$ where $\kappa_{2}$ is the limit superior of this delay period. The term $e^{-\hslash_{2}\theta}$ represents the probability of surviving from time $t-\theta$ to time $\theta$.

● The time necessary for the newly produced virions to become mature and infectious is a random variable with a probability distribution $\Lambda _{3}(\theta)$ over the time interval $\left[0, \kappa_{3}\right],$ where $\kappa_{3}$ is the limit superior of this delay period. The term $e^{-\hslash_{3}\theta}$ denotes the probability of surviving the immature virions during the delay period ^[37]. Here $\hslash_{i},$ $i = 1, 2, 3$ are positive constants.

The function $\Lambda_{i}(\theta),$ $i = 1, 2, 3$ satisfies $\Lambda_{i} (\theta) > 0$ and

where $u > 0$. Let us denote

Thus $0 < \mathcal{H}_{i}\leq1,$ $i = 1, 2, 3$. The initial conditions of system (2.1) is given by:

where $\epsilon_{j}(\ell)\in \mathcal{C}([-\kappa, 0], \mathbb{R}_{\geq0})$, $j = 1, 2, ..., 6$ and $\mathcal{C} = \mathcal{C}([-\kappa, 0], \mathbb{R}_{\geq0})$ is the Banach space of continuous functions mapping the interval $[-\kappa, 0]\ $ into $\mathbb{R}_{\geq0}$ with norm $\Vert \epsilon_{j}\Vert = \underset{-\kappa \leq m\leq0}{\sup}\left \vert \epsilon_{j}(m)\right \vert$ for $\epsilon_{j}\in \mathcal{C}$. Therefore, system (2.1) with initial conditions (2.2) has a unique solution by using the standard theory of functional differential equations (see ^[49,50]). All parameters and their definitions are summarized in Table 1.

Functions $\yen$, $\aleph_{i}$, $i = 1, 2, 3$ and $\mathcal{J}_{k}$, $k = 1, 2, ..., 5$, are continuously differentiable and satisfy the following conditions in ^[6,51,52]:

Condition (H1). (i) there exists $S_{0}$ such that $\yen (S_{0}) = 0$ and $\yen (S) > 0$ for $S\in \lbrack0, S_{0})$,

(ii) $\yen ^{\prime}(S) < 0$ for all $S > 0$,

(iii) there are $\rho > 0$ and $\alpha_{0} > 0$ such that $\yen (S)\leq \rho -\alpha_{0}S$ for $S\geq0$.

Condition (H2). (i) $\aleph_{i}(S, U) > 0$ and $\aleph _{i}(0, U) = \aleph_{i}(S, 0) = 0$ for all $S > 0$, $U > 0,$ $i = 1, 2, 3,$

(ii) $\dfrac{\partial \aleph_{i}(S, U)}{\partial S} > 0,$ $\dfrac{\partial \aleph_{i}(S, U)}{\partial U} > 0$ and $\left. \dfrac{\partial \aleph_{i} (S, U)}{\partial U}\right \vert _{U = 0} > 0$ for all $S > 0,$ $U > 0$, $i = 1, 2, 3,$

(iii) $\dfrac{d}{dS}\left(\left. \dfrac{\partial \aleph_{i}(S, U)}{\partial U}\right \vert _{U = 0}\right) > 0$ for all $\ S > 0$, $i = 1, 2, 3$.

Condition (H3).(i) $\mathcal{J}_{k}(x) > 0$ for all $x > 0$, $\mathcal{J}_{k}(0) = 0$, $k = 1, 2, ..., 5,$

(ii) $\mathcal{J}_{k}^{\prime}(x) > 0$ for all $x > 0,$ $k = 1, 2, ..., 5$. Further, $\mathcal{J}_{k}^{\prime}(0) > 0$, $k = 1, 2, 3$,

(iii) there are $\alpha_{k} > 0$ such that $\mathcal{J}_{k} (x)\geq \alpha_{k}x$ for all $x\geq0$, $k = 1, 2, ..., 5.$

Condition (H4). $\dfrac{\partial}{\partial V}\left(\dfrac{\aleph_{1}(S, V)}{\mathcal{J}_{3}(V)}\right) \leq0$, $\dfrac{\partial }{\partial L}\left(\dfrac{\aleph_{2}(S, L)}{\mathcal{J}_{1}(L)}\right) \leq0$

and $\dfrac{\partial}{\partial I}\left(\dfrac{\aleph_{3}(S, I)} {\mathcal{J}_{2}(I)}\right) \leq0$ for all $\ S,$ $L,$ $I,$ $V > 0$.

3.   Well-posedness of solutions

Proposition 1. Suppose that conditions H1-H3 are satisfied. Then all solutions of system (2.1) with initial conditions (2.2) are nonnegative and ultimately bounded.

Proof. First, we show the nonnegativity of solutions. The proof is similar to the one given in ^[53]. System (2.1) can be written as: $\dot{X}(t) = \mathcal{W}(X(t))$, where $X(t) = \left(S(t), L(t), I(t), V(t), C(t), A(t)\right) ^{T}$, $\mathcal{W} = (\mathcal{W} _{1}, \mathcal{W}_{2}, \mathcal{W}_{3}, \mathcal{W}_{4}, \mathcal{W} _{5}, \mathcal{W}_{6})^{T}$ , and

It is easy to see that the function $\mathcal{W}$ satisfies the following condition

Due to Lemma 2 in ^[54], any solution of system (2.1) with initial conditions (2.2) satisfies $X(t)\in \mathbb{R}_{\geq0}^{6}$ for all $t\geq0.$ It means that model (2.1) is biologically acceptable in the sense that no population goes negative. In addition, the orthant $\mathbb{R}_{\geq0}^{6}$ is positively invariant for system (2.1). Next, we establish the boundedness of the model's solutions. The nonnegativity of the model's solution together with condition H1 implies that $\lim \sup_{t\rightarrow \infty}S(t)\leq \dfrac{\rho}{\alpha_{0}}$. To show the ultimate boundedness of $L(t)$ we let $\Psi_{1}(t) = \int \limits_{0}^{\kappa _{1}}\mathcal{\bar{H}}_{1}(\theta)S(t-\theta)d\theta+L(t),$ then using conditions H1 and H3 we get

where $\phi_{1} = \min \{ \alpha_{0}, \alpha_{1}\left(\lambda+\gamma \right) \}$. It follows that, $\lim \sup_{t\rightarrow \infty}\Psi_{1}(t)\leq \Omega_{1}$, where $\Omega_{1} = \dfrac{\rho}{\phi_{1}}$. Since $\int \limits_{0} ^{\kappa_{1}}\mathcal{\bar{H}}_{1}(\theta)S(t-\theta)d\theta$ and $L(t)$ are nonnegative, then $\lim \sup_{t\rightarrow \infty}L(t)\leq \Omega_{1}$. Moreover, we let $\Psi_{2}(t) = I(t)+\dfrac{\mu}{\sigma}C(t)$, then using condition H3 we obtain

where $\phi_{2} = \min \{a\alpha_{2}, \pi \alpha_{4}\}$. It follows that, $\lim \sup_{t\rightarrow \infty}\Psi_{2}(t)\leq \Omega_{2}$, where $\Omega_{2} = \dfrac{\lambda \mathcal{J}_{1}(\Omega_{1})}{\phi_{2}}$. Since $I(t)\geq0$ and $C(t)\geq0$, then $\lim \sup_{t\rightarrow \infty}I(t)\leq \Omega_{2}$ and $\lim \sup_{t\rightarrow \infty}C(t)\leq \Omega_{3}$, where $\Omega_{3} = \dfrac{\sigma}{\mu}\Omega_{2}$. Finally, let $\Psi_{3}(t) = V(t)+\dfrac{\varpi }{\tau}A(t)$, then applying condition H3 we get

where $\phi_{3} = \min \{ \varepsilon \alpha_{3}, \zeta \alpha_{5}\}$. It follows that, $\lim \sup_{t\rightarrow \infty}\Psi_{3}(t)\leq \Omega_{4}$, where $\Omega_{4} = \dfrac{b\mathcal{J}_{2}(\Omega_{2})}{\phi_{3}}$. Since $V(t)\geq0$ and $A(t)\geq0$, then $\lim \sup_{t\rightarrow \infty}V(t)\leq \Omega_{4}$ and $\lim \sup_{t\rightarrow \infty}A(t)\leq \Omega_{5}$, where $\Omega_{5} = \dfrac{\tau}{\varpi}\Omega_{4}$.

According to Proposition 1 we can show that the region

is positively invariant with respect to system (2.1).

4.   Equilibria

In this section, we study the equilibria of the model and derive the conditions for their existence.Let $Ð _{1} = (S, L, I, V, C, A)$ be any equilibrium satisfying the following system of algebraic equations:

If $V = 0$, then model (2.1) always admits an infection-free equilibrium, $Ð _{0} = (S_{0}, 0, 0, 0, 0, 0)$, where $\yen (S_{0}) = 0$. This case describes the situation of healthy state where the HIV infection is absent. If $V\neq0$, then from Eqs. (4.5) and (4.6) we have four possibilities:

(i) $\mathcal{J}_{4}(C) = \mathcal{J}_{5}(A) = 0;$ which leads to $C_{1} = A_{1} = 0$. From Eqs. (4.1)-(4.4) we get

Condition H3 implies that $\mathcal{J}_{k}^{-1}$ exists, continuous and strictly increasing. From Eq. (4.7), we obtain

where

Obviously from condition H1, $f_{i}(S) > 0$ for all $S\in \lbrack 0, S_{0})$ and $f_{i}(S_{0}) = 0,$ $i = 1, 2, 3$ . Let us define

Then from conditions H1-H3, we have

Moreover,

Condition H2 implies that $\frac{\partial \aleph_{i}(S_{0}, 0)}{\partial S} = 0,$ $i = 1, 2, 3$. Also, from condition H3, we have $\mathcal{J}_{3}^{\prime}(0) > 0,$ then

From Eqs. (4.7) and (4.8), we obtain

From condition H1, we have $\yen ^{\prime}(S_{0}) < 0$. Therefore, if

then $\mathcal{F} _{1}^{\prime}\left(S_{0}\right) < 0$ and there exists $S_{1}\in(0, S_{0})$ such that $\mathcal{F} _{1}\left(S_{1}\right) = 0$. From Eq. (4.8) and condition H3, we have

It follows that $Ð _{1} = (S_{1}, L_{1}, I_{1}, V_{1}, 0, 0)$ exists when

We call $Ð _{1}$ as a chronic HIV infection equilibrium with inactive immune responses. In order to state the threshold dynamics of infection-free equilibrium, it is necessary to define the basic HIV reproduction number $\Re_{0}$ of the model. The basic HIV reproduction number of model (2.1) can be calculated by different methods such as (a) the next-generation matrix method of van den Driessche and Watmough ^[55], (b) local stability of the infection-free equilibrium, and (c) the existence of the chronic HIV infection equilibrium with inactive immune responses. In the present paper, we derive $\Re_{0}$ by method (c) as follows:

where

The parameter $\Re_{0}$ determines whether or not the infection will be chronic. In fact, $\Re_{01}$ measures the average number of secondary HIV-infected cells caused by free HIV particles due to VTC transmission, while $\Re_{02}$ and $\Re_{03}$ measure the average numbers of secondary HIV-infected cells caused by silent and active HIV-infected cells, respectively, due to CTC transmission.

(ii) $\mathcal{J}_{4}(C)\neq0$, $\mathcal{J}_{5}(A) = 0;$ which leads to $\mathcal{J}_{2}(I_{2}) = \dfrac{\pi}{\sigma},$ $A_{2} = 0\ $ and this gives $I_{2} = \mathcal{J}_{2}^{-1}\left(\dfrac{\pi}{\sigma}\right)$. From Eqs. (2.1)-(4.3) we get

According to condition H3 and from Eq. (4.4) we have

Then, we obtain

From Eq. (4.9), we get

Obviously from condition H1 we have $f_{4}(S) > 0$ for all $S\in \lbrack0, S_{0})$ and $f_{4}(S_{0}) = 0$ . Let $V = V_{2}$, $I = I_{2}$ and using Eq. (4.11) in Eq. (4.1), we define

Conditions H1 and H2 imply that $\mathcal{F} _{2}(0) = \yen (0) > 0$ and $\mathcal{F} _{2}\left(S_{0}\right) = -\left[\aleph_{1}(S_{0}, V_{2})+\aleph_{3} (S_{0}, I_{2})\right] < 0$. Thus, from the intermediate value property there exists $S_{2}\in(0, S_{0})$ such that $\mathcal{F} _{2}(S_{2}) = 0$.From Eq. (4.11) and condition H3, we obtain

Further, from Eq. (4.9), we have

Clearly, $C_{2} > 0$ when $\dfrac{\lambda \mathcal{H}_{1}\mathcal{H}_{2}\left[\aleph_{1}(S_{2}, V_{2})+\aleph_{2}(S_{2}, L_{2})+\aleph_{3}(S_{2}, I_{2})\right] }{a\left(\lambda+\gamma \right) \mathcal{J}_{2}(I_{2})} > 1.$ Now we define the HIV-specific CTL-mediated immunity reproduction number as follows:

From Eq. (4.10), we get

Thus, $C_{2} = \mathcal{J}_{4}^{-1}\left(\dfrac{a}{\mu}\left(\Re _{1}-1\right) \right)$. The parameter $\Re_{1}$ determines whether or not the HIV-specific CTL-mediated immune response is stimulated. Therefore, $Ð _{2} = (S_{2}, L_{2}, I_{2}, V_{2}, C_{2}, 0)$ exists when $\Re_{1} > 1$. We call $Ð _{2}$ as a chronic HIV infection equilibrium with only active CTL-mediated immune response.

(iii) $\mathcal{J}_{4}(C) = 0$, $\mathcal{J}_{5}(A)\neq0;$ which leads to $C_{3} = 0$, $\mathcal{J}_{3}(V_{3}) = \dfrac{\zeta}{\tau}$ and this gives $V_{3} = \mathcal{J}_{3}^{-1}\left(\dfrac{\zeta}{\tau}\right)$. From Eqs. (2.1)-(4.4) we get

From Eq. (4.12), we get

Obviously from condition H1 we have $f_{i}(S) > 0$ for all $S\in \lbrack0, S_{0})$ and $f_{i}(S_{0}) = 0,$ $i = 5, 6$ .Using Eq. (4.13) and letting $V = V_{3}$ in Eq. (4.1), we define

Then, we get

Since $\mathcal{F} _{3}\left(S\right)$ is continuous on $[0, S_{0}),$ then there exists $S_{3}\in(0, S_{0})$ such that $\mathcal{F} _{3}(S_{0}) = 0$.From Eq. (4.13) and condition H3, we obtain

Moreover, from Eq. (4.12) and condition H3, we have

Clearly, $A_{3} > 0$ when $\dfrac{b\lambda \mathcal{H}_{1}\mathcal{H} _{2}\mathcal{H}_{3}\left[\aleph_{1}(S_{3}, V_{3})+\aleph_{2}(S_{3}, L_{3})+\aleph_{3}(S_{3}, I_{3})\right] }{a\varepsilon \left(\lambda +\gamma \right) \mathcal{J}_{3}(V_{3})} > 1.$ Now we define the HIV-specific antibody immune response reproduction number

Thus, $A_{3} = \mathcal{J}_{5}^{-1}\left(\dfrac{\varepsilon}{\varpi}(\Re _{2}-1)\right)$. The parameter $\Re_{2}$ determines whether or not the HIV-specific antibody immune response is stimulated. It follows that, $Ð _{3} = (S_{3}, L_{3}, I_{3}, V_{3}, 0, A_{3})$ exists when $\Re_{2} > 1$. We call $Ð _{3}$ as a chronic HIV infection equilibrium with only active antibody immune response.

(iv) $\mathcal{J}_{4}(C)\neq0$, $\mathcal{J}_{5}(A)\neq0;$ which leads to $I_{4} = \mathcal{J}_{2}^{-1}\left(\dfrac{\pi}{\sigma}\right)$ and $V_{4} = \mathcal{J}_{3}^{-1}\left(\dfrac{\zeta}{\tau}\right)$. From Eqs. (4.1)-(4.4) we get

From Eq. (4.15), we get

Obviously from condition H1 we have $f_{7}(S) > 0$ for all $S\in \lbrack0, S_{0})$ and $f_{7}(S_{0}) = 0$ .Let $I = I_{4}$, $V = V_{4}$ and using Eq. (4.16) in Eq. (4.1), we define

Conditions H1 and H2 imply that $\mathcal{F} _{4}(0) = \yen (0) > 0$ and $\mathcal{F} _{2}\left(S_{0}\right) = -\left[\aleph_{1}(S_{0}, V_{4})+\aleph_{3} (S_{0}, I_{4})\right] < 0$. Thus, there exists $S_{4}\in(0, S_{0})$ such that $\mathcal{F} _{4}(S_{4}) = 0$.From Eq. (4.16) and condition H3, we obtain

Moreover, from Eq. (4.15), we have

It follows that $C_{4} > 0$ and $A_{4} > 0$ only when

The HIV-specific CTL-mediated immune competitive reproduction number and the HIV-specific antibody immune competitive reproduction number of system (2.1) are stated, respectively, as:

The parameters $\Re_{3}$ and $\Re_{4}$ together determine whether or not the HIV-specific CTL-mediated and antibody immune responses are both stimulated. Clearly, $Ð _{4} = (S_{4}, L_{4}, I_{4}, V_{4}, C_{4}, A_{4})$ exists when $\Re _{3} > 1$ and $\Re_{4} > 1$ and we can write $C_{4} = \mathcal{J}_{4}^{-1}\left(\dfrac{a}{\mu}\left(\Re_{3}-1\right) \right),$ $A_{4} = \mathcal{J} _{5}^{-1}\left(\dfrac{\varepsilon}{\varpi}\left(\Re_{4}-1\right) \right)$. We call $Ð _{4}$ as a chronic HIV infection equilibrium with active CTL-mediated and antibody immune responses.

The threshold parameters are given as follows:

Considering the above discussion, we sum up the following result:

Lemma 1. Suppose that conditions H1-H3 are hold true, then there exist five positive threshold parameters $\Re_{0},$ $\Re_{1}$, $\Re_{2},$ $\Re_{3}$ and $\Re_{4}$ such that

(i) if $\Re_{0}\leq1,$ then there exists only one equilibrium $Ð _{0}$,

(ii) if $\Re_{1}\leq1 < \Re_{0}$ and $\Re_{2}\leq1$ then there exist only two equilibria $Ð _{0}$ and $Ð _{1}$,

(iii) if $\Re_{1} > 1,$ then there exist three equilibria $Ð _{0}$, $Ð _{1}$ and $Ð _{2}$,

(iv) if $\Re_{2} > 1,$ then there exist three equilibria $Ð _{0}$, $Ð _{1}$ and $Ð _{3}$, and

(v) if $\Re_{3} > 1$ and $\Re_{4} > 1,$ then there exist five equilibria $Ð _{0}$, $Ð _{1},$ $Ð _{2}$, $Ð _{3}$ and $Ð _{4}$.

5.   Global stability analysis

In this section we prove the global asymptotic stability of all equilibria by constructing Lyapunov functional following the method presented in ^{[56,57,58,59]}. Let us state the function $\mathcal{K}:\mathbb{(}0, \infty \mathbb{)}\rightarrow \mathbb{[}0, \infty \mathbb{)}$ as $\mathcal{K}(\ell) = \ell-1-\ln \ell$. In addition, we define

From conditions H2 and H3 we obtain

moreover,

Therefore, the parameter $\Re_{0}$ can be rewritten as

To investigate the next theorem we need the following condition ^[60]:

Condition (H5). (i) The supremum of $\frac{\digamma_{2} (S)}{\digamma_{1}(S)}$ is achieved at $S = S_{0}$ for all $S\in(0, S_{0}],$

(ii) The supremum of $\frac{\digamma_{3}(S)}{\digamma_{1}(S)}$ is achieved at $S = S_{0}$ for all $S\in(0, S_{0}].$

Theorem 1. Let $\Re_{0}\leq1$ and conditions H1-H5 are satisfied, then $Ð _{0}$ is globally asymptotically stable (G.A.S).

Remark 1. From conditions H2 and H4 we get

which leads to

Define the following functions ^[60]:

We state the following condition

Condition(H6)

for all $L,$ $L_{i},$ $I,$ $I_{i} > 0,$ $i = 1, 2, 3, 4, \ S\in \left(0, S_{0}\right)$.

Remark 2. From Condition H6 we get

We consider the following equalities to be used in the proceeding theorems:

Theorem 2. Suppose that $\Re_{1}\leq1 < \Re_{0},$ $\Re_{2}\leq1$ and conditions H1-H4, H6 are hold true, then $Ð _{1}$ is G.A.S.

Theorem 3. Let $\Re_{1} > 1,$ $\Re_{4}\leq1$ and conditions H1-H4, H6 are satisfied, then $Ð _{2}$ is G.A.S.

Theorem 4. Suppose that $\Re_{2} > 1$, $\Re_{3}\leq1$ and conditions H1-H4, H6 are satisfied, then $Ð _{3}$ is G.A.S.

Theorem 5. If $\Re_{3} > 1$, $\Re_{4} > 1$ and conditions H1 -H4, H6 are hold true, then $Ð _{4}$ is G.A.S.

6.   Example and numerical simulations

In this section we present an example and perform some numerical simulations to illustrate our theoretical results. For numerical purposes we transform the distributed-time delay model (2.1) to a discrete-time delay one by a dirac delta function $\bar{\Lambda}(.)$ as a specific form of the kernel $\Lambda_{i}(\varsigma)$ as ^[14]:

The constants $\theta_{i}\in \left[0, \kappa_{i}\right],$ $i = 1, 2, 3$ are discrete-time delays which are special cases of the three distributed-time delays presented in model (2.1). Let $\kappa_{i}$ tends to $\infty$, then using the properties of Dirac delta function we get

Then, model (2.1) reduces to the following model with discrete-time delays:

From Theorems 1-5, the corresponding stability results of system (6.1) reads as:

Corollary 1. Let $\Re_{i}$, $i = 0, 1, ..., 4$ be defined as in (4.17). The following statements hold true.

(i) If $\Re_{0}\leq1$ and conditions H1-H5 are satisfied, then $Ð _{0}$ is G.A.S.

(ii) If $\Re_{1}\leq1 < \Re_{0},$ $\Re_{2}\leq1$ and conditions H1 -H4, H6 are statisfied, then $Ð _{1}$ is G.A.S.

(iii) If $\Re_{1} > 1,$ $\Re_{4}\leq1$ and conditions H1-H4, H6 are satisfied, then $Ð _{2}$ is G.A.S.

(iv) If $\Re_{2} > 1$, $\Re_{3}\leq1$ and conditions H1-H4, H6 are satisfied, then $Ð _{3}$ is G.A.S.

(v) If $\Re_{3} > 1$, $\Re_{4} > 1$ and conditions H1-H4, H6 are hold true, then $Ð _{4}$ is G.A.S.

Let us consider the following example:

This example is a special case of system (6.1) by considering the following particular forms:

● The intrinsic growth rate of healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells is chosen as

Here we consider another source for producing healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells which is the proliferation of existing healthy cells in the body ^[61]. The maximum proliferation rate of healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells is given by $p > 0$. It is well known that there is a maximum level of healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cell concentration in the body which is described by the parameter $S_{\max} > 0$. If the concentration reaches $S_{\max}$, it should decrease. We assume that $p < \alpha$ ^[62]. It is clear that $\yen (0) = \rho > 0$ and $\yen (S_{0}) = 0$, where

In addition, we have

Clearly, $\yen (S) > 0$ whereas $\yen ^{\prime}(S) < 0$ for all $S\in \lbrack0, S_{0})$. Hence, condition H1 is hold true.

● The virus-cell, silent infected cell-cell, and active infected cell-cell incidence rates of infection are, respectively, given by:

The parameters $\eta_{i} > 0,$ $i = 1, 2, 3$ account for the infection rate constants. Parameters $q,$ $\delta,$ $\beta_{i},$ $i = 1, 2, 3$ are positive constants. It is clear that

Further, we have

for all $S,$ $L,$ $I,$ $V > 0$. Furthermore, we have

All above discussion ensures that condition H2 is confirmed.

● The natural death rate of the silent/active HIV-infected cells, HIV particles, HIV-specific CTLs and HIV-specific antibodies are given by

Obviously, condition H3 is valid.

In addition, we have

for all $S,$ $L,$ $I,$ $V > 0$. Therefore, condition H4 is also verified. On the other hand, we have $\mathcal{J}_{k}^{\prime}(x) = 1$ and then

Clearly, $\dfrac{\digamma_{2}(S)}{\digamma_{1}(S)} = \dfrac{\eta_{2} }{\eta_{1}}$ and $\dfrac{\digamma_{3}(S)}{\digamma_{1}(S)} = \dfrac{\eta_{3}}{\eta_{1}},$ hence, condition H5 is satisfied. In addition,

and

for all $L,$ $I > 0,$ $S\in \left(0, S_{0}\right),$ where $i = 1, 2, 3, 4$. Hence, condition H6 is ensured. Consequently, the validity of conditions H1-H6 guarantees that the global stability results demonstrated in Theorems 1-5 are valid for this example. Thus, the threshold parameters for system (4.2) are given by:

To solve system (6.2) numerically we fix the values of some parameters (see Table 2) and the others will be varied. In the coming subsections, we present some numerical simulations for model (6.2) to illustrate the theoretical results. Moreover, we study the influence of time delays and silent HIV-infected CTCtransmission on the stability behavior of equilibria and HIV dynamics.

6.1.   Stability of the equilibria

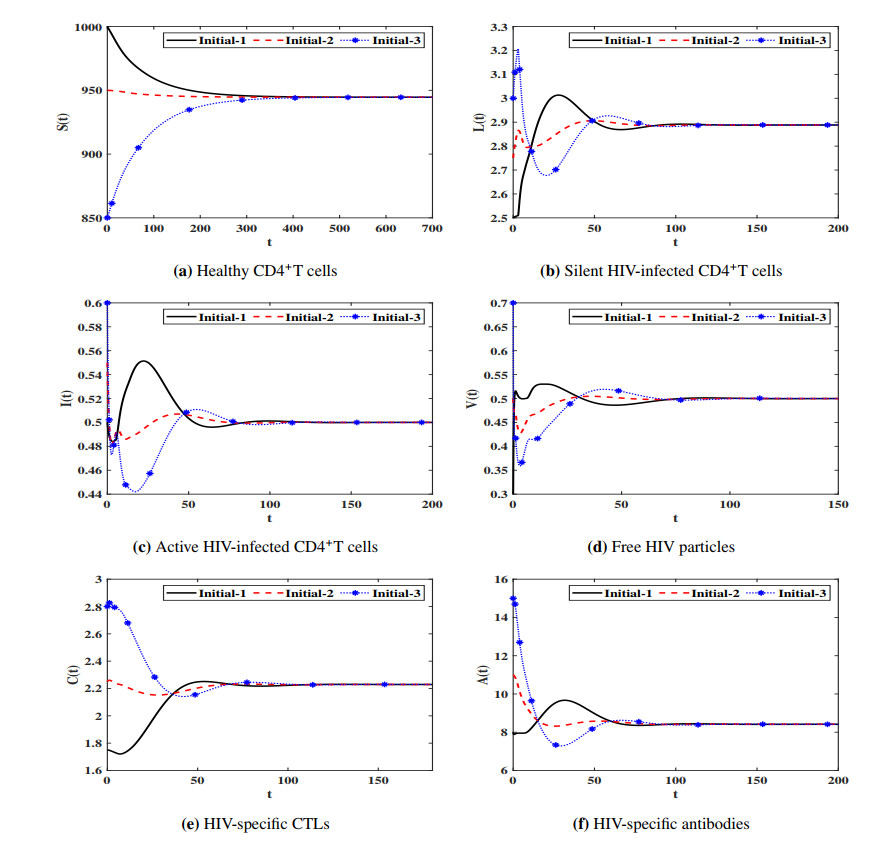
In this subsection, we illustrate the stability results given in Theorems 1-5. To do so, we fix the values $\theta_{1} = 3,$ $\theta_{2} = 2$ and $\theta_{3} = 1.$ We consider the following initial conditions for model (4.2):

Initial-1: $(S(\theta), L(\theta), I(\theta), V(\theta), C(\theta), A(\theta)) = (1000, 2.5, 0.5, 0.3, 1.75, 8)$,

Initial-2: $(S(\theta), L(\theta), I(\theta), V(\theta), C(\theta), A(\theta)) = (950, 2.75, 0.55, 0.5, 2.25, 11),$

Initial-3: $(S(\theta), L(\theta), I(\theta), V(\theta), C(\theta), A(\theta)) = (850, 3, 0.6, 0.7, 2.8, 15)$, where $\theta \in \lbrack-3, 0].$

We choose the values $\eta_{1}$ , $\eta_{2}$ , $\eta_{3},$ $\sigma$ and $\tau$ as follows:

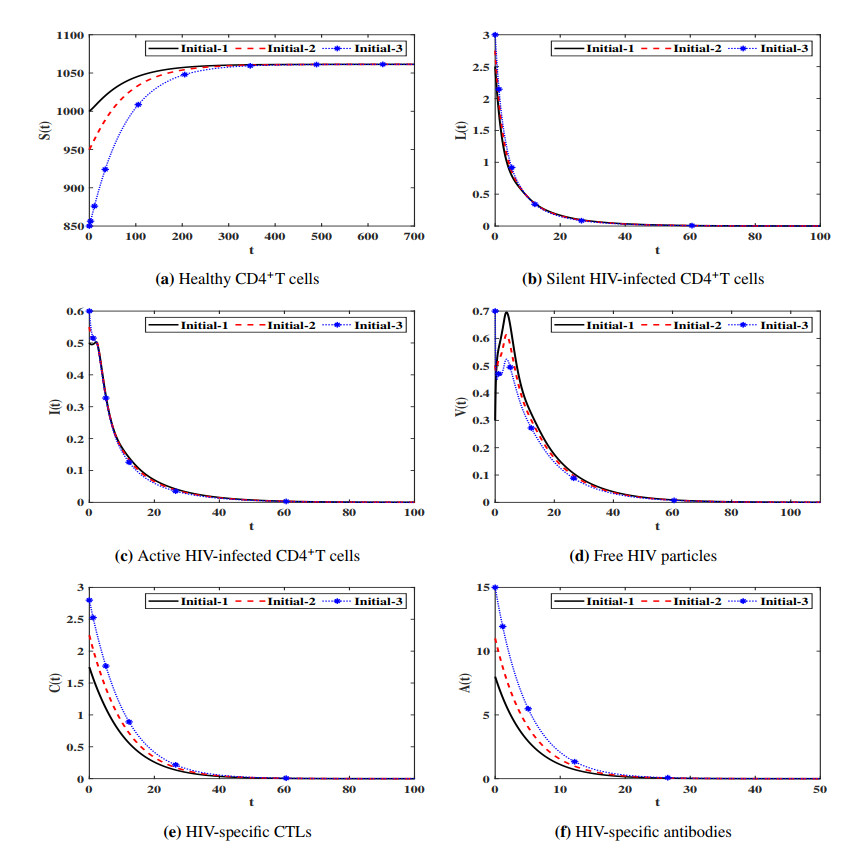
Stability of $Ð _{0}$ : $\eta_{1} = 0.1,$ $\eta_{2} = 0.05$ , $\eta_{3} = 0.2,$ $\sigma = 0.02$ and $\tau = 0.004$. For this set of parameters, we have $\Re_{0} = 0.50 < 1$. Figure 1 displays that the trajectories initiating with Initial-1, Initial-2 and Initial-3 reach the equilibrium $Ð _{0} = (1061.32, 0, 0, 0, 0, 0)$. This shows that $Ð _{0}$ is G.A.S according to Theorem 1. In this case, the HIV particles will be cleared from the body.

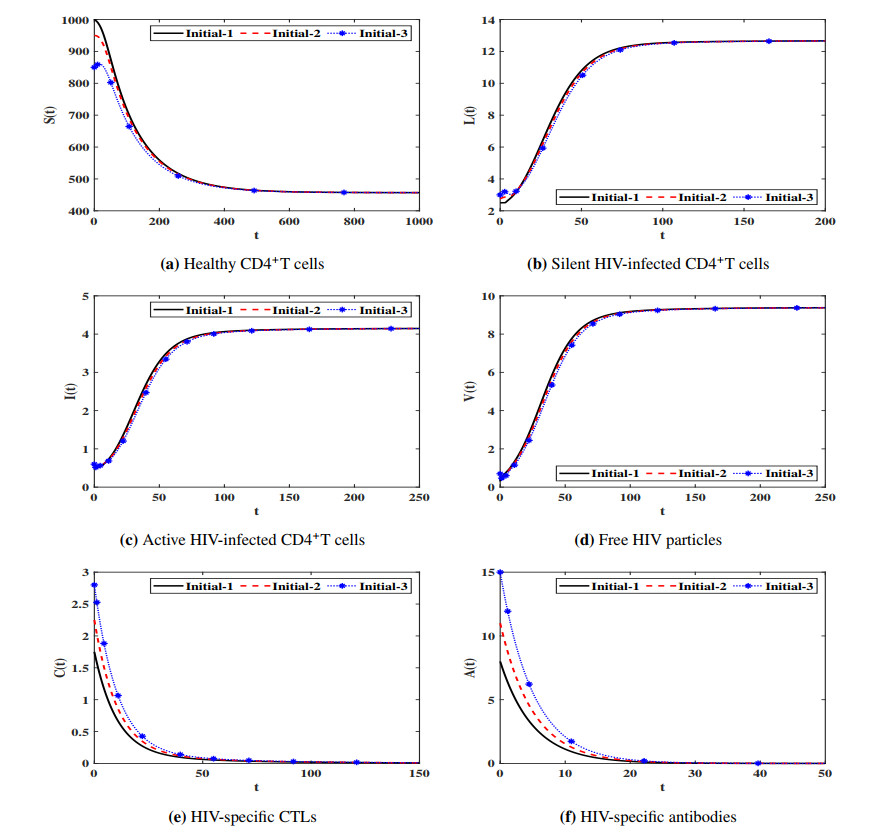
Stability of $Ð _{1}$ : $\eta_{1} = 0.5,$ $\eta_{2} = 0.3$ , $\eta_{3} = 0.7,$ $\sigma = 0.02$ and $\tau = 0.004$. With such choice we get $\Re_{1} = 0.89 < 1 < 2.38 = \Re_{0}$ and $\Re_{2} = 0.27 < 1$. It is clear that the equilibrium point $Ð _{1}$ exists with $Ð _{1} = \left(456.98, 12.68, 4.15, 9.39, 0, 0\right)$. Figure 2 displays that the trajectories initiating with Initial-1, Initial-2 and Initial-3 tend to $Ð _{1}$. Therefore, the numerical results supports Theorem 2. This case represents the persistence of the HIV infection but with unstimulated immune responses.

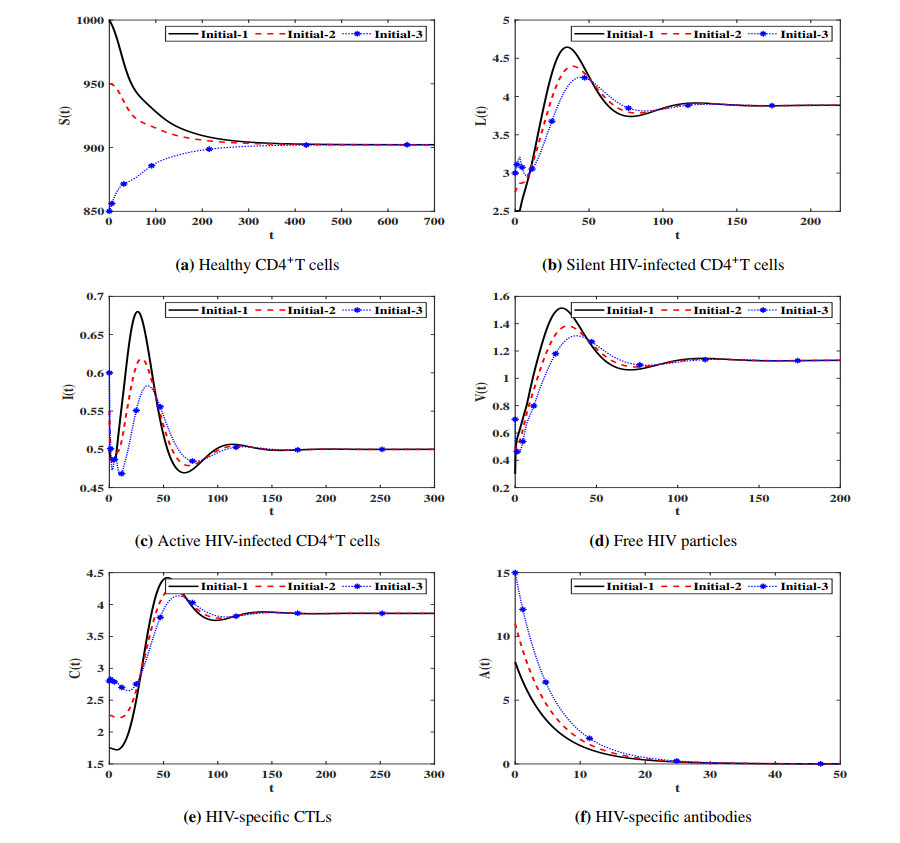
Stability of $Ð _{2}$ : $\eta_{1} = 0.5,$ $\eta_{2} = 0.3$ , $\eta_{3} = 0.7,$ $\sigma = 0.2$ and $\tau = 0.04$. Then, we calculate $\Re_{1} = 2.54 > 1$ and $\Re_{4} = 0.23 < 1$. In Figure 3 we show that $Ð _{2} = \left(902.20, 3.88, 0.50, 1.13, 3.86, 0\right)$ exists and it is G.A.S and this agrees with Theorem 3. Hence, a chronic HIV infection with only CTL-mediated immune response is attained.

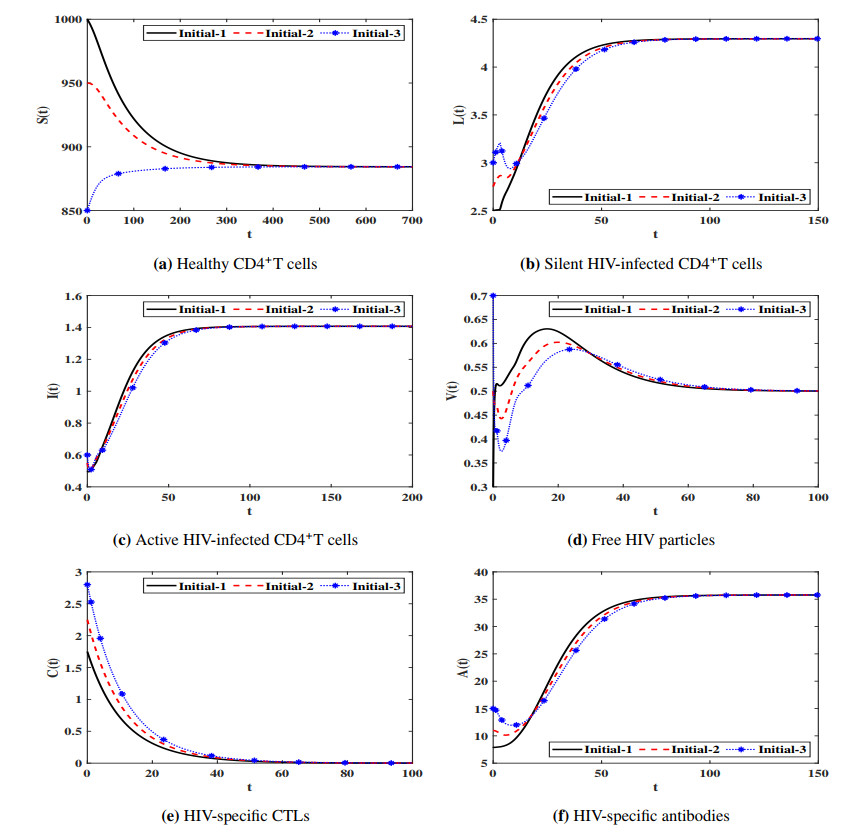
Stability of $Ð _{3}$ . $\eta_{1} = 0.5,$ $\eta_{2} = 0.3$ , $\eta_{3} = 0.7,$ $\sigma = 0.02$ and $\tau = 0.4$. Then, we calculate $\Re_{2} = 6.37 > 1$ and $\Re_{3} = 0.43 < 1$. The numerical results plotted in Figure 4 show that $Ð _{3} = \left(884.32, 4.30, 1.41, 0.50, 0, 35.77\right)$ exists and it is G.A.S and this agrees with Theorem 4. As a result, a chronic HIV infection with only antibody immune response is attained.

Stability of $Ð _{4}$ . $\eta_{1} = 0.5,$ $\eta_{2} = 0.3$ , $\eta_{3} = 0.7,$ $\sigma = 0.2$ and $\tau = 0.4$. Then, we calculate $\Re_{3} = 1.89 > 1$ and $\Re_{4} = 2.26 > 1$. The numerical results displayed in Figure 5 show that $Ð _{4} = \left(944.58, 2.89, 0.50, 0.50, 2.23, 8.41\right)$ exists and it is G.A.S according to Theorem 5. In this case, a chronic HIV infection is attained where both CTL-mediated and antibody immune responses are working.

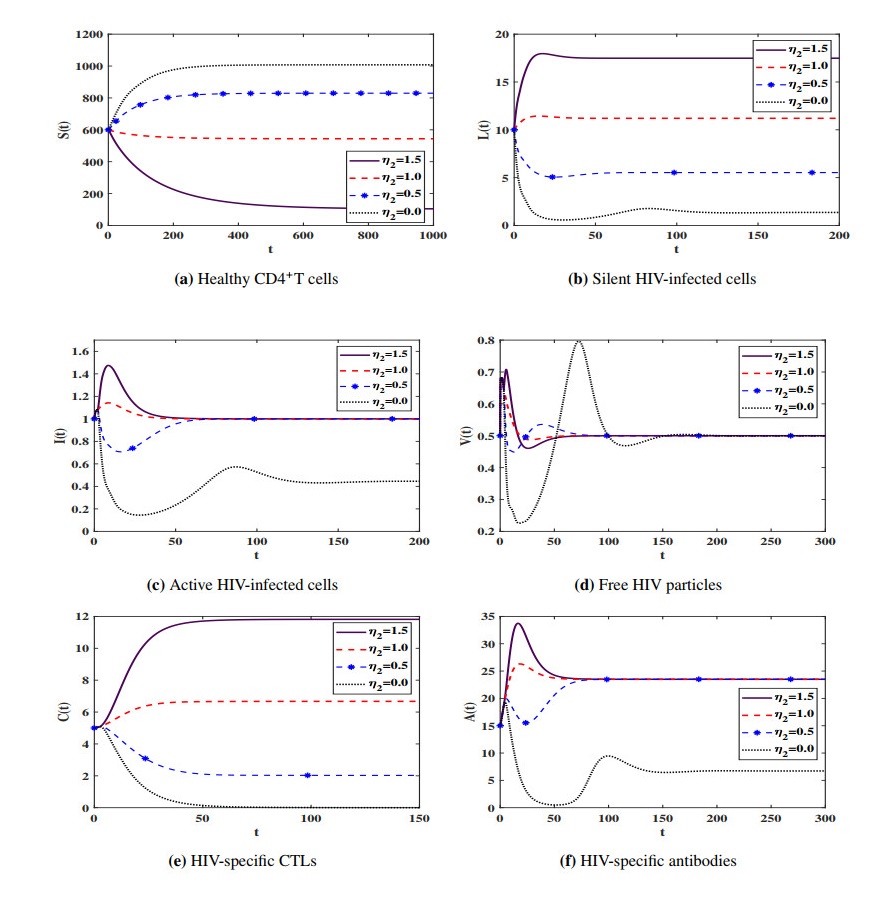
6.2.   Effect of silent HIV-infected CTC transmission

In this subsection, we investigate the influence of silent HIV-infected CTCtransmission on the HIV dynamics (4.2). We use the parameters given in Table 2 and fix the parameters $\eta_{1} = 0.5,$ $\eta_{3} = 0.7,$ $\sigma = 0.1$, $\tau = 0.4,$ $\theta_{1} = 3,$ $\theta_{2} = 2$, $\theta_{3} = 1$. We consider the following initial condition:

Initial-4: $(S(\theta), L(\theta), I(\theta), V(\theta), C(\theta), A(\theta)) = (600, 10, 1, 0.5, 5, 15),$ where $\theta \in \lbrack-3, 0].$

We vary the parameter $\eta_{2}$ as shown in Table 3 which displays that as the silent cell-cell incidence rate constant $\eta_{2}$ is changed the dynamical behavior is also changed. Figure 6 and Table 3 illustrate the effect of parameter $\eta_{2}$ on the solution trajectories of the system. We observe that, as $\eta_{2}$ is decreased, the concentration of the healthy cells is increased, while the concentrations of silent/active HIV-infected cells, free HIV particles, HIV-specific CTLs and HIV-specific antibodies are decreased.

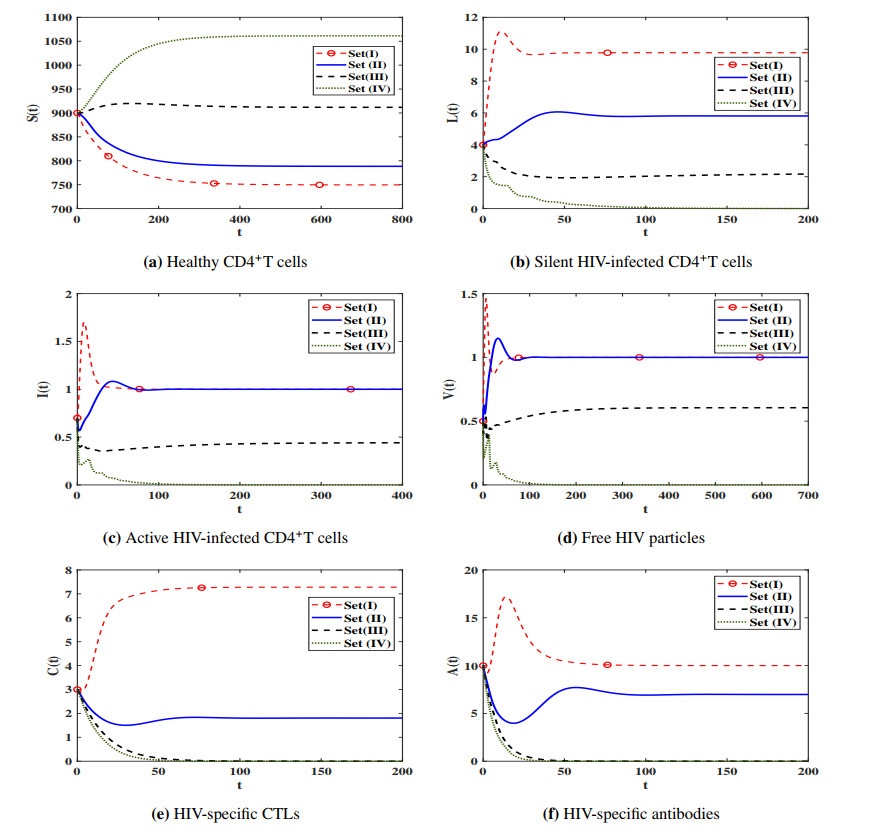
6.3.   Effect of time delays on the HIV dynamics

In this subsection, we study the influence of time delays $\theta_{1},$ $\theta_{2}$ and $\theta_{3}$ on the stability of the equilibria. We fix the parameters $\eta_{1} = 0.6,$ $\eta_{2} = 0.5$ , $\eta_{3} = 0.7$, $\sigma = 0.1$ and $\tau = 0.2$ and the remaining values will be used as given in Table 2. We observe from Eq. (6.4) that the threshold parameter $\Re_{0}$ depends on the delay parameters which leads to a significant change in the stability of the equilibria. To illustrate this situation, we consider the following initial condition:

Initial-5: $(S(\theta), L(\theta), I(\theta), V(\theta), C(\theta), A(\theta)) = (900, 4, 0.7, 0.5, 3, 10),$ where $\theta \in \lbrack-\max \left \{ \theta_{1}, \theta_{2}, \theta_{3}\right \}, 0].$

Further, we choose the following sets of parameters $\theta_{1},$ $\theta_{2}$ and $\theta_{3}$ :

Set (I): $\theta_{1} = \theta_{2} = \theta_{3} = 0$,

Set (II): $\theta_{1} = 4,$ $\theta_{2} = 3$ and $\theta_{3} = 2$,

Set (III): $\theta_{1} = 8,$ $\theta_{2} = 7$ and $\theta_{3} = 6$,

Set (IV): $\theta_{1} = 15,$ $\theta_{2} = 14$ and $\theta_{3} = 13$.

Table 4 demonstrates that as the delay parameters $\theta_{1},$ $\theta_{2}$ and $\theta_{3}$ are increased the threshold parameter $\Re_{0}$ is decreased and the stability behavior of the infection-free equilibrium $Ð _{0}$ is changed. Figure 7 shows the effect of time delay on the solution trajectories of the system. We observe that as time delays are increased, the concentration of the healthy cells is increased, while the concentrations of silent/active HIV-infected cells, free HIV particles, HIV-specific CTLs and HIV-specific antibodies are decreased. Let us fix the parameters $\theta_{2}$ and $\theta_{3}$. Using Eq. (6.4) we can define the threshold parameter $\Re_{0}$ as a function of $\theta_{1}$ as:

When $\Re_{0}\left(\theta_{1}\right) \leq1$, we obtain

Therefore, if $\theta_{1}\geq \theta_{1}^{\min}$, then the infection-free equilibrium $Ð _{0}$ is G.A.S. We select the values $\theta_{2} = 7$ and $\theta_{3} = 6$ to compute $\theta_{1}^{\min}$ as $\theta_{1}^{\min} = 10.5302$. As a result, we have the following scenarios:

(i) If $\theta_{1}\geq10.5302$, then $\Re_{0}(\theta_{1})\leq1$ and $Ð _{0}$ is G.A.S,

(ii) If $\theta_{1} < 10.5302$, then $\Re_{0}(\theta_{1}) > 1$ and one of the other equilibria is G.A.S.

The above discussion gives us a significant insights that the increase of time delays period can play the same influence as antiviral treatment

7.   Conclusion

In this paper, we formulated an HIV dynamics model with three types of distributed-time delays. Both CTL and antibody immune responses were considered. The model incorporated two routes of transmission, VTC and CTC. The CTC transmission is due to (i) the contact between healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells and silent HIV-infected cells, and (ii) the contact between healthy ${\rm{CD}}{4^ + }{\rm{T}}$ cells and active HIV-infected cells. We proved that the solutions of the model are nonnegative and bounded. We showed that the model has five possible equilibria, and their existence is determined by five threshold parameters. The global asymptotic stability of all equilibria was investigated by constructing Lyapunov functionals and utilizing LaSalle's invariance principle. Theorems 1-5 and Corollary 1 extend many existing results in the literature. We performed numerical simulations to support our theoretical results. We studied the effect of the time delay and CTC transmission on the HIV dynamics. We showed that the inclusion of time delay can significantly increase the concentration of the healthy CD4 $^{+}$ T cells and reduce the concentrations of the infected cells and free HIV particles. This gives us a significant observation that increasing the delay period can play the same influence of antiviral treatment. We showed that the presence of CTC transmission reduces the number of healthy CD4 $^{+}$ T cells and raises the numbers of infected cells and free HIV particles. We observed that the presence of silent and active HIV-infected CTC transmissions into the HIV infection model increases the basic HIV reproduction number $\Re_{0}$, since $\Re_{0} = \sum_{i = 1}^{3}\Re_{0i} > \Re_{01}$. Therefore, neglecting the CTC transmission will lead to under-evaluated basic HIV reproduction number. Our proposed HIV dynamics model can be generalized and extended to incorporate different biological phenomena such as reaction-diffusion ^{[63,64,65,66,67,68]} and stochastic interactions ^[69].

Acknowledgment

This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under grant no. (KEP-PhD-20-130-41). The authors, therefore, acknowledge with thanks DSR technical and financial support.

Conflict of interest

The authors declare that they have no conflict interests.

8.   Appendix

In this appendix we present the proof of Theorems 1-5.

Proof of Theorem 1. Constructing a Lyapunov functional candidate:

We note that, $\Phi_{0}(S, L, I, V, C, A) > 0$ for all $S, L, I, V, C, A > 0,$ and $\Phi_{0}(S_{0}, 0, 0, 0, 0, 0) = 0$. We calculate $\frac{d\Phi_{0}}{dt}$ along the solutions of model (2.1) as:

Collecting terms of Eq. (8.1), we get

From condition H4 and Eq. (5.1), we get

Then,

Therefore, Eq. (8.2) will become

Condition H5 implies that

Substituting inequality (8.4) into Eq. (8.3) and using $\yen (S_{0}) = 0$, we get

Conditions H1, H2 and Eq. (5.2) provide that $\yen (S)$ is a strictly decreasing function of $S$, while $\digamma_{1}(S)$ is a strictly increasing function of $S$. Then,

Therefore, $\frac{d\Phi_{0}}{dt}\leq0$ for all $S, L, I, V, C, A > 0$ with equality holding when $S = S_{0}$ and $L = C = A = 0.$ Let $\Upsilon_{0} = \left \{ (S, L, I, V, C, A):\frac{d\Phi_{0}}{dt} = 0\right \}$ and $\Upsilon_{0}^{^{\prime}}$ be the largest invariant subset of $\Upsilon_{0}$. Therefore, the solutions of system (2.1) converge to $\Upsilon_{0}^{^{\prime}}$ ^[49]. The set $\Upsilon_{0}^{^{\prime}}$ is invariant and contains elements which satisfy $S(t) = S_{0}$ and $L(t) = C(t) = A(t) = 0$. According to LaSalle's invariance principle we have $\lim \limits_{t\rightarrow \infty}$ $S(t) = S_{0}$ and $\lim \limits_{t\rightarrow \infty}$ $L(t) = \lim \limits_{t\rightarrow \infty }C(t) = \lim \limits_{t\rightarrow \infty}A(t) = 0$. Then, $\dot{S}(t) = 0$ and $\dot{L}(t) = \dot{C}(t) = \dot{A}(t) = 0.$ From the third and fourth equations of system (2.1), we have

Let us define a Lyapunov function as follows:

Therefore, the time derivative of $\tilde{\Phi}_{0}$ along the solutions of system (8.5)-(8.6) can be calculated as follows:

Utilizing condition H3it is clear that $\frac{d\tilde{\Phi}_{0}} {dt} = 0$ if and only if $I(t) = V(t) = 0$ for all $t$. Let $\Upsilon_{0} ^{^{^{\prime \prime}}} = \left \{ (S, L, I, V, C, A)\in \Upsilon_{0}^{^{\prime}} :\frac{d\tilde{\Phi}_{0}}{dt} = 0\right \}$. Then, $\Upsilon_{0}^{^{^{\prime \prime}}} = \left \{ (S, L, I, V, C, A)\in \Upsilon_{0}^{^{\prime}}:S = S_{0}, L = I = V = C = A = 0\right \} = \left \{ \text{\DJ }_{0}\right \}$. Hence, all solutions trajectories approach $Ð _{0}$ and this means that $Ð _{0}$ is G.A.S ^[49].

Proof of Theorem 2. Define $\Phi_{1}(S, L, I, V, C, A)$ as:

Calculating $\frac{d\Phi_{1}}{dt}$ as:

Collecting terms of Eq. (8.7), we derive

Using the equilibrium conditions for $Ð _{1}$, we get

In addition,

Then, we obtain

Considering the equalities given by (5.6) in case of $n = 1$ and after some calculations we get

Using the definition of $\mathcal{G}_{1}^{U}(S, U)$ given in (5.4), we obtain

and

Then,

We have $C_{2} = \mathcal{J}_{4}^{-1}\left(\dfrac{a}{\mu}\left(\Re _{1}-1\right) \right) \leq0$ when $\Re_{1}\leq1$. It follows that $\dot {C}(t) = \sigma \left(\mathcal{J}_{2}(I(t))-\dfrac{\pi}{\sigma}\right) \mathcal{J}_{4}(C(t)) = \sigma \left(\mathcal{J}_{2}(I(t))-\mathcal{J} _{2}(I_{2})\right) \mathcal{J}_{4}(C(t))\leq0$ for all $C > 0$, which implies that $\mathcal{J}_{2}(I_{1})\leq \mathcal{J}_{2}(I_{2})$. Further, $A_{3} = \mathcal{J}_{5}^{-1}\left(\dfrac{\varepsilon}{\varpi}(\Re _{2}-1)\right) \leq0$ when $\Re_{2}\leq1$. This implies that $\dot{A} (t) = \tau \left(\mathcal{J}_{3}(V(t))-\dfrac{\zeta}{\tau}\right) \mathcal{J}_{5}(A(t)) = \tau \left(\mathcal{J}_{3}(V(t))-\mathcal{J}_{3} (V_{3})\right) \mathcal{J}_{5}(A(t))\leq0$ for all $A > 0$, which ensures the inequality $\mathcal{J}_{3}(V_{1})\leq \mathcal{J}_{3}(V_{3})$. Furthermore, $\Phi_{1}$ is always positive and approaches its global minimum at $Ð _{1}$. Therefore, from Eq. (8.8) we have $\frac{d\Phi_{1}}{dt}\leq0$ for all $S, L, I, V, C, A > 0$ with equality holding when $S = S_{1},$ $L(t) = L_{1}$, $I(t) = I_{1},$ $V(t) = V_{1}$ and $C = A = 0.$ Let $\Upsilon_{1}^{\prime}$ be the largest invariant subset of $\Upsilon_{1} = \left \{ (S, L, I, V, C, A):\frac {d\Phi_{1}}{dt} = 0\right \}$. The solutions of system (2.1) are confined to $\Upsilon_{1}^{^{\prime}}$. It can be seen that $\Upsilon_{1}^{\prime } = \left \{ \text{ $Ð_{1}$ }\right \}$ and $Ð _{1}$ is G.A.S using LaSalle's invariance principle.

Proof of Theorem 3. Define a function $\Phi_{2}(S, L, I, V, C, A)$ as:

We calculate $\frac{d\Phi_{2}}{dt}$ as:

Collecting terms of Eq. (8.9), we derive

Using the equilibrium conditions for $Ð _{2}$:

Moreover,

Therefore, we obtain

Considering the equalities given by (5.6) in case of $n = 2$ and after some calculations we get

Using the definition of $\mathcal{G}_{2}^{U}(S, U)$ given in (5.4), we obtain

and

Then,

Hence, if $\Re_{4}\leq1$, then $Ð _{4}$ does not exists since $A_{4} = \mathcal{J}_{5}^{-1}\left(\dfrac{\varepsilon}{\varpi}\left(\Re _{4}-1\right) \right) \leq0$. This implies that, $\dot{A}(t) = \tau \left(\mathcal{J}_{3}(V(t))-\frac{\zeta}{\tau}\right) \mathcal{J}_{5} (A(t)) = \tau \left(\mathcal{J}_{3}(V(t))-\mathcal{J}_{3}(V_{4})\right) \mathcal{J}_{5}(A(t))\leq0$ for all $A > 0$, which ensures the inequality $\mathcal{J}_{3}(V_{2})\leq \mathcal{J}_{3}(V_{4})$. Hence, if $\Re_{1} > 1$, then $\frac{d\Phi_{2}}{dt}\leq0$ for all $S, L, I, V, C, A > 0$ and $\frac{d\Phi_{2} }{dt} = 0$ when $S = S_{2},$ $L(t) = L_{2},$ $I(t) = I_{2}$, $V(t) = V_{2}$ and $A = 0.$ Define $\Upsilon_{2} = \left \{ (S, L, I, V, C, A):\frac{d\Phi_{2}}{dt} = 0\right \}$ and $\Upsilon_{2}^{^{\prime}}$ is the largest invariant subset of $\Upsilon_{2}$. The solutions of system (2.1) converge to $\Upsilon _{2}^{^{\prime}}$ which contains elements with $L(t) = L_{2}$ and $I(t) = I_{2}$. Hence, $\dot{I}(t) = 0$ and from the third equation of system (2.1), we have $0 = \dot{I}(t) = \lambda \mathcal{H}_{2}\mathcal{J}_{1}(L_{2})-a\mathcal{J} _{2}(I_{2})-\mu \mathcal{J}_{4}(C(t))\mathcal{J}_{2}(I_{2})$, which gives $C(t) = C_{2}$ for all $t.$ Therefore, $\Upsilon_{2}^{^{\prime}} = \left \{ \text{ $Ð_{2}$ }\right \}$. Applying LaSalle's invariance principle we get that $Ð _{2}$ is G.A.S.

Proof of Theorem 4. Define a function $\Phi_{3}(S, L, I, V, C, A)$ as:

Calculating $\frac{d\Phi_{3}}{dt}$ as:

Collecting terms of Eq. (8.11), we derive

Using the equilibrium conditions for $Ð _{3}$, we get

In addition,

Then, we obtain

Considering the equalities given by (5.6) in case of $n = 3$ and after some calculations we get

Using the definition of $\mathcal{G}_{3}^{U}(S, U)$ given in (5.4), we obtain

and

Then,

We have $C_{4} = \mathcal{J}_{4}^{-1}\left(\frac{a}{\mu}\left(\Re _{3}-1\right) \right) \leq0$ when $\Re_{3}\leq1$. It follows that $\dot {C}(t) = \sigma \left(\mathcal{J}_{2}(I(t))-\frac{\pi}{\sigma}\right) \mathcal{J}_{4}(C(t)) = \sigma \left(\mathcal{J}_{2}(I(t))-\mathcal{J} _{2}(I_{4})\right) \mathcal{J}_{4}(C(t))\leq0$ for all $C > 0$, which implies that $\mathcal{J}_{2}(I_{3})\leq \mathcal{J}_{2}(I_{4})$. Hence, $\frac {d\Phi_{3}}{dt}\leq0$ for all $S, L, I, V, C, A > 0$ and $\frac{d\Phi_{3}}{dt} = 0$ when $S = S_{3},$ $L = L_{3},$ $I = I_{3},$ $V = V_{3}$ and $C = 0$. Let $\Upsilon _{3}^{\prime} be the largest invariant subset of$ \Upsilon_{3} = \left \{ (S, L, I, V, C, A):\frac{d\Phi_{3}}{dt} = 0\right \} $. The solutions of system (2.1) converge to$ \Upsilon_{3}^{^{\prime}} $which contains elements with$ I(t) = I_{3} $and$ V(t) = V_{3} $. Then$ \dot{V}(t) = 0 $and from the fourth equation of system (2.1) we have$ 0 = \dot{V}(t) = b\mathcal{H} _{3}\mathcal{J}_{2}(I_{3})-\varepsilon \mathcal{J}_{3}(V_{3})-\varpi \mathcal{J}_{5}(A(t))\mathcal{J}_{3}(V_{3}) $, which gives$ A(t) = A_{3} $for all$ t. $Then,$ \Upsilon_{3}^{\prime} = \left \{ \text{ $Ð_{3}$ }\right \} $and utilizing LaSalle's invariance principle we can say that$Ð _{3} $ is G.A.S.

Proof of Theorem 5. Define $\Phi_{4}(S, L, I, V, C, A)$ as:

We calculate $\frac{d\Phi_{4}}{dt}$ as:

Collecting terms of Eq. (8.12), we derive

Using the equilibrium conditions for $Ð _{4}$, we get

In addition,

Then, we obtain

Considering the equalities given by (5.6) in case of $n = 4$ and after some calculations we get

Using the definition of $\mathcal{G}_{4}^{U}(S, U)$ given in (5.4), we obtain

and

Then,

Hence, if $\Re_{3} > 1$ and $\Re_{4} > 1$, then $\frac{d\Phi_{4}}{dt}\leq0$ for all $S, L, I, V, C, A > 0$. Moreover, $\frac{d\Phi_{4}}{dt} = 0$ when $S = S_{4}$, $L = L_{4},$ $I = I_{4}$ and $V = V_{4}.$ Let $\Upsilon_{4}^{\prime}$ be the largest invariant subset of $\Upsilon_{4} = \left \{ (S, L, I, V, C, A):\frac{d\Phi_{4}} {dt} = 0\right \}$. The solutions of system (2.1) converge to $\Upsilon_{4}^{^{\prime}}$ which contains elements with $L(t) = L_{4},$ $I(t) = I_{4}$, $V(t) = V_{4}$, then $\dot{I}(t) = \dot{V}(t) = 0$ and from the third and fourth equations of system (2.1) we have $0 = \dot{I}(t) = \lambda \mathcal{H}_{2}\mathcal{J}_{1}(L_{4})-a\mathcal{J}_{2}(I_{4})-\mu \mathcal{J}_{4}(C(t))\mathcal{J}_{2}(I_{4})$ and $0 = \dot{V}(t) = b\mathcal{H} _{3}\mathcal{J}_{2}(I_{4})-\varepsilon \mathcal{J}_{3}(V_{4})-\varpi \mathcal{J}_{5}(A(t))\mathcal{J}_{3}(V_{4})$. This implies that $C(t) = C_{4}$, $A(t) = A_{4}$ for all $t.$ Then, $\Upsilon_{4}^{\prime} = \left \{ \text{ $Ð_{4}$ }\right \}$ and utilizing LaSalle's invariance principle ensures that $Ð _{4}$ is G.A.S.