Stability and Hopf bifurcation in a virus model with self-proliferation and delayed activation of immune cells

1.   Introduction

Recently, different kinds of viral infection such as HIV (human immunodeficiency virus), HCV (hepatitis C virus) and HBV (hepatitis B virus) have received many attention. Different mathematical models have been formulated to describe the dynamics of virus population in vivo ^{[1,2,3,4,5,6]}. The basic viral infection model of within-host can be described by the following three dimensional system ^[7]:

Here $x(t), y(t),$ and $v(t)$ represent uninfected target cells, infected cells and free virus, respectively. Uninfected cells are produced at a constant rate $s$, die at rate $d_{1}x$, and become infected at rate $\beta xv$. Infected cells are produced at rate $\beta xv$ and die at rate $by$. Free virus are produced from infected cells at rate $ky$ and die at rate $u v$. It was showed that, for system (1.1), there exist a critical threshold named as the basic reproduction number of virus $R_{0} = \frac{\beta sk}{d_{1}d_{2}}$ to determine its global dynamical behavior ^[8].

During viral infections, the adaptive immune response is mediated by lymphocytes expressing antigen specific receptors, T and B lymphocytes, namely, humoral and cellular immunity. To study the population dynamics of immune response, Nowak et al. ^[9] introduced the CTL population into system (1.1) and obtain the following four dimensional system:

Here $z(t)$ denotes CTLs, which is produced at rate $cyz$ because of the stimulation of infected cells, and die at rate $d_{3}z$. The infected cells are eliminated by CTLs at rate $pyz$. Following ^[9], many authors present and develop mathematical models for the cell-mediated immune response ^{[10,11,12,13]} and the humoral immunity ^{[14,15,16,17]}.

Recently study indicates that the self-proliferation of immune cells can not be neglected besides the stimulation of infected cells. In order to mimic the spontaneous proliferation of CTLs, a logistic proliferation term for CTLs was incorporated in virus infection models in ^[18], where a rigorous mathematical analysis of the effect of self-proliferation of CTLs on the dynamics of viral infection is necessary. In order to understand the effect of self-proliferation and delayed activation of immune cells in a virus model, we propose the following virus infection model:

Here the logistic proliferation term $rz(1-z/m)$ describes the self-proliferation of CTLs, in which parameter $r$ denotes a per capita self-proliferation rate, and $m$ means the capacity of CTLs population. Time delay term $cy(t-\tau)z(t-\tau)$ represents a sequence of events such as antigenic activation and selection. It has been shown that time delays cannot be ignored in models for viral immune response including intracellular delay during viral infection ^{[19,20,21,22]} and time delay of CTLs stimulating proliferation ^[23,24].

Note that the turnover of virus is much faster than that of infection cells within-host ^[25,26]. A plausible quasi steady-state assumption is proposed to mimic the fast time-scale^[27,28]. In other words, $v$ can be replaced by $\frac{ky}{u}$ in (1.3). Let $\hat{\beta} = \frac{\beta k}{u}$ and also note as $\beta$ to simplify the parameter, system (1.3) can be written as:

This paper is organized as follows. In section 2, some preliminary results are obtained, including non-negativity and boundedness of the solution of system (1.4), the existence of equilibria under different self-proliferation intensities of CTLs. Section 3 investigate the local and global stability of the boundary equilibria. Section 4 study the effects of delayed activation of immune cells on the existence of Hopf bifurcation. The direction and stability of Hopf bifurcation is investigated in section 5. Some numerical simulations are given to quantify the impact of self-proliferation and delayed activation of CTLs in section 6. Finally, some conclusions and discusses are presented in section 7.

2.   Preliminary results

In this section, we first discuss the non-negativity and boundedness of solutions of system (1.4). For $\tau > 0$, let $\mathcal{C} = \mathcal{C}([-\tau, 0], \mathbb{R}^{3}_{+})$ denote the Banach space of continuous function mapping the interval $[-\tau, 0]$ into $\mathbb{R}^{3}_{+}$ with the topology of uniform convergence. The initial conditions are given by

with $\phi_{i}(\xi)\geq 0$, $\xi\in[-\tau, 0]$ and $\phi_{i}(0) > 0$ $(i = 1, 2, 3)$.

Theorem 2.1. The solutions of system (1.4) satisfying the initial conditions (2.1) are non-negative and ultimately bounded.

Proof. We first define the right-hand side function of system (1.4) as

where $K(t) = (K_{1}(t), K_{2}(t), K_{3}(t))^{T}$ and $K_{1}(t) = x$, $K_{2}(t) = y$, $K_{3}(t) = z.$ It is obvious that the function $G(t, K(t))$ is locally Lipschitz and by the standard theory of functional differential equation, we know that there exists a unique solution for a given initial conditions. To prove the non-negativity of solutions of system (1.4), we first prove the non-negativity over the time interval $[0, \tau]$. Considering the right-hand side functions of system (1.4) over the time interval $[0, \tau]$, we have

where $\xi\in[-\tau, 0]$. Note that the positivity of parameters and nonnegativity of initial functions. It can be seen from the above expression that each component $G_{i}(t, K(t))\geq0$. It follows that the solutions of system (1.4) remain nonnegative in $[0, \tau]$. Similarly, we can repeat the process over $[\tau, 2\tau]$ and so on by using the method of steps ^[29], it can be proved that for any finite interval $[0, t]$, the solutions of system (1.4) remains non-negative.

Now we consider the boundeness of the solutions. Define a new variable $X(t) = x(t)+y(t)+\dfrac{p}{c}z(t+\tau)$, and let $d = \min\{1, d_{1}, d_{2}\}$. By the non-negativity of the solutions of system (1.4), we have

Taking $M = s+\dfrac{pm(1+r)^2}{4rc}$, we know $\limsup_{t\rightarrow\infty}X(t)\leq\dfrac{M}{d}$. So the solutions of system(1.4) are ultimately bounded. The equilibria of (1.4) are the solutions of the following algebraic equations:

It is easy to see that system (1.4) always has infection-free equilibrium $E_{0}^{yz} = (x_{0}, 0, 0)$, where $x_{0} = \dfrac{s}{d_{1}}$. According to the definition in ^[30], we obtain the basic reproduction number of virus $R_{0} = \dfrac{\beta s}{d_{1}d_{2}}$. Now we define $x_{1} = \dfrac{d_{2}}{\beta}, y_{1} = \dfrac{d_{1}(R_{0}-1)}{\beta}, x_{2} = \dfrac{s}{d_{1}}, z_{2} = \dfrac{m(r-d_{3})}{r}$. Based on (2.3), after some simple calculations, it is easy to get the following results.

Proposition 2.2. (i) Suppose that $R_{0} > 1$. The immunity-inactivated infection equilibrium $E_{0}^{z} = (x_{1}, y_{1}, 0)$ always exists. Especially, besides $E_{0}^{z}$, an infection-free but immunity-activated equilibrium $E_{0}^{y} = (x_{2}, 0, z_{2})$ will appear if $r > d_{3}$. (ii) Suppose that $0\leq r\leq d_{3}$. If $R_{0} > 1+\dfrac{\beta(d_{3}-r)}{cd_{1}}$, system (1.4) has a unique immunity-activated infection equilibrium $E_{1}^{*} = (x_{1}^{*}, y_{1}^{*}, z_{1}^{*})$, where

and $z_{1}^{*}$ is the unique positive root of the quadratic equation $A_{1}z^{2}+B_{1}z+C_{1} = 0$, in which

(iii) Suppose that $r > d_{3}$. If $R_{0} > 1+\dfrac{pm(r-d_{3})}{rd_{2}}$, system (1.4) has a unique immunity-activated infection equilibrium $E_{2}^{*} = (x_{2}^{*}, y_{2}^{*}, z_{2}^{*})$, where

and $y_{2}^{*}$ is the unique positive root of the quadratic equation $A_{2}y^{2}+B_{2}y+C_{2} = 0$, in which

3.   Global stability analysis of boundary equilibria

In order to study the stability of equilibrium, we linearize system (1.4) about one equilibrium $E^* = (x^{*}, y^{*}, z^{*})$ and obtain the following linear system

When $r = 0$, it follows from the study of Michael Y. Li and Hongying Shu ^[23] that time delay $\tau$ does not change the stability of the boundary equilibria.

When $r > 0$, by using the linear system (3.1) and constructing Lyapunov function, we can obtain the following results.

Proposition 3.1. Suppose that $0 < r < d_{3}$. Then we have

(i) The infection-free equilibrium $E_{0}^{yz}$ is globally asymptotically stable if $R_{0} < 1$, and it is unstable when $R_{0} > 1$.

(ii) The immunity-inactivated infection equilibrium $E_{0}^{z}$ is globally asymptotically stable if $1 < R_{0} < 1+\dfrac{\beta(d_{3}-r)}{cd_{1}}$, and it is unstable when $R_{0} > 1+\dfrac{\beta(d_{3}-r)}{cd_{1}}$.

Proof. (ⅰ) By the linear system (3.1), we can obtain the characteristic equation of system(1.4) at $E_{0}^{yz}$ as

So the eigenvalues are

As a result, if $R_{0} < 1$, the infection-free equilibrium $E_{0}^{yz}$ is locally asymptotically stable, and $E_{0}^{yz}$ is unstable if $R_{0} > 1$.

In order to obtain the global stability of equilibrium $E_{0}^{yz}$, we consider a Lyapunov function given by

Taking the time derivative of $L_{1}$ along the solution of system (1.4), we have

Notice that $r < d_{3}$ and $R_{0} < 1$. We have $L_{1}^{'}\leq0$ for all $x(t), y(t), z(t) > 0$, and $L_{1}^{'} = 0$ only if $x = x_{0}$, $y = 0$ and $z = 0$. It can be verified that the maximal compact invariant set in ${L_{1}^{'} = 0}$ is the singleton $E_{0}^{yz}$. By the LaSalle's invariance principle, we know the infection-free equilibrium $E_{0}^{yz}$ is globally asymptotically stable.

(ⅱ) The characteristic equation of system(1.4) at $E_{0}^{z}$ is

When $\tau = 0$ and $R_{0} < 1+\dfrac{\beta(d_{3}-r)}{cd_{1}}$, the roots of (3.3) are negative. When $\tau > 0$, the local stability of equilibrium $E_{0}^{z}$ is solely determined by

Let $\lambda = i\omega(\tau) (\omega(\tau) > 0)$ be the root of Eq (3.4). Separating real and imaginary parts yields

Squaring and adding Eq (3.5) gives

Note that

if $R_{0} < 1+\dfrac{\beta(d_{3}-r)}{cd_{1}}$. Then we konw that (3.3) has no root that can across the imaginary axis, which indicate that the immunity-inactivated infection equilibrium $E_{0}^{z}$ is locally asymptotically stable when $R_{0} < 1+\dfrac{\beta(d_{3}-r)}{cd_{1}}$.

In order to obtain the global stability of $E_{0}^{z}$, we construct the following Lyapunov functions:

Taking the time derivative of $L_{2}$ along the solution of system(1.4), we get

Using $s = \beta x_{1}y_{1}+d_{1}x_{1}$ and $d_{2} = \beta x_{1}$, we have

Using the LaSalle's invariance principle, we can obtain that $E_{0}^{z}$ is globally asymptotically stable.

Proposition 3.2. Suppose that $r = d_{3}$. Then we have

(i) The infection-free equilibrium $E_{0}^{yz}$ is globally asymptotically stable if $R_{0} < 1$, and it is unstable when $R_{0} > 1$.

(ii) The immunity-inactivated infection equilibrium $E_{0}^{z}$ is unstable as long as it appears, i.e., $R_{0} > 1$.

Proof. (ⅰ) The characteristic equation of system (1.4) at $E_{0}^{yz}$ is

So the eigenvalues are

So if $R_{0} < 1$, the infection-free equilibrium $E_{0}^{yz}$ is locally asymptotically stable and if $R_{0} > 1$, the equilibrium $E_{0}^{yz}$ is unstable.

In order to obtain the global stability of $E_{0}^{yz}$, we construct the following Lyapunov functions:

Taking the time derivative of $L_{3}$ along the solution of system (1.4), we have

Using the LaSalle's invariance principle, we can obtain that $E_{0}^{yz}$ is globally asymptotically stable.

(ⅱ)The characteristic equation of system (1.4) at $E_{0}^{z}$ is

It can be showed that there exist positive real root for the characteristic Eq (4.3), which indicates that the infection-free equilibrium $E_{0}^{z}$ is unstable. This completes the proof.

Proposition 3.3. Suppose that $r > d_{3}$. Then we have

(i) The infection-free equilibrium $E_{0}^{yz}$ is unstable.

(ii) The immunity-inactivated infection equilibrium $E_{0}^{z}$ is unstable.

(iii) If $R_{0} < 1+\dfrac{pm(r-d_{3})}{rd_{2}}$, the infection-free equilibrium $E_{0}^{y}$ is locally asymptotically stable, moreover if $R_{0} < 1$, the infection-free equilibrium $E_{0}^{y}$ is globally asymptotically stable; if $R_{0} > 1+\dfrac{pm(r-d_{3})}{rd_{2}}$, $E_{0}^{y}$ is unstable.

Proof. (ⅰ) The characteristic equation of system (1.4) at $E_{0}^{yz}$ is

So the eigenvalues are

It follows from $\lambda_{2} = r-d_{3} > 0$ that the infection-free equilibrium $E_{0}^{yz}$ is always unstable. So we can easily get the infection-free equilibrium $E_{0}^{yz}$ is always unstable when $\tau > 0$.

(ⅱ) The characteristic equation of system (1.4) at $E_{0}^{z}$ is

Note that $r > d_{3}$. It can be shown that there exist positive real root for the characteristic equation above, which indicates that the immunity-inactivated infection equilibrium $E_{0}^{z}$ is unstable.

(ⅲ) The characteristic equation of system (1.4) at $E_{0}^{y}$ is

The eigenvalues are

Note that

Thus, the infection-free equilibrium $E_{0}^{y}$ is locally asymptotically stable if $R_{0} < 1+\dfrac{pm(r-d_{3})}{rd_{2}}$, and $E_{0}^{y}$ is unstable if $R_{0} > 1+\dfrac{pm(r-d_{3})}{rd_{2}}$.

In order to obtain the global stability of $E_{0}^{y}$, we construct the following Lyapunov function:

Taking the time derivative of $L_{4}$ along the solution of system (1.4) and using a computation process similar to that of Theorem 3.9, we have

Thus, $\dfrac{dL_{4}}{dt}\leq0$ if $R_{0} < 1$, and $\dfrac{dL_{4}}{dt} = 0$ only if $x = x_{2}, y = 0$ and $z = z_{2}$, i.e., the maximal invariant subset in $\{(x, y, z): \dfrac{dL_{4}}{dt}\Big|_{(1.4)} = 0\}$ is the singleton $\{E_{0}^{y}\}$. As a result, $E_{0}^{y}$ is globally asymptotically stable based on the LaSalle's invariance principle. This complete the proof.

Remark 3.4. From Proposition 3.1 to Proposition 3.3, we can see that the delay $\tau$ does not affect the stability of infection-free equilibrium $E_{0}^{yz}$, $E_{0}^{y}$ and immune-unactivated $E_{0}^{z}$ equilibrium.

4.   Stability of positive equilibrium and Hopf bifurcation

In this section, we take the discrete delay $\tau$ as a bifurcation parameter and show that when the positive equilibrium $E_{2}^{*}$ loses its stability and a Hopf bifurcation appears when the delay $\tau$ passes through a critical value. We point out there also exists a Hopf bifurcation at positive equilibrium $E_{1}^{*}$ as the delay $\tau$ passes through a critical value and the proof is similar.

The characteristic equation of system (1.4) at $E_{2}^{*}$ is

where

When $\tau = 0,$ the characteristic equation of system (1.4) at $E_{2}^{*}$ is

where

After some calculations, we have

It follows from the Routh-Hurwitz criterion that $E_{2}^{*}$ is locally asymptotically stable when time delay is absent.

When $\tau > 0,$ putting $\lambda = i\omega$ into characteristic Eq (4.1) and separating real and imaginary parts, we have

Since $\sin^{2}(\omega\tau)+\cos^{2}(\omega\tau) = 1$, squaring and adding the two Eqs (4.2) and (4.3), we have

where

Let $u = \omega^{2}$, Eq (4.4) becomes

If Eq (4.5) has a positive real root $u$, the characteristic Eq (4.1) has a purely imaginary root $i\omega = i\sqrt{u}$; otherwise, Eq (4.1) has no purely imaginary root.

Note that

Let

Then we know that $G(u)$ is monotonically increasing if $\Delta\leq0$, which indicates that Eq (4.5) has no positive root when $p_{3}\geq0$ and $\Delta\leq0$.

If $\Delta > 0$, the function $G(u)$ has two critical points

Thus we know that Eq (4.5) has unique positive root $u_{0}$ with $G'(u_{0}) > 0$ if one of the following two conditions hold:

$(H_{1})\;$$\Delta > 0$, $p_{3} < 0$, $u^{**} < 0$ and $u^{*} > 0$;

$(H_{2}) \;$$\Delta > 0$, $p_{3} < 0$, $u^{*} > 0$ and $G(u^{**}) < 0$.

Equation (4.5) has two positive roots $u_{1} < u_{2}$ with $G'(u_{1}) < 0$ and $G'(u_{2}) > 0$ if the following assumption is satisfied:

$(H_{3})\;$$\Delta > 0$, $p_{3} > 0$, $u^{*} > 0$ and $G(u^{*}) < 0$.

Let $\omega_{k} = \sqrt{u_{k}}, k = 0, 1, 2$. It follows from Eqs (4.2) and (4.3) that the value of $\tau$ associated with the purely imaginary root $i\omega_{k}$ should satisfy

For $k = 0, 1, 2$, we define

Then at increasing sequences of $\tau$ values,

Eq (4.1) has purely imaginary roots $i\omega_{k}, k = 0, 1, 2$.

Now we consider the transversality conditions associated with Hopf bifurcation. Substituting $\lambda(\tau)$ into Eq (4.1) and differentiating the resulting equation in $\tau$, we obtain

which indicates that

Since $G'(u_{0}) > 0$, $G'(u_{1}) < 0$ and $G'(u_{2}) > 0$, then for $n = 0, 1, 2, ...,$ we have

and

Then we know that at each $\tau_{n}^{0}$ and $\tau_{n}^{2}$, $n = 0, 1, 2, \cdot\cdot\cdot$, a pair of characteristic roots of Eq (4.1) cross the imaginary axis to the right. At each $\tau_{n}^{1}$, $n = 0, 1, 2, \cdot\cdot\cdot$, a pair of characteristic roots of Eq (4.1) cross the imaginary axis to the left. Then the transversality condition required by the Hopf bifurcation theorem is satisfied.

Note that $\omega_{k} = \sqrt{u_{k}}$ and $u_{1} < u_{2}$. We have $\omega_{1} < \omega_{2}$, which indicates that

Then there exists a positive integer $k$ such that

We thus obtain the following result.

Theorem 4.1. For system (1.4), we have

(i) If $\Delta\leq0$ and $p_{3}\geq0$ holds, $E_{2}^{*}$ is asymptotically stable for all $\tau > 0$.

(ii) If one of the conditions ($H_{1}$) and ($H_{2}$) holds, $E_{2}^{*}$ is asymptotically stable when $\tau\in[0, \tau^{0}_{0})$ and unstable when $\tau > \tau^{0}_{0}$, that is system (1.4) undergoes a Hopf bifurcation at $E_{2}^{*}$ when $\tau = \tau^{0}_{0}$.

(iii) If the condition ($H_{3}$) holds, system (1.4) undergoes a Hopf bifurcation at $E_{2}^{*}$ along two sequences of $\tau$ values $\tau_{n}^{1, 2}$, $n = 0, 1, 2$.... Furthermore there exists a positive integer $k$ such that $E_{2}^{*}$ is stable when

$E_{2}^{*}$ is unstable when

5.   Direction and stability of the Hopf bifurcation

In the previous section, we know that system (1.4) undergoes a Hopf bifurcation at $E_{2}^{*}$ along some sequences of $\tau$ values. Let $\tau^{*}$ be one of the Hopf bifurcation points. As pointed out in Hassard et al. ^[31], it is interesting to determine the direction, stability and period of these periodic solutions.

Let $\mu = \tau-\tau^{*}$, and then $\mu$ is new bifurcation parameter of the system. Define

System (1.4) may be written as:

where

and

By Riesz representation theorem, there exists a matrix $\eta(\theta, \mu):[-\tau, 0]\rightarrow \mathbb{ R}^{3}$ whose components are bounded variation functions such that

where

and $\delta(\theta)$ is the Dirac delta function.

For $\phi\in C([-\tau, 0], R^{3})$, we define

and

Then system (1.4) is equivalent to the following operator equation

For $\varphi\in C([0, \tau], R^{3})$, we define the adjoint operator of $A(0)$ as $A^{\ast}(0)$, where

For the convenience of research, we simply write $A$ for $A(0)$, $A^{\ast}$ for $A^{\ast}(0)$, $R$ for $R(0)$, $\eta(\theta)$ for $\eta(\theta, 0)$, for $\varphi\in C([0, \tau], R^{3})$ and $\phi\in C([-\tau, 0], R^{3})$.

Define a bilinear form as

Let $q(\theta)$ and $q^{\ast}(s)$ to be the eigenvectors of matric $A$ and $A^{\ast}$ corresponding to eigenvalue $i\omega_{0}$ and $-i\omega_{0}$, respectively. Then

We can choose appropriate $q(\theta)$ and $q^{\ast}(s)$ such that $< q(\theta), q^{\ast}(s) > = 1$,

where

and

Note that

Then we can choose $\bar{D}$ as

such that $< q(\theta), q^{\ast}(s) > = 1$.

According to the notations in Hassard et al. ^[31], we need to compute the center manifold $C_{0}$ at $\mu = 0$. Let $u_{t}$ be the solution of Eq (5.1) when $\mu = 0$ and define

On the center manifold $C_{0}$, we have $W(t, 0) = W(Z(t), \bar{Z}(t), \theta)$, where

$Z$ and $\bar{Z}$ are local coordinates for center manifold $C_{0}$ in the direction of $q^{\ast}$ and $\bar{q}^{\ast}$. Note that if $X_{t}$ is real, $W$ is real. We only consider the real solutions. For the solution of the Eq (5.1) $X_{t}\in C_{0}$, we have

Now we rewrite this equation as $\dot{Z}(t) = i\omega Z+g(Z, \bar{Z})$, where

Note that $u_{t}(\theta) = W(t, \theta)+Zq(\theta)+\bar{Z}\bar{q}(\theta)$. We have

Comparing the coefficients with Eq (5.4), we have

It remains to compute $W_{11}(0)$ and $W_{20}(0)$ in $g_{21}$. From Eqs (5.2) and (5.3), we have

We rewrite the Eq (5.6) as

where

Thus

From Eq (5.7), we know that for $\theta\in[-1, 0)$

Comparing the coefficients with Eq (5.8), we obtain

From Eqs (5.8) and (5.9) and the definition of $A$, we have

where $q(\theta) = (1, q_{2}, q_{3})^{\mathrm{T}}e^{i\theta\omega\tau}$. Hence

where

Similarly, from Eqs (5.8) and (5.10) we obtain

where

So far, we have calculated $g_{20}$, $g_{11}$, $g_{02}$, $g_{21}$ in Eq (5.5) and then we can obtain

It is well known that $\nu_{2}$ and $\beta_{2}$ will determine the direction and stability of the Hopf bifurcation, and $T_{2}$ determines the period of the bifurcated periodic solutions, respectively. In particular, the Hopf bifurcation is supercritical (subcritical) if $\nu_{2} > 0 (\nu_{2} < 0)$, and the bifurcated periodic solutions exist for $\tau > \tau_{0} (\tau < \tau_{0})$. The bifurcated periodic solutions are stable (unstable) if $\beta_{2} < 0$ ($\beta_{2} > 0$) and the period will become longer (shorter) if $T_{2} > 0$ ($T_{2} < 0$).

6.   Numerical simulations

In this section, we carry out some numerical simulations to display some qualitative behaviours of system (1.4). Table $1$ lists the values or ranges of parameters for system (1.4) referring to ^[21].

We first study the effect of logistic growth on the dynamics of system (1.4). According to the ranges of parameters in Table 1, we take the following parameters

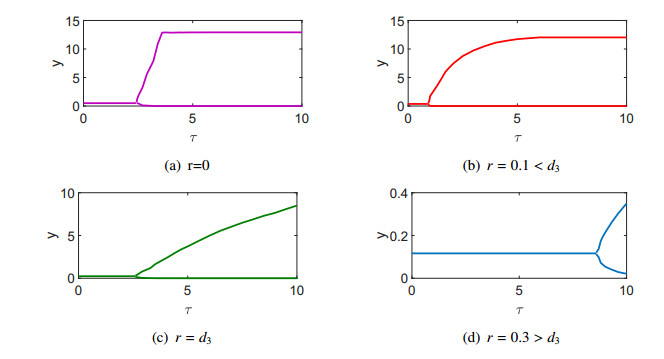
Figure 1 presents the bifurcation diagrams of the solutions for system (1.4) with respect to $\tau$ and different logistic growth rate $r$. One can see that the positive equilibrium $E_{1}^{*}$ of system (1.4) is local asymptotically stable when $\tau < \tau^{*} = 0.8$ and the bifurcated periodic solutions occurs through Hopf bifurcations when $\tau > \tau^{*}$. Similarly, the positive equilibrium $E_{2}^{*} = (49.42, 0.12, 9.77)$ of system (1.4) is local asymptotically stable when $\tau = 8 < \tau^{*} = 8.655$ and the bifurcated periodic solutions occur through Hopf bifurcations when $\tau = 9 > \tau^{*}$. At the same time, one can note that, except $r = 0$, the values of Hopf bifurcation points increase with the increase of $r$. On the other hand, the amplitude of the bifurcated periodic solution increase with the increase of time delay $\tau$ and decrease with the increase of $r$.

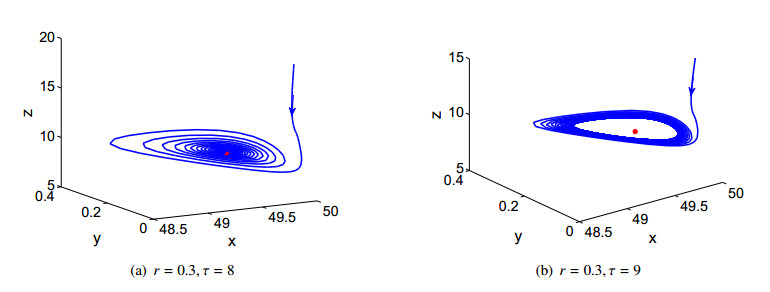
Figure 2 presents phase diagrams of the solutions for system (1.4) with $r = 0.3$ and different values of $\tau$. One can see that the positive equilibrium $E_{2}^{*} = (49.42, 0.12, 9.77)$ is local asymptotically stable when $\tau = 8 < \tau^{*} = 8.655$ and the bifurcated periodic solutions occur through Hopf bifurcations when $\tau = 9 > \tau^{*}$. Furthermore, using the given parameter values (6.1), we can obtain $c_{1}(0) = -19.651+26.769 i$ by some calculations and then we know that $\mu_{2} > 0,$ $\beta_{2} < 0,$ $T_{2} < 0$ by (5.11). According to the conclusion in ^[31], we know that the Hopf bifurcation at $\tau^{*} = 8.655$ is supercritical, and the bifurcating periodic solution is stable.

In order to investigate the stability switch of equilibrium, we take the following parameters

We obtain there exists positive equilibrium $E_{2}^{*} = (18.8775, 1.6487, 69.5102)$ and the characteristic equation of system (1.4) have two pure virtual roots $\omega_{1} = 0.4464$ and $\omega_{2} = 1.4748$. Then by (4.7) we get

and

Noting that $\tau^{2}_{1} > \tau^{1}_{2}$, we know that $E_{2}^{*}$ is asymptotically stable when $\tau\in[0, \tau_{0}^{1})\cup(\tau_{0}^{2}, \tau_{1}^{1})$ and is unstable when $\tau\in(\tau_{0}^{1}, \tau_{0}^{2})\cup(\tau_{1}^{1}, +\infty)$. Figure 3 presents time series diagrams of the solutions for system (1.4) with different values of $\tau$. One can see that there exists stability switch of equilibrium $E_{2}^{*}$ as $\tau$ increases and some periodic solutions are bifurcated by Hopf bifurcation.

7.   Conclusions and discussions

In this paper, a viral infection model with self-proliferation of cytotoxic T lymphocytes (CTLs) and activation time delay of immune cells is proposed. We mainly focus on two topics. First, we study the global dynamics of system (1.4) through constructing appropriate Lyapunov functions. Then we examine the impact of the activation time delay of immune cells on the existence of periodic solutions. The global dynamical properties of system (1.4) can be summarized in the following Table 2. Numerical simulations verify the theoretical analyses. In particular, we find that for different values of the delay in CTL response, the system can stabilize at the positive equilibrium when the delay is small, or stabilize at a stable periodic oscillation when the delay is large. The amplitudes of bifurcated periodic solutions increase with the increase of activation time delay of immune cells and decrease with the increase of $r$ (Figure 1). It is also found that there exists stability switch phenomenon under some conditions (Figure 3). The results indicate that the self-proliferation intensity and activation time delay of immune cells can significantly affect the kinetics of viral infection.

Some aspects of the viral infection problem remain to be studied in the future. For instance, we plan to extend our analysis to global Hopf bifurcation analysis. Some other factors that influence the dynamics of viral infection including the heterogeneity of space and movement of cells may be investigated.

Acknowledgments

The authors would like to thank the reviewers and the editor for their careful reading, helpful comments and suggestions that greatly improved the paper. This work is supported by the National Natural Science Foundation of China (Grant Nos. 11701472, 11771448, 11871403).

Conflict of interest

The authors declare that they have no conflict of interest.