Citation: Giulio Caravagna, Alex Graudenzi, Alberto d’Onofrio. Distributed delays in a hybrid model of tumor-Immune system interplay[J]. Mathematical Biosciences and Engineering, 2013, 10(1): 37-57. doi: 10.3934/mbe.2013.10.37
| [1] | Yaw Chang, Wei Feng, Michael Freeze, Xin Lu, Charles Smith . Elimination, permanence, and exclusion in a competition model under Allee effects. AIMS Mathematics, 2023, 8(4): 7787-7805. doi: 10.3934/math.2023391 |
| [2] | Guillaume Cantin, Cristiana J. Silva . Complex network near-synchronization for non-identical predator-prey systems. AIMS Mathematics, 2022, 7(11): 19975-19997. doi: 10.3934/math.20221093 |
| [3] | Haiping Pan, Yiqiu Mao . Transition and bifurcation analysis for chemotactic systems with double eigenvalue crossings. AIMS Mathematics, 2023, 8(10): 24681-24698. doi: 10.3934/math.20231258 |
| [4] | Lini Fang, N'gbo N'gbo, Yonghui Xia . Almost periodic solutions of a discrete Lotka-Volterra model via exponential dichotomy theory. AIMS Mathematics, 2022, 7(3): 3788-3801. doi: 10.3934/math.2022210 |
| [5] | M. Adel, M. M. Khader, Hijaz Ahmad, T. A. Assiri . Approximate analytical solutions for the blood ethanol concentration system and predator-prey equations by using variational iteration method. AIMS Mathematics, 2023, 8(8): 19083-19096. doi: 10.3934/math.2023974 |
| [6] | Yinyin Wu, Fanfan Chen, Qingchi Ma, Dingbian Qian . Subharmonic solutions for degenerate periodic systems of Lotka-Volterra type with impulsive effects. AIMS Mathematics, 2023, 8(9): 20080-20096. doi: 10.3934/math.20231023 |
| [7] | Nazmul Sk, Bapin Mondal, Abhijit Sarkar, Shyam Sundar Santra, Dumitru Baleanu, Mohamed Altanji . Chaos emergence and dissipation in a three-species food web model with intraguild predation and cooperative hunting. AIMS Mathematics, 2024, 9(1): 1023-1045. doi: 10.3934/math.2024051 |
| [8] | Xuechao Zhang, Yuhan Hu, Shichang Lu, Haomiao Guo, Xiaoyan Wei, Jun li . Dynamic analysis and control of online information dissemination model considering information beneficiaries. AIMS Mathematics, 2025, 10(3): 4992-5020. doi: 10.3934/math.2025229 |
| [9] | Li Wang, Hui Zhang, Suying Liu . On the existence of almost periodic solutions of impulsive non-autonomous Lotka-Volterra predator-prey system with harvesting terms. AIMS Mathematics, 2022, 7(1): 925-938. doi: 10.3934/math.2022055 |
| [10] | Iqra Batool, Naim Bajcinca . Stability analysis of a multiscale model including cell-cycle dynamics and populations of quiescent and proliferating cells. AIMS Mathematics, 2023, 8(5): 12342-12372. doi: 10.3934/math.2023621 |
In the United States of America, human papillomavirus (HPV) is the most common sexually transmitted infection (STI) in males and females [8]. Most sexually active males and females will get at least one type of HPV infection at some point in their lives [5]. In the United States, about 79 million are currently infected with HPV and about 14 million people become newly infected each year [8]. There are more than 150 different types of HPV [7]. Health problems related to HPV include genital warts and cancer. Most people infected with genital HPV do not know they are infected and never develop symptoms or health problems from it. Some people find out they have HPV when they get genital warts. Females may find out they have HPV when they get an abnormal Pap test result during cervical cancer screening. Others may only find out once they have developed more serious problems from HPV, such as cancer [5]. Most HPV infections cause no symptoms and are not clinically significant, but persistent infection can lead to disease or cancer.
Mathematical epidemic models have been used to study HPV infections in various populations. For example, Alsaleh and Gummel [1] in a recent paper, used a deterministic model to assess the impact of vaccination on both high-risk and low-risk HPV infection types. Ribassin-Majed and Clemencon [14] used a deterministic mathematical model to assess the impact of vaccination on non-cancer causing HPV (6/11) in French males and females. Lee and Tameru [13] used a deterministic model to assess the impact of HPV on cervical cancer in African American females (AAF). In all these studies, the HPV models have a constant recruitment function for the demographic equations.
In this paper, we use a two-sex HPV model with "fitted" logistic demographics to study the HPV disease dynamics in AAF and African American males (AAM) of 16 years and older. Using US Census Bureau data for AAF and AAM populations, we illustrate that the "fitted" logistic demographic equation captures the African American (AA) population better than the constant recruitment demographic equation. We compute the basic reproduction number,
The paper is organized as follows: In Section 2, we introduce a demographic equation for AAF (respectively, AAM) and we "fit" it to the US Census Bureau data of AAF (respectively, AAM) of 16 years and older. We introduce, in Section 3, a two-sex African American HPV model. In Section 4, we study disease-free equilibria and compute the basic reproduction number
In [14], Ribassin-Majed et al. used a HPV model with constant recruitment rate in the demographic equation to study HPV disease dynamics in male and female populations of France. In the absence of the HPV disease, the demographic equation of their model is the following ordinary differential equation:
| $\frac{dN}{dt}=\Lambda-\mu N\label{eq:l},$ | (1) |
where
In this paper, we use logistic models that are "fitted" to the
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
| AAF population 16 years and older [12,16] | 13,825,055 | 14,041,520 | 14,259,413 | 14,473,927 | 14,707,490 | 14,952,963 | 15,224,330 | 15,486,244 | 15,743,096 | 15,992,822 | 16,176,048 | 16,471,449 | 16,696,303 | 16,918,225 | 17,139,986 |
| AAF total population [12,16] | 18,787,192 | 19,013,351 | 19,229,855 | 19,434,349 | 19,653,829 | 19,882,081 | 20,123,789 | 20,374,894 | 20,626,043 | 20,868,282 | 21,045,595 | 21,320,013 | 21,543,051 | 21,767,521 | 21,988,307 |
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
| AAM population 16 years and older [12,16] | 11,909,507 | 12,124,810 | 12,332,791 | 12,518,252 | 12,756,370 | 12,996,123 | 13,266,163 | 13,517,841 | 13,765,707 | 14,006,594 | 14,181,655 | 14,490,027 | 14,724,637 | 14,950,933 | 15,176,189 |
| AAM total population [12,16] | 17,027,514 | 17,249,678 | 17,454,795 | 17,631,747 | 17,856,753 | 18,079,607 | 18,319,259 | 18,560,639 | 18,803,371 | 19,033,988 | 19,260,298 | 19,487,042 | 19,719,238 | 19,945,997 | 20,169,931 |
From Tables 1 and 2, we note that both male and female populations of African Americans of 16 years and older as well as the total populations exhibit increasing trends from 2000 to 2014. In the next section, we use a logistic differential equation model to "capture" the AA population data of Tables 1 and 2.
In [3], Brauer and Castillo-Chavez used the logistic equation "fitted" to United States Census Bureau data to model the total United States population. We use the same approach to "fit" the solution of the following logistic equation to the AAF population of 16 years and older (see Table 1) and the AAM population of 16 years and older (see Table 2).
| $\frac{dN_i}{dt}=(r_i-\mu_i)N_i(1-\frac{N_i}{K_i(r_i-\mu_i)/r_i}), t\geq0,\label{eq:a}$ | (2) |
where index
| $N_i(t)=0 \;\;\text{and} \;\;N_i(t)=\frac{K_i(r_i-\mu_i)/r_i}{1+(\frac{K_i(r_i-\mu_i)/r_i}{N_i^0}-1)e^{-(r_i-\mu_i)t}}.\label{eq:b}$ | (3) |
Let
| $R_{d_i}=\frac{r_i}{\mu_i}.$ |
| $K_i^*=\frac{K_i(r_i-\mu_i)}{r_i}, \;\;\text{as}\;\; t\rightarrow \infty,$ |
and the population persists. However, when
Equation (2) gives the per capita growth rate,
| $ \frac{dN_i/dt}{N_i}=(r_i-\mu_i)(1-\frac{N_i}{K_i(r_i-\mu_i)/r_i}). $ | (4) |
Using the
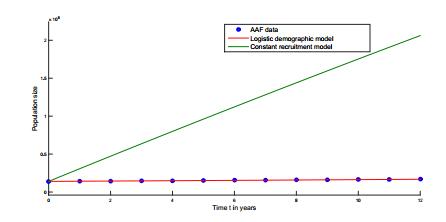 Figure 1. The logistic demographic model "fits"
Figure 1. The logistic demographic model "fits" 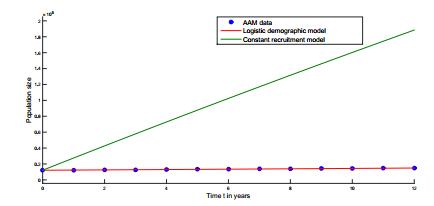 Figure 2. The logistic demographic model "fits"
Figure 2. The logistic demographic model "fits" Fitting the line to the curve gives
Using our estimates, we express the nontrivial solution (3) of the logistic growth model for AAF of 16 years and older as
| $N_f(t) = \frac{52,967,117}{1+2.772176873e^{-0.021298978t}},\label{eq:c}$ | (5) |
and for AAM of 16 years and older as
| $N_m(t) = \frac{99,484,673}{1+7.205050059e^{-0.019877926t}},\label{eq:c-m}$ | (6) |
where year 2001 is taken as
The plot of the data of AAF of 16 years or older and solution (5) in Figure 1 show that our "fitted" model captures the AAF data of Table 1. Similarly, the plot of the data of AAM of 16 years or older and solution (6) in Figure 2 show that our "fitted" model captures the AAM data of Table 2.
When the population in equation (1) consists only of AAF (
| $ N_i(t)=\frac{\Lambda_i}{\mu_i}+(N_i^0-\frac{\Lambda_i}{\mu_i})e^{-\mu_i t}.\label{eq:e} $ | (7) |
Using the initial condition
| $ N_f(t)=2,315,038,811-2,300,997,291\;e^{-0.007266 t},\label{eq:o} $ | (8) |
and
| $ N_m(t)=1,887,409,019-1,875,284,209\;e^{-0.008227 t}.\label{eq:o-m} $ | (9) |
In Figure 1, we compare the "fitted" solution (8) of Model (1), and our "fitted" solution (5) of Model (2), to the US Census Bureau data in Table 1. Figure 1 shows that Model (2), the "fitted" logistic model, captures better the
Similarly, Figure 2 shows that, as in the female population, the "fitted" solution (9) of Model (1) over estimates the AAM US Census Bureau data while our "fitted" solution (5) of Model (2) captures it.
To study the HPV dynamics in male and female African American populations of 16 years and older, we assume that the total AAF population (respectively, total AAM population) of 16 years and older is governed by Model (2) with
| $ \left\{ dSfdt=rfNf(1−NfKf)−σfSfImNf+Nm+δIf−μfSf,dSmdt=rmNm(1−NmKm)−σmSmIfNf+Nm+δIm−μmSm,dIfdt=σfSfImNf+Nm−(δ+μf)If,dImdt=σmSmIfNf+Nm−(δ+μm)Im,\right. $ | (10) |
where
| Parameter (per day) | Description | Reference |
| Death rate for AAF population | [6] | |
| Death rate for AAM population | [6] | |
| Clearance rate | [11] | |
| Intrinsic growth rate for AAF population | Estimated | |
| Intrinsic growth rate for AAM population | Estimated | |
| Carrying capacity for AAF population | Estimated | |
| Carrying capacity for AAF population | Estimated | |
| Infection rate for AAF population | [1] | |
| Infection rate for AAM population | [1] |
Notice that since
| $N_f(t)=S_f(t)+I_f(t)\;\;\text{and}\;\;N_m(t)=S_m(t)+I_m(t),$ |
adding the
Consequently, in Model (10), the total AAF and AAM populations, governed by our "fitted" logistic equations (5) and (6) are bounded. We will study Model (10) with the parameter values listed in Table 3 and with the initial conditions listed in Table 4.
| = | 8,618,960 | |
| = | 7,119,370 | |
| = | 5,422,560 | |
| = | 5,005,440 |
Notice that in Table 4,
In this section, we show that Model (10) is well-posed. In particular, we obtain that all orbits are nonnegative and there is no population explosion in Model (10).
Theorem 3.1. All solutions of Model (10) are nonnegative and bounded.
Proof. Consider the following nonnegative initial conditions
If
Similarly, if
If
Similarly, if
Recall that
Let
Then Model (10) is equivalent to
| $\frac{dX}{dt}=F(X).$ |
In AAF population,
Unlike in [14], it is possible for Model (10) to exhibit up to four disease-free equilibrium points (DFEs), where
Since
Since
To determine the stability of
| $J|_{P_{f0}}=[μf−rf02μf−rf+δ−σf0rm−μm02μm−rm+δ00−(δ+μf)σf000−(δ+μm)].$ |
Similarly, to determine the stability of
| $J|_{P_{m0}}=[rf−μf0rf+δ00μm−rm−σm2μm−rm+δ00−(δ+μf)000σm−(δ+μm)].$ |
To determine the stability of
| $ \left\{ dIfdt=σf(K∗f−If)ImK∗f+K∗m−(δ+μf)If,dImdt=σm(K∗m−Im)IfK∗f+K∗m−(δ+μm)Im,dSfdt=rfK∗f(1−K∗fKf)−σfSfImK∗f+K∗m+δIf−μfSf,dSmdt=rmK∗m(1−K∗mKm)−σmSmIfK∗f+K∗m+δIm−μmSm.\right. $ | (11) |
Using the next generation matrix method [17] we obtain the following two matrices
| $ \mathcal{F}=[σf(K∗f−If)ImK∗f+K∗mσm(K∗m−Im)IfK∗f+K∗m00]$ |
| $\text{and}\;\;\mathcal{V}=[(δ+μf)If(δ+μm)Im−rfK∗f(1−K∗fKf)+σfSfImK∗f+K∗m−δIf+μfSf−rmK∗m(1−K∗mKm)+σmSmIfK∗f+K∗m−δIm+μmSm].$ |
Then, using the Jacobian matrices of
| $D\mathcal{F}(Q_{fm})=\left[ F000\right]\;\;\text{and}\;\;D\mathcal{V}(Q_{fm})=\left[ V0WU\right],$ |
where
Hence,
| $FV^{-1}=\frac{1}{K_f^*+K_m^*}[0σfK∗fδ+μmσmK∗mδ+μf0].$ |
By the next generation matrix method [17], the reproduction number for Model (10),
| $\mathcal{R}_0=\rho(FV^{-1})=\sqrt{\mathcal{R}_{0f}\mathcal{R}_{0m}},\text{where }$ |
| $\mathcal{R}_{0f}=\frac{\sigma_f K_f^*}{(\delta+\mu_f)(K_f^*+K_m^*)}\;\;\text{and}\;\;\mathcal{R}_{0m}=\frac{\sigma_m K_m^*}{(\delta+\mu_m)(K_f^*+K_m^*)}.$ |
When
It is interesting to note that in [13], Lee and Tameru, obtained
To find an effective mitigation strategy that seeks to reduce HPV infection in AA population within the shortest time possible, in the next section, we use sensitivity analysis to study the impact of each model parameter on
Sensitivity indices are used to measure the relative change in a state variable when a parameter changes. Typically, the normalized forward sensitivity index of a variable to a parameter is defined as the ratio of the relative change in the variable to the relative change in the parameter. When the variable is a differential function of the parameter, the sensitive index may be alternatively defined using partial derivatives [4,10,18,19].
Definition 4.1([4,10,18,19]). The normalized forward sensitivity index of a variable,
| $\Upsilon^u_q:=\frac{\partial u}{\partial q}\times\frac{q}{u}.$ |
We use Definition 4.1 to derive the sensitivity indices of the basic reproduction number
Increasing (respectively, decreasing) the clearance rate,
To illustrate the impact of HPV on AAF and AAM populations of 16 years and older, we simulate Model (10) with the parameter values listed in Table 3 and the initial conditions listed in Table 4.
| Parameter | Sensitivity index of | Order of Importance |
| -0.9915 | 1 | |
| 0.5000 | 2 | |
| 0.5000 | 3 | |
| 0.1526 | 4 | |
| -0.1526 | 5 | |
| -0.0631 | 6 | |
| 0.0586 | 7 | |
| -0.0561 | 8 | |
| 0.0520 | 9 |
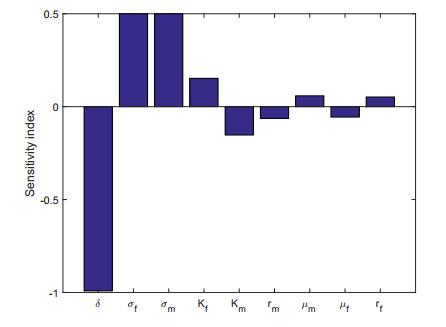 Figure 3. Normalized sensitivity indices of
Figure 3. Normalized sensitivity indices of Simulations of our HPV Model (10) are performed using Matlab software, and are illustrated in Figure 4. Figure 4 (a) shows that susceptible population of AAF of 16 years and older,
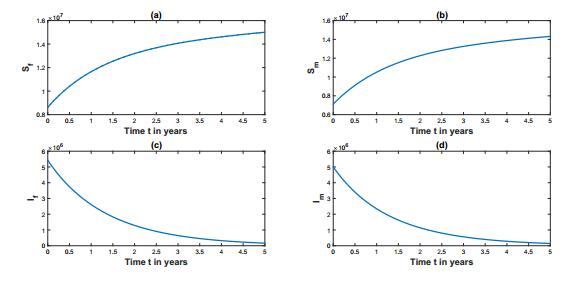 Figure 4. African American male and female HPV model simulations.
Figure 4. African American male and female HPV model simulations.To protect against HPV infections, HPV vaccines are available for males and females. Gardasil and Cervarix are two HPV vaccines that have market approval in many countries. Next, we introduce an extension of Model (10) with vaccinated male and female classes. We will use the extended model to study the impact of vaccination on Figure 4.
To introduce HPV vaccination in AAF and AAM populations of Model (10), we let
As in [14], we divide the AA population into eight compartments.
| $ \left\{ dSfdt=rf(1−pf)Nf(1−NfKf)−σfSfIm+IvmNf+Nm+δIf−μfSf,dSvfdt=pfrfNf(1−NfKf)−(1−τ)σfSvfIm+IvmNf+Nm+δIvf−μfSvf,dSmdt=rm(1−pm)Nm(1−NmKm)−σmSmIf+IvfNf+Nm+δIm−μmSm,dSvmdt=pmrmNm(1−NmKm)−(1−τ)σmSvmIf+IvfNf+Nm+δIvm−μmSvm,dIfdt=σfSfIm+IvmNf+Nm−(δ+μf)If,dIvfdt=(1−τ)σfSvfIm+IvmNf+Nm−(δ+μf)Ivf,dImdt=σmSmIf+IvfNf+Nm−(δ+μm)Im,dIvmdt=(1−τ)σmSvmIf+IvfNf+Nm−(δ+μm)Ivm,\right. $ | (12) |
where
| = | 5,257,566 | |
| = | 3,361,394 | |
| = | 5,667,019 | |
| = | 1,452,351 | |
| = | 5,086,421 | |
| = | 336,139 | |
| = | 4,860,205 | |
| = | 145,235 |
Note that in Table 6,
Proceeding exactly as in Theorem 3.1, we obtain the following result.
Theorem 5.1. All solutions of Model (12) are nonnegative and bounded.
Notice that when all vaccinated classes are missing
From Model (12), the demographic equations for the female and male total populations are respectively the following:
| $ \left\{ dNfdt=rfNf(1−NfKf)−μfNf,dNmdt=rmNm1−NmKm)−μmNm.\right. $ | (13) |
The equilibrium points of Model (13) are
As in Model (10), to state the "limiting" system of Model (12), we replace
| $ \left\{ dSfdt=rf(1−pf)K∗f(1−K∗fKf)−σfSfIm+IvmK∗f+K∗m+δIf−μfSf,dSmdt=rm(1−pm)K∗m(1−K∗mKm)−σmSmIf+IvfK∗f+K∗m+δIm−μmSm,dIfdt=σfSfIm+IvmK∗f+K∗m−(δ+μf)If,dIvfdt=(1−τ)σf(K∗f−Sf−If−Ivf)Im+IvmK∗f+K∗m−(δ+μf)Ivf,dImdt=σmSmIf+IvfK∗f+K∗m−(δ+μm)Im,dIvmdt=(1−τ)σm(K∗m−Sm−Im−Ivm)If+IvfK∗f+K∗m−(δ+μm)Ivm,\right. $ | (14) |
DFE of System (14) is
| $ \mathcal{F}=\left[σfSfIm+IvmK∗f+K∗m(1−τ)σf(K∗f−Sf−If−Ivf)Im+IvmK∗f+K∗mσmSmIf+IvfK∗f+K∗m(1−τ)σm(K∗m−Sm−Im−Ivm)If+IvfK∗f+K∗m00\right]$ |
| $\text{and}\;\; \mathcal{V}=\left[(δ+μf)If(δ+μf)Ivf(δ+μm)Im(δ+μm)Ivm−rf(1−pf)K∗f(1−K∗fKf)+σfSfIm+IvmK∗f+K∗m−δIf+μfSf−rm(1−pm)K∗m(1−K∗mKm)+σmSmIf+IvfK∗f+K∗m−δIm+μmSm\right].$ |
Let
| $D\mathcal{F}(Q)=\left[ F000\right]\;\;\text{and}\;\;D\mathcal{V}(Q)=\left[ V0WU\right],$ |
where
| $F=\left[00σf(1−pf)K∗fK∗f+K∗mσf(1−pf)K∗fK∗f+K∗m00(1−τ)σfpfK∗fK∗f+K∗m(1−τ)σfpfK∗fK∗f+K∗mσm(1−pm)K∗mK∗f+K∗mσm(1−pm)K∗mK∗f+K∗m00(1−τ)σmpmK∗mK∗f+K∗m(1−τ)σmpmK∗mK∗f+K∗m00\right],$ |
| $V=\left[δ+μf0000δ+μf0000δ+μm0000δ+μm\right], U=\left[μf00μm\right]$ |
| $ \text{and}\;\; W=\left[−δ0σf(1−pf)K∗fK∗f+K∗mσf(1−pf)K∗fK∗f+K∗mσm(1−pm)K∗mK∗f+K∗mσm(1−pm)K∗mK∗f+K∗m−δ0\right].$ |
Hence,
| $FV^{-1}=[00σf(1−pf)K∗f(δ+μm)(K∗f+K∗m)σf(1−pf)K∗f(δ+μm)(K∗f+K∗m)00(1−τ)σfpfK∗f(δ+μm)(K∗f+K∗m)(1−τ)σfpfK∗f(δ+μm)(K∗f+K∗m)σm(1−pm)K∗m(δ+μf)(K∗f+K∗m)σm(1−pm)K∗m(δ+μf)(K∗f+K∗m)00(1−τ)σmpmK∗m(δ+μf)(K∗f+K∗m)(1−τ)σmpmK∗m(δ+μf)(K∗f+K∗m)00].$ |
By the next generation matrix method [17], the reproduction number for Model (12),
| $\mathcal{R}_0^v=\rho(FV^{-1})=\sqrt{\mathcal{R}_{0f}^v\mathcal{R}_{0m}^v},\text{where }$ |
| $\mathcal{R}_{0f}^v=\frac{(1-\tau p_f)\sigma_f K_f^*}{(\delta+\mu_f)(K_f^*+K_m^*)}\;\;\text{and}\;\;\mathcal{R}_{0m}^v=\frac{(1-\tau p_m)\sigma_m K_m^*}{(\delta+\mu_m)(K_f^*+K_m^*)}.$ |
| $\mathcal{R}_{0f}^v=(1-\tau p_f)\mathcal{R}_{0f}\text{and}\mathcal{R}_{0m}^v=(1-\tau p_m)\mathcal{R}_{0m}.$ |
Since
Thus, adopting a HPV vaccination program decreases the basic reproduction number,
Using the parameter values of Table 3,
In the next section, we use sensitivity analysis to illustrate the impact of model parameters on
We use Definition 4.1 to derive the sensitivity indices of the basic reproduction number
From Table 7 and Figure 5, increasing (respectively, decreasing) the clearance rate,
| Parameter | Sensitivity index of | Order of Importance |
| -0.9915 | 1 | |
| 0.5000 | 2 | |
| 0.5000 | 3 | |
| -0.3829 | 4 | |
| -0.2704 | 5 | |
| 0.1526 | 6 | |
| -0.1526 | 7 | |
| -0.1124 | 8 | |
| -0.0631 | 9 | |
| 0.0586 | 10 | |
| -0.0561 | 11 | |
| 0.0520 | 12 |
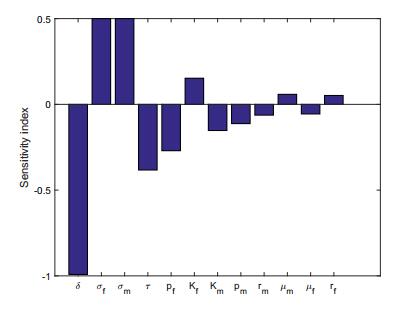 Figure 5. Normalized sensitivity indices of
Figure 5. Normalized sensitivity indices of To illustrate the impact of HPV on AAF and AAM populations of 16 years and older when a vaccination program is applied with
Simulations of our HPV Model (12) are performed using Matlab software, and are illustrated in Figure 6. Figures 6 (a-b) show that susceptible population of AAF of 16 years and older,
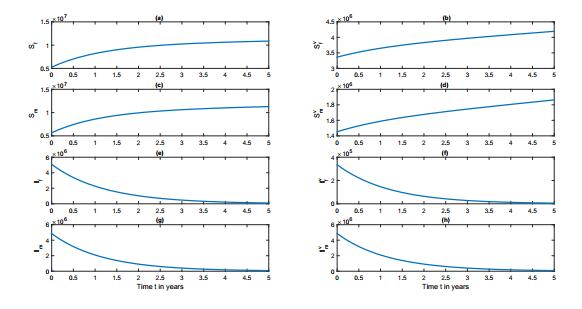 Figure 6. African American male and female HPV model with vaccination simulations.
Figure 6. African American male and female HPV model with vaccination simulations.To study the impact of the presence of the vaccinated class on the results of Figure 4, we simulate Model (12) using initial conditions in Table 8. For these simulations of Model (12), we keep all the parameter values at their current values in Figure 4, where
 | |||
| 5,257,566 | 4,309,480 | 2,585,688 | |
| 3,361,394 | 4,309,480 | 6,033,272 | |
| 5,667,019 | 3,559,685 | 2,135,811 | |
| 1,452,351 | 3,559,685 | 4,983,559 | |
| 5,086,421 | 4,991,612 | 4,819,233 | |
| 336,139 | 430,948 | 603,327 | |
| 4,860,205 | 4,649,472 | 4,507,084 | |
| 145,235 | 355,969 | 498,356 |
Note that in Figure 6 and Table 6,
In AA population,
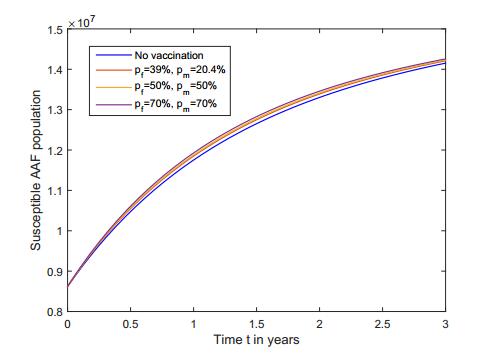 Figure 7. Susceptible AAF population.
Figure 7. Susceptible AAF population.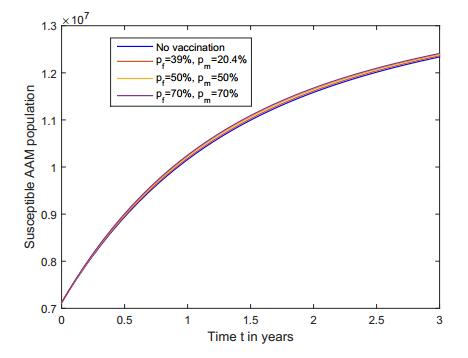 Figure 8. Susceptible AAM population.
Figure 8. Susceptible AAM population.Furthermore, in both AAF and AAM populations, Figures 9 and 10 show that the number of infected populations is lower when the population is under a vaccination policy than when the population is not being vaccinated. Thus, HPV vaccines that provide partial immunity to both AAF and AAM populations of 16 years and older not only lower the number of HPV infectives but increase the number of susceptibles in both female and male populations.
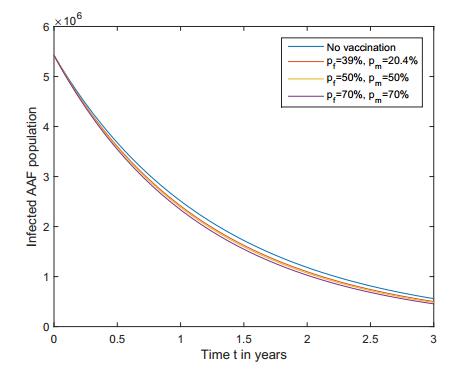 Figure 9. HPV Infected AAF population.
Figure 9. HPV Infected AAF population.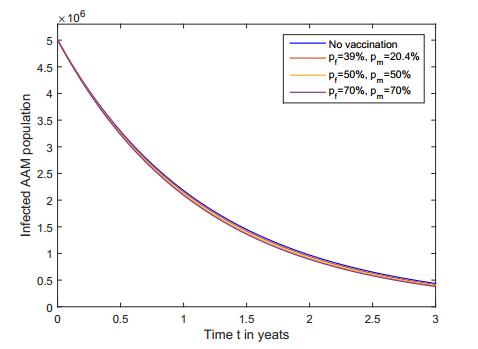 Figure 10. HPV Infected AAM population.
Figure 10. HPV Infected AAM population.Furthermore, we obtained in Figures 7-10 that the increase (respectively, decrease) in the susceptible (respectively, HPV infective) populations is larger when a bigger proportion of the population is vaccinated.
We use a two-sex HPV model with "fitted" logistic demographics to study HPV disease dynamics in AAF and AAM populations of 16 years and older. In agreement with Lee and Tameru [13], we obtained that in AA population,
Using sensitivity analysis on
● Increasing (respectively, decreasing) the clearance rate,
● Increasing (respectively, decreasing) the infection rate of the AAF population,
● Increasing (respectively, decreasing) the infection rate of the AAM population,
In the second part of the paper, we extended our model to include vaccination classes in both male and female AA populations of 16 years and older. We obtained that in AA population when the vaccination program is implemented,
● Increasing (respectively, decreasing) the clearance rate,
● Increasing (respectively, decreasing) the infection rate of the AAF population,
● Increasing (respectively, decreasing) the infection rate of the AAM population,
● Increasing (respectively, decreasing) the success rate of vaccination,
● Increasing (respectively, decreasing) the proportion of HPV vaccinated females,
Furthermore, using the extended model with vaccination we obtained the following results:
● Adopting a vaccination policy lowers HPV infections in both AAF and AAM populations.
● Vaccinating a larger proportion of AAF and AAM populations leads to fewer cases of HPV infections in the vaccinated population.
This research was partially supported by National Science Foundation under grant DUE-1439758.
| [1] | S. A. Agarwala (Guest Editor), Sem. Onc., Special Issue 29-3 Suppl. 7. 2003. |
| [2] | C.Priami et al.(Eds.): Trans. Comp. Sys. Bio. XIII, LNBI, 6575 (2011), 61-84. |
| [3] | PLoS Comp. Bio., (9), 2 (2006). |
| [4] | Curr. Top. Dev. Bio., 81 (2008), 485-502. |
| [5] | J. Math. Bio., 26 (1988), 661-688. |
| [6] | Europ. Urol., 44 (2003), 65-75. |
| [7] | Transf., 30 (1990), 291-294. |
| [8] | Bull. Math. Bio., 72 (2010), 490-505. |
| [9] | J. Log. Comp., (2011). |
| [10] | ENTCS, 229 (2009), 75-92. |
| [11] | Theoret. Comp. Sci., 282 (2002), 5-32. |
| [12] | Cha. Sol. Fract., 13 (2002), 645-655. |
| [13] | Ph.D. Thesis, Universit\`a di Pisa. 2011. |
| [14] | J. Th. Biology, 265 (2010), 336-345. |
| [15] | Proc. of the First Int. Work. on Hybrid Systems and Biology (HSB), EPTCS, 92 (2012), 106-121. |
| [16] | Th. Comp. Sc., 419 (2012), 26-49. |
| [17] | Submitted. Preprint at http://arxiv.org/abs/1206.1098. |
| [18] | J. Chem. Phys., 74 (1981), 3852-3858. |
| [19] | Proc. Cambridge Phil. Soc., 51 (1955), 433-440. |
| [20] | in "Complex Time-Delay Systems: Theory and Applications" (ed. F.M. Atay), Springer, (2010), 263-296. |
| [21] | Proc. 5th Int. Workshop on Process Algebra and Performance Modeling, CTIT technical reports series 97-14, University of Twente, 1-16. (1997). |
| [22] | in "Publication on The Microsoft Research - University of Trento Centre for Computational and Systems Biology Technical Reports" 2012. http://www.cosbi.eu/index.php/research/publications?abstract=6546. |
| [23] | Math. Mod. Meth. App. Sci., 16 (2006), 1375-1401. |
| [24] | Ch. Sol. Fract., 31 (2007), 261-268. |
| [25] | J. Th. Bio., 256 (2009), 473-478. |
| [26] | Math. Biosc. Eng., 7 (2010), 579-602. |
| [27] | BMC Bioinformatics, (4), 13 (2012). |
| [28] | Phys. Rev. E, 81 (2010), Art. n. 021923. |
| [29] | Phys. Rev. E, 84 (2011), Art. n. 031910. |
| [30] | Biology Direct, in press. 2012. |
| [31] | Math. Comp. Mod., 51 (2010), 572-591. |
| [32] | J. Roy. Stat. So. Series B, 46 (1984), 353-388. |
| [33] | J. Immunol., 134 (1985), 2748-2758. |
| [34] | Cancer Res., 65 (2005), 7950-7958. |
| [35] | J. P. Lippincott. 2005. |
| [36] | Ann. Rev. of Immun., 22 (2004), 322-360. |
| [37] | Ned. Tijdschr. Geneeskd., 5 (1909), 273-290. |
| [38] | Theoretical Biology and Medical Modelling, 9 (2012), Art.n. 31. |
| [39] | Springer-Verlag, Berlin and New York, 1994. |
| [40] | Int. J. Biomath., 3 (2010), 1-18. |
| [41] | Int. J. App. Math. and Comp. Sci., 13 (2003), 395-406. |
| [42] | (2nd edition). Springer. 1985. |
| [43] | Blood, 41 (1973), 771-783. |
| [44] | J. of Comp. Phys., 22 (1976), 403-434. |
| [45] | J. of Phys. Chem., 81 (1977), 2340-2361. |
| [46] | Proc. of the 15th conference on Winter simulation, 1 (1983), 39-44. |
| [47] | Biophys. J., 88 (2005), 2530-2540. |
| [48] | Proc. Roy. Soc. Edinburgh A, 130 (2000), 1275-1291. |
| [49] | Nonlin. Dyn., 69 (2011), 357-370. |
| [50] | University of Waterloo, available at http://uwspace.uwaterloo.ca/bitstream/10012/6403/1/Jessop_Raluca.pdf. 2011. |
| [51] | J. Clin. Invest., 117 (2007), 1466-1476. |
| [52] | Canc. Treat. Rev., 29 (2004), 199-209. |
| [53] | Blood, 35 (1970), 751-760. |
| [54] | Discr. Cont. Dyn. Systems, 4 (2004), 39-58. |
| [55] | J. Math. Biol., 37 (1998), 235-252. |
| [56] | Academic Press, 1993. |
| [57] | Sourcebook in Theoretical Ecology, Hastings and Gross ed., University of California Press, 2011. |
| [58] | Math. Comp. Mod., 33 (2001). |
| [59] | Bull. Math. Biol., 56 (1994), 295-321. |
| [60] | Sc., 197 (1977), 287-289. |
| [61] | Oxford University Press, USA. 2007. |
| [62] | A. Hem. 63 (1980), 68-70. |
| [63] | third edition, Springer Verlag, Heidelberg, 2003. |
| [64] | Ann. Rev. Immun., 21 (2003), 807-839. |
| [65] | Math. Med. and Bio., 24 (2007), 287-300. |
| [66] | Wiley-Blackwell, 2011. |
| [67] | in "NATO Science Series" (eds. O. Arino, M.L. Hbid and E. Ait Dads), 1 (205), Delay Differential Equations and Applications IV, 477-517. |
| [68] | JAMA, 244 (1980), 264-265. |
| [69] | Cancer, 79 (1997), 2361-2370. |
| [70] | Sem. Canc. Biol., 2 (2002), 33-42. |
| [71] | J. of Math. Bio., 47 (2003), 270-294. |
| [72] | New Engl. J. of Med., 286(1972), 284-290. |
| [73] | Sem. Canc. Biol., 12 (2002), 43-50. |
| [74] | Nonlin., 1 (1988), 115-155. |
| [75] | Int. J. Bifur. Chaos Appl. Sci. Eng., 19 (2009), 2283-2294. |
| 1. | O.M. Ogunmiloro, Modelling the Human Papilloma Virus Transmission in a Bisexually Active Host Community, 2020, 13, 20710216, 80, 10.14529/mmp200207 | |
| 2. | Mo’tassem Al-arydah, Two-Sex Logistic Model for Human Papillomavirus and Optimal Vaccine, 2021, 1793-5245, 2150011, 10.1142/S179352452150011X | |
| 3. | Xinwei Wang, Haijun Peng, Boyang Shi, Dianheng Jiang, Sheng Zhang, Biaosong Chen, Optimal vaccination strategy of a constrained time-varying SEIR epidemic model, 2019, 67, 10075704, 37, 10.1016/j.cnsns.2018.07.003 | |
| 4. | Shasha Gao, Maia Martcheva, Hongyu Miao, Libin Rong, The impact of vaccination on human papillomavirus infection with disassortative geographical mixing: a two-patch modeling study, 2022, 84, 0303-6812, 10.1007/s00285-022-01745-z | |
| 5. | Mo'tassem Al‐arydah, Mathematical modeling for relation between parents' health education and vaccine uptake, 2022, 0170-4214, 10.1002/mma.8860 | |
| 6. | Shasha Gao, Maia Martcheva, Hongyu Miao, Libin Rong, A two-sex model of human papillomavirus infection: Vaccination strategies and a case study, 2022, 536, 00225193, 111006, 10.1016/j.jtbi.2022.111006 | |
| 7. | Ramziya Rifhat, Zhidong Teng, Lei Wang, Ting Zeng, Liping Zhang, Kai Wang, Dynamical behavior and density function of a stochastic model of HPV infection and cervical cancer with a case study for Xinjiang, China, 2023, 00160032, 10.1016/j.jfranklin.2023.06.008 | |
| 8. | Praveen Kumar Rajan, Murugesan Kuppusamy, Abdullahi Yusuf, A fractional-order modeling of human papillomavirus transmission and cervical cancer, 2023, 2363-6203, 10.1007/s40808-023-01843-x | |
| 9. | Najat Ziyadi, A discrete-time nutrients-phytoplankton-oysters mathematical model of a bay ecosystem*, 2023, 17, 1751-3758, 10.1080/17513758.2023.2242720 | |
| 10. | Tuan Anh Phan, Farhana Sarower, Jinqiao Duan, Jianjun Paul Tian, Stochastic dynamics of human papillomavirus delineates cervical cancer progression, 2023, 87, 0303-6812, 10.1007/s00285-023-02018-z | |
| 11. | Shayidan Abuduwaili, Lei Wang, Zhidong Teng, Abidan Ailawaer, Ramziya Rifhat, Estimating real-time reproduction number for HPV infection in Xinjiang, China, 2025, 2025, 2731-4235, 10.1186/s13662-025-03896-x | |
| 12. | M. Arunkumar, Praveen Kumar Rajan, K. Murugesan, Mathematical Analysis of an Optimal Control Problem for Mitigating HPV Transmission and Cervical Cancer Progression through Educational Campaigns, 2025, 2731-8095, 10.1007/s40995-025-01804-2 |
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
| AAF population 16 years and older [12,16] | 13,825,055 | 14,041,520 | 14,259,413 | 14,473,927 | 14,707,490 | 14,952,963 | 15,224,330 | 15,486,244 | 15,743,096 | 15,992,822 | 16,176,048 | 16,471,449 | 16,696,303 | 16,918,225 | 17,139,986 |
| AAF total population [12,16] | 18,787,192 | 19,013,351 | 19,229,855 | 19,434,349 | 19,653,829 | 19,882,081 | 20,123,789 | 20,374,894 | 20,626,043 | 20,868,282 | 21,045,595 | 21,320,013 | 21,543,051 | 21,767,521 | 21,988,307 |
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
| AAM population 16 years and older [12,16] | 11,909,507 | 12,124,810 | 12,332,791 | 12,518,252 | 12,756,370 | 12,996,123 | 13,266,163 | 13,517,841 | 13,765,707 | 14,006,594 | 14,181,655 | 14,490,027 | 14,724,637 | 14,950,933 | 15,176,189 |
| AAM total population [12,16] | 17,027,514 | 17,249,678 | 17,454,795 | 17,631,747 | 17,856,753 | 18,079,607 | 18,319,259 | 18,560,639 | 18,803,371 | 19,033,988 | 19,260,298 | 19,487,042 | 19,719,238 | 19,945,997 | 20,169,931 |
| Parameter (per day) | Description | Reference |
| Death rate for AAF population | [6] | |
| Death rate for AAM population | [6] | |
| Clearance rate | [11] | |
| Intrinsic growth rate for AAF population | Estimated | |
| Intrinsic growth rate for AAM population | Estimated | |
| Carrying capacity for AAF population | Estimated | |
| Carrying capacity for AAF population | Estimated | |
| Infection rate for AAF population | [1] | |
| Infection rate for AAM population | [1] |
| = | 8,618,960 | |
| = | 7,119,370 | |
| = | 5,422,560 | |
| = | 5,005,440 |
| Parameter | Sensitivity index of | Order of Importance |
| -0.9915 | 1 | |
| 0.5000 | 2 | |
| 0.5000 | 3 | |
| 0.1526 | 4 | |
| -0.1526 | 5 | |
| -0.0631 | 6 | |
| 0.0586 | 7 | |
| -0.0561 | 8 | |
| 0.0520 | 9 |
| = | 5,257,566 | |
| = | 3,361,394 | |
| = | 5,667,019 | |
| = | 1,452,351 | |
| = | 5,086,421 | |
| = | 336,139 | |
| = | 4,860,205 | |
| = | 145,235 |
| Parameter | Sensitivity index of | Order of Importance |
| -0.9915 | 1 | |
| 0.5000 | 2 | |
| 0.5000 | 3 | |
| -0.3829 | 4 | |
| -0.2704 | 5 | |
| 0.1526 | 6 | |
| -0.1526 | 7 | |
| -0.1124 | 8 | |
| -0.0631 | 9 | |
| 0.0586 | 10 | |
| -0.0561 | 11 | |
| 0.0520 | 12 |
 | |||
| 5,257,566 | 4,309,480 | 2,585,688 | |
| 3,361,394 | 4,309,480 | 6,033,272 | |
| 5,667,019 | 3,559,685 | 2,135,811 | |
| 1,452,351 | 3,559,685 | 4,983,559 | |
| 5,086,421 | 4,991,612 | 4,819,233 | |
| 336,139 | 430,948 | 603,327 | |
| 4,860,205 | 4,649,472 | 4,507,084 | |
| 145,235 | 355,969 | 498,356 |
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
| AAF population 16 years and older [12,16] | 13,825,055 | 14,041,520 | 14,259,413 | 14,473,927 | 14,707,490 | 14,952,963 | 15,224,330 | 15,486,244 | 15,743,096 | 15,992,822 | 16,176,048 | 16,471,449 | 16,696,303 | 16,918,225 | 17,139,986 |
| AAF total population [12,16] | 18,787,192 | 19,013,351 | 19,229,855 | 19,434,349 | 19,653,829 | 19,882,081 | 20,123,789 | 20,374,894 | 20,626,043 | 20,868,282 | 21,045,595 | 21,320,013 | 21,543,051 | 21,767,521 | 21,988,307 |
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
| AAM population 16 years and older [12,16] | 11,909,507 | 12,124,810 | 12,332,791 | 12,518,252 | 12,756,370 | 12,996,123 | 13,266,163 | 13,517,841 | 13,765,707 | 14,006,594 | 14,181,655 | 14,490,027 | 14,724,637 | 14,950,933 | 15,176,189 |
| AAM total population [12,16] | 17,027,514 | 17,249,678 | 17,454,795 | 17,631,747 | 17,856,753 | 18,079,607 | 18,319,259 | 18,560,639 | 18,803,371 | 19,033,988 | 19,260,298 | 19,487,042 | 19,719,238 | 19,945,997 | 20,169,931 |
| Parameter (per day) | Description | Reference |
| Death rate for AAF population | [6] | |
| Death rate for AAM population | [6] | |
| Clearance rate | [11] | |
| Intrinsic growth rate for AAF population | Estimated | |
| Intrinsic growth rate for AAM population | Estimated | |
| Carrying capacity for AAF population | Estimated | |
| Carrying capacity for AAF population | Estimated | |
| Infection rate for AAF population | [1] | |
| Infection rate for AAM population | [1] |
| = | 8,618,960 | |
| = | 7,119,370 | |
| = | 5,422,560 | |
| = | 5,005,440 |
| Parameter | Sensitivity index of | Order of Importance |
| -0.9915 | 1 | |
| 0.5000 | 2 | |
| 0.5000 | 3 | |
| 0.1526 | 4 | |
| -0.1526 | 5 | |
| -0.0631 | 6 | |
| 0.0586 | 7 | |
| -0.0561 | 8 | |
| 0.0520 | 9 |
| = | 5,257,566 | |
| = | 3,361,394 | |
| = | 5,667,019 | |
| = | 1,452,351 | |
| = | 5,086,421 | |
| = | 336,139 | |
| = | 4,860,205 | |
| = | 145,235 |
| Parameter | Sensitivity index of | Order of Importance |
| -0.9915 | 1 | |
| 0.5000 | 2 | |
| 0.5000 | 3 | |
| -0.3829 | 4 | |
| -0.2704 | 5 | |
| 0.1526 | 6 | |
| -0.1526 | 7 | |
| -0.1124 | 8 | |
| -0.0631 | 9 | |
| 0.0586 | 10 | |
| -0.0561 | 11 | |
| 0.0520 | 12 |
 | |||
| 5,257,566 | 4,309,480 | 2,585,688 | |
| 3,361,394 | 4,309,480 | 6,033,272 | |
| 5,667,019 | 3,559,685 | 2,135,811 | |
| 1,452,351 | 3,559,685 | 4,983,559 | |
| 5,086,421 | 4,991,612 | 4,819,233 | |
| 336,139 | 430,948 | 603,327 | |
| 4,860,205 | 4,649,472 | 4,507,084 | |
| 145,235 | 355,969 | 498,356 |