The POD-based reduced-dimension study on the two-grid finite element method for the nonlinear time-fractional wave equation

1.   Introduction

The partial differential equations (PDEs) with fractional derivatives have an important physics background, can be used to describe some natural phenomena, and have been applied in many fields, such as nonlinear dynamics ^[1], physics ^[2], and bioengineering ^[3]. Due to the complexity of the fractional PDEs, their analytical solutions are usually not available. Hence, the numerical methods of the fractional PDEs have received much attention. For instance, a high-order finite difference (FD) scheme of the two-dimensional (2D) time-space tempered fractional diffusion wave equation was studied in ^[4], a high-order FD algorithm for the fractional diffusion wave equation with the Caputo fractional derivative was addressed in ^[5], a higher order FD algorithm of the fractional-order reaction and anomalous diffusion equation was presented in ^[6], a reduced-order FD scheme of the fractional-order parabolic-type sine-Gordon equations was posed in ^[7], an optimized FD scheme of the fractional-order parabolic-type sine-Gordon equations was proposed in ^[8], a Crank–Nicolson finite element (FE) method of the symmetric tempered fractional diffusion equation was constructed in ^[9], and a meshless method for solving a wide class of time-fractional PDEs was developed in ^[10]. However, these time-fractional PDEs are linear, so only single-layer grid numerical methods are needed to solve them. Recently, a two-grid FE (TGFE) method for the nonlinear time-fractional wave (NTFW) equation with two strong nonlinear terms was established in ^[11], which was composed of a nonlinear FE system of equations on the coarser grids and a linear FE system of equations on the finer grids with sufficient accuracy, thus simplifying the calculation and improving the computational efficiency.

The TGFE method was initially used to solve nonlinear elliptic equations (see ^[12]). Afterward, Shi's and Liu's teams ^[13,14,15] used the method to solve some more complicated nonlinear PDEs. Though the classical TGFE (CTGFE) method for solving the NTFW equations in ^[11] can greatly simplify the calculation and improve the computational efficiency, when it is used for the actual engineering calculations, the unknowns can be as high as tens of millions. Therefore, the main purpose of this paper is to create a new reduced-dimension TGFE (RDTGFE) method by using proper orthogonal decomposition (POD) in [16, Sec. 5.1] to reduce the dimension of unknown coefficient vectors in the CTGFE solutions in ^[11] and keep the FE basic functions unchanged. Thus, the created RDTGFE method can not only have the advantages of the CTGFE method, but also greatly reduce unknowns, mitigate calculation burden, retard the accumulation of computation errors, and enhance computation efficiency. Therefore, it is a study with practical application value.

A large number of numerical tests, such as the natural boundary element space reduced-dimension method in ^[17], the FE space reduced-dimension methods in ^[18,19], and the Galerkin space reduced-dimension methods in ^[20,21,22], show that the POD method is one of the most effective approaches for reducing the unknowns of numerical methods. However, the above reduced-dimension methods all belong to the category of dimensionality reduction methods of FE space, i.e., FE basic functions (since FE subspace is spanned by the FE basic functions) for the Galerkin and FE methods, which are thoroughly distinct from the RDTGFE method in this article and are further explained as follows.

It is well known that the unknown Galerkin and FE solutions $w_h^k$ at moment $t_k$ are equal to the linear combination of the known FE basis functions $\zeta_1({\mathit{\boldsymbol{x}}}),$ $\zeta_2({\mathit{\boldsymbol{x}}}), \cdots,$ $\zeta_{M_h}({\mathit{\boldsymbol{x}}})$ and unknown solution coefficients $w_1^k,$ $w_2^k,$ $\cdots, w_{M_h}^k$ at moment $t_k$, i.e., are equal to the inner product of the known FE bases function vectors ${\mathit{\boldsymbol{\zeta}}} = (\zeta_1({\mathit{\boldsymbol{x}}}), \zeta_2({\mathit{\boldsymbol{x}}}), \cdots,$ $\zeta_{M_h}({\mathit{\boldsymbol{x}}}))^T$ and unknown solution coefficient vectors ${\mathit{\boldsymbol{w}}}^k = (w_1^k, w_2^k,$ $\cdots, w_{M_h}^k)^T$, namely that

where $M_h$ is the number of FE basic functions, which is equal to the number of FE grid nodes, and $K$ is the number of time nodes.

Both the Galerkin reduced-dimension methods and FE reduced-dimension methods mentioned above are designed by reducing the dimension of the FE basic function vectors ${\mathit{\boldsymbol{\zeta}}}$, while the RDTGFE method of this paper is created by reducing the dimension of unknown solution coefficient vectors ${\mathit{\boldsymbol{w}}}^k$ and keeping the FE basic function vectors ${\mathit{\boldsymbol{\zeta}}}$ unchanged. Therefore, the RDTGFE method is quite different from the previous reduced-dimension method of the FE basic function vectors, i.e., FE subspace.

Although the RDTGFE methods for the nonlinear wave equation ^[23], the 3D nonlinear elastodynamic sin-Gordon problem ^[24], the unsaturated soil water flow problem ^[25], the nonlinear fourth-order reaction diffusion equation with a temporal fractional derivative ^[26], and the spatial fractional nonlinear Allen-Cahn equations ^[27] have been developed, the NTFW equation with two strong nonlinear terms and a time-fractional derivative as well as a second time derivative in this paper is much more complicated that the above five equations with only a nonlinear term. Hence, both the design of the RDTGFE format and the theory analysis for the existence, unconditional stableness, and error estimations for the RDTGFE solutions are confronted with more difficulties and require more techniques than all the previous works. But, as just mentioned above, the RDTGFE method for the equation with two strong nonlinear terms has more important applications than the previous works. Hence, it is very valuable to study the RDTGFE method of the NTFW equation.

The rest of this article is organized as follows. First, in Section 2, we review the CTGFE method in ^[11] and provide the existence and unconditional stableness as well as error estimates of the CTGFE solutions. Thereafter, in Section 3, we create a new RDTGFE method by using the POD method only to reduce the dimension of unknown coefficient vectors in the CTGFE solutions and keep the FE basis functions unchanged, and prove the existence and stableness as well as error estimates of the RDTGFE solutions by using matrix analysis. Afterward, in Section 4, we use some numerical tests to confirm the effectiveness of the RDTGFE method and correctness of our theory results. Finally, in Section 5, we generalize the main conclusions to this article and provide some expectations for the future research.

2.   The CTGFE method

The NTFW equation with two strong nonlinear terms is found in ^[11], which is restated as follows:

Problem 1. Find $w:[0, \; t_e)\to C^2(\bar{\Omega})$ such that

where $t_e$ is the given last moment, $C^2(\bar{\Omega})$ represents a space consisting of functions with second-order continuous derivatives, $\Omega\subset \mathbb{R}^n$ $(n = 1, 2, 3)$ is a connected bounded region with boundary $\partial\Omega$, $w_{t} = \partial w/\partial t$, $w_{tt} = \partial^{2} w/\partial t^{2}$, $\partial_{t}^{\gamma} w({\mathit{\boldsymbol{x}}}, t)$ $(1 < \gamma < 2)$ is the Caputo time-fractional derivative, defined as follows:

$a(w) > 0$ and ${f}(w)$ are two nonlinear functions that can be arbitrarily selected according to the needs of the object of study and are bounded second-order derivatives, namely, there are two positive numbers $\alpha_i > 0$ $(i = 1, 2)$ such that

and the source term $g({\mathit{\boldsymbol{x}}}, t)$, and the initial values $w^0({\mathit{\boldsymbol{x}}})$ and $w^1({\mathit{\boldsymbol{x}}})$ are three sufficiently smooth known functions.

The Sobolev spaces and norms used hereinafter are standard (see ^[16,28,29]). For example, the Sobolev space $H^m(\Omega)$ is also a Hilbert space, which is defined as follows:

where $m{\geqslant}0$ and $\alpha_i{\geqslant}0$ $(i = 1, 2, \cdots, n)$ are integers. Especially, the subspace $H_0^m(\Omega)$ of $H^m(\Omega)$ is defined as follows:

The norm and semi-norm are respectively defined as follows:

Let $\mathbb{U} = H_0^1(\Omega)$. Thus, by Green's formula, we can build the following variational format of Problem 1.

Problem 2. For any $t\in (0, \; t_e)$, find $w\in\mathbb{U}$ such that

where $(w, \upsilon) = \int_{\Omega}w({\mathit{\boldsymbol{x}}}, t)\upsilon({\mathit{\boldsymbol{x}}}, t){{{\rm{d}}}}{\mathit{\boldsymbol{x}}}$ is the $L^2$ inner product.

The existence and stability for the generalized solutions to Problem 2 can be proved by the proof method of Theorem 3.3.1 in ^[16].

To create the CTGFE method, we need to employ, respectively, difference quotient and the two-grid FE method to discretize the time derivative and the spatial variables in Problem 2. For this end, we first assume that $K > 0$ is an integer, $\Delta t = t_e/K$ is the time step increment, $w^k$ ($0{\leqslant} k{\leqslant} K$) is the approximations to $w({\mathit{\boldsymbol{x}}}, t)$ at $t_k = k\Delta t$, and

Thus, when $w\in c^3[0, t_e]$, by Taylor's formula, we get

When $w\in c^3[0, t_e]$, if we set that

then, by the technique in ^[11], the mean value $\hat{\partial}_t^{\gamma}w^{k}$ of the Caputo time-fractional derivative $\partial_{t}^{\gamma} w({\mathit{\boldsymbol{x}}}, t)$ $(1 < \gamma < 2)$ can be approximated by

where $b_j = (j+1)^{2-\gamma}-j^{2-\gamma} > 0$, satisfying

Then, we assume that $\mathfrak{J}_H$ is a coarse grid on $\bar{\Omega}$ that is quasi-uniformly divided, which is composed of two-dimensional triangles or quadrangles and three-dimensional tetrahedrons or hexahedrons, and $H$ represents the maximum diameter of all $E\in\mathfrak{J}_H$. Thus, the FE space defined on the coarse grids is expressed by

where $\mathbb{P}_l(E)$ $(l{\geqslant} 1)$ stands for the space of polynomials with degree ${\leqslant} l$ defined on the coarse grid element $E\in\mathfrak{J}_H$.

Afterward, we assume that $\mathfrak{J}_h$ is a fine grid on $\bar{\Omega}$ that is a quasi-uniform division and $h$ represents the maximum diameter of all $e\in\mathfrak{J}_h$ $(h\ll H)$. Likewise, the FE space defined on the fine grids $\mathfrak{J}_h$ is denoted by

If we assume that $R_\delta:\mathbb{U}\to \mathbb{U}_\delta$ $(\delta = H, h)$ are two Ritz projections, i.e., for any $u\in \mathbb{U}$, there are two unique $R_\delta u\in \mathbb{U}_\delta$ such that

then we get the following error estimates:

Thus, the CTGFE method can be created in the following.

Problem 3. Step 1. Find $w_H^k\in \mathbb{U}_H$ $(1{\leqslant} k{\leqslant} K)$ defined on the coarse grid $\mathfrak{J}_H$ such that they satisfy the following nonlinear system of equations:

Step 2. Find $w_h^k\in\mathbb{U}_h$ $(1{\leqslant} k{\leqslant} K)$ defined on the fine grid $\mathfrak{J}_h$ such that they satisfy the following linear system of equations:

The following results of existence, stability, and error estimates of the CTGFE solutions for Problem 3 have been provided in [11, Theorems 4.1 and 4.2].

Theorem 1. Problem 3 has a unique set of solutions $\{w_H^k\}_{k = 1}^K\subset\mathbb{U}_H$ defined on the coarse grid $\mathfrak{J}_H$ and a unique set of solutions $\{w_h^k\}_{k = 1}^K\subset\mathbb{U}_h$ defined on the fine grid $\mathfrak{J}_h$, respectively, satisfying the following unconditional boundedness, i.e., unconditional stability:

where and hereinafter $c$ is also a positive constant independent of $H$, $h$, and $\Delta t$. Furthermore, when $H = O(\Delta t^{3-\gamma})$ and $h = O(H^{{1+1/l}})$, they have the following error estimations:

where $w(t_k) = w({\mathit{\boldsymbol{x}}}, t_k)$.

Remark 1. Theorem 1 shows that the CTGFE solutions are unconditionally stable and can theoretically achieve an optimal order error estimate.

3.   The RDTGFE method

3.1.   The matrix form of the CTGFE method

The most critical step in creating the RDTGFE method is to rewrite the CTGFE method in matrix form. By the orthogonalization principle in functional analysis in [30, Sect. 1.6.3] and the existence of orthonormal basis functions in [30, Proposition 1.6.21], we claim that the FE subspaces $\mathbb{U}_H$ and $\mathbb{U}_h$ have, respectively, a set of orthonormal basis functions $\left\{\zeta_i\right\}_{i = 1}^{M_H}$ and $\left\{\xi_i\right\}_{i = 1}^{M_h}$ under the $L^2$ inner product $(\cdot, \cdot)$, where $M_H$ and $M_h$ are the dimensions of the FE subspaces $\mathbb{U}_H$ and $\mathbb{U}_h$, respectively. Thus, the FE subspaces $\mathbb{U}_H$ and $\mathbb{U}_h$ can be reexpressed by

By using the basis functions $\left\{\zeta_i\right\}_{i = 1}^{M_H}$ and $\left\{\xi_i\right\}_{i = 1}^{M_h}$, the CTGFE solutions $w_H^k$ and $w_h^k$ can be respectively denoted by

where ${\mathit{\boldsymbol{\zeta}}} = (\zeta_1, \zeta_2, \cdots, \zeta_{M_H})^T$ and ${{\mathit{\boldsymbol{\xi}}}} = (\xi_1, \xi_2, \cdots, \xi_{M_h})^T$ are, respectively, the basis function vectors formed by the orthonormal bases $\left\{\zeta_i\right\}_{i = 1}^{M_H}$ and $\left\{\xi_i\right\}_{i = 1}^{M_h}$, and ${\mathit{\boldsymbol{W}}}^k = (W_{1}^k, W_{2}^k, \cdots,$ $W_{M_H}^k)^T$ and ${{\mathit{\boldsymbol{w}}}}^k = ({w}_{1}^k, {w}_{2}^k, \cdots,$ ${w}_{M_h}^k)^T$ are, respectively, vectors formed by the unknown coefficients in the CTGFE solutions $w_{H}^k$ and $w_{h}^k$. Thus, Problem 3 may be rewritten as the follow matrix form.

Problem 4. Step 1. Find ${\mathit{\boldsymbol{W}}}^k\in\mathbb{R}^{M_H}$ and $w_H^k\in\mathbb{U}_H$ $(1{\leqslant} k{\leqslant} K)$ such that they satisfy the following nonlinear system of equations:

where $\hat{D}_t^{\gamma}{\mathit{\boldsymbol{W}}}^{k}$ are obtained by replacing $w^k$ in (2.6) with ${\mathit{\boldsymbol{W}}}^{k}$, and

are three $M_H$-dimensional vectors.

Step 2. Find ${{\mathit{\boldsymbol{w}}}}^k\in\mathbb{R}^{M_h}$ and $w_h^k\in\mathbb{U}_h$ $(1{\leqslant} k{\leqslant} K)$ such that they satisfy the following linear system of equations:

where $\hat{D}_t^{\gamma}{\mathit{\boldsymbol{w}}}^{k}$ are obtained by replacing $w^k$ in (2.6) with ${\mathit{\boldsymbol{w}}}^{k}$, and

are three $M_h$-dimensional vectors.

For Problem 4, we get the following conclusion.

Theorem 2. Under the same conditions as Theorem 1, Problem 4 has two unique sets of CTGFE solution coefficient vectors $\{{\mathit{\boldsymbol{W}}}^k\}_{k = 1}^{K}\subset\mathbb{R}^{M_H}$ and $\{{\mathit{\boldsymbol{w}}}^k\}_{k = 1}^{K}\subset\mathbb{R}^{M_h}$, and two unique sets of CTGFE solutions $\{w_H^k\}_{k = 1}^{K}\subset\mathbb{U}_H$ and $\{w_h^k\}_{k = 1}^{K}\subset\mathbb{U}_h$, defined respectively on the coarse grid division $\Im_H$ and the fine grid division $\Im_h$, satisfying the following unconditional boundedness, i.e., unconditional stability:

where $\|{{\mathit{\boldsymbol{W}}}}^k\|$ $(1{\leqslant} k{\leqslant} K)$ are the Euclidean norm for the vectors ${{\mathit{\boldsymbol{W}}}}^k$.

Proof. Respectively multiplying (3.1) by the FE basis vectors ${\mathit{\boldsymbol{\zeta}}}$ and ${{\mathit{\boldsymbol{\xi}}}}$ yields

Thus, by Theorem 1, we assert that Problem 4 has two unique sets of CTGFE solution coefficient vectors $\{{\mathit{\boldsymbol{W}}}^k\}_{k = 1}^{K}\subset\mathbb{R}^{M_H}$ and $\{{\mathit{\boldsymbol{w}}}^k\}_{k = 1}^{K}\subset\mathbb{R}^{M_h}$. Further, by the third subsystem of equations in (3.2) and (3.3), we claim that Problem 4 has two unique sets of CTGFE solutions $\{w_H^k\}_{k = 1}^{K}\subset\mathbb{U}_H$ and $\{w_h^k\}_{k = 1}^{K}\subset\mathbb{U}_h$.

With the inverse estimate theorem and Theorem 1, we get

Thereupon, the CTGFE solution coefficient vectors ${{\mathit{\boldsymbol{W}}}}^k$ and ${{\mathit{\boldsymbol{w}}}}^k$ $(1{\leqslant} k{\leqslant} K)$ of Problem 4 are unconditionally bounded, i.e., unconditionally stable. This completes the proof of Theorem 2. □

Remark 2. If the time-step increment $\Delta t$, the coarse and fine division parameters $H$ and $h$, $a(\cdot)$, $f(\cdot)$, $g({\mathit{\boldsymbol{x}}}, t)$, and the initial functions $w_0({\mathit{\boldsymbol{x}}})$ and $w_1({\mathit{\boldsymbol{x}}})$ are given, a set of CTGFE solutions $\{w_h^k\}_{k = 1}^K\subset\mathbb{U}_h$ can be solved by Problem 4. However, when Problem 4 is used to solve an actual engineering problem, it could contain many unknowns (often more than millions). Thereby, it is extremely necessary to employ the POD technique to reduce the dimension of the unknown coefficient vectors of the CTGFE solutions in the CTGFE method, i.e., Problem 4, and create a new RDTGFE method.

3.2.   Construction of POD basis vectors

The POD basis vectors can be constructed by the following three steps.

(1) Find two sets of coefficient vectors of CTGFE solutions $\{{{\mathit{\boldsymbol{W}}}}^k\}_{k = 1}^L$ and $\{{{\mathit{\boldsymbol{w}}}}^k\}_{k = 1}^L$ by the first and second equations of (3.3) and (3.4) at the first $L$ time steps and make up two matrices ${\mathit{\boldsymbol{A}}}_{H} = ({\mathit{\boldsymbol{W}}}^1, {\mathit{\boldsymbol{W}}}^2,$ $\cdots, {\mathit{\boldsymbol{W}}}^L)$ and ${\mathit{\boldsymbol{A}}}_{h} = ({\mathit{\boldsymbol{w}}}^1, {\mathit{\boldsymbol{w}}}^2,$ $\cdots, {\mathit{\boldsymbol{w}}}^L)$. When solving a practical engineering problem, ${\mathit{\boldsymbol{A}}}_{H}$ and ${\mathit{\boldsymbol{A}}}_{h}$ may be formed by observations on the coarse grid division $\mathfrak{J}_H$ and fine grid division $\mathfrak{J}_h$ without solving the CTGFE method (Problem 4).

(2) Find two sets of normalized eigenvectors $\hat{{\mathit{\boldsymbol{\varphi}}}}_{{\kappa} i}$ $(1{\leqslant} i{\leqslant} r_{{\kappa}}$ $= :$rank$({\mathit{\boldsymbol{A}}}_{{\kappa}}))$ of matrices ${\mathit{\boldsymbol{A}}}_{{\kappa}}^T{\mathit{\boldsymbol{A}}}_{{\kappa}}$ corresponding to two sets of positive eigenvalues $\lambda_{{\kappa}1}{\geqslant}\lambda_{{\kappa}2}{\geqslant}\cdots{\geqslant}\lambda_{{\kappa} r_{{\kappa}}} > 0$ ($\kappa = {H}, {h}$).

(3) Find two most-important sets of $d_{{\kappa}}$ (${d}_{\kappa}{\leqslant} r_{\kappa})$ normalized vectors $\left\{{\mathit{\boldsymbol{\varphi}}}_{{\kappa}1}, {\mathit{\boldsymbol{\varphi}}}_{{\kappa}2}, \cdots, \right.$ $\left. {\mathit{\boldsymbol{\varphi}}}_{{\kappa}{d}_{\kappa}}\right\}$ of matrices ${\mathit{\boldsymbol{A}}}_{{\kappa}}{\mathit{\boldsymbol{A}}}_{{\kappa}}^T$ by the formulas ${\mathit{\boldsymbol{\varphi}}}_{{\kappa}i} =$ ${\mathit{\boldsymbol{A}}}_{\kappa}\hat{{\mathit{\boldsymbol{\varphi}}}}_{{\mathit{\boldsymbol{\kappa}}} i}/\sqrt{\lambda_{{\mathit{\boldsymbol{\kappa}}} i}}$ $(1{\leqslant} i{\leqslant}{d}_{\kappa})$ to construct two matrices ${\bf{\Phi}}_{{\kappa}} = ({\mathit{\boldsymbol{\varphi}}}_{{\kappa}1}, {\mathit{\boldsymbol{\varphi}}}_{{\kappa}2},$ $\cdots,$ ${\mathit{\boldsymbol{\varphi}}}_{{\kappa}{d}_{\kappa}})$ (${\kappa} = {H}, {h}$), which are called two sets of POD basis vectors.

By Sect. 5.1.2 in ^[16], we get that ${\bf{\Phi}}_{\kappa}$ have the following properties:

in which $\|{\mathit{\boldsymbol{A}}}_{\kappa}\|_{2, 2} = \sup_{{\mathit{\boldsymbol{v}}}\in\mathbb{R}^{L}}\|{\mathit{\boldsymbol{A}}}_{\kappa}{\mathit{\boldsymbol{v}}}\|/\|{\mathit{\boldsymbol{v}}}\|$ $({\kappa} = {H}, {h})$ and $\|{\mathit{\boldsymbol{v}}}\|$ still represents the Euclidean norm of vector ${\mathit{\boldsymbol{v}}}$.

By (3.5), we get

where ${\mathit{\boldsymbol{e}}}^{k}$ $(1{\leqslant} k{\leqslant} L)$ represent the $L$-dimension normalized vectors with $k$-th element $1$.

3.3.   Establishment of the RDTGFE method

If we assume that

then the RDTGFE solutions can be denoted by

Thus, the first $L$ coefficient vectors of RDTGFE solutions are immediately obtained by

Thus, by replacing ${\mathit{\boldsymbol{W}}}^k$ and ${\mathit{\boldsymbol{w}}}^k$ in Problem 4 with ${\mathit{\boldsymbol{W}}}_{{d}}^k = {\bf{\Phi}}_{H}{\mathit{\boldsymbol{\beta}}}_{H}^{k}$ and ${\mathit{\boldsymbol{w}}}_{{d}}^k = {\bf{\Phi}}_{h}{\mathit{\boldsymbol{\beta}}}_{h}^{k}$ $(L+1{\leqslant} k{\leqslant} K)$ and using the orthogonality of vectors in ${\bf{\Phi}}_{\kappa}$, respectively, a novel RDTGFE method is created as follows.

Problem 5. Step 1. Find ${\mathit{\boldsymbol{\beta}}}_H^k\in\mathbb{R}^{d_H}$ and $w_{Hd}^k\in\mathbb{U}_H$ $(1{\leqslant} k{\leqslant} K)$ such that they satisfy the following system of nonlinear equations:

where $\hat{D}_t^{\gamma}{\mathit{\boldsymbol{\beta}}}_H^{k}$ are obtained by replacing $w^k$ in (2.6) with ${\mathit{\boldsymbol{\beta}}}_H^{k}$, and

are three $M_H$-dimensional vectors.

Step 2. Find ${\mathit{\boldsymbol{\beta}}}_{h}^k\in\mathbb{R}^{{d}_h}$ and $(w_{hd}^k, u_{hd}^k)\in\mathbb{U}_h\times\mathbb{U}_h$ $(1{\leqslant} k{\leqslant} K)$, satisfying the following system of linear equations:

where $\hat{D}_t^{\gamma}{\mathit{\boldsymbol{\beta}}}_h^{k}$ are obtained by replacing $w^k$ in (2.6) with ${\mathit{\boldsymbol{\beta}}}_h^{k}$, and

are three $M_H$-dimensional vectors.

Remark 3. It is clear that Problem 4 has $(M_H+M_h)$ unknowns per time step, while Problem 5 has only $(d_H+d_h)$ unknowns per time step, and $d_H\ll M_H$ and ${d}_h\ll M_h$ (for example, the numerical tests in Sect. 4, $d_H = d_h = 6$, but $M_H = 10^{3}$ and $M_h = 10^{6}$). Therefore, Problem 5 can greatly lessen the unknowns, thus greatly alleviating the computation load and saving the CPU time. In particular, Problem 5 has the same basis functions and accuracy as Problem 4. In other words, not only are the unknowns of Problem 5 greatly reduced, but the precision of the RDTGFE solutions of Problem 5 remains unchanged. Hence, the RDTGFE method is far superior over the CTGFE method.

3.4.   Theoretical analysis of RDTGFE solutions

The theoretical analysis of the existence, stability, and error estimates of RDTGFE solutions needs the following lemma, see [11, Lemma 3.1].

Lemma 1 (Discrete Gronwall's inequality). Let $\{a_k\}$ be a series of nonnegative real numbers, $\{c_k\}$ be a non-descending series of nonnegative numbers, and $\{\delta_k\}$ be a series of nonnegative real numbers, satisfying

Then they also satisfy

For Problem 5, we get the following results:

Theorem 3. Under the same conditions as Theorem 1, Problem 5 has two unique sets of RDTGFE solutions $\{w_{Hd}^k\}_{k = 1}^K\subset\mathbb{U}_H$ and $\{w_{hd}^k\}_{k = 1}^K\subset\mathbb{U}_h$, satisfying the following unconditional stability:

Furthermore, when $h = O(H^{1+1/l})$, they satisfy the following error estimates:

where $w(t_k) = w({\mathit{\boldsymbol{x}}}, t_k)$ $(1{\leqslant} k{\leqslant} K)$.

Proof. The demonstration of Theorem 3 is divided into the following two steps.

(1) Discuss the existence as well as stability of RDTGFE solutions.

(ⅰ) When $1{\leqslant} k{\leqslant} L$, by the first and third subsystems of (3.7) and (3.8), and Theorems 1 and 2, we assert that Problem 5 has two unique sets of RDTGFE solutions $\{w_{Hd}^k\}_{k = 1}^L\subset\mathbb{U}_H$ and $\{w_{hd}^k\}_{k = 1}^L\subset\mathbb{U}_h$, satisfying (3.9) when $1{\leqslant} k{\leqslant} L$.

(ⅱ) When $L+1{\leqslant} k{\leqslant} K$, by using ${\mathit{\boldsymbol{W}}}_{{d}}^k = {\bf{\Phi}}_{H}{\mathit{\boldsymbol{\beta}}}_{H}^{k}$ and ${\mathit{\boldsymbol{w}}}_{{d}}^k = {\bf{\Phi}}_{h}{\mathit{\boldsymbol{\beta}}}_{h}^{k}$, we can rewrite (3.7) and (3.8) as the following two systems of equations:

Noting that the second and third equations in (3.12) and (3.13) have the same form as the second and third equations in (3.2) and (3.3) of Problem 4, by using the same proof as Theorems 1 and 2, we can prove that when $L+1{\leqslant} k{\leqslant} K$, Problem 5 has two unique sets of RDTGFE solutions $\{w_{Hd}^k\}_{k = L+1}^K\subset\mathbb{U}_H$ and $\{w_{hd}^k\}_{k = L+1}^K\subset\mathbb{U}_h$, satisfying (3.9) when $L+1{\leqslant} k{\leqslant} K$.

Synthesizing (ⅰ) and (ⅱ), we assert that Problem 5 has two unique sets of RDTGFE solutions $\{w_{Hd}^k\}_{k = 1}^K\subset\mathbb{U}_H$ and $\{w_{hd}^k\}_{k = 1}^K\subset\mathbb{U}_h$, satisfying (3.9).

(2) Discuss the errors of the RDTGFE solutions.

(a) When $1{\leqslant} k{\leqslant} L$, noting that $w_H^k = {\mathit{\boldsymbol{\zeta}}}^T{\mathit{\boldsymbol{W}}}$, $w_h^k = {{\mathit{\boldsymbol{\xi}}}}^T{{\mathit{\boldsymbol{w}}}}$, $\|{\mathit{\boldsymbol{\zeta}}}\|_1{\leqslant} c$, and $\|{{\mathit{\boldsymbol{\xi}}}}\|_1{\leqslant} c$, and using (3.6), we obtain

(b) When $L+1{\leqslant} k{\leqslant} K$, by subtracting the second equations of (3.12) and (3.13) from the second equations of (3.2) and (3.3), respectively, setting ${\mathit{\boldsymbol{\theta}}}^k = {\mathit{\boldsymbol{W}}}^k-{\mathit{\boldsymbol{W}}}_d^k$ and $\tilde{{\mathit{\boldsymbol{\theta}}}}^k = {{\mathit{\boldsymbol{w}}}}^k-{{\mathit{\boldsymbol{w}}}}_d^k$, taking the inner product by left multiplying with $({\mathit{\boldsymbol{\theta}}}^{k}-{\mathit{\boldsymbol{\theta}}}^{k-2})^T$ and $(\tilde{{\mathit{\boldsymbol{\theta}}}}^{k}-\tilde{{\mathit{\boldsymbol{\theta}}}}^{k-2})^T$, respectively, and using the Lagrange differential mean value theorem, (2.7), and (3.6), we get

Summing (3.16) and (3.17) from $L+2$ to $k$ ($k{\leqslant} K$), by (3.6), we obtain

where $L+1{\leqslant} k{\leqslant} K.$ Thus, when $\Delta t$ is sufficiently small such that $c\Delta t^{3-\gamma}{\leqslant} 1/2$, simplifying (3.18) and (3.19) yields

where $L+1{\leqslant} k{\leqslant} K.$

By Lemma 1, from (3.20) and (3.21) we get

By (3.22) and (3.23), we get

By combining Theorem 1 with (3.14), (3.15), (4.1), and (3.25), we immediately get (3.10) and (3.11), which finishes the demonstration of Theorem 3. □

Remark 4. By comparison, we find that the errors of Theorem 3 have two more terms $\sqrt{\lambda_{H(d_H+1)}}$ and $\sqrt{\lambda_{h(d_h+1)}}$ than those of Theorem 1. Fortunately, the two extra terms $\sqrt{\lambda_{H(d_H+1)}}$ and $\sqrt{\lambda_{h(d_h+1)}}$ serve as suggestions for selecting the number of POD base vectors. In fact, as long as the selected $d_h$ and $d_H$ satisfy $\sqrt{\lambda_{h(d_h+1)}}+\sqrt{\lambda_{H(d_H+1)}}{\leqslant} (\Delta t^2+h^{l+1})$, the total errors will not be affected. A large number of numerical tests conducted in ^[16] demonstrate that the eigenvalue rapidly drops to $0$. Generally, when $d_h$ and $d_H = 5\sim 7$, they are already very small and satisfy $\sqrt{\lambda_{h(d_h+1)}}+\sqrt{\lambda_{H(d_H+1)}}{\leqslant} (\Delta t^2+h^{l+1})$. The biggest advantage of the RDTGFE method is that it can calculate the numerical solutions at all time nodes satisfying the appointed accuracy by updating the POD base vectors and reconstructing the RDTGFE method. The specific way is that if the RDTGFE solution $(w_{hd}^{k_0+1}, u_{hd}^{k_0+1})$ at time node $t_{k_0+1}$ does not meet the required accuracy, but $(w_{hd}^{k}, u_{hd}^{k})$ at time nodes $t_{k}{\leqslant} t_{k_0}$ still meet accuracy requirements, then we can retake two sets of new solution vectors to form two new matrices ${\mathit{\boldsymbol{A}}}_H = ({\mathit{\boldsymbol{W}}}^{k_0-L+1}, {\mathit{\boldsymbol{W}}}^{k_0-L+2}, \cdots, {\mathit{\boldsymbol{W}}}^{k_0})$ and ${{\mathit{\boldsymbol{A}}}}_h = ({{\mathit{\boldsymbol{w}}}}^{k_0-L+1}, {{\mathit{\boldsymbol{w}}}}^{k_0-L+2}, \cdots, {{\mathit{\boldsymbol{w}}}}^{k_0})$ and reconstruct two sets of new POD bases and a new RDTGFE method to find the RDTGFE solutions satisfying the appointed accuracy. In this way, we can obtain the RDTGFE solutions satisfying the specified accuracy at all time nodes, which is unmatched by the CTGFE method.

4.   Some numerical experiments

In this section, we employ some numerical experiments to verify the correctness of our theoretical results and demonstrate the advantage of the RDTGFE method.

To facilitate the calculation of the errors of CTGFE and RDTGFE solutions, we use the 2D NTFW equation with analytic solutions as an example. In general, there is no analytical solution to the NTFW equation. If we take

then Problem 1 has an analytical solution $w({\mathit{\boldsymbol{x}}}, t) = \sin x_1\sin x_2\exp(-t)$.

The fine grid division $\mathfrak{J}_h$ is composed of the squares with diagonal $h = \sqrt{2}\times10^{-3}$. When $l = 1$, in order to satisfy $h = O(H^{1+1/l})$, i.e., $h = O(H^{2})$, the coarse grid division $\mathfrak{J}_H$ is composed of the squares with diagonal $H = \sqrt[4]{2}/\sqrt{1000}$. When $\Delta t = 10^{-2-\frac{2\gamma}{3-\gamma}}$ and $\sqrt{\lambda_{h(d_h+1)}}+\sqrt{\lambda_{H(d_H+1)}} = O(10^{-6})$, according to Theorems 1 and 3.2, the $L^2$ norm errors of the CTGFE and RDTGFE solutions of the NTFW equation can theoretically achieve $O(10^{-6})$.

The RDTGFE solutions can be found by the following flowchart.

(1) Experientially, calculate two sets of the first $20$ ($L = 20$) CTGFE solution vectors ${\mathit{\boldsymbol{W}}}^1, {\mathit{\boldsymbol{W}}}^2, \cdots,$ ${\mathit{\boldsymbol{W}}}^{20}$ and ${\mathit{\boldsymbol{w}}}^1, {\mathit{\boldsymbol{w}}}^2, \cdots, {\mathit{\boldsymbol{w}}}^{20}$ when $\gamma = 1.5$ to make up two matrices ${\mathit{\boldsymbol{A}}}_H = ({\mathit{\boldsymbol{W}}}^1, {\mathit{\boldsymbol{W}}}^2, \cdots, {\mathit{\boldsymbol{W}}}^{20})$ and ${\mathit{\boldsymbol{A}}}_h = ({\mathit{\boldsymbol{w}}}^1, {\mathit{\boldsymbol{w}}}^2, \cdots, {\mathit{\boldsymbol{w}}}^{20})$.

(2) Calculate two sets of orthonormal eigenvectors $\hat{{\mathit{\boldsymbol{\varphi}}}}_{\epsilon i}$ $(1{\leqslant} i{\leqslant} 20)$ for matrices ${\mathit{\boldsymbol{A}}}_{\epsilon}^T{\mathit{\boldsymbol{A}}}_{\epsilon}$ associated with two sets of eigenvalues $\lambda_{\epsilon1}{\geqslant}\lambda_{\epsilon2}{\geqslant}\cdots{\geqslant}\lambda_{\epsilon 20}{\geqslant}0$ $(\epsilon = H, h)$.

(3) By estimation, we get that $\sqrt{\lambda_{H7}}$ ${\leqslant}\sqrt{\lambda_{H7}}+\sqrt{\lambda_{h7}}$ ${\leqslant} 3.126\times10^{-6}$. Thus, we only need to extract two sets of the first six orthonormal eigenvectors $\hat{{\mathit{\boldsymbol{\varphi}}}}_{\epsilon i}$ $(1{\leqslant} i{\leqslant} 6)$ to form two sets of POD bases ${\bf{\Phi}}_{\epsilon} = ({\mathit{\boldsymbol{\varphi}}}_{\epsilon1}, {\mathit{\boldsymbol{\varphi}}}_{\epsilon2}, \cdots,$ ${\mathit{\boldsymbol{\varphi}}}_{\epsilon6})$ by formulas ${\mathit{\boldsymbol{\varphi}}}_{\epsilon i} = {\mathit{\boldsymbol{A}}}_{\epsilon}\hat{{\mathit{\boldsymbol{\varphi}}}}_{\epsilon i}/\sqrt{\lambda_{\epsilon i}}$ $(\epsilon = H, h$ and $1{\leqslant} i{\leqslant} 6)$.

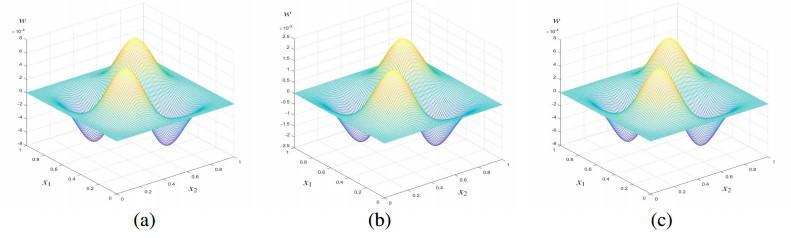
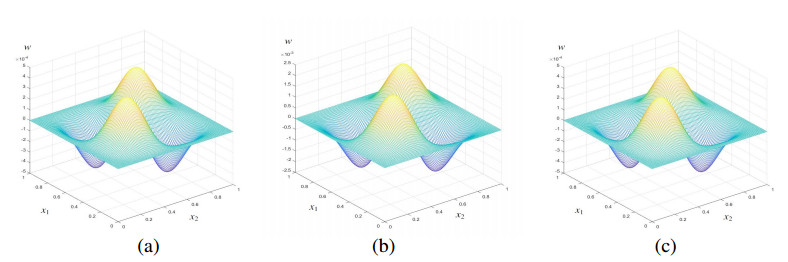
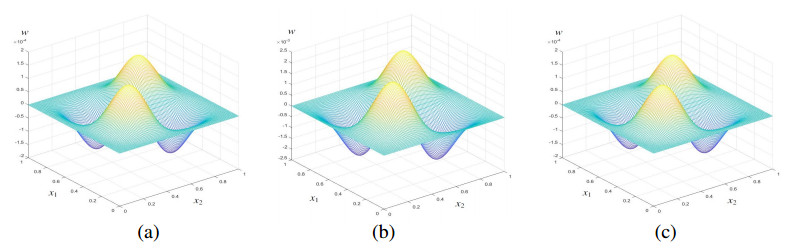
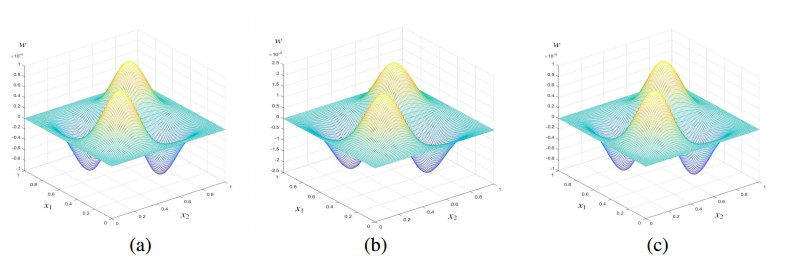
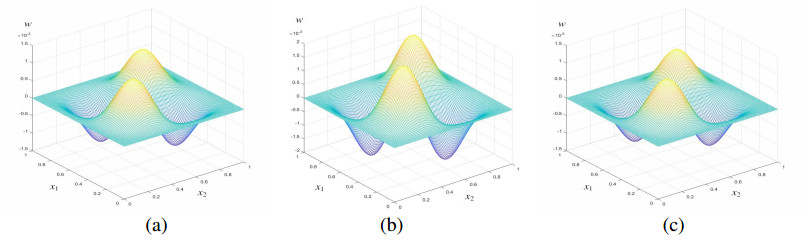
(4) Substitute ${\bf{\Phi}}_\epsilon$ ($\epsilon = H, h$) into Problem 5 and find the RDTGFE solutions $w_{hd}^k$ when $\gamma = 1.5$, $t = 0.5$, $1.0$, $1.5$, $2.0$, $2.5$, and $3.0$, as shown in Figures 1(a)–6(a).

To show that the RDTGFE method precedes the CTGFE method, we also calculate the CTGFE solutions $w_h^k$ of the NTFW equation when $\gamma = 1.5$, $t = 0.5$, $1.0$, $1.5$, $2.0$, $2.5$, and $3.0$, as shown in Figures 1(b)–6(b). In practical application, it is unnecessary to find the CTGFE solutions, which may be replaced by the observations on the coarse grid $\mathfrak{J}_H$ and fine grid $\mathfrak{J}_h$ and to find the RDTGFE solutions by the above four steps.

To expediently compare the difference between the RDTGFE solutions and the CTGFE solutions with the analytical solutions, we also provide the analytical solutions $w({\mathit{\boldsymbol{x}}}, t)$ when $\gamma = 1.5$, $t = 0.5$, $1.0$, $1.5$, $2.0$, $2.5$, and $3.0$, in Figures 1(c) to 6(c).

By comparing each set of graphs in Figures 1–6, it can be easy to see that when $\gamma = 1.5$, $t = 0.5$, $1.0$, $1.5$, $2.0$, $2.5$, and $3.0$, the RDTGFE solutions are very close to the analytical solutions, but the CTGFE solutions deviate from the analytical solutions. This deviation is caused by the accumulation of truncation errors. Because the CTGFE method has $(10^{3}+10^{6})$ unknowns per time step, while the RDTGFE method has only $2\times6$ unknowns per time step, the RDTGFE method can greatly reduce the unknowns and is obviously superior to the CTGFE method.

To truly showcase the benefits of the RDTGFE method, we record, when $\gamma = 1.5$, $t = 0.5$, $1.0$, $1.5$, $2.0$, $2.5$, and $3.0$, the CPU running time for finding the CTGFE and RDTGFE solutions by using MATLAB R2024a software on a laptop and their errors under the $L^2$ norm, shown in Table 1.

The data in Table 1 show that when $\gamma = 1.5$, $t = 0.5$, $1.0$, $1.5$, $2.0$, $2.5$, and $3.0$, the numerical errors of CTGFE and RDTGFE solutions achieve $O(10^{-6})$, which matches with the obtained theoretical errors, but the CPU runtime for finding CTGFE solutions is almost fifty times as long as that for finding RDTGFE solutions. Hence, the RDTGFE method is far superior to the CTGFE method and the RDTGFE method is very valid to find the numerical solutions of the NTFW equation.

5.   Conclusions and prospects

In this paper, we have created a new RDTGFE method of the NTFW equation, and have strictly proved the existence, stability, and error estimates of the RDTGFE solutions, theoretically. We have also employed some numerical experiments to verify the correctness of our theoretical results and demonstrate the superiorities of the RDTGFE method. The RDTGFE method of the NTFW equation is first proposed in this paper, which is completely different from the existing methods, including those in ^{[23,24,25,26,27]}. Therefore, they are completely original.

Although we have developed the RDTGFE method only for the NTFW equation, the method and ideas in this paper can be extended to more complicated unsteady nonlinear PDEs, for example, the nonlinear Schrödinger equation and Cahn-Hilliard equation, even to real engineering nonlinear problems. Hence, it has a wide range of applications.

Author contributions

Liang He: Conceptualization, Investigation, Methodology, Validation, Writing-original draft, Formal analysis; Yihui Sun: Conceptualization, Methodology, Formal analysis, Writing-review and editing; Zhenglong Chen: Conceptualization, Methodology, Formal analysis, Writing-review and editing; Fei Teng: Validation, Visualization, Writing-review and editing; Chao Shen: Inspection, Writing-review and editing; Zhendong Luo: Conceptualization, Investigation, Methodology, Formal analysis, Writing-original draft, Writing-review, and editing. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This work is jointly supported by the Natural Science Foundation of Changsha City (No. kq2208085), the Guangxi Key Laboratory of Special Engineering Equipment and Control, Guilin University of Aerospace Technology (No. 2411KFYB03), and the National Natural Science Foundation of China (No. 11671106).

Conflicts of interest

The authors declare that they have no conflicts of interest to report regarding the present study.