An improved approximate method for solving two-dimensional time-fractional-order Black-Scholes model: a finite difference approach

1.   Introduction

The fractional-order differential equations have become a powerful tool for explaining real phenomena in the last decades after they were introduced more than three hundred years ago. Fractional calculus has the ability to describe the real situation more adequately than traditional calculus ^[1].

There are many mathematical models that have been used for fractional calculus in various areas such as finance, engineering, control systems, epidemiology, etc. For example, Kumar et al. ^[2] studied the time-fractional Navier-Stokes equation and presented the technique to find the approximation analytical solution of the equation. Huang and Zhdanov ^[3] used group analysis to analyze the time-fractional Harry-Dym equation in the sense of the Riemann-Liouville fractional derivative. Chen et al. ^[4] studied the time-fractional Black-Scholes equation for pricing double barriers. The analytical solution was carried out using the eigenfunction expansion method composed with the Laplace transform. Senol et al. ^[5] investigated the time fractional order of the Burgers equation and its family. The approximate solutions of the equations were carried out using the residual power series method (RPSM). The obtained solutions can be compared to the exact solution. Mathur et al. ^[6] studied the space-time fractional-order diffusion equation and found its solution. The solution could express the behavior of the diffusion process. Bonyah et al. ^[7] proposed the mathematical model for dengue fever in the sense of the Caputo-Fabrizio derivative. They found the steady-state solutions and studied their stability. Mandal ^[8] constructed the fractional-order epidemic model with fear effect. They found the condition of the control parameter to control the disease. Chen ^[9] improved the mathematical model for the financial system from the integer-order system of differential equations to the fractional order model with incommensurate-order in the sense of the Caputo-type derivative. The chaotic behavior was found in the fractional-order model. Xu et al. ^[10] proposed an improved financial model with fractional order. They also applied the time-delayed to the proposed model to study the chaotic behavior. The sufficient conditions for the existence and stability of Hopf bifurcation were investigated. He et al. ^[11] proposed the fractional-order financial model and studied its dynamic behaviors. They found that the chaos exists in their model and the numerical simulations confirm the theoretical results. Gao and Baskonus ^[12] analyzed the fractional-order financial model. They proved that the solution of the model exists and found some impact of the parameters on the financial components.

It is known that the financial markets have affected people around the world. The mathematical model is a good choice for understanding financial market behavior. In 1973, Black, Merton, and Scholes ^[13] proposed the mathematical model based on the partial differential equation to describe the option price in the financial market. The major components of the Black-Scholes model are strike price, volatility, expiration time, risk-free rate, and underlying asset price. The Black-Scholes model is widely used to find the option price in the market. In the beginning, the model can only fit the European-style options. Recently, this model can compute the option price not only for European style options but it can also be used to compute option price for American ^[14] and Asian ^[15] style options.

The time fractional-order calculus has been used to improve the Black-Scholes model for getting the different results when applied with recent parameters. There is plenty of research that has been studied for the improved fractional-order Black-Scholes model ^{[16,17,18,19,20,21]}. Jamarie et al. ^[22] presented the derivation of fractional-order Black-Scholes model in one dimension. The time-fractional Black-Scholes model was also derived to find the numerical solution ^[23]. The fractional-order can provide the different values of the option price when the fractional-order changes. This is the main feature of the fractional calculus.

There are several methods that have been improved to solve the Black-Scholes model numerically and analytically. For example, Gulka ^[24] applied the homotopy perturbation method to find the analytical approximate solution for the Black-Scholes equation which was represented in the form of a convergence power series. Elbeleze et al. ^[25] combined the homotopy perturbation method and Sumudu transform to obtain the solution of the fractional Black-Scholes equation in Caputo sense. The obtained solution could be written as a convergence power series. They also compared the result to the Laplace homotopy perturbation method. Saratha et al. ^[26] solved the fractional Black-Scholes type equations in one dimension by using the fractional generalized homotopy analysis method (FGHAM). This method provided analytical solutions that were faster and more accurate than other numerical methods. Achdou and Pironneau ^[27] investigated the finite element method and finite difference method to obtain the solution of the Black-Scholes equation. Bungartz et al. ^[28] introduced the sparse grids to discretize the Black-Scholes equation and found the numerical solution using the finite element method. They also presented the algorithm to compute the solution in the multi-core CPU to reduce the computationl time. By proposing the weights of the radial basis function generated finite difference (RBF-FD) formulas, Soleymani and Zhu ^[29] found the solution of the Black-Scholes model which was in the form of a partial integro-differential equation composed of stochastic volatility with contemporaneous jumps. Chen et al. ^[30] combined two methods, which are the neural network model and the finite element method (FEM) for solving the Black-Scholes-Merton equation in European-style and American-style markets. Fei et al. ^[31] applied the RBF and Crank-Nicholson scheme to find the approximate solution of the Black-Scholes equation. The obtained solution agreed with the theoretical statement. Ravi Kanth and Aruna ^[16] found the solution of the time-fractional Black-Scholes equation for the European style option using the modified fractional differential transform method (MFDTM). This method gave the analytical solution, which was simpler to compute the option price. Zhou et al. ^[32] proposed a direct finite difference scheme for solving a time-fractional tempered Black-Scholes model by combining two methods. The convergence of this method is unconditionally stable.

In the last two decades, the multidimensional Black-Scholes models have been investigated to find the option price that depends on more than one asset. The concept of the multidimensional model is based on the option price that cannot depend on only one asset. A number of researchers studied the methods that can solve the multidimensional Black-Scholes equation, especially the two-dimensional Black-Scholes equation. Guillaume ^[33] studied the multidimensional Black-Scholes partial differential equation and its properties. The equation could be transformed into a standard heat equation. He also found the fundamental solution. Chacon-Acosta and Salas ^[34] applied Zwanwig's projection method to reduce the dimension of the two-dimensional Black-Scholes equation to one dimension. They also studied the effects of parameters on the option price. Chen and Wang ^[35] improved a second-order Crank-Nicolson alternating direction implicit method to solve the two-dimensional fractional Black-Scholes equation. Wang et al. ^[36] used a practical finite difference method to find the solution of the multidimensional Black-Scholes model with fractional order. Heo et al. ^[37] proposed the explicit finite difference method for solving the Black-Scholes equation with a hybrid boundary condition in two dimensions. Their method reduced the domain by eliminating some boundary conditions. Soleymani and Zhu ^[38] presented a (2-$\alpha$)-order discretization scheme for solving the fractional-order Black-Scholes model based on the meshless RBF-FD method.

As mentioned above, fractional-order differential equations serve as powerful tools for enhancing mathematical models. The Black-Scholes model, which is widely used for determining option prices, traditionally relies on a single asset. However, in real-world scenarios, option prices are influenced by multiple assets. By integrating the key aspects of each concept, we investigate the fractional-order multidimensional Black-Scholes model, enabling the determination of option prices through the model's solution. The method that can solve the model is the essential tool. Due to the complexity of the model, exact solutions for the fractional-order multidimensional Black-Scholes model are unattainable. Therefore, this paper focuses on studying numerical methods capable of solving the model.

There are various numerical methods that have been proposed to find its solution, one of which is the finite difference method (FDM). FDM is favored due to its ease of implementation compared to other numerical techniques. It can accommodate complex geometries and boundary conditions and is efficient for domains with regular grids. These are the advantages of FDM. However, traditional FDM cannot handle fractional-order partial differential equations. Therefore, improving FDM to solve fractional-order problems is important for solving the multidimensional fractional-order Black-Scholes equation.

In this work, we introduce a numerical method based on the Crank-Nicolson finite difference method to obtain the numerical solution of the time fractional-order Black-Scholes model with two assets in the Liouville-Caputo sense. This method combines a difference scheme for the time-fractional heat equation ^[39] and a Crank-Nicolson scheme for multidimensional Black-Scholes partial differential equations ^[40].

The modified method is derived from two primary aspects of each method: the capability to solve time-fractional partial differential equations and the ability to obtain numerical solutions for multidimensional partial differential equations. The Black-Scholes equation can be expressed as a heat-like equation. The stability condition of the modified method is investigated in the subsequent section. Additionally, we conduct a study on the convergence of the proposed method.

Furthermore, numerical simulations of the fractional-order Black-Scholes equation with two assets are provided to illustrate the determination of option prices. The comparison between the proposed method and analytical approximation method, that is, the Laplace homotopy perturbation method (LHPM), is studied.

The organization of the rest of this paper is as follows. Section 2 presents the two-dimensional time fractional-order Black-Scholes model and provides preliminaries about fractional calculus. The fractional derivative considered in this paper is the Liouville-Caputo fractional derivative. Section 3 introduces the discretization of the time fractional-order Black-Scholes model, along with stability and convergence analyses. Numerical examples and discussions are provided in Section 4. Finally, Section 5 presents the conclusions.

2.   The fractional-order Black-Scholes model with two assets

In this section, we first introduce some definitions of fractional derivatives that are mentioned in this work. Second, the fractional-order Black-Scholes model investigated in this work is presented.

2.1.   Preliminaries on fractional calculus

There are many definition-types of the fractional-order derivative, for example, Riemann-Liouville ^[41], Liouville-Caputo ^[42], Jaumarie ^[22], tempered ^[43], Caputo-Fabrizio ^[44], and Atangana-Baleanu ^[45] derivatives. In this work, we use the Liouville-Caputo type derivative because its initial condition satisfies the integer-order derivative ^[46].

Definition 2.1. The $\alpha$-order Liouville-Caputo ^[42] fractional derivative for a function $U:\mathbb{R} \to \mathbb{R}$ is defined by the formula

2.2.   The mathematical model

The mathematical model is based on the Black-Scholes model, applicable to European options under certain assumptions: no arbitrage, no dividends, borrowing and lending at the risk-free rate, no fees, and no transaction costs ^[47,48]. Initially, the Black-Scholes model was a one-dimensional equation. However, it has recently evolved into a multidimensional model, assuming that the option price cannot depend solely on one asset.

The fractional-order Black-Scholes partial differential equation with two assets for European-style options, which can be derived from the integer-order equation, is investigated. We aim to find an approximate solution using a modified finite difference method, as presented in the next section.

The model parameters and variables are defined as follows:

$\begin{array}{l l l} & U & \text{the option price depending on the underlying asset prices} \; S_1, \; S_2\; \text{at time } \; t, \\ & S_1, S_2 & \text{the underlying asset price}, \\ & \sigma_{1}, \sigma_{2} & \text{the volatility of the underlying asset} \; S_1\; \text{and} \; S_2, \text{respectively}, \\ & \rho & \text{the correlation between the underlying asset prices } \; S_1\; \text{and} \; S_2\; ,\\ & \beta_{i} & \text{the coefficient so that all risky asset prices are at the same level}\; S_{i}\; \text{for} \; i = 1, 2, \\ & K & \text{the strike price of the underlying stock, }\\ & r & \text{the risk-free interest rate to expiration, } \\ & T & \text{the expiration date.} \end{array}$

The fractional-order Black-Scholes model with two assets in Liouville-Caputo sense for the time forward can be represented as

for $S_1, S_2 \in [ 0, \infty), \tau \in [0, T],$ with the terminal conditions and boundary conditions define as the following equations.

For the European call option, the terminal condition is

The boundary conditions for the call option are defined by

For the European put option, the terminal condition is

The boundary conditions for the put option are defined by

The fractional-order Black-Scholes model can be rewritten in the initial boundary value problem by changing it to a forward time $t$. Let $t = T-\tau$. Equation (2.2) becomes

Equation (2.3) can be expressed as the following equation when $S_1$ and $S_2$ are specified to be $x$ and $y$, respectively. We obtain

3.   Discretization of the time fractional order Black-Scholes model with two assets

In this section, we present the concept for solving the time fractional-order Black-Scholes model with two assets by applying the Crank-Nicolson technique. This method is a combination of two methods, which are the Crank-Nicolson method for Black-Scholes multi-dimensions ^[40] and a new difference scheme for the time fractional heat equations based on the Crack-Nicholson method ^[39]. By this technique, we define $M_x$ as the grid size in the space of asset one, $M_y$ as the grid size in the space of asset two, and $N$ as the grid size in the time. To divide the domain, we let $x_i \in [0, X], y_j \in [0, Y],$ and $t \in [0, T]$. The grid points are defined as follows:

In this work, the time step is the uniform grid size, i.e., $\tau = T/N$.

Let $U^n_{i, j}$ be the value of the option price, which is the function of the underlying asset price $x_i, y_j$ and time $t_n$.

By the Crank-Nicolson discritization, we use the following scheme ^[40].

The fractional Liouville-Caputo derivative for the option price can also be written as follows ^[39]:

where $U(\cdot, \cdot, t) \in C^2([0, T])$, $\boldsymbol{\sigma} = \dfrac{1}{\Gamma(2-\alpha)}\dfrac{1}{\tau^{\alpha}},$ and $\omega_{j} = \boldsymbol{\sigma}((j+1/2)^{1-\alpha}-(j-1/2)^{1-\alpha})$.

By substituting Eq (3.7) and Eqs (3.1)–(3.6) into Eq (2.4), the two-dimensional fractional-order Black Scholes model, we obtain

By rearranging the above equation, we get

We investigate the equaled step size of the underlying asset. Let $h_{i-1} = h_i, k_{j-1} = k_j$, then the grid point of the underlying asset can be written as $x_i = ih, y_j = jk$, where $h = X/M_x$ and $k = Y/M_y$. This means that we use the uniform grid size. We then obtain

where

Equation (3.8) can be written in matrix form as follows:

Case $j = 2, 3, \ldots, M_{y}-2$ and $i = 1, 2, \dots, M_{x}-1$:

Case $j = 1$ and $i = 1, 2, \dots, M_{x} - 1$:

Case $j = M_y -1$ and $i = 1, 2, \dots, M_{x} - 1$:

where

${}^{1}A_{j} = \begin{bmatrix} {}^{4}\Lambda_{1, j} & {}^{3}\Lambda_{1, j} & 0 & \cdots & 0\\ {}^{1}\Lambda_{2, j} & {}^{4}\Lambda_{2, j} & {}^{3}\Lambda_{2, j} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0\\ \vdots & \ddots & {}^{1}\Lambda_{M_{x} - 2, j} & {}^{4}\Lambda_{M_{x} - 2, j} & {}^{3}\Lambda_{M_{x} - 2, j}\\ 0 & \cdots & 0 & {}^{1}\Lambda_{M_{x} - 1, j} & {}^{4}\Lambda_{M_{x} - 1, j} \\ \end{bmatrix},$

${}^{2}A_{j} = \begin{bmatrix} {}^{5}\Lambda_{1, j}+\frac{\boldsymbol{\sigma}}{2^{1-\alpha}} & {}^{7}\Lambda_{1, j} & 0 & \cdots & 0\\ {}^{2}\Lambda_{2, j} & {}^{5}\Lambda_{2, j}+\frac{\boldsymbol{\sigma}}{2^{1-\alpha}} & {}^{7}\Lambda_{2, j} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0\\ \vdots & \ddots & {}^{2}\Lambda_{M_{x} - 2, j} & {}^{5}\Lambda_{M_{x} - 2, j}+\frac{\boldsymbol{\sigma}}{2^{1-\alpha}} & {}^{7}\Lambda_{M_{x} - 2, j}\\ 0 & \cdots & 0 & {}^{2}\Lambda_{M_{x} - 1, j} & {}^{5}\Lambda_{M_{x} - 1, j} +\frac{\boldsymbol{\sigma}}{2^{1-\alpha}}\\ \end{bmatrix},$

${}^{3}A_{j} = \begin{bmatrix} {}^{6}\Lambda_{1, j} & {}^{1}\Lambda_{1, j} & 0 & \cdots & 0\\ {}^{3}\Lambda_{2, j} & {}^{6}\Lambda_{2, j} & {}^{1}\Lambda_{2, j} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0\\ \vdots & \ddots & {}^{3}\Lambda_{M_{x} - 2, j} & {}^{6}\Lambda_{M_{x} - 2, j} & {}^{1}\Lambda_{M_{x} - 2, j}\\ 0 & \cdots & 0 & {}^{3}\Lambda_{M_{x} - 1, j} & {}^{6}\Lambda_{M_{x} - 1, j} \\ \end{bmatrix},$

${}^{1}B_{j} = \begin{bmatrix} -{}^{4}\Lambda_{1, j} & -{}^{3}\Lambda_{1, j} & 0 & \cdots & 0\\ -{}^{1}\Lambda_{2, j} & -{}^{4}L_{2, j} & -{}^{3}\Lambda_{2, j} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0\\ \vdots & \ddots & -{}^{1}\Lambda_{M_{x} - 2, j} & -{}^{4}\Lambda_{M_{x} - 2, j} & -{}^{3}\Lambda_{M_{x} - 2, j}\\ 0 & \cdots & 0 & -{}^{1}\Lambda_{M_{x} - 1, j} & -{}^{4}\Lambda_{M_{x} - 1, j} \\ \end{bmatrix},$

$^{2}B_{j} = \begin{bmatrix} -{}^{5}\Lambda_{1, j}+\frac{\boldsymbol{\sigma}}{2^{1-\alpha}}-\omega_{1} & -{}^{7}\Lambda_{1, j} & 0 & \cdots & 0\\ -{}^{2}\Lambda_{2, j} & -{}^{5}\Lambda_{2, j}+\frac{\boldsymbol{\sigma}}{2^{1-\alpha}}-\omega_{1} & -{}^{7}\Lambda_{2, j} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0\\ \vdots & \ddots & -{}^{2}\Lambda_{M_{x} - 2, j} & -{}^{5}\Lambda_{M_{x} - 2, j}+\frac{\boldsymbol{\sigma}}{2^{1-\alpha}}-\omega_{1} & -{}^{7}\Lambda_{M_{x} - 2, j}\\ 0 & \cdots & 0 & -{}^{2}\Lambda_{M_{x} - 1, j} & -{}^{5}\Lambda_{M_{x} - 1, j}+\frac{\boldsymbol{\sigma}}{2^{1-\alpha}}-\omega_{1} \\ \end{bmatrix},$

${}^{3}B_{j} = \begin{bmatrix} {}^{6}\Lambda_{1, j} & {}^{1}\Lambda_{1, j} & 0 & \cdots & 0\\ {}^{3}\Lambda_{2, j} & {}^{6}\Lambda_{2, j} & {}^{1}\Lambda_{2, j} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0\\ \vdots & \ddots & {}^{3}\Lambda_{M_{x} - 2, j} & {}^{6}\Lambda_{M_{x} - 2, j} & {}^{1}\Lambda_{M_{x} - 2, j}\\ 0 & \cdots & 0 & {}^{3}\Lambda_{M_{x} - 1, j} & {}^{6}\Lambda_{M_{x} - 1, j} \\ \end{bmatrix},$

$\vec U_{j}^{n+1} = \begin{bmatrix} U_{1, j}^{n+1}\\ U_{2, j}^{n+1}\\ \vdots \\ U_{M_{x} - 1, j}^{n+1} \end{bmatrix}, \; \; \vec U_{j}^{n} = \begin{bmatrix} U_{1, j}^{n}\\ U_{2, j}^{n}\\ \vdots \\ U_{M_{x} - 1, j}^{n} \end{bmatrix},$

${}^{1} \vec c_{j}^{n} = \begin{bmatrix} -{}^{1}\Lambda_{1, j}(U_{0, j-1}^{n}+U_{0, j-1}^{n+1})\\ 0\\ \vdots \\ 0\\ -{}^{3}\Lambda_{M_{x}, j}(U_{M_{x}, j-1}^{n}+U_{M_{x}, j-1}^{n+1}) \end{bmatrix}, \; {}^{2} \vec c_{j}^{n} = \begin{bmatrix} -{}^{3}\Lambda_{1, j}(U_{0, j}^{n}+U_{0, j}^{n})\\ 0\\ \vdots \\ 0\\ -{}^{7}\Lambda_{M_{x}, j}(U_{M_{x}, j}^{n}+U_{M_{x}, j}^{n}) \end{bmatrix},$

${}^{3} \vec c_{j}^{n} = \begin{bmatrix} -{}^{3}\Lambda_{1, j}(U_{0, j+1}^{n}+U_{0, j+1}^{n})\\ 0\\ \vdots \\ 0\\ -{}^{1}\Lambda_{M_{x}, j}(U_{M_{x}, j+1}^{n}+U_{M_{x}, j+1}^{n}) \end{bmatrix}, \; \vec C_{j}^{n} = \begin{bmatrix} \vec U_{j-1}^{n}-U_{j-1}^{n+1}\\ 0\\ \vdots \\ 0\\ \vec U_{M_{y}}^{n}-U_{M_{y}}^{n+1} \end{bmatrix},$

$D^n = \begin{bmatrix} \omega_{n} & 0 & 0 & \dots & 0\\ 0 & \omega_{n} & 0 & \dots & \vdots\\ \vdots & \ddots & \ddots & \ddots & 0\\ 0 & \dots & 0 & \dots & \omega_{n} \end{bmatrix}, \; E_{j}^{n} = \begin{bmatrix} \sum_{m = 1}^{n-1}(\omega_{n-m+1}-\omega_{n-m})U^{m}_{1, j} \\ \sum_{m = 1}^{n-1}(\omega_{n-m+1}-\omega_{n-m})U^{m}_{2, j} \\ \vdots \\ \sum_{m = 1}^{n-1}(\omega_{n-m+1}-\omega_{n-m})U^{m}_{M_{x} - 1, j} \\ \end{bmatrix}.$

From Eqs (3.9)–(3.11), we can rewrite it in the following matrix form:

for $i = 1, 2, \dots, M_{x} - 1$ and $j = 1, 2, \dots, M_{y} -1$, where

In Eq (3.12), $A$ and $B$ are triangular block matrices of dimension $[(M_x-1)(M_y-1)]\times [(M_x-1)(M_y-1)]$.

3.1.   Stability of the modification finite difference method

The stability of the investigated scheme is analyzed by using a Fourier analysis. The uniform spatial grid nodes are introduced. Define $x_i = ih_x, y_j = jh_y$ where $h_x = X/M_x, h_y = Y/M_y$. This means that this part is available for the scheme with uniform meshes. Let $U^n_{i, j}$ be the approximate solution and define $\vartheta^n_{i, j} = u^n_{i, j}-U^n_{i, j}$, for $n = 0, 1, \dots, N, i = 0, 1, \dots, M_x,$ and $j = 0, 1, \dots, M_y$. The round-off error equation can be written as

The grid function is defined by $\vartheta ^n_{i, j} (t, x, y) = \vartheta^n_{i, j}$ when $x_{i-\frac{h}{2}} < x < x_{i+\frac{h}{2}}, y_{j-\frac{h}{2}} < y < y_{j+\frac{h}{2}}$, and $\vartheta ^n_{i, j} (t, x, y) = 0$ when $0\le x \le \frac{h}{2}, 0\le y \le \frac{h}{2}$ or $L-\frac{h}{2} < x\le L, L-\frac{h}{2} < y \le L$.

The Fourier series of $\vartheta ^n_{i, j} (t, x, y)$ can be represented in the form

where $I$ is the imaginary unit. The Fourier coefficients $\lambda^n(\zeta_1, \zeta_2)$ are given by

Introduce the norm of $\vartheta^{n}$ as

Then, apply the Parseval's equality

to obtain

Let $\vartheta^{n}_{i, j} = \lambda^{n}e^{I(i \gamma_{1} h_x +j\gamma_{2} h_y)}, \; \gamma_{1} = 2\pi \zeta_{1}/l, \; \gamma_{2} = 2\pi \zeta_{2}/l$, and $l = 1$. Equation (3.12) becomes

or

So, we get

or

The next proposition is an essential tool for helping us consider the stability of the proposed scheme.

Proposition 3.1. If $\dfrac{3}{2} \leq 3^\alpha$, then $|\lambda^{n}|\leq |\lambda^{0}|$, $n = 1, 2, \dots, N$ where $\lambda^n$ is the solution of Eq (3.13).

Proof. Let $\psi_{1} = \left(\frac{\rho \sigma_{1} \sigma_{2} x_iy_j}{8} \right)\cos(\gamma_{1} h_x+\gamma_{2} h_y)$, $\psi_{2} = \left(\frac{\rho \sigma_{1} \sigma_{2} x_iy_j}{8} \right)\cos(-\gamma_{1} h_x+\gamma_{2} h_y)$, $\psi_{3} = \left(\frac{rx_i - \sigma_{1}^{2}x_i^{2}}{4}\right)I\sin(\gamma_{1} h_x)$, $\psi_{4} = \left(\frac{ry_j - \sigma_{2}^{2}y_j^{2}}{4} \right) I\sin(\gamma_{2} h_y).$

To prove this proposition, we will use the mathematical induction.

Start with $n = 0$, then

So, $|\lambda^{1}|\leq |\lambda^{0}|$.

Now, assume that $|\lambda^{k}|\leq |\lambda^{0}|,$ for $k = 1, 2, \ldots, n$. We need to prove this for $k = n+1$.

Consider

If $\psi_{1}-\psi_{2}+\psi_{3}+\psi_{4}- \frac{\sigma_{1}^{2}i^{2}}{2} - \frac{\sigma_{2}^{2}j^{2}}{2} -\frac{r}{2}+ \frac{\boldsymbol{\sigma}}{2^{1-\alpha}} -\omega_{1} > 0$, then

If $\psi_{1}-\psi_{2}+\psi_{3}+\psi_{4}- \frac{\sigma_{1}^{2}i^{2}}{2} - \frac{\sigma_{2}^{2}j^{2}}{2} -\frac{r}{2}+ \frac{\boldsymbol{\sigma}}{2^{1-\alpha}} -\omega_{1} < 0$, then

Here, $|\lambda^{n+1}|\leq|\lambda^{0}|$, then

or

So, we have $2\omega_{1}\leq \dfrac{2\boldsymbol{\sigma}}{2^{1- \alpha}}$, then $\left(1+\tfrac{1}{2} \right)^{1- \alpha}-\left(1-\tfrac{1}{2} \right)^{1- \alpha} \leq \dfrac{1}{2^{1- \alpha}}$, that is, $\dfrac{3}{2} \leq 3^{\alpha}.$ □

The following theorem can tell us about the stability of the method, which is conditionally stable. This means that the proposed scheme is stable for some condition of fractional order $\alpha$.

Theorem 3.2. The Crank-Nicolson finite difference scheme (3.8) is stable if $\dfrac{3}{2} \leq 3^{\alpha}$.

Proof. Suppose that $\frac{3}{2} \leq 3^{\alpha}$. By applying Proposition 3.1 and using the Parseval equality, we consider

This means that $|| \vartheta^{n}||_2 \leq || \vartheta^{0}||_2$, for $n = 0, 1, \ldots, N$.

Thus, the proposed Crank-Nicolson finite difference scheme (3.8) is conditionally stable. □

3.2.   Convergence analysis

The convergent of the proposed finite different method can be proved by using the following statements.

Denote the truncation error at $(t_{n+\frac{1}{2}}, x_i, y_j)$ by $R^{n+ 1/2}_{i, j}$. We let $\varepsilon^n_{i, j} = u(x_i, y_j, t_n)-U^n_{i, j}$. For this part, we assume that $h = h_x = h_y$. This means that this part is available for the scheme with uniform meshes. From Eqs (2.4) and (3.7), we consider

From Eq (2.4), there is a positive constant $C_1$ such that

Similar to the stability analysis part, we can write $\eta_n(x, y)$ and $R^{n+1/2}(x, y)$ as Fourier series.

where the Fourier coefficients $\eta _n$ and $\varphi_n$ are defined by

By the Parseval's equality and $L^2$ norm, we obtain

By the above expression, we suppose that

By using the assumption (3.17) and Eq (3.14), we obtain

After simplification, we have

Next, we want to show that if $\eta^n$ for $n = 1, 2, \ldots, N$ is the solution of (3.18), then there is a positive constant $C_2$ such that

Suppose that $\eta^{n+1}$ and $\varphi^{n+1/2}$ satisfy Eq (3.18). Then, we have

We show this by using the mathematical induction.

Suppose that $\eta^{0} = \eta^{0}(\zeta_1, \zeta_2) = 0$. Then, we have $\eta^0 = 0$. Next, we consider

Assume that $|\eta^{s+1}|\leq C_2(s+1)|\varphi^{1/2}|$ for $s = 0, 1, \dots, n-1$. We need to show that it is true for $s = n$. From Eq (3.18), we have

If $\psi_{1}-\psi_{2}+\psi_{3}+\psi_{4}- \frac{\sigma_{1}^{2}i^{2}}{2} - \frac{\sigma_{2}^{2}j^{2}}{2} -\frac{r}{2}+ \frac{\boldsymbol{\sigma}}{2^{1-\alpha}} -\omega_{1} > 0$, then we have

If $\psi_{1}-\psi_{2}+\psi_{3}+\psi_{4}- \frac{\sigma_{1}^{2}i^{2}}{2} - \frac{\sigma_{2}^{2}j^{2}}{2} -\frac{r}{2}+ \frac{\boldsymbol{\sigma}}{2^{1-\alpha}} -\omega_{1} < 0$, then we have

Then, we need to have $\left(1+\frac{1}{2} \right)^{1- \alpha}-\left(1-\frac{1}{2} \right)^{1- \alpha} \leq \dfrac{1}{2^{1- \alpha}}$.

This means that the inequality holds when $\dfrac{3}{2} \leq 3^{\alpha}.$

Theorem 3.3. If $\frac{3}{2}\leq3^{\alpha}$, the Crank-Nicolson finite difference scheme (3.8) is convergent and the order of convergence is $O(\tau^{2 -\alpha} + h^2).$

Proof. Suppose that $\eta^{n+1}$ and $\varphi^{n+1/2}$ satisfy Eq (3.18). If $\dfrac{3}{2}\leq3^{\alpha}$, we have

Notice that $(n+1)\leq T$. Let $C = C_1C_2T$. From Eq (3.15), we have

The Crank-Nicolson finite difference scheme (3.8) is convergent and the order of convergence is $O(\tau^{2-\alpha}+h^{2})$. □

4.   Numerical examples

In this section, we apply the proposed scheme to find the solution of a fractional-order Black-Scholes model with two assets for European call and put options.

4.1.   The numerical example for European call option

The investigated Black-Scholes model with two assets can be expressed as

with the initial condition:

and boundary conditions:

Set the parameter values as the strike price, $K = 50$, the risk-free interest rate (per year), $r = 0.02$, the maturity time, $T$ (year)$= 1$, the volatility of the underlying of $x$ assets (per year), $\sigma_1 = 0.15$, the volatility of the underlying of $y$ assets (per year), $\sigma_2 = 0.2$, and the correlation, $\rho = 0.5$, $\beta_1 = 2$, $\beta_2 = 1$.

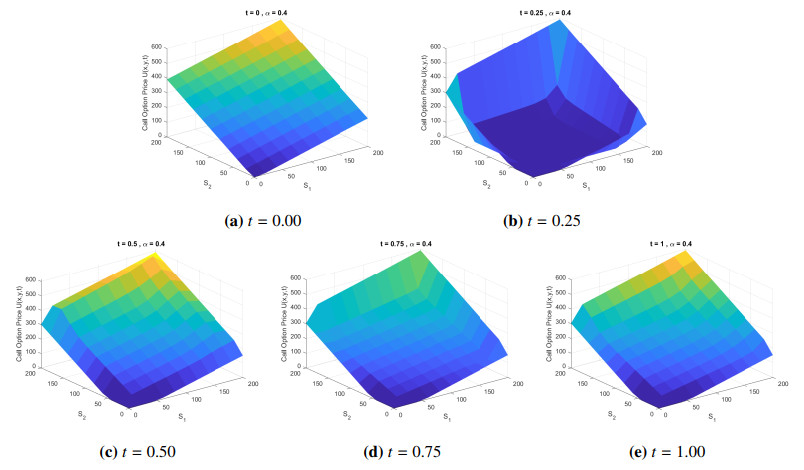
Figure 1 shows the solution of the Black-Scholes model by using the proposed Crank-Nicolson finite difference method for $\alpha = 0.4$ with $N = 4, \; M_x = 10, \; M_y = 10$. The results show that the European call option price increases as the underlying assets increase.

Figure 2 illustrates the value of European call options for various fractional orders $\alpha = 0.2$, $\alpha = 0.4$, $\alpha = 0.6$, $\alpha = 0.8$, and $\alpha = 1$. The results indicate that by increasing the value fractional order, a decreasing occurs in the value of option price.

By comparing the numerical result to the analytical approximate solution of the fractional-order Black-Scholes model for call option, the approximate solution from the LHPM ^[49] is applied. The relative root mean square error (RRMSE) is used to compare the result.

Table 1 shows the RRMSE for call option price for various times and fractional-orders $\alpha$. The value of errors confirms that the proposed finite difference scheme provides the option price not significant from another approximate method.

4.2.   The numerical example for European put option

The European put option based on the model of the Black-Scholes model with two assets thai is investigated in this example is given as follows:

with the initial condition:

and boundary conditions:

To illustrate the numerical solutions, we set the values of parameters as the strike price, $K = 150$, the risk-free interest rate (per year), $r = 0.02$, the maturity time, $T$ (year) $= 1$, the volatility of the underlying of $x$ assets (per year), $\sigma_1 = 0.15$, the volatility of the underlying of $y$ assets (per year), $\sigma_2 = 0.2$, and the correlation, $\rho = 0.5$, $\beta_1 = 2$, $\beta_2 = 1$. The domain is discritized by $N = 4$, $M_x = 10$, and $M_y = 10$.

Figure 3 shows the numerical solution of the fractional order Black-Scholes model which is solved by the proposed finite difference method. The results show that the put option price decreases when the underlying asset price increases. The put option price will reach zero when $S_1$ is greater than 100 and $S_2$ is greater than 50.

Figure 4 illustrates the value of European put options for various fractional order $\alpha = 0.2$, $\alpha = 0.4$, $\alpha = 0.6$, $\alpha = 0.8$, and $\alpha = 1$. The results show that the put option price decreases when we increase the fractional order.

By comparing the numerical result to the analytical approximate solution of the fractional-order Black-Scholes model for put option, the approximate analytical solution from LHPM ^[50] is applied.

Table 2 displays the RRMSE for put option prices at various times and fractional-orders $\alpha$. It is noted that approximate analytical solutions generally require less computational time than numerical solutions, as they can be computed directly at specified points. However, analytical solutions may not always be feasible due to dependencies on equations, domains, initial conditions, and boundary conditions. Analytical solutions are specific to each problem and may differ from numerical solutions. While analytical solutions typically offer high accuracy, the approximate analytical solution provided by LHPM is selected for comparison with the proposed finite difference method. The error values in the table affirm that the proposed finite difference scheme provides option prices that are not significantly different from other approximate methods.

4.3.   The numerical analysis

Let $g(t) = t^2+1$. The formula for the max norm of errors is given by

where $G(t_{n+1/2})$ is the approximation to $D^{\alpha}_t g(t)$, which is obtained by formula (3.7) at $t_n = 1$. Table 3 shows the order of the fractional-order difference method.

Since the investigated model has no exact solution, we compared the value of the option price obtained from the proposed method to the one obtained from the approximate analytical method (LHPM) as a reference. The setting parameters are similar to Sections 4.1 and 4.2, and the fractional-order is $\alpha = 0.5$ at time $t = 1$. The computational times of the two methods are shown in Table 4. The RRMSE is used to represent the error. The results show that the error decreases as the number of intervals increases. The computational time of the proposed method is higher than the approximate analytical method (LHPM) because the finite difference method deals with matrices, but the LHPM calculates only at the specific points. The benefit of the proposed method is suitable for many types of problems, but the analytical method is used for specific problems, or some problems that cannot find the analytical solution.

5.   Conclusions

The multidimensional Black-Scholes model has become popular because the option price does not depend on only one asset. The Black-Scholes model is widely used to compute the option price in European-style options and is suitable for both call and put options. Recently, fractional-order derivatives have become powerful tools for improving theoretical understanding. The two-dimensional time-fractional-order Black-Scholes model is a model that can be used to find the option price depending on two assets. The solution of this model is crucial for determining a suitable price for investors. However, some fractional-order partial differential equations do not have closed-form solutions. As a results, the numerical solutions is the only viable method for determining the price. Thus, we propose a modified Crank-Nicolson finite difference method for solving the time-fractional-order Black-Scholes model with two assets. The fractional-order Liouville-Caputo derivative is applied to the ordinary Black-Scholes model. This method combines the concepts of the finite difference method for solving the multidimensional Black-Scholes model and the finite difference method for solving the fractional-order heat equation. Analysis of the proposed method reveals conditional stability, and the order of convergence is also investigated. Numerical examples are illustrated to demonstrate the trend of option prices for call and put options. By comparing the numerical results with solutions from analytical approximation techniques and the LHPM, we observe only small differences, indicating in the results, which mean that the proposed method is suitable for solving the two-dimensional fractional-order Black-Scholes model.

Author contributions

Din Prathumwan: Conceptualization, Formal analysis, Investigation, Methodology, Software, Visualization, Writing-original draft, Writing-review & editing; Inthira Chaiya: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing-original draft, Writing-review & editing; Narisara Phoochalong: Formal analysis, Methodology, Software, Visualization, Writing-original draft; Thipsuda Khonwai: Investigation, Methodology, Software, Visualization, Writing-original draft; Kamonchat Trachoo: Conceptualization, Data curation, Formal analysis, Methodology, Software, Validation, Visualization, Writing-original draft, Writing-review & editing. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work (Grant No. RGNS 64-047) was supported by the Office of the Permanent Secretary, Ministry of Higher Education, Science, Research and Innovation (OPS MHESI), Thailand Science Research and Innovation (TSRI), and Khon Kaen University. This research project was financially supported by Mahasarakham University. The first author also thanks Kamsing Nonlaopon for his suggestions.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.