Existence, and Ulam's types stability of higher-order fractional Langevin equations on a star graph

1.   Introduction

The field of fractional calculus, which focuses on the application of fractional derivatives, has been rapidly developing in recent years. Compared to traditional integer calculus, fractional calculus has a broader range of applicability in both temporal and spatial scales, enabling more accurate descriptions of real-world problems. As an important branch of fractional calculus, fractional differential equations (FDEs) contain fractional derivatives and have been widely applied in various fields, including chemistry, physics, electrical engineering, economics, and biology^[1,2,3]. These equations hold significant practical value and have had a profound impact on the theoretical development of calculus, serving as one of the key foundations in its research. Currently, boundary value problems (BVPs) of FDEs are a hot topic of study. Scholars have mainly used fixed point theory ^[4,5,6,7,8], such as the Banach fixed point theorem, Schaefer fixed point theorem, and Krasnoselskii fixed point theorem, to establish sufficient conditions for the existence and uniqueness (EU) of FDEs solutions. These achievements have been highly important for deepening our understanding of FDEs and promoting their practical applications.

Fractional differential equations are of great significance in describing actual network structures, such as pipelines, gas pipelines, molecular structures, and computer network extensions. In 1980, Lumer^[9] proposed the theory of differential equations on graphs based on the branching space framework, and this field has since been widely developed for application in multiple disciplines such as chemical engineering, biology, and physics. Therefore, researchers have a strong interest in the existence and stability of solutions to BVPs of differential equations and their fractional mathematical models on graphs.

Graet et al.^[10] published their first work in the field in 2014, where they utilized known fixed point theorems to prove the EU of solutions to fractional BVPs on star graphs. That is, the authors studied a star graph $\mathcal{\tilde{G}} = \mathcal{\tilde{V}}(\tilde{\mathcal{G}})\cup \tilde{\mathcal{E}}(\tilde{\mathcal{G}})$, where $\tilde{\mathcal{V}} = \{{\epsilon_0}, {\epsilon_1}, {\epsilon_2}\}$ and $\tilde{\mathcal{E}} = \{\overrightarrow {{\epsilon_1}{\epsilon_0}}, \; \overrightarrow {{\epsilon_2}{\epsilon_0}}\}$ are sets of three vertices and of two edges, respectively; ${{\epsilon_0}}$ is the junction node and $\overrightarrow {{\epsilon_i}{\epsilon_0}}$ are the edges connecting nodes ${{\epsilon_i}}$ to ${{\epsilon_0}}$ with length ${\rho_i} = \left|{\overrightarrow {{\epsilon _i}{\epsilon_0}}} \right|$ for $i = 1, 2$. The nonlinear fractional BVPs system on each edge $\overrightarrow {{\epsilon _i}{\epsilon_0}}$ in their work^[10] is defined as follows:

where $\mathfrak{D}_{0}^\alpha$ and $\mathfrak{D}_{0}^\beta$ represent the Riemann-Liouville fractional derivative of orders $\alpha \in (1, 2]$ and $\beta \in (0, \alpha)$, respectively; ${\mathfrak{m}_i}:[0, {\rho _i}]\to \mathbb{R}$ are continuous functions with ${\mathfrak{m}_i}(t) \ne 0$ on $[0, {\rho_i}]$, and ${\mathcal{F}_i}:[0, {\rho _i}] \times \mathbb{R} \to \mathbb{R}$ are continuous functions. The EU of solutions for the BVPs (1.1) are derived by applying Scheafer's fixed point theorem and the Banach contraction principle. In 2019, Mehandirata et al. ^[11] expanded upon Graef's earlier work by generalizing it to apply to star graphs comprising $k+1$ nodes and $k$ edges as follows:

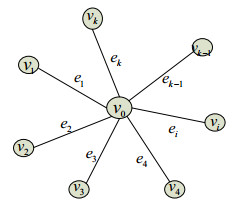
where ${}^C\mathfrak{D}_{0}^\alpha$ and ${}^C\mathfrak{D}_{0}^\beta$ represent the Caputo fractional derivative of orders $\alpha \in (1, 2]$ and $\beta \in (0, \alpha-1)$, ${\mathcal{F}_i}:[0, {\rho _i}] \times \mathbb{R} \to \mathbb{R}$ are continuous functions; $\tilde{\mathcal{G}} = \tilde{\mathcal{V}}(\tilde{\mathcal{G}}) \cup \tilde{\mathcal{E}}(\tilde{\mathcal{G}})$ with $\tilde{\mathcal{V}}(\tilde{\mathcal{G}}) = \{{\epsilon_0}, {\epsilon_1}, \cdots, {\epsilon_k}\}$ and $\tilde{\mathcal{E}}(\tilde{\mathcal{G}}) = \{e_i = \overrightarrow{{\epsilon_i}{\epsilon_0}}, \; i = 1, 2, \cdots, k\}$, ${\rho_i} = \left| {\overrightarrow {{\epsilon_i}{\epsilon_0}} }\right|, i = 1, 2, \cdots, k$ (a collection of $k$ edges incident to a single node point (see Figure 1)). The EU of the solution to the BVPs (1.2) was proven using the same fixed-point theorem as in prior work^[10].

The BVPs of FDEs on graphs have attracted widespread attention from scholars, and some interesting research results have been achieved^{[12,13,14,15,16,17,18,19]}. For instance, in 2020, Etemad^[12] proved the existence of solutions to fractional BVPs on ethane graphs using Schaefer's fixed point theorem and Krasnoselskii's fixed point theorem. In the same year, Mophou and Leugering^[13] proved the EU of the solution through their study of the optimal control of fractional Sturm-Liouville BVPs on star graphs. In 2021, Turab^[14] verified the existence of solutions to fractional BVPs on hexagonal graphs using Krasnoselskii's fixed point theorem and Schaefer's fixed point theorem. In Han's study^[15], the Banach contraction mapping principle and Schaefer's fixed point theorem were applied to the EU of solutions for BVPs of nonlinear fractional differential equations on star graphs. In 2021, Ali ^[16] considered the existence of solutions to fractional BVPs on cyclohexane graphs. Additionally, Zhang et al.^[17] studied the BVPs of fractional Langevin equations on star graphs as follows:

where $\alpha \in (0, 1)$ and $\beta\in (0, \alpha)$, ${\lambda_i} \in {\mathbb{R}^+}$, $\mathcal{D}$ is the ordinary derivative, ${\mathcal{F}_i}:[0, {\rho _i}] \times \mathbb{R} \to \mathbb{R}$ are continuous functions, and the two fractional operators ${}^C\mathfrak{D}_{0}^\alpha$ and ${}^C\mathfrak{D}_{0}^\beta$ denote the Caputo fractional derivatives. The^[17] studied a star graph $\mathcal{\tilde{G}} = \mathcal{\tilde{V}}(\tilde{\mathcal{G}})\cup \tilde{\mathcal{E}}(\tilde{\mathcal{G}})$, where $\tilde{\mathcal{V}} = \{{\epsilon_0}, {\epsilon_1}, \cdots, {\epsilon_k}\}$ and $\tilde{\mathcal{E}} = \{{e_i} = \overrightarrow {{\epsilon_i}{\epsilon_0}}$, $i = 1, 2, \cdots, k\}$ are sets of $k + 1$ nodes and set of $k$ edges, with ${\rho_i} = \left|{\overrightarrow {{\epsilon_i}{\epsilon_0}}}\right|$. The author proved the EU of the BVP (1.3) solution by utilizing Schaefer's fixed point theorem and Banach contraction principle.

On the other hand, Ulam stability analysis was proposed by Ulam in the 1940s and further developed by Hyers. This analysis primarily studies whether the behavior of a system remains stable when there are slight changes in its parameters. Regarding Banach spaces, S. Banach introduced the famous fixed-point theorem in 1932. Later, Gleason, Ricciardi, and Ulam provided the theoretical foundation for Ulam stability by extending this theorem to additive mappings in metric spaces. In the field of FDEs, scholars began to study the stability of Ulam in the late 20th century and have achieved some notable results^{[20,21,22,23,24,25,26]}. In 2017, Khan et al.^[20] studied the Ulam stability of solutions to fractional differential equation systems using topological degree methods. In 2019, the same author ^[21] utilized the Guo-Krasnoselskii theorem to study the uniqueness of solutions and Ulam stability for differential equations containing Atangana-Baleanu-Caputo fractional derivatives. The same year, Devi et al.^[22] proved the Ulam stability of specific FDEs and provided examples illustrating their application. More recently, Zhang et al.^[23] studied the existence and Ulam-type stability of solutions to BVPs containing Caputo fractional derivatives on star graphs. These research studies show that the analysis of stability for solutions of FDEs is an active and important field of study with significant implications for understanding the long-term behavior of complex dynamic systems.

Inspired by the above-mentioned research^[15,17,23], it can be seen that how to solve the mixed boundary conditions for a class of nonlinear higher-order fractional Langevin equations on a star graph consisting of $k+1$ nodes and $k$ edges has not yet been examined. Specifically, this work examines the following problems:

where $\alpha \in (0, 1)$ and $\beta\in (0, \alpha)$, ${\lambda_i} \in {\mathbb{R}^+}$, $\mathcal{D}^2$ is the ordinary second-order derivative, ${\mathcal{F}_i}:[0, {\rho _i}] \times \mathbb{R} \to \mathbb{R}$ are continuous functions, and the two fractional operators ${}^C\mathfrak{D}_{0}^\alpha$ and ${}^C\mathfrak{D}_{0}^\beta$ denote the Caputo fractional derivatives. The star graph is $\mathcal{\tilde{G}} = \mathcal{\tilde{V}}(\tilde{\mathcal{G}})\cup \tilde{\mathcal{E}}(\tilde{\mathcal{G}})$, where $\tilde{\mathcal{V}} = \{{\epsilon_0}, {\epsilon_1}, \cdots, {\epsilon_k}\}$ and $\tilde{\mathcal{E}} = \{{e_i} = \overrightarrow {{\epsilon_i}{\epsilon_0}}$, $i = 1, 2, \cdots, k\}$ are sets of $k + 1$ nodes and set of $k$ edges, and ${\rho_i} = \left|{\overrightarrow {{\epsilon_i}{\epsilon_0}}}\right|$. We consider a local coordinate system with ${\epsilon_i}$ as the origin and coordinates $t$ in the interval $(0, \rho_i)$.

This study investigates the existence, uniqueness, and Ulam stability of solutions to nonlinear fractional BVP (1.4). The EU of the solution to problem (1.4) can be demonstrated by utilizing Krasnoselskii's fixed point theorem and Banach's contraction mapping principle. Meanwhile, the Ulam stability of this system was verified using the matrix eigenvalue method. Compared with existing research results, the innovative results presented in this article can be summarized as follows: First, we extend the fractional Langevin equation on a star graph to higher-order fractional cases. Second, compared with other research^{[10,11,15,23]}, the Langevin equation in this paper introduces nonlocal terms, which increases the difficulty of prior estimation. Third, compared with another study^[17], we not only investigated the existence and uniqueness of solutions to higher-order fractional Langevin equations, but also extended the relevant results on their Ulam stability. Fourth, compared with prior research^{[10,11,15,17,23]}, the fractional BVP (1.4) considered in this paper are more generalized and complex, as its nonlinear terms and boundary conditions depend not only on unknown functions, but also on fractional derivatives. Finally, Theorem 3.1 (see Section 3) proves that the problem (1.4) has at least one solution. This theorem proposes a linear growth condition for nonlinear terms, reduces the existence conditions, and thus makes the required existence condition more relaxed than condition $(H_3)$ used in previous literature ^[11,15].

The remaining parts of this manuscript are structured as follows. Section 2 proposes the auxiliary Lemma 2.5, which transforms the BVP (1.4) into an equivalent system (2.1), while reviewing the main relationships in fractional calculus. Section 3 proves the uniqueness and existence of solutions to the fractional differential BVP (1.4). Section 4 establishes sufficient conditions for the Ulam stability of the solution to system (2.1). Section 5 illustrates the main results of this paper regarding the existence, uniqueness, and Ulam stability of solutions through two examples. Finally, some conclusions are given in the last section.

2.   Preliminaries

In this section, we will revisit the concept of fractional calculus and outline some basic results that will provide a basis for the subsequent discussions in this paper.

Definition 2.1. ^[1]. Let $f \in C([a, b], \mathbb{R})$. Then the Riemann-Liouville fractional integral is given by

where $\Gamma(\cdot)$ is the classical Euler gamma function.

Definition 2.2. ^[1]. Let $f \in C^n([a, b], \mathbb{R})$. Then the Caputo fractional derivative operator of order $\alpha > 0$ is defined by

where $n-1 < \alpha\leq n$ and $n\in N$.

Lemma 2.1. ^[1]. Let $\alpha > 0$. Suppose that $u\in A{C^n}[0, 1]$. Then

where ${c_i} \in \mathbb{R}, \; i = 1, 2, \cdots n$, $n = [\alpha ]+1$.

Lemma 2.2. ^[27]. Suppose that $({\mathfrak{D}^n}t)(\tau)$ and $({}^C\mathfrak{D}_{a, \tau}^{\alpha + n}t)(\tau)$ exist. Then

where $n\in \mathbb{N}$ and $\mathfrak{D} = d/d{\tau}$.

Lemma 2.3. ^[1]. If $\alpha > 0$, $\beta > \alpha-1$, $\tau > 0$, then

Theorem 2.1 (Urs). ^[28] Suppose $\mathcal{A}$ is a square matrix of order $n$ with positive real entries, i.e., $\mathcal{A}\in M_{nn}(\mathbb{R}^+)$. Then, the following statements are equivalent:

$(i)$ The eigenvalues of matrix $\mathcal{A}$ (in the open unit disc), denoted by $\lambda$, $\forall \lambda \in \mathbb{C}$ with det($\lambda I-\mathcal{A}$) = 0, i.e., $\left|\lambda\right| < 1$;

$(ii)$ The matrix $(I - \mathcal{A})$ is nonsingular;

$(iii)$ The matrix $(I-\mathcal{A})^{-1}$ has nonnegative elements and $(I-\mathcal{A})^{-1} = I+\mathcal{A}+\cdots+{\mathcal{A}^n}+ \cdots.$

Theorem 2.2 (Krasnoselskii's fixed point theorem). ^[29]. Let $P$ be a closed, bounded, convex, and nonempty subset of a Banach space $Z$. Let $A$ and $B$ be two operators such that

$(a)\; Az + B\bar{z}\in P$ for all $z, \bar{z}\in P$,

$(b)\; A$ is compact and continuous on $P$,

$(c)\; B$ is a contraction mapping on $P$.

Then there exists $\hbar\in P$ such that $\hbar = A\hbar + B\hbar$.

Lemma 2.4. ^[11]. Let $\alpha > 0$, $\varphi$ be a function defined on $[0, \rho]$, and $z(\tau) = \varphi(\rho \tau)$. Suppose that ${}^C\mathfrak{D}_{0, t}^\alpha \varphi$ exists on $[0, \rho]$, $t\in [0, \rho]$, then

Lemma 2.5. Let $\alpha\in (n-1, n)$, $\varphi$ be a function defined on $[0, \rho]$, and $z(\tau) = \varphi(\rho \tau)$. Suppose that ${}^C\mathfrak{D}_{0, t}^\alpha \varphi$ exists on $[0, \rho]$, $t\in [0, \rho]$, then

Proof. By means of Definition 2.2 and Lemma 2.2, we obtain

This concludes the proof of Lemma 2.5.□

Under the direct application of Lemmas 2.4 and 2.5, BVP (1.4) is equivalently transformed into system (2.1) defined on [0, 1], as given by

where ${z_i}(\tau) = {\varphi_i}({\rho _i}\tau)$, ${f_i}(\tau, u, v) = \mathcal{F}_i({\rho _i}\tau, u, v)$.

Lemma 2.6. Let ${h_i}(\tau) \in C[0, 1]$, $\alpha\in (0, 1)$. Then ${z_i}(\tau)$ is a solution of the BVP

which is given by

where ${\ell _j} = \frac{{\rho _j^{ - 2}}}{{2\sum\limits_{j = 1}^k {\rho _j^{ - 2}} }}, \; j = 1, 2, \cdots k$.

Proof. Applying the integral operator $I_{0}^{\alpha+2}$ to (2.2) and using Lemma 2.1, we have

where $a_i^j \; (i = 1, 2, \cdots, k, \; j = 1, 2, 3)$ are some constants. Deriving both sides of Eq (2.4) from 0 to $\tau$ gives

and

${z'_i}(0) = 0$ implies that $a_i^{(2)} = 0$, which leads to

Since ${z''_i}(1) = {z''_j}(1)$ and $\sum\nolimits_{i = 1}^k {\rho _i^{ - 2}{{z''_i}}(1) = 0}$, we obtain

and

According to (2.5) and (2.6), there is

which implies

By substituting ${z_i}(1) = 0$ and $a_i^{(3)}$ into in (2.4), we get

Inserting the values from (2.7) and (2.8) into (2.4), we get the solution (2.3). This completes the proof. □

3.   Existence and uniqueness results

In this section, we prove the existence and uniqueness of the solution to system (2.1). We first define a Banach space $X = \{ z: z, {}^C\mathfrak{D}_{0, \tau}^\beta z \in C[0, 1]\}$, with the supremum norm

where $\|z\| = \mathop {\max }\limits_{\tau \in [0, 1]} \big| {z(\tau)} \big|, \; \|{{}^C\mathfrak{D}_{0, \tau}^\beta z} \| = \mathop {\max}\limits_{\tau \in [0, 1]}| {{}^C\mathfrak{D}_{0, \tau}^\beta z(\tau)} |.$ It is obvious that the product space $({X^k} = {X_1} \times {X_2} \times \cdots \times {X_k}, {\left\| \cdot \right\|_{{X^k}}})$ is a Banach space, where the norm is defined by

By considering Lemma 2.6, we introduce the operator $T:{X^k} \to {X^k}$, related to system (2.1) by

for $\tau\in[0, 1]$ and ${z_i} \in X, \; i = 1, 2, \cdots k,$ where

Assume that the following conditions hold:

$(H_1)$ The functions ${f_i}:[0, 1] \times {\mathbb{R}^2} \to \mathbb{R}$ are continuous, $i = 1, 2, \cdots, k$.

$(H_2)$ There exist functions ${\xi_i}(\tau), {\eta_i}(\tau), {\psi_i}(\tau) \in C([0, 1], [0, + \infty))$, such that

for all $\tau\in[0, 1]$ and $u, v\in {\mathbb{R}^2}$.

$(H_3)$ There exist functions ${w_i}(\tau) \in C([0, 1], [0, + \infty))$, such that

for all $\tau\in[0, 1]$ and $(u, v), ({u_1}, {v_1}) \in {\mathbb{R}^2}$.

For the convenience of calculation, the following symbols are given:

Theorem 3.1. Assume that $(H_1)$ and $(H_2)$ hold, then system (2.1) allows at least one solution on [0, 1], provided that

where

and

Proof. Let $\Theta = \left\{ {z = (z_1, z_2, \cdots z_k) \in X^{k}:{{\left\| z_i \right\|_X}} \le r} \right\}$, where $r$ is chosen such that

then $\Theta$ is a bounded and closed convex subset of the Banach space $X^{k}$. We define $A_i$ and $B_i$ on $\Theta$ as

where

and

for all $\tau\in[0, 1]$ and $z = (z_{1}, z_{2}, \cdots, z_{k})\in \Theta$.

Now, for every $z = ({z_1}, {z_2}, \cdots, {z_k}), \; {\bar z} = ({{\bar z}_1}, {{\bar z}_2}, \cdots, {{\bar z}_k})\in X^k$, we have

From this we can deduce the following:

By Lemma 2.3 and $(H_2)$, we also can get

By using similar computations, we obtain

From (3.3) and (3.4), we get

where

Hence,

and so $A_i (z) + B_i({\bar z})\in\Theta$.

On the other hand, the continuity of $A_i$ follows from the continuity of functions $f_i \; (i = 1, 2, \cdots, k)$. Now, we show that the operator $A_i$ is uniformly bounded. For this, note that

This shows that the operator $A_i$ is uniformly bounded on $\Theta$.

Now, we show that the operator $A_i$ is compact on $\Theta$. Let ${\tau_1}, {\tau_2}\in(0, 1)$, ${\tau_1} < {\tau_2}$, then we have

and

From (3.5) and (3.6), we get

which implies ${\left\| {{A_i}z({\tau_2}) - {A_i}z({\tau_1})} \right\|_X} \to 0$ as ${\tau_2} \to {\tau_1}$, and so ${\left\| {{A_i}z({\tau_2}) - {A_i}z({\tau_1})} \right\|_{X^k}} \to 0$ as ${\tau_2} \to {\tau_1}$. Thus, ${A_i}$ is equicontinuous and, by the Arzel$\acute{a}$-Ascoli theorem, we conclude that the operator ${A_i}$ is a completely continuous operator.

Next, we prove that the operator $B_i$ is a contraction. Letting $z, \bar{z} \in \Theta$, we have

and

Thus, from (3.7) and (3.8), we get

Furthermore, we obtain

$\sum\limits_{i = 1}^k {{L_i}} < 1$, which means that $\Theta$ is bounded. We use Theorem 2.2 to show that the operator $T$ at least has one fixed point, and then system (2.1) has at least one solution. □

Theorem 3.2. Assume that $(H_1)$ and $(H_3)$ hold. Then system (2.1) has a unique solution on [0, 1], that is,

where

Proof. We will prove that $T$ is a contraction mapping. For any $z = ({z_1}, {z_2}, \cdots, {z_k})$, $\bar z = ({\bar z_1}, {\bar z_2}, \cdots, {\bar z_k}) \in X^{k}$, $\tau\in [0, 1]$. By Eq (3.1), we get

where

Now using assumption $(H_3)$ and $1-{\tau^2} < 1 \; (0 < \tau < 1)$, ${\ell_j} \in (0, 1)$, $j = 1, 2, \cdots, k$, we have

Hence, for any $z, \bar z\in {X^k}$, we obtain

On the other hand, using Lemma 2.3,

by using similar computations, we get

this implies that, for any $z, \bar z \in {X^k}$,

It follows from (3.10) and (3.11) that

From this it follows that

As a consequence, we obtain

which, given condition (3.9), proves that operator $T$ is a contraction. This implies that $T$ has a unique fixed point on ${X^k}$, that is, system (2.1) has a unique solution on [0, 1]. □

4.   Ulam type stability analysis

In this section, we introduce Ulam type stability concepts for system (2.1). Let ${\varepsilon_i} > 0$, ${f_i}:[0, 1] \times {\mathbb{R}^2} \to \mathbb{R}$ be continuous, and ${\Phi_i}(\tau):[0, 1] \to {\mathbb{R}^+} \; (\tau\in[0, 1])$ be nondecreasing. Consider the following inequalities:

Definition 4.1. ^[23] System (2.1) is Ulam-Hyers stable if there exists a real number ${c_{{f_1}, {f_2}, \cdots, {f_k}}} > 0$ such that, for each $\varepsilon = \varepsilon ({\varepsilon _1}, {\varepsilon _2}, \cdots, {\varepsilon _k}) > 0$ and for each solution $z = ({z_1}, {z_2}, \cdots, {z_k}) \in X$ of inequalities (4.1), there exists a solution $\bar z = ({\bar z_1}, {\bar z_2}, \cdots, {\bar z_k}) \in X$ of system (2.1) with

Definition 4.2. ^[23] System (2.1) is generalized Ulam-Hyers stable if there exists a function ${\Upsilon_{{f_1}, {f_2}, \cdots, {f_k}}} \in C({\mathbb{R}^+ }, {\mathbb{R}^+ })$ with ${\Upsilon_{{f_1}, {f_2}, \cdots, {f_k}}}(0) = 0$ such that, for each $\varepsilon = \varepsilon ({\varepsilon _1}, {\varepsilon _2}, \cdots, {\varepsilon _k}) > 0$ and for each solution $v = ({z_1}, {z_2}, \cdots, {z_k}) \in X$ of inequalities (4.2), there exists a solution $\bar z = ({\bar z_1}, {\bar z_2}, \cdots, {\bar z_k}) \in X$ of system (2.1) with

Definition 4.3. ^[23] System (2.1) is Ulam-Hyers-Rassias stable with respect to $\Phi = \Phi({\Phi_1}, {\Phi_2}, \cdots, {\Phi_k}) \in C([0, 1], {\mathbb{R}^+})$ if there exists a real number ${c_{{f_1}, {f_2}, \cdots, {f_k}}}\Phi > 0$ such that, for every $\varepsilon = \varepsilon ({\varepsilon _1}, {\varepsilon _2}, \cdots, {\varepsilon _k}) > 0$ and for each solution $z = ({z_1}, {z_2}, \cdots, {z_k}) \in X$ of inequalities (4.2), there exists a solution $\bar z = ({\bar z_1}, {\bar z_2}, \cdots, {\bar z_k}) \in X$ of system (2.1) with

Definition 4.4. ^[23] System (2.1) is generalized Ulam-Hyers-Rassias stable with respect to $\Phi = \Phi({\Phi_1}, {\Phi _2}, \cdots, {\Phi_k}) \in C([0, 1], {\mathbb{R}^ + })$ if there exists a real number ${c_{{f_1}, {f_2}, \cdots, {f_k}}}\Phi > 0$ such that, for each solution $z = ({z_1}, {z_2}, \cdots, {z_k}) \in X$ of inequalities (4.2), there exists a solution $\bar z = ({\bar z_1}, {\bar z_2}, \cdots, {\bar z_k}) \in X$ of system (2.1) with

Remark 4.1. A function $z = ({z_1}, {z_2}, \cdots, {z_k}) \in X$ is a solution of (4.1), if there exist functions ${\phi _i} \in C([0, 1], \mathbb{R})$ which depend on ${z_i}$ such that

$(i) \; \left| {{\phi _i}(\tau)} \right| \le {\varepsilon _i}, \; \tau \in [0, 1], \; i = 1, 2, \cdots, k,$

$(ii) \; ^C\mathfrak{D}_{0, \tau}^\alpha ({\mathcal{D}^2} + {\lambda _i}\rho _i^2){z_i}(\tau) = \rho _i^{\alpha + 2}{f_i}(\tau, {z_i}(\tau), \rho_i^{-\beta C}\mathfrak{D}_{0, \tau}^\beta {z_i}(\tau)) + {\phi _i}(\tau), \; \tau\in [0, 1], \; i = 1, 2, \cdots, k.$

One can make similar Remarks for inequalities (4.2) and (4.3).

Lemma 4.1. If $z = ({z_1}, {z_2}, \cdots, {z_k}) \in X$ is a solution of inequality (4.1), then the following inequalities hold:

and

where

and

Proof. Given $z$ is the solution of (4.1), then according to Remark 4.1 we have

By Lemma 2.6, the solution of (4.4) is given by

From (4.5), we deduce that

Similarly, applying the operator ${}^C\mathfrak{D}_{0, \tau}^\beta$ on (4.5), we have

Then we have

The proof is completed.□

Lemma 4.2. If $z = ({z_1}, {z_2}, \cdots, {z_k}) \in X$ is the solution of inequality (4.2). then, the following inequalities hold:

and

Proof. The proof can be obtained using a similar analysis as in Lemma 4.1 and the fact that ${\Phi _i}(\tau) \; i = 1, 2, \cdots, k$ are nondecreasing functions. Therefore, the proof is omitted. □

Theorem 4.1. Suppose that $(H_1)$, $(H_3)$, and (3.9) hold. If $\left| \lambda \right| < 1$, for every $\lambda \in \mathbb{C}$ with $\det(\lambda I-\mathcal{A}) = 0$, then system (2.1) is Ulam-Hyers stable, where

and

Proof. Let $z = ({z_1}, {z_2}, \cdots, {z_k})\in X$ be the solution of inequality (4.1) and $\bar z = ({\bar z_1}, {\bar z_2}, \cdots, {\bar z_k}) \in X$ be the solution of the following BVP:

According to Lemma 2.6 and Theorem 3.1, the solution to Eq (4.6) can be expressed as

Now, by Lemma 4.1, for $\tau \in [0, 1]$, we have

and

Therefore, from (4.7) and (4.8), it follows that

Meanwhile, inequality (4.9) can also have the form

where

Using matrix $\mathcal{A}$ and Theorem 2.1, we get

set

Obviously, ${c_{ij}} \ge 0$. Choose $\varepsilon = \max \{ {\varepsilon _1}, {\varepsilon _2}, \cdots, {\varepsilon _k}\}$. Then it follows from (4.10) that

Thus, system (2.1) is Ulam-Hyers stable. □

Remark 4.2. Take ${\Upsilon_{{f_1}, {f_2}, \cdots, {f_k}}}(\varepsilon) = {\Xi _\varepsilon }$ in (4.11). Obviously, we have ${\Upsilon_{{f_1}, {f_2}, \cdots, {f_k}}}(0) = 0$. Then, using Definition 4.2, we conclude that system (2.1) is generalized Ulam-Hyers stable.

Theorem 4.2. Suppose that $(H_1)$, $(H_3)$, and (3.9) hold. Let ${\Phi_i}(\tau) \in C([0, 1], {\mathbb{R}^+}) \; (i =$$1, 2, \cdots, k)$ be nondecreasing. If $\left| \lambda \right| < 1$, for every $\lambda \in \mathbb{C}$ with $\det(\lambda I-\mathcal{A}) = 0$, where $\mathcal{A}$ is defined as before and the function $\Phi$ is defined by

and

then system (2.1) is Ulam-Hyers-Rassias stable with respect to $\Phi$.

Proof. Assume that $z = ({z_1}, {z_2}, \cdots, {z_k}) \in X$ is a solution of inequality (4.2). Also, let $\bar z = ({\bar z_1}, {\bar z_2}, \cdots, {\bar z_k}) \in X$ be the unique solution of system (2.1). Then, combining Lemma 4.2 with an analysis similar to that used to prove Theorem 4.1, we obtain

and

Hence, from (4.12) and (4.13), we get

Similarly, one can obtain

From (4.14) and (4.15), we find that

We rewrite (4.16) as:

where

Using matrix $\mathcal{A}$ and Theorem 2.1, we get

and further, we define

It is easy to verify that

and

Setting $\varepsilon = \max \{ {\varepsilon _1}, {\varepsilon _2}, \cdots, {\varepsilon _k}\}$, we have

Let

By Definition 4.3, system (2.1) is Ulam-Hyers-Rassias stable with respect to $\Phi$. □

Remark 4.3. Taking $\varepsilon = 1$ in (4.18), we conclude using Definition 4.4 that system (2.1) is generalized Ulam-Hyers-Rassias stable with respect to $\Phi$.

5.   Example

Example 5.1. Consider the BVP (1.4) with $\alpha = \frac{1}{2}, \; \beta = \frac{1}{3}, \; k = 3, \; {\lambda _1} = \frac{1}{2}, \; {\lambda _2} = \frac{1}{4}, \; {\lambda _3} = \frac{1}{8}, \; {\rho _1} = {\rho _2} =$$\frac{1}{{10}}$, ${\rho _3} = \frac{1}{5}$, and

Using Lemma 2.5, we obtain the equivalent system

then

For $\tau\in[0, 1]$, we have $\xi_1^ * = \frac{1}{5}, \; \xi _2^ * = \frac{1}{3}, \; \xi _3^ * = 2, \; \eta _1^ * = \frac{1}{{36}}, \; \eta _2^ * = \frac{1}{{128}}, \; \eta _3^ * = \frac{1}{{50}}, \; \psi _1^ * = \psi _2^ * = \frac{5}{{3}}, \; \psi _3^ * = \frac{1}{{4}}$. By calculation, we get

so, we have

and

Thus,

According to Theorem 3.1, BVP (5.1) has at least one solution on [0, 1].

Example 5.2. Consider the BVP (1.4) with $\alpha = \frac{1}{2}, \; \beta = \frac{1}{3}, \; k = 3, \; \lambda_1 = \lambda_2 = \lambda_3 = \frac{1}{10}, \; \rho_1 = \rho_2 = \rho_3 =$$\frac{1}{5}$, and

Using Lemma 2.5, we obtain the equivalent system

and for $\tau\in[0, 1]$, $u, v, u_1, v_1\in \mathbb{R}$, we can conclude that

and so, we get

By simple calculation, we obtain

Then

Since all conditions of Theorem 3.2 have been satisfied, therefore, the system (5.2) has a unique solution in [0, 1]. Using the given value, we also have

Let

Solving Eq (5.3) gives

From Theorem 4.1 and Remark 4.2, it can be seen that the system (5.2) is Ulam-Hyers stable and generalized Ulam-Hyers stable. Similarly, we obtain that system (5.2) is Ulam-Hyers-Rassia stable and generalized Ulam-Hyers-Rassia stable.

6.   Conclusions

This article discussed a class of nonlinear Caputo type higher-order fractional Langevin equations on a star graph. By utilizing Lemmas 2.4 and 2.5, BVP (1.4) was transformed into system (2.1) defined on the interval [0, 1]. The existence and uniqueness of solutions are proven using fixed point theorems, specifically the Krasnoselskii fixed point theorem and the Banach contraction mapping principle. Furthermore, the Ulam-Hyers stability, Ulam-Hyers-Rassias stability, and their generalized forms are explored based on Definitions 4.1–4.4, which may provide researchers with a new approach to analyzing the Ulam stability of higher-order fractional differential equations. The results presented in this article are new and extend some existing literature on this topic (see prior references^{[10,11,15,17,23]}). Finally, two examples demonstrated the application of the main results. One promising avenue for future research is to explore fractional differential equations on star graphs, including the fractional Sturm-Liouville equation, the fractional Langevin equation with the $p$-Laplacian operator, and fractional integral-differential equations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (11601007) and the Graduate Innovation Fund of Anhui University of Science and Technology (2023cx2146).

Conflict of interest

The authors declare that they have no competing interests.