Enhancing epidemic modeling: exploring heavy-tailed dynamics with the generalized tempered stable distribution

1.   Introduction and problematic

Utilizing mathematical modeling empowers stakeholders to simulate diverse scenarios, assess potential outcomes, and gauge the effectiveness of various intervention measures. By incorporating a range of variables such as transmission rates, population mobility, and healthcare capacity, these tools establish a comprehensive and dynamic framework for predicting the trajectory of epidemics ^[1]. The ongoing refinement and expansion of these models enhance their adaptability, allowing them to effectively address emerging infectious threats. As our understanding of pathogens evolves and new data becomes available, it is imperative to regularly update modeling and simulation frameworks to ensure continued relevance and accuracy ^[2]. In the domains of human and animal health, these analytical approaches function as navigational tools, guiding decision-makers through the intricacies of epidemic scenarios. By exploring the intricate interplay of variables, including transmission patterns, host susceptibility, and environmental factors, these approaches provide decision-makers with a forward-looking perspective. This foresight is pivotal in formulating comprehensive strategies encompassing surveillance, prevention, and containment measures ^[3]. As a result, the integration of modeling and simulation methodologies stands as a cornerstone in the toolkit employed by professionals in the field of epidemiology to effectively address and manage infectious outbreaks. However, recognizing that each epidemic possesses unique biological features is crucial. Thus, the adaptation of dynamical models describing the mechanisms of propagation becomes imperative to address the specifics of each case ^[4]. This adaptive approach is essential for effectively navigating real-world situations, acknowledging the diverse and nuanced nature of various epidemics ^[5].

Within the realm of biological modeling, "intervention measures" encompass the strategic implementation of actions aimed at curbing the spread of disease. These measures, ranging from social distancing and mask-wearing to contact tracing, isolation, quarantine, and hospitalization, constitute common strategies employed in epidemic control ^[6,7]. To simulate the ramifications of these interventions, a compartmental model is often employed ^[8]. This model categorizes the population into distinct compartments based on their infection status. Furthermore, it allows for the incorporation of parameters that denote the efficacy of interventions, such as the reduction in transmission attributed to social distancing or the effectiveness of a vaccine ^[9,10]. The adjustment of these parameters enables the simulation of diverse intervention strategies and their impacts on the progression of the illness. Consequently, this modeling approach becomes a valuable tool for assessing and optimizing the outcomes of various intervention scenarios, contributing to the refinement of public health strategies and policies.

Building on this trajectory, our study introduces and scrutinizes an expanded version of the model described in ^[11]. This novel iteration incorporates two critical additional hypotheses: demographic variations and media intervention. The primary aim of the first enhancement is to bolster the model's descriptive capacity, enabling it to elucidate the dynamics of the ongoing pandemic over an extended timeframe ^[12]. This is achieved by integrating natural birth and overall mortality rates, thereby providing a more comprehensive understanding of population dynamics ^[13]. Concurrently, the second enhancement examines the impact of media campaigns and the dissemination of daily reports through various mass communication channels, including newspapers and social media ^[6]. Recognizing the significant role of media interventions in shaping public perception and response to the pandemic, our model seeks to capture the intricate interplay between information dissemination and the dynamics of infectious spread. By incorporating these additional dimensions, our refined model aspires to offer a more nuanced and realistic representation of the complex factors influencing the progression of the pandemic over time ^[14]. The demographic variations account for the evolving population structure, while media intervention addresses the influence of public awareness and behavior changes induced by continuous information flow. Moreover, the inclusion of these supplementary hypotheses allows for a better assessment of intervention strategies and their long-term efficacy. This comprehensive approach not only enhances the predictive power of the model but also provides valuable insights for public health policy and decision-making.

Developing accurate and comprehensive mathematical models is a critical method for guiding public health measures and interventions aimed at mitigating the spread of infectious diseases ^[15,16]. Compartmental models, such as the basic SIR (Susceptible-Infected-Recovered) model and its more complex variants, including SIRS, SEIR, and SIQR, have long been used to understand the dynamics of epidemics and pandemics ^{[17,18,19,20]}. These models categorize individuals into distinct compartments based on their infection status and track the movement of individuals between these states over time. For example, since the outbreak of COVID-19, a wide array of models has been developed to better understand the virus's transmission dynamics and to predict future trends ^[21,22]. Some early studies, such as ^[23], employed a classical SIR model to analyze the spread of COVID-19, leveraging its simplicity to provide quick insights into the disease's basic transmission patterns. However, as the pandemic evolved, it became clear that more refined models were necessary to capture the complex and multifaceted nature of SARS-CoV-2 transmission. To address this complexity, several modified versions of the SIR model were introduced to better reflect the unique characteristics of COVID-19. For example, studies like ^[24] adapted the classical SIR framework by adding new parameters and compartments, making it more suitable for understanding SARS-CoV-2 dynamics. One of the most significant modifications was the transition to an SEIR (Susceptible-Exposed-Infected-Recovered) model, which incorporates an additional compartment for "Exposed" individuals who are infected but not yet infectious. This latency period is a crucial feature of COVID-19, as individuals often go through a phase where they harbor the virus but do not immediately spread it to others. Kumar et al. ^[25] employed this SEIR model to effectively describe the spread of COVID-19, taking into account various transmission pathways and the role of environmental factors. Similarly, the authors of ^[26] applied the SEIR model to study early-transmission variations during the initial stages of the pandemic in Italy, highlighting the adaptability of the model to different epidemiological settings. As the pandemic continued and more data became available, it became increasingly important to model the progression of deaths alongside infection rates. In response to this need, the SEIR model was further expanded to include a compartment for deceased individuals, resulting in the SEIRD model. The addition of the "Deceased" (D) class allowed researchers to more accurately project the number of deaths over time. The authors in ^[27] took this a step further by employing a fractional-order formulation of the SEIRD model, adding more flexibility in simulating the complex temporal dynamics of the epidemic. To generalize and extend the above works, in this paper, we consider a more comprehensive model by incorporating the impact of media interventions and additional specific compartments. Media interventions, such as public awareness campaigns and government announcements, significantly affect public behavior and adherence to preventive measures, which in turn influence the transmission dynamics of diseases. Our formulation incorporates these behavioral shifts and their effect on disease spread, making the model more robust for analyzing early-stage COVID-19 dynamics and other epidemics.

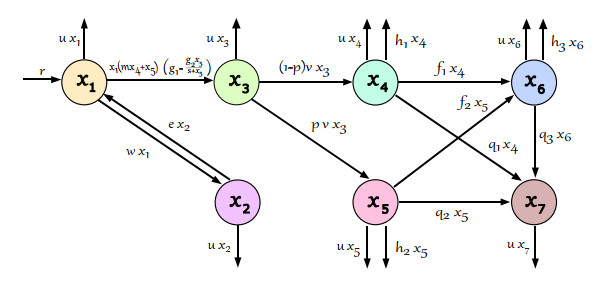
In order to establish a rigorous mathematical formulation of the model based on the preceding assumptions, we designate the entire host population at time $t$ as $T(t)$. This population is categorized into seven distinct classes representing susceptible $(x_1(t))$, quarantined or isolated $(x_2(t))$, exposed $(x_3(t))$, manifesting symptoms of contagion $(x_4(t))$, asymptomatically infected $(x_5(t))$, hospitalized $(x_6(t))$, and recovered $(x_7(t))$ individuals, each characterized by its respective density. The intricate interactions among these classes are captured by a system of deterministic ordinary differential equations, elucidating the dynamic relationships and transitions between the various compartments. This mathematical framework provides a formal representation of the epidemiological processes, enabling the quantitative analysis and simulation of the progression of the infectious disease within the host population. The structured nature of the model facilitates a detailed examination of how individuals move between different states over time, essential for understanding the dynamics of the disease and informing public health strategies. Based on the work presented in ^[11], the encompassing mathematical depiction associated with this framework is articulated as follows:

Within this system, we make certain assumptions to better capture the nuances of the epidemic dynamics. First, we consider exposed individuals $x_3(t)$ as non-infectious, representing them as carriers with low-level virus presence, a choice substantiated by existing research ^[28]. Building upon studies highlighted in ^[29,30], we assert in Eq (1.1) that vertical transmission from mother to fetus is negligible, and we consider the enforcement of a generic lockdown policy. Consequently, the recruitment rate $r$ for the uninfected population is exclusively attributed to natural births. Moreover, we incorporate a information-interaction function into our system to delineate the infection's transmission dynamics. We introduce $g_2$ as the baseline contact rate pre-media intervention, subject to reduction described by $g_2x_5(s+x_5)^{-1}$ when infective individuals are reported in the media. Here, $g_2$ represents the reduction interaction rate due to the presence of infection, and $s$ is the saturation parameter, signifying the impact of media alerts on the transmission rate. It is imperative to note that while media coverage can curtail the strength of virus generation, it lacks the ability to entirely eliminate it. Thus, we posit $g_1 > g_2 > 0$. From a logical perspective, individuals displaying symptoms of infection should manifest a higher rate of contagion compared to those who are asymptomatic. This rationale justifies our representation of the ratio between these rates as $0 < m < 1$. Regarding the population under home confinement, we introduce parameters $w$ and $e$ to signify the rates of isolation and release, respectively. The constant $v$ denotes the transition rate from the class of exposed individuals to the infected compartments $x_4$ and $x_5$, with the likelihood of remaining asymptomatic being $1-p$. Furthermore, parameters $f_1$ and $f_2$ signify the hospitalization rates of asymptomatic and symptomatic infectives, while $q_1$, $q_2$, and $q_3$ represent the recovery rates for classes $x_k(t)$, $k = 4, 5, 6,$ respectively. Finally, constants $u$, $h_1$, $h_2$ and $h_3$, respectively represent the normal mortality rate of each class and infection-related mortality rates of classes $x_k(t)$, $k = 4, 5, 6$. The graphical representation in Figure 1 vividly captures the intricate interactions among the various classes within system (1.1).

In a deterministic framework, the general epidemic model mentioned above displays two significant constraints, as delineated below:

• ${Restriction \; \; 1}$: While Gaussian noise is effective for modeling minor fluctuations, it falls short in simulating substantial and abrupt changes, particularly those induced by natural events like volcanoes and earthquakes, which can drastically affect populations ^[31]. These catastrophic events can significantly influence the transmission of human diseases, forcing people to relocate and gather in unsanitary conditions with inadequate sanitation facilities, thus increasing the risk of disease resurgence ^[32]. The inadequacy of Gaussian noise in capturing the sudden and discontinuous nature of these disaster events is clear ^[33]. Therefore, in scenarios involving substantial and abrupt environmental changes, a more robust modeling approach is necessary. This approach should more accurately reflect the profound and immediate impacts of natural disasters on population dynamics and disease transmission ^[34,35,36].

• ${Restriction \; \; 2}$: Considering epidemic models with jumps associated with standard measures reveals limitations in capturing phenomena with heavy tails (see ^[37,38]). Introducing the GTS distribution into a jump-incorporated epidemic model offers a more realistic portrayal of the stochastic nature of disease transmission. The GTS distribution, known for its flexibility, accommodates various degrees of tail heaviness, making it particularly beneficial for modeling epidemic dynamics marked by occasional extreme events or jumps ^[39]. Epidemic models often encounter rare yet impactful events that can induce sudden and substantial changes in disease dynamics, such as super-spreader gatherings, abrupt policy interventions, or unforeseen shifts in population behavior. Leveraging the GTS distribution allows for the modeling of these jump sizes, facilitating more accurate simulations of their influence on the epidemic. The GTS distribution is particularly effective in capturing the heterogeneity in disease transmission rates among individuals within an epidemic. In many epidemic scenarios, some individuals contribute more significantly to the spread of the disease than others due to varying factors such as contact rates or susceptibility. The GTS distribution is well-suited for modeling this variability because it aligns with a power-law distribution, which is known for its ability to represent extreme events and heavy-tailed phenomena where a small number of individuals account for a large proportion of the transmission. By incorporating the GTS distribution into epidemic models, researchers can account for both the stochastic nature of disease spread and the differences in transmission rates among individuals. This approach allows for a more nuanced and comprehensive understanding of how disease dynamics unfold, reflecting the real-world complexity of epidemic spread. Specifically, it helps model the influence of highly infectious individuals, often termed super-spreaders, and how their interactions disproportionately affect the overall transmission dynamics. The inclusion of the GTS distribution not only enhances the accuracy of simulations but also improves the effectiveness of public health strategies. By providing a more detailed and realistic representation of epidemic behavior, it helps in better predicting the spread of the disease, evaluating the impact of interventions, and devising more targeted and effective public health responses. This advancement ensures that models more accurately reflect the variability and complexity of real-world epidemic scenarios, leading to more informed decision-making and improved outcomes in managing disease outbreaks ^[40].

Considering the preceding discussion, the primary innovations in this paper involve the extension of previously established findings to a novel, well-defined stochastic model that is both mathematically rigorous and biologically plausible. This model addresses the constraints denoted as ${Restrictions\; 1-2}$ across a broad spectrum of human diseases. To the best of our knowledge, this marks the inaugural attempt to present an epidemic model that tackles both of these limitations simultaneously. Practically speaking, this method better mirrors real-world situations, given that the discrete factors affecting the dynamics may vary among different sub-populations. Hence, the system at hand is presented by the following interconnected perturbed formulation:

In this framework, $L_{j}\; ({j} = 1, \cdots, 7)$ represents seven mutually independent Brownian motions, each with a strength parameter ${\ell}_{j} > 0\; ({j} = 1, \cdots, 7)$. These processes are defined on $\left(\Omega, \mathcal{F}_\Omega, (\mathcal{F}_{\Omega, t})_{t\geqslant 0}, {\mathbb P}\right)$ which satisfies the usual conditions for a stochastic basis. Here, ${x}_{j}(t^-)\; ({j} = 1, \cdots, 7)$ indicates the left-hand limits of the processes of ${x}_{j}(t)\; ({j} = 1, \cdots, 7)$. Additionally, $\mathcal{Z}_{j}\; ({j} = 1, \cdots, 7)$ independent Poisson random measures, each associated with a finite Lévy measure ${Q}_{j}\; ({j} = 1, \cdots, 7)$ defined on a measurable set ${\mathbb R}^7\setminus\{0\}$. These measures are given by

where $\mathbb{1}$ is the indicator function, $\alpha\in(0, 2)$, and $R_L$ is the Rosiński measure defined on ${\mathbb R}^7\setminus\{0\}$ with $R_L(0) = 0$ and satisfying,

The compensated Poisson random measures $\widetilde{\mathcal{Z}}_{j}\; ({j} = 1, \cdots, 7)$ are defined as: $\widetilde{\mathcal{Z}}_{k}(\rm{d}t, \rm{d}\xi) = \mathcal{Z}_{k}(\rm{d}t, \rm{d}\xi)-{Q}_{k}(\rm{d}\xi) \rm{d}t$, and ${z}_{k}: {\mathbb R}^7\setminus\{0\}\to\mathbb{R}$ are the jump size functions, assumed to be continuous on ${\mathbb R}^7\setminus\{0\}$.

In this paper, we consider a GTS distribution by taking a new Lévy measure ${Q}_{0}$ defined as follows:

Let $\alpha_{-}\in(0, 2)$, $\alpha_{+}\in(0, 2)$, $\beta_{-} > 0$, $\beta_{+} > 0$, $\sigma_{-} > 0$ and $\sigma_{+} > 0$, then

The tempered stable distribution associated with the measure defined in (1.4) is a general framework of some well-known special cases presented in the literature:

• By picking out $\alpha_{+} = \alpha_{-} = 0$ and $\beta_{+} = \beta_{-}$, we get the variance Gamma distribution exhibited in ^[38].

• By selecting $\alpha_{+} = \alpha_{-}$, we get the KoBoL distribution discussed in ^[39].

• By choosing $\alpha_{+} = \alpha_{-} = 0$, we get the bilateral Gamma distribution explained in ^[40].

• By picking $\alpha_{+} = \alpha_{-}$ and $\sigma_{+} = \sigma_{-}$, we get the infinitely divisible distribution linked to a truncated Lévy flight introduced in ^[41].

• By choosing $\alpha_{+} = \alpha_{-}$ and $\beta_{+} = \beta_{-}$, we get the CGMY-distribution presented in ^[42].

The key advantage of this paper lies in presenting a comprehensive framework that offers a more intricate modeling perspective compared to existing works. A distinguishing feature of our approach is the incorporation of the GTS distribution, which introduces a novel methodology requiring deeper analytical assumptions and careful consideration in numerical simulations. This is especially critical in capturing the severe environmental fluctuations that are often oversimplified in traditional models. From a technical standpoint, our stochastic system diverges from conventional epidemic models, which typically exhibit well-defined endemic or disease-free states. In classical epidemiological models, these states represent stable conditions where a disease either persists at a constant level (endemic) or is completely eradicated (disease-free). These equilibrium points provide researchers with a framework for predicting the long-term behavior of the disease by examining how the system behaves in proximity to these stable states. However, our model challenges this paradigm by introducing a perturbed system where clear-cut stable states do not exist. This absence of distinct endemic or disease-free conditions leads to a more complex and dynamic interpretation of disease transmission. The disease does not settle into predictable long-term behaviors, making it impossible to categorize the outcomes as simple persistence or eradication. Instead, the model reflects the reality of fluctuating, unpredictable patterns of disease spread driven by stochastic forces, such as environmental variability or behavioral changes in the population.

The structure of this paper unfolds in the following manner: In Section 2, we introduce the vectorial representation of our stochastic model, accompanied by a generic compilation of notations and hypotheses. Employing analytical analysis, we verify the well-posedness of our model and establish sufficient conditions for both the extinction and persistence of the infection. Section 3 represents the realm of numerical simulations, providing a crucial validation of our results. Additionally, we emphasize the influence of GTS distribution on the dynamics of our model. The paper culminates with concluding remarks and a glimpse into potential future perspectives.

2.   Theoretical results

This section is dedicated to the examination of an adapted version of the general model, as articulated by the stochastic differential system denoted in (1.2). In order to streamline our discourse and facilitate clarity in notation moving forward, we present the initial-value system linked to (1.2) in the following standardized format:

where

• $S(t) = \big(x_i(t)\big)_{i\in\{1, \dots, 7\}} = \big(x_1(t), x_2(t), x_3(t), x_4(t), x_5(t), x_6(t), x_7(t) \big),$

• ${ } D_1\left(S(t)\right) = \big(D_i\left(S(t)\right)\big)_{i\in\{1, \dots, 7\}} = \left(\begin{matrix} r-\left(g_1-g_2\dfrac{x_5}{s+x_5}\right)x_1\left(m x_4+x_5\right)+e x_2 -(u+w)x_1 \\ wx_1-(u+e)x_2 \\ \left(g_1-g_2\dfrac{x_5}{s+x_5}\right) x_1\left(m x_4+x_5\right)-(u+v)x_3 \\ \left(1-p\right)v x_3-\left(u+f_1+q_1+h_1\right)x_4 \\ v p x_3-\left(u+f_2+q_2+h_2\right)x_5 \\ f_1 x_4+f_2 x_5-\left(u+h_3+q_3\right)x_6 \\ q_1 x_4+q_2 x_5+q_3 x_6-u x_7 \end{matrix} \right),$

• ${ } D_2\left(S(t)\right) = \mathrm{diag}\left(\left(\ell_iS_i(t)\right)_{i\in\{1, \dots, 7\}}\right) = \begin{pmatrix} \ell_1 S_1(t) & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \ell_7 S_7(t) \end{pmatrix},$

• ${ } L(t) = \left(L_1(t), L_2(t), \cdots, L_7(t) \right),$

• ${ } D_3\left(S(t)\right) = \mathrm{diag}\left(\left({z}_i(\xi)S_i(t^{-})\right)_{i\in\{1, \dots, 7\}}\right) = \begin{pmatrix} {z}_1(\xi)S_1(t^{-}) & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {z}_7(\xi)S_7(t^{-}) \end{pmatrix},$

• ${ } \widetilde{\mathcal{Z}}(\rm{d}t, \rm{d}\xi) = \left(\int^t_0\int_{{\mathbb R}^7\setminus\{0\}} \widetilde{\mathcal{Z}}_1(\rm{d}t, \rm{d}\xi), \int^t_0\int_{{\mathbb R}^7\setminus\{0\}} \widetilde{\mathcal{Z}}_2(\rm{d}t, \rm{d}\xi), \cdots, \int^t_0\int_{{\mathbb R}^7\setminus\{0\}} \widetilde{\mathcal{Z}}_7(\rm{d}t, \rm{d}\xi) \right).$

To ensure simplicity and streamline mathematical computations, we will consistently use the following notations and definitions throughout this paper. This deliberate choice aims to facilitate concise mathematical expressions and enhance clarity in our presentation.

• ${ } \chi_1: = \underset{k \in \{1, \cdots, 7\}}{\max}\left\{\int_{{\mathbb R}^7\setminus\{0\}}{z}_{k}^2(\xi){Q}_k(\rm{d}\xi)\right\}$.

• ${ } \chi_2: = \underset{k \in \{1, \cdots, 7\}}{\max} \left\{\int_{{\mathbb R}^7\setminus\{0\}}\Big\{-\ln\left(1+{z}_{k}(\xi)\right)+{z}_{k}(\xi)\Big\}{Q}_k(\rm{d}\xi)\right\}$.

• ${ } \chi_3: = \underset{{k}\in\{1, \cdots, 7\}}{\max}\big\lbrace {\ell}_{k}^2 \big\rbrace$.

• ${ } \chi_4(\xi): = \underset{{k}\in\{1, \cdots, 7\}}{\max}\big\lbrace {z}_{k}(\xi) \big\rbrace = {z}_{k^*}(\xi)$, where $k^*$ denotes the index for which the maximum is attained.

• ${ } \chi_5(\xi): = \underset{{k}\in\{1, \cdots, 7\}}{\min}\big\lbrace {z}_{k}(\xi) \big\rbrace = {z}_{\overline{k}}(\xi)$, where $\overline{k}$ denotes the index for which the minimum is attained.

• ${ } \chi_6(\xi): = \left(1+\chi_4(\xi)\right)^v-v\times\chi_4(\xi)-1$.

• ${ } \chi_7(\xi): = \left(1+\chi_5(\xi)\right)^v-v\times\chi_5(\xi)-1$.

• ${ } \chi_8(\xi): = \max\left\lbrace\chi_6(\xi), \chi_7(\xi)\right\rbrace$.

• ${ } \chi_9: = {\int_{{\mathbb R}^7\setminus\{0\}}} \chi_8(\xi) \mathbb{1}_{\left\{\chi_6(\xi)\geq \chi_7(\xi)\right\}} {Q}_{k^*}(\rm{d}\xi)+ {\int_{{\mathbb R}^7\setminus\{0\}}} \chi_8(\xi) \mathbb{1}_{\left\{\chi_7(\xi) > \chi_6(\xi)\right\}} {Q}_{\overline{k}}(\rm{d}\xi).$

Furthermore, to ensure both mathematical rigor and biological coherence in the proposed model, we introduce the following technical assumptions. These assumptions are essential for maintaining the integrity of the model, aligning it with both mathematical principles and biological accuracy.

• Assumption 1. ${z}_{k}(\xi)+1\; \; \text{are {positive}}, \; \; \forall k \in \{1, \cdots, 7\}$ and $\underset{{{k}\in \{1, 2\}}}{\max} \chi_k < \infty$.

• Assumption 2. $\exists v > 2$ such that ${ }\chi_{10} = r-0.5(v-1)\chi_3-v^{-1}\chi_9 > 0$.

Remark 2.1. To fully appreciate the importance of Assumption 2, we refer the reader to [43, Lemma 2.5]. In their work, the authors provide crucial insights that underpin the primary outcomes of our study. The general findings detailed in [43, Lemma 2.5] are instrumental in supporting and validating the key results derived from our investigation.

Remark 2.2. In the context of this section, we proceed under the assumption that both Assumptions 1 and 2 are upheld.

For the well-posedness of the generic model (2.1), we present the following theorem.

Theorem 2.1. For any started data $S(0)$ in the positive real seven-dimensional space ($\mathbb{R}_+^7$), there is a single solution $S(t)$ to (2.1) for $t \geqslant 0$. In addition, this single solution will persist within $\mathbb{R}_+^7$ with a probability of one. In other words, if the initial state $S(0)$ belongs to $\mathbb{R}_+^7$, then $S(t) \in \mathbb{R}_+^7$ holds for all $t \geqslant 0$ almost surely (abbreviated as a.s.).

Proof. Let $S(t) = \big(x_k(t)\big)_{k\in\{1, \cdots, 7\}} = \big(x_1(t), x_2(t), x_3(t), x_4(t), x_5(t), x_6(t), x_7(t) \big)$. In system (2.1), the associated coefficients exhibit continuous differentiability within their respective domains of definition, satisfying the local Lipschitz criterion. Consequently, for any given initial solution $S(0)$ in the positive real seven-dimensional space ($\mathbb{R}_+^7$), there exists a unique maximal local solution $S(t)$ defined for $t$ in the interval $\left(0, \gamma_{e}\right),$ where $\gamma_{e}$ represents the explosion time ^[44]. Our objective at this juncture is to establish the global nature of this solution; specifically, to demonstrate that $\gamma_{e} = \infty$ almost surely. For this objective, consider a sufficiently large natural number $\beta_0\in\mathbb{N}$ such that $S(0)\in [\beta_0^{-1}, \beta_0]$. For each integer $\beta\geqslant \beta_0$, define the stopping time $\gamma_k$ as follows:

Define $\gamma_\infty$ as the limit of $\gamma_\beta$ as $\beta$ approaches infinity. It is evident that the sequence $\left(\gamma_\beta\right)_{\beta \geqslant \beta_0}$ is monotonically increasing. Therefore, the limit of $\gamma_k$ as $k$ tends to infinity is equivalent to the supremum of $\gamma_\beta$ for $\beta\geqslant \beta_0$. By applying the theory presented in ^[45], which states that the supremum of a sequence of stopping times is itself a stopping time, we conclude that $\gamma_\infty$ is also a stopping time. Utilizing the convention $\inf \emptyset = \infty$ throughout this paper, it is straightforward to assert that $\gamma_\infty \leqslant\gamma_e$ almost surely. Therefore, establishing $\gamma_e = \infty$ almost surely directly hinges on demonstrating that $\gamma_\infty = \infty$ almost surely. This is precisely the objective we are poised to achieve to conclude the proof. Suppose that the statement $\gamma_\infty = \infty$ almost surely is false. This implies the existence of $D > 0$ such that ${\mathbb P}\left(\gamma_\infty\leqslant D\right) > 0$. Hence, there exists $x > 0$ such that

Examine the $\mathcal{C}^2$ function $F$ defined for $s = \left(x_1, \cdots, x_7\right)\in \mathbb{R}_+^7$ as follows:

In this context, $q$ represents a positive constant that will be carefully chosen at a later stage. Utilizing the multi-dimensional Ito's formula for $F(S(t))$, we derive expressions valid for all $\beta \geqslant \beta_0$ and $t\in\left(0, \gamma_\beta \right)$:

where

and

So,

Henceforth,

Selecting $q$ as $0.5\min\left\{\dfrac{u+h_1}{m g_1}, \dfrac{u+h_2}{g_1}\right\}$ ensures that the coefficients of $x_4$ and $x_5$ become negative; thus,

Therefore, for every $\beta \geqslant \beta_0$ and $t\in\left(0, \gamma_\beta \right)$, we obtain

Then,

Given that $F(\epsilon)\geq 0$ holds for all $\epsilon > 0$, then

Observe that for any $\omega\in \Omega$ that verifies $\gamma_\beta(\omega)\leqslant D$, there exists a component of $F\left(S(\gamma_\beta)\right)$ equal to either $\beta$ or $\beta^{-1}$; thus,

We deduce that

Allowing $\beta$ to approach infinity results in the contradiction $F\left(S(0)\right)+\mathcal{O}D = \infty$, thereby concluding the proof. □

2.1.   Stochastic eradication of a generic model (2.1)

In this subsection, we present the sufficient condition for the exponential extinction of the disease.

Theorem 2.2. Let us employ the notation $S(t)$ to represent the solution trajectory of the dynamical system defined by (2.1). This solution initiates from a specified initial condition denoted as $S(0)\in \mathbb{R}_+^7$. If $\frac{1}{6}\min(\ell_3^2, \ell_4^2, \ell_5^2) > g_1x_1^\star-u-\widetilde{\chi}$, with ${ } x_1^\star = \dfrac{r(e+u)}{u(w+u+e)}$ and

where

then

This signifies that the disease is anticipated to undergo exponential decay with a certainty of one in terms of probability.

Proof. By harnessing Itô's formula alongside the dynamics delineated in the system (2.1), we obtain the following expression:

Subsequently

By applying the renowned Cauchy-Schwarz inequality, we can confidently affirm that

Based on the inherent properties of the GTS measure, it follows that

where

As a result, we obtain

By integrating Eq (2.7) over the interval from $0$ to $t$ and subsequently dividing both sides by $t$, we arrive at the following expression:

Conversely, the initial equation in (2.1) yields the following information:

Then,

Furthermore, the second equation in (2.1) provides additional insights:

This observation underscores that

Integrating (2.9) with (2.10) leads to

Henceforth,

One can deduce, in accordance with the insights derived from [43, Lemma 2.5] and the inequality (2.11), that

In accordance with the strong law of large numbers for local martingales, as expounded in ^[44], it follows that:

From (2.8), (2.12), and (2.13), we obtain

This result precisely aligns with the intended conclusion. □

Remark 2.3. Unquestionably, the theorem preceding this assertion establishes the stochastic extinction of individuals infected within the system. This implication, rooted in the positivity of the solution, invariably leads to the convergence of key variables towards zero as time tends to infinity. Specifically, as denoted by $\lim\limits_{t\to\infty}x_k(t) = 0, \; \; \forall\; k = 3, 4, 5$, this convergence occurs almost surely (a.s.).

Corollary 2.1. Within the framework of the present analysis, adopting identical notations and adhering to the hypotheses stipulated in Theorem 2.2, we hereby establish the following assertions:

(1) ${ } {\mathbb P}\left(\lim_{t\to\infty}\frac{1}{t}\int^t_0 x_k(s){\rm{d}} s = x_k^{\star}\right) = 1, \; \forall\; k = 1, 2$.

(2) ${ } {\mathbb P}\left(\lim_{t\to\infty}\frac{1}{t}\int^t_0 x_k(s){\rm{d}} s = 0\right) = 1, \; \forall\; k = 6, 7$.

Proof. For all time instances $t\geqslant 0$, we have

By executing the integration of Eq (2.14) over the interval from $0$ to $t$, followed by subsequent division by $t$ on both sides, we obtain the following expression:

Substituting the expression for ${ }\frac{1}{t}\int^t_0 x_2(s){\rm{d}} s$ from (2.10) into the final equality results in

Then,

As we allow the variable $t$ to approach infinity on both sides of Eq (2.15), the ensuing outcome is

In light of the considerations presented in Remark 2.3, we can affirm the following: $\lim\limits_{t\to \infty} x_3(t) = 0, \quad\text{a.s.}$ This leads to an implication derived from the continuous version of Cesàro's result suggesting that

So,

Concurrently, it is imperative to acknowledge that

As a result, through a rigorous application of the limit to the aforementioned procedure, we derive

The aforementioned rationale holds true for the final two assertions posited in our theorem

Thus, the conclusion of the proof is reached. □

2.2.   Stochastic persistence of the generic model (2.1)

In the interest of conciseness and clarity in presenting forthcoming results, we find it appropriate to introduce the following notational conventions. These notations, meticulously selected for their brevity and simplicity, will prove instrumental in succinctly articulating subsequent findings.

• $\mathfrak{h}^\star(s) = 3\times\sqrt[3]{r \left(g_1-g_2\right)v}\times\left(\sqrt[3]{m(1-p)s}+\sqrt[3]{p\times(1-s) }\right), \quad \forall \; 0 < s < 1,$

• $\mathfrak{h}_\mathfrak{c} = 7u+v+\left(f_1+q_1+h_1\right)+\left(f_2+q_2+h_2\right)+\left(h_3+q_3\right)+\left|r-w\right| +{ } 2^{-1}\sum\limits_{k = 1}^7\ell_k^2+\sum\limits_{k = 1}^7\int_{{\mathbb R}^7\setminus\{0\}} \Big({z}_k(\xi)+\ln\big(1+{z}_k(\xi)\big)\Big)Q_k(\rm{d}\xi),$

• $\widehat{s} = \dfrac{\sqrt{m(1-p)}}{\sqrt{m(1-p)}+\sqrt{p}}.$

Lemma 2.1. For every $s$ belonging to the open interval $(0, 1)$, the ensuing inequality holds true: $\mathfrak{h}^\star(s)\leqslant \mathfrak{h}^\star (\widehat{s})$. Alternatively expressed, $\mathfrak{h}^\star (\widehat{s})$ represents the supremum of $\mathfrak{h}^\star(s)$ over the open interval $(0, 1)$. In more precise terms, it denotes the maximum value attained by $\mathfrak{h}^\star(s)$ within this specified interval.

Proof. Commencing our demonstration, we initiate by acknowledging the differentiability property inherent in the function $\mathfrak{h}^\star(s)$ over the open interval $(0, 1)$. To establish this, we explicitly define the first derivative of this function as

Evidently, the derivative $\mathfrak{h}^{\star\prime}(s)$ and the linear function $f_L(s) = \widehat{s} - s$ exhibit concordant signs. Consequently, the behavior of the function $\mathfrak{h}^\star(s)$ is characterized by a decreasing trend for $s$ within the interval $(0, \widehat{s})$ and an increasing trend for $s$ within the interval $(\widehat{s}, 1)$. This implies that the critical points of $\mathfrak{h}^\star(s)$ coincide with the zeros of the linear function $f_L(s)$, emphasizing the pivotal role of $\widehat{s}$ in the function's behavior. Thus, within the interval $(0, 1)$, the maximum value attained by $\mathfrak{h}^\star(s)$ is precisely at $\widehat{s}$, aligning with the assertion encapsulated in the lemma. This mathematical observation solidifies the lemma's claim, establishing the supremacy of $\mathfrak{h}^\star (\widehat{s})$ as the zenith within the specified interval. □

Theorem 2.3. Should $\mathfrak{h}^\star(\widehat{s})$ surpass $\mathfrak{h}_\mathfrak{c}$, then for every $S(0) \in \mathbb{R}_+^7$, the solution $S(t)$ of the initial-value problem defined by (2.1) satisfies the ensuing property:

This implies that the presence of infectious individuals, denoted by $x_4(t)$ and $x_5(t)$, exhibits a persistent behavior on average.

Proof. Contemplate the following mathematical function:

Leveraging Ito's formula in conjunction with the dynamics described by system (2.1), we obtain the following expression:

Given the positivity constraint inherent in the solution, we derive the following mathematical implication:

Observing that $\min(r, w) = 2^{-1}(r+w-\left|r-w\right|)$ and $\left(x_1 x_2^{-1}+x_2x_1^{-1}\right)\geqslant 2$, we establish the following inequality for all $t \geqslant 0$:

Exploiting the relationship between arithmetic and geometric averages, we deduce the following:

Upon integrating from $0$ to $t$ and subsequently dividing both sides of Eq (2.18) by $t$, we obtain the following expression:

Then,

Given that $\ln(z)+1 \leqslant z\leqslant z+1$ for all positive $z$, it follows that one can confidently affirm the inequality ${ }\widehat{\mathcal{G}}(z) \leqslant \sum\limits_{k = 1}^7z_i$ for any $z \in \mathbb{R}_+^7$. Therefore,

Utilizing the strong law of large numbers for local martingales, we derive the following expression:

This inequality constitutes the essential result we sought, thereby establishing the required assertion. □

3.   Numerical experiments and discussion

In this section, we present a series of numerical examples to validate the various results proposed in this study, utilizing the parameter values listed in Table 1. These parameters are predominantly chosen for numerical verification purposes. The simulations focus on solving our general model, considering both its perturbed and non-perturbed forms. For the initial data, we choose $S(0) = (100, 15, 2, 2, 50, 10, 10)$. It is important to note that the selected parameter values for these simulations are not arbitrary; they are derived from empirical data sourced from reputable sources, ensuring a realistic and meaningful exploration of our model's behavior. The simulation results will be thoroughly analyzed in the subsequent subsections, offering insights into the dynamics and implications of our general model (1.2).

3.1.   Simulation techniques and verification of the theoretical findings

Crafting stochastic processes through computer methodologies entails the application of two refined discretization techniques. Initially, it necessitates the precise discretization of the time parameter, succeeded by the intricate task of approximating random variables utilizing meticulously generated finite time series datasets. When confronted with the complexities of a Lévy process, distinguished by its property of stationary and independent increments, the most effective approach to simulate it at discrete time points mirrors the process of generating random numbers from an infinitely divisible distribution. In this subsection, we present a method for simulating GTS distributions and tempered stable processes. Although numerous techniques exist for simulating Lévy processes, many prove unsuitable for the task of simulating tempered stable processes due to the intricate nature of their Lévy measure. Consider the sequences $\{S_{1, j}\}_{j\geqslant 1}$, $\{S_{2, j}\}_{j\geqslant 1}$, and $\{S_{3, j}\}_{j\geqslant 1}$, representing independent and identically distributed (i.i.d.) random variables in the real numbers following the distribution (1.3). Additionally, let $\{S_{2, j}\}_{j\geqslant 1}$ and $\{S_{3, j}\}_{j\geqslant 1}$ be i.i.d. sequences of uniform random variables within the intervals $(0, 1)$ and $(0, T)$, respectively. Furthermore, consider $\{S_{4, j}\}_{j\geqslant 1}$ and $\{S_{5, j}\}_{j\geqslant 1}$ as i.i.d. sequences of random variables following an exponential distribution with a rate coefficient of $1$. It is assumed that all the aforementioned random variables are mutually independent. Now, let

Noticeably, $\{S_{6, j}\}$ can be regarded as a Poisson point process on the interval ${\mathbb R}_+$ with random intensity measure. In reference to the theory outlined in ^[37], if $\alpha\in(0, 2)$, then

converges almost surely and uniformly for t within the interval $[0, T]$ to a Lévy process, where

Ultimately, we can formulate a method for generating a GTS process with specified parameters at discrete time instances $t_i$, where $\{t_i\}_{i\in[0, I]}$ represents a partition of the interval $[0, T]$ with uniformly sized subintervals and mesh $\Delta t = T/I$, $I\in \mathbb{N}$. Then, we use the following algorithm:

(1) Select a specific time duration T and create a division of the time interval $[0, T]$ into $I$ equally sized segments.

(2) Select and fix a number $N$.

(3) Numerically replicate or emulate independent quantities $\{S_{i, j}\}$, $i\in\{1, \cdots, 6\}$ of range $N$.

(4) Determine the value of $G_t$.

Using the aforementioned algorithm, we can generate the complete path of a GTS process associated with system (1.2).

In the upcoming analysis, our goal is to evaluate the accuracy of the results presented in Theorems 2.2 and 2.3, focusing specifically on the influence of the GTS distribution on the dynamics of infection. Setting the stability index at $\alpha = 1.5$, we provide three types of trajectories for comparison: deterministic trajectories (without any noise), solutions incorporating jumps with a standard measure (with standard distribution), and stochastic trajectories with jumps and GTS distribution (with GTS distribution). This generic approach allows us to explore a range of potential scenarios. It is crucial to emphasize that our assumptions hold true in the following three experiments.

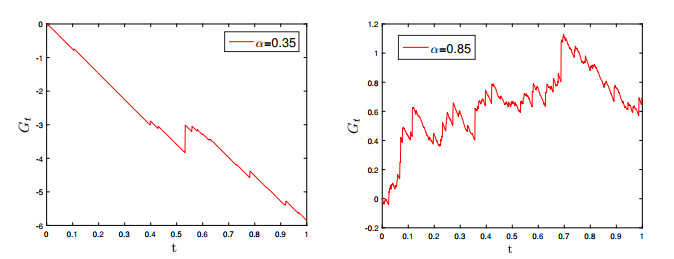
Remark 3.1. The parameter $\alpha$, referred to as the stability index, offers significant insights into the tail characteristics of a tempered $\alpha$-stable distribution. A value of $\alpha$ less than 1 indicates heavy tails, suggesting a higher probability of extreme events. Conversely, when $\alpha$ exceeds 1, the tails become lighter, resembling a distribution closer to normal. This distinction is visually evident in the representations depicted in Figures 2.

3.2.   Case 1: Total elimination of the infection

We parameterize our system based on the data provided in the third column of Table 1. Specifically, we assign values to $\ell_k$ ($k \in \{1, \ldots, 7\}$) as 1.2, 1.22, 1.02, 1.27, 1.23, and 1.26 respectively. The jump intensities are characterized by the function $z_k(\xi) = \frac{-u_k \xi}{0.5 + \xi^2}$, where $k \in \{1, \ldots, 7\}$ and $\xi = 0.22$. Correspondingly, $u_k$ ($k \in \{1, \ldots, 7\}$) take values 0.02, 0.03, 0.02, -0.0770, 0.02, and 0.03. These parameter selections give the following result:

Consequently, we have verified that the condition stated in Theorem 2.2 has been satisfied, thereby confirming that

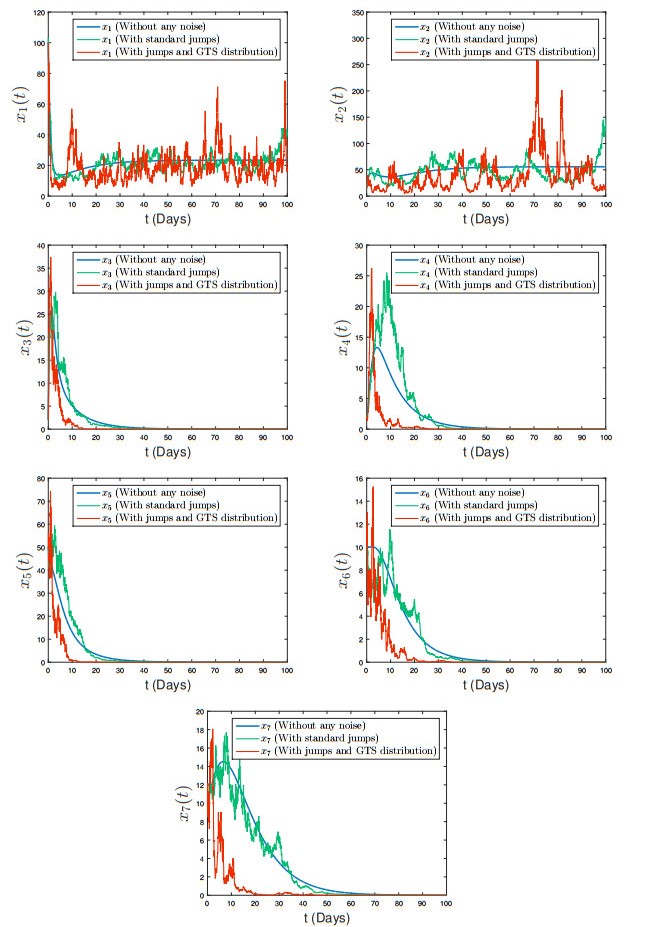
To validate this finding through numerical analysis, we have depicted three distinct types of trajectories associated with system (1.2) in Figure 3. Our observations confirm that the model consistently converges to an infection-free state across all trajectory types. Specifically, focusing on the initial data mentioned earlier, we note that over time, $x_1(t)$ stabilizes at a constant value of 23.4155, while $x_2(t)$ reaches an equilibrium point at 55.7512. Interestingly, regardless of the trajectory type, the solutions for $x_k(t)$ ($k = 3, \ldots, 7$) eventually extinguish after a certain duration. This phenomenon exemplifies stochastic extinction, where the solutions converge towards complete eradication of the disease. Importantly, this behavior holds true for all trajectories—whether they are noise-free, follow a standard distribution, or adhere to a GTS distribution—showcasing a consistent and identical pattern across different scenarios.

An additional observation worth noting is the marked contrast in the speed of extinction between paths governed by the GTS distribution and those following standard jumps. Notably, trajectories characterized by GTS distribution exhibit a notably swifter extinction process compared to their counterparts with standard jumps. This implies that the modeling incorporating GTS distribution captures a higher degree of external perturbations and more abrupt noises, thus creating a more realistic framework. The accelerated extinction in GTS-driven paths suggests a heightened sensitivity to external factors, lending credence to the notion that this distribution effectively incorporates and reflects a greater level of real-world dynamics.

To underscore the significance of incorporating the GTS distribution, we present a pivotal case in the ensuing example. This illustrative instance serves as a compelling demonstration of the pivotal role played by GTS distribution, emphasizing its essential contribution to the overall modeling framework.

3.3.   Case 2: Specific instance of the eradication of the infection

In the specific context at hand, our initial procedural step involves assigning numerical values to the system parameters. This critical process aligns these values with the data presented in the third column of Table 1. By meticulously calibrating the numerical parameters to match the provided data, we establish a foundational framework for deeper analysis and exploration within this specific context. For instance, setting $u_4 = -2.2$ yields

Consequently, we confirm that the essential condition described in Theorem 2.2 is satisfied. To empirically validate this result, we provide visual representations of three distinct system trajectories for Eq (1.2) in Figure 4. These figures emphasize the critical importance of incorporating the GTS distribution into our model. Specifically, the comparison reveals a stark difference between a system influenced by the standard Lévy distribution and one utilizing the GTS distribution. In a system driven by standard Lévy jumps (as in model (1.2) with standard Lévy distribution), the disease persists indefinitely within the population. However, when the GTS distribution is employed, the disease ultimately goes extinct. This observation highlights the pivotal role of the GTS distribution in shaping the dynamics of disease transmission, addressing a key limitation in the conventional Lévy jump framework where extinction does not occur. The incorporation of the GTS distribution is therefore a decisive factor, fundamentally altering the system's behavior and providing a more nuanced understanding of disease dynamics. Lévy processes, especially when using the GTS distribution, exhibit heavy-tailed characteristics, meaning that extreme events (such as sudden spikes in infection rates) are far more likely compared to systems governed by Gaussian (normal) distributions. In the context of infectious disease transmission, this implies a significant chance of experiencing rapid outbreaks, where the number of infections surges within a short period, potentially leading to the rapid spread of the disease and its eventual extinction. The stochastic nature of Lévy jumps, when combined with the GTS distribution, introduces the possibility of large, sudden increases in the number of infected individuals, which could drive the system toward a stochastic extinction event. If this surge results in a substantial proportion of the population becoming infected and if conditions are unfavorable for sustained transmission, the disease may self-extinguish. This phenomenon illustrates the importance of considering not only the average dynamics of the system but also the extreme tail behaviors introduced by the GTS distribution. These tail behaviors play a critical role in understanding the full range of possible outcomes in epidemic scenarios, allowing us to explore extreme scenarios where rapid disease propagation could lead to its extinction. The GTS distribution provides a richer framework for studying these complex dynamics, offering valuable insights into the behavior of infectious diseases under varying conditions.

3.4.   Case 3: Continuation of the infection

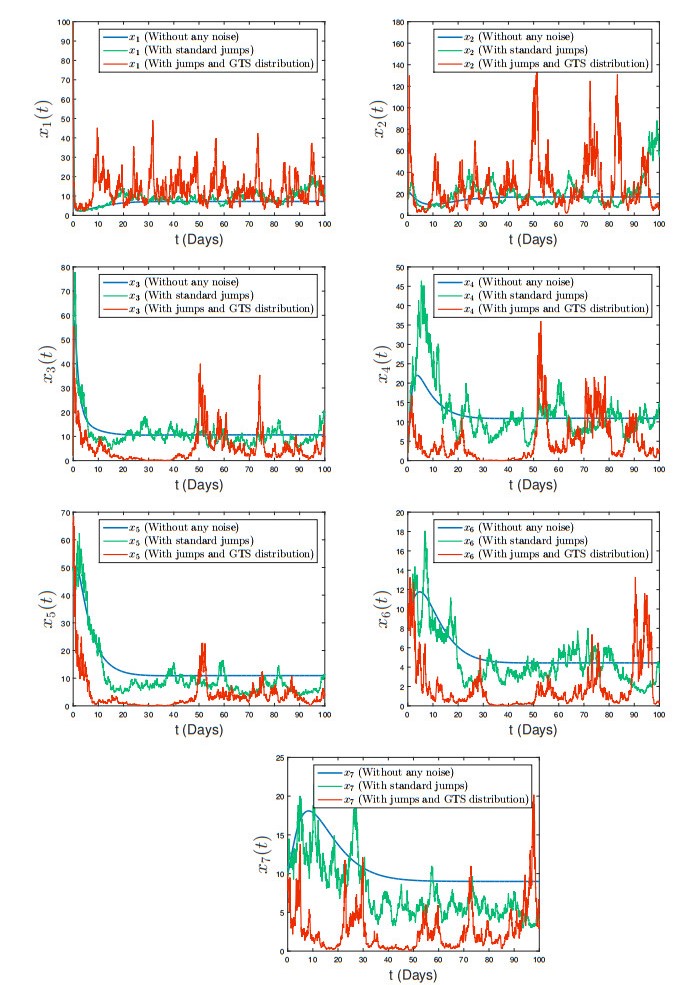
Exploring the scenario of sustained infection dynamics, we focus on setting specific values for $\ell_k$ ($k \in \{1, \ldots, 7\}$), choosing 0.9, 0.49, 0.28, 0.98, 0.39, and 0.26, respectively. These parameter choices are informed by empirical data and are crucial for modeling realistic infection spread scenarios. The jump intensities are defined by the function $z_k(\xi) = \frac{-u_k \xi}{0.5 + \xi^2}$, where $k$ ranges from 1 to 7, and $\xi$ is fixed at 0.24. Correspondingly, $u_k$ ($k \in \{1, \ldots, 7\}$) are specified as 0.02, 0.03, 0.02, 0.81, 0.02, and 0.03. By leveraging the numerical values from the last column of Table 1, we confirm the validity of our hypotheses, and derive

Thus, in accordance with Theorem 2.3, we confidently affirm that our model exhibits persistent infection dynamics on average, as consistently observed in the patterns depicted in Figure 5. Notably, unlike the deterministic version where an endemic equilibrium prevails, the stochastic model (1.2) does not settle into a stable state over extended time spans. The influence of noise intensity becomes pronounced, significantly impacting the fluctuations around deterministic equilibria.

Moreover, the temporal average closely approximates the endemic equilibrium, particularly evident in scenarios with lower noise intensities. This underscores the necessity of accounting for environmental fluctuations in biological systems. Figure 5 provides a detailed comparison between the volatility patterns of standard jumps and those governed by the GTS distribution. It reveals that GTS-distributed jumps exhibit greater volatility with heavier tails compared to those modeled by a normal distribution. Stochastic volatility occasionally experiences sharp upward spikes and clusters, contrasting sharply with the smoother trajectories observed in standard scenarios.

Further analysis of Figure 5 illustrates how adopting the GTS distribution mitigates infection intensity. This distribution not only modulates volatility but fundamentally reshapes infection dynamics, introducing unpredictability and resilience into biological systems. This deeper understanding enhances our grasp of infection dynamics and underscores the practical advantages of employing advanced distributional models in epidemiological studies.

4.   Conclusions

The core objective of an epidemic model is to thoroughly encapsulate the complex dynamics of disease transmission, capturing a broad spectrum of biological and environmental factors ^[46,47,48]. In our work, we advance this objective by introducing a generalized epidemic model that integrates two crucial elements: the effects of quarantine measures and media interventions on populations, and the stochastic impact of significant environmental fluctuations modeled using the GTS distribution. This model employs a compartmental approach, articulated as a system of interconnected stochastic differential equations influenced by Lévy noise. Our rigorous mathematical analysis has confirmed the model's robustness, biological relevance, and its behavior over extended periods in the absence of disease. By carefully calibrating stochastic parameters, we have identified conditions that influence whether infections can persist or be eradicated within human populations. This model's flexibility in capturing diverse transitions between compartments makes it particularly useful for studying diseases such as Zika virus, West Nile virus, Chikungunya virus, and Dengue fever. This comprehensive approach significantly enhances our understanding of disease transmission dynamics and aids in developing effective public health strategies and interventions. Despite these advancements, our research faces inherent limitations that present compelling avenues for future investigation:

(1) Existence of a stationary distribution for model (1.2): The stochastic system outlined in (1.2) does not possess a traditional endemic equilibrium state, necessitating the exploration of alternative concepts of stochastic stability. It is essential to investigate the existence of a stationary distribution for (1.2), as this would suggest the potential for persistent disease dynamics within both mosquito and human populations. Understanding the conditions under which such a distribution emerges remains a key unresolved issue in the realm of human epidemic models influenced by Lévy noise and the GTS distribution.

(2) Parameter estimation for model (1.2): Although our study addresses the model with assumed known parameters, the challenge of parameter identification is significant when adapting the model to specific diseases. This process involves determining appropriate values for the model parameters and stochastic noise based on observed data from population dynamics over time. Achieving an optimal fit to empirical data remains a complex and unresolved challenge, particularly for epidemic models driven by Lévy noise and the GTS distribution.

Given the complexity and importance of these questions, we plan to explore them in future research endeavors, aiming to further refine our model and enhance its applicability to real-world epidemic scenarios.

Author contributions

Yassine Sabbar: Conceptualization, Writing Original Draft, Software, Formal Analysis; Aeshah A. Raezah: Conceptualization, Software, Validation; Mohammed Moumni: Validation, Reviewing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP 1/78/45.

Conflicts of interest

The corresponding author states that there is no conflict of interest.