A new type of generic, self-evolving and efficient automated deduction algorithm based on category theory

1.   Introduction

In the recent papers [7,9] two functionals were introduced, measuring the amount of light collected by the leaves, and the amount of water and nutrients collected by the roots of a tree. In connection with a ramified transportation cost [1,14,18], these lead to various optimization problems for tree shapes.

Quite often, optimal solutions to problems involving a ramified transportation cost exhibit a fractal structure [2,3,4,12,15,16,17]. In the present note we analyze in more detail the optimization problem for tree branches proposed in [7], in the 2-dimensional case. In this simple setting, the unique solution can be explicitly determined. Instead of being fractal, its shape reminds of a solar panel.

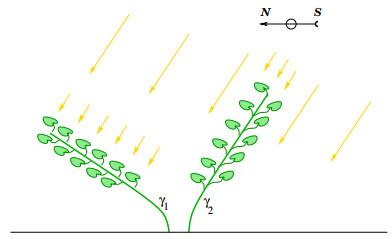
The present analysis was partially motivated by the goal of understanding phototropism, i.e., the tendency of plant stems to bend toward the source of light. Our results indicate that this behavior cannot be explained purely in terms of maximizing the amount of light collected by the leaves (Fig. 1). Apparently, other factors must have played a role in the evolution of this trait, such as the competition among different plants. See [6] for some results in this direction.

The remainder of this paper is organized as follows. In Section 2 we review the two functionals defining the shape optimization problem and state the main results. Proofs are then worked out in Sections 3 to 5. Finally, in Section 6 we show the sharpness of the assumptions used in Theorem 2.5 and discuss various possible extensions.

2.   Statement of the main results

We begin by reviewing the two functionals considered in [7,9].

2.1.   A sunlight functional

Let $\mu$ be a positive, bounded Radon measure on ${{\mathbb R}}^d_+\doteq\{(x_1, x_2, \ldots, x_d)\, ;\; x_d\geq 0\}$. Thinking of $\mu$ as the density of leaves on a tree, we seek a functional ${{\mathcal S}}(\mu)$ describing the total amount of sunlight absorbed by the leaves. Fix a unit vector

and assume that all light rays come parallel to ${{\bf n}}$. Call $E_{{\bf n}}^\perp$ the $(d-1)$-dimensional subspace perpendicular to ${{\bf n}}$ and let $\pi_{{\bf n}}:{{\mathbb R}}^d\mapsto E_{{\bf n}}^\perp$ be the perpendicular projection. Each point ${{\bf x}}\in {{\mathbb R}}^d$ can thus be expressed uniquely as

with ${{\bf y}}\in E_{{\bf n}}^\perp$ and $s\in{{\mathbb R}}$.

On the perpendicular subspace $E_{{\bf n}}^\perp$ consider the projected measure $\mu^{{\bf n}}$, defined by setting

Call $\Phi^{{\bf n}}$ the density of the absolutely continuous part of $\mu^{{\bf n}}$ w.r.t. the $(d-1)$-dimensional Lebesgue measure on $E_{{\bf n}}^\perp$.

Definition 2.1. The total amount of sunlight from the direction ${{\bf n}}$ captured by a measure $\mu$ on ${{\mathbb R}}^d$ is defined as

More generally, given an integrable function $\eta\in {{\bf L}}^1(S^{d-1})$, the total sunlight absorbed by $\mu$ from all directions is defined as

In the formula (4), $\eta({{\bf n}})$ accounts for the intensity of light coming from the direction ${{\bf n}}$.

Remark 1. According to the above definition, the amount of sunlight ${{\mathcal S}}^{{\bf n}}(\mu)$ captured by the measure $\mu$ only depends on its projection $\mu^{{\bf n}}$ on the subspace perpendicular to ${{\bf n}}$. In particular, if a second measure $\tilde{\mu}$ is obtained from $\mu$ by shifting some of the mass in a direction parallel to ${{\bf n}}$, then ${{\mathcal S}}^{{\bf n}}(\tilde{\mu}) = {{\mathcal S}}^{{\bf n}}(\mu)$.

2.2.   Optimal irrigation patterns

Consider a positive Radon measure $\mu$ on ${{\mathbb R}}^d$ with total mass $M = \mu({{\mathbb R}}^d)$, and let $\Theta = [0, M]$. We think of $\xi\in \Theta$ as a Lagrangian variable, labeling a water particle.

Definition 2.2. A measurable map

is called an admissible irrigation plan for the measure $\mu$ if

(ⅰ) For every $\xi\in \Theta$, the map $t\mapsto \chi(\xi, t)$ is Lipschitz continuous. More precisely, for each $\xi$ there exists a stopping time $T(\xi)$ such that, calling

the partial derivative w.r.t. time, one has

(ⅱ) At time $t = 0$ all particles are at the origin: $\chi(\xi, 0) = {\bf 0}$ for all $\xi\in\Theta$.

(ⅲ) The push-forward of the Lebesgue measure on $[0, M]$ through the map $\xi\mapsto \chi(\xi, T(\xi))$ coincides with the measure $\mu$. In other words, for every open set $A\subset{{\mathbb R}}^d$ there holds

One may think of $\chi(\xi, t)$ as the position of the water particle $\xi$ at time $t$.

To define the corresponding transportation cost, we first compute how many particles travel through a point $x\in{{\mathbb R}}^d$. This is described by

We think of $|x|_\chi$ as the total flux going through the point $x$. Following [13,14], we consider

Definition 2.3. For a given $\alpha\in [0, 1]$, the total cost of the irrigation plan $\chi$ is

The $\alpha$-irrigation cost of a measure $\mu$ is defined as

where the infimum is taken over all admissible irrigation plans for the measure $\mu$.

Remark 2. Sometimes it is convenient to consider more general irrigation plans where, in place of (6), for a.e. $t\in [0, T(\xi)]$ the speed satisfies $|\dot\chi(\xi, t)|\leq 1$. In this case, the cost (9) is replaced by

Of course, one can always re-parameterize each trajectory $t\mapsto \chi(\xi, t)$ by arc-length, so that (6) holds. This does not affect the cost (11).

Remark 3. In the case $\alpha = 1$, the expression (9) reduces to

Of course, this length is minimal if every path $\chi(\cdot, \xi)$ is a straight line, joining the origin with $\chi(\xi, T(\xi))$. Hence

On the other hand, when $\alpha<1$, moving along a path which is traveled by few other particles comes at a high cost. Indeed, in this case the factor $\bigl|\chi(\xi, t) \bigr|_\chi^{\alpha-1}$ becomes large. To reduce the total cost, it is thus convenient that many particles travel along the same path.

For the basic theory of ramified transport we refer to the monograph [1]. For future use, we recall that optimal irrigation plans satisfy

Single Path Property. If $\chi(\xi, \tau) = \chi(\xi', \tau')$ for some $\xi, \xi'\in\Theta$ and $0<\tau\leq \tau'$, then

Another property that will be repeatedly used in the sequel is the following.

Lemma 2.4. Let $\chi$ be an admissible irrigation plan for the measure $\mu$. Let ${{\bf C}}\subset {{\mathbb R}}^d$ be a closed convex set containing the origin, and let $p_{{\bf C}}:{{\mathbb R}}^d\mapsto {{\bf C}}$ be the perpendicular projection. Consider the projected measure $\tilde{\mu}$ supported on ${{\bf C}}$, obtained as the push-forward of $\mu$ by the map $p_{{\bf C}}$. Then the composed map ${\tilde{\chi}} (\xi, t)\; = \; p_{{\bf C}}(\chi(\xi, t))$ is an admissible irrigation plan for the measure $\tilde{\mu}$. Moreover, for every $\alpha\in [0, 1]$ one has

If $\tilde{\mu}\not = \mu$, then the above inequality is strict.

Proof. The first statement is obvious. As in Lemma 5.15 in [1], the inequality (13) follows from the fact that, in the projected irrigation plan, the length of particle trajectories decreases while the multiplicity increases. Indeed,

2.3.   The general optimization problem for branches

Combining the two functionals (4) and (10), one can formulate an optimization problem for the shape of branches:

${\bf (OPB)}$ Given a light intensity function $\eta\in {{\bf L}}^1(S^{d-1})$ and two constants $c>0$, $\alpha\in [0, 1]$, find a positive measure $\mu$ supported on $R^d_+$ that maximizes the payoff

2.4.   Optimal branches in dimension $d=2$

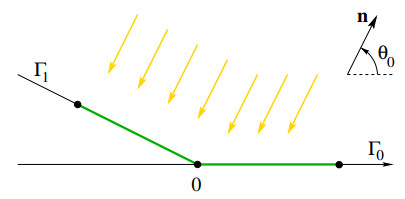
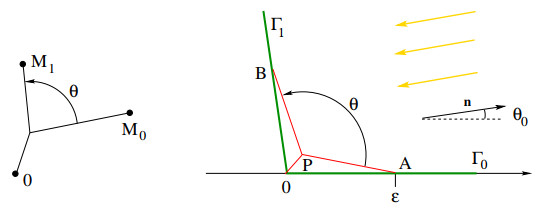
We consider here the optimization problem for branches in the planar case $d = 2$. We assume that the sunlight comes from a single direction ${{\bf n}} = (\cos\theta_0, \sin\theta_0)$, so that the sunlight functional takes the form (3). Moreover, as irrigation cost we take (10), for some fixed $\alpha\in \, ]0, 1]$. For a given constant $c>0$, this leads to the problem

over all positive measures $\mu$ supported on the half space ${{\mathbb R}}^2_+\doteq \{x = (x_1, x_2)\, ;\; \; x_2\geq 0\}$. To fix ideas, we shall assume that $0\leq \theta_0\leq \pi/2$. Our main goal is to prove that for this problem the "solar panel" configuration shown in Fig. 2 is optimal, namely:

Theorem 2.5. In dimension $d = 2$, assume that $0\leq\theta_0\leq \pi/2$ and $1/2 \leq \alpha \leq 1$. Then the optimization problem (15) has a unique solution. The optimal measure is supported along two rays, namely

When $0<\alpha<1/2$, the same conclusion holds if either $\theta_0 = 0$, or else the angle $\theta_0$ satisfies

In the case $\alpha = 1$ the result is straightforward. Indeed, for any measure $\mu$ we can consider its projection $\tilde{\mu}$ on $\Gamma_0\cup\Gamma_1$, obtained by shifting the mass in the direction parallel to the vector ${{\bf n}}$. In other words, for $x\in {{\mathbb R}}^2$ call $\phi^{{\bf n}}(x)$ the unique point in $\Gamma_0\cup\Gamma_1$ such that $\phi^{{\bf n}}(x)-x$ is parallel to ${{\bf n}}$. Then let ${\tilde{\mu}}$ be the push-forward of the measure $\mu$ w.r.t. $\phi^{{\bf n}}$. Since this projection satisfies $|\phi^{{\bf n}}(x)|\leq |x|$ for every $x\in {{\mathbb R}}^2_+$, the transportation cost decreases. On the other hand, by Remark 1 the sunlight captured remains the same. We conclude that

with strict inequality if $\mu$ is not supported on $\Gamma_0\cup\Gamma_1$.

In the case $0<\alpha<1$, the result is not so obvious. A proof of Theorem 2.5 will be worked out in Sections 3 and 4.

Having proved that the optimal measure $\mu$ is supported on the two rays $\Gamma_0\cup\Gamma_1$, the density of $\mu$ w.r.t. one-dimensional measure can then be determined using the necessary conditions derived in [6]. Indeed, the density $u_0$ of $\mu$ along the ray $\Gamma_0$ provides a solution to the scalar optimization problem

among all non-negative functions $u:{{\mathbb R}}_+\mapsto{{\mathbb R}}_+$. Here $s$ is the arc-length variable along $\Gamma_0$.

We write (18) in the form

subject to

The necessary conditions for optimality (see for example [8,11]) now yield

where the dual variable $q$ satisfies

Notice that, by (21), $u>0$ only if $q<1$. Combining (20) with (22) one obtains an ODE for the function $q\mapsto z(q)$, with $q \in [0, 1]$. Namely

This equation admits the explicit solution

Inserting (24) in (22), we obtain an implicit equation for $q(s)$:

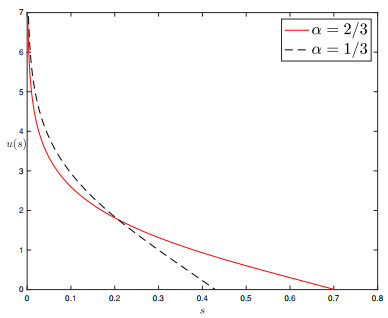
In turn, the density $u(s)$ of the optimal measure $\mu$ along $\Gamma_0$, as a function of the arc-length $s$, is recovered from (21). Notice that this measure is supported only on an initial interval $[0, \ell_0]$, determined by

In particular, the total mass $M_0$ along the ray $\Gamma_0$ is computed setting $q = 0$ in (24), namely

The density of the optimal measure along the ray $\Gamma_1$ is computed in an entirely similar way. In fact, it corresponds to the special case of setting $\theta_0 = \pi/2$ in the previous computations. Along $\Gamma_1$, the optimal measure $\mu$ is supported on an initial interval $[0, \ell_1]$, where

while the total mass is given by

An illustration of how the corresponding density profile $u(s)$ looks like for different values of $\alpha$ is displayed in Fig. 3.

2.5.   The case $\alpha=0$

In the analysis of the optimization problem (OPB), the case $\alpha = 0$ stands apart. Indeed, the general theorem on the existence of an optimal shape proved in [7] does not cover this case.

When $\alpha = 0$, a measure $\mu$ is irrigable only if it is concentrated on a set of dimension $\leq 1$. When this happens, in any dimension $d\geq 3$ we have ${{\mathcal S}}^\eta(\mu) = 0$ and the optimization problem is trivial. The only case of interest occurs in dimension $d = 2$. In the following, $\langle\cdot, \cdot\rangle$ denotes the inner product in ${{\mathbb R}}^2$.

Theorem 2.6. Let $\alpha = 0$, $d = 2$. Let $\eta\in {{\bf L}}^1(S^1)$ and define

(i) If $K>c$, then the optimization problem (OPB) has no solution, because the supremum of all possible payoffs is $+\infty$.

(ii) If $K\leq c$, then the maximum payoff is zero, which is trivially achieved by the zero measure.

A proof will be given in Section 5.

3.   Properties of optimal branch configurations

In this section we consider the optimization problem (15) in dimension $d = 2$. As a step toward the proof of Theorem 2.5, some properties of optimal branch configurations will be derived.

By the result in [7] we know that an optimal measure $\mu$ exists and has bounded support, contained in ${{\mathbb R}}^2_+\; \doteq\; \{(x_1, x_2)\, ;\; \; x_2\geq 0\}$. Call $M = \mu({{\mathbb R}}^2_+)$ the total mass of $\mu$ and let $\chi:[0, M]\times{{\mathbb R}}_+\mapsto{{\mathbb R}}^2_+$ be an optimal irrigation plan for $\mu$.

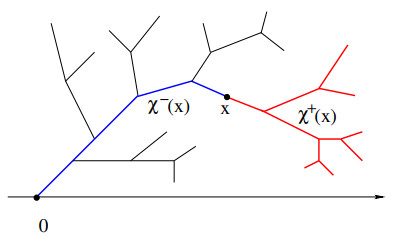
Next, consider the set of all branches, namely

By the single path property, we can introduce a partial ordering among points in ${{\mathcal B}}$. Namely, for any $x, y\in {{\mathcal B}}$ we say that $x\preceq y$ if for any $\xi\in [0, M]$ we have the implication

This means that all particles that reach the point $y$ pass through $x$ before getting to $y$.

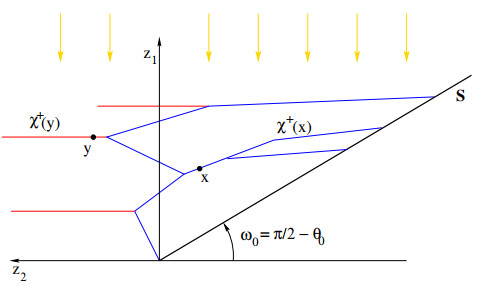
For a given $x\in {{\mathcal B}}$ the subsets of points $y\in {{\mathcal B}}$ that precede or follow $x$ are defined as

respectively (see Fig. 4).

We begin by deriving some properties of the sets $\chi^+(x)$. Introducing the unit vectors ${{\bf e}}_1 = (1, 0)$, ${{\bf e}}_2 = (0, 1)$, we denote by ${{\mathbb R}}{{\bf e}}_1$ the set of points on the $x_1$-axis. As before, ${{\bf n}} = (\cos\theta_0, \sin\theta_0)$ denotes the unit vector in the direction of the sunlight. Throughout the following, the closure of a set $A$ is denoted by $\bar{A}$, while $\langle \cdot, \cdot\rangle$ denotes an inner product.

Lemma 3.1. Let the measure $\mu$ provide an optimal solution to the problem (15), and let $\chi$ be an optimal irrigation plan for $\mu$. Then, for every $x\in {{\mathcal B}}$, one has

where $a_x\; \doteq\; \langle {{\bf n}}, x\rangle$, while $b_x$ is defined as follows.

● If $\overline{\chi^+(x)} \cap {{\mathbb R}}{{\bf e}}_1 = \emptyset$, then $b_x = a_x = \langle {{\bf n}}, x\rangle$.

● If $\overline{\chi^+(x)}\cap {{\mathbb R}}{{\bf e}}_1\not = \emptyset$, then

Proof. The right-hand side of (32) is illustrated in Fig. 5. To prove the lemma, consider the set of all particles that pass through $x$, namely

1. We first show that, by the optimality of the solution,

Indeed, consider the perpendicular projection on the half plane

Define the projected irrigation plan

Then the new measure $\mu^\sharp$ irrigated by $\chi^\sharp$ is still supported on ${{\mathbb R}}^2_+$ and has exactly the same projection on $E^\perp_{{\bf n}}$ as $\mu$. Hence it gathers the same amount of sunlight. However, if the two irrigation plans do not coincide a.e., then the cost of $\chi^\sharp$ is strictly smaller than the cost of $\chi$, contradicting the optimality assumption.

2. Next, we show that

Indeed, call

If $b''\leq b_x$, we are done. In the opposite case, by a continuity and compactness argument we can find $\delta>0$ such that the following holds. Introducing the perpendicular projection on the half plane

one has

Similarly as before, define the projected irrigation plan

Then the new measure $\mu^\flat$ irrigated by $\chi^\flat$ is supported on ${{\mathbb R}}^2_+\cap S^\flat$ and has exactly the same projection on $E^\perp_{{\bf n}}$ as $\mu$. Hence it gathers the same amount of sunlight. However, if the two irrigation plans do not coincide a.e., then the cost of $\chi^\flat$ is strictly smaller than the cost of $\chi$, contradicting the optimality assumption. This completes the proof of the Lemma.

Based on the previous lemma, we now consider the set

It will be convenient to rotate coordinates by an angle of $\pi/2 - \theta_0$, and choose new coordinates $(z_1, z_2)$ oriented as in Fig. 6. In these new coordinates, the direction of sunlight becomes vertical, while the positive $x_1$-axis corresponds to the line

Calling $\bigl(z_1(\xi, t), z_2(\xi, t)\bigr)$ the corresponding coordinates of the point $\chi(\xi, t)$, from Lemma 3.1 we immediately obtain

Lemma 3.2. Let $\chi$ be an optimal irrigation plan for a solution to (15). Then

(i) For every $\xi\in [0, M]$, the map $t\mapsto z_1(\xi, t)$ is non-decreasing.

(ii) If $\bar z = (\bar z_1, \bar z_2)\notin {{\mathcal B}}^*$, then $\chi^+(\bar z)$ is contained in a horizontal line. Namely,

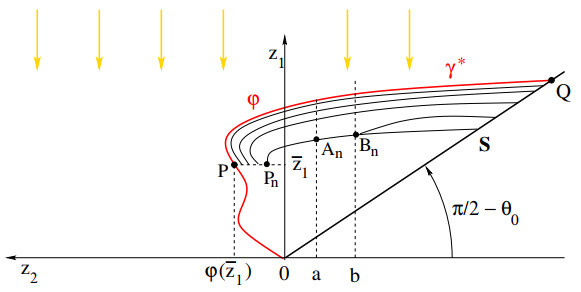
To make further progress, we define

Moreover, on the interval $[0, z_1^{max}[\,$ we consider the function

Lemma 3.3. For every $z_1\in [0, z_1^{max}[\,$, the supremum ${\varphi}(z_1)$ is attained as a maximum.

Proof. 1. Assume that, on the contrary, for some $\bar z_1$ the supremum is not a maximum. In this case, as shown in Fig. 7, there exist a sequence of points $P_n\to P$ with $P_n = (\bar z_1, s_n)$, $P = (\bar z_1, \bar z_2)$, $s_n\uparrow \bar z_2$. Here $P_n\in {{\mathcal B}}^*$ for every $n\geq 1$ but $P\notin {{\mathcal B}}^*$. Without loss of generality, we can assume that all points $P_n$ lie on distinct branches (i.e., there is no couple $m\not = n$ such that $P_m\preceq P_n$ or $P_n\preceq P_m$). Otherwise, we could group all these points into finitely many horizontal branches. But since every horizontal branch intersects the horizontal line through $P$ in a closed interval, this would already imply that the supremum in (39) is attained.

2. Choose two values $a, b$ such that

By construction, for every $n\geq 1$ the set $\overline {{\chi ^ + }\left( {{P_n}} \right)}$ intersects ${{\bf S}}$. Therefore we can find points

all in ${{\mathcal B}}^*$, with

3. Since the total mass $M$ is finite, we have

We can thus find $N$ large enough so that the amount of particles ${\varepsilon}_N\; \doteq\; |A_N|_\chi$ going through $A_N$ is so small that

Consider the modified transport plan $\tilde{\chi}$, obtained from $\chi$ by removing all particles that go through the point $B_N$. More precisely, $\tilde{\chi}$ is the restriction of $\chi$ to the domain

Let $\tilde{\mu}$ be the measure irrigated by $\tilde{\chi}$.

Calling $\sigma_0>0$ the total amount of particles going through $B_N$, since $\tilde{\mu}\leq\mu$, the total amount of sunlight gathered by the measure $\tilde{\mu}$ satisfies

We now estimate the reduction in the transportation cost, achieved by replacing $\mu$ with $\tilde{\mu}$. Let $\gamma:[s_A, s_B]\mapsto {{\mathbb R}}^2$ be an arclength parameterization of the branch from $A_N$ to $B_N$. Along this arc, when all the particles reaching $B_N$ are removed, the multiplicity (8) decreases from $|\gamma(s)|_\chi$ to $|\gamma(s)|_\chi-\sigma_0$. The transportation cost through $\gamma$ is reduced in the amount

This yields

If (40) holds, combining (41)-(42) one obtains

Hence the measure $\mu$ is not optimal. This contradiction proves the lemma.

By the previous result, the graph of ${\varphi}$ is contained in one single maximal trajectory of the transport plan $\chi$. As in Figure 8, we denote this curve by $\gamma$, which provides the left boundary of the set ${{\mathcal B}}^*$.

Along the curve $\gamma$, we now consider the set of points $C_j = (z_{1, j}, z_{2, j})$ where some horizontal branch bifurcates on the left. A property of such points is given below.

Lemma 3.4. In the above setting, for every $j$, one has

Proof. If (43) fails, there exists another point $C_j^* = (z_{1, j}^*, z_{2, j})$ along the curve $\gamma$, with $z_{1, j}^*<z_{1, j}$. We can now replace the measure $\mu$ by another measure $\tilde{\mu}$ obtained as follows. All the mass lying on the horizontal half-line $\{(z_{1, j}, s)\, ;\; \; s\geq z_{2, j}\}$ is shifted downward on the half-line $\{(z_{1, j}^*, s)\, ;\; \; s\geq z_{2, j}\}$. Since the functional ${{\mathcal S}}^{{\bf n}}$ is invariant under vertical shifts, we have ${{\mathcal S}}^{{\bf n}}(\tilde{\mu}) = {{\mathcal S}}^{{{\bf n}}}(\mu)$. However, the transportation cost is strictly smaller: ${{\mathcal I}}^\alpha(\tilde{\mu}) < {{\mathcal I}}^\alpha(\mu)$. This contradicts the optimality of $\mu$.

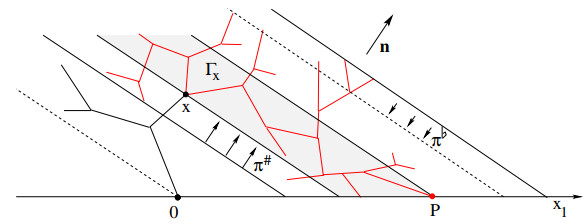
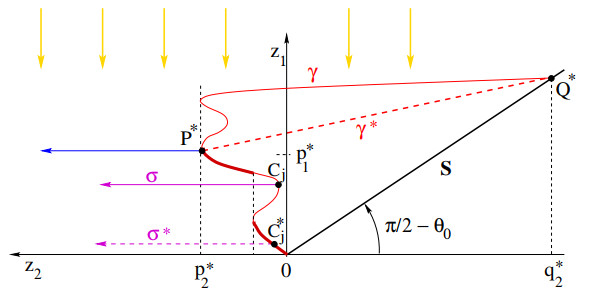
Next, as shown in Fig. 8, we consider a point $P^* = (p_1^*, p_2^*)\in \gamma$ where the component $z_2$ achieves its maximum, namely

Notice that such a maximum exists because $\gamma$ is a continuous curve, starting at the origin. If this maximum is attained at more than one point, we choose the one with smallest $z_1$-coordinate, so that

Moreover, call

and let $Q^* = (q_1^*, q_2^*) \in {{\bf S}}$ be the point on the ray ${{\bf S}}$ whose second coordinate is $q_2^*$. Recalling the notation of Lemma 3.1, we note that $q_1^* = b_x$ for $x = (0, 0)$. We claim that, by the optimality of the solution, all paths of the irrigation plan $\chi$ must lie within the convex set

Otherwise, call $\pi^*:{{\mathbb R}}^2\mapsto \Sigma^*$ the perpendicular projection on the convex set $\Sigma^*$, and let $\mu^*$ be the push-forward of $\mu$ by the map $\pi^*$. By Lemma 2.4 the composed map

is an irrigation plan for $\mu^*$ and satisfies ${{\mathcal E}}^\alpha(\chi^*)< {{\mathcal E}}^\alpha(\chi)$. Hence

contradicting the optimality assumption.

By a projection argument we now show that, in an optimal solution, all the particle paths remain below the segment $\gamma^*$ with endpoints $P^*$ and $Q^*$.

Lemma 3.5. In the above setting, let

be the segment with endpoints $P^*, Q^*$. If

is an optimal irrigation plan for the problem (15), then for a.e. $\xi \in \Theta$ we have the implication

Proof. 1. It suffices to show that the maximal curve $\gamma$ lies below $\gamma^*$. If this is not the case, consider the set of particles which go through the point $P^*$ and then move to the right of $P^*$, namely

Notice that, by the single path property (see Section 7.1 in [1]), all these particles follow the same path from the origin to $P^*$. Hence the length $t^*$ of this path is the same for all $\xi\in \Omega^*$.

2. Consider the convex region below $\gamma^*$, defined by

Let $\pi:{{\mathbb R}}^2\mapsto\Sigma$ be the perpendicular projection. Then the irrigation plan

has total cost strictly smaller than $\chi$. Indeed, for all $x$ and a.e. $\xi, t$ we have

Notice that, in (50), equality can hold for a.e. $\xi, t$ only in the case where $\chi = \chi^\dagger$.

3. We now observe that the perpendicular projection on $\Sigma$ can decrease the $z_2$-component. As a consequence, the measures $\mu$ and $\mu^\dagger$ irrigated by $\chi$ and $\chi^\dagger$ may have a different projections on the $z_2$ axis. If this happens, we may have ${{\mathcal S}}^{{\bf n}}(\mu)\not = {{\mathcal S}}^{{\bf n}}(\mu^\dagger)$.

To address this issue, we observe that all particles $\xi\in \Omega^*$ satisfy $\chi^\dagger(\xi, t^*) = \chi(\xi, t^*) = P^*$. In terms of the $z_1, z_2$ coordinates, this implies

By continuity, for each $\xi\in\Omega^*$ we can find a stopping time $\tau(\xi)\in [t^*, T(\xi)]$ such that

Call $\tilde{\chi}$ the truncated irrigation plan, such that

By construction, the measures $\mu$ and $\tilde{\mu}$ irrigated by $\chi$ and $\tilde{\chi}$ have exactly the same projections on the $z_2$-axis. Hence ${{\mathcal S}}^{{\bf n}}(\tilde{\mu})\; = \; {{\mathcal S}}^{{\bf n}}(\mu)$. On the other hand, the corresponding costs satisfy

This contradicts optimality, thus proving the lemma.

4.   Proof of Theorem 2.5

In this section we give a proof of Theorem 2.5. We recall that the functional (15) to be maximized is the difference between a payoff, i.e. the sunlight ${{\mathcal S}}^{{\bf n}}(\mu)$ absorbed by the measure $\mu$, and the ramified transportation cost $c{{\mathcal I}}^\alpha(\mu)$. Together with the measure $\mu$, at various steps of the proof we shall construct a second measure $\tilde{\mu}$, obtained by shifting part of the mass in a direction parallel to ${{\bf n}}$. As in Remark 1, this will not change the sunlight gathered: ${{\mathcal S}}^{{\bf n}}(\tilde{\mu}) = {{\mathcal S}}^{{\bf n}}(\mu)$. On the other hand, the irrigation cost of $\tilde{\mu}$ is strictly smaller: ${{\mathcal I}}^\alpha(\tilde{\mu})< {{\mathcal I}}^\alpha(\mu)$. We shall conclude that $\mu$ is not optimal.

As shown in Fig. 8, let $P^* = (p_1^*, p_2^*)$ be the point defined at (44). We consider two cases:

(ⅰ) $P^* = 0\in {{\mathbb R}}^2$,

(ⅱ) $P^*\not = 0$.

Assume that case (ⅰ) occurs. Then, by Lemma 3.4, the only branch that can bifurcate to the left of $\gamma$ must lie on the $z_2$-axis. Moreover, by Lemma 3.5, the path $\gamma$ cannot lie above the segment with endpoints $P^*$, $Q^*$. Therefore, the restriction of the measure $\mu$ to the half space $\{z_2\leq 0\}$ is supported on the line ${{\bf S}}$. Combining these two facts we achieve the conclusion of the theorem.

The remainder of the proof will be devoted to showing that the case (ⅱ) cannot occur, because it would contradict the optimality of the solution.

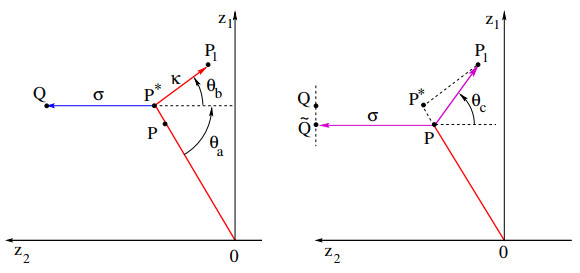
To illustrate the heart of the matter, we first consider the elementary configuration shown in Fig. 9, left, where all trajectories are straight lines. Water is first transported from the origin to the point $P^*$. Then, an amount $\sigma>0$ is moved horizontally to the point $Q$, while an amount $\kappa>0$ is moved to $P_1$. This yields a transport plan $\chi$, which irrigates the measure $\mu$ consisting of a mass $\sigma$ at $Q$ and a mass $\kappa$ at $P_1$.

Next, as shown in Fig. 9, right, we consider a point $P$ along the segment $0P^*$. A new transport plan $\tilde{\chi}$ is defined, where water is first transported from the origin to $P$. Then, an amount $\sigma$ is moved horizontally to a point $\tilde{Q}$ located along the same vertical line as $Q$. The remaining amount $\kappa$ is moved in a straight line from $P$ to $P_1$. Notice that the new transport plan $\tilde{\chi}$ now irrigates a measure $\tilde{\mu}$ consisting of a mass $\sigma$ at $\tilde{Q}$ and a mass $\kappa$ at $P_1$.

To fix ideas, we denote the lengths of the segments $PP^*$ and $P^*P_1$ as

The angles between these segments and a horizontal line will be denoted by $\theta_a, \theta_b$, respectively. The next lemma provides a comparison between the costs of the two irrigation plans $\chi$ and $\tilde{\chi}$.

Lemma 4.1. Let $\sigma\geq 0$, $\kappa>0$ be given, together with angles $\theta_a\in [0, \pi/2]$ and $\theta_b\in [0, \pi/2[\,$. Let $\chi, \tilde{\chi}$ be the irrigation plans defined above, as shown in Fig. 9. If $0<\alpha<1/2$ and $\theta_b$ satisfies the additional bound

or if $\alpha\geq 1/2$, then there exists ${\varepsilon}>0$ such that $\ell_a/\ell_b\leq{\varepsilon}$ implies

Proof. 1. To compute the difference between the quantities in (55), notice that the old transportation cost along $PP^*$ and $P^*P_1$,

is replaced by the new cost

Notice that the last term in (56) accounts for the fact that an amount $\sigma$ of particles need to cover a longer horizontal distance, traveling along the segment $P\tilde{Q}$ instead of $P^*Q$.

The difference in the cost is thus expressed by the function

2. Introducing the variables

we obtain

Setting

we are thus led to study the function

and to find conditions which imply the positivity of $F$.

3. The function $F$ in (58) can be written in terms of an inner product:

To prove that $F> 0$ it thus suffices to show that the second vector on the right hand side of (59) has length smaller than one, namely

This inequality holds provided that

Two cases must be considered. If $\alpha\geq 1/2$, then

Hence (60) trivially holds for all $\theta_b<\pi/2$.

On the other hand, if $\alpha<1/2$, consider the function

We observe that, for $0 \le \alpha \le \tfrac12$, one has

while

From (61) it now follows that the condition (54) guarantees that (60) holds, hence $F\geq 0$, as required.

Summarizing the previous analysis, for any $\lambda\in \, ]0, 1[\,$ and $\theta_a\in [0, \pi/2]$, we have proved:

(ⅰ) When $\alpha\geq 1/2$, one has $F(\lambda, \theta_a, \theta_b)> 0$ for all $\theta_b\in [0, \pi/2[\,$.

(ⅱ) When $0<\alpha<1/2$ one has $F(\lambda, \theta_a, \theta_b)> 0$ provided that $\theta_b$ satisfies the additional bound (54).

4. Combining (57) with (58), we obtain

By the previous step, in both cases (ⅰ) and (ⅱ) the right hand side of (62) is strictly positive provided that the ratio $\ell_a/\ell_b$ is sufficiently small. This yields (55).

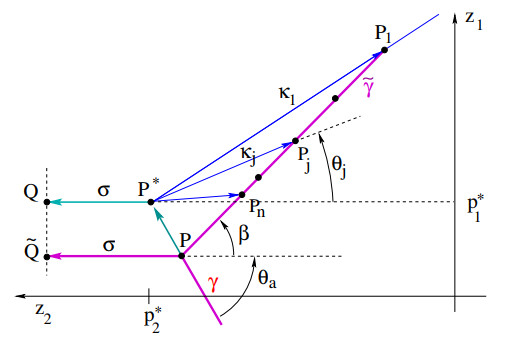
We now consider a more general irrigation plan $\chi$, shown in Fig. 10. Water is transported from the origin along a straight path $\gamma$, up to the point $P^*$. Then the flux is split into a finite number of straight paths. One goes horizontally to the left, with flux $\sigma\geq 0$, reaching a point $Q$. The other paths go to the right, with fluxes $\kappa_1, \ldots, \kappa_n >0$, at angles

until they reach points $P_1, \ldots, P_n$. This provides an irrigation plan for the measure concentrating a mass $\sigma$ at the point $Q$ and masses $\kappa_1, \ldots, \kappa_n$ at the points $P_1, \ldots, P_n$. As shown in Fig. 10, we assume that all points $P_i$ lie on the same straight line $\tilde{\gamma}$, which intersects $\gamma$ at a point $P$.

We compare this configuration with a modified irrigation plan $\tilde{\chi}$ defined as follows. First, the plan $\tilde{\chi}$ moves all the mass from the origin along the straight line $\gamma$ up to the point $P$. Then an amount of mass $\sigma$ is moved horizontally to the left, until it reaches a point $\tilde{Q}$ on the same vertical line as $Q$. The remaining mass $\kappa = \kappa_1+\cdots +\kappa_n$ is moved along the segment $\tilde{\gamma}$, until it reaches the various points $P_1, \ldots, P_n$. Notice that $\tilde{\chi}$ is an irrigation plan for a measure $\tilde{\mu}$ which concentrates a mass $\sigma$ at the point $\tilde{Q}$ and masses $\kappa_1, \ldots, \kappa_n$ at the points $P_1, \ldots, P_n$. As shown in Fig. 10, we call $\theta_a\in [0, \pi/2]$ the angle between $\gamma$ and a horizontal line, and let $\beta\in [0, \pi/2[\,$ be the angle between $\tilde{\gamma}$ and a horizontal line.

Lemma 4.2. Let the masses $\sigma\geq 0$ and $\kappa_1, \ldots, \kappa_n>0$ be given, together with angles $\theta_a\in [0, \pi/2]$ and $\theta_i\in [0, \pi/2[\,$ as in (63). Let $\chi, \tilde{\chi}$ be the irrigation plans defined above, as shown in Fig. 10. If $0<\alpha<1/2$ and $\theta_1$ satisfies the additional bound

or if $\alpha\geq 1/2$, then there exists ${\varepsilon}>0$ such that $0<\beta-\theta_1<{\varepsilon}$ implies

Proof. 1. The left-hand side of (65), describing the difference between the old and the new transportation cost, can be expressed as

where, for notational convenience, we set $P_{n+1} \doteq P$. According to (66) we can write

where

2. Notice that the quantity $A$ in (68) would describe the difference in the costs if all the mass $\kappa = \kappa_1+\cdots+\kappa_n$ were flowing through the point $P_1$. We claim that

Indeed, the last two terms within the square brackets in (70) are derived from

Using Lemma 4.1, we can now choose ${\varepsilon}'>0$ small enough such that, if

then the right hand side of (70) is strictly positive. It now suffices to observe that, given all the angles $\theta_a, \theta_1, \ldots, \theta_n$, by choosing ${\varepsilon}>0$ small enough one achieves the implication

In turn, this implies the strict inequality

3. To complete the proof of the lemma, it remains to prove that $S_n \ge 0$. This will be proved by induction on $n$. Starting from (69) and using the inequalities

we obtain

where in the second equality we have used $|P_{n-1}-P_1| = |P_{n}-P_1|-|P_{n}-P_{n-1}|$. Repeating this same argument, by induction we obtain

Observing that

the proof of the lemma is completed.

Remark 4. As soon as all the masses $\sigma, \kappa_1, \ldots, \kappa_n$ and all the angles $\theta_a, \beta, \theta_1, \ldots, \theta_n$ have been assigned, the difference between the two irrigation costs in (65) is a positive homogeneous function of the distance $|P_1-P^*|$. We can thus replace (65) with the inequality

for some $c_0>0$ depending on all the above constants. Notice that, by continuity, the bound (75) remains valid if $\theta_a$ is replaced by some other angle $\theta_a'$, with $|\theta'_a-\theta_a|$ sufficiently small.

4.1.   Completion of the proof

Let $\mu$ be an optimal measure, maximizing the functional (15), and let $\chi:\Theta\times{{\mathbb R}}_+\mapsto{{\mathbb R}}^2$ be an optimal irrigation plan for $\mu$. According to (6), we assume that all paths are parameterized by arc-length.

As remarked at the beginning of this section, a proof of Theorem 2.5 can be achieved by showing that, for an optimal solution, the point $P^* = (p_1^*, p_2^*)$ introduced at (44) must coincide with the origin. We recall that by definition we must necessarily have $p_2^* \geq 0$ since the maximal curve $\gamma$ contains the origin. Moreover, $p_2^* = 0$ implies $p_1^* = 0$, since by a projection argument, this leads to a lower irrigation cost. Throughout the following we shall thus assume $p_2^*>0$ and derive a contradiction.

1. Call

the set of particles that move through $P^*$. Notice that, by the single path property, there exists a unique path $\gamma:[0, t^*]\mapsto {{\mathbb R}}^2$ such that

As a consequence, in (76) the time $t^*$ is the same for all $\xi\in \Theta^*$.

Within the set $\Theta^*$ of all particles reaching $P^*$, we distinguish the ones which proceed to the left or to the right of $P^*$, namely

Here $\Theta_l$ denotes the set of particles that, after reaching $P^*$, move along the horizontal line $\{ (z_1, z_2);\; \; z_1 = p_1^*, \; z_2>p_2^*\}$ to the left of $P^*$. Moreover, $\Theta_r = \Theta^*\setminus\Theta_l$ is the set of particles which, after reaching $P^*$, move to the right. For all $\xi\in \Theta_r$ and $t>t^*$, we thus have

For future use, we denote

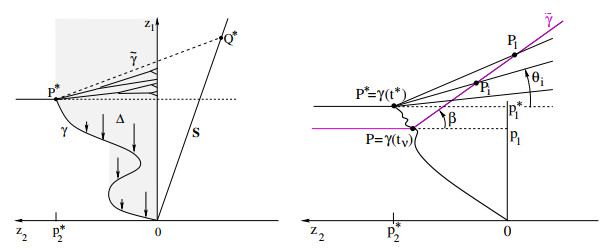
2. In connection with the path $\gamma$ at (77), consider the set (the shaded region in Fig. 11)

We claim that the measure $\mu$ cannot concentrate any mass on the open set $\Delta$. Indeed, if $\mu(\Delta)>0$, then we consider the measure $\widehat{\mu}$ obtained by vertically shifting all the mass in $\Delta$ until it touches some point on the curve $\Gamma$. More precisely, let $\phi:\Delta\mapsto \{\gamma(t); t\in [0, t^*]\}$ be a measurable map such that $\phi(z_1, z_2) = (\widehat{z}_1, z_2)$, with $\widehat{z}_1$ as in (81). Furthermore, outside the set $\Delta$ we extend the map by the identity, that is, $\phi(z_1, z_2) = (z_1, z_2)$. Let $\widehat{\mu}$ be the push-forward of the measure $\mu$ by the map $\phi$. This new measure $\mu$ would then satisfy

contradicting the optimality of $\mu$.

3. The previous argument shows that there are no sinks inside $\Delta$. Hence all particles $\xi\in \Theta_r$ continue to move to the right of $P^*$, eventually crossing the $z_1$-axis. For $\xi\in \Theta_r$ we can thus define the stopping time

and introduce the measure $\bar{\mu}$, supported on the $z_1$-axis, defined by

We observe that the restriction of $\chi$ to the set

yields an optimal transport plan from a point mass located at $P^*$ to the measure $\bar{\mu}$.

By the interior regularity property (see Theorem 8.16 in [1], or Theorem 4.10 in [19]), outside a neighborhood of the support of $\bar{\mu}$, the optimal transport plan is supported on a finite union of line segments. In particular, restricted to the set $\{ z_2 > p_2^*/2\}$, all paths $\chi(\xi, \cdot)$, with $\xi\in \Theta_r$, $t>t^*$ are contained within finitely many line segments.

4. By the previous step, within a neighborhood of $P^*$, all particle paths which move out of $P^*$ are contained in finitely many straight lines starting at $P^*$.

Adopting the same notation used in Lemma 4.2, we call $\sigma = {\hbox{meas}}(\Theta_l)$ the amount of mass which moves horizontally to the left of $P^*$. As in (63), we call $\theta_1, \ldots, \theta_n$ the angles formed by the line segments to the right of $P^*$ with a horizontal line (see Fig. 11, right). The fluxes along these line segments are denoted by $\kappa_1, \ldots, \kappa_n$. We introduce the decomposition

where $\Theta_i$ denotes the set of particles $\xi\in \Theta_r$ that move along the $i$-th segment. Notice that, with this notation, one has $\kappa_i = {\hbox{meas}}(\Theta_i)$.

We recall that, by Lemma 3.5, all particle paths $\chi(\xi, t)$, $\xi\in \Theta_r$, lie below the segment $\gamma^*$ with endpoints $P^*$, $Q^*$. This implies that all angles $\theta_1, \ldots, \theta_n$ are strictly smaller than ${\pi\over 2}-\theta_0$. By the assumption (17), we are led to consider two cases.

Case 1: $1/2\leq \alpha\leq 1$ and $0\leq \theta_1<\pi/2$,

Case 2: $0<\alpha< 1/2$ and

5. In this step, under the assumption that $p_2^*>0$, we construct a competing measure $\tilde{\mu}$. Using Lemma 4.2, this will eventually allow us to conclude that the measure $\mu$ is not optimal.

For $t<t^*$, consider the unit vector

By compactness, there exists an increasing sequence $t_\nu\to t^*-$ such that

for some unit vector ${\bar{\bf {w}}} = \; ({\bar{w}}_1, {\bar{w}}_2)$, with ${\bar{w}}_1\leq 0$, ${\bar{w}}_2\leq 0$. Call $\theta_a\in [0, \pi/2]$ the angle between ${\bar{\bf {w}}}$ and a horizontal line.

In connection with the masses $\sigma, \kappa_1, \ldots, \kappa_n$ and the angles $\theta_1, \ldots, \theta_n$ defined above, we now choose an angle $\beta>\theta_1$, sufficiently close to $\theta_1$, so that the conclusion of Lemma 4.2 holds. In particular, by Remark 4 the inequality (75) holds.

Next, we choose $\nu\geq 1$ sufficiently large (its precise value will be determined later), and consider the point $P = (p_1, p_2) = \gamma(t_\nu)$. Again referring to Fig. 11, right, we denote by $\tilde{\gamma}$ the straight line through $P$, forming an angle $\beta$ with a horizontal line. As in Lemma 4.2, we denote by $P_1, \ldots, P_n$ the points where $\tilde{\gamma}$ intersects the line segments through $P^*$, forming angles $0\leq \theta_n<\cdots <\theta_1$ with a horizontal line.

A new measure $\tilde{\mu}$ and a new irrigation plan $\tilde{\chi}$ are now defined as follows.

● The measure $\tilde{\mu}$ is obtained from $\mu$ by vertically shifting all the mass located on the horizontal line to the left of $P^*$ downward on the horizontal line to the left of $P$. More precisely, $\tilde{\mu}$ is the push-forward of $\mu$ by the map

● Recalling (78), for $\xi\notin \Theta^*$ we simply set $\tilde{\chi}(\xi, t) = \chi(\xi, t)$ for all $t\geq 0$.

● Particles $\xi\in \Theta_l$ move along the path $\gamma$ up to the point $P$. Then the move horizontally to the left of $P$, stopping at a point $\tilde{\chi}(\xi, \tilde{T}(\xi))$ on the same vertical line as $\chi(\xi, T(\xi))$.

● Particles $\xi\in \Theta_r$ move along the path $\gamma$ up to the point $P$. Then they move along $\tilde{\gamma}$ until they reach the corresponding points $P_1, \ldots, P_n$. Afterwards, the remaining portions of their trajectories are exactly as before.

6. By construction we have ${{\mathcal S}}^{{\bf n}}(\tilde{\mu}) = {{\mathcal S}}^{{\bf n}}(\mu)$. To analyze the cost of the new irrigation plan $\tilde{\chi}$, consider the set

This is the set of particles that go through $P$, but do not reach $P^*$ afterwards: either they stop along $\gamma$, or they move to some other branch bifurcating from $\gamma$ before reaching $P^*$.

We observe that, in the case where $\Theta^\dagger_\nu = \emptyset$, one can immediately apply Lemma 4.2 and conclude

The following analysis will show that the same conclusion can still be reached, provided that $P$ is sufficiently close to $P^*$ and

is sufficiently small. For future use, we observe that

We are now ready to estimate the difference between the two irrigation costs, in the general case.

(1) For $\xi\notin \Theta^*\cup\Theta^\dagger_\nu$, we have

for all $t>0$. Hence these particles do not contribute to the difference in the transportation cost.

(2) For $\xi\in\Theta^\dagger_\nu$, the first identity in (88) still holds for all $t>0$. However, the second one holds only for $t\notin [t_\nu, \tau(\xi)]$, where

is the time when the particle $\xi$ either stops, or leaves the path $\gamma$. We estimate the difference

(3) It remains to estimate the difference in the cost for transporting particles $\xi\in \Theta^*$, namely

The estimate of $B$ is based on the following observation. If the portion of the curve $\gamma$ between $P$ and $P^*$ were a straight segment, and if on this segment the multiplicity were constantly equal to $\sigma + \kappa$, then we could use Lemma 4.2 and Remark 4. By (75) we could thus conclude

In the general case, recalling (86), the multiplicity along $\gamma$ is estimated by

The presence of the additional particles $\xi\in \Theta^\dagger_\nu$ increases the multiplicity and hence reduces the cost of $\chi$. The amount by which this cost is reduced can be bounded above by

On the other hand, the fact that the curve $\gamma$ is not necessarily a straight line increases the cost of $\chi$ in an amount which is bounded below by

Combining all the previous observations, from (89), (91), (92), and (93), we conclude

We claim that, for some choice of $\nu\geq 1$ large enough, the right hand side of (94) becomes negative, thus contradicting the optimality of the measure $\mu$. We consider two cases.

Case 1: $(t^*-t_\nu)\leq 2 |\gamma(t_\nu) -P^*|$ for infinitely many integers $\nu\geq 1$. When this inequality holds, (94) yields

We now observe that the limit (84) implies an inequality of the form

for a suitable constant $C$ and all $\nu$ sufficiently large. Therefore, as $\delta_\nu\to 0$, it is clear that the right hand side of (95) becomes negative. This contradicts the optimality of $\mu$.

Case 2: $(t^*-t_\nu)\geq 2 |\gamma(t_\nu) -P^*|$ for infinitely many integers $\nu\geq 1$. When this inequality holds, (94) yields

When $\delta_\nu$ is sufficiently small, the right hand side of (96) becomes negative. Once again, this contradicts the optimality of $\mu$.

5.   The case $d=2$, $\alpha=0$

We give here a proof of Theorem 2.6.

1. Assume that there exists a unit vector ${{\bf w}}^*\in {{\mathbb R}}^2$ such that

Let ${{\bf v}} = (\cos \beta, \sin\beta)$ be a unit vector perpendicular to ${{\bf w}}^*$, with $\beta\in[0, \pi]$. Let $\mu$ be the measure supported on the segment $\{r{{\bf v}}\, ;\; r\in [0, \ell]\}$, with constant density $\lambda$ w.r.t. 1-dimensional Lebesgue measure.

Then the payoff achieved by $\mu$ is estimated by

By choosing $\lambda>0$ large enough, the first factor on the right hand side of (97) is strictly positive. Hence, by increasing the length $\ell$, we can render the payoff arbitrarily large.

2. Next, assume that $K\leq c$. Consider any Lipschitz curve $s\mapsto \gamma(s)$, parameterized by arc-length $s\in [0, \ell]$. Then, for any measure $\mu$ supported on $\gamma$, the total amount of sunlight from the direction ${{\bf n}}$ captured by $\mu$ satisfies the estimate

Indeed, it is bounded by the length of the projection of $\gamma$ on the line $E_{{\bf n}}^\perp$ perpendicular to ${{\bf n}}$. Integrating over the various sunlight directions, one obtains

More generally, $\mu = \sum_i \mu_i$ can be the sum of countably many measures supported on Lipschitz curves $\gamma_i$. In this case, since the sunlight functional is sub-additive, one has

Hence

This concludes the proof of case (ⅱ) in Theorem 2.6.

6.   Concluding remarks

We first clarify the role of the assumption (17), used in Theorem 2.5 when $0<\alpha<1/2$.

Consider the problem of irrigating two masses $M_0, M_1>0$ from the origin. Then, as shown in Fig. 12, left, the optimal bifurcation angle satisfies

For a proof, see Lemma 12.2 of [1]. As a consequence, we have the implications

Notice that $\cos\theta = 2^{2\alpha-1} -1$ when $M_0 = M_1$ and hence $\lambda = 1/2$. As a consequence, regardless of the relative sizes of $M_0, M_1$, we have:

● When $\alpha\geq 1/2$, a bifurcation with an angle $\theta>\pi/2$ cannot be optimal.

● When $\alpha< 1/2$, a bifurcation with an angle $\theta$ such that $\cos\theta < 2^{2\alpha-1}-1$ cannot be optimal.

This is the underlying motivation for the assumption (17), repeatedly used in the proofs. Notice that a similar assumption (54) was introduced in Lemma 4.1.

It is interesting to speculate whether the conclusion of Theorem 2.5 may still hold when $\alpha<1/2$ while the angle $\theta_0>0$ is arbitrarily small. Consider any measure $\mu$ supported on the two half-lines $\Gamma_0\cup\Gamma_1$ as shown in Fig. 12, right. The necessary conditions derived for the problem (18) allow us to compute the total mass concentrated by the measure $\mu$ on each of these half-lines. Indeed, according to (26) and (27), we have

Therefore

In order for this configuration to be optimal, a necessary condition is

Indeed, if (101) fails, a better configuration could be constructed as shown in Fig. 12, right. Here $A$ and $B$ are points along $\Gamma_0$ and $\Gamma_1$ respectively, at distance ${\varepsilon}>0$ from the origin, while $P$ is a suitable point such that the angle between $PA$ and $PB$ equals $\theta$. To uniquely determine $P$, we again refer to the necessary conditions in Lemma 12.2 of [1]. Replacing the segments $0A$ and $0B$ with the three segments $0P$, $PA$, and $PB$, we can obtain a new configuration where the transportation cost is reduced by ${{\mathcal O}}(1)\cdot {\varepsilon}$, while keeping the same value of the sunlight functional. Therefore, our initial configuration where the measure $\mu$ is supported on $\Gamma_0\cup\Gamma_1$ would not be optimal.

The inequality (101) is precisely what is needed to rule out this possibility. Namely, if (101) holds, then the point $P$ cannot lie inside the sector bounded by $\Gamma_0$ and $\Gamma_1$. Recalling (100), we can write (101) in the form

Equivalently:

We observe that $\phi(0) = 0$ while $\phi(1) = -2$. In addition,

for $0 < \lambda < 1$. This implies that $\phi(\lambda) < 0$ for $0 < \lambda < 1$. Therefore, the necessary conditions for optimality (101) are always satisfied, even when the angle $\theta_0$ is very small.

We conclude this paper by discussing possible extensions of our results.

(I) Motivated by the previous analysis, we conjecture that the conclusion of Theorem 2.5 remains valid even without the assumption (17). Namely, for all $0<\alpha<1/2$ and every $\theta_0\in [0, \pi/2]$, the optimal measure $\mu$ is still supported on the union of the two rays $\Gamma_0\cup\Gamma_1$. To achieve a proof, however, an additional argument will be needed. More specifically, the assumption (54) in Lemma 4.1 can be removed only by imposing some additional restriction on the value of $\lambda = {\sigma\over \kappa+\sigma}\in [0, 1]$. Our construction in Section 4, however, does not yield such information.

(II) In Theorem 2.5 it was assumed that sunlight comes from one single direction. In the case considered at (4), where sunlight comes with varying intensity from different directions, one may conjecture that a similar result still holds true. This guess seems very reasonable if the support of the function $\eta\in {{\bf L}}^1(S^1)$ is contained within a small sector, say $[\theta_0-\delta, \theta_0+\delta]$. We remark, however, that proving such a result will require a substantially different approach. In the proof of Theorem 2.5, we repeatedly used the fact (highlighted in Remark 1) that, shifting part of the mass of $\mu$ along the direction ${{\bf n}}$ of sunlight, one obtains a new measure $\tilde{\mu}$ which collects exactly the same amount of sunlight: ${{\mathcal S}}^{{\bf n}}(\tilde{\mu}) = {{\mathcal S}}^{{\bf n}}(\mu)$. This crucial property fails as soon as we replace ${{\mathcal S}}^{{\bf n}}$ with ${{\mathcal S}}^\eta$, allowing sunlight to come from different directions.

(III) It would be interesting to analyze the optimal branch configuration in three space dimensions. To fix ideas, assume that sunlight comes from the direction parallel to ${{\bf n}} = (\cos\theta_0, 0, \sin\theta_0)$, and call ${{\bf e}} = (0, 0, 1)$ the unit vector in the vertical direction. Then it is easy to see that the optimal measure $\mu$ must be supported within the convex closure of the two half-planes

In addition, the Hausdorff measure of Supp$(\mu)$ must be $\geq 2$. Otherwise, the collected sunlight would be ${{\mathcal S}}^{{\bf n}}(\mu) = 0$. A challenging question is whether the support of $\mu$ is indeed contained in a two-dimensional surface. In this case, the optimal irrigation plan should have a structure similar to the one studied in [16].

Acknowledgments

The research of the first author was partially supported by NSF with grant DMS-1714237, "Models of controlled biological growth". The research of the second author was partially supported by a grant from the U.S.-Norway Fulbright Foundation.