Analysis of a deterministic-stochastic oncolytic M1 model involving immune response via crossover behaviour: ergodic stationary distribution and extinction

1.   Introduction

In natural and social systems, an individual's strategy is often shaped by complex game processes that influence not only personal outcomes but also the evolutionary trajectory of group behavior ^[1,2,3,4]. The dynamic equilibrium between cooperation and defection significantly impacts the system's long-term stability. However, maintaining cooperation is challenging under limited resources and competitive pressure, particularly when defection yields short-term gains ^[5,6,7,8]. Researchers are focusing on mechanisms such as rewards to promote cooperation or punishments to deter defection ^[9,10]. Understanding the dynamic balance between cooperation and defection, and the factors that affect this balance, is crucial for developing effective incentive policies and sustaining stable cooperative relationships. This issue is both a theoretical and practical challenge with broad implications for economics ^[11], sociology ^[12], and biology ^[13].

In the past, most of the classical game theory simply considered the change of strategy, but now more and more researchers are beginning to address the influence of the surrounding environment on strategy. Strategy and environment change and interact with each other ^[14,15]. Individual strategies within a group can alter the environmental state, which in turn affects subsequent strategy choices. Environmental feedback is a crucial factor influencing participant behavior and the evolution of group dynamics. For instance, plants' nitrogen fixation strategies can change soil nitrogen content ^[16], and over time, this nitrogen content influences plant selection strategies. In microbial communities, collaborators produce enzymes to decompose nutrients for microorganisms. Conversely, changes in nutrient availability affect whether microorganisms choose to collaborate ^[17]. Positive environmental feedback following a decision increases the likelihood of that decision being repeated, thereby raising the group's adoption rate of the strategy. Rewarding cooperators is one of the most direct ways to promote individual selection and cooperation in the population ^[18,19]. Li et al. explored the influence of reciprocal rewards on cooperative evolution in the dilemma of voluntary society by adding the third strategy, the loner strategy ^[20]. Besides, it is also interesting to study different game models in the complex network structure ^[21,22]. In previous studies, the reward for collaborators was treated as a constant. However, in real life, cooperative reward can change with the change of collaborators and betrayers in the population. It has been verified that dynamic reward is more beneficial to cooperation than fixed reward in the game of space public goods^[23].

Time delay plays a significant and complex role in systems^[24,25]. It not only influences the response speed and stability of the system but also plays a crucial role in its dynamic behavior and long-term regulation ^{[26,27,28,29]}. It takes time to complete many biological processes, which leads to time lag. Biological systems often experience various types of delays, such as latency delays ^[30] and growth delays ^[31]. Despite numerous studies attempting to reveal the dynamic characteristics and stability conditions of cooperation and defection strategies in game models, most models assume immediate payoff feedback, neglecting the delay effects present in many real-world scenarios. Tao and Wang incorporated time delay into an evolutionary game model with two strategies, finding that it influences the stability of equilibria. They analyzed the stability conditions for both systems with and without time delay ^[32]. Khalifa et al. studied how discrete and distributed delays affect evolutionary stable strategies. They found that evolutionary stable strategies are asymptotically stable regardless of the rate parameters under an exponential delay distribution ^[33].

Therefore, this paper not only considers that the reward intensity can be affected by the strategic proportion, but also further explores the role of time delay in the feedback game system through the replicator equation ^[34,35]. In section 2, a feedback game system is constructed for the classical payoff matrix, and the existence and stability of the equilibrium points of the system without time delay and the conditions for the system to experience transcritical bifurcation are analyzed. In section 3, we consider the payoff delay and find the critical delay of Hopf bifurcation in time-delay systems. In section 4, we explore the related properties of hopf bifurcation. Numerical simulation and biological significance analysis of strategic dynamics are exhibited in section 5. The sixth section summarizes the paper and presents future prospects.

2.   Model and results without time delay

This section investigates an infinitely mixed group, in which the payoff matrix of cooperative strategy and defective strategy is the classical payoff matrix as follows

where non-negative parameters $a$ and $b$ represent the payoffs of the collaborator meeting the collaborator and the betrayer, respectively. Non-negative parameters $c$ and $d$ represent the payoffs of the betrayer meeting the collaborator and the betrayer, respectively.

To incentivize cooperators to enhance their cooperative efforts, they will be rewarded with an additional amount $r$ on top of their original payoff. This adjustment modifies the payoff matrix to

Let the proportion of cooperators among the participants be $x\left (t\right)$, and the proportion of defectors be $y\left (t\right)$. According to the matrix (2.2), the payoff equations for cooperators and defectors are given by

Then according to the replicator equation, we have

where $\bar{f}\left (t\right) = \pi _{C}\left (t\right)x\left (t\right)+\pi _{D}\left (t\right)y\left (t\right)$.

Here, we assume that the reward intensity $r$ is a variable that changes over time, ranging from a minimum value of $0$ to a maximum value of $m$. To more effectively promote cooperation, the reward for cooperators is influenced by the proportions of defectors and cooperators within the population. Specifically, the presence of more defectors increases the reward for cooperators, while a higher proportion of cooperators decreases the reward. In other words, as the number of defectors rises, the reward for cooperators increases. Therefore the dynamic equation for reward intensity is described by

where $u_{1}$ and $u_{2}$ represent the growth rates of defectors and cooperators, respectively. Letting $\beta = \frac{u_{1}}{u_{2}}$, we have

In the above equations, $\pi _{C}\left (t\right)$ and $\pi _{D}\left (t\right)$ represent the payoffs of the group that chooses to cooperate and defect in the population, respectively, and $\bar{f}\left (t\right)$ represents the average payoff. We eliminate $y\left (t\right) = 1-x\left (t\right)$, substitute Eq (2.4) into the above equation, and combining with the reward intensity Eq (2.6), where $\epsilon$ indicates the relative speed between the influence reward intensity and the strategy. The inequality $\epsilon < 1$ ($\epsilon > 1$) means that the strategy evolves faster (slower) than the reward intensity. So we obtain a high-order evolutionary game system with reward feedback and the classical payoff matrix as follows:

2.1.   Existence and stability of numerous equilibrium points

The system (2.7) may have seven equilibrium points: $E_{1}\left (0, 0\right)$, $E_{2}\left (0, m\right)$, $E_{3}\left(1, m\right)$, $E_{4}\left(1, 0\right)$, $E_{5}\left (x_{5}, 0\right)$, $E_{6}\left (x_{6}, m\right)$, and $E_{7}\left (x_{7}, r_{7}\right)$, where $x_{5} = \frac{d-b}{a-b-c+d}$, $x_{6} = \frac{d-b-m}{a-b-c+d}$, $x_{7} = \frac{\beta}{\beta+1}$, and $r_{7} = \frac{d-b-\beta a+\beta c}{\beta +1}$. Obviously, $E_{1}$, $E_{2}$, $E_{3}$, and $E_{4}$ always exist.

Define

where $x_{5}, x_{6},$ and $x_{7}\in(0, 1)$ and $r_{7}\in(0, m)$ in the game.

For the equilibrium point $E_{5}$, we have $\frac{d-b}{a-b-c+d} \in (0, 1)$. Thus, $E_{5}$ exists when $(a-c)(b-d)< 0$, that is, $H_{1}$ holds.

For the equilibrium point $E_{6}$, we have $\frac{d-b-m}{a-b-c+d} \in (0, 1).$ Thus, $E_{6}$ exists when $(a-c+m)(b-d+m)<0$, that is, $H_{2}$ holds.

For the equilibrium point $E_{7}$, given $\frac{\beta}{\beta+1} \in (0, 1)$ and $\frac{d-b-\beta a+\beta c}{\beta +1} \in (0, m),$ we obtain $0 < d-b-\beta a+\beta c < m(\beta+1),$ that is, $H_{3}$ and $H_{4}$ hold.

Thus the existence of equilibria is summarized as follows:

Lemma 2.1. (1) The boundary equilibria $E_{1}$, $E_{2}$, $E_{3}$, and $E_{4}$ always exist.

(2) $E_{5}(x_{5}, 0)$ exists when $H_{1}$ holds.

(3) $E_{6}(x_{6}, m)$ exists when $H_{2}$ holds.

(4) $E_{7}(x_{7}, r_{7})$ exists when $H_{3}$ and $H_{4}$ hold.

Next, we determine the stability conditions for the above seven equilibria. The Jacobian matrix of system (2.7) is known to be

The stability of the equilibrium points can be assessed by examining the real parts of the eigenvalues of the Jacobian matrix evaluated at those equilibrium points.

The following theorem is utilized to elucidate the local stability of system (2.7).

Theorem 2.1. (1) The equilibrium $E_{1}$ is always unstable.

(2) $E_{2}$ is locally asymptotically stable when $H_{5}$ is true.

(3) $E_{3}$ is always unstable.

(4) $E_{4}$ is locally asymptotically stable when $H_{6}$ is true.

(5) $E_{5}$ is locally asymptotically stable when $H_{3}$ is not true and $H_{7}$ is true.

(6) $E_{6}$ is locally asymptotically stable when $H_{4}$ is not true and $H_{7}$ is true.

(7) $E_{7}$ is locally asymptotically stable when $H_{7}$ is true.

Proof. (1) The Jacobian matrix at $E_{1}$ is

We obtain $\lambda_{11} = b - d$ and $\lambda_{12} = \epsilon m\beta$. It is easy to see that $E_{1}$ is unstable since $\lambda_{12} > 0$.

(2) The matrix (2.8) at the equilibrium point $E_{2}$ is

Given that $\lambda_{21} = b - d+m$ and $\lambda_{22} = -\epsilon m\beta$, $E_{2}$ is locally asymptotically stable when $H_{5}$ is satisfied.

(3) The matrix (2.8) at the equilibrium point $E_{3}$ is

We obtain $\lambda_{31} = c - a - m$ and $\lambda_{32} = \epsilon m>0$. So $E_{3}$ is unstable.

(4) The matrix (2.8) at $E_{4}$ is

It is easy to see that $\lambda_{41} = c-a$ and $\lambda_{42} = -\epsilon m < 0$. Therefore, $E_{4}$ is locally asymptotically stable when $H_{6}$ is true.

(5) The matrix (2.8) at $E_{5}$ is

where $j_{51} = -\frac{(d-b)(c-a)}{{a-b-c+d}}$, $j_{52} = -\frac{(d-b)(c-a)}{{(a-b-c+d)}^{2}}$, and $j_{53} = \frac{\epsilon m(d-b-\beta a+\beta c)}{b+c-a-d}$.

Thus, given that $\lambda_{51} = j_{51}$ and $\lambda_{52} = j_{53},$ the equilibrium $E_{5}$ is locally asymptotically stable when condition $H_{7}$ is true and $H_{3}$ is not.

(6) For system (2.7) at $E_{6}$, the Jacobian matrix (2.8) is

where $j_{61} = -\frac{(d-b-m)(c-a-m)}{{a-b-c+d}}$, $j_{62} = -\frac{(d-b-m)(c-a-m)}{{(a-b-c+d)}^{2}}$, and $j_{63} = -\frac{\epsilon m(d-b-\beta a+\beta c-m\beta -m)}{b+c-a-d}$. Thus, given that $\lambda_{61} = j_{61}$ and $\lambda_{62} = j_{63},$ the equilibrium point $E_{6}$ is locally asymptotically stable when $H_{7}$ is true and $H_{4}$ is not.

(7) The Jacobian matrix of sysytem (2.7) at $E_{7}$ is

where $j_{71} = \frac{(-a-b+c+d-2r)\beta^{2}+(2a-3b-2c+3d-r)}{(\beta+1)^{2}})$, $j_{72} = \frac{\beta}{(\beta+1)^{2}}$, and $j_{73} = -\epsilon \frac{(d-b-\beta a+\beta c)(m\beta+m-d+b+\beta a-\beta c)}{\beta+1}.$ One has

If $\text{Det}(J_{7}) > 0$ and $\text{tr}(J_{7}) < 0$, at this time, $a-b-c+d < 0$, that is, $H_{7}$ is true. Therefore, $E_{7}$ is locally asymptotically stable when $H_{7}$ is true. □

In summary, Table 1 provides a recap of the information discussed above.

Thus the bistability of the equilibrium points can be obtained.

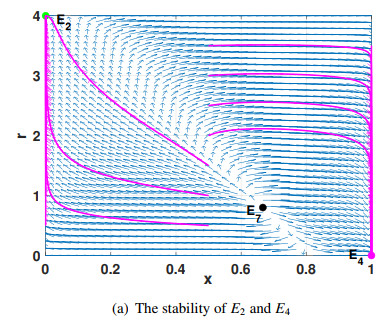
Theorem 2.2. When conditions $H_{5}$ and $H_{6}$ are both true, the equilibrium points $E_{2}$ and $E_{4}$ are stable.

2.2.   Bifurcation analysis

Next, we use the Sotomayor theorem to explore the bifurcation scenarios of system (2.7) ^[36].

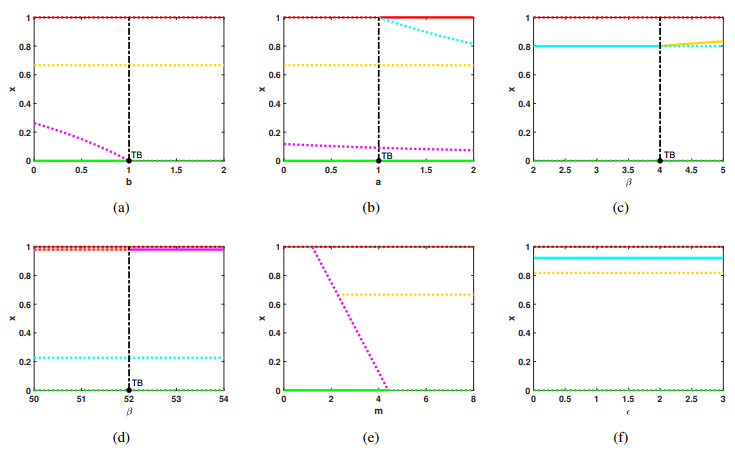
Theorem 2.3. (1) When the cooperator meets the defector, the payoff of the cooperator is $b = b^{*} = d - m$, and a transcritical bifurcation occurs at $E_{2}$.

(2) When a cooperator meets the cooperator, the payoff of the cooperator is $b \ne d$ and $a = a^{*} = c$, and a transcritical bifurcation occurs at $E_{4}$.

(3) When the ratio of the defective strategy promotion reward to the cooperator inhibition reward is $\beta = \beta^{*} = \frac{d - b}{a - c}$, a transcritical bifurcation occurs at $E_{5}$.

(4) When $\beta = \beta^{**} = \frac{d - b - m}{a - c + m}$, a transcritical bifurcation occurs at $E_{6}$.

Proof. (1) The Jacobian matrix $J_{2}$ has eigenvalues $\lambda_{21} = b - d + m$ and $\lambda_{22} = -\epsilon m\beta$. Let $\lambda_{21} = 0$, and we get $b = b^{*} = d - m$, and at this time $\lambda_{22} < 0$. In this case, the eigenvectors corresponding to the zero eigenvalue for $J_{2}$ and $J_{2}^{T}$ are

We rewrite Eq (2.7) as

Then we get

and

Further, we have

Therefore, when $b = b^{*} = d - m$, a transcritical bifurcation occurs at $E_{2}$.

(2) According to the the Jacobian matrix $J_{4}$, it has eigenvalues $\lambda_{41} = c - a$ and $\lambda_{42} = -\epsilon m$. Let $\lambda_{41} = 0$, and we get $a = a^{*} = c$, that is $\lambda_{2} < 0$. The eigenvectors corresponding to the eigenvalue $0$ for $J_{4}$ and $J_{4}^{T}$ are

Thus one has

and

Further, we have

Therefore, when $b \neq d$ and $a = a^{*} = c$, a transcritical bifurcation occurs at $E_{4}$.

(3) The Jacobian matrix $J_{5}$ has eigenvalues $\lambda_{51} = \frac{\epsilon m(d-b-\beta a+\beta c)}{b+c-a-d}$ and $\lambda_{52} = -\frac{(d-b)(c-a)}{a-b-c+d}$. Let $\lambda_{51} = 0$, that is $d-b-\beta a+\beta c = 0$, and we get $\beta = \beta^{*} = \frac{d-b}{a-c}$. At this time, $\lambda_{2} < 0$. The eigenvectors corresponding to the eigenvalue $0$ for $J_{5}$ and $J_{5}^{T}$ are

Thus we have

and

where $L = -\frac{2(x+1)}{a-b-c+d}+\frac{2(a-2b-c+2d)}{(a-b-c+d)^{2}}$.

Further, we have

Hence, when $\beta = \beta^{*} = \frac{d-b}{a-c}$, a transcritical bifurcation occurs at $E_{5}$.

(4) The Jacobian matrix at $E_{6}$ has eigenvalues $\lambda_{61} = -\frac{\epsilon m(d-b-\beta a+\beta c-m\beta -m)}{b+c-a-d}$ and $\lambda_{62} = -\frac{(d-b-m)(c-a-m)}{a-b-c+d}.$ Let $\lambda_{61} = 0$, that is $d-b-\beta a+\beta c -m\beta - m = 0$, and we get $\beta = \beta^{**} = \frac{d-b-m}{a-c+m}$. At this time, $\lambda_{62} < 0$. The eigenvectors corresponding to the zero eigenvalue for $J_{6}$ and $J_{6}^{T}$ are

Then one has

and

Similarly, the calculation of $D^{2}F_{\beta}(E_{6}, \beta^{**})$ follows the same method as above. Substituting the values of $E_{6}$ and $\beta^{**}$ yields

We have

Therefore, when $\beta = \beta^{**} = \frac{d-b-m}{a-c+m}$, a transcritical bifurcation occurs at $E_{6}$. □

3.   Model and results with time delay

In the real world, games are not instantaneous and involve time delays, such as a payoff time delay and feedback time delay. This section introduces the concept of a payoff time delay, denoted as $\tau$, which represents the time required for players to realize revenue during the game. In other words, a player's income at time $t$ depends on the proportion of players at time $(t-\tau)$. Consequently, the average expected payoffs for cooperation and defection strategies are, respectively,

Based on the replicator equation, the evolutionary game system with reward feedback and a time delay is described by

Theorem 3.1. For the time-delay system (3.2),

(1) when $\tau\in(0, \tau_{k})$, system (3.2) is stable at $E_{7}$,

(2) when $\tau\in(\tau_{k}, +\infty)$, system (3.2) is unstable at $E_{7}$,

(3) when $\tau = \tau_{k}$, system (3.2) incurs a Hopf bifurcation at $E_{7}$.

Proof. Linearizing system (3.2) at the equilibrium point $E_{7}$, we obtain

where

From the second equation of the system (3.2), we obtain

Differentiating the above equation can get

Substituting Eqs $(3.4)$ and $(3.5)$ into the first equation of the system $(3.2)$, one has

Letting $r = {e}^{\lambda t}$ and substituting into the above equation, the following characteristic equation can be obtained:

Let

Then we obtain the simplified form of the characteristic equation:

Let $\lambda = i\omega$, and then Eq (3.8) become

Substituting ${e}^{-i\omega \tau} = \cos(\omega\tau)-i\sin(\omega\tau)$ into Eq $(3.9)$, one has

Then we obtain

Taking the square sum of the two equations in the above system yields

Let $\bar{\omega} = \omega^{2}$, and substituting into the above equation, we obtain

If $s_{2}^{2}-s_{3}^{2} < 0$ is true, then Eq (3.12) has at least one positive root $\bar{\omega}$,

According to the above equation, one has

Furthermore, from the system of Eq (3.10), we have

Then the critical time delay is

□

The following lemma proves that $\tau$ satisfies the transversal condition of bifurcation.

Lemma 3.1. If $s_{2}^{2}-s_{3}^{2} < 0$ holds, then

Proof. According to Eq (3.8), we have

Then

Substituting $\lambda = i\omega$ into the above equation results in

Therefore, its real part is

Substituting the value from Eq (3.16) into the above equation leads to

Then

□

4.   Stability and direction of Hopf bifurcation

Next, we explore various properties of Hopf bifurcation including direction, stability, and period changes^[37].

Theorem 4.1. For system (3.2) with time delay,

(1) the Hopf bifurcation is supercritical (subcritical) when $\iota > 0\ (\iota < 0),$

(2) the bifurcating periodic solution is stable (unstable) if $\chi < 0\ (\chi > 0)$,

(3) when $\varkappa > 0\ (\varkappa < 0)$, the period increases (decreases).

The values of $\iota$, $\chi$, and $\varkappa$ are given by Eq (4.2) below.

Proof. Let $\dot{x}\left (t\right) = x\left (t\right)-x_{7}$, $\dot{r}\left (t\right) = r\left (t\right)-r_{7}$, and $\tau = \tau_{0}+\upsilon \in \mathbb{R}$. System (3.2) is rewritten as

where $Z(t) = (x(t), r(t))^{T}\in \mathbb{R}^{2}$, $L_{\upsilon }: C \to \mathbb{R}$, and $S : \mathbb{R} \times C \to \mathbb{R}$ are given by $L_{\upsilon }(\varphi) = (\tau_{0}+\upsilon)J_{7}\varphi (-1)$, $S(\upsilon, \varphi) = (\tau_{0} + \upsilon)(S_{1}, S_{2})^{T}$, and $\varphi = (\varphi _{1}, \varphi _{2})^{T}$. $S_{1}$ and $S_{2}$ are

where

We have a bounded variational function $\kappa (\gamma, \upsilon), (\gamma \in \left [0, 1\right])$, according to the Riesz representation theorem, satisfying

Next

and

Define

and

System (4.1) is rewritten as

where $Z_{t}(\gamma) = Z(t+\gamma) \in C, \gamma \in [-1, 0]$. For $\phi \in C([0, 1], R^{2*})$, we get

and

where $\kappa(\gamma) = \kappa(\gamma, 0)$. $P = P(0)$ and $P^{*}$ are adjoint operators. Since for eigenvalue $i\omega_{0}\tau_{0}$, the eigenvector of $P(0)$ is $v(\gamma) = (1, v_{7})^{T}\mathrm{e}^{i\omega_{0}\tau_{0}\gamma }$ and the eigenvector of $P^{*}$ is $v^{*}(q) = U(1, v_{7}^{*}) e^{i\omega_{0}\tau_{0}q}$ when the eigenvalue is $-i\omega_{0}\tau_{0}$, we have $\left \langle v^{*}(q), v(p)\right \rangle = 1$ and

One has

and

The values of $\Omega_{1}$ and $\Omega_{2}$ are given by

Therefore, we define

The proof of this theorem is complete. □

5.   Numerical simulation and analysis

This section uses numerical simulations to confirm the previous theoretical derivations, and analyzes its biological significance.

5.1.   Non-delay system

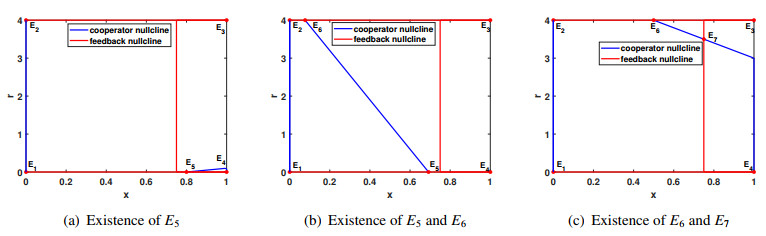
Figure 1 exhibits the equilibrium points of system (2.7) under varying parameter settings. The equilibrium points $E_{1}$, $E_{2}$, $E_{3}$, and $E_{4}$ consistently exist across all parameter configurations. Specifically, the parameters depicted in Figure 1(a) satisfy the conditions necessary for the existence of $E_{5}$. Figure 1(b) demonstrates the presence of both $E_{5}$ and $E_{6}$, while Figure 1(c) reveals the existence of $E_{6}$ and $E_{7}$.

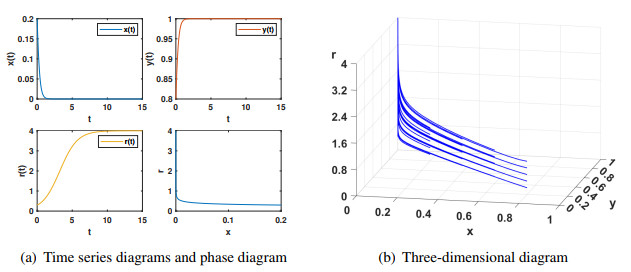
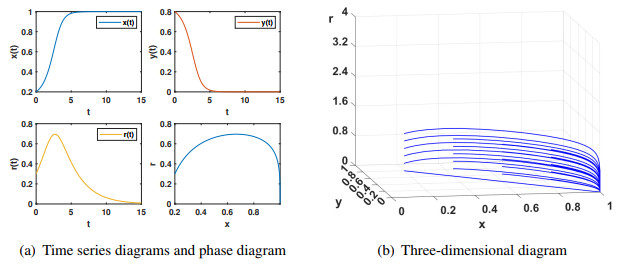
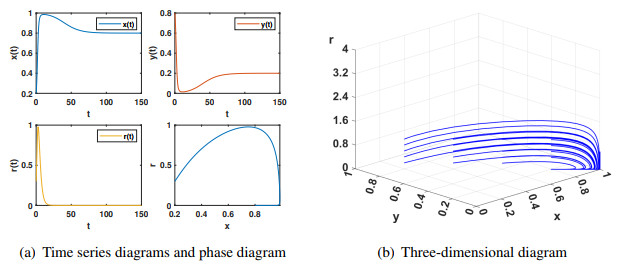
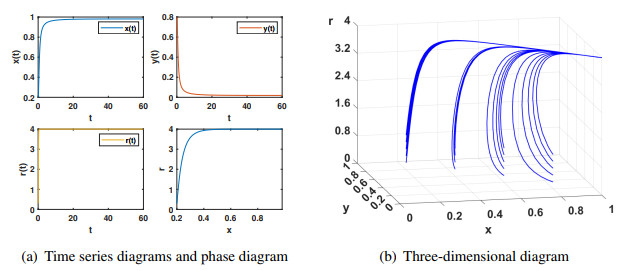
Subsequent figures, Figures 2–6, depict the stabilization of system (2.7) at the equilibria $E_{2}$, $E_{3}$, $E_{4}$, $E_{5}$, $E_{6}$, and $E_{7}$, respectively. Irrespective of the initial conditions, the system consistently converges to a stable equilibrium point, in accordance with Theorem 2.1. The analysis reveals that the stable values of cooperation strategy and reward intensity vary with different parameter settings. By tuning these parameters, one can achieve the desired proportions of cooperation strategy and reward intensity. It shows five different situations: defectors and reward intensity dominate, cooperators exist independently and stably, cooperators and defectors coexist, and reward intensity reaches the maximum, and defectors, cooperators, and reward intensity coexist. When the reward intensity reaches the maximum, there is a phenomenon that no player chooses to cooperate, as shown in Figure 2. Notably, when the reward intensity is minimized, the cooperation strategy can potentially reach its maximum, as illustrated in Figure 3. Similarly, Figure 6 shows that cooperators, defectors, and reward intensity can reach a stable coexistence state. This is conducive to maintaining population diversity.

Figure 7 illustrates the bistable phenomenon of equilibrium points $E_{2}$ and $E_{4}$. We observe that the final stable equilibrium point of system (2.7) is influenced by the initial states. Different initial values result in the system converging to various equilibrium points. At this stage, the maximum value of the cooperator is influenced by the initial condition of the number of collaborators and reward intensity. This indicates that even when the reward intensity reaches its maximum, the proportion of the cooperation strategy can still be zero due to the different initial values.

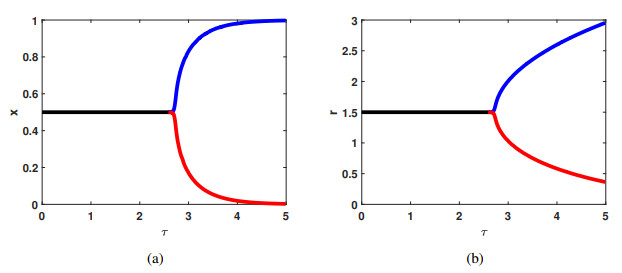
Theorem 2.3 is illustrated in Figure 8. Figure 8 provides a clear depiction of the state of each equilibrium point. In Figure 8(a), the equilibrium point $E_{2}$ transitions from stable to unstable. Figure 8(b) shows that the equilibrium point $E_{4}$ initially exhibits instability but becomes stable subsequently; additionally, a bistable phenomenon involving equilibrium points $E_{2}$ and $E_{4}$ is observed following the transcritical bifurcation. Figure 8(c) reveals that the previously stable equilibrium $E_{5}$ becomes unstable, giving rise to a new stable equilibrium $E_{6}$. Finally, (d) demonstrates that the stable equilibrium $E_{6}$ transitions to instability, while a new stable internal equilibrium $E_{7}$ emerges. These observations highlight that variations in parameters are intricately linked to the system's final stable state and influence the dynamics of cooperative strategies.

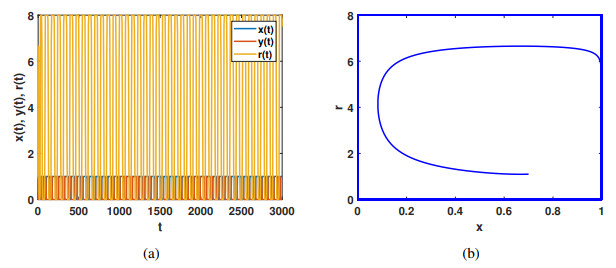
Fix the parameter values in Figure 2 and change the maximum value of the reward intensity, as shown in Figure 8(e). At this time, all the equilibrium points in the system (2.7) are no longer stable. The reward intensity oscillates between the highest and lowest intensity, while the players oscillate between complete cooperation and complete defection, which forms an evolutionary oscillation dynamic as shown in Figure 9. The influence of different relative speeds, $\epsilon$, on the system is shown in Figure 8(f). When $\epsilon$ changes from $0$ to $3$, the equilibrium points of the system are not affected, and the original stability is maintained. This suggests that, in this case, changes in relative speed do not impact the player's choice of strategy or the intensity of rewards.

5.2.   Time-delay system

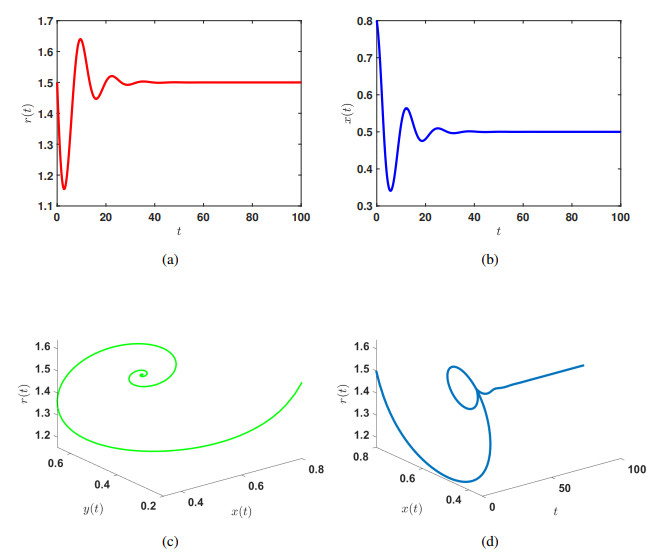
We continue to study the dynamic behavior of the time-delay system (3.2) by selecting the parameters in Figure 6. Then the internal equilibrium point is $E_{7}\left(0.5, 1.5\right)$, and the following results can be obtained through calculation.

Therefore, Hopf bifurcation is supercritical, and the periodic solution of the bifurcation is stable and the period increases.

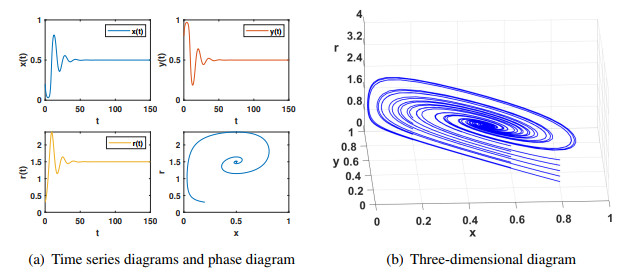
Regarding the system (3.2), we first examine the behavior of the system under a small time delay, as illustrated in Figure 10. When the time delay is minimal, the ratio of reward intensity to cooperation strategy stabilizes following a minor perturbation. At this stage, the time-delay system remains stable at $E_{7}$. Additionally, as evidenced by Figure 10(c), the system ultimately approaches a stable state.

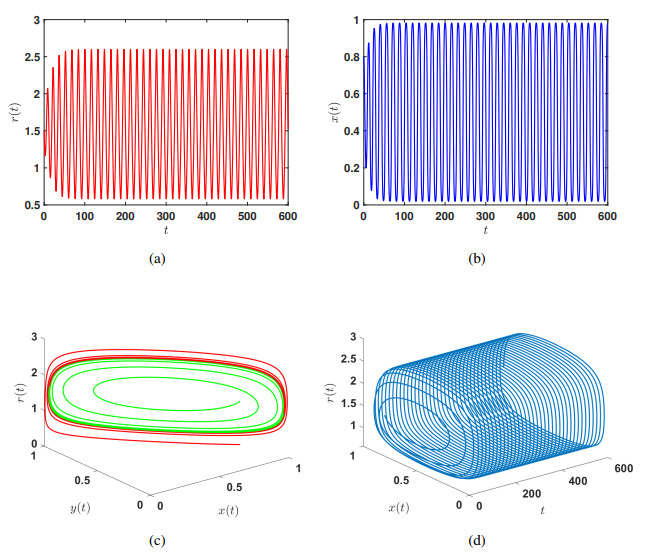
An oscillatory phenomenon emerges as the time delay gradually increases as depicted in Figure 11. At this point, the variables $x(t)$ and $r(t)$ begin to oscillate periodically rather than remaining stable at a single value, leading to the instability of the previously stable internal equilibrium point $E_{7}$. Subsequently, a stable limit cycle is observed in Figure 11(c). Simultaneously, the increase in time delay causes the stable strategy to begin oscillating, leading to a Hopf bifurcation at the critical time delay. After the Hopf bifurcation, the proportion of the cooperative strategy and reward intensity oscillate between the blue and the red lines, as illustrated in Figure 12. This shows that the time delay induces the switching of different stable states of the system.

6.   Conclusions

Building upon the classical evolutionary game theory framework, this paper introduces the concepts of reward feedback and time delay. To facilitate a more nuanced application of reward feedback for enhancing cooperation, the model posits that the proportion of the defection strategy promotes a modest reward for cooperators, while a higher proportion of the cooperative strategy suppresses the reward intensity. Under certain conditions, even when the reward intensity reaches its maximum value, the cooperation strategy may still yield a minimum value of zero. Additionally, in systems without a time delay, bistability is observed, and the attainment of the maximum cooperation strategy is contingent upon the initial values of the cooperative strategies and reward intensity. Specifically, variations in initial conditions lead to differing final states of stability for the cooperation strategy. In the system incorporating a time delay, the previously stable equilibrium point becomes unstable as the time delay increases. At the critical time delay, Hopf bifurcation occurs, causing oscillations in both strategies and the reward intensity rather than maintaining a stable constant value. The delayed system yields a series of delayed dynamical behaviors including Hopf bifurcation, period, stability, and direction of bifurcation. This shows that the time delay induces the switching of different stable states of the system.

With the advancement of feedback evolutionary game theory, exploring various feedback mechanisms and enhancing the evolutionary game model remain key areas of future investigation ^[38,39]. Cheng et al. have examined the evolutionary game system within spatial and temporal contexts, uncovering numerous interesting phenomena ^[40]. However, time delay emerges as a critical factor in spatiotemporal games, warranting further research in this area ^[41,42]. This aspect represents a significant direction for our future studies.

Author contributions

Writing-original draft preparation, Haowen Gong and Huijun Xiang; writing-review and editing, Haowen Gong and Yifei Wang; visualization, Haowen Gong and Yifei Wang; supervision, Huaijin Gao and Xinzhu Meng; project administration, Xinzhu Meng; and funding acquisition, Xinzhu Meng. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 12271308) and the SDUST Innovation Fund for Graduate Students.

Conflict of interest

The authors declare no conflicts of interest.