Threshold behaviour of a triple-delay SIQR stochastic epidemic model with Lévy noise perturbation

1.   Introduction

Governments have been prioritizing public health policies and taking decisions, plans and actions to save human lives from deadly infectious diseases. For this issue, computational biologists study the dynamics of epidemics in order to prevent and control the spread of infections in the population ^[1,2]. Recently, an epidemic named Corona Virus Disease 2019 (COVID-19) by the World Health Organization (WHO) has been spreading worldwide, especially in the United States, Brazil, India and South Africa, and the spread of the epidemic has caused a huge impact on industrial production and social life ^{[2,3,4,5,6,7,8]}. The virus has spread widely from person to person, although its origin remains unclear ^[9,10,11,12]. According to the data released by WHO Coronavirus (COVID-19) Dashboard. As of 14 February 2022, there have been 416,614,051 confirmed cases of COVID-19, including 5,844,097 deaths. COVID-19 has generated many mutant strains so far, and some of them have higher transmission and lethality rates, posing new challenges to the prevention and control of the epidemic.

In the 14th century, the authorities of the city of Venice adopted quarantine measures for access to the port, where each crew member of each ship was examined and could be cleared from land once the entire population was free of symptoms. This idea was adopted as the main measure to prevent the spread of infectious diseases such as Ebola and malaria. Recently, quarantine measures have proven to be effective in the extinction of COVID-19 disease in China ^[13], which has led many countries to adopt this strategy in the absence of a vaccine or cure for Neocoronavirus. To understand the effect of quarantine on epidemic behavior ^{[14,15,16,17,18]}. Liu et al. ^[19] proposed a model with quarantine to describe isolated individuals in a segregation model.

When studying the spread of epidemics, researchers now consider the impact of environmental noise, such as high temperature, freezing, drought, humidity, hurricanes, and so on. And they show that the existence of random factors such that the development of infectious diseases can be interfered ^[20]. The stochastic model can make up for the shortcomings of the deterministic model. Gard points out that the population dynamics is often disturbed by random perturbations ^[21], Cai et al. revealed that disease outbreaks can be suppressed by white noise ^[22]. Du et al. ^[23,24] propose the following model

where $F(S, I) = \frac{{\beta SI}}{{1 + {\alpha _1}S + {\alpha _2}I }},$ $\alpha_1, \alpha_2$ are positive constants measuring the suppression effect. On the other hand, a novel delayed stochastic model is proposed to describe the role of time delays in reality ^[25], which leads to a more complex behavior of dynamical system stability. This concept was described as temporary immunity in ^[26] and as a vaccine effect in ^[27]. However, temporary immunity can also affect isolated individuals. To better reflect reality, motivated by the study of ^[23,24], we propose the following triple-delay SIQR epidemic model with vaccination and isolation strategies

where $S(t)$ stands for the susceptible individuals, $I(t)$ for infected individuals, $R(t)$ for recovered compartment and $Q(t)$ for isolated or quarantined compartment. The parameter $\delta$, $\epsilon$, $\Lambda$, $\beta$ and $\rho$ denotes the rate of infectious individuals who were isolated, the recovered people coming from isolation, the population recuritment rate, the transmission coefficient from susceptible to infected individuals, the natural death rate respectively. $\gamma, \omega, \mu$ and $q$ represents the recovery rate of the infective individual, the death rate for infected, quarantined individuals due to infection complications and the proportional coefficient of vaccinated for the susceptible respectively. The time $\tau_1 > 0$, $\tau_2 > 0$ and $\tau_3 > 0$ represents the delay for the efficiency of vaccine, the length of the immunity period, the delay for isolated individuals to get back their immunity respectively. The term $S(t-\tau_1)e^{-\mu \tau_1}$ reflects the fact that some individuals remains susceptible even after the vaccine for a specific time. The term $I(t-\tau_2)e^{-\mu \tau_2}$ represents the individuals who became susceptible because of the lose of immunity for a specific time. The term $Q(t-\tau_3)e^{-\mu \tau_3}$ represents the individuals coming out from isolation with immunity impairment. The $B_i(t) \; (i = 1, 2, 3, 4)$ are independent standard Brownian motions defined on a complete probability space $(\Omega, \mathcal{F}, \mathbb{P})$ with the filtration $(\mathcal{F}_t)_{t\ge 0}$, satisfying the usual conditions, and $\sigma_i \ge 0$ represent the intensities of $B_i(t)$. The incidence of model (1.1) is of the form

where $\alpha_1, \alpha_2, \alpha_3$ and $\alpha_4$ are constants measuring the suppression effect.

As we know, population systems may suffer severe environmental perturbations, such as tsunami, volcanoes, avian influenza, hurricanes, earthquakes, toxic pollutants, etc. These phenomena cannot be described by stochastic continuous models. And so it is feasible to introduce a jump process into the underlying population systems (see e.g., ^[28,29,30]). Our goal in this work is to extend the model presented in ^[23] to a model with Lévy noise perturbation and also take in consideration a special incidence $f(S, I)$ and this model can be practically applied to describe hepatitis B epidemic ^[31].

where $S(t^-), I(t^-), Q(t^-)$ and $R(t^-)$ is the left limit of $S(t), I(t), Q(t)$ and $R(t)$. $\tilde{N} = N(dt, dy)$ is a poisson counting measure with the stationary compensator $v(dy)dt$. $v$ defined on a measurable subset $Y$ of $[0, \infty)$ with $v(Y) < \infty$ and $\eta _i > -1, \quad i = 1, 2, 3, 4$.

Noticing the first three stochastic differential equations in system (1.2) do not depend on the function $R(t)$, and so we can exclude the fourth one without loss of generality. Hence, we will only discuss the following system

$\mathbb{R}_+^3 = \left \{(x_1, x_2, x_3)\in \mathbb{R}^3, x_1 > 0, x_2 > 0, x_3 > 0 \right\}$. Let $C([-\tau, 0], \mathbb{R}_+^3)$ be the Banach space of continuous function mappings $[-\tau, 0] \quad \mathrm{into} \quad \mathbb{R}^3_+$ with norm $\left \| \phi \right \| = \sup_{-\tau \le \theta \le 0}\left | \phi(\theta) \right |$, where $\tau = \max\left\{\tau_1, \tau_2, \tau_3 \right\}$. We assume that

The innovation of this paper as follow:

● We consider the delay and Lévy noise based on the model in ^[23], a threshold $R_0^l$ of model (1.3) is obtained. If we disregard Lévy jumps, then $R_0^s = R_0^l$, here $R_0^s$ is the threshold of the random model (1.1).

● A complex incidence function $f(S, I)$ is considered, and the function can contain the following form:

(1) Holling Type II incidence $f(S, I)I = \frac{\beta SI}{1+\alpha_2S}$ ^[32], Saturation incidence $f(S, I)I = \frac{\beta SI}{1+\alpha_1I}$ ^[33], Bilinear functional response $f(S, I)I = \beta SI$ ^[34].

(2) if $\alpha_4 = \alpha_3 = 0$, we obtain Beddington-DeAngelis rate $f(S, I)I = \frac{\beta SI}{1+\alpha_1I+\alpha_2S}$ ^[35].

(3) if $\alpha_4 = 0, \alpha_3 = \alpha_1 \alpha_2$, Crowly-Martin functional response $f(S, I)I = \frac{\beta SI}{1+\alpha_1I+\alpha_2S+\alpha_1\alpha_2SI}$ ^[36].

(4) if $\alpha_1 = \alpha_2 = \alpha_3 = 0$, Non-monotonous incidence $f(S, I)I = \frac{\beta SI}{1+\alpha_4I^2}$ ^[37].

(5) if $\alpha_1 = \alpha_3 = 0$, Holling Type IV incidence $f(S, I)I = \frac{\beta SI}{1+\alpha_2I+\alpha_4I^2}$ ^[38].

● The numerical simulations compare the effects of Lévy noise and white noise on infectious diseases, and further conclude that Lévy noise can make diseases extinct.

Throughout this paper, we define the operator $\mathcal{L}$ associated with the following $n$-dimensional stochastic differential equation(SDE)

$X = (x_1, x_2, \cdots, x_n)$. If $\mathcal{L}$ acts on a function ${ G\in C^{1, 2} (\mathbb{R}^n; \mathbb{R}_+)}$, then

and

then by Itô's formula, we obtain

The rest of this article is organized as follows. In Section 2, the existence and uniqueness of the global positive solution of a stochastic system with Lévy noise is proven. In Section 3, the result of the analysis is the extinction can be determined when $R_0^l < 1$. In Section 4, we show that disease will persistence in the mean when $R_0^l > 1$. In Section 5, some numerical simulations to summarize related results, and provides direction for future research.

2.   Existence and uniqueness of the positive solution

Throughout this section, we will establish the existence of a global positive solution for our delayed stochastic epidemic model with jumps. For the sake of convenience, we shall impose a standard assumption (H1), which is essential to prove the existence and uniqueness of a global positive solution of (1.3).

(H1) $1 + {\eta_i}(y) > 0, y \in \mathbb Y, i = 1, 2, 3, \left| {\ln (1 + {\eta_i}(y))} \right| \le C$, where $C$ is a positive constant.

Theorem 2.1. For any initial condition $(S(0), I(0), Q(0))\in L^1([-\tau, 0];\mathbb{R}_{+}^{3})$. There is a unique solution $(S(t), I(t), Q (t))$ of the stochastic system $\mathrm{(1.3)}$ for $t\geq -\tau$ and the solution will remain in $\mathbb{R}_{+}^{3}$ with probability one.

Proof. For any initial condition $(S(0), I(0), Q(0))\in \mathbb{R}_{+}^{3}$, the local Lipschitz condition can make the system (1.3) exist solution $(S(t), I(t), Q(t))$ for any $t \in [-\tau, \tau _{e})$ almost surely ($\tau _{e}$ is the explosion time ^[39]). So, in order to prove the existence of a global positive solution, we need to prove that $\tau _{e} = \infty$. In other words, $(S(t), I(t), Q(t))$ will not explode to infinity in a finite time. We choose a positive constant $m_{0} > 0$. In order to keep $S(0)$, $I(0)$, and $Q(0)$ all lie within the interval $[\frac{1}{m_{0}}, m_{0}]$, we let $m_{0}$ be sufficiently large. Next, we construct a set $\{ \tau_m, m\geq m_0\}$ related to this positive number $m_{0} > 0$:

Clearly, we can find that $\tau _{m}$ is a monotonically increasing function of the independent variable $m$. According to the definition above, set $\tau _{\infty} = \lim_{m \to \infty} \tau _{m}$, we know that $\tau _{\infty} \le \tau _{e}$ holds. In order to prove $\tau _{e} = \infty$ we just need to ensure that $\tau _{\infty} = \infty$ for $(S(0), I(0), R(0))\in \mathbb{R}_{+}^{3}$. We write $\phi$ as the empty set and define $\inf \phi = \infty$ in this paper. We assume that $\tau _{\infty} < \infty$ holds, then there exist a pair of constant $T > 0$ and $\epsilon \in \left (0, 1 \right)$ such that $\mathbb{P}(\tau _{\infty}\le T)\ge \epsilon.$ From the above discussion, we know that there is an integer $m_{1} \ge m_{0}$ such that

for all $m\ge m_{1}.$

Define $C^{2} -\mathrm{function} \; V(S, I, Q) :\mathbb{R}_{+}^{3} \longrightarrow \mathbb{R}_{+}$ by

where $a$ is a positive constant determined later, the non-negativity of this function occurs from $u-1-\ln u\ge 0$ for $\forall u > 0$. With Itô's formula, then

From $\frac{f(S, I)I}{S} \le \beta I$ and $a = \frac{\rho + \omega}{ \beta }$, we get

Then,

Integrating both side of (2.2) from $0$ to $\tau_{m}\wedge T = \min \{\tau_{m}, T\}$, then

Take the expectations to (2.3)

so, we have

Let $\Omega _{m} = \left \{\tau_{m}\wedge T \right \}$ for $m\ge m_{1}$, and by $(2.1)$, we derive that $\mathbb{P} (\Omega _{m})\ge \epsilon$. For $\forall \omega \in \Omega _{m}$, there is at least one of $S(\tau_{m}\wedge T), I(\tau_{m}\wedge T)$ and $Q(\tau_{m}\wedge T)$ that equals either $\frac{1}{m}$ or $m$. It follows that $V(S(\tau_{m}\wedge T), I(\tau_{m}\wedge T), Q(\tau_{m}\wedge T))$ is no less than $m-1-\ln m$ or $\frac{1}{ m}-1-\ln \frac{1}{ m}$ or $a m-1-\ln a m$ or $\frac{a}{ m}-1-\ln \frac{a}{ m }$. From this we obtain

where $1_{\Omega _{m} }(\omega)$ is a indicator function of $\Omega _{m}(\omega)$. Let $m\longrightarrow \infty$, then we attain

From this we conclude that the above equation is a contradiction, then $S(t), I(t)$ and $Q(t)$ will not explode in a finite time.

We consider the region

Theorem 2.2. The region $\Gamma$ is almost surely (a.s.) positive invariant for the stochastic model $\mathrm{(1.3)}$.

Proof. Suppose $(S(\theta), I(\theta), Q(\theta)) \in \Gamma, \theta \in[-\tau, 0]$ and $n_{0} \geq 0$ be sufficiently large such that $S(\theta) \in\left(\frac{1}{n_{0}}, \overline{M}\right]$, $I(\theta) \in\left(\frac{1}{n_{0}}, \overline{M}\right]$ and $Q(\theta) \in\left(\frac{1}{n_{0}}, \overline{M}\right]$. For each integer $n \geq n_{0}$, the stopping times are defined as follows

We need to show that $\mathbb{P}(\tau < t) = 0$ for all $t > 0$.

Notice that $\mathbb{P}(\tau < t) \leq \mathbb{P}\left(\tau_{n} < t\right)$, then we have to prove $\lim \sup _{n \rightarrow +\infty} \mathbb{P}\left(\tau_{n} < t\right) = 0$. Define the function

then

here,

Then

where

Taking integral and expectation on both sides of (2.4) and by virtue of Fubini Theorem, then we derive

Applying Gronwall Lemma, we obtain that

for all $s \in\left[0, t \wedge \tau_{n}\right]$. Thus,

In consideration of $W\left(X\left(t \wedge \tau_{n}\right)\right) > 0$ and some component of $X\left(\tau_{n}\right)$ being less than or equal to $\frac{1}{n}$, we achieve

By (2.5), we obtain that

for all $t \geq 0$. Therefore,

The proof is completed.

3.   Extinction of the disease

In the study of infectious disease models, the search for thresholds is an important aspect, and in this section we investigate a threshold condition that can determine the extinction and persistence of the disease. Define a parameter

Let ${R_0^s} = {R_0} - \frac{1}{{(\rho + \omega + \gamma + \delta)}}\left(\frac{{\sigma _2^2}}{2} \right)$ be the threshold of our stochastic model (1.3) and $R_0^l$ be the threshold of our model (1.3) defined as follows

To simplify, we consider the following notation $\left \langle x(t) \right \rangle = \frac{1}{t}\int_0^tx(s)\mathrm{d}s$.

Lemma 3.1. ^[40] $M = \left \{ M_{t} \right \} _{t \ge 0}$ be a real-valued continuous local martingle vanishing at $t = 0$ then

and also

Theorem 3.1. For any initial value $(S(\theta), I(\theta), Q(\theta))\in \Gamma, \quad \theta\in[-\tau, 0]$, let $(S(t), I(t), Q(t))$ be the solution of stochastic system $\mathrm{(1.3)}$. If $R_{0}^{l} < 1$, then

The disease will be extinct exponentially. Moreover

Proof. We consider the following function

Using the Itô's formula, we get

and

Then,

Therefore, intergrating both sides of (3.1), we obtain

where

Since $(S, I, Q)\in \Gamma$, and taking expectation of $\phi(t)$, we obtain $\lim_{t \to \infty} \phi(t) = 0.$ Now, applying Itô's formula to the function $\ln I(t)$ we get

Noticing that the function $f(S, I)$ can be written as

Then

Hence, integrating both sides of (3.3) and by dividing by t we obtain

By the strong of large number law for local martingales ^[41], and for $R_0^l < 1$, we get

which leads to $\lim_{t \to \infty }I(t) = 0$.

From (3.2) we obtain

Integrating third equation of system (1.3),

Hence, from $\lim_{t \to \infty }I(t) = 0$ and by the strong law of large numbers for local martingales

So our proof is complete.

4.   Persistence in mean of the disease

In this section, we investigate the persistence of the disease. First, we recall the following definition.

Definition 4.1. ^[42] The solution of the stochastic model $\mathrm{(1.3)}$ is said to persistence in the mean, if

Lemma 4.1. ^[42] Let $f\in C([0, \infty), (0, +\infty))$ and $F\in C([0, +\infty), \mathbb{R})$ such thatif there exist positive constants $m_1, m_2$ and $T$, such that

and $\lim_{t \to \infty}\frac{F(t)}{t} = 0 \ \ a.s.$, then

Let

Theorem 4.1. Let $(S(t), I(t), Q(t))$ be the solution of system (1.3) with initial value $(S(\theta), I(\theta), Q(\theta))\in \Gamma, \quad \theta\in[-\tau, 0]$. If $R_0^l > 1$, then

where $I^* = (R_0^l-1) \frac{(\rho + \omega + \delta + \gamma)}{ \lambda }$.

Proof. From Theorem 2.2, we can get

Applying the Itô's formula to the second equation of model (1.3) yields

where

Then

From the result (3.2) and integrating (4.1) between 0 and t we have

where

By the strong law of large numbers for local martingales that

Hence, by Lemma 4.1 we get

Then, we get

From (3.2) and (4.2), we can check that

Also, from Theorem 2.2 and the first equation of (1.3) gives

Then

By the law of large numbers for martingales and $S(t)\in \Gamma$, we obtain

From the third equation of the system (1.3), we have

Hence, from the strong law of large numbers for local martingales we get

So our proof is complete.

5.   Numerical simulations

In this section, we shall use Euler-Maruyama numerical approximation ^[43] to illustrate the rigor of our analytical results. The two examples are given below concern the results obtained in Theorems 3.1 and 4.1. Moreover, we numerically simulate the solution of a corresponding system (1.2) for the comparison.

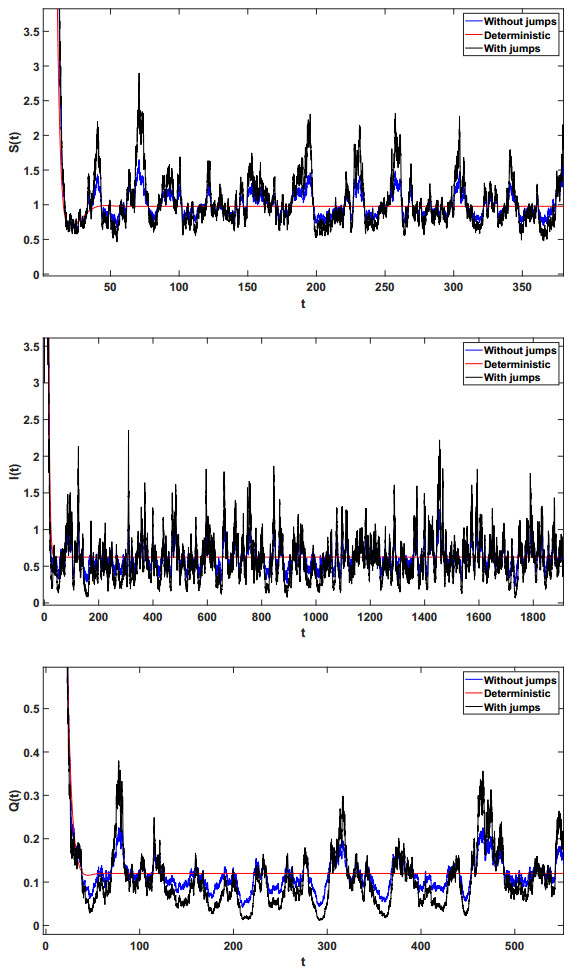
Example 5.1. According to the parameters in the paper ^[31], Choose $\Lambda = 0.5$, $\beta = 0.2$, $\rho = 0.1$, $q = 0.1$, $\delta = 0.15$, $\gamma = 0.11, \omega = 0.12, \mu = 0.2, \epsilon = 0.3, \tau_1 = 0.1, \tau_2 = 0.5, \tau_3 = 0.5, \alpha_1 = 0.22, \alpha_2 = \alpha_3 = \alpha_4 = 0.2$, $\eta_1 = 0.01, \eta_2 = 0.1, \eta_3 = 0.03$ and $Y = (0, \infty), v(Y) = 1$, $\sigma _{1} = \sigma _{2} = \sigma _{3} = 0.1$. Then $R_0 = 1.04 > 1, R_0^s = 1.024 > 1$, however $R_0^l = 0.9921 < 1$.

The computer simulation illustrated by Figure 1, support the result of Theorem 3.1. That is to say, the disease in system (1.3) (with jump) dies out exponentially with probability one, although the disease in system (1.1) (without jumps) persists. If we decrease $\beta$ to $0.19$, we get $R_0 = 0.995 < 1, R_0^s = 0.97 < 1$, and $R_0^l = 0.9421 < 1$. By Theorem 3.1, the disease will tend to zero exponentially with probability one.

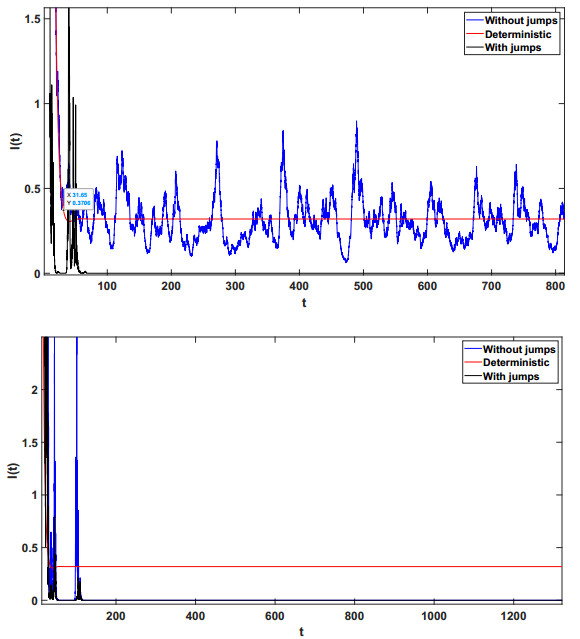
Example 5.2. Choose $\beta = 0.19$ and other parameters be the same as Example 5.1. Then $R_0 = 1.15 > 1$, $R_0^s = 1.12 > 1$, $R_0^l = 1.09121 > 1$. By Theorem 4.1, We can get $\lim_{t \to \infty }\left \langle S(t) \right \rangle = 1.0921 > 0,$ $\lim_{t \to \infty }\left \langle I(t) \right \rangle = 0.593 > 0,$ $\lim_{t \to \infty }\left \langle Q(t) \right \rangle = 0.1201 > 0.$ This means that the disease persists almost surely. The come simulations showed in Figure 2 support the result 4.1 clearly.

6.   Conclusions

Since the role of isolation has been shown to be meaningful for the prevention and control of infectious diseases such as for the recent influenza disease COVID-19. Therefore the dynamical behavior of a delayed SIQR stochastic epidemic model with Lévy noise is studied. In comparison with the studies of ^[23], we explore a new response function $f(S, I)$ and consider the Lévy noise. Where the reaction function can contain forms such as Holling Type II incidence $f(S, I)I = \frac{\beta SI}{1+\alpha_2S}$, Saturation rate $f(S, I)I = \frac{\beta SI}{1+\alpha_1I}$, Bilinear functional response $f(S, I)I = \beta SI$, Beddington-DeAngelis rate $f(S, I)I = \frac{\beta SI}{1+\alpha_1I+\alpha_2S}$, Crowly-Martin functional response $f(S, I)I = \frac{\beta SI}{1+\alpha_1I+\alpha_2S+\alpha_1\alpha_2SI}$, Non-monotonous incidence $f(S, I)I = \frac{\beta SI}{1+\alpha_4I^2}$, Holling Type IV incidence $f(S, I)I = \frac{\beta SI}{1+\alpha_2I+\alpha_4I^2}$. A threshold value $R_0^l$ is derived

● If $R_{0}^{l} > 1$, the disease will persistence in mean.

● If $R_{0}^{l} < 1$, the disease will tend to extinction exponetially.

We can also compare the expressions for $R_{0}^{l}$ and the parameter $R_{0}$. Obviously, when we ignore the environmental noise and Lévy noise, we show that $R_{0}^{l} = R_0^s = R_{0}$, this implies that the stochastic model is an extension of corresponding deterministic model.

The following topics deserve further discussion. Since white noise is a continuous stochastic perturbation, some discontinuous perturbations such as the color noises can be further investigated and the effect of the impulsive can also be considered. At the same time, we can also try to find the probability density function by solving the Fokker-Planck equation of stochastic model (1.3). We left the above topics for future work.

Acknowledgments

We will say thanks to reviewers for the valuable ideas and comments on improving the article. The said article is supported by Funding for National Nature Science Foundation of China (11571088) and National Nature Science Foundation of China (12071105).

Conflict of interest

The authors declare that there are no conflicts of interest.