À Italo Capuzzo Dolcetta, en signe d'affection, de profonde estime et d'amitié.
1.
Motivation and framework
Introduced by Kermack and McKendrick [48] as one particular instance of a family of models, the SIR compartmental type model and its host of variants are basic tools of epidemiology. They have given rise to a vast literature. The SIR system features two populations: the Susceptible, represented by S(t,x), and the Infected, represented by I(t,x). These are supplemented by the compartment of removed R(t,x). In its simplest form (with spatial component x) and Brownian diffusion, the model is written as the following system of reaction-diffusion equations:
together with the equation for the recovered R(t,x)
Since (1.1) does not involve R (which is derived from I), we can overlook it.
This system is essential in epidemiology, both from the point of view of theory [41,42,43,55,64,67,72] and applications [3,7,59]. Most of the available mathematical approaches are quite specific to this system and do not lend themselves to be generalized to a broader class of systems. Given the variety of extensions and variants of this model, it is natural to seek a unified mathematical framework and to identify the core general properties of this class of system. This is one of the aims of this paper.
Similar models have been used since long to describe the spread of riots and, more generally, of collective behaviors in various social contexts (see e.g., the survey of Dietz [28]). One may trace this use of epidemiology models in the context of social phenomena to the analogy between the mechanisms of contagion and social imitation.
The mechanism of social imitation implies that the inclination of an individual to join a social movement is largely influenced by the intensity of the movement itself. Once the movement has reached a certain size, owing to several mechanisms such as imitation or social influence, more people are prone to join it and the movement grows. The celebrated work of Granovetter Threshold Models of Collective Behavior [39] described the formal analogy between epidemics and collective behavior in the following visionary terms*:
*we left out the references
"There is also some similarity between the present models and models used in epidemiology, the diffusion of information and innovations, and the evolution of behavior in groups over time."
This approach is also developed by Burbeck et al. [23] in their pioneering paper about the dynamics of riots:
"Patterns within three major riots suggest that the dynamics of the spread of riot behavior during a riot can be fruitfully compared to those operative in classical epidemics. We therefore conceptualize riots as behavioral epidemics, and apply the mathematical theory of epidemics [...]."
It is only relatively recently that several works have developed the actual epidemiology approach for the modeling of riots [13,16,18,61,76]. This approach proved very effective in fitting data from observations [20,25].
Similar ideas have also been applied to other instances of collective behaviors: the propagation of ideas (see the pioneering works of Goffman & Newill [37] and Daley & Kendall [26], and also the more recent contributions on the propagation of scientific knowledge [24,44,46,49,57], rumors [1,47,78,79], and extreme ideology in a society [65]), the diffusion of a new product in a market (as originally studied by Bass [8] and more recently included in numerous works dealing both with the theory [19,32,33,63] and the applications [38,40]), the growth of political parties [45] and the propagation of memes and hashtags [35,68,73,75].
Conversely, the analogy between epidemics and collective behaviors shows us that to a large extent epidemics are a social phenomenon. The impacts and challenges of the current COVID-19 epidemic remind us of this fact. The website [53] of the Institute of Development Studies formulates it explicitly:
"As the COVID-19 pandemic rages across the world, one thing is clear: this epidemic, like all others, is a social phenomenon. The dynamics of the virus, infection and immunity, not to mention on-going efforts to revise and improve clinical care, and endeavors to develop medical treatments and vaccines, are a critical part of the unfolding story. So, too, are peoples' social responses to the disease and interactions with each other."
Since epidemics and collective behaviors, although very different in nature, have structural similarities, they can be modeled and studied within a unified mathematical paradigm. A question of particular importance is to understand whether a triggering event, i.e., a small initial social movement, can result in a significant movement by means of social imitation and other self-reinforcement mechanisms. The answer to this question typically involves a threshold phenomenon on an ambient level of susceptibility. In a context of low susceptibility, the triggering event fades out and the system promptly returns to a calm situation, whereas in a context of high susceptibility, the triggering event leads to a significant movement.
Our main goal in [15] and in the present article is to develop a unified mathematical framework to deal with this general setting. We aim to unify, generalize, and open new fields of application for epidemiology and collective behavior models. This article can also be seen as a contribution to the program proposed by Granovetter:
"To develop these analogies in more detail would require that (1) my models, expressed below as difference equations in discrete time, be translated into differential equations in continuous time, and that (2) some way be found to introduce the "threshold" concept into these other models, which generally do not stress individual differences. While some work in this direction has been accomplished, it is incomplete"
Let us emphasize that spatial diffusion plays a key role in the dynamics of many collective behaviors [20,22,69,76]. Therefore, in [15] and here we include spatial dependence and we are especially interested in spatial propagation.
In our approach, we consider the coupled dynamics of a level of activity, denoted by u, representing the intensity of activity (e.g., rioting activity, fraction of population having adopted a belief or a technology, etc.), and an underlying level of susceptibility, denoted by v, representing the ambient context. We emphasize that these two quantities play an asymmetric role: u is thought of as the actual observed or explicit quantity while v is a potential field that modulates the growth of u. From a modeling perspective, the level of activity u often represents an explicit quantity that is tractable empirically, whereas the level of susceptibility v is an implicit field. In a sense, we postulate the existence of such a field which is a lumped variable that results from several complex social interactions. Then, these two quantities interact: the field v modulates the dynamics of the activity level, and there is also a feedback mechanism whereby the level of activity influences the field of susceptibility. This is why we call this general class of models the activity/susceptibility systems.
Assuming that u and v are subject to diffusion and coupled reaction, the resulting mathematical model takes the following general form:
We aim at keeping the assumptions on the terms in the system as general as possible. In fact, the form of Φ and Ψ given in (1.2) is only suggested in this introduction to give an insight of our approach, but later on we deal with more general nonlinear terms, see Section 2.3 below.
Let us briefly justify the structural form of the above system. In a normal situation, i.e., in the absence of any exogenous event, we consider the system at equilibrium at some steady state (u,v)≡(0,vb), where the level of activity u is null and the social tension v is at its base value vb. Note that the special form of Φ, Ψ in (1.2) ensures that (0,vb) is indeed a steady state. We also assume that the steady-state (0,vb) is, in a sense, weakly stable in a situation where u=0, that is, H(0,v)≥0.
We consider that an exogenous event occurs at t=0 affecting the activity and propose to study its effect on the system. This exogenous event is encoded in the initial condition u0(⋅)≩0.
As we will see, the class of systems (1.2) gives rise to many diverse qualitative behaviors. This variety is illustrated by two subclasses that we will investigate in more details, namely, the tension inhibiting systems (where Ψ≤0) which give rise to ephemeral episodes of activity, and the tension enhancing systems (where Ψ≥0) which give rise to time-persisting episodes of activity.
The SI epidemiology model (1.1) is recovered from (1.2) by taking Φ(u,v)=βuv−γu and Ψ(u,v)=−βuv, In this context, the Susceptible are represented by v, and the Infected are represented by u: this exeplifies the role of potential field assumed by v – here the susceptibles. Actually, we will see that the SI belongs to the subclass of tension inhibiting systems. The terms ±βuv (which could be described as law of mass action type terms) account for the contagion mechanism and derive from the assumption that the contagion is proportional to the rate of encounter between susceptible and infected individuals in a evenly mixed population. Many papers consider variants of the model where this term is replaced by a more elaborate contagion term. For example, the Michaelis-Menten interaction assumes the existence of a saturation effect on the contagion term and amounts to substitute ±βSI by ±βSI1+b(S+I). Most of these variant fit our general framework (1.2) and are therefore included in our study.
As further discussed in our other paper [15], a number of systems used in other modeling areas (such as propagation in excitable media, population dynamics, etc.) also fall into the setting defined by (1.2a). When dealing with solid combustion (which is a typical example of propagation in an excitable media), one can choose u to represent the temperature, v to represent the chemical fuel, and assume that their dynamics is governed by (1.2a) with Φ(u,v)=qF(u)v and Ψ(u,v)=−F(u)v, where q>0 is a constant, see [6,12,14] and references therein. The function F derives from the Arrhenius law and is typically taken to be of the form F(u)=(u−θ)+g(u), where θ∈(0,1) is the ignition temperature and g is some postive function involving the activation energy.
Another famous system that fit our framework is the classical Lotka-Volterra predator-prey model, obtained by taking (overlooking various parameters) Φ(u,v)=u(v−ω) and Ψ(u,v)=−uv+v(1−v) (with vb=1) in (1.2a). In this context, u represents the density of predators and v the density of preys. The term ±uv represents the transfer between prey and predators (through a law of mass action type term); −ωu represents the natural death rate of predators; v(1−v) represents the natural birth rate and saturation effect (due, for instance, to the limitations of ressources) in the prey population.
In our paper [15], we propose a theoretical study of (1.2) in a general framework. In the present article, we discuss the significance of the results for modeling purposes while assuming a slightly more specific structure to the system. We also prove some new theoretical results concerning the long-time behavior of solutions in the tension inhibiting and the tension enhancing cases, dealing with the behaviors of solutions far from the leading edge of the front. Those results deal with both the traveling wave problem and the Cauchy problem. We accompany our analysis with several numerical simulations which also reveal a number of interesting open questions.
To fix ideas, we place ourselves in the context of modeling of social unrest, which is a historical example and a textbook case of a propagating collective behavior. The epidemiology approach is particularly relevant in this context, as highlighted by the pioneering work of Burbeck et al. [23] already mentioned. However, our approach can be envisioned to model other sociological phenomena in social sciences and population dynamics. Let us also mention that the literature on the modeling of social unrest often considers models with very particular forms, even though the quantities at stake (especially the susceptibility, or social tension) are not directly accessible from data. It thus seems important to us to develop a unified approach with mild assumptions on the parameters.
In this paper, our aim is to illustrate the richness of the framework and to discuss its qualitative relevance regarding the topic, while keeping the mathematical approach quite general.
Outline. We start with presenting, in Section 2.1, the social phenomena that we aim at describing, pointing out the basic sociological assumptions that lead, in Section 2.2, to the mathematical derivation of our model. The model and the assumptions are then stated in Sections 2.3 and 2.4. In Section 2.5, we discuss the existing literature on this and related topics. Section 3 is devoted to a general analysis of the model. Applying the results of [15], we enlighten a threshold phenomenon on the initial level of social tension for the ignition of a social movement. We present some estimates on the speed of propagation of the movement and comment on the interpretation of the mathematical results in terms of modeling. Next, we focus on two important classes of models: the tension inhibiting systems (Section 4), which generate ephemeral movements of social unrest, and the tension enhancing systems (Section 5), which give rise to time-persisting movements of social unrest. In both cases, we present some new results about the behavior of solutions far from the leading edge of the propagating front, as well as for traveling wave solutions. These results are corroborated by numerous numerical simulations. In Section 6, we examine several mixed cases which are neither tension inhibiting nor tension enhancing, and that exhibit more complex dynamics. Section 7 deals with extensions of the model including spatial heterogeneity. Section 8 contains all the proofs of our results. Finally, Section 9 is devoted to concluding remarks and perspectives.
Remark on the numerical simulations. Numerical simulations are performed with a standard explicit Euler finite-difference scheme, with time-step dt=0.05, and space-step dx=1. In the caption of each figure, we give a clickable URL link and the reference to a video of the simulation available online†.
†Temporary address: https://sites.google.com/view/samuelnordmann/research/modeling-social-unrest-videos Definite address to be specified in the published paper.
2.
The model
2.1. The dynamics of social unrest
In this section, we introduce our modeling assumptions on the dynamics of social unrest in society and other collective behaviors. We do not aim at discussing the sociological origins of social unrest, which is the topic of an abundant literature and continues to be studied. Instead, we propose a model built from simple ingredients to account for recurrent patterns observed in these phenomena [20,27]. Our purpose here is to identify some possible features and mechanisms that land themselves to mathematical analysis. Of particular importance in this respect is the dynamical unfolding and spatial spreading of social unrest.
Our approach consists of using epidemiology models to account for the coupled dynamics of social unrest and social tension. This approach, introduced by Burbeck et al. [23] and further developped in [13,16,18], turns out to be remarkably efficient to account for data from the field. In particular, a model [20] of the class we consider here reproduces rather precisely the dynamics and spreading of the French riots of 2005, which was triggered by the death of two young men trying to escape the police in Clichy-sous-Bois, a poor suburb of Paris. This event occurred in a context of high social tension and was the spark for the riots that spread throughout the country and lasted over three weeks.
For literature on the modeling of social unrest, riots, and related topics, we refer the reader to [13,21,39,71] and references therein. We return in Section 2.5 to the existing literature and give a more detailed comparison between our model and several others.
We define the level of social unrest, abbreviated to SU, as the number of rioting activities or civil disobedience. We can think of SU as the level of illegal actions resulting from rioting, measured in some homogeneous way (e.g., number of rioting incidents reported by the police). Our model also features a level of Social Tension, abbreviated to ST, accounting for the resentment of a population towards society, be it for political, economic, or for social reasons. This implicit quantity can be seen as the underlying (or potential) field of susceptibility for an individual to join a social movement. The guiding principle of our approach rests on the hypothesis that SU and ST follow coupled dynamics.
Let us now review the most common characteristics of the dynamics of SU and define some vocabulary. To begin with, even if social movements can take many different forms, it appears that they often occur as episodic bursts. A first simplistic classification would be to distinguish an ephemeral movement of social unrest, that we call here a "riot", which lasts at most a couple of weeks and then fades (e.g., the London riots of 2011 [9,27] or the French riot of 2005 [20]), from a long-duration or persisting movement of social unrest, that we call here a "lasting upheaval", which lasts longer and can result in significant political or sociological changes (e.g., the Yellow Vest Movement [58,74], the Arab Spring [50,52], the Russian revolution of 1905-1907 [60], or the French Revolution. See also [4]).
However, most social protests are commonly considered to have been ignited by a single triggering event [30].
Accordingly, we assume that in a normal situation, the level of SU is null and that ST is at equilibrium at its base value. To account for the triggering event, we assume that the system is perturbed at t=0.
We therefore expect that whether the triggering event ignites a burst of SU depends on the level of ST. If ST is high enough, a small triggering event triggers a burst of SU; whereas if ST is low, the same event is followed by a prompt return to calm. This threshold phenomenon is studied in the famous work of Granovetter [39].
These observations suggest that, in a context of low ST, an intrinsic mechanism of relaxation occurs on SU. The relaxation rate accounts for various sociological features after a burst, such as fatigue, police repression, incarceration, etc.
On the other hand, a high ST activates an endogeneous growth of SU. In other words, if ST is above a threshold level, then a mechanism of self-reinforcement occurs on SU. This is analogous to a flame propagation (an endogenous growth is activated when the temperature is high enough) and pertains, more generally to "excitable media". One can think of this endogeneous feature as the gregarious dimension of social movements: the larger the movement, the more prone an individual is to join it [62,66].
Naturally, this self-reinforcement mechanism can be counterbalanced by a saturation effect, accounting for the limited number of individuals, resources, goods to be damaged, etc.
Another important feature usually observed during movements of SU is the geographical spread [22,76]. A striking example is the case of the 2005 riots in France [20,70]. This phenomenon is either caused by the rioters movement as in London 2011, or by a diffusion of the riot as in France 2005. However, the role played by the geography in the dynamics of ST is less clear. For example, one could consider that ST is, or is not, affected by diffusion, or even that it is affected by a non-local diffusion (see Section 9.2.1) since information nowadays is often available instantaneously through global media.
With this vocabulary at hand, a riot (i.e., an ephemeral movement of social unrest) will typically be observed in a case where the burst of SU results in a decrease of ST. Once ST falls below a threshold value, SU fades and eventually stops. We call this case tension inhibiting. It is qualitatively comparable to the outburst of a disease, which propagates until the number of susceptible individuals falls below a certain threshold. This behavior is well captured by the famous SI epidemiology model, with S= ST and I= SU.
On the contrary, a lasting upheaval (i.e., a time-persisting movement of social unrest) will typically be observed in a case where the burst of SU results in an increases of ST. In this case, the dynamics escalates towards a sustainable state of high SU. We call this case tension enhancing. From a modeling point of view, it points to a cooperative system.
These two model classes give a first good idea of the variety of behaviors generated by the model. They suggest different classes of systems: epidemiology models on the one hand and monotone systems on the other hand. Those two classes of model are studied quite separately in the literature. Our aim here is to take advantage of the unified framework of [15] to propose a single model able to encompass both behaviors.
Of course, one can also consider more complex scenarios where the feedback of SU on ST is neither positive nor negative. This situation is included in our framework and illustrated with numerous examples later on.
2.2. Construction of the model
We propose a mathematical model inspired from [13,16,18] to account for the dynamics of SU and ST. We let u(t,x) denote the level of SU at given time t and position x, and let v(t,x) be the level of ST. We consider the general form of systems of Reaction-Diffusion equations
The diffusion terms d1Δu(t,x) and d2Δv(t,x) describe the influence that one location has on its geographical neighbors. The reaction terms Φ and Ψ model the endogenous growths and feebacks of u and v.
The level u=0 represents the absence of social unrest, or activity. The value vb stands for the base value of the social tension in the normal (quiet) regime. We assume that the system is at equilibrium in the quiet regime, that is, (u≡0,v≡vb) is a steady state for (2.1) (Φ(0,vb)=Ψ(0,vb)=0). For example, we can choose, as in (1.2),
We further assume that vb is a weakly stable state for the second equation when u≡0, i.e., Ψ(0,v)≥0 if v≤vb and Ψ(0,v)≤0 if v≥vb. Under the particular form (2.2), it amounts to saying that H(0,⋅)≥0 (which is the case of the SI system, where H≡0).
We then introduce a triggering event. This corresponds to a small perturbation of the steady-state (u=0,v=vb) and is encoded in the initial condition. For clarity, we suppose that the initial perturbation only occurs on the u component, that is, we take v0(⋅)≡vb. The case of more general initial conditions v0 can be adapted from the results of [15]).
We choose the term Φ in the first equation of (2.1) to be of the form
The term f(u) represents the endogenous factor (or self-reinforcement/saturation mechanism). We take f nonincreasing (to account for a saturation effect) and positive at u=0; for example, f(u)=1−u or f(u)=1.
The parameter ω>0 is the natural rate of relaxation of SU in absence of self-reinforcement.
The endogenous factor is regulated by r(v), which models the role of activator played by ST. We choose r(⋅) to be nonnegative and increasing. We can think of this term as an on-off switch of the endogenous growth. For example, r(⋅) can be linear r(v)=v, or take the form of a sigmoïd
where, α≥0 is a threshold value while β>0 measures the stiffness of the transition between the relaxed state and the excited state (if we formally take β=+∞, then r is a step function which equals 0 if v<α and equals 1 if v>α).
Let us now describe the reaction term Ψ in the second equation of (2.1). For the sake of clarity, we want to normalize v such that it ranges in (0,1); thus we will assume that v0∈(0,1), Ψ(u,0)≥0 and Ψ(u,1)≤0. We devote a particular attention to the following two classes of models. Each case illustrates a typical qualitative behavior.
1). The tension inhibiting case: Ψ(u,v)<0 for u>0, v∈(0,1). In this case, a burst of u causes a decrease of v. We expect this case to give rise to an ephemeral riot and to behave comparably to the SI epidemiology model (1.1), in which
with β>0.
2). The tension enhancing case: Ψ(u,v)>0 for u>0, v∈(0,1). In this case, a burst of u causes an increase of v. We expect this case to give rise to a lasting upheaval and to behave comparably to a cooperative system (although we do not assume that Ψ is monotonic). As an example, we can take
2.3. The model: assumptions and notations
We consider u(t,x), which stands for the level of social unrest at time t≥0 and location x∈Rn, and v(t,x), which stands for the level of social tension, solution of
Here are our standing assumptions, that will be understood throughout the paper:
a) d1>0, d2≥0, ω>0.
b) f(u) is smooth and nonincreasing on [0,+∞), with f(0)>0; for example, f(u)=1 or f(u)=1−u.
c) r(v) is smooth, nonnegative and increasing on (0,1); for example, r(v)=v.
d) r(0)<ωf(0)<r(1), and we define
e) Ψ(0,⋅) has a (weakly) stable zero vb∈(0,1), i.e.,
for example, Ψ(0,⋅)≡0.
f) Ψ(u,v) is smooth and satisfies the saturation conditions at v=0,1
g) u0(x)≩0 is bounded and v0≡vb, where vb is the constant in (2.5).
The structure assumed on the system (2.3) is slightly more specific here than in the general framework developped in [15] where no monotony is assumed and Φ can have a more generic form; yet, our set of assumptions encompasses many diverse systems, which may be highly non-monotone and exhibit quite different qualitative behaviors, as illustrated in the sequel.
Note that if Ψ(0,⋅)≡0 then (2.5) is automatically satisfied and so any vb∈(0,1) is suitable for our set of assumptions.
The following property is an immediate consequence of our assumptions.
Lemma 2.1. Any solution of (2.3) satisfies
Proof. Recall that u0≩0 and v0∈(0,1). For the range of v, we notice that in view of (2.6), v satisfies the inequalities
and
This implies that v(t,x) has range in (0,1), thanks to the parabolic strong comparison principle if d2>0, or simple ODE considerations if d2=0. Analogously, since the constant 0 is a solution of the first equation in (2.3), we have that u(t,x)>0 for t>0, x∈Rn.
The quantity v⋆ defined by (2.4) coincides with the value of v where ∂uΦ(0,v) changes sign, i.e.,
We will see in the sequel that v⋆ is the threshold value on v0≡vb which determines the regime of dynamics:
● if vb<v⋆, a small triggering event is followed by a return to calm,
● if vb>v⋆, a small triggering event ignites a burst of social unrest. This is akin to the Hair-trigger effect in KPP equations.
The assumption (2.4) allows us to cover both possibilities of a burst or a return to calm depending on the choice of vb∈(0,1).
The above dichotomy is readily revealed by the analysis of the constant steady states of (2.3). Consider the scalar equation (with unknown u)
under the assumption that f is strictly decreasing and f(1)=0. Call
Note that, since r(⋅) is increasing, the sign of Kb coincides with that of vb−v⋆. We have the following dichotomy:
● If vb<v⋆, then Kb<0, and (2.7) has exactly one solution u=0 (stable). See Figure 1a.
● If vb>v⋆, then Kb>0, and (2.7) has exactly two solutions, u=0 (unstable) and u=u⋆(vb) (stable), defined by
See Figure 1b. Note that v↦u⋆(v) is continuous increasing and that u⋆(v)↘0 as v↘v⋆. For example, if f(u)=1−u and r(v)=v, then v⋆=ω and u⋆(v):=1−ωv.
2.4. Traveling waves
It is reasonable to expect that, when a burst of social unrest occurs, the solution of (2.3) converges to a traveling wave, that is, an identical profile moving at a constant speed. Although we do not prove such a result, we corroborate it with numerical evidence in the sequel. It is thus interesting to study the existence, non-existence, and the shape of traveling waves.
A traveling wave is defined as a solution of (2.3) of the form u(t,x)=U(x⋅e+ct), v(t,x)=V(x⋅e+ct), with c>0, e∈Sn−1 and prescribed values at −∞. The profiles U(ξ) and V(ξ) thus satisfy the elliptic problem
We complete it with the semi-boundary conditions at −∞
The term semi-boundary conditions comes from the fact that we do not impose a prescribed value at +∞. The traveling waves under consideration might not be unique and may take many diverse forms, such as monotone waves or bumps. This will be illustrated in the following sections.
2.5. Comparison with previous models and remarks
Our model is directly inspired by a series of papers [13,16,18] which introduce a system of Reaction-Diffusion equation, comparable to (2.3), to model the dynamics of riots. As before, the quantity u(t,x), depending on time t≥0 and location x∈Rn, represents the level of social unrest, and v(t,x) represents the level of social tension. In most cases, the model reduces to the following system
This model has been first introduced [13].
Let us describe the model (2.12) and discuss the main differences with our model (2.3). The parameters r(⋅), f(⋅) and ω are the same as described in the previous section. The quantity θ>0 stands for the natural relaxation rate on the level of social tension to the base rate vb in absence of any rioting activity.
The function ub(x) stands for the low recurrent rioting activity in the absence of any unusual factors. Accordingly, vb(x) denotes the base level of social tension in absence of any rioting activity. Our model (2.3) corresponds to the case where ub and vb are constant (using the change of variable ˜u:=u−ub).
With non-constant ub(x) and vb(x), the model (2.12) is spatially heterogenous. On the contrary, our model (2.3) is spatially homogeneous. The non-homogeneous setting is however an interesting perspective and is discussed in Section 7.
The parameter p∈R models the feedback of u on v. If p>0, then a burst of u will slow down the relaxation of v; if p<0, then a burst of u will speed up the relaxation of v. If p=0, the system is decoupled. In [16,18], the cases p<0 and p>0 are called respectively tension enhancing and tension inhibiting, however it does not correspond to what we call tension enhancing and tension inhibiting in the present work. Let us be more precise. Assume for simplicity that vb≡0 and S≡0. In (2.12), the cases p>0 and p<0 model respectively a negative and a positive feedback of u on v. However, since −θ1(1+u)pv is negative we deduce that t↦v(t,x) is decreasing and decays to 0, regardless of the sign of p. This implies that any burst of social unrest eventually vanishes. Therefore, both the case p>0 and the case p<0 are contained in what we call tension inhibiting in the present work (Section 4). System (2.12) does not model a situation where a burst of social unrest results in an increase of the social tension. Yet, this case is reasonable from the modeling perspective and allows to account for time-persisting movement of social unrest (see Section 5).
In [13,16,18], the source term S(t,x) accounts for exogenous events. In the present paper, we consider that a single exogenous event occurs at time t=0, and so we encode it in the initial conditions.
In [18], the authors focus on the effect of a restriction of information, which is modeled by substituting the KPP term uf(u) with the combustion term (u−α)+f(u), α∈(0,1), where the subscript + denotes the positive part. The paper [16] considers (2.12) without space (i.e., d=0) and studies the dynamics of the system for a periodic source term
We also mention [76] in which a numerical analysis is conducted to investigate the influence of the parameters on the shape and speed of traveling waves. The article [17] also proposes a model comparable to (2.12) for criminal activity.
A recent work [61] proposes an other reaction-diffusion model to account for the dynamics of social unrest quite different in spirit from the model we discuss here. In [61], u(t,x) represents the number of individuals that take part in the social movement. It is assumed to satisfy the equation
where 0ε, ε, a and h are positive constants. The term 0ε+uε stands for the rate at which people are willing to join the social movement. The nonlinear term au2h2+u2 accounts for a saturation effect. The quantity m(t,x) represents the rate at which individuals exit the movement. It can be thought as a field of non-susceptibility, and is somehow opposite to v in our model. It is assumed in [61] that m is either constant, or given by the explicit formula
or by the equation
Let us emphasize that, for some range of parameters, the equation on u is of the bistable type. For example, if 0ε=0 and m is a constant lying in the interval (ε,ε+a2h), then Eq (2.13) admits three constant steady states (two of them are stable and the third one is unstable). This differs from our model in which u satisfies a monostable equation.
Finally, we mention that many other mathematical approaches have been taken to model the dynamics of riots, protests and social unrest, such as individual-based models [31,34], cost/benefits analysis [27], or diffusion on networks [77].
3.
General properties
In this section, we state general properties on the system (2.3) under the assumptions presented in Section 2.3. These results are established in [15]. Here, we apply the results of [15] in our context and discuss the implications in terms of modeling. In particular, we highlight a threshold phenomenon on the initial level of social tension for a small triggering event to ignite a movement of social unrest.
3.1. Return to calm
First, let us observe that in a context of low social tension, a small triggering event is followed by a return to calm. Mathematically speaking, if vb<v⋆, with v⋆ defined in (2.4), the steady state (u=0,v=vb) is stable with respect to a small perturbation on u. Indeed, from [15,Theorem 1], if d2>0 and v0≡vb<v⋆, then any solution with u0 sufficiently small and compactly supported, satisfies
This has two implications from the modeling point of view. First, it means that a triggering event with small intensity has no effect in the long run. Furthermore, since the convergence is uniform in space, it means that a localized triggering event has a localized effect.
Under the same conditions, but with d2=0, and u0<ε small but not necessarily compactly supported, there holds that
for some constant C independent of u0 and ε. This expresses the fact that a triggering event with small intensity, even if spread out, will have a small effect on the system.
We point out that, in the tension inhibiting case (c.f. assumption (4.1) below), the above results hold true for u0 not necessarily small, see [15,Proposition 6].
3.2. Burst of social unrest
In contrast with the above return to calm, when the initial level of social tension is sufficiently large, an arbitrarily small triggering event ignites a movement of social unrest. This feature is usually called a Hair-trigger effect.
In other words, if v0≡vb>v⋆ defined by (2.4), the steady state (0,vb) is unstable. Namely, from [15,Theorem 1], we know that for any x0∈Rn and r>0, there holds that
This means that even a small event is sufficient to trigger a burst of social unrest, which will drive the system away from the initial condition. This can be put in contrast with the scenario when v0≡vb<v⋆ for which (3.1) occurs.
Aside from property (3.2), the asymptotic behavior of the solution can be diverse, as revealed by numerical simulations presented later on in this paper. Nevertheless, we are able to detail the picture for two important and general classes of systems: the tension inhibiting systems or tension enhancing systems, see Sections 4 and 5 respectively.
3.3. Spatial propagation
Next, we investigate the long-range effect and the geographical spreading of a burst. When v0≡vb>v⋆ given by (2.4), we define
Note that cb<c1 because r(⋅) is increasing and vb<1. Then [15,Theorem 2] states that, for any x0∈Rn and any direction e∈Sn−1, the following hold:
From the modeling point of view, it means that a localized triggering event leads to a movement of social unrest that propagates through space. More precisely, an observer moving at a speed c eventually outruns the propagation if c>c1, whereas, if c<cb, he will face situations away from the quiet state (0,vb).
Properties (3.4) and (3.5) do not allow us to assert the existence of an asymptotic speed of propagation, as usually intended, because of the gap between cb and c1 and also of the fact that we only have a "lim sup" in (3.4) and not a "lim inf". The gap between cb and c1 is filled in the inhibiting case, because we show in [15,Theorem 8] that in this case property (3.5) holds with c1 replaced by cb. That is, in this case, cb is the asymptotic speed of propagation. The numerical simulation in Section 5.3.3 shows that in the general case the asymptotic speed of propagation may be different from both cb and c1. We also show in [15,Theorem 11] that, in the enhancing case, we can replace the "lim sup" with a "lim inf" in (3.4). This means that an observer moving at speed c<cb faces an excited scenario for all sufficiently large times.
4.
Tension Inhibiting – dynamics of a riot
We consider our main Eq (2.3). The tension inhibiting structure relies on following negativity assumptions on Ψ:
In particular, in view of the saturation assumption (2.6), there holds that Ψ(u,0)=0 for all u≥0.
Assumptions (4.1) essentially mean that u has a negative feedback on v (however, we do not assume any monotonicity on u↦Ψ(u,v) as in the SI model (1.1)). As a direct consequence of this assumption and the parabolic comparison principle (or ODE considerations if d2=0), we have that
A typical example of a tension inhibiting system is the SI epidemiology model (1.1). This system enters the general class (2.3) by taking r(v)=v, f(u)=u, and Ψ(u,v)=−uv in (2.3). Note that the SI model is inhibiting for any vb∈(0,1).
As we will see, the tension inhibiting case typically grasps the dynamics of a limited-duration movement of social unrest, that we call a riot. A good heuristics of the behavior of the model is given by a formal analysis of the underlying ODE system. Consider a constant initial datum u0, hence the solutions u(t,x) and v(t,x) of (2.3) do not depend on x. In this case, we easily see that if the initial level of social tension vb is above the threshold v⋆ then the system features a Hair-trigger effect, that is, any triggering event (i.e., u0>0) ignites a movement of social unrest. Then, from assumption (4.1), the level of social tension decreases, until it goes below than the threshold value v⋆. At this point, the level of social unrest begins to fade and eventually goes to 0, while the level of social tension converges to some final state smaller than the initial one.
The same qualitative behavior is observed in the context of epidemiology, where v represents the number of susceptible and the number of infected. When an epidemic spreads out, the susceptible population decreases until it goes below a threshold value, after what the infection dies out.
The goal of this section is to recover, at least partially, the above properties for the PDE general system (2.3). We begin with the study of traveling waves, next we present partial results for solutions of the Cauchy problem. We conclude this section with detailed numerical simulations.
4.1. Traveling waves
Let us first reclaim from [15] the existence and non-existence results for traveling waves, i.e., solutions to (2.10) and (2.11). Recalling that the sign of vb−v⋆ (from definition (2.4)) coincides with the one of Kb (from (2.8)), [15,Theorem 4] implies that the following hold under the inhibiting assumption (4.1):
● if vb<v⋆, there exists no traveling wave;
● if vb>v⋆, there exists no traveling wave with speed c<cb and there exists a traveling wave for any speed c>cb, where cb is defined in (3.3).
Then, we quote from [15,Theorem 5] further qualitative properties of traveling waves, concerning monotonicity and identification of their limit at +∞. Namely, under the inhibiting assumption (4.1), any traveling wave (U,V) satisfies
where V∞∈[0,vb) is a root of Ψ(0,⋅) and moreover V∞≤v⋆. In addition,
Roughly speaking, U has the shape of a bump and V has the shape of a monotone wave.
Recall that assumptions (2.6) and (4.1) yield Ψ(0,0)=0, hence Ψ(0,⋅) has at least one root. If Ψ(0,⋅) has many roots (e.g., if Ψ(0,⋅)≡0 as in the SI model (1.1)), an important issue is the identification of the limiting state V∞ among them. From a modeling perspective, the quantity vb−V∞ measures the amount of social tension dissipated by the movement of social unrest. In the context of epidemiology, vb−V∞ represents the total number of individuals that has been infected during the epidemic. As stated previously, we have the a priori bound V∞≤v⋆ from [15,Theorem 5]. To derive a more precise estimate on V∞, one can integrate the equation on V (and use V′(±∞)=0) to find
Analogously, from U(±∞)=U′(±∞)=0, integrating the equation on U gives
However, this formula is not explicit. In some particular cases (including the SI model (1.1) with d2=0), one can obtain a rather explicit expression for V∞.
Proposition 4.1. Let (U,V) be a solution (2.10)–(2.11) with d2=0, f≡1 and Ψ(U,V)=UG(V), that is
and assume that G<0 on (0,1).
Then, letting Q be a primitive of v↦ω−r(v)G(v), there holds that
In particular, V∞ does not depend on c, nor on d1.
In the particular case of the SI model (1.1) with d2=0, we have
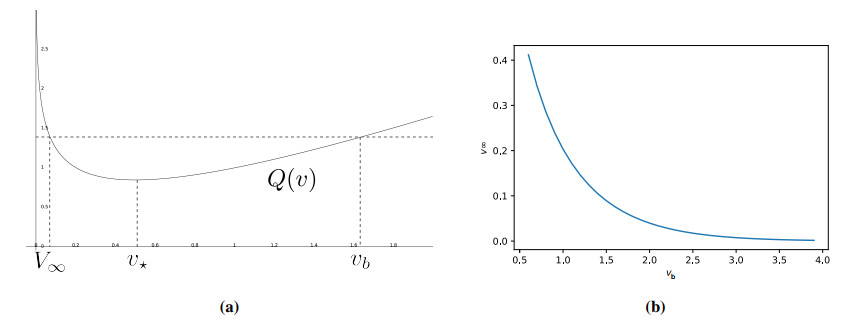
See Figure 2. In this case, V∞ is uniquely determined by the conditions
The numerical values of V∞ as a function of vb are plotted in Figure 2 for β=12. We see that V∞ is a decreasing convex function of vb∈(v⋆,+∞). From a modeling perspective, it means that the higher the initial level of social tension, the lower the final level of social tension after the burst of a riot.
4.2. Large time behavior for the Cauchy problem
We now turn to the more intricate question of studying the large time behavior of solutions to (2.3). Compared with the previous section on traveling waves, we are only able to establish partial results. We have seen in Section 3.1 that when v0≡vb<v⋆, perturbations of the steady state (0,vb) (not necessarily small) eventually disappear as t→+∞. On the contrary, if v0≡vb>v⋆, perturbations do not tend to 0 as t→+∞, at least in one of the (u,v) components, see Section 3.2. However, solutions can exhibit many qualitatively diverse behaviors in general. We are able to obtain some informations in the inhibiting case.
Theorem 4.2. Assume that the inhibiting hypothesis (4.1) holds, that d2>0, and that the dimension is n=1 or 2.
Then any solution of (2.3) satisifes
If in addition v(t,x) converges pointwise to some v∞(x) as t→+∞, then v∞ is a constant in [0,v⋆] and u(t,x)→0 as t→+∞ locally uniformly in x∈Rn.
The first part of Theorem 4.2 is a consequence of [15,Proposition 7] and states that the movement of social unrest vanishes along some sequences of time. We establish in the second part of Theorem 4.2 that, if we assume that v converges as t→+∞, u converges to 0. This means that only the v component matters in the estimate (3.2) for the case vb>v⋆.
As discussed in the previous section about the traveling waves, an interesting question is to estimate the final state v∞. The following result concerns the homogeneous case, i.e., when u0(⋅) is constant.
Proposition 4.3. Assume that (4.1) holds.
Let (u,v) and (˜u,˜v) be the solutions of (2.3) with initial conditions (u0,v0) and (u0,˜v0) respectively, where u0 is constant and v0≡vb, ˜v0≡˜vb. If vb>˜vb>v⋆, the corresponding final states v∞ and ˜v∞ satisfy
Moreover,
The above proposition states that the final level v∞ is decreasing with respect to vb. From the modeling point of view, it implies that a higher initial level of social tension will lead to a lower final level of social tension. On the contrary, the higher the initial level of social tension, the higher the maximal level of social unrest. This enlightens very well the non monotone structure of the inhibiting case.
4.3. Numerical simulations
Let us illustrate the dynamics of (2.3) in the inhibiting case (4.1) with numerical simulations.
4.3.1. Threshold between calm and riot
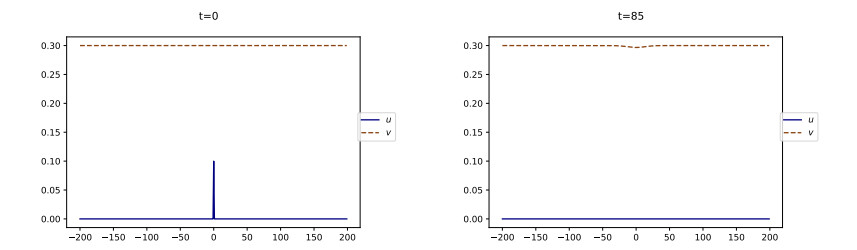
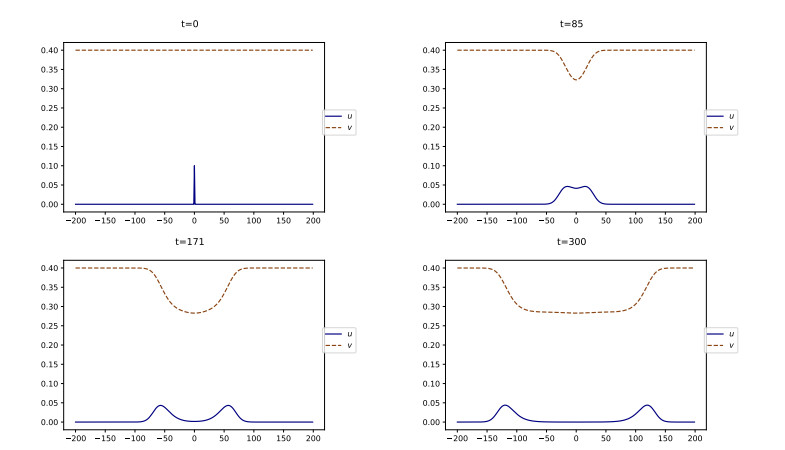
Consider the following particular instance of (2.3):
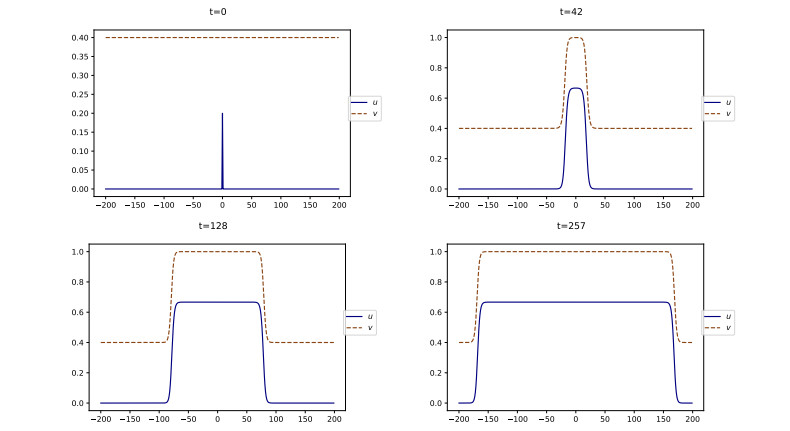
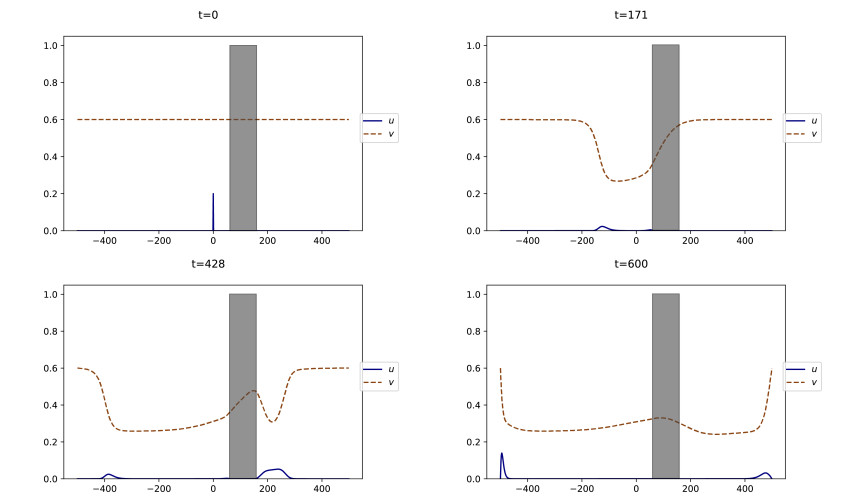
As for the initial datum, we take u0(x)=0.2(1−x2100)+, where (⋅)+ denotes the positive part, and v0≡vb. Observe that any vb∈(0,1) is allowed by the stability hypothesis (2.5). System (4.7) satisfies the inhibiting assumption (4.1). The quantities defined in (2.4) and (2.8) are given by v⋆=110 and Kb=5vb−12.
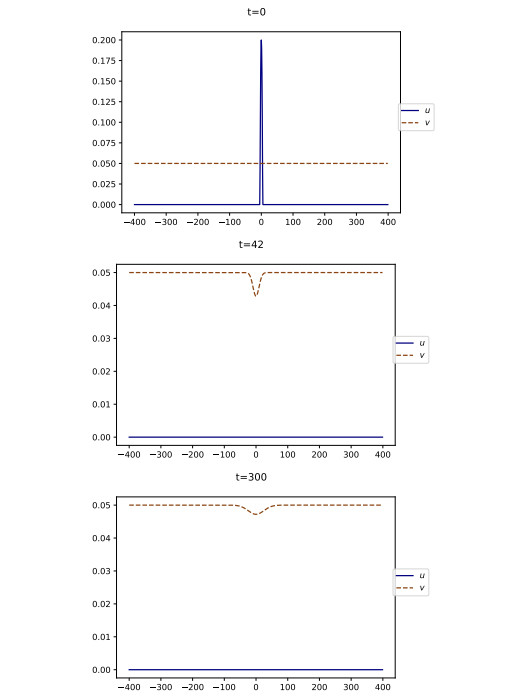
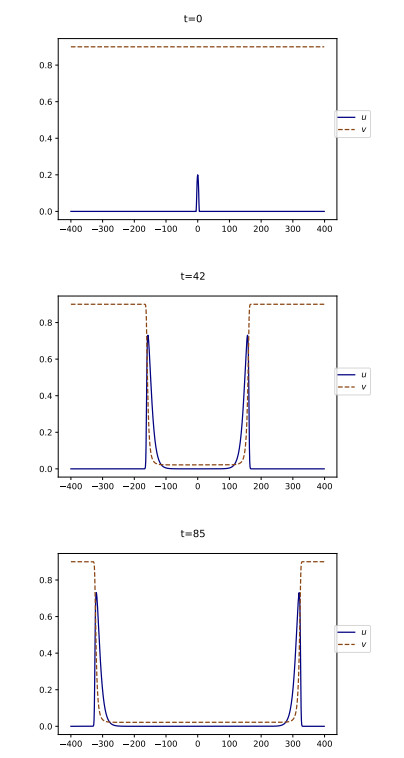
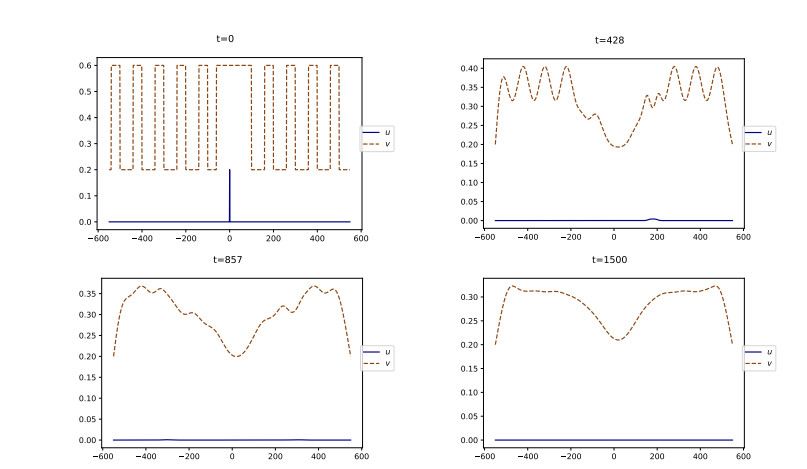
First, if vb<v⋆ we observe in Figure 3 that a triggering event is promptly followed by a return to calm, i.e., u rapidly vanishes. Next, v converges in long time to its initial value vb. This is in agreement with the property (3.1).
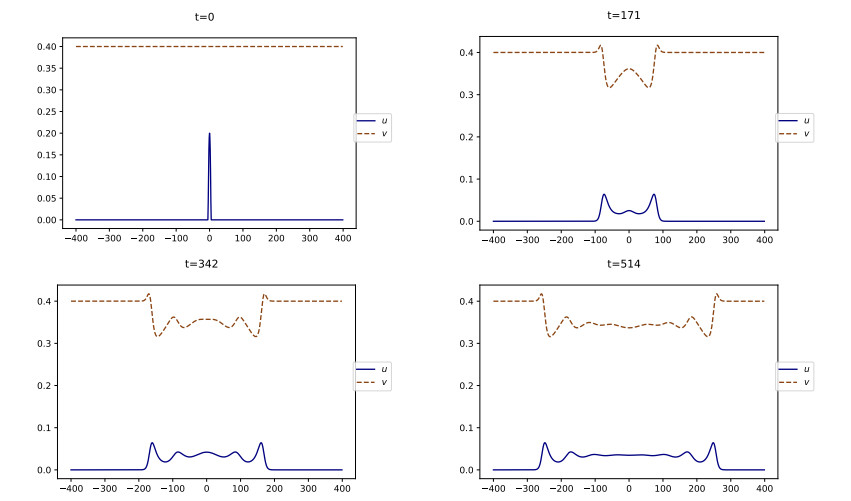
On the contrary, when vb=0.15>v⋆, Figure 4 shows that the solution does not vanish uniformly in space, but rather develops two traveling waves –one leftward and the other rightward– i.e., two fixed profiles propagating at constant speed. This is in agreement with the discussion in Sections 3.2, 3.3. The profile of u has the shape of a bump, while the profile of v is a decreasing wave, as stated in (4.3) and (4.4). The fact that the level of SU decays as t→+∞, which was expected from Theorem 4.2, means that social movements get extinct after some times. Thus, the dynamics describe a limited-duration movement of social unrest, that we call a riot.
4.3.2. Speed of propagation
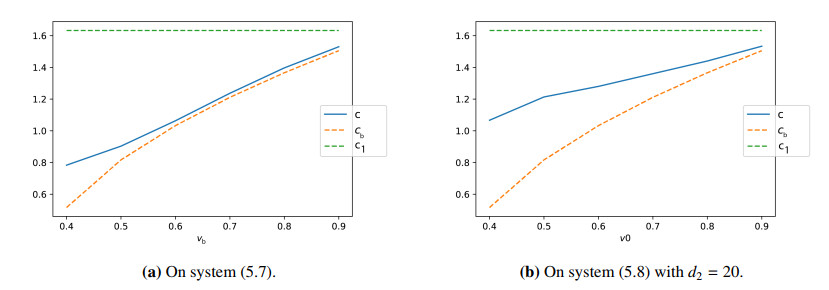
Let us investigate in more details the dependence of the speed of propagation with respect to v0≡vb on the system
We consider u0(x)=0.2(1−x2)+ as an initial datum for u, then we will study the asymptotic speed of propagation as the initial datum for v, v0≡vb, varies in (0,1).
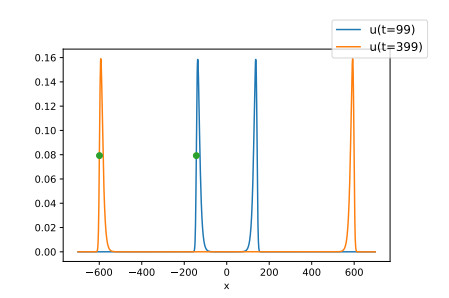
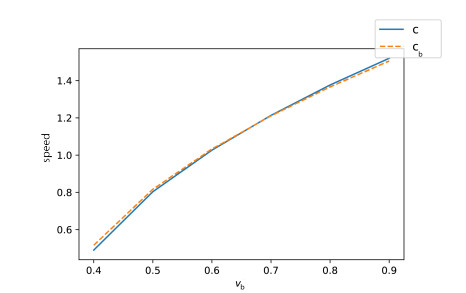
Let us briefly explain how we numerically compute the speed of propagation. For each simulation and two given times t1=99 and t2=399, we track the leftmost locations xi where the solution u(ti,⋅) reaches half its supremum, i.e., the value 12supx∈Ru(ti,x). See Figure 5.
Then, we compute the speed as
We recall that, according to Section 3.3, the speed of propagation of the solution is equal to
We plot in Figure 6 the computed speed c and the theoretical speed cb, and we see that the two speeds are indeed equal.
4.3.3. Eventual level of social tension
As we can see in Figure 4 and Figure 7, the solution (u,v) converges to some (0,v∞) as t→+∞. We can verify numerically that v∞≤v⋆, which is in agreement with Theorem 4.2.
It is an interesting question to estimate more precisely the final level of social tension v∞. Theoretical results in this direction are given by Propositions 4.1 and 4.3. Let us now study this question with numerical simulations.
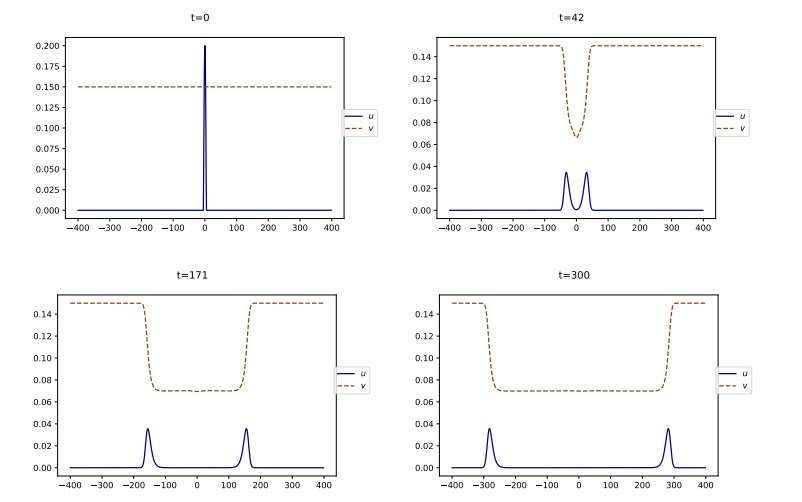
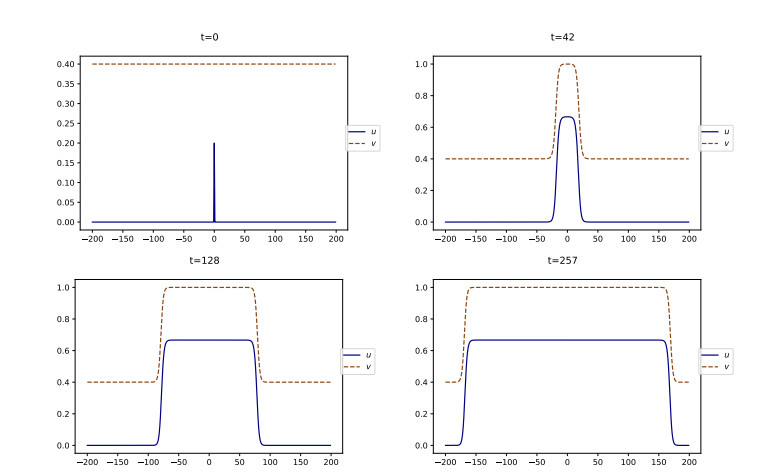
We plot in Figure 7 the simulation of Eq (4.7) with a high initial level of social tension vb=0.9. Compared with the simulation for vb=0.15, in Figure 4, we observe that u reaches higher values, that its shape is sharper, and that the speed of propagation is larger.
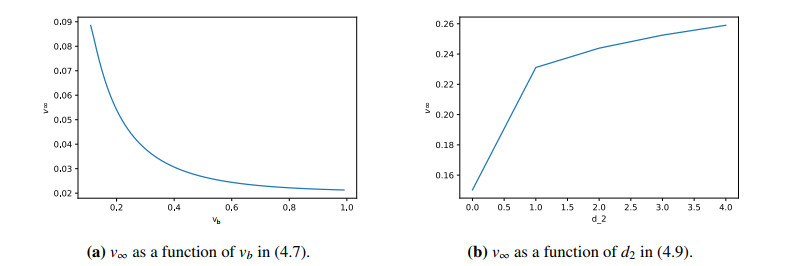
We also observe in Figure 7 that the eventual level of social tension v(t=+∞) is very low. To see this more precisely, we plot in Figure 8a the value of v∞ as a function of vb on the system (4.7). We observe that v∞ is indeed a decreasing function of vb. From a modeling perspective, it means that the higher the initial level of social tension, the lower the final level of social tension. This phenomenon is in agreement with what was observed in Figure 2 for the SI model.
Now, let us focus on the dependence of v∞ with respect to the diffusion on social tension d2. We consider (4.8) with a varying diffusion on the second equation, that is,
We fix v0≡vb=0.5 and u0(x)=0.2(1−x210)+. We plot in Figure 8b the value of v∞ as a function of d2. We observe that d2↦v∞ is increasing. From a modeling point of view, it means that the higher the diffusion on the social tension, the higher the final level of social tension. Heuristically, this is explained by the fact that lim|x|→+∞v(t,x)=vb>v∞ and that, the larger d2, the more v(t,x) is influenced by its value at far distances.
5.
Tension enhancing – dynamics of a lasting upheaval
The tension enhancing structure relies on the following saturation assumptions on f and positivity on Ψ:
The assumption on f accounts for the saturation effect on the level of social unrest. A typical example is to take f(u)=M−u. As a direct consequence, the parabolic comparison principle yields
The assumption on Ψ essentially means that u has a positive feedback on v (we do not assume, however, that u↦Ψ(u,v) is increasing). Again, as a direct consequence of the positivity of Ψ we have that
A typical example of the tension enhancing case is the cooperative system
obtained by taking r(u,v)=v, f(u,v)≡1−u, Ψ(u,v)=uv(1−v) in (2.3).
The tension enhancing assumption typically grasps the dynamics of a persisting movement of social unrest, that we refer to here as a lasting upheaval. A good heuristic of the behavior of the model is given by a formal analysis of the underlying ODE system. Taking u0 constant implies that the solutions u and v of (2.3) do not depend on x. If the initial level of social tension is above the threshold v⋆=ω from (2.4), then any triggering event ignites a burst of social unrest. The level of social tension then increases, which enhances the growth of social unrest. Eventually, both the level of social tension and social unrest converge to an excited state, v→1 and u→u⋆(1)=1−ω from definition (2.9).
We begin by stating qualitative properties for the traveling waves, then we investigate the large time behavior of solutions to (2.3). On this latter question, we obtain more complete results than in the inhibiting case (Section 4), since we prove the convergence of the solution to an excited state as t→+∞. We then present some numerical simulations to illustrate the results and to investigate further properties.
5.1. Traveling waves
Let us first discuss the existence and non-existence of traveling solutions of (2.10)–(2.11) using the results of [15]. Consider the function γ:[c1,+∞)→R defined by
where cb and c1 are defined in (3.3). Because cb<c1, we have that γ is positive and decreasing, with γ(c1)=12√1−c2bc21 and γ(+∞)=0. Let us define
We point out that
Recall that the sign of vb−v⋆ (from definition (2.4)) coincides with the one of Kb (from (2.8)).
Under assumptions (5.1), we know from [15,Theorem 4] that if vb>v⋆ then the following hold:
● there exists no traveling wave with speed c<cb;
● there exists a traveling wave with any speed c>cγ.
In particular, if d2 is sufficiently small, then cγ=c1, and so there exists a traveling wave for any c>c1.
We then reclaim [15,Theorem 9] which eastablish properties on the shape of the traveling waves. Namely, under the enhancing assumption (5.1), any traveling wave satisfies
We also recall that u⋆(1) is defined in (2.9) as the only positive root of r(1)f(⋅)−ω. Note that, contrarily to the analogous result in the inhibiting case in (4.3) and (4.4), we are here able to determine explicitely the limit of U in +∞.
5.2. Large time behavior for the Cauchy problem
In the previous section, we have identified the limits of traveling waves as ξ→+∞. We now show that the same limits hold for the solution of (2.3) as t→+∞.
Theorem 5.1. Assume that (5.1) holds and that vb>v⋆. Then any solution of (2.3) with v0≡vb and u0 compatcly supported satisfies
locally uniformly in x∈Rn.
This theorem states that the level of social unrest converges to a sustainable excited state u⋆(1). From a modeling point of view, this corresponds to a persisting social movement, that we refer to as a lasting upheaval.
5.3. Numerical simulations
In this section we provide some numerical illustrations of the dynamics of system (2.3) in the enhancing case (5.1).
5.3.1. Threshold between calm and lasting upheaval
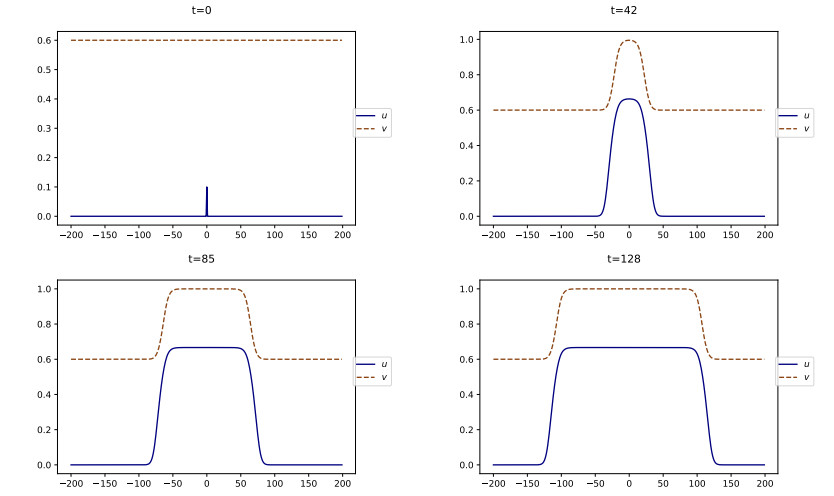
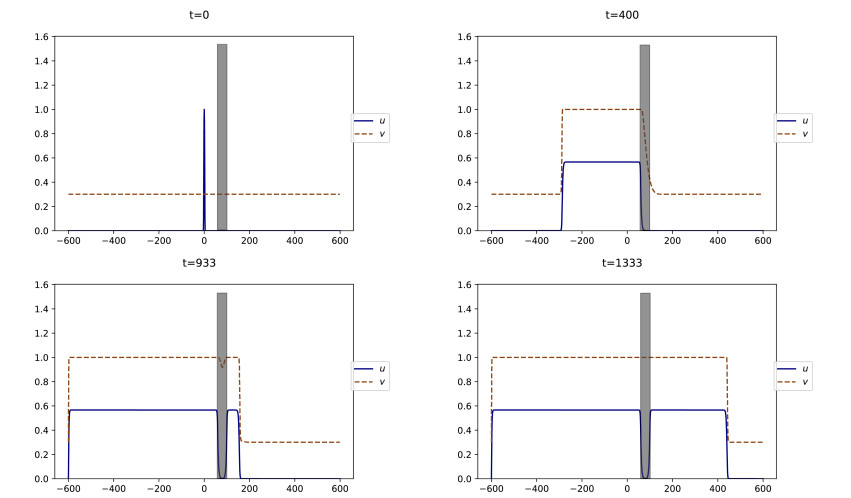
Let us consider the following particular instance of (2.3) satisfying the enhancing assumption (5.1):
with initial condition u0(x)=0.2(1−x2)+ and v0≡vb ranging in (0,1). In this case we have v⋆=1╱3 and Kb:=vb−1╱3.
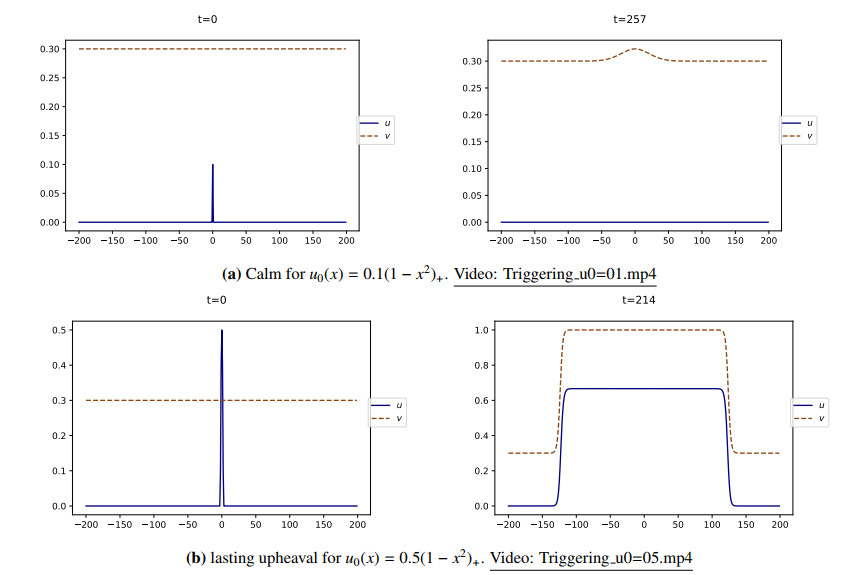
Figure 9 refers to the case vb<v⋆. We observe there that a triggering event is promptly followed by a return to calm, namely, u rapidly vanishes. Next, v converges in long time to its initial value vb. This is in agreement with the discussion in Section 3.1. Let us emphasize, however, that this is only true when considering a sufficiently small initial condition u0(x), see Section 5.3.2 for more details.
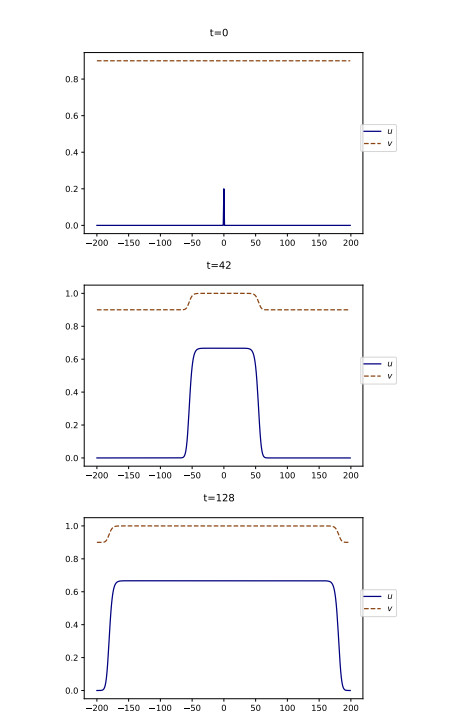
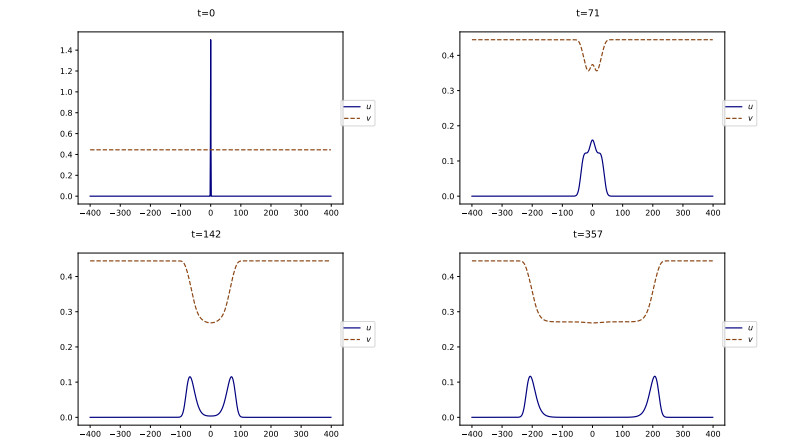
On the contrary, if vb>v⋆, a small triggering event ignites a burst of social unrest that spreads through space, as can be seen on Figure 11. This is in agreement with Sections 3.2 and 3.3. More precisely, the simulation shows that the solution converges to two traveling waves, one leftwards and the other one rightwards, i.e., two fixed profiles moving at a constant speed. The profiles for both u and v have the shape of monotone waves, as stated in Equation 4.4. In addition, the solution converges pointwise to (u⋆(1),1) as t→+∞, in agreement with Theorem 5.1.
Since the asymptotic state as t→+∞ features a positive level of activity, the dynamics describe a persisting movement of social unrest, that we call a lasting upheaval.
5.3.2. Magnitude of the triggering event
In the tension enhancing case, the magnitude of the triggering event (i.e., the size of u0(x)) may be of crucial importance to determine the regime of the dynamics when v0≡vb<v⋆. This has to be put in contrast with tension inhibiting case (described in Section 4) for which the regime of the dynamics do not depends on the size of u0(x).
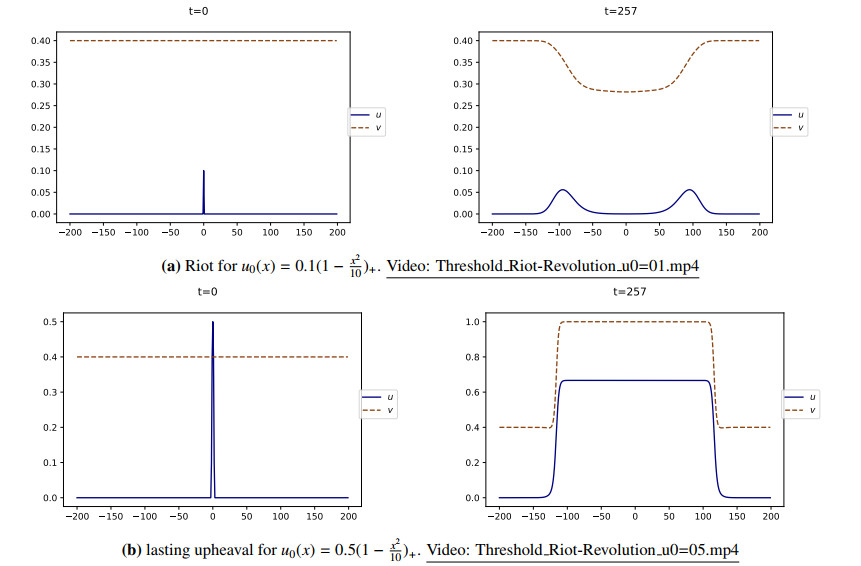
Figure 12 depicts two distinct dynamics for system (5.7) corresponding to vb=0.3<v⋆=1/3: the initial condition u0(x)=0.1(1−x2)+ exhibits a return to calm, see Figure 12a, whereas u0(x)=0.5(1−x2)+ ignites a lasting upheaval, see Figure 12b.
The phenomenon depicted by Figure 12 can be explained by the following heuristic: if u0 is large enough, then u(t,⋅) remains at high values for a sufficiently long time so that v increase and reach values above the threshold v⋆.
5.3.3. Speed of propagation
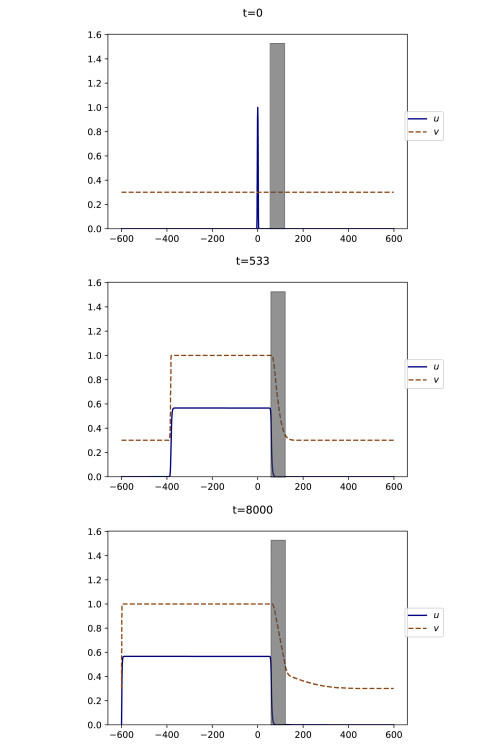
We see in Figure 11 that, if the initial level of social tension vb is above the threshold v⋆, the solution of (5.7) propagates through space at a constant speed. If we increase the initial social tension, we observe that the solution propagates faster through space. See Figure 13 for a numerical simulation of (5.7) with vb=0.9.
To see this phenomenon more clearly, we plot the speed of propagation c of the solution of (5.7) as a function of vb in Figure 14a (the speed is computed with the method presented in Section 4.3.2). We see that c is indeed an increasing function of vb.
The theoretical result presented in Section 3.3 states that c ranges in (cb,c1) defined in (3.3). This is confirmed numerically in Figure 14a.
Figure 14a could suggest that c≈cb, or that c does not depend on the equation on v (i.e., d2 and Ψ) like in the inhibiting case (Section 4.3.2). However, numerical experiment shows that it is not the case in general. This is a substential difference with the inhibiting case, for which c=cb. To see this, let us consider the same system (5.7) with a diffusion coefficient d2 on the second equation:
We plot in Figure 14b the speed of propagation c of the solution of (5.8) with d2=20 as a function of vb. We see that c and cb largely differ, especially for small values of vb. This is a numerical evidence that vb depends on d2. Fixing vb=0.9, we see on Figure 15a that c is indeed an increasing function of d2. Again, this has to be put in contrast with the inhibiting case, for which c=cb does not depend on d2.
Let us now investigate how the speed depends on the magnitude of Ψ. Consider the analogous of system (5.7) with a variable magnitude for the reaction term in the second equation, namely,
where k≥0 is a parameter, and vb=0.5. We plot the speed c as a function of k in Figure 15b. We see that c is an increasing function of k, and so that it indeed depends on the magnitude of Ψ.
These observations motivate the following questions.
Open problem: Do we have limd2→+∞c=c1 in (5.8)? Do we have limk→0c=cb or limk→+∞c=c1 in (5.9)?
6.
Mixed cases
We propose in this section to focus on some particular instances of (2.3) which exhibit more complex behaviors. We begin with a model featuring a double threshold phenomenon which can give rise to both ephemeral riots and lasting upheaval. Next, we present other models where oscillating traveling waves appear.
6.1. Double threshold: calm-riot-lasting upheaval
Consider the system
and some initial conditions u0(x)≩0 and vb∈(0,1). We find v⋆=1/3 from definition (2.4). Depending on the value of vb, we have the following dichotomy:
● if v0≡vb<1/2: the system is tension inhibiting (4.1),
● if v0≡vb>1/2: the system is tension enhancing (5.1).
Indeed, note that v0<1/2 implies that v(t,x)∈(0,1/2) and v0>1/2 that v(t,x); one can thus restrict Ψ to a suitable range where Ψ(⋅,v(t,x)) is either positive or negative.
We can then apply the results of the previous sections to infer that a small triggering event can lead to three different situations:
● For a small initial level of social tension vb∈(0,v⋆): return to calm (Section 3).
● For an intermediate initial level of social tension v∈(v⋆,1/2): burst of an ephemeral riot (Section 4).
● For a high initial level of social tension v∈(1/2,1): burst of a lasting upheaval (Section 3).
From the modeling point of view, this double threshold phenomenon means that, in the model (6.1), the initial level of social tension determines whether a small triggering event ignites a social movement, and also whether the movement will be ephemeral or persisting.
We propose to illustrate this double threshold phenomenon with numerical simulations of (6.1). We take v0≡vb∈(0,1) and u0(x)=0.1(1−x2)+. Figure 16 illustrates the return to calm for vb=0.3; Figure 17 the propagation of a riot for vb=0.4; Figure 18 the propagation of a lasting upheaval for vb=0.6.
6.2. Oscillating traveling waves
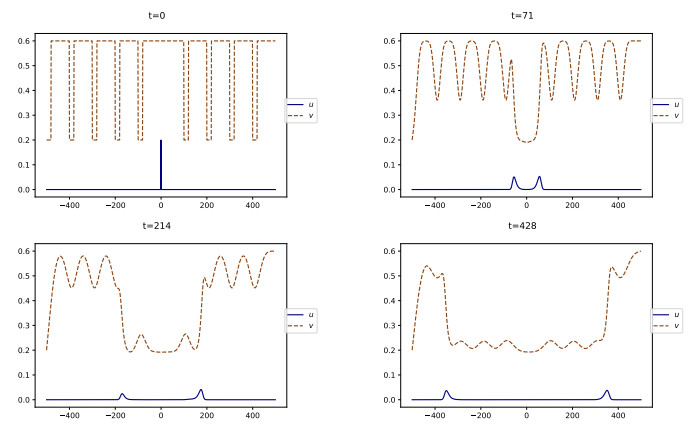
We saw in Sections 4.1 and 5.1 that the traveling wave can have the shape of a bump or a monotonic wave. Yet, some traveling waves may have a more complex shape. For example, consider the following particular instance of (2.3)
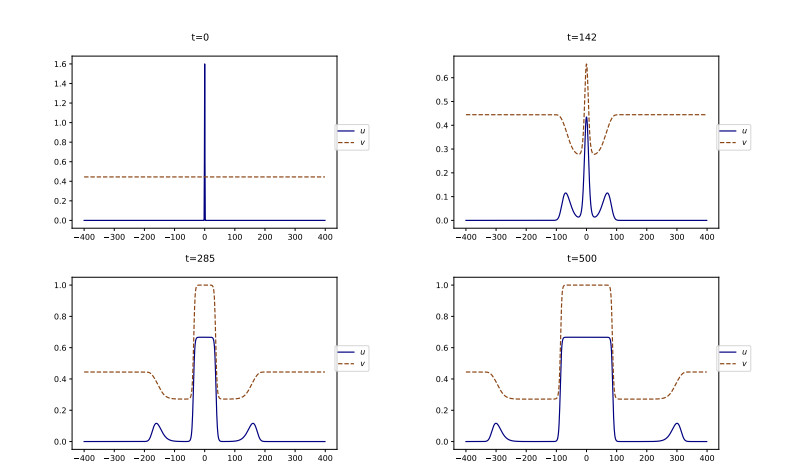
We see in Figure 19 that the solution converges to a traveling wave which features damped oscillations on its tail.
We suspect that some well-chosen parameters could generate travelings wave with undamped oscillation; yet, we are not able to produce such an example.
6.3. Magnitude of the triggering event and terraces
As described in Section 5.3.2, when the system is not tension inhibiting, the magnitude of the triggering event (i.e., the size of u0) may be of crucial importance to determine the regime of the dynamics when v0≡vb<v⋆.
The same phenomenon may occur even in the case v0≡vb>v⋆. Indeed, consider the system
We find v⋆=1/3 from definition (2.4). Fixing v0≡vb>v⋆ close to the threshold 1/2, we expect that the magnitude of the triggering event determines whether the dynamics give rise to an ephemeral riot or a lasting upheaval. We see in Figure 20a that, taking vb=0.4 and u0(x)=0.1(1−x210)+, system (6.3) gives rise to an ephemeral riot. On the contrary, with the same initial level of social tension vb=0.4, but with a larger triggering event u0(x)=0.5(1−x210)+, we observe a lasting upheaval in Figure 20b.
There are also some examples where a sufficiently large triggering event generates a fast riot followed by a slower persisting upheaval. Mathematically speaking, this consists of a terrace, that is, the superposition of two traveling waves traveling at different speeds. Consider
with vb=0.44 and u0=ε(1−x2)+. Taking ε=1.5, we see in Figure 21 that the dynamics correspond to that of a riot. However, if we consider a triggering event with a larger magnitude by taking ε=1.6, we observe a terrace in Figure 22, featuring an ephemeral riot followed by a lasting upheaval (the traveling speed of the upheaval equals approximately half the one of the riot).
The same phenomenon can also be observed on the following example
for vb=0.5 and u0=ε(1−x2)+. Loosely speaking, this system can be interpreted as tension inhibiting for u<1/4 and tension enhancing for u>1/4. We observe a riot for ε=0.5 (video: Terrace2_eps = 05.mp4) and a terrace consisting of a riot followed by a lasting upheaval for ε=0.6 (video: Terrace2_eps = 06.mp4).
7.
Spatially heterogeneous models
Data show that the dynamics of social unrest is highly influenced by many factors that are not homogeneous in space, such as the density of population, poverty, etc. See, e.g., [20]. An interesting extension of our model is to introduce spatial heterogeneity in the system (2.3). In this section, we propose some possible ways to do this and provide some numerics.
7.1. Gap problem
The first approach to account for space heterogeneity is to assume that the function Φ(u,v) (which, we recall, stands for the growth of the level of social unrest u) depends explicitly on the space variable x. We may assume that some areas in space are not favorable to the growth of social unrest. It is then an interesting problem to determine whether a propagating movement of social unrest can overcome those areas.
For some interval K:=(a,a+L), representing the gap (or the obstacle), we choose Φ of the form
Namely, in dimension n=1, we consider the system
We ask the following question: is there a threshold on the length L of the obstacle above which the propagation of the solution is blocked?
First, let us remark that, if v0≡vb>v⋆, then our system enjoys a Hair-Trigger effect: it means that arbitrarily small initial conditions ignites a social movement (see Sections 3.1 and 3.2). Since, for all t>0, we have that u(t,⋅)>0, we deduce that there exists no gap that can block the propagation. We illustrate this remark with a numerical simulation on Figure 23 for the system (4.8), that is
with vb=0.6 (we recall that v⋆=1/3) and u0(x)=0.2(1−x2)+. We see on Figure 23 that a riot begins to propagate, but then fades as it reaches the obstacle. However, after some times, the riot grows again and continue to propagate beyond the obstacle.
However, if we are in a situation where v0≡vb<v⋆ but u0 is large enough to triggers a social movement (as described in Sections 5.3.2, 6.3), there might exists a length L above which the gap blocks the propagation. Let us consider the following system
with vb=0.3 and u0(x)=(1−x210)+. We plot in Figure 24 a numerical simulation of the above system for L=40. We observe that an upheaval propagates until it reaches the obstacle. Then, after some time, the upheaval manages to overpass the obstacle and continue to propagate. If now we increase the length of the gap to L=60, we see in Figure 25 that the spreading of the upheaval is blocked by the gap (even after a long time).
Of course, one could also consider that Ψ depends on the space variable x, but we omit this case for conciseness.
7.2. Non-uniform initial social tension
So far, we have only dealt with a constant initial level of social tension v0≡vb (although more general results are available in [15] when v0−vb is compactly supported). Another way to encode space heterogeneity in our model is to consider the case of a non-constant initial level of social tension v0. This case is relevant from a modeling perspective, since the social tension may indeed vary between, for examples, cities and suburbs, or poor and rich areas (see [20]). To account for this situation with a model case, we may assume that v0(x):=v(t=0,x) is periodic and oscillates around the threshold v⋆.
Consider the inhibiting system (4.8), that we recall here,
with u0(x)=0.2(1−x2)+ and
for some parameter L∈(0,100). We recall that, for Eq (7.4), we have v⋆=13 (where v⋆ is defined in (2.4)). Therefore, v0(x) oscillates periodically around v⋆, creating zones of length 100−L that are favorable for propagation (v0(x)=0.6>v⋆), and zones of length L that are unfavorable (v0(x)=0.2<v⋆). If the favorable zone is sufficiently large, then the solution manages to propagate, as can be seen on Figure 26 for L=20. On the contrary, if the favorable zone is too thin, then the propagation is blocked, as can be seen on Figure 27 for L=60. (We point out that, for the numerical simulation, we impose v0(x)=0.6 on (−60,60) to ensure that the movement of social unrest gets properly ignited at x=0 before being affected by the oscillations of vb).
We leave for future works the rigorous analysis of the case of a non-constant initial level of social tension v0(⋅)≡vb(⋅). In this case, however, let us indicate that the threshold phenomenon on the initial level of social tension may not involve the sign of vb−v⋆, but rather the sign of λb defined as the lowest eigenvalue of the operator, ∀φ∈C2(Ω),
and given by the expression
7.3. Including geometry
Another possible way to include spatial heterogeneity in our model is to consider the system (2.3) on a domain Ω⊂Rn rather than on the entire space. We may impose Neumann boundary condition
with ∂ν the outer normal derivative, accounting for the fact that there is no flux of individuals across the boundary.
From the modeling point of view, the boundary ∂Ω could stand for various structural spatial obstructions for rioters, such as streets, highways, fences, rivers, mountains etc. These features play sometimes a significant role; for example, the ring around Paris in the 2005 riots [20].
Mathematically speaking, it is known that heterogeneous geometry can largely affect the propagation properties of Reaction-Diffusion equations (e.g., see [11,29]). However, fewer papers deal with systems of Reaction-Diffusion such as our system (2.3). We leave further investigations on this topic for future works.
8.
Proofs
8.1. The tension inhibiting case
We begin with the proof of Propositions 4.1 and 4.3.
Proof of Proposition 4.1. First of all, we know from (4.3) that U(±∞)=0, whence U′(±∞)=0 by elliptic estimates. From the equation on V, we get
Injecting this formula into the equation on U, and integrating over (−∞,+∞) we find
that is,
and so Q(V∞)−Q(vb)=0
Proof of Proposition 4.3. The smallness of u0 is determined by the following condition:
which can be achieved since vb≥˜vb>v⋆ and so r(v)f(0)>ω for all v∈[˜vb,˜v]. For all time t≥0, both u(t,⋅) and v(t,⋅) are constant. We thus omit to write the dependence on x. The proof relies on a simple argument in the phase plane. Denote γ(t) and ˜γ(t) the trajectories in the plane (u,v), namely γ(t):=(u(t),v(t)) and ˜γ(t):=(˜u(t),˜v(t)). By the inhibiting assumption (4.1), these trajectories are nonincreasing in the v component and, by Theorem 4.2, they have two endpoints (0,v∞), (0,˜v∞) respectively. In addition, by uniqueness of solutions of the Cauchy problem, they cannot cross each other, nor can γ cross the segment {u0}×(˜vb,vb), because there u′>0 thanks to (8.1). The result then follows.
Let us now turn to the proof of Theorem 4.2. The first statement of the theorem is a consequence of [15,Proposition 7]. In order to prove the second statement, we make use of the following classical lemma, whose proof is inspired from that of [10,Theorem 1.8].
Lemma 8.1. Let w∈C2(Rn) be a bounded function satisfying wΔw≥0 in Rn. If n≤2, then w is constant.
Proof. For R>0, we define a cut-off function
for χ a smooth nonnegative function such that
Multiplying the equation on w by χ2R, integrating on Rn and using the divergence theorem, we find
Using the Cauchy-Schwarz inequality, we deduce
where BR is the ball of radius R and center 0. Recall that w is bounded and that |∇χR|2≤R−2‖∇χ‖∞. As n≤2, we deduce that
From (8.2), we have that ∫Rnχ2R|∇w|2 is uniformly bounded. Therefore, ∫B2R∖BRχ2R|∇w|2 converges to 0 as R→+∞, and so the term on the left-hand side of (8.2) also converges to 0. At the limit, we find ∫Rn|∇w|2≤0. Hence ∇w≡0, which ends the proof.
Proof of the second statement of Theorem 4.2. Assume that v(t,x) converges pointwise to some v∞(x) as t→+∞. From classical parabolic estimates, the convergence actually occurs in C2loc. Since ∂tv−Δv≤0, when t→+∞ we find
Lemma 8.1 implies that v∞ is constant.
We claim that v∞≤v⋆. By contradiction, assume v∞>v⋆, then, for t large enough, u satisfies
with α:=v∞+v⋆2>v⋆. Thus, u is a supersolution of a classical KPP equation, we deduce
We reach a contradiction with the first assertion of Theorem 5.1, namely (4.6), which we proved previsouly.
Finally, let us show that u(t,⋅) converges locally uniformly to 0 when t→+∞. Let us first consider the case v∞≠0. By contradiction, assume that there exists a diverging sequence of times tk>0 and a ball B⊂Rn such that
We use the notation
Since v∞∈(0,1), the inhibiting assumption (4.1) implies
From the equation on v, we can write
From the convergence of v(t,⋅), we deduce that u(t,⋅)˜Ψ(t,⋅) converges locally uniformly to 0 as t→+∞. From (8.5), we thus have that u(tk,x) converges to 0 as k→+∞ and x∈B: we reach a contradiction with (8.4).
Let us now consider the case v∞=0. Fixing ε∈(0,v⋆), for t large enough u satisfies
where C:=ω−r(ε)f(0)>0. It proves that u(t,⋅) converges uniformly to 0 as t→+∞.
8.2. The tension enhancing case
Let us prove Theorem 5.1 which deal with the asymptotic behavior of the solution in the tension enhancing case. The proof follows the same line as the proof of Proposition 10 in [15] but, here, we derive a more precise result on the limit of U in +∞, and so we give a full proof for completeness.
Proof of Theorem 5.1 in the case d2>0. First of all, we know from Lemma 2.1 that u>0 and 0<v<1 for all t>0, x∈Rn. The proof is achieved in four steps: we first derive an upper bound for u, next a lower bound for v, then for u, and we finally conclude.
Upper bound for u.
Let us derive the upper bound for u as t→+∞. We see that, by the monotonicity of r,
where f+:=max{f,0} is the positive part of f. Let U be the solution of the ODE U′=U(r(1)f+(U)−ω) with initial datum U(0)=max{M,supu0}. There holds that U↘u⋆(1) given by (2.9), i.e., the zero of u↦r(1)f(u)−ω, whose existence and uniqueness is guaranteed by (2.4) and (5.1). Then, by comparison, we get the desired upper bound:
It follows that there exist M′<M and T>0 such that
Lower bound for v.
Consider a sequence (xk)k∈N in Rn such that |xk|→+∞. By parabolic estimates, the functions u(⋅,xk+⋅), v(⋅,xk+⋅) converge (up to subsequences) as k→+∞, locally uniformly in [0,+∞)×Rn, to some functions ˜u, ˜v which are still solutions of (2.3), with initial datum (0,vb). Hence (˜u,˜v)≡(0,vb) because Φ(0,vb)=Ψ(0,vb)=0. This means that (u(t,x),v(t,x))→(0,vb) as |x|→+∞, for any given t≥0. In particular, for any fixed t≥0 and v_∈(v⋆,vb), we have that v(t,x)>v_ for |x| sufficiently large. Moreover, (5.1) and (8.6) imply that Ψ(u,v)>0 for t≥T, x∈Rn, that is, v is a supersolution of the heat equation, and we know that at time T it is larger than v_ outside a large ball. By comparison with the heat equation, one readily deduces that, for given v_′∈(v⋆,v_), there exists T′>T such that
Lower bound for u.
Consider the equation
which is a standard scalar KPP equation. Observe indeed that r(v_′)f(0)−ω>0>r(v_′)f(M)−ω by the definition (2.4) of v⋆ and (5.1). We consider the solution of this KPP equation starting at time T′ with the datum ˆu(T′,x)=min{u(T′,x),u⋆(v_′)}, where u⋆(v_′)>0 is given by (2.9), i.e., r(v_′)f(u⋆(v_′))=ω. It follows from the classical result of [5] that ˆu(t,x)↗u⋆(v_′) as t→+∞, locally uniformly in x∈Rn. For t≥T′, using that ˆu(t,⋅)≤u⋆(v_′) and v(t,⋅)≥v_′ by (8.7), we see that ˆu is a subsolution of the first equation in (2.3), whence, by comparison,
Conclusion.
Let (tk)k∈N be an arbitrary sequence diverging to +∞. The functions u(tk+⋅,⋅), v(tk+⋅,⋅) converge (up to subsequences) as k→+∞, locally uniformly in R×Rn, to some functions u∞, v∞ which are entire solutions (i.e., for t∈R, x∈Rn) of the equations in (2.3). Moreover, (8.6), (8.7), (8.8) yield u⋆(v_′)≤u∞≤u⋆(1) and v∞≥v_′. From (5.1) we deduce that necessarily v∞≡1 and then that u∞≡u⋆(1).
Proof of Theorem 5.1 in the case d2=0. We immediately see that 0<u<max{supu0,M}, owing to (5.1) and the parabolic strong maximum principle, and that 0<v<1, by elementary ODE considerations, for all t>0, x∈Rn. Moreover, we observe that the upper bound (8.6) for u is derived in the above proof for the case d2>0 only by arguing on the first equation in (2.3), hence it holds true when d2=0. We want to derive now the upper bound
for some possibly very large R. For this we consider, for any given direction e∈Sn−1, the function
It is readily seen that there exists σ sufficiently large so that this is a supersolution of the first equation in (2.3). Moreover, since u0 is compactly supported, we can choose σ, possibly even larger and independent of e, so that in addition ue(0,x)>u0(x) for all x∈Rn. Therefore, by comparison, u≤ue for all t≥0 and x∈Rn, which, being true for any e∈Sn−1, yields u(t,x)≤eσ(t+1)−|x|. We deduce in particular that u(t,x)<M for all t∈[0,T) an |x|≥σ(T+1)−logM. Combining this with (8.6) eventually gives (8.9) with R=σ(T+1)−logM.
We now use the upper bound (8.9) for u in the equation for v. Owing to (5.1), it implies that, for t≥0 and |x|≥R, ∂tv=Ψ(u,v)>0, hence
Let us derive a lower bound on u. Let λρ be the Dirichlet principal eigenvalue of −Δ in Bρ, and φρ be the associated (positive) eigenfunction. It is well known that λρ↘0 as ρ→+∞, hence in particular d1λρ<r(vb)f(0)−ω for ρ large enough, because vb>v⋆ defined by (2.4) and therefore r(vb)f(0)>ω. It follows that, for such a ρ and for ε>0 small enough,
whence, by (8.10), εφρ(x−x0) is a subsolution to the first equation in (2.3) for t>0 and x∈Bρ(x0) whenever |x0|>R+ρ. Take x0 satisfying |x0|>R+ρ and ε>0 small enough so that the above property holds and moreover εφρ(x−x0)<u(1,x) for all x∈Bρ(x0). The comparison principle yields u(t,x)>εφρ(x−x0) for all t≥1, x∈Bρ(x0), thus, using the parabolic Harnack inequality, we find, for any compact set K⊂Rn,
We are now in a position to conclude. For s≥0 call
This function satisfies g(s)>0 for s∈(0,1) by (5.1) and g(1)=0 by (2.6). For t≥max{T,2} and x∈K, since m≤u(t,x)≤M′ by (8.6) and (8.11), we see that
As a consequence, because minx∈Kv(max{T,2},x)>0, by the continuity of v, we infer that v(t,x)→1 as t→+∞ uniformly in x∈K. We have thereby shown that v(t,x)→1 as t→+∞ locally uniformly in x∈Rn. Finally, for any sequence (tk)k∈N diverging to +∞, the function u(tk+⋅,⋅) converges (up to subsequences) as k→+∞, locally uniformly in R×Rn, to a nonnegative, bounded solution ˜u of
which satisfies ˜u(t,x)≥m for all t∈R, x∈K thanks to (8.11). It is a straightforward consequence of [5] that the only entire solution of this standard KPP equation satisfying such a property is ˜u≡u⋆(1). This concludes the proof.
9.
Conclusions
9.1. Main findings
An increasing number of papers consider systems of Reaction-Diffusion equations to model the dynamics of epidemics or collective behaviors such as riots. However, most of the work study particular and different cases. In this paper, we try to propose a unified mathematical approach, based on the theoretical framework developed in [15]. Although we focus on the problem of modeling social unrest, our goal is to keep a rather general mathematical approach that can be transposed to other topics in social dynamics.
Our model involves two quantities, the level social unrest u and the level of social tension v, which play asymmetric roles. We examine the problem of a system initially at equilibrium u=0, v=vb, for which a triggering event u0(⋅)≩0 occurs at t=0. After stating our modeling assumptions, we derive the Reaction-Diffusion system (2.3).
In Section 3, we highlight a threshold phenomenon on the initial level of social tension v0≡vb. On the one hand, if vb is below a threshold value v⋆ and the triggering event is small enough, the system returns to equilibrium quickly, and we speak of a return to calm. On the other hand, if vb is above v⋆, an arbitrarily small triggering event causes an eruption of social unrest. Then, the movement of social unrest spreads through space with an asymptotically constant speed.
We are able to derive more complete theoretical and numerical results on two subclasses of models. The first one, called tension inhibiting, is such that the movement of social unrest dissipates social tension. Once the level of social tension falls below the threshold value v⋆, in turn, the level of social unrest fades until it is extinguished as t→+∞. This behavior is exhibited by both traveling wave solutions, c.f. (4.3), as well as by solutions of the Cauchy problem, c.f. Theorem 4.2. Tension inhibiting models thus give rise to limited duration movement of social agitation, that we call "riots". An interesting property is that the intensity of the triggering event has no influence on the qualitative dynamic of the system. We numerically observe that the solution converges to two opposite traveling waves moving with the speed cb:=2√r(vb)f(0)−ω (which does not depend on the parameters of the equation on v) and link the steady state (0,vb) to another one (0,v∞), the profile of u having the shape of a bump, and that of v a monotonous decreasing wave, linking. We also invesigate theoretically and numerically the question of estimating the final level of social tension v∞, revealing the non-monotonic structure underlying the inhibiting system, see Theorem 4.3.
The second specific class of models we examine is the tension enhancing. For such systems, if the initial level of social tension vb is higher than the threshold value v⋆, the dynamics gives rise to a movement of social agitation that converges in a long time to a sustainable excited state. This case typically accounts for time-persisting social movements, which we call here lasting upheaval. We numerically observe that if vb<v⋆, the solution converges towards two opposite traveling waves, whose speed can take intermediate values between cb and c1:=2√r(1)f(1)−ω (depending on the parameters of the equation on v, c.f. Figure 15). These waves connect (0,vb) to (u⋆(1),1) (defined in (2.9)), the profiles of u and v having the shape of increasing waves, c.f. Theorem 4.4. If vb<v⋆, contrarily to the tension inhibiting case, we observe that a sufficiently strong triggering event can still ignite a lasting upheaval, see Figure 12.
The tension inhibiting and tension enhancing classes of models give a good idea of the variety of behaviors that our model can generate. In Section 6, we examine mixed cases that exhibit more complex behaviors; some models feature a double threshold effect between return to calm, riot and lasting upheaval, others generate oscillating traveling waves or terraces (consisting of a riot followed by a lasting upheaval).
In Section 7, we propose several ways to include spatial heterogeneity in our model. We first consider the case of heterogeneous coefficients and study how an obstacle (i.e., an area of depressed growth for social unrest) affects the propagation of a social movement. On the one hand, if vb>v⋆, the propagation of the social movement is guaranteed in any case. On the other hand, if vb<v⋆, propagation is only possible if the triggering event is sufficiently large and the gap is sufficiently small. We then consider the case of an initial level of social tension v0 that is not constant. This case accounts for the variability of populations according to the neighborhood (for example, between a city and its suburbs) which may have a significant impact on social movement according to data. Finally, we mention that our framework allows to include geometrical heterogeneity through the domain on which we pose the system of equations (2.3).
9.2. Possible extensions and perspectives
We conclude by mentionning several other extensions which are relevant regarding the modeling of social unrest.
9.2.1. Non-local diffusion
A possible extension of our model is two replace the Laplace operator in (2.3) with some non-local diffusion operator. One can consider, for example, that the classical diffusion is replaced by the convolution with an integrable kernel K(⋅)
Another interesting example is the fractional Laplacian, for s∈(0,1),
with cn,s a normalization constant.
On the one hand, a non-local diffusion on the level of activity u could account for the fact that rioters can travel to another location. On the other hand, a nonlocal on the level of social tension could account for the global spreading of information through media.
Non-local diffusion is increasingly used in various modeling situations (e.g., [16] deals with the modeling of riots, and [54] contains many other topics), and often leads to some anomalous behaviors. We let the reader refer to [51,54] and references therein for more details.
9.2.2. Compartmental models
An underlying hypothesis of our modeling approach is that all individuals are identical. Yet, the variability of individuals sometimes plays an important role in collective behaviors [36,39]. It is often admitted that certain social and economic classes are more prone to trigger or drive a social movement, such as students [2], rural population [60], activists [56], etc.
One way to include individuals variability in our model is to consider two different levels of activity u1 and u2, the first accounting for the rioting activity of activist and leaders, the other accounting for the rioting activity of more reluctant individuals. It remains unclear how our conclusions would be affected by this additional feature, and we leave this question as an open problem.
Acknowledgments
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement n. 321186 - ReaDi - Reaction-Diffusion Equations, Propagation and modeling held by Henri Berestycki. This work was also partially supported by the French National Research Agency (ANR), within project NONLOCAL ANR-14-CE25-0013.
Conflict of interest
The authors declare no conflict of interest.
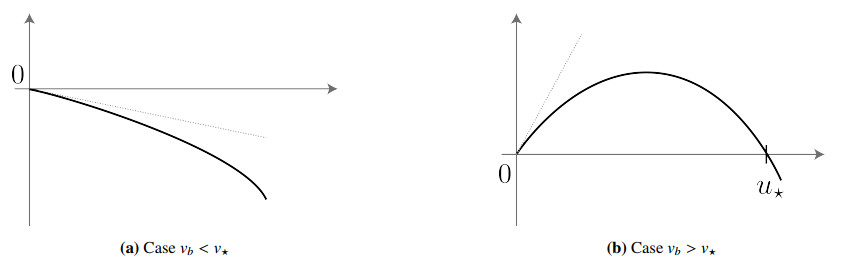









 DownLoad:
DownLoad: