Soliton solutions and periodic solutions for two models arises in mathematical physics

F. A. Mohammed; Mohammed K. Elboree; F. A. Mohammed; Mohammed K. Elboree

doi:10.3934/math.2022247

AIMS Mathematics

2022, Volume 7, Issue 3: 4439-4458. doi: 10.3934/math.2022247

Previous Article Next Article

Research article Special Issues

Soliton solutions and periodic solutions for two models arises in mathematical physics

F. A. Mohammed ^{1,2
,
,},
Mohammed K. Elboree ²

1.
Department of mathematics, College of Science and Arts, Jouf university, Al-Gurayat, Kingdom of Saudi Arabia
2.
Department of mathematics, Faculty of Science, South Valley University, Qena, Egypt

Received: 21 October 2021 Revised: 09 December 2021 Accepted: 16 December 2021 Published: 22 December 2021
MSC : 35Q51, 37K40, 35G20, 35Q60

We aimed in this paper to acquire the periodic wave solutions and soliton solutions and other solutions such as kink-wave solutions for the cubic nonlinear Schrödinger equation with repulsive delta potential ( $\delta$ -NLSE) and complex coupled Higgs field equation via two mathematical methods Jacobi elliptic function method and generalized Kudryashov method. Some of these solutions are degenerated to solitary wave solutions and periodic wave solutions in the limit case. We also gave the meaning of these solutions physically and the numerical simulation by some figures.

Keywords:

Citation: F. A. Mohammed, Mohammed K. Elboree. Soliton solutions and periodic solutions for two models arises in mathematical physics[J]. AIMS Mathematics, 2022, 7(3): 4439-4458. doi: 10.3934/math.2022247

Related Papers:

[1]	Nafissa Toureche Trouba, Mohamed E. M. Alngar, Reham M. A. Shohib, Haitham A. Mahmoud, Yakup Yildirim, Huiying Xu, Xinzhong Zhu . Novel solitary wave solutions of the (3+1)–dimensional nonlinear Schrödinger equation with generalized Kudryashov self–phase modulation. AIMS Mathematics, 2025, 10(2): 4374-4411. doi: 10.3934/math.2025202
[2]	Nafissa T. Trouba, Huiying Xu, Mohamed E. M. Alngar, Reham M. A. Shohib, Haitham A. Mahmoud, Xinzhong Zhu . Soliton solutions and stability analysis of the stochastic nonlinear reaction-diffusion equation with multiplicative white noise in soliton dynamics and optical physics. AIMS Mathematics, 2025, 10(1): 1859-1881. doi: 10.3934/math.2025086
[3]	Abeer S. Khalifa, Hamdy M. Ahmed, Niveen M. Badra, Wafaa B. Rabie, Farah M. Al-Askar, Wael W. Mohammed . New soliton wave structure and modulation instability analysis for nonlinear Schrödinger equation with cubic, quintic, septic, and nonic nonlinearities. AIMS Mathematics, 2024, 9(9): 26166-26181. doi: 10.3934/math.20241278
[4]	Ninghe Yang . Exact wave patterns and chaotic dynamical behaviors of the extended (3+1)-dimensional NLSE. AIMS Mathematics, 2024, 9(11): 31274-31294. doi: 10.3934/math.20241508
[5]	M. Mossa Al-Sawalha, Safyan Mukhtar, Azzh Saad Alshehry, Mohammad Alqudah, Musaad S. Aldhabani . Chaotic perturbations of solitons in complex conformable Maccari system. AIMS Mathematics, 2025, 10(3): 6664-6693. doi: 10.3934/math.2025305
[6]	Abeer S. Khalifa, Hamdy M. Ahmed, Niveen M. Badra, Jalil Manafian, Khaled H. Mahmoud, Kottakkaran Sooppy Nisar, Wafaa B. Rabie . Derivation of some solitary wave solutions for the (3+1)- dimensional pKP-BKP equation via the IME tanh function method. AIMS Mathematics, 2024, 9(10): 27704-27720. doi: 10.3934/math.20241345
[7]	Ahmed A. Gaber, Abdul-Majid Wazwaz . Dynamic wave solutions for (2+1)-dimensional DJKM equation in plasma physics. AIMS Mathematics, 2024, 9(3): 6060-6072. doi: 10.3934/math.2024296
[8]	Wafaa B. Rabie, Hamdy M. Ahmed, Taher A. Nofal, Soliman Alkhatib . Wave solutions for the (3+1)-dimensional fractional Boussinesq-KP-type equation using the modified extended direct algebraic method. AIMS Mathematics, 2024, 9(11): 31882-31897. doi: 10.3934/math.20241532
[9]	A. K. M. Kazi Sazzad Hossain, M. Ali Akbar . Solitary wave solutions of few nonlinear evolution equations. AIMS Mathematics, 2020, 5(2): 1199-1215. doi: 10.3934/math.2020083
[10]	Hamood-Ur-Rahman, Muhammad Imran Asjad, Nayab Munawar, Foroud parvaneh, Taseer Muhammad, Ahmed A. Hamoud, Homan Emadifar, Faraidun K. Hamasalh, Hooshmand Azizi, Masoumeh Khademi . Traveling wave solutions to the Boussinesq equation via Sardar sub-equation technique. AIMS Mathematics, 2022, 7(6): 11134-11149. doi: 10.3934/math.2022623

Abstract

1. Introduction

Soliton solutions for nonlinear evolution equations (NEEs) play a significant role in soliton theory, physical sciences and engineering. So the finding of exact solutions for NEEs is very important for mathematicians and physicists. Many powerful methods have been suggested to obtain the soliton solutions, such as homogeneous balance technique ^{[1,2,3,4,5,6]}, extended tanh method ^[7,8], soliton-like, multisoliton-like ^[9], truncated expansion technique ^[10,11], sech-function method ^[12], Jacobi elliptic function method ^[13,14] and Kudryashov's method ^[15,16], generalized( $G'/G$ )-expansion method ^[17,18], rational generalized( $G'/G$ )-expansion method ^[19], exp( $\Phi(\eta)$ )-expansion method ^[20,21], the fractional sub-equation method ^[22] and optical solutions ^{[23,24,25,26]}.

We implemented the Jacobi elliptic function method ^[27,28,29] and generalized Kudryashov's method to obtain the Jacobi elliptic function solutions, periodic solutions and soliton solutions for the ( $\delta$ -NLSE) and complex coupled Higgs field.

Some exact solutions are based on the generalized Hirota bilinear ^[30] method.

We introduce a brief summary for the two methods which have been applied Jacobi elliptic function method and generalized Kudryashov's method in Section 2. Jacobi elliptic function, periodic solutions and soliton solutions for the cubic nonlinear Shrödinger's equation with repulsive delta potential ( $\delta$ -NLSE) and complex coupled Higgs field equation using two methods were derived analytically and numerically in Sections 3 and 4. We explained the results in a view of physical perspective in Section 5. Finally, some results were deduced in Section 6.

2. Materials and methods

Suppose that we have a given nonlinear partial differential equations (NPDEs) as follows

$\begin{eqnarray} &&H_\gamma(x, u, u_{1}, u_{2}, ...., u_{n}) = 0, \qquad \gamma = 1, 2, ..., m. \end{eqnarray}$

(2.1)

For $m = 2$ such that $u^1 = u, u^2 = v$ , and $n = 2$ such as $x^1 = t, x^2 = x$ ,

Step 1. By using a wave transformation $u(x, t) = u(l x-n t+f), v(x, t) = v(l x-n t+f)$ , $n$ is the wave speed and the function.

Transformed Eq (2.1) into an ordinary differential equation (ODE)

$\begin{eqnarray} &&H_{1}(u, v, u_{\zeta}, v_{\zeta}, u_{\zeta\zeta}, v_{\zeta\zeta}, ....) = 0, \\&&H_{2}(u, v, u_{\zeta}, v_{\zeta}, u_{\zeta\zeta}, v_{\zeta\zeta}, ....) = 0, \end{eqnarray}$

(2.2)

where $\zeta = l x-n t+d$ .

Step 2. Suppose the solutions is as follows

$\begin{align} u(\zeta)& = \Sigma_{i = 0}^Na_i\varphi(\zeta)^i, \\ v(\zeta)& = \Sigma_{i = 0}^Mb_i\varphi(\zeta)^i, \end{align}$

(2.3)

where $N$ , and $M$ determined by balancing the highest order derivatives with the nonlinear term, the parameters $a_i$ and $b_i$ to be determined.

2.1. The Jacobi elliptic function method

The variable $\varphi(\zeta)$ is the solutions of the anzata ^[31]

$\begin{equation} \varphi'(\zeta) = \sqrt{d_0+d_1\varphi(\zeta)+d_2\varphi^{2}(\zeta)+d_3\varphi^{3}(\zeta)+d_4 \varphi^{4}(\zeta)} \end{equation}$

(2.4)

where $d_0, d_1, d_2, d_3$ and $d_4$ are real parameters.

We substitute anzatz Eqs (2.4) and (2.3) into Eq (2.2) with the aid of computerized symbolic computation, we obtain a set of algebraic equations for $d_0, d_1, d_2, d_3, d_4, c, k, a_{i}$ and $b_{i}$ .

Inserting the solutions of Eq (2.4) and setting $\zeta = lx\pm n t+f$ , then we obtain the exact traveling wave solutions of Eq (2.2).

The Jacobi elliptic functions $sn\zeta = sn(\zeta\mid m)$ , $cn\zeta = cn(\zeta\mid m)$ and $dn\zeta = dn(\zeta\mid m)$ , m $(0 < m < 1)$ is the modulus of the elliptic function, are double periodic posses properties of triangular functions, namely

$\begin{eqnarray} &&sn^{2}(\zeta)+cn^{2}(\zeta) = 1, \\ &&dn^{2}(\zeta)+m^{2}sn^{2}(\zeta) = 1, \\ &&(cn(\zeta))' = -sn(\zeta) dn(\zeta), \\ && (sn(\zeta))' = cn(\zeta) dn(\zeta), \\ &&(dn(\zeta))' = -m^{2}sn(\zeta) cn(\zeta). \end{eqnarray}$

(2.5)

When $m\longrightarrow0$ , the Jacobi elliptic function degenerate to

$\begin{eqnarray} &&sn(\zeta)\rightarrow \sin(\zeta), \quad cn(\zeta)\rightarrow \cos(\zeta), \quad dn(\zeta)\rightarrow 1, \\&& cs(\zeta)\rightarrow \cot(\zeta), \quad ds(\zeta)\rightarrow csc(\zeta). \end{eqnarray}$

(2.6)

While $m\longrightarrow1$ , the Jacobi elliptic function degenerate to

$\begin{eqnarray} &&sn(\zeta)\rightarrow \tanh(\zeta), \quad cn(\zeta)\rightarrow sech(\zeta), \quad dn(\zeta)\rightarrow sech(\zeta), \\&& cs(\zeta)\rightarrow csch(\zeta), \quad ds(\zeta)\rightarrow csch(\zeta), \end{eqnarray}$

(2.7)

where $\zeta = l x-n t+f$ .

2.2. {The generalized Kudryashov's method}

For $m = 1$ , we suppose the solutions of Eq (2.1) can be expressed in the following rational form ^[32]

$\begin{eqnarray} u(\zeta) = \frac{\Sigma_{i = 0}^Na_i\varphi(\zeta)^i}{\Sigma_{i = 0}^Mb_i\varphi(\zeta)^i} \end{eqnarray}$

(2.8)

where $N$ , and $M$ determined by balancing the highest order derivatives with the nonlinear term, the parameters $a_i$ and $b_i$ to be determined.

The variable $\varphi(\zeta)$ is the solutions which satisfy the first order Bernoulli differential equation

$\begin{eqnarray} \varphi'(\zeta) = \varphi(\zeta)^2-\varphi(\zeta), \end{eqnarray}$

(2.9)

which has the solution

$\begin{eqnarray} \varphi(\zeta) = \frac{1}{1+c_1 e^{l x-n t+f}}. \end{eqnarray}$

(2.10)

Inserting the solutions of Eq (2.9) into Eqs (2.8) and (2.1), then we obtain the exact traveling wave solutions such as soliton solutions of Eq (2.1).

3. $\delta$ -NLSE equation

3.1. Jacobi elliptic function method

Consider the $\delta$ -NLSE equation ^[33]

$\begin{eqnarray} &&iu_{tt}+\frac{1}{2}\, u_{xx} -\alpha\, \delta \, u \left( x, t \right) -\upsilon\, \left | u \right| ^{2} u = 0, \qquad i = \sqrt{-1}. \end{eqnarray}$

(3.1)

Where $\alpha, \upsilon\neq0$ are real constants, $\delta$ is the Dirac measure ^[34]. The $\delta$ potential is called repulsive for $\alpha > 0$ and attractive for $\alpha < 0$ . The $\delta$ -NLSE equation is a simpler model which describes the resonant nonlinear propagation of light through optical waves ^[34].

To find the Jacobi elliptic solutions for $\delta$ -NLSE equation via Jacobi elliptic function method, we start by assuming a solution of the form ^[35]

$\begin{eqnarray} &&{\it u} \left( x, t \right) = U(\zeta) {\rm e}^{i \left( k x+\omega\, t \right) }. \end{eqnarray}$

(3.2)

Where $\zeta = l x-n\, t+f$ , $l, n$ represent the wave number and wave frequency of the light pulse, respectively, and $U(\zeta)$ is the cnoidal wave or periodic wave or solitary wave solutions.

We transform the (3.1) into ODE wave transformation using (3.2)

$\begin{eqnarray} &&\upsilon\, U^{3}+\alpha\, \delta \, U +\frac{{n}^{2 }}{2 l^2}\, {U}+U \omega-\frac{1}{2}\, U'' {l} ^{2} = 0. \end{eqnarray}$

(3.3)

Balancing $U''$ with $U^3$ , we get $N = 1$ . Then, the Jacobi elliptic function solutions for Eq (3.1) as follows:

$\begin{eqnarray} &&U(\zeta) = a_0+a_1\varphi(\zeta) \end{eqnarray}$

(3.4)

where $a_i, i = 0, 1$ are constants which are to be determined later and $\varphi$ satisfies (2.4) which has the solutions in Table 1.2 in ^[36].

Inserting (3.4) along (2.4) into (3.3) and collecting the terms with the same order of $\varphi(\zeta)$ , and setting it to zero we obtain the Jacobi elliptic function solutions for $\delta$ -NLSE equation for $d_0 = 1-m^2, d_1 = d_3 = 0, d_2 = 2m^2-1$ and $d_4 = -m^2$ .

$\begin{eqnarray} &&\!\!\!\!\!u(x, t) = \pm\gamma m{\it cn} \left( {\frac {-2\, {m}^{2}nt+2\, f{m}^{2}+\sqrt { \left( 2\, { m}^{2}-1 \right) \sigma }x+nt-f}{2\, {m}^{2}-1}}, m \right){\rm e}^{i \left( k x+\omega\, t \right) }, \end{eqnarray}$

(3.5)

where

$\sigma = \left( \alpha\, \delta+\sqrt {{\alpha}^{2}{\delta}^{2 }+2\, {m}^{2}{n}^{2}+2\, \alpha\, \delta\, \omega-{n}^{2}+{\omega}^{2}}+ \omega \right),$

$\gamma = \sqrt {-{\frac {\sigma}{\upsilon\, \left( 2\, {m}^{2}-1 \right) }}}.$

When $m\longrightarrow1$ , we obtain the soliton solutions for $\delta$ -NLSE equation

$\begin{eqnarray} &&\!\!\!\!\!u(x, t) = \pm\gamma m{\it sech} \left( {\frac {-2\, {m}^{2}nt+2\, f{m}^{2}+\sqrt { \left( 2\, { m}^{2}-1 \right) \sigma }x+nt-f}{2\, {m}^{2}-1}}\right){\rm e}^{i \left( k x+\omega\, t \right) }, \end{eqnarray}$

(3.6)

For $d_0 = 1, d_1 = d_3 = 0, d_2 = -(m^2+1)$ and $d_4 = m^2$ .

$\begin{eqnarray} &&u(x, t) = a_{{1}}{\it sn} \left( lx-nt+f, m \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&& u(x, t) = a_{{1}}{\it cd} \left( lx-nt+f, m \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \end{eqnarray}$

(3.7)

where $k = \frac{n }{l}$ . When $m\longrightarrow0$ , we obtain the periodic solutions for $\delta$ -NLSE equation

$\begin{eqnarray} &&u(x, t) = a_{{1}}{\it sin} \left( lx-nt+f \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&& u(x, t) = a_{{1}}{\it cos} \left( lx-nt+f \right) {\rm e}^{i \left( k x+\omega\, t \right) }. \end{eqnarray}$

(3.8)

When $m\longrightarrow1$ , we obtain the soliton solutions for $\delta$ -NLSE equation

$\begin{eqnarray} &&u(x, t) = a_{{1}}{\it tanh} \left( lx-nt+f \right) {\rm e}^{i \left( k x+\omega\, t \right) }. \end{eqnarray}$

(3.9)

And for $d_0 = m^2, d_1 = d_3 = 0, d_2 = -(m^2+1)$ and $d_4 = 1$ .

$\begin{eqnarray} &&u(x, t) = a_{{1}}{\it ns} \left( lx-nt+f, m \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&& u(x, t) = a_{{1}}{\it dc} \left( lx-nt+f, m \right) {\rm e}^{i \left( k x+\omega\, t \right) }. \end{eqnarray}$

(3.10)

When $m\longrightarrow0$ , we obtain the periodic solutions for $\delta$ -NLSE equation

$\begin{eqnarray} &&u(x, t) = a_{{1}}{\it csc} \left( lx-nt+f \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&& u(x, t) = a_{{1}}{\it sec} \left( lx-nt+f \right) {\rm e}^{i \left( k x+\omega\, t \right) }. \end{eqnarray}$

(3.11)

When $m\longrightarrow1$ , we obtain the soliton solutions for $\delta$ -NLSE equation

$\begin{eqnarray} &&u(x, t) = a_{{1}}{\it coth} \left( lx-nt+f \right) {\rm e}^{i \left( k x+\omega\, t \right) }. \end{eqnarray}$

(3.12)

3.2. Generalized Kudryashov's method

In this section we will find the soliton solutions for $\delta$ -NLSE equation via generalized Kudryashov's method.

Suppose the solution for Eq (3.1) in the rational form (2.8). Balancing $U''$ with $U^3$ , in (3.3) we get $N = M+1$ , we choose $N = 2, M = 1$ Then, we can obtain the soliton solutions for Eq (3.1) according to (2.8) as follows:

$\begin{eqnarray} &&U(\zeta) = \frac{a_0+a_1\varphi(\zeta)+a_2\varphi(\zeta)^2 }{b_0+b_1\varphi(\zeta)} \end{eqnarray}$

(3.13)

where $a_i, b_j, i = 0, 1, 2, j = 0, 1$ are constants to be determined and $\varphi$ satisfies (2.9) which has the solutions (2.10).

Inserting (3.13) along (2.9) into (3.3) and collecting the terms with the same order of $\varphi(\zeta)$ , we obtain the family of soliton solutions for $\delta$ -NLSE equation as follows:

Case 1.

$\begin{eqnarray} &&u(x, t) = -{\frac {a_{{1}}{{\rm e}^{-lx+nt-f}}}{{\it c_1 }\, b_{{1}}}}{\rm e}^{i \left( k x+\omega\, t \right) } , \end{eqnarray}$

(3.14)

Case 2.

$\begin{eqnarray} &&u(x, t) = -{\frac {a_{{1}}{{\rm e}^{lx-nt+f}}{\it c_1}}{ b_{{1}}}}{\rm e}^{i \left( k x+\omega\, t \right) } , \end{eqnarray}$

(3.15)

Case 3.

$\begin{eqnarray} &&u(x, t) = {\frac {a_{{0}} \left( {{\rm e}^{lx-nt+f}}{\it c_1}\, b_{{0}}-b_{{0}}-b_{{1}} \right) }{ \left( {{\rm e}^{lx-nt+f}}{ \it c_1}\, b_{{0}}+b_{{0}}+b_{{1}} \right) b_{{0}}}}{\rm e}^{i \left( k x+\omega\, t \right) } , \end{eqnarray}$

(3.16)

Case 4.

$\begin{eqnarray} &&u(x, t) = -2\, {\frac {a_{{1}}{{\rm e}^{lx-nt+f}}{\it c_1 }}{b_{{1}} \left( {{\rm e}^{2\, lx-2\, nt+2\, f}}{{\it c_1}}^{2}-1 \right) }}{\rm e}^{i \left( k x+\omega\, t \right) }, \end{eqnarray}$

(3.17)

Case 5.

$\begin{eqnarray} &&u(x, t) = -\, {\frac { \left( {{\rm e}^{lx-nt+f}}{\it c_1}-1 \right) a_{{2}}}{2b_{{1}} \left( 1+{{\rm e}^{lx-nt+f}}{\it c_1 } \right) }}{\rm e}^{i \left( k x+\omega\, t \right) } , \end{eqnarray}$

(3.18)

Case 6.

$\begin{eqnarray} &&u(x, t) = -{\frac {a_{{2}} \left( {{\rm e}^{2\, lx-2\, nt+2 \, f}}{{\it c_1}}^{2}+1 \right) }{b_{{1}} \left( {{\rm e}^{2\, lx-2\, nt +2\, f}}{{\it c_1}}^{2}-1 \right) }}{\rm e}^{i \left( k x+\omega\, t \right) }, \end{eqnarray}$

(3.19)

where $k = \frac{n }{l}$ .

3.3. Physical discussions

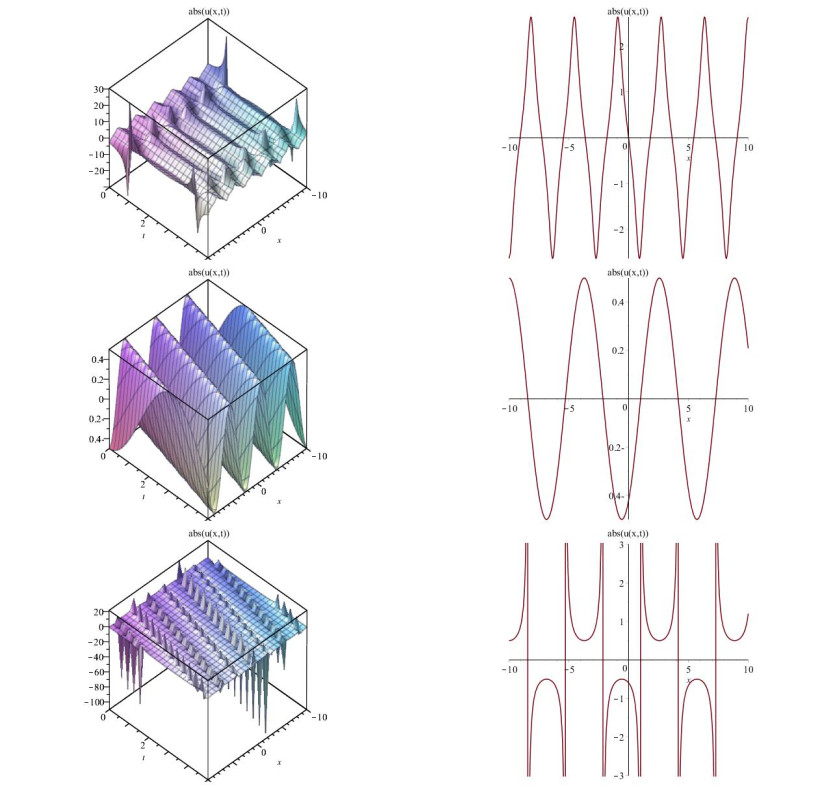
In this section, we give the physical meanings of the solutions obtained for $\delta$ -NLSE equation (3.1), for (3.5), (3.7) and (3.10) which are Jacobi elliptic pattern solutions, which are the solutions in terms of the Jacobi elliptic functions or cnoidal solutions.

It is interesting to point out that the delicate balance between the nonlinearity effect of $|u|^2u$ and the dissipative effect of $u_{xx}$ gives rise to solitons, that after full interaction with others, the solitons come back retaining their identities with the same speed and shape. The $\delta$ -NLSE equation (3.1) has solitary wave solutions that have exponentially decaying wings. If two solitons of the $\delta$ -NLSE equation (3.1) collide, the solitons just pass through each other and emerge unchanged.

We showed the time growth of these Jacobi elliptic solutions by some figures to describe the dynamical properties in 3D graphs and 2D graphs in . The solutions (3.8) and (3.11), which are periodic solutions, displayed in 3D graphs and 2D graphs in . The solution (3.9), which is kink-soliton solution which has a permanent profile displayed in 2D graph and 3D graph, solutions in (3.12) and (3.14)–(3.19), which soliton-like solutions which is occurred from the balance between nonlinearity $U^3$ and dispersion $U''$ , displayed in . All figures in 2D for the space evolution $-10 < x < 10$ and figures in 3D for the time evolution $0 < t < 5$ for Jacobi elliptic function, kink-soliton solutions and soliton-like, space evolution for periodic solutions in the interval $-5 < x < 5$ and $-20 < x < 20$ .

Figure 1. The cnoidal wave solutions of (3.5), (3.7) and (3.10).

DownLoad: Full-Size Img PowerPoint

Figure 2. The for periodic wave profiles for various times scale for (3.8) and (3.11).

DownLoad: Full-Size Img PowerPoint

Figure 3. The for kink-soliton solutions and soliton-like wave profiles for different times scale for (3.9), (3.12), (3.14) and (3.16).

DownLoad: Full-Size Img PowerPoint

We note that the wave speed $n$ acts a vital role in a physical structure for solutions for $\delta$ -NLSE equation.

Remark: The solutions (3.5), (3.7), (3.10), (3.8), (3.11), (3.9), (3.12), (3.14) and (3.16) of $\delta$ -NLSE equation (3.1) are not previously found, that is in ^[33] the optical solitons obtained using the complex envelope function ansatz method.

4. Complex coupled Higgs field equation

4.1. Jacobi elliptic function method

Consider the complex coupled Higgs field equation ^[37]

$\begin{eqnarray} &&u_{tt} -u_{xx} -\alpha_{\mbox{\tt }}\, u +\beta\, \left( \left| u \right| \right) ^{2}u -2\, u v = 0, \\&& v_{tt}+v_{xx} -\beta (\mid u\mid^{2})_{xx} = 0, \end{eqnarray}$

(4.1)

describes a system of conserved scalar nucleons interacting with neutral scalar mesons, where $v$ is a complex scalar nucleon field and $u$ is a real scalar meson field ^[38]. In case of $\alpha < 0, \beta < 0$ , the Eq (4.1) transformed into nonlinear Klein-Gordon equation and for $\alpha > 0, \beta > 0$ , the Eq (4.1) transformed into coupled Higgs field equation.

To find the Jacobi elliptic solutions for complex coupled Higgs field equation via Jacobi elliptic function method, we start by assuming a solution of the form ^[35]

$\begin{eqnarray} &&{\it u} \left( x, t \right) = U(\zeta) {\rm e}^{i \left( k x+\omega\, t \right) }, \qquad v(x, t) = V(\zeta). \end{eqnarray}$

(4.2)

Where $\zeta = l x-n\, t+f$ , $l, n$ represent the wave number and wave frequency of the light pulse, respectively, and $U(\zeta)$ and $V(\zeta)$ are the periodic wave profile.

We transform the (4.1) into ODE wave transformation using (4.2)

$\begin{align} \beta\, U ^{3}+{\frac {U {n}^{2}{\omega}^{2}}{{l}^{2}}} -U {\omega}^{2}&-2\, {\frac { U ^{3}{l}^{2}\beta}{{l}^{2}+{n}^{2}}}-\alpha\, U + U'' ({n}^{2}- {l}^{2} )\ = 0, \\ & V = {\frac {{l}^{2}\beta\, U^{2}}{{l}^{2}+{n}^{2}}} . \end{align}$

(4.3)

Balancing $U''$ with $U^3$ , we get $N = 2$ . Then, the Jacobi elliptic function solutions for Eq (4.1) as follows:

$\begin{eqnarray} &&U(\zeta) = a_0+a_1\varphi(\zeta), \end{eqnarray}$

(4.4)

where $a_i, i = 0, 1$ are constants which are to be determined later and $\varphi$ satisfies (2.4).

Inserting (4.4) along (2.4) into (4.3) and collecting the terms with the same order of $\varphi(\zeta)$ , and setting it to zero we obtain the Jacobi elliptic function solutions for complex coupled Higgs field equation for $d_0 = 1-m^2, d_1 = d_3 = 0, d_2 = 2m^2-1$ and $d_4 = -m^2$ .

$\begin{eqnarray} && u(x, t) = a_{{1}}{\it cn} \left( lx-nt+f, \sqrt {{\frac { \beta}{2({l}^{2}+{n}^{2})}}}a_{{1}} \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\ &&v(x, t) = {\frac {\beta\, {l}^{2}{a_{{1}}}^{2}}{{l}^{2}+{n}^{2}} \left( {\it cn} \left( lx-nt+f, -\sqrt {{\frac {\beta}{2({l}^{2}+ {n}^{2})}}}a_{{1}} \right) \right) ^{2}}, \end{eqnarray}$

(4.5)

where $k = -\frac{n \omega}{l}$ .

When $m\longrightarrow1$ , we obtain the soliton solutions for complex coupled Higgs field equation

$\begin{eqnarray} && u(x, t) = sech \left( x-1 \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&&v(x, t) = 2\, sech^2 \left( x-1 \right) . \end{eqnarray}$

(4.6)

For $d_0 = 1, d_1 = d_3 = 0, d_2 = -(m^2+1)$ and $d_4 = m^2$ .

$\begin{eqnarray} &&u(x, t) = a_{{1}}{\it sn} \left( lx-nt+f, m \right){\rm e}^{i \left( k x+\omega\, t \right) }, \\&&v(x, t) = {\frac {{l}^{2}\beta\, \left( a_{{0}}+a_{{1}}{\it sn} \left( lx- nt+f, m \right) \right) ^{2}}{{l}^{2}+{n}^{2}}}, \\&& u(x, t) = a_{{1}}{\it cd} \left( lx-nt+f, m \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&&v(x, t) = {\frac {{l}^{2}\beta\, \left( a_{{0}}+a_{{1}}{\it cd} \left( lx- nt+f, m \right) \right) ^{2}}{{l}^{2}+{n}^{2}}}. \end{eqnarray}$

(4.7)

When $m\longrightarrow1$ , we obtain the soliton solutions for complex coupled Higgs field equation

$\begin{eqnarray} &&u(x, t) = a_{{1}}\tanh \left( x-1 \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&&v(x, t) = 2\, \left( \left| \tanh \left( x-1 \right) \right| \right) ^{2}. \end{eqnarray}$

(4.8)

And for $d_0 = m^2, d_1 = d_3 = 0, d_2 = -(m^2+1)$ and $d_4 = 1$ .

$\begin{eqnarray} &&u(x, t) = a_{{1}}{\it ns} \left( lx+I \sqrt {\, \frac{\beta\, {a_{{1}}}^{2}}{2}+{l}^ {2}}t+f, m \right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&&v(x, t) = -2\, {l}^{2} \left( {\it ns} \left( lx+I \sqrt {\, \frac{\beta\, {a_{{1}}}^{2}}{2}+{l}^ {2}}t+f, m \right) \right) ^{2} , \\&& u(x, t) = a_{{1}}{\it dc} \left( lx+I \sqrt {\, \frac{\beta\, {a_{{1}}}^{2}}{2}+{l}^ {2}}t+f, m \right){\rm e}^{i \left( k x+\omega\, t \right) }, \\&&v(x, t) = -2\, {l}^{2} \left( {\it dc} \left( lx+I \sqrt {\, \frac{\beta\, {a_{{1}}}^{2}}{2}+{l}^ {2}}t+f, m \right) \right) ^{2}, \end{eqnarray}$

(4.9)

where

$m = -{\frac {1}{l}\sqrt {-{\frac {\beta\, {l}^{2}{a_{{1}}}^{2}- \beta\, {\omega}^{2}{a_{{1}}}^{2}+4\, {l}^{4}-4\, {l}^{2}{\omega}^{2}-2\, {l}^{2}\alpha}{\beta\, {a_{{1}}}^{2}+4\, {l}^{2}}}}}.$

When $m\longrightarrow1$ , we obtain the soliton solutions for complex coupled Higgs field equation

$\begin{eqnarray} &&u(x, t) = {\rm coth} \left(-x+i\sqrt {2}t\right) {\rm e}^{i \left( k x+\omega\, t \right) }, \\&&v(x, t) = 2\, \left( \left| {\rm coth} \left(x-2\, i\sqrt {2}\right) \right| \right) ^{2}. \end{eqnarray}$

(4.10)

4.2. Generalized Kudryashov's method

In this section we will find the soliton solutions for complex coupled Higgs field equation using generalized Kudryashov's method.

Let us assume the solution for Eq (4.1) in the rational form (2.8). Balancing $U''$ with $U^3$ , in (3.3) we get $N = M+1$ , we choose $N = 2, M = 1$ Then, we can obtain the soliton solutions for Eq (4.1) according to (2.8) as follows:

$\begin{eqnarray} &&U(\zeta) = \frac{a_0+a_1\varphi(\zeta)+a_2\varphi(\zeta)^2 }{b_0+b_1\varphi(\zeta)}, \\&& V(\zeta) = {\frac {{l}^{2}\beta\, U^{2}}{{l}^{2}+{n}^{2}}}, \end{eqnarray}$

(4.11)

where $a_i, b_j, i = 0, 1, 2, j = 0, 1$ are constants to be determined.

The family of soliton solutions for complex coupled Higgs field equation as follows

$\begin{eqnarray} &&u(x, t) = -\, {\frac {{c_1^{2}a_{{2}}{\rm e}^{\zeta }}-4\, c_1\, a_{{1}}{{\rm e}^{ \frac{\zeta}{2}}}+2\, c_1\, a_{{2 }}{{\rm e}^{\frac{\zeta}{2}}}-4\, a_{{1}}-3\, a_{{2}}}{2b_{{1}} \left( {c_1{\rm e}^{\frac{\zeta}{2}}}+3 \right) \left( 1+{c_1{\rm e}^{\zeta /2}} \right) }} {\rm e}^{i \left( k x+\omega\, t \right) } , \\&&v(x, t) = {\frac{l^2\beta}{(l^2+n^2)}({\frac {{c_1^{2}a_{{2}}{\rm e}^{\zeta }}-4\, c_1\, a_{{1}}{{\rm e}^{ \frac{\zeta}{2}}}+2\, c_1\, a_{{2 }}{{\rm e}^{\frac{\zeta}{2}}}-4\, a_{{1}}-3\, a_{{2}}}{2b_{{1}} \left( {c_1{\rm e}^{\frac{\zeta}{2}}}+3 \right) \left( 1+{c_1{\rm e}^{\zeta /2}} \right) }})^2}{} \end{eqnarray}$

(4.12)

for

$n = {\pm\frac { \sqrt {-4\, {l}^{2}{b _{{1}}}^{2}-2\, {a_{{2}}}^{2}\beta}}{2b_{{1}}}} \, \, and \, \, \omega = \mp \left( \sqrt {{\frac {4\, {l} ^{2}{b_{{1}}}^{2}+{a_{{2}}}^{2}\beta-4\, {b_{{1}}}^{2}\alpha}{2(4\, {l}^{2}{b_{{1}}}^{2}+{a_{{2}}}^{2}\beta)}}} \right),$

where

$\zeta = {\frac {2\, lxb_{{1}}+\sqrt {-4\, {l}^{2}{b_{{1}}}^{2}-2\, {a_{{2}}}^{2} \beta}t+2\, fb_{{1}}}{b_{{1}}}}, \, k = -\frac{n \omega}{l}.$

4.3. Physical interpretation

In this section, we will display numerical simulations to the problem of this paper that add extra flavor to our analytical solutions of Eq (4.1), the physical meanings of the solutions obtained for complex coupled Higgs field equation (4.1), for (4.5), (4.7) and (4.9) which are Jacobi elliptic pattern solutions, which are cnoidal solutions, we showed the time growth of these Jacobi elliptic solutions by some figures to describe the dynamical properties in 3D graphs and 2D graphs in Figures 4–6. The solutions (4.6), which is soliton-solutions, (4.8) and (4.10), which is kink-soliton solutions which have a permanent profile displayed in 2D graph and 3D graph by taking suitable values of the parameters to visualize the mechanism of the (4.1) in –., solutions in (4.12), which are soliton-like solutions from balance between nonlinearity $U^3$ and dispersion $U''$ , displayed in . All figures in 2D for the space evolution $-10 < x < 10$ and figures in 3D for the time evolution $0 < t < 5$ for Jacobi elliptic function, kink-soliton solutions and soliton-like, space evolution for periodic solutions in the interval $-5 < x < 5$ and $-20 < x < 20$ .

Figure 4. The for periodic wave profiles for various times scale for (4.5)using Jacobi elliptic function method.

DownLoad: Full-Size Img PowerPoint

Figure 5. The for periodic wave profiles for various times scale for (4.7) using Jacobi elliptic function method.

DownLoad: Full-Size Img PowerPoint

Figure 6. The for periodic wave profiles for various times scale for (4.9) using Jacobi elliptic function method.

DownLoad: Full-Size Img PowerPoint

Figure 7. The for soliton wave solutions for various times scale for (4.6) using Jacobi elliptic function method.

DownLoad: Full-Size Img PowerPoint

Figure 8. The for kink-soliton solutions for various times scale for (4.8) using Jacobi elliptic function method.

DownLoad: Full-Size Img PowerPoint

Figure 9. The for kink-soliton solutions for various times scale for (4.10) using Jacobi elliptic function method.

DownLoad: Full-Size Img PowerPoint

Figure 10. The for soliton like solutions for various times scale for (4.12) using generalized Kudryashov's method.

DownLoad: Full-Size Img PowerPoint

Remark: The solutions (4.5)–(4.10) and (4.12) for complex coupled Higgs field equation (4.1) are not previously found, that is some of them were explored before and in this paper we gave new solutions, in ^[39], which is used an algebraic method is applied to construct solitary wave solutions and Jacobi periodic wave solutions, the authors in ^[40] constructed the traveling wave solutions using (G' /G)-expansion method and the authors in ^[37] constructed the soliton solutions and triangular solutions using tanh method.

5. Conclusions

In this paper we successfully constructed the Jacobi elliptic function solutions, periodic wave solutions and soliton solutions, which obtained as a limit of the periodic wave solutions for $\delta$ -NLSE equation (3.1) and complex coupled Higgs field equation (4.1) using the Jacobi elliptic function method and generalized Kudryashov method utilized in treating the equations with the aid of symbolic computation using Mathematica. Other soltions are constructed such as kink-soliton solutions. We investigate these results numerically by some figures. As such, we compared the obtained results with previously works to prove that we explored some results and new results were derived and evaluated computationally owing to the less constant parameters. These solutions with free parameters have rich structures and may be important to explain some physical phenomena. It is worthy to note that the two methods are straightforward, concise and can be widely used to other nonlinear partial differential equations which arise in the theory of solitons in mathematical physics.

Acknowledgments

The authors would like to express their sincere thanks to the referees for suggestions.

Conflict of interest

There is no conflict of interests regarding the publication of this paper.

References

[1]	Y. Gurefe, E. Misirli, Y. Pandir, A. Sonmezoglu, M. Ekici, New exact solutions of the Davey-Stewartson equation with power-law nonlinearity, Bull. Malays. Math. Sci. Soc., 38 (2015), 1223–1234. https://doi.org/10.1007/s40840-014-0075-z doi: 10.1007/s40840-014-0075-z
[2]	M. Khalfallah, Exact traveling wave solutions of the Boussinesq-Burgers equation, Math. Comput. Model., 49 (2009), 666–671. https://doi.org/10.1016/j.mcm.2008.08.004 doi: 10.1016/j.mcm.2008.08.004
[3]	M. Khalfallah, New exact traveling wave solutions of the (3+1) dimensional Kadomtsev-Petviashvili (KP) equation, Commun. Nonlinear Sci. Numer. Simulat., 14 (2009), 1169–1175. https://doi.org/10.1016/j.cnsns.2007.11.010 doi: 10.1016/j.cnsns.2007.11.010
[4]	A. S. Abdel Rady, M. Khalfallah, On soliton solutions for Boussinesq-Burgers equations, Commun. Nonlinear Sci. Numer. Simulat., 15 (2010), 886–894. https://doi.org/10.1016/j.cnsns.2009.05.039 doi: 10.1016/j.cnsns.2009.05.039
[5]	A. S. Abdel Rady, E. S. Osman, M. Khalfallah, On soliton solutions for a generalized Hirota-Satsuma coupled KdV equation, Commun. Nonlinear Sci. Numer. Simul., 15 (2010), 264–274. https://doi.org/10.1016/j.cnsns.2009.03.011 doi: 10.1016/j.cnsns.2009.03.011
[6]	A. S. Abdel Rady, E. S. Osman, M. Khalfallah, The homogeneous balance method and its application to the Benjamin-Bona-Mahoney (BBM) equation, Appl. Math. Comput., 217 (2010), 1385–1390. https://doi.org/10.1016/j.amc.2009.05.027 doi: 10.1016/j.amc.2009.05.027
[7]	A. M. Wazwaz, New solitary wave solutions to the Kuramoto-Sivashinsky and the Kawahara equations, Appl. Math. Comput., 182 (2006), 1642–1650. https://doi.org/10.1016/j.amc.2006.06.002 doi: 10.1016/j.amc.2006.06.002
[8]	A. M. Wazwaz, New solitary wave solutions to the modified forms of Degasperis-Procesi and Camassa-Holm equations, Appl. Math. Comput., 186 (2007), 130–141. https://doi.org/10.1016/j.amc.2006.07.092 doi: 10.1016/j.amc.2006.07.092
[9]	R. Guo, J. Y. Song, H. T. Zhang, F. H. Qi, Soliton solutions, conservation laws and modulation instability for the discrete coupled modified Korteweg-de Vries equations, Mod. Phys. Lett. B, 32 (2018), 1850152. https://doi.org/10.1142/S021798491850152X doi: 10.1142/S021798491850152X
[10]	J. Weiss, M. Tabor, G. Carnevalle, The Painlevé property for partial differential equations, J. Math. Phys., 24 (1983), 522–526. https://doi.org/10.1063/1.525721 doi: 10.1063/1.525721
[11]	N. A. Kudryashov, Exact solutions of the generalized Kuramoto-Sivashinsky equation, Phys. Lett. A, 147 (1990), 287–291. https://doi.org/10.1016/0375-9601(90)90449-X doi: 10.1016/0375-9601(90)90449-X
[12]	W. X. Ma, Travelling wave solutions to a seventh order generalized KdV equation, Phys. Lett. A, 180 (1993), 221–224. https://doi.org/10.1016/0375-9601(93)90699-Z doi: 10.1016/0375-9601(93)90699-Z
[13]	S. Z. Rida, M. Khalfallah, New periodic wave and soliton solutions for a Kadomtsev-Petviashvili (KP) like equation coupled to a Schrödinger equation, Commun. Nonlinear Sci. Numer. Simul., 15 (2010), 2818–2827. https://doi.org/10.1016/j.cnsns.2009.10.024 doi: 10.1016/j.cnsns.2009.10.024
[14]	M. K. Elboree, The Jacobi elliptic function method and its application for two component BKP hierarchy equations, Comput. Math. Appl., 62 (2011), 4402–4414. https://doi.org/10.1016/j.camwa.2011.10.015 doi: 10.1016/j.camwa.2011.10.015
[15]	M. Mirzazadeh, M. Eslami, A. Biswas, Dispersive optical solitons by Kudryashov's method, Optik, 125 (2014), 6874–6880. https://doi.org/10.1016/j.ijleo.2014.02.044 doi: 10.1016/j.ijleo.2014.02.044
[16]	A. Neirameh, Exact analytical solutions for 3D-Gross-Pitaevskii equation with periodic potential by using the Kudryashov method, J. Egypt. Math. Soc., 24 (2016), 49–53. https://doi.org/10.1016/j.joems.2014.11.004 doi: 10.1016/j.joems.2014.11.004
[17]	H. O. Roshid, M. N. Alam, M. F. Hoque, M. A. Akbar, A new extended ( $G'/G$ )-expansion method to find exact traveling wave solutions of nonlinear evolution equations, Math. Stat., 1 (2013), 162–166.
[18]	M. N. Alam, M. A. Akbar, Some new exact traveling wave solutions to the simplified MCH equation and the (1+1)-dimensional combined KdV-mKdV equations, J. Assoc. Arab Univ. Basic Appl. Sci., 17 (2015), 6–13. https://doi.org/10.1016/j.jaubas.2013.12.001 doi: 10.1016/j.jaubas.2013.12.001
[19]	M. A. Akbar, N. H. M. Ali, M. T. Islam, Multiple closed form solutions to some fractional order nonlinear evolution equations in physics and plasma physics, AIMS Math., 4 (2019), 397–411. https://doi.org/10.3934/math.2019.3.397 doi: 10.3934/math.2019.3.397
[20]	H. O. Roshid, M. N. Alam, M. A. Akbar, Traveling wave solutions for fifth order (1+1)-dimensional Kaup-Kupershmidt equation with the help of exp( $-\Phi(\eta)$ )-expansion method, Walailak J. Sci. Tech., 12 (2015), 1063–1073.
[21]	M. N. Alam1, M. G. Hafez, M. A. Akbar, H. O. Roshid, Exact solutions to the (2+1)-dimensional Boussinesq equation via exp( $-\Phi(\eta)$ )-expansion method, J. Sci. Res., 7 (2015), 1–10.
[22]	S. T. Mohyud-Dina, T. Nawaz, E. Azhar, M. A. Akbar, Fractional sub-equation method to space-time fractional Calogero-Degasperis and potential Kadomtsev-Petviashvili equations, J. Taibah Uni. Sci., 11 (2017), 258–263. https://doi.org/10.1016/j.jtusci.2014.11.010 doi: 10.1016/j.jtusci.2014.11.010
[23]	I. Jaradata, M. Alquran, S. Momani, A. Biswas, Dark and singular optical solutions with dual-mode nonlinear Schrödinger's equation and Kerr-law nonlinearity, Optik, 172 (2018), 822–825. https://doi.org/10.1016/j.ijleo.2018.07.069 doi: 10.1016/j.ijleo.2018.07.069
[24]	M. Alquran, I. Jaradat, Multiplicative of dual-waves generated upon increasing the phase velocity parameter embedded in dual-mode Schr ${\rm{\ddot d}}$ inger with nonlinearity Kerr laws, Nonlinear Dyn., 96 (2019), 115–121. https://doi.org/10.1007/s11071-019-04778-0 doi: 10.1007/s11071-019-04778-0
[25]	T. A. Sulaiman, A. Yusuf, M. Alquran, Dynamics of optical solitons and nonautonomous complex wave solutions to the nonlinear Schrodinger equation with variable coefficients, Nonlinear Dyn., 104 (2021), 639–648. https://doi.org/10.1007/s11071-021-06284-8 doi: 10.1007/s11071-021-06284-8
[26]	M. Alquran, Optical bidirectional wave-solutions to new two-mode extension of the coupled KdV-Schrodinger equations, Opt. Quant. Electron., 53 (2021), 588. https://doi.org/10.1007/s11082-021-03245-8 doi: 10.1007/s11082-021-03245-8
[27]	M. Alquran, A. Jarrah, Jacobi elliptic function solutions for a two-mode KdV equation, J. King Saud Univ. Sci., 31 (2019), 485–489. https://doi.org/10.1016/j.jksus.2017.06.010 doi: 10.1016/j.jksus.2017.06.010
[28]	M. Al Ghabshi, E. V. Krishnan, M. Alquran1, K. Al-Khaled, Jacobi elliptic function solutions of a nonlinear Schrodinger equation in metamaterials, Nonlinear Stud., 24 (2017), 469–480.
[29]	M. Alquran, A. Jarrah, E.V. Krishnan, Solitary wave solutions of the phi-four equation and the breaking soliton system by means of Jacobi elliptic sine-cosine expansion method, Nonlinear Dyn. Syst. Theory, 18 (2018), 233–240.
[30]	L. Huang, J. Manafian, G. Singh, K. S. Nisar, M. K. M. Nasution, New lump and interaction soliton, N-soliton solutions and the LSP for the (3+1)-D potential-YTSF-like equation, Results Phys., 29 (2021), 104713. https://doi.org/10.1016/j.rinp.2021.104713 doi: 10.1016/j.rinp.2021.104713
[31]	Y. Z. Peng, Exact solutions for some nonlinear partial differential equations, Phys. Lett. A, 314 (2003), 401–408. https://doi.org/10.1016/S0375-9601(03)00909-5 doi: 10.1016/S0375-9601(03)00909-5
[32]	K. A. Gepreel, T. A. Nofal, A. A. Alasmari, Exact solutions for nonlinear integro-partial differential equations using the generalized Kudryashov method, J. Egypt. Math. Soc., 25 (2017), 438–444. https://doi.org/10.1016/j.joems.2017.09.001 doi: 10.1016/j.joems.2017.09.001
[33]	D. Baleanu, M. Inc, A. I. Aliyu, A. Yusuf, Optical solitons, nonlinear self-adjointness and conservation laws for the cubic nonlinear Shrödinger's equation with repulsive delta potential, Superlattices Microstruct., 111 (2017), 546–555. https://doi.org/10.1016/j.spmi.2017.07.010 doi: 10.1016/j.spmi.2017.07.010
[34]	R. H. Goodman, P. J. Holmes, M. I. Weinstein, Strong NLS soliton-defect interactions, Phys. D: Nonlinear Phenom., 192 (2004), 215–248. https://doi.org/10.1016/j.physd.2004.01.021 doi: 10.1016/j.physd.2004.01.021
[35]	H. Triki, A. M. Wazwaz, Combined optical solitary waves of the Fokas-Lenells equation, Waves Random Complex Media, 27 (2017), 587–593. https://doi.org/10.1080/17455030.2017.1285449 doi: 10.1080/17455030.2017.1285449
[36]	L. H. Zhang, Travelling wave solutions for the generalized Zakharov-Kuznetsov equation with higher-order nonlinear terms, Appl. Math. Comput., 208 (2009), 144–155. https://doi.org/10.1016/j.amc.2008.11.020 doi: 10.1016/j.amc.2008.11.020
[37]	M. A. Abdelkawy, A. H. Bhrawy, E. Zerrad, A. Biswas, Application of tanh method to complex coupled nonlinear evolution equations, Acta Phys. Pol. A, 129 (2016), 278–283. http://dx.doi.org/10.12693/APhysPolA.129.278 doi: 10.12693/APhysPolA.129.278
[38]	M. Tajiri, On N-soliton solutions of coupled Higgs field equations, J. Phys. Soc. Japan, 52 (1983), 2277–2280.
[39]	Y. C. Hon, E. G. Fan, A series of exact solutions for coupled Higgs field equation and coupled Schrödinger-Boussinesq equation, Nonlinear Anal.: Theory Methods Appl., 71 (2009), 3501–3508. https://doi.org/10.1016/j.na.2009.02.029 doi: 10.1016/j.na.2009.02.029
[40]	S. Kumar, K. Singh, R. K. Gupta, Coupled Higgs field equation and Hamiltonian amplitude equation: Lie classical approach and (G' /G)-expansion method, Pramana J. Phys., 79 (2012), 41–60. https://doi.org/10.1007/s12043-012-0284-7 doi: 10.1007/s12043-012-0284-7

This article has been cited by:

1.	F. A. Mohammed, Soliton solutions for some nonlinear models in mathematical physics via conservation laws, 2022, 7, 2473-6988, 15075, 10.3934/math.2022826
2.	Marwan Alquran, Ahmad Alqawaqneh, New bidirectional wave solutions with different physical structures to the complex coupled Higgs model via recent ansatze methods: applications in plasma physics and nonlinear optics, 2022, 54, 0306-8919, 10.1007/s11082-022-03685-w
3.	Musawa Yahya Almusawa, Hassan Almusawa, Exploring the Diversity of Kink Solitons in (3+1)-Dimensional Wazwaz–Benjamin–Bona–Mahony Equation, 2024, 12, 2227-7390, 3340, 10.3390/math12213340
4.	Muslum Ozisik, Mustafa Bayram, Aydin Secer, Melih Cinar, On the analytical soliton solutions of (1 + 1)-dimensional complex coupled nonlinear Higgs field model, 2024, 233, 1951-6355, 1331, 10.1140/epjs/s11734-023-00954-x

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(2476) PDF downloads(80) Cited by(4)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(10)

AIMS Mathematics

Soliton solutions and periodic solutions for two models arises in mathematical physics

Related Papers:

Abstract

1. Introduction

2. Materials and methods

2.1. The Jacobi elliptic function method

2.2. {The generalized Kudryashov's method}

3. $\delta$ -NLSE equation

3.1. Jacobi elliptic function method

3.2. Generalized Kudryashov's method

3.3. Physical discussions

4. Complex coupled Higgs field equation

4.1. Jacobi elliptic function method

4.2. Generalized Kudryashov's method

4.3. Physical interpretation

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Soliton solutions and periodic solutions for two models arises in mathematical physics

Related Papers:

Abstract

1. Introduction

2. Materials and methods

2.1. The Jacobi elliptic function method

2.2. {The generalized Kudryashov's method}

3. δ \delta -NLSE equation

3.1. Jacobi elliptic function method

3.2. Generalized Kudryashov's method

3.3. Physical discussions

4. Complex coupled Higgs field equation

4.1. Jacobi elliptic function method

4.2. Generalized Kudryashov's method

4.3. Physical interpretation

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

3. $\delta$ -NLSE equation