Existence of positive periodic solutions for a class of in-host MERS-CoV infection model with periodic coefficients

1.   Introduction

Middle East Respiratory Syndrome (MERS) is an acute respiratory disease caused by MERS-CoV, which was first reported in Saudi Arabia in 2012 ^[1]. Its main clinical features are fever, cough, dyspnea, shortness of breath, abdominal pain, nausea and diarrhea, etc ^[2,3]. Since the clinical symptoms may be non-specific, it is not always possible to identify patients with MERS-CoV in a timely manner. MERS-CoV probably originated in bats, and the intermediate host is dromedary camels ^[4]. It is a zoonotic virus, which means that it can be transmitted between animals and humans. Since its outbreak in 2012, cases have been reported in 27 countries (mostly in the Middle East), and more than 850 people are known to have died from the infection and related complications, with a case fatality rate of about $35\%$ ^[5]. To date, no specific antiviral therapy has been approved for MERS-CoV infection, so treatment is primarily supportive and based on the patient's clinical condition; potential vaccines are in the early stages of development ^[4,5,6].

Usually, viruses can only invade a host by binding to specific receptors in the host body. Raj et al. ^[7] reported for the first time that dipeptidyl peptidase-4 (DPP4, also known as CD26) is a functional receptor for MERS-CoV. Studies have shown that DPP4 is mainly expressed in bronchial epithelial cells and lung tissue cells, and can also be expressed in MERS-CoV sensitive cells (such as Vero and Huh-7 cells) ^[7]. The binding of the MERS-CoV spike protein to DPP4 mediates the attachment of the virus to host cells and the virus-cell fusion, thus triggering infection ^[8]. Therefore, DPP4 plays an important role in MERS-CoV infection, which provides valuable input into the development of potential receptor-targeted vaccines and drugs. In recent decades, the dynamic model of viral infection has become an effective tool for people to understand the replication and clearance of various viruses (such as human immunodeficiency virus (HIV), hepatitis B virus (HBV) and hepatitis C virus (HCV)) in host ^[9,10,11].

Recently, in order to describe the interactions among uninfected cells, infected cells, MERS-CoV and DPP4, the authors in ^[12] proposed the following novel four dimensional autonomous ordinary differential equation model:

where $T(t)$, $I(t)$, $v(t)$ and $D(t)$ represent the concentrations of uninfected cells, infected cells, free virus and DPP4 on the surface of uninfected cells at time $t$, respectively. $\lambda$, $\beta$, $d$, $d_{1}$, $M$, $c$, $\lambda_{1}$, $\beta_{1}$ and $\gamma$ are positive constants. $\lambda$ is the rate at which uninfected cells are produced. $\beta$ is the rate at which uninfected cells are infected by the free virus (i.e., infected cells are increased at a mount of $\beta D(t)v(t)T(t)$, because uninfected cells are infected by the free virus). $d$ and $d_{1}$ represent the death rates of uninfected cells and infected cells, respectively. $M$ represents the number of the free viruses released by lysis of each infected cell after death. $c$ represents the death rate of the free viruses. $\lambda_{1}$ represents the rate at which DPP4 is produced on the surface of uninfected cells. $\beta_{1}$ represents the rate at which DPP4 is decreased (i.e., DPP4 is decreased at a mount of $\beta_{1} \beta D(t) v(t) T(t)$, because uninfected cells are infected by the free virus). $\gamma$ represents the natural decay rate of DPP4. More detailed biological explanations can be found in literature ^[12].

The basic reproductive number of model (1.1) is given by $R_{0} = (\lambda\beta M\lambda_{1})/(dc\gamma)$. By constructing the appropriate Lyapunov functions and combining with the Lyapunov-LaSalle invariance principle, the authors in ^[12] obtained that, if $R_{0} < 1$, then the infection-free equilibrium of model (1.1) is globally asymptotically stable; if $R_{0} > 1$ and some additional conditions hold, then the infected equilibrium is also globally asymptotically stable. The results suggest that MERS-CoV infection can also be controlled by reducing the expression rate ($\lambda_1$) of DPP4. In addition, In ^[13], the authors applied the modeling idea of model (1.1) to the modeling of SARS-CoV-2 infection, and also took into consideration the effects of CTL immune response and pulsed administration therapy. It is shown that proper dosing intervals and drug dosages are both important in the eradication of viral infections.

It is well known that, periodic phenomena, such as the changes in the host's microenvironment with day and night, are common features in viral infection models. For example, some scholars have considered periodic drug therapy in viral infection models ^[14,15]. Therefore, it may be more reasonable to describe MERS-CoV infection using the model with periodic coefficients. Inspired by the research efforts above, in this paper, we will consider the following non-autonomous MERS-CoV dynamic model with periodic coefficients:

In model (1.2), $\lambda(t)$, $\beta(t)$, $d(t)$, $d_{1}(t)$, $M(t)$, $c(t)$, $\lambda_{1}(t)$, $\beta_{1}(t)$ and $\gamma(t)$ are all assumed to be positive, continuous and periodic functions with positive upper and lower bounds and share the same period $\omega > 0$. All the parameters in model (1.2) have exactly the same biological significance with those in model (1.1).

There are abundant research results on the existence of periodic solutions of nonlinear ordinary differential equations. The main research methods mainly include fixed point theorems, Lyapunov's second method, coincidence degree theory and so on. Especially, in recent years, the continuation theorem of the coincidence degree theory ^[16] has been successfully applied to the study of the existence of periodic solutions of some classic biological models, such as the models in population biology ^{[17,18,19,20]}, the models in epidemiology ^[21,22], and the models in microbiology ^[23,24], etc.

The main purpose of this paper is to establish some sufficient conditions for the existence of positive $\omega$-periodic solutions of model (1.2) by using the continuation theorem in the coincidence degree theory.

The remaining part of this paper is organized as follows. In Section 2, some sufficient conditions are given for the existence of positive $\omega$-periodic solutions of model (1.2). In Section 3, the conclusions and some numerical simulations are presented.

2.   Existence of positive periodic solutions

For convenience, let us first introduce the following well-known the continuation theorem in the coincidence degree theory ^[16].

Let $X$ and $Z$ be two Banach spaces, $L: \mathrm{Dom\; L}\subset X\rightarrow Z$ be a linear mapping, $N: X\rightarrow Z$ be a continuous mapping. The mapping $L$ will be called a Fredholm mapping of index zero, if $\operatorname{dim} \operatorname{Ker} L = \operatorname{codim} \operatorname{Im} L < +\infty$ and $\mathrm{Im}\; L$ is closed in $Z$. If $L$ is a Fredholm mapping of index zero and there exist continuous projectors idempotent operator $P: X\rightarrow X$ and $Q: Z\rightarrow Z$ such that $\operatorname{Im} P = \operatorname{Ker} L$, $\operatorname{Im} L = \operatorname{Ker} Q = \operatorname{Im}(I-Q)$, it follows that $L \mid \operatorname{Dom} L \cap \operatorname{Ker} P:(I-P) X \rightarrow \operatorname{Im} L$ is invertible. We denote the generalized inverse of that map by $K_{P}$. Let $\Omega$ be an open bounded subset of $X$. The mapping $N$ will be called $L$-compact on $\overline{\Omega}$, if $Q N(\overline{\Omega})$ is bounded and $K_{P}(I-Q) N: \overline{\Omega} \rightarrow \operatorname{Im} L$ is compact. Since $\operatorname{Im} Q$ is isomorphic to $\operatorname{Ker} L$, there exists an isomorphism $J: \operatorname{Im} Q \rightarrow \operatorname{Ker} L$.

Lemma 2.1. $(Continuation \; theorem)$ ^[16] Assume that $\Omega\subset X$ be an open bounded set. Let $L$ be a Fredholm mapping of index zero and let $N: \overline{\Omega} \rightarrow Z$ be $L$-compact on $\overline{\Omega}$. Assume

$\rm{(ⅰ)}$ for each $\mu \in(0, 1)$, $x \in \partial \Omega \cap \operatorname{Dom} L$, $L x \neq \mu N x$;

$\rm{(ⅱ)}$ for each $x \in \partial \Omega \cap \operatorname{Ker} L$, $Q N x \neq 0$;

$\rm{(ⅲ)}$ $\operatorname{deg}\{JQ N, \Omega \cap \operatorname{Ker} L, 0\} \neq 0$.

Then the operator equation $L x = N x$ has at least one solution in $\operatorname{Dom} L \cap \overline{\Omega}$.

For the sake of convenience in the presentation, for any continuous $\omega$-periodic function $f(t)$ defined on $\mathbb{R}$, we define the following notations,

Furthermore, let us define the following parameters,

The following two conditions will be used:

(H1) $2(\widehat{d}+\widehat{\beta} \exp\{M_{3}+M_{4}\})\omega < 1$;

(H2) $2(\widehat{\gamma}+\widehat{(\beta_{1}\beta)} \exp\{M_{1}+M_{3}\}) \omega < 1$.

Let us give the main result of this paper.

Theorem 2.1. If $R^{*} > 1$ and conditions $\rm{(H1)}$ and $\rm{(H2)}$ hold, then model $(1.2)$ has at least one positive $\omega$-periodic solution.

Proof. By using the following variable transformation,

model (1.2) can be rewrite as

Obviously, if model (2.1) exists a $\omega$-periodic solution, then model (1.2) exists a positive $\omega$-periodic solution. Therefore, we only need to study the existence of $\omega$-periodic solutions of model (2.1).

We define

with the norm

It is easily to verify that $X$ and $Z$ are Banach spaces. Define

where $\text{Dom}\; L = \{x\in X, \; \dot{x}\in X\}$. Then it follows that

Obviously, $\text{Im}\; L$ is closed in $Z$ and $\text{dim}\; \text{Ker}\; L = \text{codim}\; \text{Im}\; L = 4$. Thus, $L$ is a Fredholm mapping of index zero. Furthermore, the generalized (to $L$) inverse $K_{P}:\; \text{Im}\; L\rightarrow \text{Dom}\; L\cap \text{Ker}\; P$ exists and is given by

Thus

and

It is not difficult to show that $QN$ and $K_{P}(I-Q)N$ are continuous. By using Arzela-Ascoli theorem, we can also show that $QN(\overline{\Omega})$ and $K_{P}(I-Q)N(\overline{\Omega})$ are compact for any open bounded set $\Omega$ in $X$. Furthermore, it is obvious that $QN(\overline{\Omega})$ is bounded. Thus $N$ is $L$-compact on $\overline{\Omega}$ for any open bounded set $\Omega$ in $X$.

Corresponding to the operator equation $Lx = \mu Nx$, $\mu\in(0, 1)$, we have

Assume that $x = (x_{1}(t), x_{2}(t), x_{3}(t), x_{4}(t))^{T}\in X$ is an arbitrary solution of model (2.3) for the parameter $\mu\in(0, 1)$. It is obvious that, $(T(t), I(t), v(t), D(t))^{T}: = (\exp\{x_{1}(t)\}, \exp\{x_{2}(t)\}, \exp\{x_{3}(t)\}$, $\exp\{x_{4}(t)\})^{T}$ is a solution of the following model,

Integrating the left and right sides of (2.3) and (2.4) over the interval $[0, \omega]$, we have

and

From (2.5) and the second and third equations of (2.3), we have

In addition, from (2.6) and the first and fourth equations of (2.4), we have

For $x\in X$, there exist $\xi_{i}, \; \eta_{i}\in[0, \omega]$ $(i = 1, 2, 3, 4)$ such that

Obviously, it has $\dot{x}_{i}(\xi_{i}) = 0$, $\dot{x}_{i}(\eta_{i}) = 0$ ($i = 1, 2, 3, 4$).

From the first equation of (2.5), we have

which, together with (2.4) and (2.8), imply that

Hence, we have

Similarly, we can obtain

Adding the first and the second equations of (2.6), we have

which implies that

From (2.7) and (2.11), we have

From the third equation of (2.5), we have

which implies that

Hence, from (2.7), we have

In the following, let us further give lower bounds of $x_{i}(t)$ $(i = 1, 2, 3, 4)$. It should be mentioned here that, due to the particularity of mode (1.2), we will use a method different from that in the literature to obtain the estimations of the lower bounds.

From the first equation of (2.5), (2.10) and (2.13), we have

which implies that

Further, from condition (H1) and (2.8), we have

which implies that

Similarly, using condition (H2), we can obtain

In the following, to obtain lower bounds for $x_{2}(t)$ and $x_{3}(t)$, we need the following two important claims.

Claim (ⅰ).

If Claim (ⅰ) is not true, then it has $\min\limits_{t\in[0, \omega]} \{\exp\{x_{1}(t)+x_{4}(t)\}\} > \frac{1}{E^{*}}$. We define

Obviously, $G(0) = G(\omega)$. Calculating the derivative of $G(t)$ along the solution of model (2.3) yields

which implies that $G(\omega) > G(0)$. This is a contradiction. Thus, Claim (ⅰ) is true.

If $R^{*} > 1$, then there exists a positive constant $\delta^{*} > 0$ such that

Claim (ⅱ). If $R^{*} > 1$, then

If Claim (ⅱ) is not true, then it has $\max\limits_{t\in[0, \omega]}\{x_{3}(t)\} < \ln(\delta^{*})$, i.e. $\max\limits_{t\in[0, \omega]}\{\exp\{x_{3}(t)\}\} < \delta^{*}$. From $\dot{x}_{1}(\xi_{1}) = 0$ and (2.10), we have

Similarly, from $\dot{x}_{4}(\xi_{4}) = 0$ and (2.9), we can obtain

From (2.15)–(2.17), we have

which implies that

This contradicts with Claim (ⅰ). Thus Claim (ⅱ) is proved.

From Claim (ⅱ) and (2.7), we have

From the second equation of (2.5), we have

which implies that

Further, from (2.7), we have

Obviously, $M_{i}$, $L_{i}$ $(i = 1, 2, 3, 4)$ are independent of $\mu$.

Let $(x_{1}, x_{2}, x_{3}, x_{4})^{T}\in \mathbb{R}^{4}$ satisfy the following algebraic equations

It is not difficult to show that if $R^{*} > 1$, then it has

Completely similar to the results of the existence of positive equilibrium in ^[12], we can easily obtain that if $\overline{R_{0}} > 1$, then (2.18) has a unique solution $(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, x_{4}^{*})^{T}\in \mathbb{R}^{4}$ which satisfies

where

We define the set $\Omega = \{x\in X\; |\; ||x|| < U\}$, where

It is clear that $\Omega$ satisfies the condition(ⅰ) in Lemma 2.1. When $\widetilde{x} = (x_{1}, x_{2}, x_{3}, x_{4})^{T}\in \partial \Omega\cap Ker\; L = \partial \Omega \cap \mathbb{\mathbb{R}}^{4}$, then $\widetilde{x}$ is a constant vector in $\mathbb{R}^{4}$ with $|x_{1}|+|x_{2}|+|x_{3}|+|x_{4}| = U > |x_{1}^{*}|+|x_{2}^{*}|+|x_{3}^{*}|+|x_{4}^{*}|$. Then, we have

This shows that $\Omega$ satisfies the condition (ⅱ) in Lemma 2.1. Next, let us prove that the condition (ⅲ) in Lemma 2.1 is also satisfied. Let

Note that $J = I$ since $\text{Im}\; Q = \text{Ker}\; L$. Furthermore, by simple calculation, we have

In addition, from (2.19), we can obtain

Then, from (2.20), we have

Thus, the condition (ⅲ) in Lemma 2.1 is also satisfied. Therefore, from Lemma 2.1, we have that model (2.1) has at least one $\omega$-periodic solution. Thus, model (1.2) has at least one positive $\omega$-periodic solution.

Remark 2.1. It should be mentioned here that, if all the periodic coefficients in model $(1.2)$ are taken as positive constants, then model $(1.2)$ degenerates to model $(1.1)$, and $R^*$ naturally becomes $R_0$. Furthermore, note that, for model $(1.1)$, the conditions $({\rm{H1}})$ and $({\rm{H2}})$ are naturally satisfied, and the condition $R_{0} > 1$ implies the existence of unique positive equilibrium. These show that, for the existence of positive periodic solutions of model $(1.2)$, the conditions $({\rm{H1}})$ and $({\rm{H2}})$ in Theorem $2.1$ may be reasonable.

3.   Conclusions and simulations

In this paper, the existence of positive periodic solutions of a class of MERS-CoV infection dynamic model (1.2) with periodic coefficients is studied by using the continuation theorem of the coincidence degree theory. By estimating technically the upper and lower bounds of the prior solutions of the corresponding operator equation ($Lx = \mu N x$), we obtain the sufficient conditions for the existence of positive periodic solutions of model (1.2). If model (1.2) degenerates to an autonomous one, our sufficient conditions become the basic reproductive number $R_0 > 1$.

In model (1.2) ((1.1)), the interaction between DPP4 and virus infection is considered. From the expression of the basic reproductive number $R^*$ ($R_0$), it can be seen that adjusting the growth rate $\lambda_1(t)$ ($\lambda_1$) of DPP4 may be one of control strategies for the controlling of virus infection as well as drug therapy. In addition, for model (1.2) ((1.1)) it may be interesting to introduce the time lags in the process of virus infection and immune response in the bodies, which will be discussed in another papers.

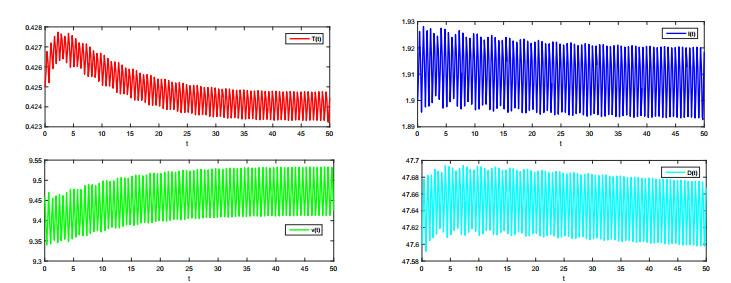
At the end of the paper, we present numerical simulations to illustrate our theoretical results. The following parameters are taken

Obviously, $\omega = \pi/5$. The calculation gives $R^{*}\approx3.43 > 1$, $M_{1}\approx2.327$, $M_{2}\approx0.819$, $M_{3}\approx2.504$, $M_{4}\approx3.925$,

Thus, conditions (H1) and (H2) hold. From Theorem 2.1, model (1.2) has at least one positive $(\pi/5)$-periodic solution (see Figure 1).

Acknowledgments

This paper is supported by National Natural Science Foundation of China (No.11971055) and Beijing Natural Science Foundation (No.1202019).

Conflict of interest

The authors declare there is no conflict of interest in this paper.