1.
Introduction
Gorenstein homological algebra, roughly speaking, which is a relative version of homological algebra with roots on one hand in commutative algebra and on the other hand in modular representation theory of finite groups, has been developed to a high level. We refer the reader to [6] for some basic knowledge. It is well known that a very natural and important way to study homological algebra is by extending the homological theory on the category of modules to one on the category of complexes. Based on this idea, Gorenstein homological theory of complexes concerned many scholars, see [5,8,12,20,22,27] and so on. In particular, Gorensein injective complexes were introduced and studied by Enochs and García Rozas in [5]. It was shown that for each n∈Z, a complex C is Gorenstein-injective if and only if Cn is a Gorenstein-injective module over an n-Gorenstein ring. Liu and Zhang proved that this result holds over left Noetherian rings [12]. These have been further developed by Yang [22], Yang and Liu [27], independently.
Cartan-Eilenberg projective and injective complexes play important roles not only in the category of complexes but also in homotopy category of complexes, see [2,Sections 12.4 and 12.5]. In 2011, Enochs further studied Cartan-Eilenberg projective, injective and flat complexes, and meanwhile, introduced and investigated Cartan-Eilenberg Gorenstein-injective complexes in [4]. In particular, he proved that a complex X is Cartan-Eilenberg Gorenstein-injective if and only if Bn(X) and Hn(X) are Gorenstein-injective modules for all n∈Z. Recently, Cartan-Eilenberg complexes have attracted a lot of attention. For instance, Yang and Liang in [23,24] studied the notion of Cartan-Eilenberg Gorenstein projective and flat complexes. For a self-orthogonal class W of modules, Lu et al. studied Cartan-Eilenberg W-Gorenstein complexes and stability [17].
The notion of m-complexes has important applications in theoretical physics, quantum theory and representation theory of algebras, and has concerned many authors, see [1,7,9,11,14,15,16,19,25,26,28] and so on. For instance, Bahiraei, Gillespie, Iyama, Yang and their collaborators [1,9,11,19,26,28] investigate the homotopy category and the derived category of m-complexes. Yang and Wang in [28] introduce the notions of dg-projective and dg-injective m-complexes, and study the existence of homotopy resolutions for m-complexes. Estrada investigates the notion of Gorenstein-injective m-complexes in [7]. Recently, Lu et al. in [13,15,16] investigate the notions of Cartan-Eilenberg m-complexes and Gorenstein m-complexes. For a self-orthogonal subcategory W of an abelian category A, it is shown that a Cartan-Eilenberg injective m-complex can be divided into direct sums of an injective m-complex and an injetive grade module, a m-complex G is Gorenstein-injective if and only if G is a m-complex consisting of Gorenstein modules which improves a result of Estrada in [7].
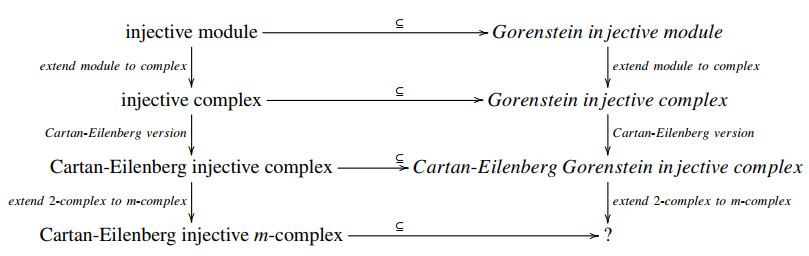
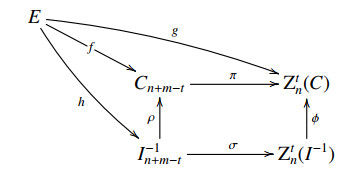
The motivation of this paper comes from the following incomplete diagram of related notions:
The main purpose of the present paper is to define and investigate Cartan-Eilenberg Gorenstein injective m-complexes such that the above diagram will be completed. We establish the following result which gives a relationship between a Cartan-Eilenberg Gorenstein-injective m-complex and the corresponding level modules, cycle modules, boundary modules and homology modules.
Theorem 1.1. (= Theorem 3.8) Let G be a m-complex. Then the following conditions are equivalent:
(1) G is a Cartan-Eilenberg Gorenstein-injective m-complex.
(2) Gn, Ztn(G), Btn(G) and Htn(G) are Gorenstein-injective modules for each n∈Z and t=1,2,…,m.
The stability of Gorenstein categories, initiated by Sather-Wagstaff et al. in [18], is an important research subject, and has also been considered by Ding, Liu, Lu, Xu and so on, see [17,21]. In this paper, as an application of Theorem 1.1 we prove a stability result for Cartan-Eilenberg Gorenstein-injective m-complexes, see Theorem 4.2.
We conclude this section by summarizing the contents of this paper. Section 2 contains necessary notation and definitions for use throughout this paper. In section 3, we mainly give an equivalent characterization of Cartan-Eilenberg Gorenstein-injective m-complexes. An application of Theorem 1.1 is given in Section 4.
In what follows, we will use the abbreviation 'CE' for Cartan-Eilenberg.
2.
Preliminaries
In this section we recall some necessary notation and definitions. Throughout the paper, R denotes an associative ring with an identity and by the term "module" we always mean a left R-module. For two modules M and N, we will let HomR(M,N) denote the group of morphisms from M to N. ExtiR for i≥0 denotes the groups we get from the right derived functor of Hom.
A m-complex X (m≥2) is a sequence of left R-modules
satisfying dm=dXn+1dXn+2⋯dXn+m=0 for any n∈Z. That is, composing any m-consecutive morphisms gives 0. So a 2-complex is a chain complex in the usual sense. We use dlnX to denote dXn−l+1⋯dXn−1dXn. A chain map or simply map f:X→Y of m-complexes is a collection of morphisms fn:Xn→Yn making all the rectangles commute. In this way we get a category of m-complexes of left R-modules, denoted by Cm(R), whose objects are m-complexes and whose morphisms are chain maps. This is an abelian category having enough projectives and injectives. Let C and D be m-complexes. We use HomCm(R)(C,D) to denote the abelian group of morphisms from C to D and ExtiCm(R)(C,D) for i≥0 to denote the groups we get from the right derived functor of Hom. In particular, we use Hom(C,D) to denote the abelian group of morphisms from C to D whenever m=2.
Unless stated otherwise, m-complexes will always the m-complexes of left R-modules. For a m-complex X, there are m−1 choices for homology. Indeed for t=1,⋯,m, we define Ztn(X)=Ker(dn−t+1⋯dn−1dn), Btn(X)=Im(dn+1dn+2⋯dn+t), and Htn(X)=Ztn(X)/Bm−tn(X) the amplitude homology modules of X. In particular, we have
and
We say X is m-exact, or just exact, if Htn(X)=0 for all n and t. Given a left R-module A, we define m-complexes Dtn(A) for t=1,⋯,m as follows: Dtn(A) consists of A in degrees n,n−1,⋯,n−t+1, all joined by identity morphisms, and 0 in every other degree.
Two chain maps f,g:X→Y are called chain homotopic, or simply homotopic if there exists a collection of morphisms {sn:Xn→Yn+m−1} such that
If f and g are homotopic, then we write f∼g. We call a chain map f null homotopic if f∼0. There exists an additive category Km(R), called the homotopy category of m-complexes, whose objects are the same as those of Cm(R) and whose Hom sets are the ∼ equivalence classes of Hom sets in Cm(R). An isomorphism in Km(R) is called a homotopy equivalence. We define the shift functor Θ:Cm(R)⟶Cm(R) by
for X=(Xi,dXi)∈Cm(R). The m-complex Θ(ΘX) is denoted Θ2X and inductively we define ΘnX for all n∈Z. This induces the shift functor Θ:Km(R)⟶Km(R) which is a triangle functor.
Recall from [6,Definition 10.1.1] that a left R-module M is called Gorenstein-injective if there exists an exact sequence of injective left R-modules
with M≅Ker(E0→E1) and which remains exact after applying HomR(I,−) for any injective left R-module I.
A complex I is injective if and only if I is exact with Zn(I) injective in R-Mod for each n∈Z. A complex X is said to be Gorenstein-injective if there exists an exact sequence of injective complexes
with X≅Ker(E0→E1) and which remains exact after applying Hom(I,−) for any injective complex I [8,Definition 3.2.1].
A complex I is said to be CE injective if I,Z(I),B(I) and H(I) are complexes consisting of injective modules [4,Definition 3.1]. A sequence of complexes
is CE exact if ⋯→C−1→C0→C1→⋯ and ⋯→Z(C−1)→Z(C0)→Z(C1)→⋯ are exact by [4,Lemma 5.2 and Definition 5.3]. Eonchs also introduced and studied the concept of CE Gorenstein-injective complexes, see [4,Definition 8.4]. A complex G is said to be CE Gorenstein-injective, if there exists a CE exact sequence
of CE injective complexes such that G=Ker(I0→I1) and the sequence remains exact when Hom(E,−) is applied to it for any CE injective complex E.
Remark 2.1. (1) For any injective module E, E is a Gorenstein-injective module and ⋯⟶0⟶E1⟶E⟶0⟶⋯ is an injective complex.
(2) For any Gorenstein-injective module E, ⋯⟶0⟶E⟶0⟶⋯ is a Gorenstein-injective complex by [27,Proposition 2.8].
(3) According to [4,Theorem 8.5] and [27,Proposition 2.8], any injective complex is CE Gorenstein-injective, and any CE Gorenstein-injective complex is Gorenstein-injective.
(4) Note that strongly Gorenstein-injective modules are Gorenstein-injective by [3,Definition 2.1]. The Gorenstein injective modules are not necessarily injective by [3,Example 2.5]. Thus Gorenstein-injective complexes and CE Gorenstein-injective complexes are not necessarily injective by [4,Theorem 8.5] and [27,Proposition 2.8].
3.
Cartan-Eilenberg Gorenstein-injective m-complexes
In this section, we will give an equivalent characterization on Cartan-Eilenberg Gorenstein-injective m-complexes. To this end, we first give some preparations.
Definition 3.1. ([16,Definition 1]) A sequence of m-complexes
is said to be CE exact if
(1) ⋯→C−1n→C0n→C1n→⋯,
(2) ⋯→Ztn(C−1)→Ztn(C0)→Ztn(C1)→⋯,
(3) ⋯→Btn(C−1)→Btn(C0)→Btn(C1)→⋯,
(4) ⋯→C−1/Ztn(C−1)→C0/Ztn(C0)→C1/Ztn(C1)→⋯,
(5) ⋯→C−1/Btn(C−1)→C0/Btn(C0)→C1/Btn(C1)→⋯,
(6) ⋯→Htn(C−1)→Htn(C0)→Htn(C1)→⋯ are all exact for t=1,⋯,m and n∈Z. $
Remark 3.2. ([16,Remark 1]) Obviously, in the above definition, exactness of (1) and (2)(or (1) and (3), or (1) and (4), or (2) and (3), or (2) and (5), or (3) and (4), or (3) and (5), or (4) and (5)) implies exactness of all (1)–(6).
Definition 3.3. ([16,Remark 2]) A m-complex I is called CE CE if In,Ztn(I),Btn(I),Htn(I) are injective left R-modules for n∈Z and t=1,⋯,m.
The following lemma palys an important role in the proof of Theorem 3.8.
Lemma 3.4. ([16,Proposition 3] and [15,Proposition 4.1]) Let I be a m-complex. Then
(1) I is injective if and only if I=⨁n∈ZDmn+m−1(En), where En is an injective module for each n∈Z.
(2) I is CE injective if and only if I can be divided into direct sums I=I′⨁I″, where I′ is an injective m-complex and I″ is a graded module with I″n injective modules. Specifically,
Here, we give the notion of CE Gorenstein-injective objects in the category of m-complexes.
Definition 3.5. A m-complex G is said to be CE Gorenstein-injective, if there exists a CE exact sequence
of CE injective m-complexes such that
(1) G=Ker(I0→I1);
(2) the sequence remains exact when HomCm(R)(E,−) is applied to it for any CE injective m-complex V.
In this case, I is called a complete CE injective resolution of G.
Remark 3.6. (1) It is clear that any CE injective m-complex is CE Gorenstein-injective.
(2) Any CE Gorenstein-injective m-complex is Gorenstein-injective.
(3) Take m=2. Then CE Gorenstein-injective m-complexes are CE Gorenstein-injective complexes.
The following lemma is used to prove Theorem 3.8.
Lemma 3.7. ([25,Lemma 2.2]) For any module M, X,Y∈Cm(R) and n∈Z,i=1,2,⋯,m, we have the following natural isomorphisms.
(1) HomCm(R)(Dmn(M),Y)≅HomR(M,Yn).
(2) HomCm(R)(X,Dmn+m−1(M))≅HomR(Xn,M).
(3) HomCm(R)(Din(M),Y)≅HomR(M,Zin(Y)).
(4) HomCm(R)(X,Din(M))≅HomR(Xn−(i−1)/Bin−(i−1)(Y),M).
(5) Ext1Cm(R)(Dmn(M),Y)≅Ext1R(M,Yn).
(6) Ext1Cm(R)(X,Dmn+m−1(M))≅Ext1R(Xn,M).
(7) If Y is m-exact, then Ext1Cm(R)(Din(M),Y)≅Ext1R(M,Zin(Y)).
(8) If X is m-exact, then Ext1Cm(R)(X,Din(M))≅Ext1R(Xn−(i−1)/Bin−(i−1)(X),M).
Now, we give the following result which gives an equivalent characterization of m-complexes which extends the corresponding result [4,Theorem 8.5] to the setting of m-complexes.
Theorem 3.8. Let G be a m-complex. Then the following conditions are equivalent:
(1) G is a CE Gorenstein-injective m-complex.
(2) Gn, Ztn(G), Btn(G) and Htn(G) are Gorenstein-injective modules for each n∈Z and t=1,2,…,m.
In this case, Gn/Ztn(G) and Gn/Btn(G) are Gorenstein-injective modules.
Proof. (1) ⇒(2). Suppose that
is a complete CE injective resolution of G such that G=Ker(I0→I−1). Then, there is an exact sequence of injective modules
such that Gn=Ker(I0n→I−1n) for all n∈Z by Definition 3.3. For any injective module E, Dmn(E) is a CE injective m-complex for each n∈Z by Definition 3.3 again. It follows from Lemma 3.7 that there is a natural isomorphism
for all i,n∈Z. Then the following commutative diagram with the first row exact
yields that the lower row is exact. Hence, Gn is a Gorenstein-injective module.
We notice that Ztn(Ii)=Iin for t=m. So we only to show that Ztn(G) is a Gorenstein-injective module for t=1,2,⋯,m−1. Since I is CE exact, then, for any n∈Z and t=1,2,⋯,m−1, the sequence
is exact with Ztn(Ii) injective module since Ii is CE injective for each i∈Z.
For any injective module E, Dtn(E) is a CE injective m-complex for each n∈Z and t=1,2,⋯,m, and there is a natural isomorphism HomCm(R)(Dtn(E),Ii)≅HomR(E,Ztn(Ii)) by Lemma 3.7 for each i∈Z. Applying HomCm(R)(Dtn(E),−) to the sequence I, we obtain that Ztn(I) is HomR(E,−) exact. Note that Ztn(G)=Ker(Ztn(I0)→Ztn(I−1)). Thus Ztn(G) is a Gorenstein-injective module.
Meanwhile, there are exact sequences of modules
and
for all n∈Z and t=1,2,⋯,m. Then we get that Btn−t(G) and Htn(G) are Gorenstein-injective by [10,Theorem 2.6].
(2) ⇒ (1). For a fixed n∈Z, there exist the following exact sequences of modules
with Bm−1n−i(G) and H1n(G) Gorenstein-injective modules for i=0,1,2,⋯,m−1.
Suppose Ei is a complete injective resolution of Bm−1n(G), and Fn is a complete injective resolution of H1n(G) respectively, i=0,1,2,⋯,m−1, n∈Z. In an iterative way, we can construct a complete injective resolution of Gn+m
by the Horseshoe Lemma.
Put
and define
for any (xn,xn−1,⋯,xn−m+2,xn−m+1,yn)∈Iln. Then (Il,dn) is a m-complex and Gn≅Ker(Iln→Il−1n). It is easily seen that Il is a CE injective m-complex for all l∈Z and G=Ker(Il→Il−1). For any n∈Z and t=1,2,⋯,m,
is a complete injective resolution of Ztn(G), and
is a complete injective resolution of Gn, so they both are exact. Hence, we can get that
is CE exact by Remark 3.2.
It remains to prove that, for any CE injective m-complex I, I is still exact when HomCm(R)(I,−) applied to it. However, it suffices to prove that the assertion holds when we pick I particularly as I=Dmn(E) and I=D1n(E) for any injective module E and all n∈Z by Lemma 3.4. Note that In and Ztn(I) are complete injective resolutions, hence from Lemma 3.7, the desired result follows.
Moreover, if G is a CE Gorenstein-injective m-complex. then Gn/Ztn(G) and Gn/Btn(G) are also Gorenstein-injective modules by [10,Theorem 2.6].
Take m=2 in Theorem 3.8. We obtain the following corollary which is a main result of [4].
Corollary 3.9. [4,Theorem 8.5] Let G be a complex. Then the following conditions are equivalent:
(1) G is a CE Gorenstein-injective complex.
(2) Gn, Zn(G), Bn(G) and Hn(G) are Gorenstein-injective modules for each n∈Z.
Take m=3 in Theorem 3.8. We obtain the following result.
Corollary 3.10. Let G be a 3-complex. Then the following conditions are equivalent:
(1) G is a CE Gorenstein-injective 3-complex.
(2) Gn, Z1n(G), B1n(G) , H1n(G), Z2n(G), B2n(G) and H2n(G) are Gorenstein-injective modules for each n∈Z.
The following result establishes a relationship between an m-exact m-complex and its cycle modules under certain hypotheses.
Proposition 3.11. Let C be a m-exact m-complex with HomR(D1n(E),C) exact for any injective module E. Then C is a Gorenstein-injective complex if and only if Ztn(C) is a Gorenstein-injective module for each n∈Z and t=1,2,⋯,m.
Proof. (⇒) Let C be a Gorenstein-injective m-complex. There exists an exact sequence of injective m-complexes
with C=Kerf0 such that I is HomCm(R)(E,−) exact for any injective m-complex E. We also have Ker(fi) is m-exact for all i∈Z since Ker(f0)=C and Ii are m-exact.
Applying HomCm(R)(Dtn(R),−) to the sequence (⋆), there is a commutative diagram:
with the upper exact since Ext1Cm(R)(Dtn(R),Kerfi)=0 by Lemma 3.7. Then the second row is exact. Thus we obtain an exact sequence of injective modules
with Ztn(C)≅Ker(Ztn(I0)→Zn(I1)). So we only need to show that HomR(E,−) leave the sequence (⋆⋆) exact for any injective module E.
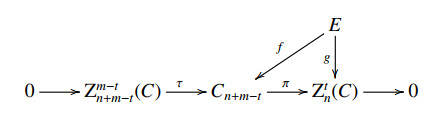
Let E be an injective module and g:E→Ztn(C) be a morphism of modules. Since HomR(D1n(E),C) is m-exact, there exists a morphism f:E→Cn+m−t such that the following diagram:
commutes.
Note that I is HomCm(R)(Dmn+m−t(E),−) exact since Dmn+m−t(E) is an injective m-complex by [15,Proporition 4.1 and Corollary 4.4]. For the exact sequence
there is an exact sequence
It follows from Lemma 3.7 that
is exact. Thus, for f∈HomR(E,Cn+m−t), there exists a morphism h:E→I−1n+m−t such that f=hρ. Therefore, we obtain the following commutative diagram:
where
and
is induced by the morphism I−1→C, which means g=ϕσh. We notice that
Then
is exact. Similarly, we can prove that
is exact. Hence, HomR(E,−) leaves the sequence (⋆⋆) exact. This completes the proof.
(⇐) Note that there is an exact sequence
and Zm−tn+m−t(C) and Ztn(C) are Gorenstein-injective modules. Then Cn is a Gorenstein-injective module for each n∈Z by [10,Theorem 2.6], as desired.
As an immediately consequence of Proposition 3.11, we establish the following Corollary which appears in [22,Theorem 4].
Corollary 3.12. Let C be an exact complex with HomR(E,C) exact for any injective module E. Then C is a Gorenstein-injective complex if and only if Zn(C) is a Gorenstein-injective module for each n∈Z.
4.
An application
In this section, as an application of Theorem 3.8, we investigate the stability of CE Gorenstein-injective categories of CE Gorenstein-injective m-complexes. That is, we show that an iteration of the procedure used to define the CE Gorenstein-injective m-complexes yields exactly the CE Gorenstein-injective m-complexes. We first introduce the notion of two-degree CE Gorenstein-injective m-complexes.
Definition 4.1. A m-complex C is said to be two-degree CE Gorenstein-injective if there is a CE exact sequence of CE Gorenstein-injective m-complexes
such that C≅Ker(G0→G1) and the functors HomCm(R)(H,−) leave G exact whenever H is a CE Gorenstein-injective m-complex. In this case, G is called a complete CE Gorenstein-injective resolution of C.
It is obvious that any CE Gorenstein-injective m-complex is two-degree CE Gorenstein-injective. In the following, we prove that two-degree CE Gorenstein-injective m-complexes are CE Gorenstein-injective.
Theorem 4.2. Let C be a m-complex. Then the following statements are equivalent:
(1) C is two-degree CE Gorenstein-injective.
(2) C is a CE Gorenstein-injective.
Proof. (2)⇒(1) is trivial.
(1)⇒(2). We need to show that Gn, Ztn(G), Btn(G) and Htn(G) are Gorenstein-injective modules for each n∈Z and t=1,2,…,m by Theorem 3.8. By (1), there exists a CE exact sequence of CE Gorenstein-injective m-complexes
with C=Ker(G0→G1) and such that the functor HomCm(R)(H,−) leave G exact whenever H is a CE Gorenstein-injective m-complex. Then there is an exact sequence of Gorenstein-injective modules
with Cn=Ker(G0n→G1n) for all n∈Z by Theorem 3.8.
Let E be an injective module. Then Dmn(E) is a CE Gorenstein-injective m-complex for each n∈Z by Theorem 3.8. We apply the functor HomCm(R)(Dmn(E),−) to the sequence (†), we get the following exact sequence
by Lemma 3.7. Thus, Cn is a Gorenstein-injective module for each n∈Z by Corollary 3.12.
There also exists an exact sequence
of Gorenstein-injective modules with Ztn(C)=Ker(Ztn(G0)→Ztn(G1)) for all n∈Z and t=1,2,⋯,m.
We notice that, for any injective module E, Dtn(E) is CE Gorenstein-injective m-complexes for each n∈Z and t=1,2,⋯,m by Theorem 3.8. Applying the functor HomCm(R)(Dtn(E),−) to the sequence (†), we get the following exact sequence
by Lemma 3.7. Hence, Ztn(C) is a Gorenstein-injective module for each n∈Z by Corollary 3.12 again.
Meanwhile, there are exact sequences of modules
and
for all n∈Z and t=1,2,⋯,m. Then we get that Btn−t(G) and Htn(G) are Gorenstein-injective by [10,Theorem 2.6]. Therefore, C is a CE Gorenstein-injective m-complexes using Theorem 3.8 again.
Take m=2, as a consequence of Theorem 4.2, we obtain the following corollary which establishes the stability for CE Gorenstein-injective complexes.
Corollary 4.3. Let C be a complex. Then the following statements are equivalent:
(1) C is a two-degree CE Gorenstein-injective complex.
(2) C is a CE Gorenstein-injective complex.
Take m=3, as a consequence of Theorem 4.2, we obtain the following corollary.
Corollary 4.4. Let C be a 3-complex. Then the following statements are equivalent:
(1) C is two-degree CE Gorenstein-injective 3-complex.
(2) C is a CE Gorenstein-injective 3-complex.
We can construct the following example by Corollary 3.10 and Corollary 4.4.
Example 4.5. The 3-complex
is CE Gorenstein-injective if and only if G is a Gorenstein-injective module if and only if H is two-degree CE Gorenstein-injective.
Acknowledgments
This work was partially supported by National Natural Science Foundation of China (No. 12061061), Innovation Team Projec of Northwest Minzu University (No. 1110130131), and first-rate discipline of Northwest Minzu University. We would like to thank the referee for a careful reading of the paper and for many useful comments and suggestions.
Conflict of Interest
All authors declare no conflicts of interest.









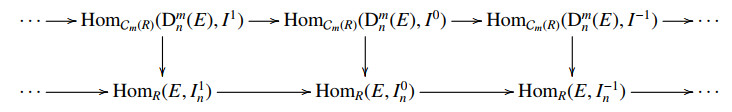
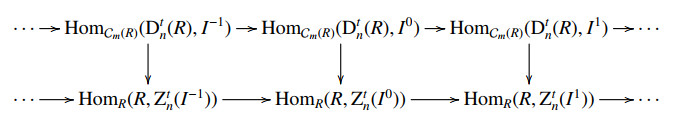




 DownLoad:
DownLoad: