Some aspects in Noetherian modules and rings

1.   Introduction

Researchers have extensively studied Noetherian rings; we list some of the important results. E. Matlis ^[6] demonstrated that, under direct sum, the class of injective right $\mathrm{R}$-modules is closed if the ring $\mathrm{R}$ is right Noetherian. I. Amin, M. Yousif and N. Zeyada ^[1] showed that the ring $\mathrm{R}$ is right Noetherian if and only if every direct sum of strongly $\mathrm{soc}$-injective right $\mathrm{R}$-modules is strongly $\mathrm{soc}$-injective. N. Zeyada ^[10] proved that the ring $\mathrm{R/S_{r}}$ is Noetherian, where $\mathrm{S_{r}}$ is the right socle of $\mathrm{R}$, if and only if every direct sum of strongly $\mathrm{R}$-injective right $\mathrm{R}$-modules is strongly $\mathrm{R}$-injective. Beidar and Ke ^[3] obtained that the class of modules that are direct sums of injective $\mathrm{R}$-modules is closed under essential extensions if and only if the ring $\mathrm{R}$ is right Noetherian. M. Kosan and T. Quynh ^[5] extended Beider and Ke's result (mentioned above) and showed that $\mathrm{R}$ is right Noetherian if and only if every essential extension of a direct sum of injective hulls of simple right $\mathrm{R}$-modules is a direct sum of either injective right $\mathrm{R}$-modules or projective right $\mathrm{R}$-modules. Our aim in this article is to study the rings such that every essential extension of a direct sum of injective hulls of singular simple right $\mathrm{R}$-modules is a direct sum of either injective right $\mathrm{R}$-modules or projective right $\mathrm{R}$-modules. Also, we investigate how these extensions are close to Noetherian rings. Moreover, we aim to get new characterizations of Noetherian rings.

All rings have an associative ring with identity throughout this article, and all modules are unitary $\mathrm{R}$-modules. The socle of a right $\mathrm{R}$-module $\mathrm{M}$ is represented by $\mathrm{soc(M)}$. $\mathrm{S_r}$ and $\mathrm{S_l}$ are used to denote $\mathrm{R}$'s right and left socles, respectively. The notations $\mathrm{N\subseteq ^{ess}M}$ and $\mathrm{N\subseteq ^{\oplus }M}$ indicate that a submodule $\mathrm{N}$ of $\mathrm{M}$ is essential and a direct summand, respectively. For all unspecified concepts in this article, we refer to ^[2,4,7,9].

2.   $\mathrm{Soc}$-injectivity and Noetherian rings

$\mathrm{Soc}$-injectivity was first proposed by I. Amin, M. Yousif and N. Zeyada ^[1].

Definition 2.1. ^[1] $\mathrm{M}$ is $\mathrm{soc}$-$\mathrm{N}$-injective for any modules $\mathrm{M}$ and $\mathrm{N}$ if every $\mathrm{R}$-homomorphism $\mathrm{f:soc(N)\rightarrow M}$ extends to $\mathrm{N}$. If $\mathrm{M}$ is $\mathrm{soc}$-$\mathrm{N}$-injective for all modules $\mathrm{N}$, it is strongly $\mathrm{soc}$-injective.

Theorem 2.1. ^[3] Consider $\mathrm{M_R}$ to be a module. The following are equivalent:

(1) $\mathrm{M}$ is locally Noetherian.

(2) The essential extension in $\mathrm{\sigma[M]}$ of a direct sum of any family of injective modules in $\mathrm{\sigma[M]}$ is a direct sum of injective modules in $\mathrm{\sigma[M]}$.

(3) If $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of simple modules in $\mathrm{\sigma[M]}$, any essential extension of $\mathrm {\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ is a direct sum of injective modules in $\mathrm{\sigma[M]}$.

$\mathrm{M}$ is locally Noetherian if and only if every direct sum of strongly $\mathrm{soc}$-injective modules in $\mathrm{\sigma[M]}$ is strongly $\mathrm{soc}$-injective in $\mathrm{\sigma[M]}$, according to Özcan, D. Tütüncü and M. Yousif ^[8]. Theorem 2.1 is extended to strongly $\mathrm{soc}$-injectivity in the following theorem.

Theorem 2.2. Assume $\mathrm{M_R}$ is a module. The following are equivalent:

(1) $\mathrm{M}$ is locally Noetherian.

(2) The essential extension in $\mathrm{\sigma[M]}$ of a direct sum of any family of strongly $\mathrm{soc}$-injective modules in $\mathrm{\sigma[M]}$ is a direct sum of strongly $\mathrm{soc}$-injective modules in $\mathrm{\sigma[M]}$.

(3) If $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of simple modules in $\mathrm{\sigma[M]}$, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ is a direct sum of strongly $\mathrm{soc}$-injective modules in $\mathrm{\sigma[M]}$.

Proof. $\mathrm{(1)\Rightarrow (2)}$. Let $\mathrm{M}$ be locally Noetherian and $\mathrm{\{N_i|i\in I\}}$ be a family of strongly $\mathrm{soc}$-injective modules. For all $\mathrm{i \in I}$, $\mathrm{N_i = L_i\bigoplus K_i}$, where $\mathrm{L_i}$ is injective with essential socle and $\mathrm{soc(K_i) = 0}$ [1,Theorem 3.1]. Furthermore, $\mathrm{\bigoplus\limits_{i\in I}{N_i}}$ is strongly $\mathrm{soc}$-injective, and $\mathrm{\bigoplus\limits_{i\in I}{N_i} = L\bigoplus K}$, where $\mathrm{L}$ is injective with essential socle, and $\mathrm{soc(K) = 0}$. As a result, any essential extension of $\mathrm{\bigoplus\limits_{i\in I}{N_i}}$ is strongly $\mathrm{soc}$-injective.

$\mathrm{(2)\Rightarrow (3)}$ Clear.

$\mathrm{(3)\Rightarrow (1)}$ Assume $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of simple modules in $\mathrm{\sigma[M]}$. Any essential extension $\mathrm{E}$ of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_i)}}$ is then strongly $\mathrm{soc}$-injective. Because $\mathrm{E(\bigoplus\limits_{i\in \mathbb{N}}{E(S_i)})}$ has an essential socle, $\mathrm{E(\bigoplus\limits_{i\in \mathbb{N}}{E(S_i)})}$ is injective. As a result, $\mathrm{M}$ is locally Noetherian.

The following Corollary is a direct result of the preceding Theorem.

Corollary 2.1. Assume $\mathrm{R}$ is a ring. The following are equivalent:

(1) $\mathrm{R}$ is Noetherian.

(2) The essential extension of a direct sum of any family of strongly $\mathrm{soc}$-injective modules is a direct sum of strongly $\mathrm{soc}$-injective modules.

(3) If $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of simple modules, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ is a direct sum of strongly $\mathrm{soc}$-injective modules.

Theorem 2.3. ^[5] Assume $\mathrm{M_R}$ is a module. The following are equivalent:

(1) $\mathrm{M}$ is locally Noetherian.

(2) If $\mathrm{\{S_i|i\in \mathbb{N}\}(\subseteq\sigma[M])}$ is a family of simple modules, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{S_{i}}}$ in $\mathrm{\sigma[M]}$ is a direct sum of modules that are either $\mathrm{M}$-injective or projective.

(3) If $\mathrm{\{S_i|i\in \mathbb{N}\}(\subseteq\sigma[M])}$ is a family of simple modules, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ in $\mathrm{\sigma[M]}$ is a direct sum of modules that are either $\mathrm{M}$-injective or projective.

Theorem 2.3 can be extended to include $\mathrm{soc}$-injectivity.

Theorem 2.4. Assume $\mathrm{M_R}$ is a module. The following are equivalent:

(1) $\mathrm{M}$ is locally Noetherian.

(2) If $\mathrm{\{S_i|i\in \mathbb{N}\}(\subseteq\sigma[M])}$ is a family of simple modules, the essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{S_{i}}}$ in $\mathrm{\sigma[M]}$ is a direct sum of modules that are either strongly $\mathrm{soc}$-injective in $\mathrm{\sigma[M]}$ or projective.

(3) If $\mathrm{\{S_i|i\in \mathbb{N}\}(\subseteq\sigma[M])}$ is a family of simple modules, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ in $\mathrm{\sigma[M]}$ is a direct sum of modules that are either strongly $\mathrm{soc}$-injective in $\mathrm{\sigma[M]}$ or projective.

Proof. $\mathrm{(1)\Rightarrow (2)}$ and $\mathrm{(2)\Rightarrow (3)}$ are clear.

$\mathrm{(3)\Rightarrow (1)}$ Assume $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of simple modules in $\mathrm{\sigma[M]}$. Then, any essential extension $E$ of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_i)}}$ is strongly $\mathrm{soc}$-injective in $\mathrm{\sigma[M]}$ or projective. Because $\mathrm{E(\bigoplus\limits_{i\in \mathbb{N}}{E(S_i)})}$ has an essential socle, any strongly $\mathrm{soc}$-injective summand of $\mathrm{E(\bigoplus\limits_{i\in \mathbb{N}}{E(S_i)})}$ is $\mathrm{M}$-injective. As a result, $\mathrm{M}$ is locally Noetherian.

Corollary 2.2. Let $\mathrm{R}$ represent a ring. The following are equivalent:

(1) $\mathrm{R}$ is right Noetherian.

(2) If $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of simple modules, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{S_{i}}}$ is a direct sum of modules that are either strongly $\mathrm{soc}$-injective or projective.

(3) If $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of simple modules, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ is a direct sum of modules that are either strongly $\mathrm{soc}$-injective or projective.

Proof. The preceding Theorem makes this clear.

If a ring $\mathrm{R}$ is right (or left) Artinian and right (or left) self-injective, it is referred to as a quasi-Frobenius ($\mathrm{QF}$-ring). Equivalently, $\mathrm{R}$ is $\mathrm{QF}$ if and only if every injective right $\mathrm{R}$-module is projective if and only if every projective right $\mathrm{R}$-module is injective.

Corollary 2.3. Let $\mathrm{R}$ represents a ring. The following are equivalent:

(1) $\mathrm{R}$ is a $\mathrm{QF}$ ring.

(2) Every essential extension of the direct sum of strongly $\mathrm{soc}$-injective right $\mathrm{R}$-modules is projective.

Proof. If $\mathrm{R}$ is $\mathrm{QF}$, then every strongly $\mathrm{soc}$-injective module is injective ^[1]. As a result, [5,Corollary 2.8] completes the proof.

3.   $\mathrm{S}$-injectivity and Noetherian rings

Let $\mathrm{M}$ be a module and $\mathrm{N}$ and $\mathrm{L}$ be members of $\mathrm{\sigma[M]}$. If any homomorphism $\mathrm{f : K\rightarrow N}$ extends to $\mathrm{L}$ for any singular submodule $\mathrm{K}$ of $\mathrm{L}$, $\mathrm{N}$ is said to be $\mathrm{s}$-$\mathrm{L}$-injective. If $\mathrm{N}$ is $\mathrm{s}$-$\mathrm{N}$-injective, a module $\mathrm{N}$ in $\mathrm{\sigma[M]}$ is called $\mathrm{s}$-quasi-injective in $\mathrm{\sigma[M]}$. If $\mathrm{N}$ is $\mathrm{s}$-$\mathrm{M}$-injective, it is called $\mathrm{s}$-injective in $\mathrm{\sigma[M]}$. If $\mathrm{N}$ is $\mathrm{s}$-$\mathrm{L}$-injective for all $\mathrm{T}$ in $\mathrm{\sigma[M]}$, it is said to be strongly $\mathrm{s}$-injective in $\mathrm{\sigma[M]}$.

Theorem 3.1. Let $\mathrm{N\in\sigma[M]}$. The following are equivalent:

(1) In $\mathrm{\sigma[M]}$, $\mathrm{N}$ is strongly $\mathrm{s}$-injective.

(2) $\mathrm{N}$ is $\mathrm{s}$-$\mathrm{E_M(N)}$-injective, where $\mathrm{E_M(N)}$ is the injective hull of $\mathrm{N}$ in $\mathrm{\sigma[M]}$.

(3) $\mathrm{N = E\oplus L}$, where $\mathrm{E}$ is injective in $\mathrm{\sigma[M]}$, and $\mathrm{L}$ is nonsingular.

Furthermore, if $\mathrm{Z(N)\neq0}$, then $\mathrm{E}$ has an essential singular submodule.

Proof. $\mathrm{(1)\Rightarrow (2)}$ Clear.

$\mathrm{(2)\Rightarrow (3)}$ We're done if $\mathrm{Z(N) = 0}$. Assume $\mathrm{Z(N)\neq0}$, and consider the diagram below.

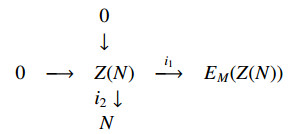
Here, $i_{1}$ and $i_{2}$ are inclusion maps. $\mathrm{N}$ is $\mathrm{s}$-$\mathrm{E_M(Z(N))}$- injective because $\mathrm{N}$ is $\mathrm{s}$-$\mathrm{E_M(N)}$-injective. As a result, there exists a homomorphism $\mathrm{\sigma:E_M(Z(N))\rightarrow N}$, which extends ${i_{2}}$. Since $\mathrm{Z(N)}$ is an embedding of $\mathrm{E_M(Z(N))}$ in $\mathrm{N}$, $\mathrm{Z(N)\subseteq^e E_M(Z(N))}$. If $\mathrm{E = E_M(Z(N))}$, then $\mathrm{N = E\oplus L}$ for some submodule $\mathrm{L}$ of $\mathrm{N}$. $\mathrm{E}$ is injective, and $\mathrm{L}$ is nonsingular.

$\mathrm{(3)\Rightarrow (1)}$ This is obvious because nonsingular modules are strongly $\mathrm{s}$-injective in $\mathrm{\sigma[M]}$, and the finite direct sum of strongly $\mathrm{s}$-injective modules is also strongly $\mathrm{s}$-injective in $\mathrm{\sigma[M]}$. The final statement of the theorem is $\mathrm{Z(E)\subseteq^e E}$. On the other hand, $\mathrm{Z(E) = Z(N) = \sigma(Z(N))\subseteq^e E}$ implies that $\mathrm{Z(E)\subseteq^e E}$.

Recall that a module $M$ satisfies ACC on essential submodules if $M$ satisfies the ascending chain condition on essential submodules.

Lemma 3.1. ^[10]For a right $\mathrm{R}$-module $\mathrm{M}$, the following areequivalent:

(1) $\mathrm{M}$ satisfies $\mathrm{ACC}$ on essential submodules.

(2) $\mathrm{M/Soc(M)}$ is right Noetherian.

Proposition 3.1. For a right $R$-module $\mathrm{M}$, the following are equivalent:

(1) $\mathrm{M/soc(M)}$ is locally Noetherian.

(2) Every direct sum of strongly $\mathrm{s}$-injective modules is strongly $\mathrm{s}$-injective in $\mathrm{\sigma[M]}$.

Proof. $\mathrm{(1)\Rightarrow (2)}$ Let $\mathrm{\{M_i\}_{i\in I}}$ represent a family of strongly $\mathrm{s}$-injective modules in $\mathrm{\sigma[M]}$. According to Theorem 3.1, write $\mathrm{M_i = E_i\oplus T_i}$ for each $\mathrm{i\in I}$, where $\mathrm{E_i}$ is injective in $\mathrm{\sigma[M]}$, and $\mathrm{Z(T_i) = 0}$. If $\mathrm{E = \oplus_{i\in I}E_i}$, and $\mathrm{T = \oplus_{i\in I}T_i}$, then $\mathrm{\oplus_{i\in I}M_i = E\oplus T}$, and $\mathrm{Z(T) = 0}$. $\mathrm{E}$ is $\mathrm{M/soc(M)}$-injective because $\mathrm{M/soc(M)}$ is locally Noetherian, and $\mathrm{E}$ can be considered in $\mathrm{\sigma[M/soc(M)]}$. As a result, $\mathrm{E}$ is injective in $\sigma[M]$, and $\mathrm{\oplus_{i\in I}M_i}$ is strongly $\mathrm{s}$-injective. Since $\mathrm{M/soc(M)}$ is locally Noetherian, and $\mathrm{E}$ may be considered in $\mathrm{\sigma[M/soc(M)]}$, $\mathrm{E}$ is $\mathrm{M/soc(M)}$-injective. As a result, $\mathrm{E}$ is injective in $\mathrm{\sigma[M]}$, and $\mathrm{\oplus_{i\in I}M_i}$ is strongly $\mathrm{s}$-injective.

$\mathrm{(2)\Rightarrow (1)}$. Consider a chain $\mathrm{L_{1}\subseteq L_{2}\subseteq......}$ of essential submodules of a submodule $\mathrm{K}$ of $\mathrm{M}$ with $\mathrm{soc(M)\subseteq K}$, and $\mathrm{K/soc(M)}$ is finitely generated. Let $\mathrm{E(K/L_{i})}$ be the injective hull of $\mathrm{K/L_{i}, }$ $\mathrm{i\geq 1, }$ and $\mathrm{f:L\longrightarrow \bigoplus\limits_{1\leq i}E(K/L_{i})}$ be a map defined by $\mathrm{f\left(l\right) = \left(l+L_{i}\right) }$ where $\mathrm{L = \bigcup\limits_{1\leq i}L_{i}}$. Since $\mathrm{\bigoplus\limits_{1\leq i}E(K/L_{i})}$ is strongly $\mathrm{s}$-injective in $\mathrm{\sigma[M]}$, and $\mathrm{\bigoplus\limits_{1\leq i}E(K/L_{i})}$ has an essential singular submodule, $\mathrm{\bigoplus\limits_{1\leq i}E(K/L_{i})}$ is injective, and $\mathrm{f}$ can be extended to an $\mathrm{R}$-homomorphism $\mathrm{\widehat{f} :K\longrightarrow \bigoplus\limits_{1\leq i}E(K/L_{i}).}$ Since $\mathrm{f\left(Soc(M)\right) = 0}$, there exists $\mathrm{h:K/soc(M)\longrightarrow \bigoplus\limits_{1\leq i}E(K/L_{i})}$ with $\mathrm{h(k+soc(M)) = \widehat{f}(k)}$ for all $\mathrm{k\in K}$.

Then $\mathrm{\widehat{f} (K)\subseteq \bigoplus\limits_{1\leq i\leq n}E(K/L_{i})}$ for some $\mathrm{n}$, and $\mathrm{ f(K)\subseteq \bigoplus\limits_{1\leq i\leq n}E(K/L_{i})}$. Thus $\mathrm{L = L_{j+n}}$ for every $\mathrm{j\geq 1}$, and $\mathrm{K}$ has $\mathrm{ACC}$ on essential submodules. It follows that $\mathrm{K/soc(K)}$ is Noetherian by the above Lemma. Since $soc(K) = soc(M)$, every finitely generated submodule of $\mathrm{M/soc(M)}$ is Noetherian. Therefore, $\mathrm{M/soc(M)}$ is locally Noetherian.

Proposition 3.2. Consider $\mathrm{M_R}$ to be a module. Then, the following are equivalent:

(1) $\mathrm{M/soc(M)}$ is locally Noetherian.

(2) The essential extension in $\mathrm{\sigma[M]}$ of a direct sum of any family of strongly $\mathrm{s}$-injective modules in $\mathrm{\sigma[M]}$ is a direct sum of $\mathrm{s}$-injective modules in $\mathrm{\sigma[M]}$.

(3) For a given family $\mathrm{\{S_i|i\in \mathbb{N}\}}$ of singular simple modules in $\mathrm{\sigma[M]}$, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ is a direct sum of injective modules in $\mathrm{\sigma[M]}$.

Proof. $\mathrm{(1)\Rightarrow (2)}$ and $\mathrm{(2)\Rightarrow (3)}$ are clear.

$\mathrm{(3)\Rightarrow (1)}$ Because the simple modules in $\mathrm{\sigma[M/soc(M)]}$ are the singular simple modules in $\mathrm{\sigma[M]}$, Theorem 2.1 completes the proof.

Theorem 3.2. Allow $\mathrm{M_R}$ to be a module. Then, the following are equivalent:

(1) $\mathrm{M/soc(M)}$ is locally Noetherian.

(2) If $\mathrm{\{S_i|i\in \mathbb{N}\}(\subseteq\sigma[M])}$ is a family of singular simple modules, then any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ in $\mathrm{\sigma[M]}$ is a direct sum of modules that are either strongly $\mathrm{s}$-injective or projective in $\mathrm{\sigma[M]}$.

(3) Provided a family of singular simple modules $\mathrm{\{S_i|i\in \mathbb{N}\}(\subseteq\sigma[M])}$, any essential extension of $\mathrm{\bigoplus\limits_{i\in \mathbb{N}}{E(S_{i})}}$ in $\mathrm{\sigma[M]}$ would be a direct sum of modules that are either strongly $\mathrm{s}$-injective in $\mathrm{\sigma[M]}$ or projective.

Proof. $\mathrm{(1)\Rightarrow (2)}$ and $\mathrm{(2)\Rightarrow (3)}$ are clear.

$\mathrm{(3)\Rightarrow (1)}$ Assume $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of singular simple modules in $\mathrm{\sigma[M]}$. Then, any essential extension $\mathrm{E}$ of $\mathrm{E(\bigoplus\limits_{i\in \mathbb{N}}(S_{i}))}$ is strongly $\mathrm{s}$-injective in $\mathrm{\sigma[M]}$ or projective. Because $\mathrm{E(\bigoplus\limits_{i\in \mathbb{N}}{S_{i}})}$ contains an essential singular submodule, every strongly $\mathrm{s}$-injective summand of $\mathrm{E(\bigoplus\limits_{i\in \mathbb{N}}{S_{i}})}$ is $\mathrm{M/soc(M)}$-injective. As a result, according to Theorem 2.3, $\mathrm{M/soc(M)}$ is locally Noetherian.

Corollary 3.1. Let $\mathrm{R}$ represent a ring. The following are equivalent:

(1) $\mathrm{R/S_r}$ is right Noetherian.

(2) The essential extension of a direct sum of any family of strongly $\mathrm{s}$-injective right $\mathrm{R}$-modules is a directsum of $\mathrm{s}$-injective modules.

(3) The essential extension of a direct sum of any family of injective right $\mathrm{R}$-modules is a direct sum of modules that areeither strongly $\mathrm{s}$-injective or projective.

(4) If $\mathrm{\{S_i|i\in \mathbb{N}\}}$ is a family of singular simple right $\mathrm{R}$-modules, any essential extension of $\mathrm{\bigoplus\limits_{i\in\mathbb{N}}{E(S_{i})}}$ is a direct sum of injective modules.

(5) Given a family $\mathrm{\{S_i|i\in \mathbb{N}\}}$ of singular simple $\mathrm{R}$-modules, any essential extension of $\mathrm{\bigoplus\limits_{i\in\mathbb{N}}{E(S_{i})}}$ is a direct sum ofright $R$-modules that are either injective or projective.

Conflict of interest

The authors declare that they have no competing interests.