Nowadays, the problem of finding families of graphs for which one may ensure the existence of a vertex-labeling and/or an edge-labeling based on a certain class of integers, constitutes a challenge for researchers in both number and graph theory. In this paper, we focus on those vertex-labelings whose induced multiplicative edge-labeling assigns hyper totient numbers to the edges of the graph. In this way, we introduce and characterize the notions of hyper totient graph and restricted hyper totient graph. In particular, we prove that every finite graph is a hyper totient graph and we determine under which assumptions the following families of graphs constitute restricted hyper totient graphs: complete graphs, star graphs, complete bipartite graphs, wheel graphs, cycles, paths, fan graphs and friendship graphs.
Citation: Shahbaz Ali, Muhammad Khalid Mahmmod, Raúl M. Falcón. A paradigmatic approach to investigate restricted hyper totient graphs[J]. AIMS Mathematics, 2021, 6(4): 3761-3771. doi: 10.3934/math.2021223
| [1] | Mohammad Hamidi, Irina Cristea . Hyperideal-based zero-divisor graph of the general hyperring $ \mathbb{Z}_{n} $. AIMS Mathematics, 2024, 9(6): 15891-15910. doi: 10.3934/math.2024768 |
| [2] | Fawaz E. Alsaadi, Faisal Ali, Imran Khalid, Masood Ur Rehman, Muhammad Salman, Madini Obad Alassafi, Jinde Cao . Quantifying some distance topological properties of the non-zero component graph. AIMS Mathematics, 2021, 6(4): 3512-3524. doi: 10.3934/math.2021209 |
| [3] | Faik Babadağ, Ali Atasoy . On hyper-dual vectors and angles with Pell, Pell-Lucas numbers. AIMS Mathematics, 2024, 9(11): 30655-30666. doi: 10.3934/math.20241480 |
| [4] | Bin Zhou, Xiujuan Ma, Fuxiang Ma, Shujie Gao . Robustness analysis of random hyper-networks based on the internal structure of hyper-edges. AIMS Mathematics, 2023, 8(2): 4814-4829. doi: 10.3934/math.2023239 |
| [5] | Andromeda Sonea, Irina Cristea . Euler's totient function applied to complete hypergroups. AIMS Mathematics, 2023, 8(4): 7731-7746. doi: 10.3934/math.2023388 |
| [6] | Qi Xiao, Jin Zhong . Characterizations and properties of hyper-dual Moore-Penrose generalized inverse. AIMS Mathematics, 2024, 9(12): 35125-35150. doi: 10.3934/math.20241670 |
| [7] | Yamin Sayyari, Mehdi Dehghanian, Choonkil Park, Jung Rye Lee . Stability of hyper homomorphisms and hyper derivations in complex Banach algebras. AIMS Mathematics, 2022, 7(6): 10700-10710. doi: 10.3934/math.2022597 |
| [8] | Abdelaziz Alsubie, Anas Al-Masarwah . MBJ-neutrosophic hyper $ BCK $-ideals in hyper $ BCK $-algebras. AIMS Mathematics, 2021, 6(6): 6107-6121. doi: 10.3934/math.2021358 |
| [9] | Hashem Bordbar, Sanja Jančič-Rašovič, Irina Cristea . Regular local hyperrings and hyperdomains. AIMS Mathematics, 2022, 7(12): 20767-20780. doi: 10.3934/math.20221138 |
| [10] | Ali Al Khabyah . Mathematical aspects and topological properties of two chemical networks. AIMS Mathematics, 2023, 8(2): 4666-4681. doi: 10.3934/math.2023230 |
Nowadays, the problem of finding families of graphs for which one may ensure the existence of a vertex-labeling and/or an edge-labeling based on a certain class of integers, constitutes a challenge for researchers in both number and graph theory. In this paper, we focus on those vertex-labelings whose induced multiplicative edge-labeling assigns hyper totient numbers to the edges of the graph. In this way, we introduce and characterize the notions of hyper totient graph and restricted hyper totient graph. In particular, we prove that every finite graph is a hyper totient graph and we determine under which assumptions the following families of graphs constitute restricted hyper totient graphs: complete graphs, star graphs, complete bipartite graphs, wheel graphs, cycles, paths, fan graphs and friendship graphs.
In 2017, Khalid and Shahbaz [1] introduced the notions of totient, super totient and hyper totient numbers (see also [2]). Recall in this regard that a positive integer t is said to be totient if the sum of its co-prime residues is 2kt, with k≥1. Further, a positive integer s is called super totient if its set of co-prime residues can be divided into two nonempty disjoint subsets with equal sum. Finally, a positive integer h is said to be hyper totient if its set of co-prime residues including h can be divided into two nonempty disjoint subsets with equal sum. This paper focuses on the use of hyper totient numbers in graph labeling.
The assignment of positive integers as labels of vertices and/or edges of a graph is a classic problem in graph theory (see, for instance, [3,4,5]), with a broad range of applications in real daily life problems as networking, coding theory, digital design, database or management, amongst other areas. Nowadays, the problem of finding and characterizing new classes of integers satisfying certain given conditions, together with the problem of finding illustrative families of graphs for which a labeling based on such classes exists, constitutes a challenge for researchers in both number and graph theory. In the recent literature, one can find a wide amount of examples in this regard [6,7,8,9]. Of particular interest for the topic of this paper, it is remarkable the recent studies of Shahbaz and Khalid [1,10] on graph labelings based on super totient numbers, and the introduction of both concepts of restricted super totient labeling and super totient index of graphs by Joshua and Wong [11].
The paper is organized as follows. In Section 2, we describe some preliminary concepts and results on graph theory and hyper totient numbers that are used throughout the paper. Then, we introduce in Section 3 the concept of (restricted) hyper totient graph labeling. In particular, we prove that every finite graph is hyper totient. Finally, we investigate in Section 4 under which assumptions the following families of graphs constitute restricted hyper totient graphs: complete graphs, star graphs, complete bipartite graphs, wheel graphs, cycles, paths, fan graphs and friendship graphs.
This section deals with some preliminary concepts, notations and results on graph theory and hyper totient numbers that are used throughout the paper. For more details about these topics, we refer the reader to the manuscripts [1,10,12].
A graph is any pair G=(V,E) formed by a set V of vertices and a set E of edges so that each edge joins two vertices, which are then said to be adjacent. The number of vertices and the number of edges of G constitute, respectively, the order and size of G. A graph is said to be finite if both its order and size are finite. A subetaaph of G is any graph H=(W,F) such that W⊆V and F⊆E. The set of vertices that are adjacent to a given vertex v∈V constitutes its neighborhood NG(v). The number of such vertices constitutes the degree dG(v) of such a vertex v. The minimum vertex degree of the graph G is denoted δ(G).
From now on, let vw be the edge formed by two vertices v,w∈V. If v=w, then it is a loop. A graph is called simple if it does not contain loops. Two graphs G1=(V1,E1) and G2=(V2,E2) are said to be isomorphic if there exists a bijection f:V1→V2 such that uv∈E1 if and only if f(u)f(v)∈E2.
A finite graph is called complete if all its vertices are pairwise adjacent. The complete graph of order n is denoted Kn. Further, the complete bipartite graph Km,n is the finite graph of order m+n whose set of vertices may be partitioned into two subsets of respective sizes m and n so that every edge of the graph contains a vertex of each one of these two sets. The complete bipartite graph K1,n, with n>2, is called a star graph. Its center is the unique vertex that is contained in all the edges.
A path between two distinct vertices v and w of a given finite graph G is any ordered sequence of adjacent and pairwise distinct vertices ⟨v0=v,v1,…,vn−2,vn−1=w⟩ in G, with n>2. If v=w, then it constitutes a cycle. As such, paths and cycles are also finite graphs. From here on, let Pn and Cn respectively denote the path and the cycle of order n. A graph is connected if there always exists a path between any pair of vertices. If no subetaaph of a connected graph G is a cycle, then G is called a tree.
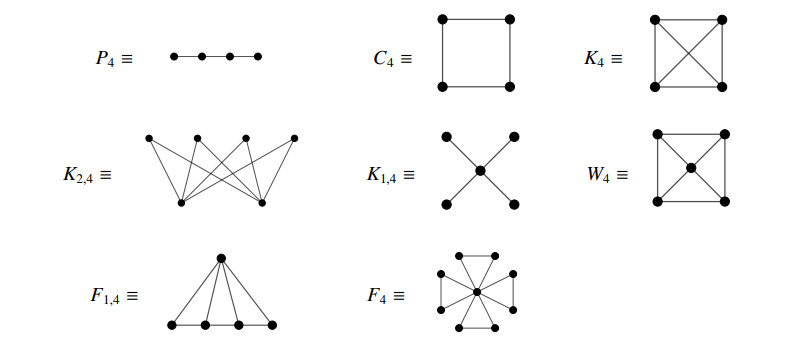
Further, the wheel graph Wn results after joining all the vertices of the cycle Cn to a new vertex, which is called the center of the wheel graph. The fan graph Fm,n is the graph that results after joining each vertex of a set of m isolated vertices with all the vertices of the path Pn. Finally, the friendship graph Fn is the graph that results after joining n copies of the cycle C3 with a common vertex. Figure 1 illustrates the different families of graphs that we have enumerated until now.
A vertex-labeling of a graph G is any map f:V→N assigning |V| positive integers or labels to the set of vertices V. It gives rise to the induced multiplicative edge-labeling f∗:E→N so that f∗(vw)=f(v)f(w), for all vw∈E. In 2017, Khalid and Shahbaz [1] defined a super totient graph as any finite graph G for which there exists an injective vertex-labeling f (which is called super totient labeling of G) whose induced multiplicative edge-labeling f∗ assigns a super totient number to each one of its edges. In particular, they proved that every finite graph is super totient. Much more recently, Joshua and Wong [11] defined the super totient index of a finite graph G as the minimum cardinality of the image of f∗, for every super totient labeling f of G. In this paper, we focus on those injective vertex-labelings f so that the image of the induced map f∗ is only formed by hyper totient numbers. To this end, the following result characterizing this type of numbers is of particular interest. It gathers together the different results on this subject that are enumerated in [2].
Theorem 2.1. Every hyper totient number is a positive integer n>2 satisfying exactly one of the following two assertions.
a) It is an even integer distinct from 10 and 30.
b) It is a prime power pk, with k≥1, where p is a prime such that p≡3(mod4).
Proof. If n<32, then the result follows readily from a simple computational check (see, for instance, [2,Table 1]). Further, according to [2,Theorem 3.6], a positive integer n≥32 is hyper totient if and only if n(φ(n)+2) is divisible by 4. Here, φ(n) denote the Euler's totient number associated to n. That is, the number of co-prime residues of n. The result holds from the following study of cases.
● If n is even, then n(φ(n)+2) is divisible by 4, because φ(m) is also even, whatever the positive integer m is. Hence, n is hyper totient.
● If n is odd, then n is hyper totient if and only if φ(n)+2 is divisible by 4. Equivalently, if n=∏mi=1pkii is the prime factorization of n, then φ(n)=∏mi=1pki−1i(pi−1)≡2(mod4). Since n is an odd integer, we have that pi is also odd, for all i≤m. Thus, φ(n)≡2(mod4) if and only if m=1 in the previous prime factorization. (Otherwise, if m>1, then φ(n) would be divisible by 4.) Hence, n=pk, for some prime p≡3(mod4). (Notice to this last end that it would be φ(n)=pk−1(p−1)≡2(mod4), where p is odd.)
In this section, we show how hyper totient numbers may be implemented in graph labeling. In this regard, we say that a finite graph G=(V,E) is an hyper totient graph if there exists an injective vertex-labeling f of G whose induced multiplicative edge-labeling f∗ assigns a hyper totient number to each edge in E. In such a case, we say that the map f is an hyper totient labeling (HTL) and that the graph G is an hyper totient graph (HTG). In order to illustrate these concepts, Figure 2 shows an HTG of order five and size ten, whose vertices are uniquely labeled by the positive integers of the subset {2,3,4,6,7}⊂N and whose set of edges is then labeled by the set of totient numbers {4,6,8,9,12,14,16,36,49}. In order to distinguish both vertex- and edge-labelings, they are respectively colored in blue and black. Notice the fact that this graph is not simple.
Similarly to the concept of super totient index, which was introduced by Joshua and Wong in [11], we define the hyper totient index of the graph G as
| h∗(G):=min{|f∗(V)|:f is an HTL of G}. |
Then, we say that an HTL f of the graph G is optimal if |f∗(V)|=h∗(G). In an analogous way to the result obtained by the mentioned authors in [11,Lemma 4.3], the following lemma holds.
Lemma 3.1. Let G be an HTG. There always exists an optimal HTL of G whose image is contained in the set {3i:i∈N}.
Proof. Let f be an optimal HTL of the graph G and let V={v1,…,vn} be its set of vertices. Then, let {p1,…,pt} be a set of primes such that f∗(vi)=∏tj=1paijj, for all positive integers i≤n, where each aij is a non-negative integer. Let m=1+max{aij:1≤i≤n,1≤j≤t}. Then, Theorem 2.1 implies that the map g:V→{3i:i∈N} that is described so that g(vi)=3∑tk=1aikmk−1 constitutes an optimal HTL of the graph G.
The previous result enables us to ensure the equivalence of super totient and hyper totient indices, and the subsequent result concerning the fact that every finite graph is an HTG.
Theorem 3.2. Both the hyper totient index and the super totient index of any given finite graph coincide.
Proof. Let f be an injective vertex-labeling of a graph G=(V,E). This map induces the additive edge-labeling f+:E→N so that f+(vw)=f(v)+f(w), for all vw∈E. In addition, it is defined the sum index of the graph G as
| min{|f+(V)|:f is an injective vertex-labeling of G}. |
As a simple consequence of Lemma 3.1, the hyper totient index of the graph G coincides with the sum index of such a graph. The result follows simply from the fact that, according to [11,Theorem 4.5], this last index also coincides with the super totient index of the graph G.
Corollary 3.3. Every finite graph constitutes an HTG.
Proof. The result follows straighforwardly from Theorem 3.2 and the fact that every finite graph is a super totient graph (see [1,Theorem 5.5]).
We say that a finite graph G=(V,E) is a restricted hyper totient graph (RHTG) if it is a simple HTG whose set of vertices may be labeled by the subset of positive integers {1,…,|V|}. The corresponding vertex-labeling is termed a restricted hyper totient labeling (RHTL) of G. Thus, for instance, Figure 3 illustrates a RHTL of order and size six, whose set of edges is labeled by the set of totient numbers {3,4,6,12}. Again, the vertex-labeling is colored in blue and the edge-labeling is colored in black.
Of particular interest for the development of our work is the RHTG having maximum size for each given order. It is described as follows. Let ℜn be the RHTG of order n that is defined so that there is an edge between the vertices labeled as i and j, with 1≤i≠j≤n, if and only if the product ij is a hyper totient number. Figure 4 illustrates this graph ℜn, for all positive integers n≤9. In order to avoid a tangled mess of labels, we remove from now on the edge-labeling of the corresponding graphs.
The following result follows straightforwardly from the previous definitions.
Lemma 4.1. For n>3, every spanning subetaaph of ℜn is an RHTG.
Lemma 4.1 enables us to ensure that the finding of RHTGs is completely solved once one may construct the graph ℜn, for every positive integer n. In this regard, and based on Theorem 2.1, Algorithm 1 describes a simple computational method of time complexity O(n2) for determining this graph ℜn.
| Algorithm 1 Construction of the graph ℜn. |
| 1. procedure R(n) |
| 2: V(ℜn)={1,…,n}; |
| 3: fori←1,n do |
| 4: forj←i+1,n do |
| 5: if ij satisfies either Condition (a) or Condition (b) in Theorem 2.1 then |
| 6: E(ℜn)←E(ℜn)∪{ij}; |
| 7: end if |
| 8: end for |
| 9: end for |
| 10: return ℜn=(V(ℜn),E(ℜn)) |
| 11: end procedure |
In this section, we study under which assumptions the following types of graphs constitute RHTGs: a complete graph Kn, a star graph K1,n, a complete bipartite graph Km,n, a wheel graph Wn, a cycle Cn, a path Pn, a fan graph F1,n and a friendship graph Fn. Notice that, according to Lemma 4.1, any subetaaph of any of these types of graphs satisfying the mentioned assumptions constitutes also an RHTG. Firstly, we focus on the complete graph Kn.
Proposition 4.2. Let n be a positive integer. Then, the complete graph Kn is an RHTG if and only if n=1.
Proof. The case n=1 is trivial. Further, the case n≥2 follows straightforwardly from the fact that the vertices labeled as 1 and 2 must be adjacent, but the induced edge label 2 is not a hyper totient number.
Proposition 4.3. Let n>2 be a positive integer. Then, the star graph K1,n is a spanning subetaaph of ℜn+1. As a consequence, every star graph constitutes an RHTG.
Proof. According to Theorem 2.1, every multiple of 4 is a hyper totient number. Hence, the spanning subetaaph of ℜn+1 having as edges those ones containing the vertex labeled as 4 constitutes a star graph K1,n. This vertex corresponds indeed to the center of the star graph. The consequence follows readily from Lemma 4.1.
Theorem 4.4. Let m and n be two positive integers such that 2≤m≤n. The complete bipartite graph Km,n is an RHTG if and only one of the following assertions hold.
a) m=n=2.
b) m=2 and n≥6.
c) 3≤m≤11 and n≥m+6.
d) m≥12 and n≥m+8.
Proof. Figure 5 illustrates the case m=n=2. Thus, let us suppose the existence of two positive integers m≥2 and n≥2 such that m+n>4 and Km,n is an RHTG. Let vi denote the vertex that is labeled as i∈{1,…,m+n} in the graph ℜm+n. Since 10 is not a hyper totient number, the two vertices v2 and v5 must belong to the same part of Km,n. Let P denote such a part. Then,
| NKm,n(v2)=NKm,n(v5)=Km,n∖P⊆Nℜm+n(v2)∩Nℜm+n(v5). |
From Theorem 2.1, we have that
| Nℜm+n(v5)={v4}∪{v2k:4≤k≤m+n2}⊂Nℜm+n(v2). |
In particular, since 2≤m≤n, it must be m+n≥8 and n=|P|. Moreover, Theorem 2.1 enables us to ensure that every vertex in the set Nℜm+n(v5), except for v10 (if m+n≥10) and v30 (if m+n≥30), is adjacent to any other vertex in the set ℜm+n. Notice to this end that all the indices of such vertices are even integers and that both vertices v10 and v30 are not adjacent to v1∈P. Due to this last aspect, it must be {v10,v30}⊂P. As a consequence,
| m+n≥{8, if m=2,2(m+3), if 3≤m≤11,2(m+4), if m≥12. |
Let αm,n denote the previous lower bound, for the positive integers m and n under consideration. Then, in order to get an RHTL of the graph Km,n, it is enough to take
| Km,n∖P={v2k:2≤k≤αm+n2}∖{v6,v10,v30}. |
Figure 6 illustrates an RHTL for the complete bipartite graph K4,13.
Theorem 4.5. Every tree containing at least 32 vertices is an RHTG.
Proof. The result follows straightforwardly from Lemma 4.1, Proposition 4.3 and Theorem 4.4 once it is noticed that every tree is a bipartite graph.
Theorem 4.6. The wheel graph Wn is an RHTG if and only if n≥9.
Proof. Throughout this proof, let vi denote the vertex labeled as i∈N in the graph under consideration. Notice in Figure 4 that δ(ℜn)≤2, for all positive integer n≤9. To this end, observe in the mentioned figure the vertex v1, if 1≤n≤5, and the vertex v5, if 6≤n≤9. Then, since δ(Wn)=3, for all positive integers n, we have from Lemma 4.1 that the wheel graph Wn is not an RHTG, if n<9.
Now, Figure 7 illustrates an RHTL of the wheel graph W9. If we replace the edge v10v6 in that figure by the path ⟨v10,v11,…,vn+1,v6⟩, so that all the vertices are joined with the center v4 by an edge, then Theorem 2.1 implies that the resulting vertex-labeling is an RHTL of the wheel graph Wn.
Theorem 4.7. Let n>2 be a positive integer. Then, the cycle graph Cn is an RHTG if and only if n=4 or n≥8.
Proof. Again, let vi denote the vertex labeled as i∈N in the graph under consideration. Notice in Figure 4 that δ(ℜn)≤1, for all positive integer n≤7, except for n=4. To this end, observe in the mentioned figure the vertex v1, if 1≤n≤3, and the vertex v5, if 5≤n≤7. Then, since δ(Cn)=2, for all positive integers n, we have from Lemma 4.1 that the cycle Cn is not an RHTG, if n∈{3,5,6,7}.
Now, Figures 5 and 8 illustrate, respectively, RHTLs of the cycles C4, which is isomorphic to the complete bipartite graph K2,2, and C8. Finally, if n≥9, then the result follows simply from Lemma 4.1 and Theorem 4.6, once it is noticed that the cycle Cn is a subetaaph of the wheel graph Wn+1.
Theorem 4.8. Every path is an RHTG.
Proof. Firstly, notice that the path P3 is isomorphic to the graph ℜ3, and hence, it constitutes an RHTG. In addition, if n=4 or n≥8, then the result follows simply from Lemma 4.1 and Theorem 4.7, once it is noticed that the path Pn is a subetaaph of the cycle Cn. Finally, the case n∈{5,6,7} is illustrated by the RHTL of the path P7 in Figure 9, which contains implicitly the RHTLs of both paths P5 and P6 as subetaaphs.
Theorem 4.9. Let n>2 be a positive integer. Then, the fan graph F1,n is an RHTG if and only if n≥9.
Proof. Since δ(F1,n)=2, for all positive integers n>2, Lemma 4.1 enables us to ensure that the fan graph F1,n is not an RHTG, for all n∈{4,5,6}, because δ(ℜn+1)=1 in such cases. Further, the case n≥9 follows simply from Lemma 4.1 and Theorem 4.6, once it is noticed that the fan graph F1,n is a subetaaph of the wheel graph Wn. Finally, the case n∈{3,7,8} is illustrated by the RHTLs of the fan graphs F1,3 and F1,8 in Figure 10. Notice to this end that the RHTL of the fan graph F1,7 is implicitly indicated in that one of the fan graph F1,8, of which the former constitutes a subetaaph.
Theorem 4.10. The friendship graph Fn is an RHTG if and only if n≥4.
Proof. Since the order of the friendship graph Fn is 2n+1 and δ(ℜn)=1, for all n∈{3,5,7}, then Lemma 4.1 implies that the friendship graph Fn is not an RHTG, for all n≤3. Further, the case n≥4 follows simply from Lemma 4.1 and Theorem 4.6, once it is noticed that the friendship graph Fn is a subetaaph of the wheel graph Wm, for all m≥2n.
In this paper, we have introduced the notion of hyper totient graph as any finite graph G=(V,E) admitting an injective vertex-labeling f:V→N so that its induced multiplicative edge-labeling assigns a hyper totient number to each edge. We have proved in particular that every finite graph is hyper totient. Furthermore, we have introduced the concept of restricted hyper totient graph as a hyper totient graph of order n whose vertices are labeled by the elements of the set {1,…,n}. Then, we have determined under which assumptions some well-known families of graphs are restricted hyper totient.
Of course, the current manuscript constitutes a starting point for the study of hyper totient graphs, but a much deeper study is required in order to characterize all the structural properties of this type of graphs. In this regard, we propose as further work the study of locating, dominating and independent sets within a given RHTG, together with their corresponding locating, dominating and independent numbers. We also propose the following open questions for further work on this subject.
Problem 5.1. In Theorem 4.5, we have determined a lower bound for the number of vertices of a tree in order to ensure that the latter is an RHTG. But, what about trees of smaller orders? A similar reasoning to that one developed by Joshua and Wong in [11,Theorem 3.9] may be done in this regard.
Problem 5.2. In 2001, Beineke and Hedge [13] defined a strongly multiplicative graph as a finite graph of order n for which there exists an injective vertex-labeling f:V→{1,…,n} so that the induced multiplicative edge-coloring f∗ is injective. In a similar way, we may introduce here the notion of strongly hyper totient graph (SHTG) as an RHTG having distinct all the hyper totient numbers that are used for labeling its edges. Notice in this regard that the majority of RHTGs appearing in the figures of this paper are not SHTGs. The study of this type of RHTGs is established as further work.
Problem 5.3. Under which assumptions is the condition of being RHTG preserved by the different graph products existing in the literature? A similar question may be dealt with concerning the just introduced notion of SHTG.
Falcón's work is partially supported by the research project FQM-016 from Junta de Andalucía. In addition, the authors want to express their gratitude to the anonymous referees for the comprehensive reading of the paper and their pertinent comments and suggestions, which helped improve the manuscript.
All authors are here with confirm that there are no competing interests between them.
| [1] | M. Khalid, A. Shahbaz, A novel labeling algorithm on several classes of graphs, Punjab Univ. J. Math., 49 (2017), 23-35. |
| [2] | A. Shahbaz, M. Khalid, New numbers on Euler's totient function with application, J. Math. Extension, 14 (2019), 61-83. |
| [3] | A. Rosa, On certain valuations of the vertices of a graph, Theory of Graphs: Int. Symp., Rome, 1966, (1967), 349-355. |
| [4] |
G. S. Bloom, S. W. Golomb, Application of numbered undirected graphs, P. IEEE, 65 (1977), 562-570. doi: 10.1109/PROC.1977.10517

|
| [5] | J. A. Gallian, A dynamic survey of graph labeling, Electron. J. Comb., 6 (2009), 1-219. |
| [6] | H. V. Dinh, M. Rosenfeld, A new labeling of C2n proves that K4+M6n decomposes K6n+4, Ars Comb., 4 (2018), 255-267. |
| [7] |
M. Hussain, A. Tabraiz, Super d-anti-magic labeling of subdivided kC5, Turk. J. Math., 39 (2015), 773-783. doi: 10.3906/mat-1501-45

|
| [8] |
M. Seoud, S. Salman, Some results and examples on difference cordial graphs, Turk. J. Math., 40 (2016), 417-427. doi: 10.3906/mat-1504-95

|
| [9] |
M. Seoud, M. Salim, Further results on edge-odd graceful graphs, Turk. J. Math., 40 (2016), 647-656. doi: 10.3906/mat-1505-67

|
| [10] | M. Khalid, A. Shahbaz, On super totient numbers with applications and algorithms to graph labeling, Ars Comb., 143 (2019), 29-37. |
| [11] |
H. Joshua, W. H. T. Wong, On super totient numbers and super totient labelings of graphs, Discrete Math., 343 (2020), 111670. doi: 10.1016/j.disc.2019.111670

|
| [12] | F. Harary, Graph Theory, Reading, Massachusetts: Addison Wesley, 1969. |
| [13] |
L. W. Beineke, S. M. Hegde, Strongly multiplicative graphs, Discuss. Math. Graph T., 21 (2001), 63-75. doi: 10.7151/dmgt.1133

|
| 1. | M. Haris Mateen, Muhammad Khalid Mahmmod, Doha A. Kattan, Shahbaz Ali, A novel approach to find partitions of $ Z_{m} $ with equal sum subsets via complete graphs, 2021, 6, 2473-6988, 9998, 10.3934/math.2021581 | |
| 2. | Nadeem Salamat, Muhammad Kamran, Shahbaz Ali, Md. Ashraful Alam, Riaz Hussain Khan, Fairouz Tchier, Several Characterizations on Degree-Based Topological Indices for Star of David Network, 2021, 2021, 2314-4785, 1, 10.1155/2021/9178444 | |
| 3. | Muhammad Usman Ghani, Muhammad Kashif Maqbool, Reny George, Austine Efut Ofem, Murat Cancan, Entropies Via Various Molecular Descriptors of Layer Structure of H3BO3, 2022, 10, 2227-7390, 4831, 10.3390/math10244831 | |
| 4. | Muhammad Usman Ghani, Francis Joseph H. Campena, Shahbaz Ali, Sanaullah Dehraj, Murat Cancan, Fahad M. Alharbi, Ahmed M. Galal, Characterizations of Chemical Networks Entropies by K-Banhatii Topological Indices, 2023, 15, 2073-8994, 143, 10.3390/sym15010143 | |
| 5. | S. Nagarajan, Muhammad Imran, P. Mahesh Kumar, K. Pattabiraman, Muhammad Usman Ghani, Degree-Based Entropy of Some Classes of Networks, 2023, 11, 2227-7390, 960, 10.3390/math11040960 | |
| 6. | Shahbaz Ali, Rashad Ismail, Francis Joseph H. Campena, Hanen Karamti, Muhammad Usman Ghani, On Rotationally Symmetrical Planar Networks and Their Local Fractional Metric Dimension, 2023, 15, 2073-8994, 530, 10.3390/sym15020530 | |
| 7. | Tayyiba Sabahat, Sufyan Asif, Asif Abd ur Rehman, On Fixed Points of Digraphs Over Lambert Type Map, 2021, 9, 2309-0022, 59, 10.21015/vtm.v9i1.1023 | |
| 8. | Sufyan Asif, Muhammad Khalid Mahmood, Amal S. Alali, Abdullah A. Zaagan, Structures and applications of graphs arising from congruences over moduli, 2024, 9, 2473-6988, 21786, 10.3934/math.20241059 | |
| 9. | Mamoona Farooq, Asif Abd ul Rehman, M. Khalid Mahmood, Daud Ahmad, Upper Bound Sequences of Rotationally Symmetric Triangular Prism Constructed as Halin Graph Using Local Fractional Metric Dimension, 2021, 9, 2309-0022, 13, 10.21015/vtm.v9i1.1020 | |
| 10. | Amal S. Alali, Shahbaz Ali, Noor Hassan, Ali M. Mahnashi, Yilun Shang, Abdullah Assiry, Algebraic Structure Graphs over the Commutative Ring Zm: Exploring Topological Indices and Entropies Using M-Polynomials, 2023, 11, 2227-7390, 3833, 10.3390/math11183833 | |
| 11. | Shahbaz Ali, Muhammad Khalid Mahmood, Sobia Ghaffar, Several topological indices and entropies for certain families of commutative graphs over Quaternion groups, 2024, 12, 2309-0022, 32, 10.21015/vtm.v12i2.1901 | |
| 12. | Muhammad Amir Asif, Rashad Ismail, Ayesha Razaq, Esmail Hassan Abdullatif Al-Sabri, Muhammad Haris Mateen, Shahbaz Ali, An application on edge irregular reflexive labeling for $ m^t $-graph of cycle graph, 2025, 10, 2473-6988, 1300, 10.3934/math.2025060 | |
| 13. | Mohammed Alsharafi, Haifa Ahmed, Saad Tobaili, Ayesha Ikram, On the Hub Number of Ring Graphs and Their Behavior Under Graph Operations, 2025, 2025, 0161-1712, 10.1155/ijmm/5522259 |
| Algorithm 1 Construction of the graph ℜn. |
| 1. procedure R(n) |
| 2: V(ℜn)={1,…,n}; |
| 3: fori←1,n do |
| 4: forj←i+1,n do |
| 5: if ij satisfies either Condition (a) or Condition (b) in Theorem 2.1 then |
| 6: E(ℜn)←E(ℜn)∪{ij}; |
| 7: end if |
| 8: end for |
| 9: end for |
| 10: return ℜn=(V(ℜn),E(ℜn)) |
| 11: end procedure |