Optimal control strategies for a heroin epidemic model with age-dependent susceptibility and recovery-age

1.   Introduction

In this paper, we present a hybrid nonlinear conjugate gradient (CG) method for solving unconstrained optimization problems:

where $f : \mathbb{R}^n \to \mathbb{R}$ is continuously differentiable and its gradient $g(x) = \nabla f(x)$ is Lipschitz continuous. CG methods are among the most prefered iterative methods for solving large-scale problems because of their simplicity in implementation, Hessian free and less storage requirements ^[14]. In view of these advantages, an encouraging number of CG methods were proposed (see, for example, ^{[1,5,10,12,13,31]}).

The conjugate gradient method for solving (1.1) generates a sequence $\{x_k\}$ via the iterative formula

where $d_k$ is the search direction defined by

and for descent methods, $d_k$ is usually required to satisfy the sufficient descent property, if there exists a constant $c > 0$ such that for all $k$

The scalar $\alpha_k > 0$ is the step-size determined by a suitable line search rule, and $\beta_k$ is the conjugate gradient parameter that characterizes different type of conjugate gradient methods based on the global convergence properties and numerical performance. Some of the well-known nonlinear conjugate gradient parameters are the Fetcher-Reeves (FR) ^[9], Polak-Ribiére-Polyak (PRP)^[25,26], Hestenes-Stiefel (HS)^[15], conjugate descent (CD) ^[8], Liu-Storey (LS) ^[22] and Dai-Yuan (DY) ^[6]. These prameters are given by the following formulae:

where $g_k = g(x_k), \; \; y_{k-1} = g_k-g_{k-1}$ and $\|\cdot\|$ is the Euclidean norm.

In order to have some of the classical CG methods possess a descent direction and trust region as well as improving their numerical efficiency, the three-term CG and hybrid CG methods were introduced for solving (1.1). For instance, Mo et al. ^[23] proposed two hybrid methods for solving unconstrained optimization problems. The methods are based on the Touati-Ahmed and Storey ^[30] and the DY methods. Under the strong Wolfe condition, the global convergence was proved. Andrei in ^[2] proposed a simple three-term CG method obtained by modifying the Broyden-Fletcher-Goldferb-Shanno (BFGS) updating formula of the inverse approximation of the Hessian. The search direction satisfies both the descent and conjugacy conditions. Numerical results were given to support the theoretical results. Also in ^[3], Andrei proposed an eliptic CG method for solving (1.1). The search direction is the sum of the negative gradient and a vector obtained by minimizing the quadratic approximation of the objective function. In addition, the search direction satisfies both Dai-Liao (DL) cojugacy and descent conditions. Eigenvalue analysis was carried out to determine parameter which the search direction depends on. In comparison with the well-known CG_DESCENT method, the proposed method was more efficient. Liu and Li ^[21] proposed a new hybrid CG with it's search direction satisfying the DL conjugacy condition and the Newton direction independent of the line search. As usual the global convergence was established under the strong Wolfe line search. In ^[16], Jian et al. proposed a new hybrid CG method based on previous classical methods. At every iteration, the method produces a descent direction independent of the line search. Global convergence was proved and numerical experiments on medium-scale problems was conducted and the results reported. By applying a mild modification on the HS method, Dong et al. proposed a new approach that generates a descent direction. Also, the approach satisfies an adaptive conjugacy condition and has a self-restarting property. The global convergence was proved for general functions and the efficiency of the approach was shown via numerical experiments on some large-scale problems. Min Li ^[19] developed a three-term PRP CG method with the search direction close to the direction of the memoryless BFGS quasi-Newton method. The method collapses to the standard PRP method when an exact line search is considered. Independent of any line search, the method satisfies the descent condition. The global convergence of the method was established using an appropriate line search. Numerical results show that the method is efficient for the standard unconstrained problems in the CUTEr library. Again, Li ^[18] proposed a nonlinear CG method which generates a search direction that is close to that of the memoryless BFGS quasi-Newton method. Moreover, the search direction satisfies the descent condition. Global convergence for strongly convex functions and nonconvex functions was established under the strong Wolfe line search. Furthermore, an efficient spectral CG method that combine the spectral parameter and a three-term PRP method was proposed by Li et al. ^[20]. The method is based on the quasi-Newton direction and quasi-Newton equation. Numerical experiments reported show the superiority of the method over the three-term PRP method.

Motivated by the works of Li ^[18,19] which originated from ^[17,27], we propose a new hybrid CG method for solving (1.1). The hybrid direction is a combination of the FR and DY directions that are both close to the direction of the memoryless BFGS quasi-Newton method. Interestingly, the hybrid direction satisfies the descent condition and is bounded independent of any line search procedure. We prove the global convergence under both the Wolfe-type and Armijo-type line searches. Numerical results are also provided to show the efficiency of the new hybrid method. Finally, application of the method in optimizing risk in portfolio selection is also considered. The remainder of this paper is organized as follows. In the next section, the hybrid method is derived together with it's convergence. In Section 3, we provide some numerical experimental results.

2.   Algorithm and theoretical results

We begin this section by recalling a three-term CG method for solving (1.1). From an initial guess $x_0$, the method compute the search direction as follows:

where $\beta_k$, $\gamma_k$ are parameters. Distict choices of the parameters $\beta_k$ and $\gamma_k$ correspond to distinct three-term CG methods. It is clear that, the three-term CG methods collapses to the classical ones when $\gamma_k = 0.$

Next, we will recall the memoryless BFGS method proposed by Nocedal ^[17] and Shanno ^[27], where the search direction can be written as

$s_{k-1} = x_k-x_{k-1} = \alpha_{k-1}d_{k-1}$ and $I$ is the identity matrix. After simplification, $d_k^{LBFGS}$ can be rewritten as

Replacing $\beta_k^{HS}$ with $\beta_k^{FR}$ and $\frac{\|y_{k-1}\|^2g_k^Td_{k-1} }{(d_{k-1}^Ty_{k-1})^2}$ with $\frac{\|g_k\|^2g_k^Td_{k-1} }{\|g_{k-1}\|^4}$ in (2.2), we define a three-term search direction as

Again, replacing $\beta_k^{HS}$ with $\beta_k^{DY}$ and $\frac{\|y_{k-1}\|^2g_k^Td_{k-1} }{(d_{k-1}^Ty_{k-1})^2}$ with $\frac{\|g_k\|^2g_k^Td_{k-1} }{(d_{k-1}^Ty_{k-1})^2}$ in (2.2), we define another three-term search direction as

To find the parameter $t_k$, we require the solution of the univariate minimal problem

Let $E_k = (y_{k-1}-s_{k-1})-t.g_k,$ then

Letting $A_k = y_{k-1}-s_{k-1},$ then

and

Differentiating the above with respect to $t$ and equating to zero, we have

which implies

Hence, we select $t_k$ as

which implies $0\leq t_k\leq \bar{t} < 1$.

Motivated by the three-term CG directions defined in (2.3) and (2.4), we propose a hybrid three-term CG based algorithm for solving (1.1), where the search direction is defined as

where

and

Remark 2.1. Observe that, because of the way $w_k$ is defined, the parameter $\beta_k^{HTT}$ is a hybrid of $\beta_k^{FR}-\frac{\|g_k\|^2g_k^Td_{k-1} }{\|g_{k-1}\|^4}$ and $\beta_k^{DY}-\frac{\|g_k\|^2g_k^Td_{k-1} }{(d_{k-1}^Ty_{k-1})^2}$ in (2.3) and (2.4), respectively. Also, the parameter $\gamma_k$ defined by (2.8) is a hybrid of $-t_k\frac{g_k^Td_{k-1} }{\|g_{k-1}\|^2}$ and $-t_k\frac{g_k^Td_{k-1} }{d_{k-1}^Ty_{k-1}}$ in (2.3) and (2.4), respectively. Finally, the search direction given by (2.7) is close to that of the memoryless BFGS method when $t_k = \frac{g_k^T(y_{k-1}-s_{k-1})}{\|g_k\|^2}$.

Remark 2.2. Note that, relation (2.9) is carefully defined such that the search direction possess a trust region (see Lemma 2.7) independent of the line search.

Lemma 2.3. The search direction $d_k$ defined by (2.7) satisfy (1.4) with $c = \frac{3}{4}$.

Proof. Multiplying both sides of (2.7) with $g_k^T$, we have

Next, we will turn our attention to establishing the convergence of the proposed scheme by first considering the standard Wolfe line search conditions ^[29],

where $0 < \vartheta < \sigma < 1$. In addition, we will assume that

Assumption 2.4. The level set $\mathcal{H} = \{x:f(x)\leq f(x_0)\}$ is bounded.

Assumption 2.5. Suppose $\mathcal{H}$ is some neighborhood of $\mathcal{L}$, then $f$ is continuously differentiable and its gradient Lipschitz continuous on $\mathcal{H}$. That is, we can find $L > 0$ such that for all $x$

From Assumption 2.4 and 2.5, we can deduce that for all $x\in \mathcal{L}$ there exist $b_1, \; b_2 > 0$ for which

● $\|x\|\leq b_1$.

● $\|g(x)\|\leq b_2$.

Furthermore, the sequence $\{x_k\}\in \mathcal{L}$ because $\{f(x_k)\}$ is decreasing. Henceforth, we will suppose that Assumption 2.4–2.5 hold and that the objective function is bounded below. We will now prove the convergence result.

Theorem 2.6. Let conditions (2.10) and (2.11) be fulfilled. If

then

Proof. Suppose by contradiction that Eq (2.14) does not hold, then there exists a nonnegative scalar $\epsilon$ such that

From Lemma 2.3 and (2.10),

Likewise, by Lemma 2.3, condition (2.11) and Assumption 2.5, we have

Combining the above inequality with (2.10), we obtain

and

since $\{f(x_k)\}$ is bounded. The above implies that

Now, inequality (2.15) with (1.4) implies that

Squaring both sides and dividing by $\|d_k\|^2\ne 0$ of (2.17), yields

This contradicts (2.16). Therefore, the conclusion of the theorem hold.

Next, we will establish the convergence of the proposed method under the Armijo-type backtracking line search procedure. The procedure was first introduced by Grippo and Lucidi ^[11], where the step size $\alpha_k$ is determined as follows: $\rho, \; \vartheta\in (0, 1)$, $\alpha_k = \rho^i$, where $i$ is the smallest nonnegative integer for which the relation

hold.

From (2.19) and the fact that $\{f(x_k)\}$ is decreasing, we can deduce that

which further implies that

Lemma 2.7. If $\{d_k\}$ is defined by (2.7), then there is $N_1 > 0$ for which $\|d_k\|\leq N_1$.

Proof. From (2.8),

Also,

Therefore, from (2.7), (2.21) and (2.22), we have

Letting $N_1 = \left(1+\frac{1+\bar{t}}{\lambda}+\frac{1}{\lambda^2}\right) b_2$, we have

Theorem 2.8. If the step size $\alpha_k$ is obtained via relation (2.19), then

Proof. Suppose by contradiction equation (2.26) is not true. Then for all $k$, we can find an $r > 0$ for which

Let $\alpha_k = \rho^{-1}\alpha_k$, then $\alpha_k$ does not satisfy (2.19). That is

Applying the mean value theorem together with Lemma 2.7, (1.4) and (2.12), there exist an $l_k\in (0, 1)$ such that

Inserting the above relation in (2.28), together with (2.25) and (2.27) we have

This and (2.20) gives

On the other hand, applying backward Cauchy-Schwartz inequality on (1.4) gives

Thus, we have $\lim_{k\to\infty}\|g_k\| = 0$. This is a contradiction and therefore (2.26) holds.

3.   Numerical experiments

This section discusses the computational efficiency of the proposed method, namely HTT method. One way to measure the efficienecy of a method is to use the test function. An important test function is used to validate and compare among optimization methods, especially newly developed methods. We selected 34 test functions and initial points as in Table 1 mostly considered by Andrei ^[4]. For each function we have taken five numerical experiments with a dimension of which is among $n$ = 10, 50, 80,100,200,400,300,500,600, 1000, 3000, 5000, 10,000, 15,000, 20,000. However, we often use dimensions that are greater than $1000$. The executed methods are coded in Matlab 2019a and compiled using personal laptop; Intel Core i7 processor, 16 GB RAM, 64 bit Windows 10 Pro operating system.

As a good comparison, for NHS+ and NPRP+ all parameters are maintained according to their articles in ^[18] and ^[19], i.e, $\vartheta = 0.1, \, \, \sigma = 0.9$. Specially, for HTT, we set the value of parameters $\vartheta = 0.0001, \, \, \sigma = 0.009$. For all methods, we use the parameter value $\bar{t} = 0.3$, $\lambda = 0.01$ and the step-size $\alpha_k$ is calculated by standard Wolfe line search. The numerical results are compared based on number of iterations (NOI), number of function evaluations (NOF), and CPU time in seconds (CPU). In this experiment, we consider a stopping condition that many researchers suggest (see ^{[16,18,21,23]}), namely that the algorithm will stop when $\|g_k\|\leq 10^{-6}$.

In Table 5 we list the numerical results obtained by compiling each method for completing each test function with different dimension sizes. If the number of iterations of the method exceeds $10,000$ or it never reaches the optimal value, the algorithm stops and we write it as 'FAIL'.

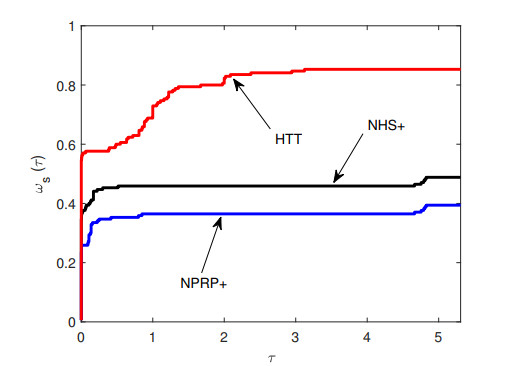
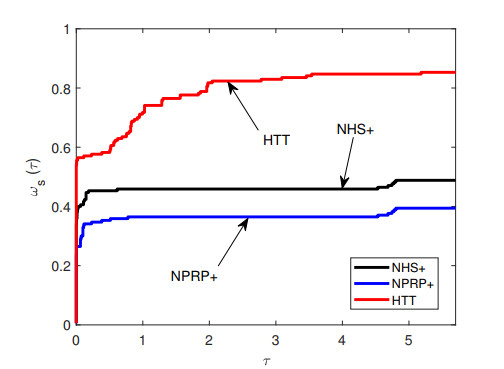
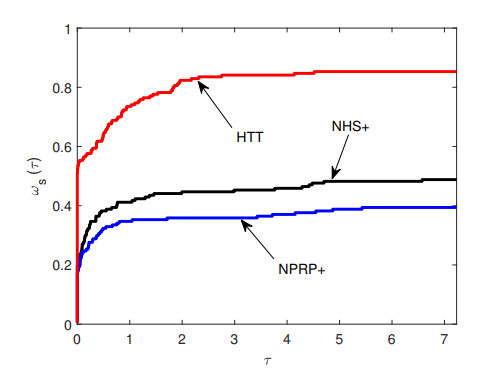
To compare the performance between methods, we use the performance profiles of Dolan and Moré ^[7] with rule as follows. Let $S$ is the set of methods and $P$ is set of the test problems with $n_p, n_s$ are the number of test problems and the number of methods, respectively.

The performance profile $\omega: \mathbb{R} \to [0, 1]$ is for each $s \in S$ and $p \in P$ defined that $a_{p, s} > 0$ is NOI or NOF or CPU time required to solve problems $p$ by method $s$. Furthermore, the performance profile is obtained by:

where $\tau > 0$, $size\, B$ is the number of the elements in the set $B$, and $r_{p, s}$ is performance ratio defined as:

In general, the method whose performance profile plot is on the top right will win the rest of the methods or represents the best method.

From Table 5, all the methods failed to solve the Raydan 1 and NONSCOMP with $n = 1,000, \, 5,000, \, 10,000, \, 15,000, \, 20,000$, the NHS+ and NPRP+ methods failed to solve Extended Powel, Hager, Generalized Tridiagonal 1, Generalized Tridiagonal 2, QP2 Extended Quadratic Penalty, DENSCHNA, Extended Block-Diagonal BD1, ENGVAL1, and ENGVAL8 for all of dimension given, and NPRP+ method has more failures for the given problem compared to other methods. So, based on the numerical results in Table 5, we can say that the HTT method has the best performance. Meanwhile, from the result in performance profile in Figures 1–3 show that the HTT method profile is always on the top right curve, whether it's based on NOI, NOF or CPU time. The final conclusion is that the HTT method has the best performance compared the NHS+ and NPRP+ methods under the test functions given.

4.   Application in portfolio selection

Investment is a commitment to invest several funds carried out at this time to obtain many benefits in the future. One investment that is quite attractive is a stock investment. An investor can invest in more than one stock. Of course, the thing to consider is whether the investment can be profitable or not. One theory that discusses investment in several assets is portfolio theory. A stock portfolio is a collection of stocks owned by an investor ^[24].

In this section, we present the problem of risk management in a portfolio of stocks. The main issue is how to balance a portfolio, that is, how to choose the percentage of each stock in the portfolio to minimize the risk ^[28]. In investing, investors expect to get a large return by choosing the smallest possible risk. Return is the income received by an investor from stocks traded on the capital market. There are several ways to calculate returns, one of which is to use arithmetic returns which can be calculated as follows:

where $P_t$ is the stock prices at time $t$ and $P_{t-1}$ is the stock prices at time $t-1$. Furthermore, we may consider the mean of return, the expected value, and the variance of the return. The mean of return of a stock $i$ is denoted by

where $n$ is number of returns on a stock and $r_{it}$ is return at time $t$ on stock $i$. The expected return of stock $i$

The variance of return of stock $i$

is called the risk of stock $i$ ^[28]. One thing that needs to be considered is the relationship between stocks, so we must also pay attention to how stocks interact, i.e, by using the covariance of individual risk. Covariance measures the directional relationship between the returns on two stocks. If positive covariance then that stock returns move together while a negative covariance means they move inversely. Usually the covariance of return between two stocks $R_i, R_j$ is denoted as $\text{Cov}(R_i, R_j)$ ^[28].

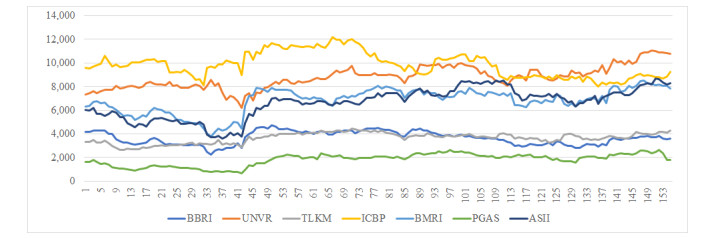
For our cases, we consider the seven blue chip stocks in Indonesia, namely, PT Bank Rakyat Indonesia (Persero) Tbk (BBRI), PT Unilever Indonesia Tbk (UNVR), PT Telekomunikasi Indonesia Tbk (TLKM), PT Indofood CBP Sukses Makmur Tbk (ICBP), PT Bank Mandiri (Persero) Tbk (BMRI), PT Perusahaan Gas Negara Tbk (PGAS), and PT Astra International Tbk (ASII). The stock price used is the weekly closing price which data history is taken from from the database http://finance.yahoo.com, over a period of 3 years (Jan 1, 2018 – Dec 31, 2020). Based on this data, we may see the movement of the closing price of each stock in Figure 4.

So that the portfolio returns for the seven stocks are defined as the weighted amount of returns for each stocks

where $w_i$ is the percentage of the value of the stock contained in the portfolio. Thus, we may define the expected return and risk on our portfolio (see ^[28]). The expected return $\mu$ on our portfolio is the expected value of the portfolio's return as follows:

and the risk of our portfolio is the variance of the portfolio's return as follows,

Since our main objective is to determine the optimal portfolio by minimizing the risk of returns, then our problem model is

The next step changes the problem (4.3) to unconstrained optimization model, i.e, considering $w_7 = 1-w_1-w_2-w_3-w_4-w_5-w_6$, then the problem (4.3) changes into an unconstrained optimization model as follows:

where ${\bf w} = (w_1, \, w_2, \, w_3, \, w_4, \, w_5, \, w_6, \, \, 1-w_1-w_2-w_3-w_4-w_5-w_6)$.

The following table shows the mean, variance, and covariance values of the returns of UNVR, BBRI, TLKM, ICBP, BMRI, PGAS, and ASII stocks.

According to Tables 2 and 3, we may execute the problem (4.4) by choosing some random initial points and still maintaining the same parameter values according to each method. The results obtained are stated in Table 4.

From Table 4, it is clear that the HTT method more efficient than NHS+ and NPRP+ methods based on NOI, NOF, and CPU time for solving the problem (4.4). Meanwhile, the algorithm executed from each method give the same result for the value of ${\bf w}$, i.e, $w_1 = 0.3877, \, w_2 = 0.3220, \, w_3 = 0.2878, \, w_4 = 0.4179, \, w_5 = -0.1642, \, w_6 = -0.0465$, and $w_7 = -0.2047$. By using the value of ${\bf w}$, (4.1), and (4.2), we obtain $\mu = 0.00094$ and $\sigma^2 = 0.00074$. Finally, the selection of stock portfolios for our case with a minimum risk can be done by allocating each stock in the following proportions, i.e, UNVR $38.77\%$, BBRI $32.22\%$, TLKM $28.78\%$, ICBP $41.79\%$, BMRI $-16.42\%$, PGAS $-4.65\%$, and ASII $-20.47\%$ with the expected return is $0.00094$ and the portfolio risk value is $0.00074$. A negative sign in the proportion indicates that investor is short selling.

5.   Conclusions

In this work, we presented a new hybrid CG method that guarantees sufficient descent direction and boundedness of the direction independent of the line search. In addition, the gloabal convergence result is established under both the Wolfe and Armijo line searches. Based on the numerical results, it can be observed that the new hybrid method is more efficient and robust than other methods, providing faster and more stable convergence in most of the problems considered. These can be seen more clearly from Figures 1–3. Finally, the practical applicability of the hybrid method is also explored in risk optimization. It's efficiency in solving portfolio selection problem was outstanding as it solves the problem with less iteration, function evaluations and CPU time compared with others.

Acknowledgments

The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Also, the (first) author, (Dr. Auwal Bala Abubakar) would like to thank the Postdoctoral Fellowship from King Mongkut's University of Technology Thonburi (KMUTT), Thailand. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under project number 64A306000005. The first author acknowledge with thanks, the Department of Mathematics and Applied Mathematics at the Sefako Makgatho Health Sciences University.

Conflict of interest

The authors declare that they have no conflict of interest.

Appendix