A mathematical study of effects of delays arising from the interaction of anti-drug antibody and therapeutic protein in the immune response system

1.   Introduction

One of the challenges in biotherapy study is the pharmacokinetics of drug therapy due to the existence of an immune response of the host such as human body against the therapeutic protein. It is an interesting study when the novel protein therapeutics should be predicted its immunogenic potential. Some cases of immunogenicity occur in patients where the immune response to protein therapy has devastating effects for that patient ^{[1,2,3,4,5,6,7,8]}. This unwanted immunogenicity is the clinical impact of the appearance of anti-drug antibodies (ADA) where it is known that the severity of the antibody-mediated toxicity depends not only on the affinity but on the functionality of the antibody ^[9,10,11]. Production of anti-drug-antibodies (ADA) will be inactivating the therapeutic effects of the treatment and anti-drug antibodies (ADA) may lead to allergic reactions, altered pharmacokinetics, and reduced efficacy ^[1,12,13]. Therefore, in practice, study the pharmacokinetics of drug therapy is conducted through the assessment of immunogenicity where antibodies that directed against the therapeutic protein are measured.

The principal role of ADA in immunogenicity has been extensively studied, including research that characterized the nature of ADA, such as the magnitude of the ADA response, bond affinity, and neutralization capacity ^[14]. Based on the right assumptions and simplified rational mechanism of the immune system, mathematical modeling can be applied as an approach tool that complements experimentation and research. This approach can be used to estimate or even be able to predict ADA responses to the therapeutic proteins. Several mathematical models of immune response have been developed ^{[15,16,17,18,19]}. For example, Bell ^[17] developed a mathematical model to predict the production of polyclonal antibodies based on the proliferation of relevant B cell species. Lee et al. ^[18] simulated and predicted the adaptive immune response to influenza A virus infection, where the virus triggers an antibody response and cytotoxic T cell proliferation. Xu et al. ^[19] considered immunogenicity as a covariate in pharmacokinetic modeling of therapeutic proteins. The study was conducted by analyzing the golimumab (a human monoclonal antibody) pharmacokinetic population in ankylosing spondylitis patients, and finding anti-golimumab antibodies that were significantly affected by golimumab release. Bonate et al. ^[20] also used a statistical approach to characterize immunogenicity. The approach was to model antibody titers using the zero-inflated Poisson random effect model. This model was able to identify patient specific factors that can influence antibody titers. Similar research was also carried out by Chen et al. ^[21] where a pharmacokinetic/ADA mathematical model was studied to estimate the ADA response quantitatively. This model was based on observing the impact of ADA on the release of protein drugs. It was assumed that the pharmacokinetic drug changes contain information about the level and time of ADA generation. This model provided an approach to the characterization of ADA generation, including maximum ADA response, sensitivity of ADA response to drug dose levels, affinity maturation rates, time lags to observe ADA responses, and elimination rates for ADA-drug complexes. Expanding their mathematical study, here, we are interested to develop model of Chen et al. by adding two natural assumptions. The first assumption comes from the fact that times are needed by the drugs to accumulate to trigger the production of ADA. There is no ADA response before the second dose and starting from the second dose, ADA is produced, and injected as a bolus dose into a depot compartment at the time of drug dosing ^[21]. This process can be considered as a delay factor in injecting therapeutic protein drug doses and a delay response of the ADA production. The second assumption is the natural delay factor that occurs on the ADA entry process from the depot into the plasma. It also can be considered as a delay process due to ADA having to go through a certain series of compartments before it enters the plasma. Instead of considering a series of compartments, in this study, the series of compartment are considered as a lumped process with a discrete-time delay. We believe that the mathematical model development will present another mathematical point of view regarding the study of the level of immunogenicity in the system.

This paper is organized as follows. In Section 2, we present several assumptions underlying the development of the mathematical model. In Section 3, we discuss the qualitative analysis of the model including the existence of a positive steady-state solution and its local stability conditions. The analysis of the appearance of a Hopf bifurcation is also presented in this section. Some numerical simulations are also provided in Section 4 to validate our analytical results and to study numerically effect of the existence of delay factor in the system to the level of immunogenicity of therapeutic protein. A summary and some concluding remarks are presented in the last section.

2.   Model formulation

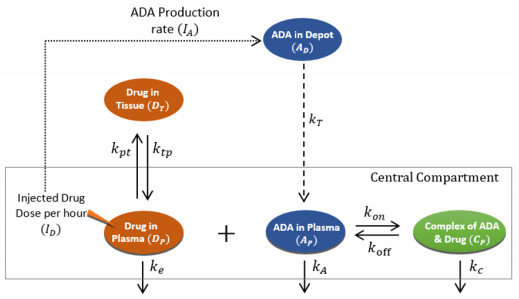
Mathematical model of the pharmacokinetic of the therapeutic protein and ADA is formulated based on the schematic diagram of protein drug-ADA interaction that is depicted in Figure 1 with appropriate assumptions and reasonable simplifications of the immune system mechanisms. The model follows the line of Chen et al. ^[21] with development on the delay compartments. The delay of entering process of ADA from the depot to the plasma is considered as a lumped process with a discreet time delay on the ADA variable.

2.1.   Non-autonomous model

Let ${A}_{D}$, ${A}_{P}$, ${D}_{P}$, ${D}_{T}$, and ${C}_{P}$ respectively denote the amount of ADA in the depot, ADA in plasma, protein therapeutic in the plasma, and complex of ADA-drug. Modeling the rate change of ${A}_{D}$, ${A}_{P}$, ${D}_{P}$, ${D}_{T},$ and ${C}_{P}$ is formulated based on the following assumptions. Therapeutic protein drugs are injected into the body at a rate ${I}_{D}$ through the subcutaneous pathway (under the skin). With repeated doses of the drug, the amount of ADA in the depot (${A}_{D}$) will be stimulated to enter the central compartment to bind the therapeutic protein drugs. The accumulated dose of the drug that affects the ADA production is illustrated by the dashed arrow in Figure 1. It is assumed that the dose of ADA is injected as a bolus into the ${A}_{D}$ compartment.

Bolus ADA starts to produce when the drug (protein therapy) was injected (at the second injection ^[21]). The dose of ADA is modeled as a saturated function that depends on the exposure to therapeutic protein drugs (cumulative drug doses) that experience delays because it requires a certain accumulated dose to stimulate ADA generation. No ADA is stimulated during the first drug dose interval, due to the delay needed to increase the body's immune response. The production of ADA is increased as the cumulative drug dose is also increased until the production saturated and reached the maximum production. Thus, the ADA dose rate that enters to the ADA depot is modeled as the following saturated function:

where ${D}_{P}(t-{\mathrm{\tau }}_{1})$ is the amount of drug dose in the plasma that triggers the production of ADA. This function depends on ${\mathrm{\tau }}_{1}$, the length of time needed for injection reaches a cumulative drug dose for stimulating ADA generation. The production of ADA reaches maximum production at ${A}_{max}$ and the half-maximum production is reached when the amount of cumulative drug dose is equal ${k}_{m}$. ADA at the depot then passes through a series of compartments before entering the central compartment with a rate constant of ${k}_{T}$. The series of compartments resulted in a delay for entering ADA to the central compartment. If the series of compartments are assumed as a lumped process then the entering process of ADA can be modeled in the form of a delay function with respect to ${A}_{D}$, namely ${A}_{D}(t-{\mathrm{\tau }}_{2})$. The variable ${\mathrm{\tau }}_{2}$ represents the length of time for ${A}_{D}$ to pass through a series of compartments before entering the central compartment to bind the therapeutic protein drug. In the central compartment (in the plasma), ADA can reversely bind the therapeutic protein drugs. As a result, the binding process will reduce the amount of ADA and drugs in the plasma by $\frac{{k}_{on}}{{V}_{p}}{A}_{P}{D}_{P}$ with ${V}_{p}$ representing the distribution volume for ADA and the ADA-drug complex and ${k}_{on}$ representing the rate constant of the ADA-drug binding process. With repeated dose, the bond between ADA and the drug to form a complex will be strengthened such that an affinity maturation achieved and the opportunity to break down the complex bond into ADA and free drug becomes smaller or almost zero. Therefore, ${k}_{\mathrm{o}\mathrm{f}\mathrm{f}}$ will decrease as the time increase. The decreasing of ${k}_{\mathrm{o}\mathrm{f}\mathrm{f}}$ is modeled as an exponential function,

where ${k}_{0}$ represents the initial value of ${k}_{\mathrm{o}\mathrm{f}\mathrm{f}}$ and a represents the rate constant for ${k}_{\mathrm{o}\mathrm{f}\mathrm{f}}$ to change with time ^[21]. In addition, the complex bond of ADA-drug is naturally eliminated by the body at a constant rate ${k}_{c}$. As well as the drugs and ADA in the plasma which are eliminated at constant rate ${k}_{e}$ and ${k}_{A}$, respectively. Besides the drug is binding to ADA to form a complex, therapeutic protein drugs in the plasma are also can be distributed to the tissues with a constant rate of ${k}_{\mathrm{p}\mathrm{t}}$. Vice versa, the protein drug in the tissues can be distributed back to the plasma with a rate constant of ${k}_{\mathrm{t}\mathrm{p}}$. By following these assumptions, we then have a nonlinear differential equation in term of a non-autonomous system that describes the dynamics of the pharmacokinetic of ADA and therapeutic protein drug,

with ${k}_{off} = {k}_{0}\cdot {e}^{-a\cdot t}$, initial conditions ${A}_{P}\left(0\right) = {{A}_{P}}_{0}>0, {C}_{P}\left(0\right) = {{C}_{P}}_{0}>0, {D}_{T}\left(0\right) = {{D}_{T}}_{0}>0,$ and the historical functions:${D}_{P}\left(t\right) = {\beta }_{1}, \forall t\in \left[-{\tau }_{1}, 0\right], {A}_{D}\left(t\right) = {\beta }_{2}, \forall t\in \left[-{\tau }_{2}, 0\right]$, for ${\beta }_{1}, {\beta }_{2}\in {R}^{+}$. Throughout the next sections, we define ${D}_{P}(t-{\tau }_{1})$ and ${A}_{D}(t-{\tau }_{2})$ as ${{D}_{p}}_{{\tau }_{1}}$ and ${{A}_{D}}_{{\tau }_{2}}$, respectively.

2.2.   Autonomous model

Consider the rate constant of decomposition of ADA and drug complex in (1). From the previous studies ^[21,22], it suggested that the ${k}_{off}$ of antibodies is more variable during affinity maturation. If we assume that a, i.e. the rate constant for ${k}_{off}$ to change with time, is a varying parameter then a can be considered as a perturbation parameter. Let ${k}_{off}$ decreases as a increases. Then as $a\to \infty$, for any time $t>0$, the ${k}_{off}$ will converge to the zero-disassociation rate meaning that the complexes are binding tightly, and affinity maturation quickly achieved. This fact can occur for some cases of high-affinity antibodies which bind quickly to the antigen ^[23,24]. As a result, the non-autonomous system (2) becomes an autonomous system as follows

Obviously, the complex with tight-binding rate (affinity maturation) is the limiting case of the immunogenicity system as the rate constant $a\to \infty$ for some $t>0$. This case will be analytically analyzed in the further section. On the other hand, the non-autonomous system (2a) can become equivalent to a six-dimensional autonomous system by introducing an additional differential equation as follows

where $\theta \left(t\right) = at$. This six-dimensional autonomous system will be numerically analyzed to calculate the numerical solutions of the system and to study effects of varying of rate constant a to the response immune system with or without delays.

3.   Results and discussions

3.1.   The qualitative analysis of the autonomous model

In this section, we study the qualitative behavior of the system (3) by considering different cases of delay. The qualitative analysis consists of the study of steady-state solutions, their local stability, and the existence of local bifurcations of the fixed point. Some discussions and interpretations are included along with the analysis of the model.

3.1.1.   Steady-state analysis

The steady-states of the model are obtained by setting the system (3) equals to zero such that we have a solution ${E}^{*} = \left({{A}_{D}}^{*}, {{{{A}_{P}}^{*}, {{D}_{P}}^{*}, {{C}_{P}}^{*}, D}_{T}}^{*}\right),$ where

The solution of ${{D}_{P}}^{*}$ is the positive roots of a cubic polynomial,

with

Since ${a}_{0}>0$ and ${a}_{3} < 0$, possible sign changes for coefficients (4) are given as follow

We can observe that there exists at most three changes of sign and at least one change of sign for the coefficients of the polynomial (4). Using Descartes’ rule of sign ^[27], we get that a unique positive steady-state exists if one of the following conditions is satisfied, i.e.

So, the condition H1 ensures that Eq (3) has only one positive root for ${D}_{P}$, the amount of free protein drugs in the plasma. Therefore system (3) has only one steady-state solution, namely ${E}^{*},$ if it fulfills condition H1.

3.1.2.   Local stability and bifurcation analysis

By linearizing system (3) using Taylor expansion around ${E}^{*}$, we get the linearized system as follows,

with

and the Jacobian matrices,

System (5) has a characteristic equation in term of implicit function that contains an exponential form that depends on λ (see for instance ^[25,26] for the references of this method), i.e.

with

Note that ${C}_{i}>0,$ for all $i = \mathrm{1, 2}, 3\dots, 12$. Solution of the implicit function (6) is difficult to find explicitly. Therefore, the local stability of ${E}^{*}$ will be studied by considering the following three cases based on the value of ${\tau }_{i}$, $i = \mathrm{1, 2}$.

Case 1: ${\tau }_{1} = {\tau }_{2} = 0$

Suppose ${\tau }_{1} = {\tau }_{2} = 0$, then Eq ($6)$ becomes

Based on the Routh-Hurwitz stability criteria ^[22], Eq ($7)$ will produce roots with negative real parts if it fulfills the following conditions (H2),

Therefore in the absence of delay, the steady-state ${E}^{*} = \left({{A}_{D}}^{*}, {{{{A}_{P}}^{*}, {{D}_{P}}^{*}, {{C}_{P}}^{*}, D}_{T}}^{*}\right)$ will be stable if it fulfills H1 and H2 conditions.

Case 2: ${\tau }_{1} = 0, {\tau }_{2}>0$

If we consider ${\tau }_{1} = 0$ and ${\tau }_{2}>0$ then Eq ($6)$ becomes,

Like Eq (6), Eq (8) forms a transcendental equation in $\lambda$ and ${\tau }_{2}$ that has infinitely many solutions. Routh-Hurwitz stability criteria are not applicable to determine the solutions of Eq (8). Since the locally asymptotically stability of ${E}^{*}$ is determined by the sign of the real part of $\lambda$, therefore investigating the stability of ${E}^{*}$ is similar to investigating the sign of the real part of the roots of (8) in the presence ${\tau }_{2}$. It is interesting to investigate whether the stability of ${E}^{*}$ loss if the root crosses the imaginary part from left to the right (a purely complex root exists). For that purpose, we can assume that Eq (8) has an imaginary root, $\lambda = i\omega$ with $\omega >0$. By substituting $\lambda = i\omega$ into Eq (8), we have the following equation,

Consider that

If we substitute (10) into Eq (9) then we get

Equation (11) is fulfilled iff

and

If Eqs ($12)$ and $\left(13\right)$ are eliminated, we get the following two solutions,

and

with

By squaring and adding both Eqs ($12)$ and ($13)$, we have

with

Let $z = {\omega }^{2}$, then Eq ($16)$ can be rewritten as

Suppose ${p}_{i}>0, i = 1\dots 4$ (H3). Since ${p}_{5} < 0$ then according to Descartes’ rule of sign, Equation ($17)$ has only one positive root, namely ${z}^{*}$ such that ${\omega }^{*} = \sqrt{{z}^{*}}$.

Let $\vartheta = \omega {\tau }_{2}$. Notice that the unique solution $\vartheta \in \left[0, 2\pi \right]$ of (14) and (15) is

if $\mathrm{sin}\left(\vartheta \right)>0$, and

if $\mathrm{sin}\left(\vartheta \right)\le 0$. If we define two sequences $\left\{{\tau }_{2}^{\left(1, j\right)}\right\}$ and $\left\{{\tau }_{2}^{\left(2, j\right)}\right\}$ for $j = \mathrm{0, 1}, 2, \cdots$ then we have solutions for ${\tau }_{2}$ corresponding to ${\omega = \omega }^{*}$ as follow

and

with

Suppose that ${{\tau }_{2}}^{*} = \min _{j \in Z^{+}}\left\{{\tau }_{2}^{(1, j)}, {\tau }_{2}^{(2, j)}\right\},$ then ${{\tau }_{2}}^{*}$ becomes the minimum critical time delay that will generate purely imaginer solutions for Eq (8). Since for ${\tau }_{2} = 0$, ${E}^{*}$ is asymptotically stable under some Routh-Hurwitz conditions then for $0 < {\tau }_{2}$ < ${{\tau }_{2}}^{*}$, the steady-state ${E}^{*}$ remains stable. To study the existence of Hopf bifurcation in model (3), it is interesting to investigate the direction of motion of $\lambda$ when ${\tau }_{2}$ is varied. It means that we must investigate the transversality condition ${\left.\frac{dRe\left(\lambda \right)}{d{\tau }_{2}}\right|}_{{|}_{{\tau }_{2} = {{\tau }_{2}}^{*}}}$. If the transversality condition is positive, then there exists at least one eigenvalue with positive real part for ${\tau }_{2}>{{\tau }_{2}}^{*}$ and preserving the conditions for the existence of a periodic solution. Now suppose that $\lambda \left({\tau }_{2}\right) = v\left({\tau }_{2}\right)+i\omega \left({\tau }_{2}\right)$ is the solution of Eq (8). So, $v\left({{\tau }_{2}}^{*}\right) = 0$ and $\omega \left({{\tau }_{2}}^{*}\right) = {\omega }^{*}.$ Next, we will investigate $sign\left\{\frac{dRe\left(\lambda \right)}{d{\tau }_{2}}|{|}_{{\tau }_{2} = {{\tau }_{2}}^{*}}\right\},$ where the $sign$ is a signum function and $Re\left(\lambda \right)$ stands for the real part of eigenvalue $\lambda$. Let us consider Eq (8). Differentiating (8) with respect to ${\tau }_{2}$, we have

which gives

From Eq (8), we have

By substituting (22) into (21) we have

Evaluate ${\left(\frac{d\lambda }{d{\tau }_{2}}\right)}^{-1}$ at ${\tau }_{2} = {{\tau }_{2}}^{*}$ and take the real part, we have

Evaluate Eq (15) at ${\omega = \omega }^{\mathrm{*}}$, we have

Substitute (25) into (24) gives

From Eq (16), for $z = {{\omega }^{*}}^{2},$ let

Then Eq (26) can be rewritten as

Since

then

Based on the assumptions applied for Descartes’ rule of sign in Eq (16), condition H2, we have ${F}^{\text{'}}\left(z\right)>0$. Then we get $sign\left\{\frac{dRe\left(\lambda \right)}{d{\tau }_{2}}|{|}_{{\tau }_{2} = {{\tau }_{2}}^{*}}\right\}>0.$ This result implies that the transversality condition holds, hence the model (2) undergo Hopf bifurcation at $\omega = {\omega }^{*}$, ${\tau }_{2} = {{\tau }_{2}}^{*}.$ Summarizing our results for the second case of analysis, we have the following theorem.

Theorem A. Under the conditions H1–H3, system (2) experiences Hopf bifurcation around the positive steady-state ${E}^{*} = \left({{A}_{D}}^{*}, {{{{A}_{P}}^{*}, {{D}_{P}}^{*}, {{C}_{P}}^{*}, D}_{T}}^{*}\right)$ at ${\tau }_{1} = 0$ and ${\tau }_{2} = {{\tau }_{2}}^{*}$. Moreover, if ${\tau }_{1} = 0$ and ${\tau }_{2} < {{\tau }_{2}}^{*}$, ${E}^{*}$ is locally asymptotically stable; otherwise, ${E}^{*}$ is unstable.

Case 3: ${\tau }_{1}, {\tau }_{2}>0$

In this case, we assume that the delays exist both in the injection of therapeutic protein and the distribution of ADA from the depot to the plasma. If ${\tau }_{1}>0$ and ${\tau }_{2}>0$ then we have

a transcendental equation which depends on $\lambda$, ${\tau }_{1}$, and ${\tau }_{2}$. In the same way, as we have done in case 2, we assume $\lambda = i\omega, \omega >0.$ Then we have

Since

and

then Eq (28) becomes

Equation (29) is fulfilled iff

and

By eliminating Eqs (30) and (31), we have

and

By dividing Eqs (32) and (33), we have

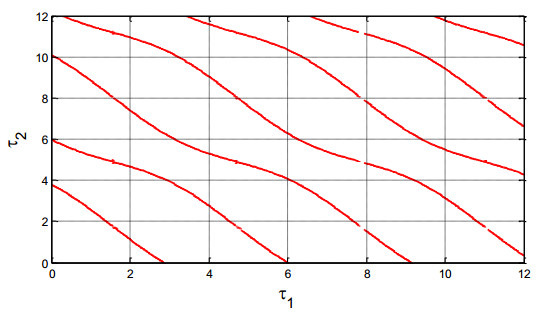
Equation (34) shows the relation between ${\tau }_{1}$ and ${\tau }_{2}$. Solutions of the transcendental function (34) are a pair of critical time delay ${\tau }_{1}^{*}$ and ${\tau }_{2}^{*}$ that will generate a periodic solution with purely imaginary eigenvalues. Suppose Eq (34) is written as an implicit function $G\left({\tau }_{1}, {\tau }_{2}\right) = 0$. We get the zeros of G numerically as presented in Figure 2. The red line in Figure 2 represents a collection of $\left({\tau }_{1}, {\tau }_{2}\right)$ that satisfies Eq (34).

3.2.   Numerical simulations

In this section, numerical solutions of the system (2) are studied by solving the nonlinear delay differential Eq (2) using dde23 function in Matlab (Runge-Kutta for delay differential equation, see ^[28] for detail about the method). The set of parameter values used in this simulation is taken from ^[21] that estimated from pharmacokinetic of Interferon-Fc Fusion which is a type of therapeutic protein (see Table 1). Some parameter values are assumed such as the number of drug doses injected into the body via subcutaneous (I_D), the constant rate of k_off (a), and the rate constant of binding ADA-drug complex (k_on). The initial amount of ADA free in plasma is $2\times {10}^{-5}$ mol/kg, the initial amount of free therapeutic protein drug in tissue is $0.5\times {10}^{-5}$ mol/kg, and the initial amount of ADA-drug complexes in plasma is $2\times {10}^{-5}$ mol/kg. Whereas, the historical functions used for compartments that experience delay is $1\times {10}^{-5}$ mol/kg for free therapeutic protein drug in plasma, and $4\times {10}^{-5}$ mol/kg for ADA in the depot.

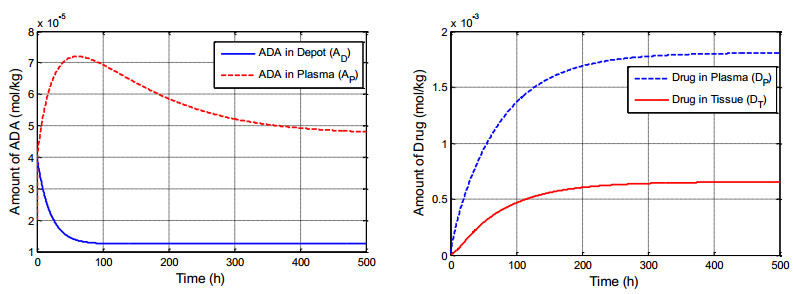
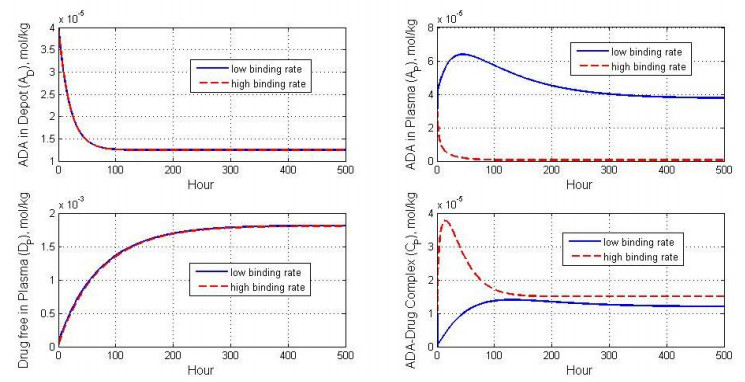
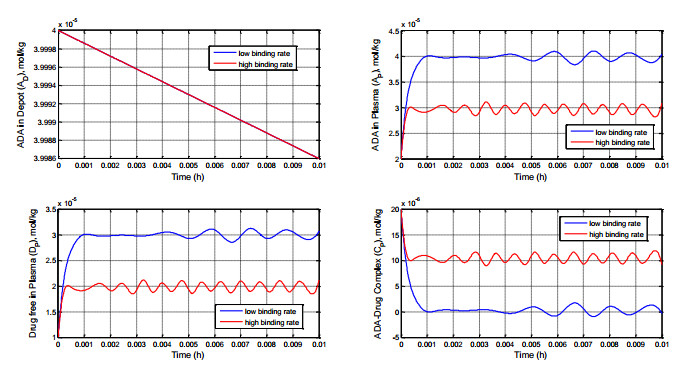
Figure 3 shows the dynamic of ADA in the depot and the plasma in the absence of delay on the distribution of ADA from depot to the plasma. We can observe that the amount of ADA in the depot is declining over time as ADA in the plasma is increasing. This occurs because the ADA in the depot enters the plasma directly without delay, which then forms a complex to bind drugs that are considered foreign to the body. Similar behavior occurs for the amount of drug wherein the absence of delay in the drug accumulation causes the amount of the drug in plasma increases, and the amount is higher than the amount in the tissue since when the injection occurs plasma is the first compartment that is entered by the drug. When the binding rate of ADA-drug complex in plasma is enlarged, the amount of ADA in plasma decreases along with the increasing of ADA-drug complex (see Figure 4). We can also observe that the increasing binding rate of ADA-drug complex only affects the amount of ADA and ADA-drug complex. High binding rate is not affect the amount of drug in the plasma due to the injection occurs directly without delay. Furthermore, when the disassociation rate constant of ADA-drug complex is variated, we can observe in Figure 5 that the perturbation is almost does not affects the change of drug amount in the plasma for long time observation. The perturbation only affects the amount of ADA and ADA-drug complexes in the plasma. The amount of ADA in the plasma decreses as the disassociation rate constant is also decrease (i.e. as $a\to \infty$). It means that the affinity maturation was achieved as the saturation of ADA-drug complex occured.

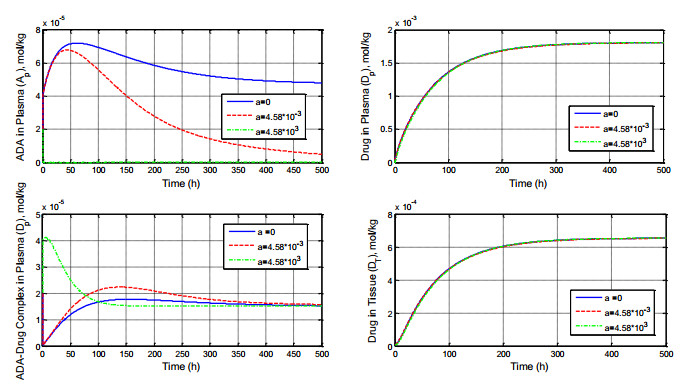
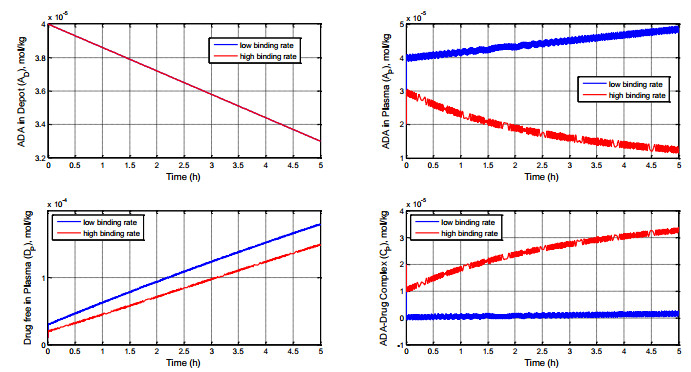
Next, assume that there exists effect of delay on the drug acumulation that affects the production of ADA bolus in the depot and assume that delay also occurs at the distribution of ADA from the depot to the plasma. Based on the previous analysis (see Figure 1) and by using parameter values in Table 1, we have ${\tau }_{1} = 7.824\mathrm{a}\mathrm{n}\mathrm{d}{\tau }_{2} = 8.208$. In Figure 6 we can observe that existence of delays affects directly the amount of ADA, drug, and ADA-drug complex in the plasma compartment. There exists ossilatory pattern in the transient behaviour of the system that clearly describes the apperance of Hopf bifurcation on the system. As we can see on Figure 6 that high binding rate of ADA-drug complexes indicates high immunogenicity on therapeutic protein pharmacokinetics with oscillatory behaviour eventhough the oscillatory occurs at a small time interval. When the time observation is increased (see Figure 7), the ocsillatory pattern almost unseen due to a small of amplitude and a high of frecuency of the solutions. It means that for a large time observation, the delays have a small effect to the immunogenicity system on the therapeutic protein pharmacokinetics.

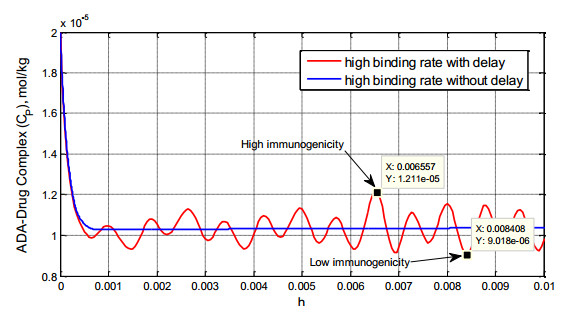
Now let us observe the time evolution of the system in a small-time observation. For studying the effect of delay on the pharmacokinetics of therapeutic protein, in Figure 8, we show the dynamic of ADA-drug complex in which the amount of the complexes represents the inactivity of the protein drug due to the appearance of immune response through the production of ADA that binds the drugs to form a complex of ADA-drug. We can observe that the existence of delays on the drug accumulation and the distribution of ADA from depot to the plasma causes the amount of the complexes in the plasma to go ups and downs. The amount of ADA-drug complex oscillates around its steady-state. There exists a certain time in which the number of complexes is high indicating high immunogenicity of a therapeutic protein, vice versa, low immunogenicity is observed at a certain time of observation. It indicates that the time lag can be adjusted especially the lag that refers to the drug accumulation that triggers the production of ADA such that the complex formation between ADA and the protein drug due to immunogenicity on the therapeutic protein pharmacokinetic can be delayed.

4.   Conclusions

We studied a mathematical model of immunogenicity on therapeutic protein pharmacokinetics by considering the interaction of ADA and the protein drug with delay on the response of the ADA production due to drug accumulation (injected therapeutic protein drug doses) and natural delay on the ADA entry process from the depot into the plasma. Effects of the delays on the system caused a change in the stability behavior and the growth rate of each compartment. With delay factor, compartments experienced slower growth or faster decline. In addition, the delay also affected the behavior of the model solutions. It was initially evolved exponentially to oscillate, and Hopf bifurcation appeared in certain compartments. The delay factor also influenced the number of ADA in the depot to be greater than in the plasma. This was a good effect on the host body because the amount of ADA in the plasma that would deactivate the drug performance was quite small, so the drug could have more optimal effects on the host body. An appropriate critical delay could be chosen based on the critical time delay obtained on the analysis results.

Acknowledgments

The authors thank the reviewer for their valuable responses to increase the quality of the paper. This work was supported by the Institute for Research and Community Service, Hasanuddin University [grantnumber 1740/UN4.21/PL.01.10/2019].

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.