In this article, a novel semi-discrete model for stochastic competitive neural networks (SCNNs) is proposed. At first, taking advantage of some famous inequalities and fixed point theory, a few conditions are obtained for the existence of 2p-th mean almost periodic sequence (MAPS) of the semi-discrete stochastic model. In the next palace, 2p-th moment global exponential stability (MGES) of the above model is discussed as well. The research findings exhibit the stochastic and delayed effects on the mean dynamics of the semi-discrete stochastic networks. In the end, some numerical illustrations are presented to visually expound the feasibility of the works in this paper. The methods in this article could be applied to investigate other models in the areas of science and engineering.
1.
Introduction
Competitive neural networks (CNNs) simulate the cortical cognitive maps with unsupervised synaptic modifications. In the structure of CNNs, it has two kinds of states: one depicts the fast neural activity and the other one depicts the slow unsupervised synaptic modifications. Recently, CNNs had been extensively used in artificial intelligence, robotics, adaptive control and combinatorial optimization, etc. In the dynamical behaviours of CNNs, (almost) periodicity and exponential stability are extremely important. Consequently, many literatures [1,2,3,4,5,6,7,8] concerned synchronization, the existence and global exponential stability of equilibrium point, (almost) periodic solutions of CNNs. Such as, Wang and Huang [6] studied the CNNs below:
where xi is the ith neuron, mij is the synaptic efficiency, fj and ˜fi are the activation functions, i,j=1,2,…,n. In [6], the authors studied the equilibrium point and exponential asymptotic stability for system (1.1).
In practical applications, stochastic disturbances frequently occur in NNs and the stochastic factors always happen in the uncertainties of the parameter process. Therefore, this paper concerns the SCNNs below:
where wj and ˜wi are the standard Brownian motions, τij(t) and ηij(t) are bounded continuous functions with 0≤τij(t)≤ˉτij, 0≤ηij(t)≤ˉηij, ∀t∈R, ˉτij and ˉηij are positive constants, i,j=1,2,…,n.
The discreteness of NNs is a very effective tool to investigate the dynamics of the networks in a digital way. Therefore, lots of research findings were gained for the dynamics of discrete-time determinant or stochastic NNs by Euler scheme [9,10,11,12,13]. In recent years, the semi-discretization [14] of determinant differential equations received wide attentions and the authors [14,15,16,17,18] displayed that semi-discrete models provide more precise approximation of continuous-time models than those by Euler method. For example, the following semi-discrete NNs had been discussed in [16]:
Assuming that all coefficients are almost periodic, the stable almost periodic sequence solution of system (1.3) was studied. Next, Huang et al. [18] studied the semi-discrete analogue of a general neural networks as follows:
In [18], some sufficient conditions were obtained for the existence of 2n locally stable almost periodic solutions of the above NNs.
In literatures [14,15,16,17,18], the disquisitive models are deterministic. To the best of authors' knowledge, few results study the semi-discrete stochastic NNs. The major contributions of this paper are as follows:
● Semi-discrete analogue of SCNNs (1.2) is achieved.
● A Volterra integral expression in difference form is got for semi-discrete model of SCNNs (1.2).
● Some new results are gained for 2p-th MAPS and MGES to semi-discrete stochastic model.
● The issues discussed in this article can motivate the researches of other discrete stochastic models.
Motivated by the above reasons, the aim of this literature is to achieve the semi-discrete SCNNs and the mean dynamic behaviours (MAPS and MGES) of the model should be discussed. The rest of this article is organized as follows. In Section 2, the semi-discrete model of system (1.2) is obtained and some preparatory works are given. In Section 3, the 2p-th MAPS of the semi-dicrete model is studied by fixed point theory. In Section 4, 2p-th MGES of the model is also discussed. An example and simulations are provided to expound the chief results of this paper in Section 5. Section 6 displays the conclusions and future perspectives of this article.
Denote by Rn the n-dimensional real vector space and (Ω,F,P) is a complete probability space. Let BC(Z,Lp(Ω,Rn)) be the space of all bounded continuous functions from Z to Lp(Ω,Rn), where Lp(Ω,Rn) is the space of all p-th integrable Rn-valued random variables. So BC(Z,Lp(Ω,Rn)) is a Banach space with ‖X‖p=supk∈Z|X|p, |X|p=max1≤i≤n(E|xi(k)|p)1p, ∀X={xi}:={x1,x2,…,xn}∈BC(Z,Lp(Ω,Rn)), where p>1 and E(⋅) stands for the expectation operator. [a,b]Z=[a,b]∩Z, ∀a,b∈R.
2.
Model description and preparatory work
2.1. Model description
Letting Si(t)=p∑j=1mij(t)yj=yTmi(t), where y=(y1,y2,…,yp)T, mi=(mi1,mi2,…,mip)T, then system (1.2) is changed to
Similar to the argument as that in [14], the semi-discrete analogue of system (2.1) is obtained as follows:
2.2. Preparatory work
Definition 2.1. ([19]) For X∈BC(Z;Lp(Ω;Rn)) and each ϵ>0, there exists an integer l(ϵ)>0 such that each interval of length l(ϵ) contains an integer ω for which
Then stochastic process X is said to be p-th MAPS.
Lemma 2.1. ([20]) If X={xi} is a solution of system (2.2), then
where k0∈Z, k∈(k0,+∞)Z, i=1,2,…,n.
Lemma 2.2. ([21]) If g∈L2([a,b],R), then
Lemma 2.3. ([20]) If {x(k):k∈Z} is real-valued stochastic process and w(k) is the standard Brownian motion, then
where Cp is defined as that in Lemma 2.2, p>0.
Let fu=supk∈Z|f(k)| and fl=infk∈Z|f(k)| for bounded function f defined on Z. In this paper, assume that the assumptions below hold:
(H1)ali>0 and ˜ali>0, i=1,2,…,n.
(H2) There are some positive constants Lfj, Lσj and L˜fi such that
for all u,v∈R, i,j=1,2,…,n.
3.
2p-th mean almost periodic sequence
Define
where
Lemma 3.1. ([22]) If X is a Banach space, Λ⊆X is closed and convex. Suppose further that B, C:Λ→X such that
(1)x,y∈Λ⇒Bx+Cy∈Λ;
(2)B is continuous and BΛ is contained in a compact set;
(3)C is contractive.
Then it has z∈Λ with z=Bz+Cz.
Theorem 3.1. Assume that (H1)–(H2) and the following conditions hold.
(AP) All of the coefficients in system (2.2) are almost periodic sequences.
(H3)r2p<1.
Then it has a 2p-th MAPS X of system (2.2) with ‖X‖2p≤β2p, p≥1.
Proof. Let Λ⊆BC(Z;L2p(Ω;Rm+n)) denote the set of all 2p-th MAPS X satisfying ‖X‖2p≤β2p.
On the basis of (2.3), define ΦX(k)=BX(k)+CX(k), where
Let X0={x0i;S0i} be given by
By the above equations, it has
Then
Homoplastically,
Thus
From (3.1–3.3), one has
which implies
where D∗∗i=D∗−Bui−∑nj=1buijLfj, i=1,2,…,n. It gains from Lemma 2.3 that
Homoplastically,
Consequently,
So
By (3.4) and similar to the argument as that in [20], (1)–(2) of Lemma 3.1 hold.
At last, ∀X={xi;Si},X∗={x∗i;S∗i}∈Λ, one has
homoplastically,
Then
By (H3), C is contractive. So (3) of Lemma 3.1 holds. By Lemma 3.1, system (2.2) has a 2p-th MAPS. The proof is finished.
Remark 3.1. In view of Theorem 3.1, (H3) is hard to be verified. For the sake of enabling (H3) to be met, the following items should be followed in applications:
(1) The coefficients ai and ˜ai in NNs (2.2), i=1,2,…,n, should be selected to be large enough.
(2) The coefficients bij, cij, Bi, dij, ˜bi and ˜di of NNs (2.2) should be selected to meet (H3) with large enough numbers, i=1,2,…,n.
(3) If the activation functions fj, σj and ˜fi in NNs (2.2) are selected by some small enough constants Lfj, Lσj and L˜fi, then (H2) is easier to be valid, i,j=1,2,…,n.
4.
2p-th moment global exponential stability
Theorem 4.1. If (H1)–(H3) hold, then system (2.2) has the property of 2p-th MGES.
Proof. Assume that X={xi;Si} with initial condition φ={φi;ψi} and X∗={x∗i;S∗i} with initial condition φ∗={φ∗i;ψ∗i} are any two solutions of system (2.2). So
where i=1,2,…,n, k∈[−μ0,+∞)Z, μ0=max(i,j){τuij,ηuij}.
To facilitate, set
Z={zi}, W={wi}, zi(k)=xi(k)−x∗i(k), wi(k)=Si(k)−S∗i(k), i=1,2,…,n, k∈Z.
By (4.1), it has
From (4.2), it induces
By (H3), it has λ>0 small enough ensuring that
Define V(k)=max{|Z(k)|2p,|W(k)|2p}, k∈Z.
Next, assume that it has M0>1 ensuring that
If (4.5) fails, then it has k0∈(0,+∞)Z such that one of the following two cases is valid:
(C1)|Z(k0)|2p>M0γ2pe−λk0 and V(k)≤M0γ2pe−λk,∀k∈[−μ0,k0)Z.
(C2)|W(k0)|2p>M0γ2pe−λk0 and V(k)≤M0γ2pe−λk,∀k∈[−μ0,k0)Z.
If (C1) holds, then
Thus (C1) fails. Homoplastically, (C2) is not satisfied. So (4.5) hold. Then system (2.2) has the property of 2p-th MGES. The proof is finished.
By Theorem 3.1, it obtains
Theorem 4.2. Assume that all conditions in Theorem 3.1 hold, then system (2.2) admits a 2p-th MAPS, which has the property of 2p-th MGES.
Remark 4.1. In literature [17], Ji discussed a delayed semi-discrete neural networks and the existence and global attractivity of a unique almost periodic sequence solution were investigated. In literatures [14,15,16,18], the authors discussed the almost periodic dynamics of various NNs. But neither of them considered the stochastic disturbances. Therefore, the work of this paper complements the works in [14,15,16,17,18].
5.
Numerical illustrations
Example 5.1. Regarding the semi-discrete stochastic CNNs below:
Referring to system (2.2), it has ˜au=˜al=au=al=1, Lf=L˜f=1, Lσ=0, bu=0.01, ˜bu=0.03, Bu=0.05, du=0.01, ˜du=0.02. Taking p=2, then
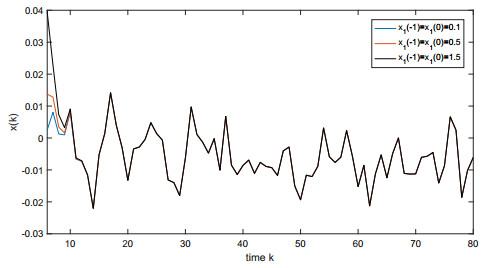
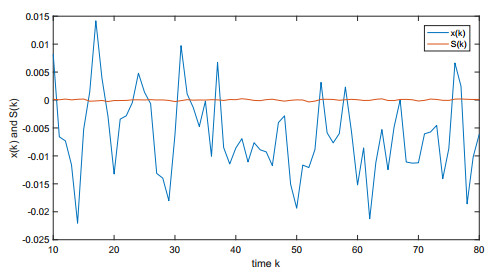
By Theorem 4.2, system (5.1) admits a 4-th MAPS, which has the property of 4-th MGES, see Figures 1–3.
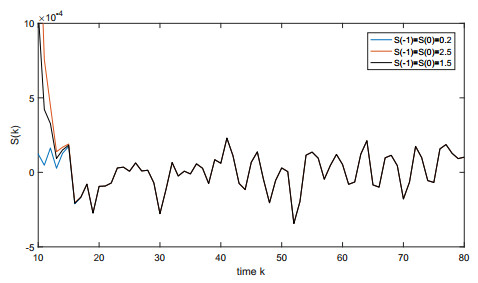
Figure 1 plots the almost periodic trajectories of state variables x and S in system (5.1). Obviously, the amplitude of state variable x is larger than that of state variable S. Figures 2,3 plot the trajectories of state variables x and S in system (5.1) with different initial values, respectively. They demonstrate that the trajectories of state variables in system (5.1) with different initial values will tend to the same trajectory since it has the property of 4-th MGES.
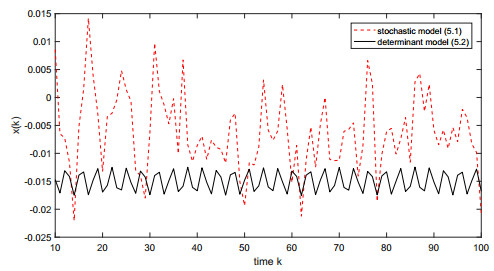
Considering the corresponding determinant model of system (5.1) below:
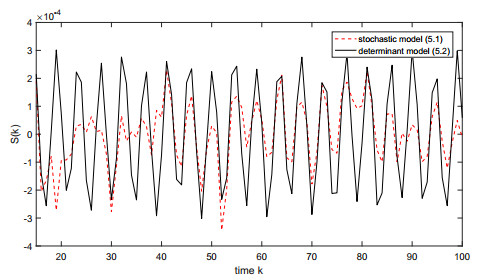
Figures 4 and 5 depict the comparison result between model (5.1) and model (5.2). Figures 4 and 5 imply that the influences of stochastic disturbances on x and S are pretty obvious. Observing Figures 4 and 5, it easily discovers that the effect of stochastic disturbance on x is larger than that on S.
6.
Conclusions and future perspectives
To date, few people consider the problems of MAPS and MGES of semi-discrete SFCNNs. Hence, this article concerns the issues of 2p-th MAPS and 2p-th MGES of semi-discrete SFCNNs. The techniques of this literatures give an effective approach to investigate 2p-th MAPS and 2p-th MGES of semi-discrete stochastic fuzzy models. By (H3), r2p<1 is important to the studies of 2p-th MAPS and 2p-th MGES. There is no influence of time delay on 2p-th MAPS and time delay has negative influence in 2p-th MGES.
In the future, the following aspects could be studied further:
(1) p∈(0,1] in NNs (2.2) could be further investigated.
(2) Other dynamics in NNs (2.2) should be further considered, e.g., hopf bifurcation, chaos, automatic control, etc.
(3) Using the idea and method of this paper, other types of dynamic systems could be studied, such as impulsive dynamic systems [23,24], biomathematical systems [25,26,27], etc.
(4) Applications of NNs (2.2) in intelligent control, machine learning, image processing, etc, should be further investigated.
Acknowledgments
This work is supported by the National Natural Sciences Foundation of People's Republic of China under Grants 11961078. The authors are grateful to anonymous referees for their excellent suggestions, which greatly improve the presentation of the paper.
Conflict of interest
All authors declare no conflict of interest.








 DownLoad:
DownLoad: