Multistep hybrid viscosity method for split monotone variational inclusion and fixed point problems in Hilbert spaces

1.   Introduction

It is known that variational inequality, as a very important tool, has already been studied for a wide class of unilateral, obstacle, and equilibrium problems arising in several branches of pure and applied sciences in a unified and general framework. Many numerical methods have been developed for solving variational inequalities and some related optimization problems; see ^{[1,2,3,4,5,6]} and the references therein.

Let $H$ be a real Hilbert space whose inner product and norm are denoted by $\langle \cdot, \cdot \rangle$ and $\| \cdot \|,$ respectively. Let $C$ be a nonempty, closed and convex subset of $H$ and $A: C \rightarrow H$ be a nonlinear mapping. The variational inequality problem (VIP) associated with the set $C$ and the mapping $A$ is stated as follows:

In particular, the $VIP \; (1.1)$ in the case $C$ is the set $Fix (T)$ of fixed points of a nonexpansive self-mapping $T$ of $C$ and $A$ is of the form $A = I-S$, with $S$ another nonexpansive self-mapping of $C$. In other words, $VIP$ is of the form

This problem, introduced by Mainge and Moudafi ^[8], is called hierarchical fixed point problem (HFPP).

Subsequently, Moudafi and Mainge ^[7] studied the explicit scheme for computing a solution of $VIP\; (1.2)$ by introducing the following iterative algorithm:

where $f:C \rightarrow C$ and $\{ \alpha_n \}, \{ \lambda_n \} \subset (0, 1)$. They also proved the strong convergence of the sequence $\{ x_n \}$ generalized by $(1.3)$ to a solution of $VIP\; (1.2)$.

Yao et al. ^[9] introduced and analyzed the following two-step iterative algorithm that generates a sequence $\{ x_n \}$ by the following explicit scheme:

Under appropriate conditions, the above iterative sequence $\{x_n\}$ converges strongly to some fixed point of $T$ where $T$ is nonexpansive mapping and $\{x_n\}$ is solves $VIP\; (1.2)$.

Marino et al. ^[10] introduced a multistep iterative method that generalizes the two-step method studied in ^[9] from two nonexpansive mappings to a finite family of nonexpansive mappings that generates a sequence $\{ x_n \}$ by the following iterative scheme:

They prove that strong convergence of the method to a common fixed point of a finite number of nonexpansive mappings that also solves a suitable equilibrium problem.

On the other hand, by combining the regularization method, the hybrid steepest descent method, and the projection method, Ceng et al. ^[11] proposed an iterative algorithm that generates a sequence via the explicit scheme and proved that this sequence converges strongly to a unique solution of the following problem.

Problem 1.1 Let $F:C \rightarrow H$ be $k$-Lipschitzian and $\eta$-strongly monotone on the nonempty, closed and convex subset $C$ of $H$, where $k$ and $\eta$ are positive constants, that is,

Let $f:C \rightarrow H$ be a $\rho$-contraction with a coefficient $\rho \in [0, 1)$ and $S, T: C \rightarrow C$ be two nonexpansive mappings with $Fix(T) \neq \emptyset.$ Let $0 < \mu < \frac{2\eta}{k^2}$ and $0 < \gamma \leq \tau$, where $\tau = 1- \sqrt{1-\mu (2 \eta -\mu k^2)}.$ Consider the following triple hierarchical variational inequality problem (THVI): find $x^* \in \Xi$ such that

where $\Xi$ denotes the solution set of the following hierarchical variational inequality problem (HVIP): find $z^* \in Fix(T)$ such that

where the solution set $\Xi$ is assumed to be nonempty.

Since Problem 1.1 has a triple hierarchical structure, in contrast to bilevel programming problems ^[12,13], that is, a variational inequality problem with a variational inequality constraint over the fixed point set $Fix(T)$, we also call (1.8) a triple hierarchical variational inequality problem (THVIP), which is a generalization of the triple hierarchical constrained optimization problem (THCOP) considered by ^[14,15].

Recently, many authors introduced the split monotone variational inequality inclusion problem, which is the core of the modeling of many inverse problems arising in phase retrieval and other real-world problems. It has been widely studied in sensor networks, intensity-modulated radiation therapy treatment planning, data compression, and computerized tomography in recent years; see, e.g., ^{[18,19,21,26,27]} and the references therein.

The split monotone variational inclusion problem (SMVIP) was first introduced by Moudafi ^[20] as follows: find $x^{*} \in H_1$ such that

where $f_1 : H_1 \rightarrow H_1$ and $f_2: H_2 \rightarrow H_2$ are two given single-valued mappings, $A:H_1 \rightarrow H_2$ is a bounded linear operator, and $B_1 : H_1 \rightarrow 2^{H_1}$ and $B_2 : H_2 \rightarrow 2^{H_2}$ are multivalued maximal monotone mappings.

If $f_1 = f_2 \equiv 0$, then (1.9) reduces to the following split variational inclusion problem (SVIP): find $x^{*} \in H_1$ such that

Additionally, if $f_1 \equiv 0$, then (1.9) reduces to the following split monotone variational inclusion problem ($SMVIP$): find $x^* \in H_1$ such that

We denote the solution sets of variational inclusion $0\in B_1 x^{*}$ and $0\in f y^{*} + B_2 y^{*}$ by $SOLVIP(B_1)$ and $SOLVIP(f+B_2)$, respectively. Thus, the solution set of $(1.11)$ can denoted by $\Gamma = \{x^*\in H_1 : x^{*} \in SOLVIP(B_1), Ax^{*} \in SOLVIP(f+B_2) \}$.

In 2012, Byrne et al. ^[21] studied the following iterative scheme for $SVIP \; (1.10)$: for a given $x_0 \in H_1$ and $\lambda > 0$,

In 2014, Kazmi and Rizvi ^[22] introduced a new iterative scheme for $SVIP \; (1.10)$ and the fixed point problem of a nonexpansive mapping:

where $A$ is a bounded linear operator, $A^{*}$ is the adjoint of $A$, $f$ is a contraction on $H_1$, and $T$ is a nonexpansive mapping of $H_1$. They obtained a strong convergence theorem under some mild restrictions on the parameters.

Jitsupa et al. ^[1] modified algorithm (1.13) for $SVIP \; (1.10)$ and the fixed point problem of a family of strict pseudo-contractions:

where $A$ is a bounded linear operator, $A^{*}$ is the adjoint of $A$, $\{ T_i \}_{i = 1}^{N}$ is a family of $k_i$-strictly pseudo-contractions, $f$ is a contraction, and $D$ is a strong positive linear bounded operator. In ^[1], they prove under certain appropriate assumptions on the sequences $\{ \alpha_{n } \}, \{ \beta_{n } \}$ and $\{ \eta_{i}^{(n)} \}_{i = 1}^{N}$ that $\{x_n\}$, defined by (1.14), converges strongly to a common solution of $SVIP \; (1.10)$ and a fixed point of a finite family of $k_i$-strictly pseudo-contractions, which solve a variational inequality problem (1.1).

In this paper, we consider the following system of variational inequalities defined over a set consisting of the set of solutions of split monotone variational inclusion, the set of common fixed points of nonexpansive mappings, and the set of fixed points of a mapping.

Problem 1.2 Let $F:C \rightarrow H$ be $k$-Lipschitzian and $\eta$-strongly monotone on the nonempty closed and convex subset $C$ of $H$, $\psi:C \rightarrow H$ be a $\rho$-contraction with coefficient $\rho \in [0, 1)$ and $S_i, S, T: C \rightarrow C$ be nonexpansive mappings for all $i\in \{ 1, \ldots, N \}$. Let $0 < \mu < \frac{2 \eta}{k^2}$ and $0 < \xi \leq \tau$, where $\tau = 1-\sqrt{1-\mu(2 \eta - \mu k^2)}$. Then, the objective is to find $x^* \in \Omega$ such that

where $\Omega = Fix(T)\cap(\bigcap_i Fix (S_i))\cap \Gamma \neq \emptyset.$

Motivated and inspired by the Moudafi and Mainge ^[7], Marino et al. ^[10], Ceng et al. ^[11] and Kazmi and Rizvi ^[22], in this paper, we consider a multistep which difference from (1.5). It is proven that under appropriate assumptions the proposed iterative method, the sequence $\{ x_n \}$ converges strongly to a unique solution to Problem 1.2 and which is solve $THVI (1.7)$. Finally, we give some example and numerical results to illustrate our main results.

2.   Preliminaries

In this section, we collect some notations and lemmas. Let $C$ be a nonempty closed convex subset of a real Hilbert space $H$. We denote the strong convergence and the weak convergence of the sequence $\{ x_n \}$ to a point $x \in H$ by $x_n \rightarrow x$ and $x_n \rightharpoonup x$, respectively. It is also well known ^[24] that the Hilbert space $H$ satisfies $Opail's \; condition$, that is, for any sequence $\{ x_n \}$ with $x_n \rightharpoonup x$, the inequality

holds for every $y\in H$ with $y \neq x$.

In the sequel, given a sequence $\{ z_n \}$, we denote with $\omega_w (z_n)$ the set of cluster points of $\{ z_n \}$ with respect to the weak topology, that is,

Analogously, we denote by $\omega_s (z_n)$ the set of cluster points of $\{ z_n \}$ with respect to the norm topology, that is,

Lemma 2.1. In a real Hilbert space $H$, the following inequalities hold:

(1) $\|x-y\|^2 = \|x\|^2-\|y\|^2-2 \langle x-y, y\rangle, \forall x, y \in H$;

(2) $\|x+y\|^2 \leq \|x\|^2+2 \langle y, x+y\rangle, \forall x, y \in H$;

(3) $\|\lambda x+(1-\lambda) y\|^2 = \lambda \|x\|^2+(1-\lambda)\|y\|^2-\lambda(1-\lambda)\|x-y\|^2, \forall \lambda \in [0, 1], \forall x, y \in H$;

An element $x \in C$ is called a $fixed \; point$ of $S$ if $x\in Sx$. The set of all fixed point of $S$ is denoted by $Fix(S)$, that is, $Fix(S) = \{ x\in C: x\in S x \}$.

Recall the following definitions. Moreover, $S:H_1 \rightarrow H_1$ is called

$(1)$ a nonexpansive mapping if

A nonexpansive mapping with $k = 1$ can be strengthened to a firmly nonexpansive mapping in $H_1$ if the following holds:

We note that every nonexpansive operator $S:H_1\rightarrow H_1$ satisfies, for all $(x, y)\in H_1 \times H_1$, the inequality

and therefore, we obtain, for all $(x, y)\in H_1\times Fix(S)$,

(see, e.g., Theorem 3 in ^[16] and Theorem 1 in ^[17]).

$(2)$ a contractive if there exists a constant $\alpha \in (0, 1)$ such that

$(3)$ an $L$-Lipschitzian if there exists a positive constant $L$ such that

$(4)$ an $\eta$-strongly monotone if there exists a positive constant $\eta$ such that

$(5)$ an $\beta$-inverse strongly monotone ($\beta-ism$) if there exists a positive constant $\beta$ such that

$(6)$ averaged if it can be expressed as the average of the identity mapping and a nonexpansive mapping, i.e.,

where $\alpha \in (0, 1), I$ is the identity operator on $H_1$ and $T:H_1 \rightarrow H_1$ is nonexpansive.

It is easily seen that averaged mappings are nonexpansive. In the meantime, firmly nonexpansive mappings are averaged.

$(7)$ A linear operator $D$ is said to be a strongly positive bounded linear operator on $H_1$ if there exists a positive constant $\bar{\tau} > 0$ such that

From the definition above, we easily find that a strongly positive bounded linear operator $D$ is $\bar{\tau}$-strongly monotone and $\|D\|$-Lipschitzian.

$(8)$ A multivalued mapping $M : D(M) \subseteq H_1 \rightarrow 2^{H_1}$ is called monotone if for all $x, y \in D(M), u\in Mx$ and $v \in My$,

A monotone mapping $M$ is maximal if the $Graph(M)$ is not properly contained in the graph of any other monotone mapping. It is well known that a monotone mapping $M$ is maximal if and only if for $x\in D(M), u\in H_1, \langle x-y, u-v \rangle \geq 0$ for each $(y, v) \in Graph (M)$, $u\in Mx$.

$(9)$ Let $M:D(M) \subseteq H_1 \rightarrow 2^{H_1}$ be a multivalued maximal monotone mapping. Then, the resolvent operator $J_{\lambda}^{M}: H_1 \rightarrow D(M)$ is defined by

for $\forall \lambda > 0$, where $I$ stands for the identity operator on $H_1$. We observe that $J_{\lambda}^{M}$ is single-valued, nonexpansive, and firmly nonexpansive.

We recall some concepts and results that are needed in the sequel. A mapping $P_C$ is said to be a metric projection of $H_1$ onto $C$ if for every point $x\in H_1$, there exists a unique nearest point in $C$ denoted by $P_C x$ such that

It is well known that $P_C$ is a nonexpansive mapping and is characterized by the following property:

Moreover, $P_C x$ is characterized by the following properties:

and

Proposition 2.2. ^[20]

(1) If $T = (1-\alpha) S + \alpha V,$ where $S: H_1 \rightarrow H_1$ is averaged, $V: H_1 \rightarrow H_1$ is nonexpansive, and if $\alpha \in [0, 1],$ then $T$ is averaged.

(2) The composite of finitely many averaged mappings is averaged.

(3) If the mappings $\{ T_i \}_{i = 1}^{N}$ are averaged and have a nonempty common fixed point, then

(4) If $T$ is a $v-ism$, then for $\gamma > 0, \gamma T$ is a $\frac{v}{\gamma}-ism.$

(5) $T$ is averaged if and only if its complement $I-T$ is a $v-ism$ for some $v > \frac{1}{2}$.

Proposition 2.3. ^[20] Let $\lambda > 0, h$ be an $\alpha-ism$ operator, and $B$ be a maximal monotone operator. If $\lambda \in (0, 2\alpha)$, then it is easy to see that the operator $J_{\lambda}^{B}(I-\lambda h)$ is averaged.

Proposition 2.4. ^[20] Let $\lambda > 0$ and $B_1$ be a maximal monotone operator. Then,

Lemma 2.5. ^[23] Let $\{s_n\}$ be a sequence of nonnegative numbers satisfying the condition

where $\{ \gamma_n \}, \{ \delta_n \}$ are the sequences of real numbers such that

(i) $\{ \gamma_n \} \subset [0, 1]$ and $\mathop {\mathop \sum \limits^\infty }\limits_{n = 1} \gamma_n = \infty$, or equivalently,

(ii) $\underset{n \rightarrow \infty}{\limsup} \delta_n \leq 0$, or

(iii) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 1} \gamma_n \delta_n$ is convergent.

Then, $\underset{n \rightarrow \infty}{\lim} s_n = 0$.

Lemma 2.6. ^[23] Let $\lambda$ be a number $(0, 1]$, and let $\mu > 0.$ Let $F:C \rightarrow H$ be an operator on $C$ such that for some constant $k, \eta > 0, F$ is $k$-Lipschitzian and $\eta$-strongly monotone. Associating with a nonexpansive mapping $T:C \rightarrow C$, we define the following the mapping $T^{\lambda}:C \rightarrow H$ by

Then, $T^{\lambda}$ is a contraction provided $\mu < \frac{2\eta }{k^2}$, that is,

where $\tau = 1- \sqrt{1-\mu (2\eta - \mu k^2)} \in (0, 1]$.

Lemma 2.7. ^[25] Let $\{ \alpha_n \}$ be a sequence of nonnegative real numbers with $\underset{n \rightarrow \infty}{\limsup} \alpha_n < \infty$ and $\{ \beta_n \}$ be a sequence of real numbers with $\underset{n \rightarrow \infty}{\limsup} \beta_n \leq 0$. Then, $\underset{n \rightarrow \infty}{\limsup} \alpha_n \beta_n \leq 0$.

Lemma 2.8. ^[28] Assume that $T$ is nonexpansive self-mapping of a closed convex subset $C$ of a Hilbert space $H_1$. If $T$ has a fixed point, then $I-T$ is demiclosed, i.e., whenever $\{ x_n \}$ weakly converges to some $x$ and $\{ (I-T) x_n \}$ converges strongly to $y$, it follows that $(I-T)x = y$. Here, $I$ is the identity mapping on $H_1.$

3.   Results

Theorem 3.1. Let $C$ be a nonempty closed convex subset of a real Hilbert space $H_1$ and $Q$ be a nonempty closed convex subset of a real Hilbert space $H_2$. Let $A:H_1\rightarrow H_2$ be a bounded linear operator, $A^*$ be the adjoint of $A$, and $r$ be the spectral radius of the operator $A^* A$. Let $f: H_2 \rightarrow H_2$ be a $\varsigma$-inverse strongly monotone operator, $B_1:C \rightarrow 2^{H_1}, B_2: H_2 \rightarrow 2^{H_2}$ be two multivalued maximal monotone operators, and $F:C \rightarrow H_1$ be $k$-Lipschitzian and $\eta$-strongly monotone. Let $\psi: C \rightarrow H_1$ be a $\rho$-contraction with a coefficient $\rho \in [0, 1)$ and $S_i, S, T:C \rightarrow C$ be nonexpansive mappings for all $i\in \{ 1, \ldots, N \}$. Let $\{ \lambda_n \}, \{ \alpha_n \}, \{ \beta_{n, i} \}, i = 1, \ldots, N$ be sequences in $(0, 1)$ such that $\beta_{n, i} \rightarrow \beta_i \in (0, 1)$ as $n \rightarrow \infty$ for all $i\in \{ 1, \ldots, N \}$, $0 < \mu < \frac{2 \eta}{k^2}$ and $0 < \xi \leq \tau$, where $\tau = 1- \sqrt{1-\mu(2\eta - \mu k^2)}$. Then, the sequence $\{ x_n \}$ is generated from an arbitrary initial point $x_1 \in C$ by the following:

Assume that Problem 1.2 has a solution. Suppose that the following conditions are satisfied:

(C1) $0 < \underset{n \rightarrow \infty}{\liminf}\alpha_n \leq \underset{n \rightarrow \infty}{\limsup}\alpha_n < 1$;

(C2) $\underset{n \rightarrow \infty}{\lim}\lambda_n = 0$ and $\mathop {\mathop \sum \limits^\infty }\limits_{n = 1} \lambda_n = \infty$;

(C3) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \alpha_{n }\lambda_{n}-\alpha_{n-1}\lambda_{n-1}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\alpha_{n }\lambda_{n}-\alpha_{n-1}\lambda_{n-1} |}{\lambda_n} = 0$;

(C4) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \lambda_{n}-\lambda_{n-1}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\lambda_{n}-\lambda_{n-1} |}{\lambda_n} = 0$;

(C5) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \beta_{n, i}-\beta_{n-1, i}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\beta_{n, i}-\beta_{n-1, i} |}{\lambda_n} = 0$ for all $i\in \{ 1, \ldots, N \}$;

(C6) $\lambda_1 > 0, 0 < \lambda_2 < 2 \varsigma, 0 < \gamma < \frac{1}{r}$.

Then, $\{ x_n \}$ converges strongly to a unique solution $x^{*} \in \Omega$ of Problem 1.2.

Proof. Let $\{ x_n \}$ be a sequence generated by scheme (4.1). First, note that $0 < \xi \leq \tau$ and

Then, it follows from the $\rho$-contractiveness of $\psi$ that

Hence, from $\xi \rho < \xi \leq \tau \leq \mu \eta$, we deduce that $\mu F - \xi \psi$ is $(\mu \eta - \xi \rho)$-strongly monotone. Since it is clear that $\mu F - \xi \psi$ is Lipshitz continuous, there exists a unique solution to the VIP:

Additionally, since Problem 1.2 has a solution, it is easy to see that Problem 1.2 has a unique solution. In addition, taking into account condition $(C1)$, without loss of generality, we may assume that $\{ \alpha_n \} \subset [a, b]$ for some $a, b \in (0, 1).$

Let $\mathcal{U} : = J_{\lambda_2}^{B_2}(I-\lambda_2 f)$; the iterative scheme (4.1) can be rewritten as

The rest of the proof is divided into several steps.

Step 1. We show that the sequences $\{ x_n\}, \{ y_{n, i} \}$ for all $i, \{ u_n \}$ are bounded.

Indeed, take a point $p\in \Omega$ arbitrarily. Then, $J_{\lambda_1}^{B_1}p = p, \mathcal{U}(Ap) = Ap$, and it is easily seen that $Wp = p$, where $W: = I+\gamma A^{*}(\mathcal{U}-I)A.$ From the definition of firm nonexpansion and Proposition 2.3, we have that $J_{\lambda_1}^{B_1}$ and $\mathcal{U}$ are averaged. Likewise, $W$ is also averaged because it is a $\frac{v}{r}-ism$ for some $v > \frac{1}{2}$. Actually, by Proposition 2.2 (5), we know that $I-\mathcal{U}$ is a $v-ism$ with $v > \frac{1}{2}$. Hence, we have

Thus, $\gamma A^{*} (I-\mathcal{U})A$ is a $\frac{v}{\gamma r}-ism.$ Due to the condition $0 < \gamma < \frac{1}{r}$, the complement $I-\gamma A^{*}(I-\mathcal{U})A$ is averaged, as well as $M: = J_{\lambda_1}^{B_1}[I+\gamma A^{*}(\mathcal{U}-I)A]$. Therefore, $J_{\lambda_1}^{B_1}, \mathcal{U}, W,$ and $M$ are nonexpansive mappings.

From $(3.2)$, we estimate

Thus, we obtain

Next, setting $\vartheta_1: = \gamma^2 \langle (\mathcal{U}-I)A x_n, A A^{*} (\mathcal{U} - I)A x_n \rangle$, we estimate

Setting $\vartheta_2: = 2\gamma \langle x_n-p, A^{*}(\mathcal{U} - I) A x_n \rangle$, we obtain from (2.5) the following:

In view of (3.4)-(3.6), we have

From $0 < \gamma < \frac{1}{r}$, we obtain

Thus, we have from $(3.2)$ and $(3.8)$ that

For all $i$ from $i = 2$ to $i = N$, by induction, one proves that

Hence, we obtain that for all $i\in \{ 1, \ldots, N \}$,

In addition, utilizing Lemma 2.6 and (3.2), we have

due to $0 < \xi \leq \tau.$ Thus, calling

by induction, we derive $\| x_n-p\| \leq M$ for all $n \geq 1$. We thus obtain the claim.

Step 2. We show that $\underset{n \rightarrow \infty}{\lim} \| x_{n+1} - x_n \| = 0$.

Indeed, for each $n\geq 1,$ we set

Then, we observe that

Let $M_{0} > 0$ be a constant such that

It follows from (3.2) and (3.13) that

By the definition of $y_{n, i}$, we obtain that for all $i = N, \ldots, 2$,

In this case $i = 1$, we have

Substituting (3.16) in all (3.15)-type inequalities, we find that for $i = 2, \ldots, N$,

Thus, we conclude that

Since $J_{\lambda_1}^{B_1}[I + \gamma A^{*}(\mathcal{U}-I)A]$ is nonexpansive, we obtain

Substituting (3.18) into (3.17), we have

If we call $M_{1} : = \max \bigg \{ M_0, \underset{n \geq 2, i = 2, \ldots, N}\sup \| S_i u_{n-1} - y_{n-1, i-1}\|, \underset{n\geq 2} \sup \|S_1 u_{n-1}-u_{n-1} \| \bigg \}$, we have

due to $0 < \xi < \tau$. By condition $(C2)-(C5)$ and Lemma 2.5, we obtain that

Step 3. We show that $\underset{n \rightarrow \infty}{\lim} \| x_{n} - u_{n} \| = 0$.

From (3.2) and (3.7), we have

which implies that

Since $\gamma (1-r \gamma) > 0, \|x_{n+1}-x_n\| \rightarrow 0, \lambda_{n} \rightarrow 0$ as $n \rightarrow \infty$, and by the boundedness of $\{ x_n \}$, we conclude that

In addition, by the firm nonexpansion of $J_{\lambda_1}^{B_1}, (3.3), (3.7),$ and $\gamma \in (0, \frac{1}{r})$, we estimate

and hence,

In view of (3.22) and (3.25),

which implies that

Since $\|x_{n+1}-x_n\| \rightarrow 0, \| (\mathcal{U}-I)Ax_n \| \rightarrow 0,$ and $\lambda_n \rightarrow 0$ as $n \rightarrow \infty$, and owing to the boundedness of $\{ x_n \}$, we conclude that

Step 4. We show that $\underset{n\rightarrow \infty}{\lim} \| S_i u_n-u_{n}\| = 0$ for $i\in \{ 1, \ldots, N \}$.

Take a point $p\in \Omega$ arbitrarily. When $i = N,$ utilizing Lemma 2.8 and (3.2), we have

Thus, we have

Since $\beta_{n, N} \rightarrow \beta_N \in (0, 1), \|x_{n+1} - x_n\| \rightarrow 0$ and $\lambda_n \rightarrow 0$ as $n \rightarrow \infty$, by the boundedness of $\{ x_n \}$, we conclude that

Take $i\in \{ 1, \ldots, N-1 \}$ arbitrarily. Then, we obtain

Hence, after $(N-i+1)$-iterations,

Again, we obtain

Since for all $k\in \{ 1, \ldots, N \}, \beta_{n, k} \rightarrow \beta_k \in (0, 1), \|x_{n+1} - x_n\| \rightarrow 0$ and $\lambda_n \rightarrow 0$ as $n \rightarrow \infty$, by the boundedness of $\{ x_n\}$, we conclude that

Obviously, for $i = 1$, we have $\underset{n\rightarrow \infty}{\lim} \| S_1 u_n-u_{n}\| = 0$. To conclude, we have that

which implies that $\underset{n\rightarrow \infty}{\lim} \| S_2 u_n-u_{n}\| = 0$. Consequently, by induction, we obtain

It is enough to observe that

Step 5. We show that $\underset{n\rightarrow \infty}{\lim} \| y_{n, N}-x_n\| = \underset{n\rightarrow \infty}{\lim} \|x_n-T x_n\| = 0$ and $\omega_w (x_n) \subset \Omega$.

Indeed, since $\|x_n-u_n\| \rightarrow 0$ as $n\rightarrow \infty$, we have $\omega_w(x_n) = \omega_w(u_n)$ and $\omega_s(x_n) = \omega_s(u_n)$. Now, we observe that

By Step 4, $\| S_1 u_n - u_n\| \rightarrow 0$ as $n\rightarrow \infty$. Hence, we obtain

This implies that $\omega_w (x_n) = \omega_w (y_{n, 1})$ and $\omega_s (x_n) = \omega_s (y_{n, 1})$.

Take a point $q\in \omega_w (x_n)$ arbitrarily. Since $q\in \omega_w (u_n)$, by Step 4 and the demiclosedness principle, we have $q\in Fix (S_i)$ for all $i \in \{ 1, \ldots, N \}$, that is, $q\in \underset{i}{\cap} Fix (S_i)$. Moreover, note that

hence,

Since $\|x_n-x_{n+1}\| \rightarrow 0, \lambda_n \rightarrow 0, \|y_{n, 1}-x_n\| \rightarrow 0, \beta_{n, k} \rightarrow \beta_k$ and $\|S_k u_n - y_{n, k-1}\| \rightarrow 0$ for all $k\in \{1, \ldots, N \}$, we obtain

Thus, by the demiclosedness principle, we have $q\in Fix (T)$.

In addition, we rewrite $u_{n_k} = J_{\lambda_1}^{B_1}[x_{n_k} + \gamma A^{*}(\mathcal{U}-I)Ax_{n_k}]$ as

Taking $k \rightarrow \infty$ in (3.44) and using (3.24), (3.28) and the fact that the graph of a maximal monotone operator is weakly strongly closed, we have $0 \in B_{1} q,$ i.e., $q\in SOLVIP(B_1)$. Furthermore, since $x_n$ and $u_n$ have the same asymptotical behavior, $A x_{n_k}$ weakly converges to $Aq$. It follows from (3.24), the nonexpansion of $\mathcal{U}$, and Lemma 2.8 that $(I-\mathcal{U})A q = 0$. Thus, by Proposition 2.4, we have $0\in f(Aq) + B_2 (Aq),$ i.e., $Aq \in SOLVIP(B_2).$ As a result, $q\in \Gamma$. This shows that $q \in \Omega$. Therefore, we obtain the claim.

Step 6. We show that $\{ x_n \}$ converges strongly to a unique solution $x^*$ to Problem 1.2.

Indeed, according to $\|x_{n+1} - x_n\| \rightarrow 0,$ we can take a subsequence $\{ x_{n_j}\}$ of $\{ x_n \}$ satisfying

Without loss of generality, we may further assume that $x_{n_j} \rightharpoonup \tilde{x};$ then, $\tilde{x} \in \Omega$, as we have just proved. Since $x^*$ is a solution to Problem 1.2, we obtain

Repeating the same argument as that of (3.46), we have

From (3.2) and (3.9), it follows (noticing that $x_{n+1} = P_C z_n$ and $0 < \xi \leq \tau$) that

It turns out that

Put $s_{n} = \|x_n-x^*\|^2, \xi_n = \alpha_n \lambda_n \xi (1-\rho)$ and

Then, (3.49) can be rewritten as

From conditions $(C1)$ and $(C2)$, we conclude from $0 < 1-\rho \leq 1$ that

Note that

and

Consequently, utilizing Lemma 2.5, we find that

Thus, this, together with Lemma 2.5, leads to $\underset{n \rightarrow \infty}{\lim} \|x_n-x^*\| = 0$. The proof is complete.

In Theorem 3.1, if $\lambda_1 = \lambda_2 = \lambda$ and $f = 0$, the we obtain the following corollary immediately.

Corollary 3.2. Let $C$ be a nonempty closed convex subset of a real Hilbert space $H_1$ and $Q$ be a nonempty closed convex subset of a real Hilbert space $H_2$. Let $A:H_1\rightarrow H_2$ be a bounded linear operator, $A^*$ be the adjoint of $A$, and $r$ be the spectral radius of the operator $A^* A$. Let $B_1:C \rightarrow 2^{H_1}, B_2: H_2 \rightarrow 2^{H_2}$ be two multivalued maximal monotone operators, and $F:C \rightarrow H_1$ be $k$-Lipschitzian and $\eta$-strongly monotone. Let $\psi: C \rightarrow H_1$ be a $\rho$-contraction with a coefficient $\rho \in [0, 1)$ and $S_i, S, T:C \rightarrow C$ be nonexpansive mappings for all $i\in \{ 1, \ldots, N \}$. Let $\{ \lambda_n \}, \{ \alpha_n \}, \{ \beta_{n, i} \}, i = 1, \ldots, N$ be sequences in $(0, 1)$ such that $\beta_{n, i} \rightarrow \beta_i \in (0, 1)$ as $n \rightarrow \infty$ for all $i\in \{ 1, \ldots, N \}$, $0 < \mu < \frac{2 \eta}{k^2}$ and $0 < \xi \leq \tau$, where $\tau = 1- \sqrt{1-\mu(2\eta - \mu k^2)}$. Then, the sequence $\{ x_n \}$ is generated from an arbitrary initial point $x_1 \in C$ by the following:

Suppose that the following conditions are satisfied:

(C1) $0 < \underset{n \rightarrow \infty}{\liminf}\alpha_n \leq \underset{n \rightarrow \infty}{\limsup}\alpha_n < 1$;

(C2) $\underset{n \rightarrow \infty}{\lim}\lambda_n = 0$ and $\mathop {\mathop \sum \limits^\infty }\limits_{n = 1} \lambda_n = \infty$;

(C3) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \alpha_{n }\lambda_{n}-\alpha_{n-1}\lambda_{n-1}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\alpha_{n }\lambda_{n}-\alpha_{n-1}\lambda_{n-1} |}{\lambda_n} = 0$;

(C4) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \lambda_{n}-\lambda_{n-1}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\lambda_{n}-\lambda_{n-1} |}{\lambda_n} = 0$;

(C5) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \beta_{n, i}-\beta_{n-1, i}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\beta_{n, i}-\beta_{n-1, i} |}{\lambda_n} = 0$ for all $i\in \{ 1, \ldots, N \}$;

(C6) $0 < \gamma < \frac{1}{r}$.

Then, $\{ x_n \}$ converges strongly to a unique solution $x^{*} \in Fix(T)\cap(\bigcap_i Fix (S_i))\cap SVIP$.

4.   Numerical illustration and application

Here as a numerical illustration, we consider a split common fixed points of a family of nonexpansive mappings, which is a particular case of problem 1.2. To that end, we have the following, which is an equivalent formulation of Theorem 3.1.

Let $C$ be a nonempty closed convex subset of a real Hilbert space $H_1$ and $Q$ be a nonempty closed convex subset of a real Hilbert space $H_2$. Let $A:H_1\rightarrow H_2$ be a bounded linear operator, $A^*$ be the adjoint of $A$, and $r$ be the spectral radius of the operator $A^* A$. Let $f: H_2 \rightarrow H_2$ be a $\varsigma$-inverse strongly monotone operator, and $F:C \rightarrow H_1$ be $k$-Lipschitzian and $\eta$-strongly monotone. Let $\psi: C \rightarrow H_1$ be a $\rho$-contraction with a coefficient $\rho \in [0, 1)$ and $S_i, S, T:C \rightarrow C$ be nonexpansive mappings for all $i\in \{ 1, \ldots, N \}$. Let $\{ \lambda_n \}, \{ \alpha_n \}, \{ \beta_{n, i} \}, i = 1, \ldots, N$ be sequences in $(0, 1)$ such that $\beta_{n, i} \rightarrow \beta_i \in (0, 1)$ as $n \rightarrow \infty$ for all $i\in \{ 1, \ldots, N \}$, $0 < \mu < \frac{2 \eta}{k^2}$ and $0 < \xi \leq \tau$, where $\tau = 1- \sqrt{1-\mu(2\eta - \mu k^2)}$. Then, the sequence $\{ x_n \}$ is generated from an arbitrary initial point $x_1 \in C$ by the following:

Assume that the problem

has a solution. Suppose that the following conditions are satisfied:

(C1) $0 < \underset{n \rightarrow \infty}{\liminf}\alpha_n \leq \underset{n \rightarrow \infty}{\limsup}\alpha_n < 1$;

(C2) $\underset{n \rightarrow \infty}{\lim}\lambda_n = 0$ and $\mathop {\mathop \sum \limits^\infty }\limits_{n = 1} \lambda_n = \infty$;

(C3) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \alpha_{n }\lambda_{n}-\alpha_{n-1}\lambda_{n-1}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\alpha_{n }\lambda_{n}-\alpha_{n-1}\lambda_{n-1} |}{\lambda_n} = 0$;

(C4) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \lambda_{n}-\lambda_{n-1}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\lambda_{n}-\lambda_{n-1} |}{\lambda_n} = 0$;

(C5) $\mathop {\mathop \sum \limits^\infty }\limits_{n = 2} | \beta_{n, i}-\beta_{n-1, i}| < \infty$ or $\underset{n \rightarrow \infty}{\lim} \frac{ |\beta_{n, i}-\beta_{n-1, i} |}{\lambda_n} = 0$ for all $i\in \{ 1, \ldots, N \}$;

(C6) $\lambda_1 > 0, 0 < \lambda_2 < 2 \varsigma, 0 < \gamma < \frac{1}{r}$.

Then, $\{ x_n \}$ converges strongly to a unique solution $x^{*} \in \Omega$ of Problem (4.2). Suppose $H = C = \mathbb{R},$ for each $x \in \mathbb{R}$ the mappings $S_i$ and $T_i$ are defined as follows

and

Observe that $S_i$ for $i \ge 1$ are nonexpansive and T is $\frac{1}{3}$-demicontractive mapping ^[29]. Take $\beta_{n, i} = \frac{6}{n^2 i^2}, \alpha_n = \frac{3}{n^2}$ and $\lambda_n = \frac{1}{n^2 + 2}$. Also define $\psi (x) = \frac{2x}{3}$ and $Ax = 2x$ with $\|A \| = 2$. Therefore it can be seen that the sequences satisfy the conditions in the (C1) - (C6).

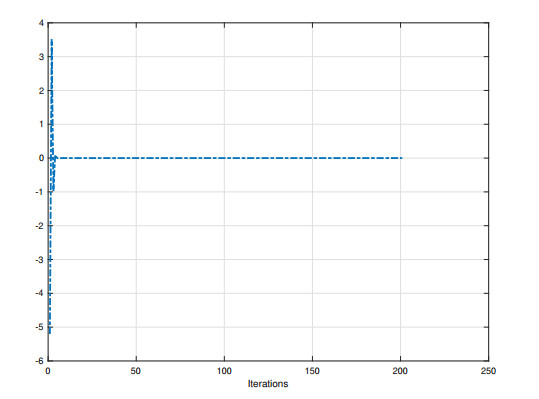
It can be observed from Figure 1, that the sequence $\{x_n\}$ generated converges to $0$, which is the only element of the solution set, i.e $\Omega = \{0\}.$

5.   Conclusion

In this paper, we first propose triple hierarchical variational inequality problem (4.1) in Theorem 3.1 and then we prove some strong convergence of the sequence $\{x_n\}$ generated by (4.1) to a common solution of variational inequality problem, split monotone variational inclusion problem and fixed point problems. We divide the proof into 6 steps and our theorem is extends and improves the corresponding results of Jitsupa et al. ^[1] and Kazmi and Rizvi ^[22].

Acknowledgments

The authors thank the referees for their comments and suggestions regarding this manuscript. The last author would like to thank King Mongkut's University of Technology North Bangkok, Rayong Campus (KMUTNB-Rayong). This research was funded by King Mongkut's University of Technology North Bangkok. Contract no. KMUTNB-63-KNOW-016.

Conflict of interest

The authors declare that they have no competing interests.