A novel class of forward-backward explicit iterative algorithms using inertial techniques to solve variational inequality problems with quasi-monotone operators

1.   Introduction

The primary objective of this study is to look into the iterative methods used to solve the variational inequality problem ^[13] including quasi-monotone operators in any real Hilbert space. Consider that $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ is a mapping. Assume $\mathcal{H}$ is an arbitrary Hilbert space and $\mathcal{K}$ is a nonempty, closed, and convex subset of $\mathcal{H}.$ The variational inequality problem for mapping $\mathcal{A}$ on $\mathcal{K}$ is defined as follows:

Conditions of convergence study. The following conditions must be met in order to investigate the strong convergence of proposed algorithms.

($\mathcal{A}$1) The solution set of a problem (1.1) is denoted by $VI(\mathcal{K}, \mathcal{A})$ and nonempty it is non-empty;

($\mathcal{A}$2) $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ is said to be quasi-monotone if

($\mathcal{A}$3) $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ is said to be Lipschitz continuous with $L > 0$ such that

($\mathcal{A}$4) $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ is sequentially weakly continuous if $\{\mathcal{A}(r_{i})\}$ weakly converges to $\mathcal{A}(r)$ for each $\{r_{i}\}$ weakly converges to $r.$

The formal formulation of the variational inequality problem is an important topic in nonlinear analysis. It is a key mathematical model that advances many important ideas in modern mathematics, such as optimization conditions for problems with the optimization process, nonlinear systems of equations, complementarity problems, finance, and network equilibrium problems (see for more details ^{[12,17,18,19,20,27,30]}). As a result, this concept has a wide range of applications in mathematics, engineering, transportation studies, network economics, game theory, and computer science. The regularized approach and the projection algorithm are both useful and general solutions for dealing with variational inequalities. It should also be noted that the first algorithm is most commonly used to deal with variational inequalities that are largely determined by the monotone operator class. The regularized subproblem is strongly monotone in this approach, and its unique solution is determined to be more convenient than the primary problem. In this study, we will look into projection methods that are well-known for their simplicity of numerical calculation. Many researchers have examined not just the theory of solution existence and stability but also iterative procedures for dealing with variational inequality problems (see for more details ^{[2,7,15,44,45,46]}) and others in ^{[24,29,32,33,34,35,36,38]}.

Furthermore, projection methods are appropriate for finding a numerical solution to variational inequalities. Many researchers have created novel projection techniques to deal with various types of variational inequalities ^{[3,5,8,9,10,16,21,26,28,37,47,48,49]} and others in ^{[4,6,39,40,41,42,43]}. All algorithms for resolving the (1.1) problem are based on computing a projection on the appropriate set $\mathcal{K}.$ The corresponding extragradient method was developed by Korpelevich ^[21] and Antipin ^[1]. Their algorithm is designed as follows:

where $0 < \varkappa < \frac{1}{L}.$ In accordance with the previous algorithm, we used two projections on the underlying set $\mathcal{K}$ for each iteration. If the feasible set $\mathcal{K}$ has a complicated structure, the method's computing capabilities may be decreased. This section will go over various methods for getting around this limitation. The first is Censor et al. ^[8] subgradient extragradient algorithm. This algorithm is defined as follows:

where $0 < \varkappa < \frac{1}{L}$ with

In this study, we will focus on Tseng's extragradient algorithm ^[37], which uses only one projection each iteration. This algorithm is defined as follows:

while $0 < \varkappa < \frac{1}{L}.$ It is worth noting that the previous two algorithms have two major flaws: a fixed stepsize rule that is dependent on the Lipschitz constant of the cost operator and generates a weakly convergent iterative sequence. The Lipschitz constant of a mapping is often unknown or difficult to approximate. A fixed stepsize criterion that influences the method's efficacy and speed of convergence. Furthermore, in the case of an infinite-dimensional Hilbert space, the investigation of a strongly convergent iterative sequence is important.

The purpose of this research is to solve variational inequalities in an infinite-dimensional Hilbert space using a quasi-monotone operator. Furthermore, the proposed algorithms take into account the extension and modification of the previous results ^[11,31]. We show that Tseng's iterative sequence for solving variational inequalities with quasi-monotone operators is strongly convergent to a solution. Tseng's inertial-type extragradient approach makes use of both monotone and non-monotone variable stepsize rules. For each algorithm, we created a series of computational studies.

The following is the format of the paper: Preliminary results are provided in Section 2. All new algorithms and their convergence analysis are described in Section 3. Finally, Section 4 presents some numerical results to show the practical usefulness of the proposed algorithms.

2.   Preliminaries

This section contains various important identities as well as significant lemmas. For any $\digamma_{1}, \digamma_{2} \in \mathcal{H},$ we have

Furthermore, a set is defined as follows:

A metric projection $P_{\mathcal{K}}(e_{1})$ of $e_{1} \in \mathcal{H}$ is defined by

Lemma 2.1. ^[23] Let $\{a_{i}\} \subset [0, +\infty)$ be a sequence satisfying the following inequality

where $\{\alpha_{i}\} \subset (0, 1)$ and $\{\beta_{i}\} \subset \mathbb{R}$ are two sequences such that

Then, $\lim_{i \rightarrow +\infty} a_{i} = 0.$

Lemma 2.2. ^[25] Let $\{a_{i}\} \subset \mathbb{R}$ be a sequence with $\{i_{j}\}$ is a subsequence of $\{i\}$ such that

Then, there exists a nondecreasing sequence $m_{k} \subset \mathbb{N}$ with

such that

Eventually, $m_{k} = \max \{ j \leq k: a_{j} \leq a_{j+1} \}.$

3.   Main results

In this section, we present three new inertial methods for solving quasi-monotone variational inequalities in a real Hilbert space. We verified that the sequences generated by the proposed algorithms are strongly convergent. The following three methods are modified variants of Tseng's extragradient method ^[37]. The nature of their use of the stepsize rule differentiates these three algorithms between each other. The primary objective of this study is to extend and modify Tseng's extragradient method ^[37] and compare the numerical efficiency of the algorithms in terms of their stepsize rule.

Lemma 3.1. Let $\{\varkappa_{i} \}$ sequence is created due to (3.7) is diminishing and converges monotonically to $\varkappa > 0.$

Proof. The proof is similar to the proof of Lemma 3.1 in ^[22].

Lemma 3.1. Let $\{\varkappa_{i} \}$ is a sequence is created due to (3.14) is convergent to $\varkappa$ with

Proof. The proof is similar to the proof of Lemma 3.1 in ^[22].

Lemma 3.2. Suppose $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ satisfies the conditions ${\rm(\mathcal{A} 1)}$–${\rm(\mathcal{A} 4)}$ and sequence $\{u_{i}\}$ generated due to Algorithm 1. For any $u^{*} \in VI(\mathcal{K}, \mathcal{A})_{+},$ we have

Proof. It is given that $u^{*} \in VI(\mathcal{K}, \mathcal{A}),$ such that

It provides that $v_{i} = P_{\mathcal{K}}[w_{i}- \varkappa \mathcal{A}(w_{i})]$ and it implies that

Thus, we have

Combining expressions (3.1) and (3.3), we obtain

It is given that $u^{*}$ is the solution of the problem (1.1) implies that

It implies that

By substituting $v = v_{i} \in \mathcal{K},$ we have

From expressions (3.4) and (3.5), we obtain

Lemma 3.4. Consider that $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ satisfies the conditions ${\rm(\mathcal{A} 1)}$–${\rm(\mathcal{A} 4)}$. Let $\{u_{i}\}$ generated due to Algorithm 2. For any $u^{*} \in VI(\mathcal{K}, \mathcal{A})_{+},$ we have

Proof. Let $u^{*} \in VI(\mathcal{K}, \mathcal{A})$ and by description of $u_{i+1},$ we obtain

It is given that $v_{i} = P_{\mathcal{K}}[w_{i}- \varkappa_{i} \mathcal{A}(w_{i})]$ and indicates that

or, in certain cases, equivalently $u^{*} \in VI(\mathcal{K}, \mathcal{A}),$ we are able to write

From (3.8) and (3.10), we have

Thus, we obtain

Because the property of $\mathcal{A}$ on $\mathcal{K},$ such as

Substituting $v = v_{i} \in \mathcal{K},$ we have

Combining expressions (3.11) and (3.12), we obtain

Lemma 3.5. Consider that $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ satisfies the conditions ${\rm(\mathcal{A} 1)}$–${\rm(\mathcal{A} 4)}$. Let $\{u_{i}\}$ generated due to Algorithm 3. For each $u^{*} \in VI(\mathcal{K}, \mathcal{A}),$ we have

Proof. The proof is similar to the proof of Lemma 3.4.

Theorem 3.1. Let a mapping $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ satisfies the conditions ${\rm(\mathcal{A} 1)}$–${\rm(\mathcal{A} 4)}$. Then, the sequence $\{u_{i}\}$ generated due to Algorithm 3 converges strongly to $u^{*} = P_{VI(\mathcal{K}, \mathcal{A})}(0).$

Proof. Due to the value of $\{w_{i}\}$ such that

where

Since $\varkappa_{i} \rightarrow \varkappa$ to use a certain number $\Im \in (0, 1 - \chi^{2})$ such that

As a result, a finite number $N_{1} \in \mathbb{N}$ appears here such that

By the use of Lemma 3.4, we obtain

Due to Eqs (3.16) and (3.18), we have

As a result, we may conclude that $\{u_{i}\}$ is a bounded sequence.

Apparently, relation (3.16) gives that

for some $K_{2} > 0.$ Combining expressions (3.13) and (3.20) we have

From expression (3.15), we can write

Due to Eqs (3.18) and (3.22), we obtain

Case 1. Consider there is a definite integer $N_{2} \in \mathbb{N}$ ($N_{2} \geq N_{1}$) such that

The relation implies that $\lim_{i \rightarrow +\infty} \| u_{i} - u^{*}\|$ exists and let $\lim_{i \rightarrow +\infty} \| u_{i} - u^{*}\| = l$, for $l \geq 0.$ Hence, we have

Because of the existence of the limits $\| u_{i} - u^{*}\|$ and $\vartheta_{i} \rightarrow 0,$ we may derive that

It follows that

The preceding statement suggests that

It continues from expression (3.26) that

Following that, we evaluate

The accompanying statement indicates that

Since $\{w_{i_{k}}\}$ weakly convergent to $\hat{u}$ and thus $\lim_{k \rightarrow +\infty} \| w_{i_{k}} - v_{i_{k}}\| = 0,$ then $\{v_{i_{k}}\}$ also convergent weakly to $\hat{u}.$ Then, we must demonstrate that is $\hat{u} \in VI(\mathcal{K}, \mathcal{A}).$ From the value of $v_{i},$ we get

that is equivalent to

The above inequality implies that

Thus, we obtain

By the use of $\lim_{k \rightarrow +\infty} \|w_{i_{k}} - v_{i_{k}} \| = 0$ and $k \rightarrow +\infty$ in (3.33), we have

Furthermore, it implies that

Since $\lim_{k \rightarrow +\infty} \|w_{i_{k}} - v_{i_{k}} \| = 0.$ Thus, we have

which together with (3.35) and (3.36), we obtain

Furthermore, consider a positive sequence $\{\epsilon_{k}\}$ that would be decreasing and converging to zero. There is indeed a least positive integer represented by $m_{k}$ for each $\{\epsilon_{k}\}$ such that

Because $\{\epsilon_{k}\}$ is a diminishing sequence, it is straightforward to observe that $\{m_{k}\}$ is increasing.

Thus, we have

Due to the above definition, we have

Moreover, from expressions (3.38) and (3.40) for all $i_{m_{k}} \geq N_{0},$ we have

By the definition of quasi-monotone, we have

Due to all integer $i_{m_{k}} \geq N_{0},$ gives that

Furthermore, we might draw the conclusion that

It is given that $\{w_{i_{m_{k}}}\} \subset \{w_{i_{k}}\}$ with $\lim_{k \rightarrow +\infty} \epsilon_{k} = 0.$ It follows from this that

By letting $k \rightarrow +\infty$ in expression (3.43), we get

Consider the case when $u \in \mathcal{K}$ is an arbitrary element and $0 < \varkappa \leq 1.$ Thus, we have

Then $\hat{u}_{\varkappa} \in \mathcal{K}$ and from expression (3.46), we have

Hence, we have

Let $\varkappa \rightarrow 0.$ Then $\hat{u}_{\varkappa} \rightarrow \hat{u}$ along a line segment. By the continuity of an operator, $\mathcal{A} (\hat{u}_{\varkappa})$ converges to $\mathcal{A} (\hat{u})$ as $\varkappa \rightarrow 0.$ It follows from expression (3.49) such that

Hence $\hat{u} \in VI(\mathcal{K}, \mathcal{A}).$ It is given that $u^{*} = P_{VI(\mathcal{K}, \mathcal{A})}(0),$ we have

As a result, we obtain

By using the fact that $\lim_{i \rightarrow +\infty} \big\lVert u_{i+1} - u_{i} \big\rVert = 0$. As a result of employing the formula (3.52), we receive

We may derive from the Eqs (3.23) and (3.53), and Lemma 1 that $\big\lVert u_{i} - u^{*} \big\rVert \rightarrow 0$ as $i \rightarrow +\infty.$

Case 2. suppose the fact that somehow there arises a subsequence $\{i_{j}\}$ of $\{i\}$ in order that

A sequence exists $\{m_{k}\} \subset \mathbb{N}$ as $\{m_{k}\} \rightarrow +\infty$ by applying Lemma 2, such that

As in Case 1, the Eq (3.25) suggests that

Due to $\vartheta_{m_{k}} \rightarrow 0,$ and following step as in Case 1

Furthermore, it follows that

Following that, we must evaluate

The preceding statement suggests that

By adopting the same argument as in Case 1, in order that

Using merging the formulae (3.23) and (3.54). Thus

Consequently, we acquire

Since $\vartheta_{m_{k}} \rightarrow 0$ and $\big\lVert u_{m_{k}} - u^{*} \big\rVert$ is a bounded sequence. Thus, Eqs (3.60) and (3.62), we get

The accompanying phrase suggests

As a result, the sequence $u_{i} \rightarrow u^{*}$ is represented as $i \rightarrow +\infty.$

Remark 3.1. The convergence studies for the Algorithms 1 and 2 are analogous to the proof of Theorem 3.1.

3.1.   Methods to solve semistrictly quasi-monotone variational inequalities

In this part, we present two new inertial methods for solving quasi-monotone variational inequalities in a real Hilbert space. Let $\mathcal{H}$ be a real Hilbert space. Given $u, v \in \mathcal{H}$ and closed line segment is defined as follows:

The segments $(u, v],$ $[u, v),$ and $(u, v)$ are defined similarly. A mapping $\mathcal{A} : \mathcal{H} \rightarrow \mathcal{H}$ is said to be semistrictly quasi-monotone ^[14] on $\mathcal{K}$ if $\mathcal{A}$ is quasi-monotone on $\mathcal{K}$ and for all distinct of points $u, v \in \mathcal{K},$ we have that

The first method (Algorithm 4) is a modified variant of the two-step extragradient method ^[21] with a non-monotone stepsize rule to solve variational inequalities involving semistrictly quasi-monotone operators.

The second method (Algorithm 5) is a modified variant of the Tseng's extragradient method ^[37] with a non-monotone stepsize rule to solve variational inequalities involving semistrictly quasi-monotone operators.

4.   Numerical illustration

This section evaluates the numerical performance of the proposed algorithms to some relevant work in the literature, as well as how changes in control parameters affect the numerical validity of the proposed algorithms.

All computations are done in MATLAB R2018b and run on HP i-5 Core(TM)i3-6200 6.00 GB (5.78 GB usable) RAM laptop.

Example 4.1. Assume that a real Hilbert space $\mathcal{H} = l_{2}$ square summable sequences

Let $\mathcal{A} : \mathcal{K} \rightarrow \mathcal{K}$ be an operator is defined by

where $\mathcal{K} = \{ u \in \mathcal{H} : \|u\| \leq 3 \}.$ It is simple to demonstrate that $\mathcal{A}$ is sequentially weakly continuous on $\mathcal{H}$ with $VI(\mathcal{K}, \mathcal{A}) = \{0\}.$ Take any two elements $u, v \in \mathcal{H},$ such that

The mappings $L$ is Lipschitz continuous through a parameter value of $L = 11.$ Take any two elements $u, v \in \mathcal{H},$ and consider $\big\langle \mathcal{A} (u), v - u \big\rangle > 0,$ with

Because $\|u \| \leq 3,$ as a result of

Take this into consideration:

It demonstrates that $\mathcal{A}$ is quasi-monotone on the set $\mathcal{K}.$ The projection formula is defined by:

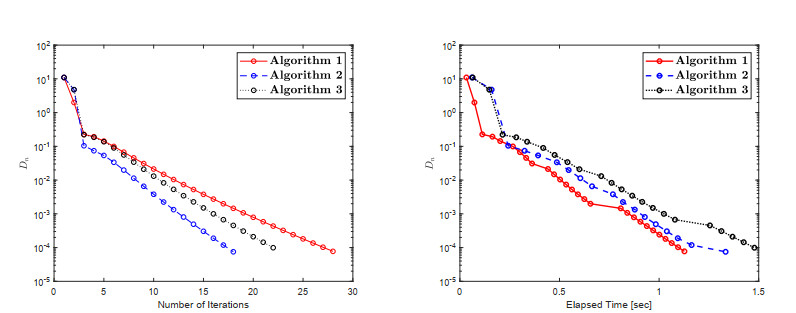
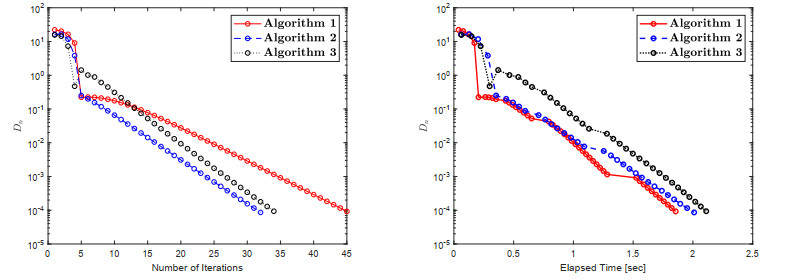
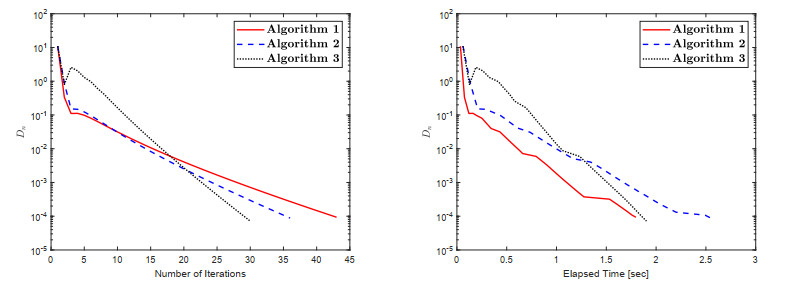
The numerical findings are shown in Table 1 and Figures 1–3. While defining the control conditions, the following factors are taken into account: ${\rm(1)}$ Algorithm 1: $\varkappa = \frac{0.5}{L}, \theta = 0.50, \epsilon_{i} = \frac{1}{(i+1)^{2}}, u_{1} = (1, 1, \cdots, 1_{50000}, 0, 0, \cdots), D_{i} = \|w_{i} - v_{i} \|;$ ${\rm(2)}$ Algorithm 2: $\varkappa_{1} = 0.55, \chi = 0.33, \theta = 0.50, u_{1} = (1, 1, \cdots, 1_{50000}, 0, 0, \cdots), \epsilon_{i} = \frac{1}{(i+1)^{2}}, D_{i} = \|w_{i} - v_{i} \|;$ ${\rm(3)}$ Algorithm 3: $\varkappa_{1} = 0.55, \chi = 0.33, \theta = 0.50,$ $\varphi_{i} = \frac{100}{(i+1)^{2}}, u_{1} = (1, 1, \cdots, 1_{50000}, 0, 0, \cdots), \epsilon_{i} = \frac{1}{(i+1)^{2}}, D_{i} = \|w_{i} - v_{i} \|.$

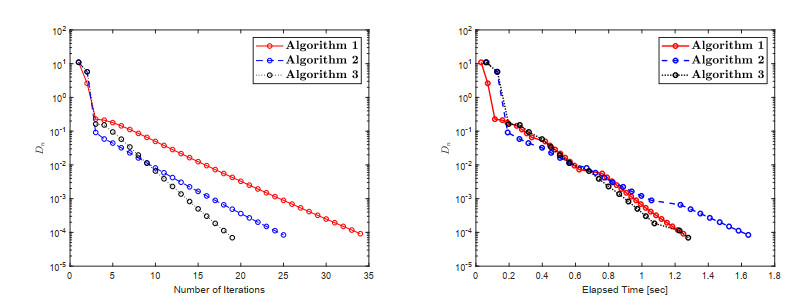
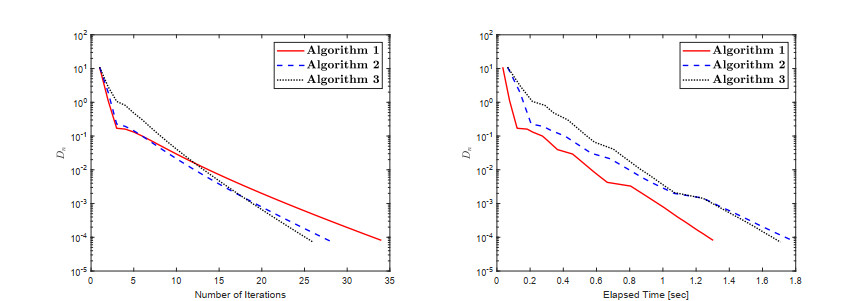
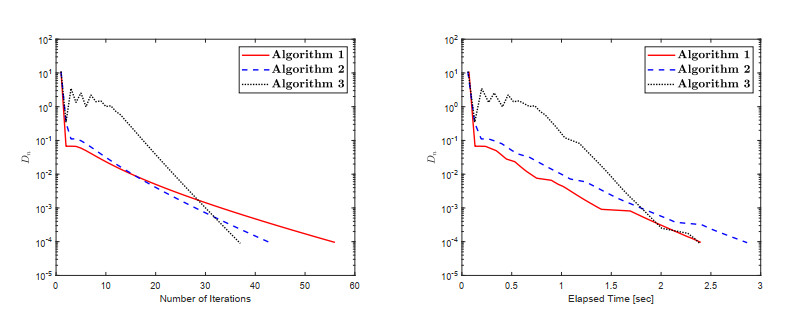
The numerical findings are shown in Table 2 and Figures 4–6. The control conditions are considered in the following way: $\rm(1)$ Algorithm 1: $\varkappa = \frac{0.7}{L}, \theta = 0.66, \epsilon_{i} = \frac{1}{(i+1)^{2}}, \vartheta_{i} = \frac{1}{(i+2)}, D_{i} = \|w_{i} - v_{i} \|;$ $\rm(2)$ Algorithm 2: $\varkappa_{1} = 0.45, \chi = 0.44, \theta = 0.66, \vartheta_{i} = \frac{1}{(i+2)}, \epsilon_{i} = \frac{1}{(i+1)^{2}}, D_{i} = \|w_{i} - v_{i} \|;$ $\rm(3)$ Algorithm 3: $\varkappa_{1} = 0.45, \chi = 0.44, \theta = 0.66, \varphi_{i} = \frac{100}{(i+1)^{2}}, \vartheta_{i} = \frac{1}{(i+2)}, \epsilon_{i} = \frac{1}{(i+1)^{2}}, D_{i} = \|w_{i} - v_{i} \|.$

5.   Conclusions

This research focused on various types of strong convergence results for variational inequalities problems involving quasi-monotone and semistrictly quasi-monotone operators in the setting of real Hilbert spaces. We modify the two forms of extragradient methods by employing an inertial scheme and two types of variable stepsize rules. The numerical results are presented to evaluate the effectiveness of the proposed algorithms in terms of their stepsize rule. These numerical experiments have shown that the variable step size has an impact on the effectiveness of the iterative sequence in this context.

Acknowledgments

The authors and would like to thank Professor Dr. Poom Kumam from King Mongkut's University of Technology Thonburi, Thailand for his advice and comments to improve the results of this paper. The first author was partially supported by Chiang Mai University and Fundamental Fund 2023, Chiang Mai University and the NSRF via the Program Management Unit for Human Resources and Institutional Development, Research and Innovation (grant number B05F640183). The third author was supported by University of Phayao and Thailand Science Research and Innovation (Grant No. FF66-UoE) and School of Science, University of Phayao (Grant no. PBTSC65007). The fourth author was financially supported by the Office of the Permanent Secretary, Ministry of Higher Education, Science, Research and Innovation (Grant No. RGNS 65-168).

Conflict of interest

All authors declare that they have no conflicts of interest.