On the theory of fractional terminal value problem with ψ-Hilfer fractional derivative

1.   Introduction

In the recent years, scientific community renders more attention on fractional differential equations, since their are effective tools in modeling many phenomena in applied sciences and engineering application such as acoustic control, rheology, polymer physics, porous media, medicine, electrochemistry, proteins, electromagnetics, economics, astrophysics, chemical engineering, signal processing, optics, chaotic dynamics, statistical physics and so on for more details, see ^[1,2,3,4]. Since boundary value problems of fractional differential equations represent an important class of applied analysis, therefore the said area was given more importance, see ^{[5,6,7,8,9,10]} and references therein.

Terminal value problems for differential equation nowadays play an essential part in the modeling of numerous phenomena in physical science, engineering, and so forth. Also, it arise naturally in the simulation of techniques that are watched at a later point, eventually after the methodology has started.

Existence theory for classical terminal value problems have been investigated by several researchers ^{[11,12,13,14,15,16,17,18,19,20,21,22]}. It is well known ^[23] that the comparison principle for initial value problems of ordinary differential equations is a very useful tool in the study of qualitative and quantitative theory. Recently, attempts have been made to study the corresponding comparison principle for terminal value problems (TVP) ^[24]. Benchohra et. al. ^[14], studied the existence results and uniqueness of solutions for a class of boundary value problems of terminal type for fractional differential equations with the Hilfer–Katugampola fractional derivative by using different types of classical fixed point theory such as the Banach contraction principle and Krasnoselskii's fixed point theorem.

Motivated by the above-mentioned works, the objective of this work is to study conditions for the existence and uniqueness of the solutions for terminal value problem for fractional differential equations of the type

where $D_{a^{+}}^{\alpha, \beta; \psi }(\cdot)$ is the $\psi$-Hilfer fractional derivative of order $\alpha \in \left(0, 1\right)$, type $\beta \in \left[0, 1\right]$ and $f:\left(a, T\right] \times \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}$ is a given function. Moreover, we study the uniqueness and continuous dependence of the $\delta$-approximate solution by generalized Gronwall inequality. To our knowledge, no papers on terminal value problem for implicit fractional differential equations exist in the literature, in particular for those involving the $\psi$-Hilfer fractional derivative.

The rest of the paper is organized as follows. In section 2, we present some necessary definitions and results which are used throughout this paper. In section 3, we study the existence and uniqueness results of $\psi$-Hilfer fractional differential equation with the terminal condition by using some fixed point theorems such as Banach and Krasnoselskii. In section 4, we study the $\delta$-approximate solution of the problem (1.1), (1.2). Also, four examples are included to illustrate the applicability of the results obtained.

2.   Preliminaries

In this section, we recall some notations, definitions of the fractional differential equation which are using throughout this paper. Let $\left[a, T \right] \subset \mathbb{R} ^{+}$ with $(0 < a < T < \infty)$, and let $C\left[a, T\right]$ be the Banach space of continuous function$\ y:\left[a, T\right] \rightarrow \mathbb{R}$ with the norm $\left\Vert y\right\Vert _{C\left[a, T\right] } = \max \{\left\vert y(t)\right\vert :a\leq t\leq T\}.$ The weighted space $C_{1-\gamma; \psi }\left[a, T\right]$ of continuous function $y$ is defined by ^[25]

Obviously, $C_{1-\gamma; \psi }\left[a, T\right]$ is a Banach space endowed with the norm

Definition 2.1. ^[26] Let $\alpha > 0,$ $y\in L_{1}\left[a, b\right]$ and $\psi \in C^{1}\left[a, b\right]$ be an increasing function with $\psi ^{\prime }(t)\neq 0,$ for all $t\in \left[a, b\right].$ Then, the left-sided $\psi$-Riemann-Liouville fractional integral of a function $y$ is defined by

where $\Gamma (\cdot)$ is the Euler gamma function defined by $\Gamma (\alpha) = \int_{0}^{\infty }s^{\alpha -1}e^{-s}ds,$ $\alpha > 0.$

Definition 2.2. ^[27] Let $n-1 < \alpha < n,$ $($ $n = \left[\alpha \right] +1),$ and $y, \psi \in C^{n}[a, b]$ be two functions with an increasing $\psi$ and $\psi ^{\prime }(t)\neq 0,$ for all $t\in \lbrack a, b].$ Then, the left-sided $\psi$-Riemann-Liouville fractional ($\psi$-Caputo) derivative of a function $y\ $of order $\alpha$ is defined by

and

respectively.

Definition 2.3. ^[25] Let $n-1 < \alpha < n,$ $($ $n\in \mathbb{N})$, and $y, \psi \in C^{n}[a, T]$ be two functions such that $\psi$ is increasing and $\psi ^{\prime }(t)\neq 0,$ for all $t\in \lbrack a, T]$. Then, the left-sided $\psi$-Hilfer fractional derivative of a function $y$ of order $\alpha$ and type $0\leq \beta \leq 1$ is defined by

In this paper we consider the case $n = 1$, because $0 < \alpha < 1.$

Lemma 2.4. ^[2] Let $\alpha > 0$ and $0\leq \gamma < 1.$ Then $I_{a^{+}}^{\alpha, \psi }$ is bounded from $C_{1-\gamma; \psi }[a, b]$ into $C_{1-\gamma; \psi }[a, b].$

Now, we introduce the following spaces

and

Lemma 2.5. ^[25] Let $\gamma = \alpha +\beta -\alpha \beta$ where $\alpha \in \left(0, 1\right),$ $\beta \in \left[0, 1\right]$, and $y\in C_{1-\gamma; \psi }^{\gamma }[a, T]$. Then

and

Lemma 2.6. ^[25] Let $\alpha > 0,$ $0\leq \gamma < 1$ and $y\in C_{1-\gamma }[a, T],$ $\beta \in \left[0, 1\right]$. Then

Lemma 2.7. ^[2] Let $t > a.$ Then for $\alpha \geq 0$ and $\gamma > 0$, we have

and

Lemma 2.8. ^[25] Let $\gamma = \alpha +\beta -\alpha \beta$ where $\alpha \in \left(0, 1\right),$ $\beta \in \left[0, 1\right]$, $y\in C_{1-\gamma; \psi }^{\gamma }[a, T]$ and $I_{a^{+}}^{1-\gamma; \psi }y\in C_{1-\gamma, \psi }^{1}[a, T]$. Then, we have

Lemma 2.9. ^[25] Let $\alpha > 0, 0\leq \gamma < \alpha$ and $y\in C_{1-\gamma, \psi }[a, T]$ $(0 < a < T < \infty)$. If $\gamma < \alpha,$ then $I_{a^{+}}^{\alpha; \psi }:C_{1-\gamma, \psi }[a, T]\rightarrow C_{1-\gamma, \psi }[a, T]$ is continuous on $[a, T]$ and satisfies

Theorem 2.10. ^[28] (Krasnoselskii fixed point theorem). Let $M$ be closed, convex, bounded and nonempty subset of a Banach space $X$ and $A, B$ be two operators such that

(1) $Au+Bv\in M$ for all $u, v\in M.$

(2) $A$ is compact and continuous.

(3) $B$ is contraction mapping.

Then there exists $z\in M$ such that $z = Az+Bz.$

Theorem 2.11. ^[29] (Banach's fixed point theorem). Let $X$ be a Banach space and $M$ be a nonempty closed subset of $X,$ then any contraction mapping $T:M\rightarrow M$ has a unique fixed point.

Lemma 2.12. ^[30] (Generalized Gronwall's Inequality Lemma) Let $\alpha > 0$ and $x, y$ be two nonnegative function locally integrable on $[a, b].$ Assume that $g$ is nonnegative and nondecreasing, and let $\psi \in C^{1}[a, b]$ be an increasing function such that $\psi ^{^{\prime }}(t)\neq 0$ for all $t\in \lbrack a, b]$. If

then

If $y$ be a nondecreasing function on $[a, b]$, then

where $E_{\alpha }(\cdot)$ is the Mittag-Leffler function defined by

3.   Existence of solutions

Theorem 3.1. Let $\gamma = \alpha +\beta -\alpha \beta,$ where $\alpha \in \left(0, 1\right)$ and $\beta \in \left[0, 1\right].$ If $\ f:\left(a, T \right] \rightarrow ~ \mathbb{R}~$ is a function such that $f(\cdot)\in C_{1-\gamma, \psi }\left[a, T\right],$ then $y\in C_{1-\gamma, \psi }^{\gamma }\left(a, T\right]$ satisfies the following problem

if and only if $y$ satisfies the following integral equation

Proof. First, let $y\in C_{1-\gamma, \psi }^{\gamma }\left(a, T\right]$ be a solution of the problem (3.1), (3.2). We prove that $y$ is also a solution of Eq (3.3). From the definition of $C_{1-\gamma, \psi }^{\gamma }\left(a, T\right]$, Lemma 2.4, and using the definition 2.3, we have

By the definition of the space $C_{1-\gamma, \psi }^{n}\left[a, T\right],$ it follows that

Using Lemma 2.8, with $\alpha = \gamma,$ we obtain

Since $y\in C_{1-\gamma, \psi }^{\gamma }\left[a, T\right]$, and using Lemma 2.5 with Eq (3.1), we have

Comparing Eqs (3.5) and (3.6), we see that

Using Eq (3.2), we get

Hence $y(t)$ satisfies the problem (3.1), (3.2).

Conversely, Let $y\in C_{1-\gamma, \psi }^{\gamma }\left[a, T\right]$ be a function satisfying Eq (3.3). We prove that $y$ is also a solution of the problem (3.1), (3.2). Apply the operator $D_{a^{+}}^{\gamma; \psi }$ on both sides of Eq (3.3). Then, from Lemmas 2.7 and 2.5, we have

From Eq (3.4), we have $D_{a^{+}}^{\gamma; \psi }y\in C_{1-\gamma; \psi } \left[a, T\right],$ and hence, Eq (3.8) implies

As $f(t)\in C_{1-\gamma; \psi }\left[a, T\right],$ and from Lemma 2.4, it follows that

From Eqs (3.9) and (3.10) and the definition of the space $C_{1-\gamma; \psi }^{n}\left(a, T\right],$ we get

Now, by applying operator $I_{a^{+}}^{\beta (1-\alpha); \psi }$ on both sides of Eq (3.9) and using Lemmas 2.9, 2.8, we have

From Eq (2.1), the Eq (3.11) reduces to

that is, Eq (3.1) holds.

Before given our main results, the following conditions must be satisfied

$\mathbf{H}_{1}$ $f:\left(a, T\right] \times \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}$ is continuous function such that $f(\cdot, x(\cdot), y(\cdot))\in C_{1-\gamma; \psi }^{\beta (1-\alpha)}$ for all $x, y\in C_{1-\gamma; \psi } \left[a, T\right].$

$\mathbf{H}_{2}$ There exist two constants $L > 0$ and $M\in \left(0, 1\right)$ such that

for all $x_{1}, y_{1}, x_{2}, y_{2}\in \mathbb{R}$ and $t\in \left(a, T\right].$

In the forthcoming theorem, by using the Banach fixed point theorem, we prove the unique solution of the problem (1.1), (1.2)

Theorem 3.2. Assume that (H$_{1}$) and (H$_{2}$) hold. If

then the problem (1.1), (1.2) has a unique solution in $C_{1-\gamma; \psi }^{\gamma }\left[a, T\right] \subset C_{1-\gamma; \psi }^{\alpha, \beta }\left[a, T\right].$

Proof. In view of Theorem 3.1, the solution of the problem (1.1), (1.2) is given by

where $K_{y}(t) = f(t, y(t), K_{y}(t)).$ Consider the operator $\mathcal{F} :C_{1-\gamma; \psi }\left[a, T\right] \rightarrow C_{1-\gamma; \psi }\left[a, T\right]$ defined by

by Lemma 2.4, we deduce that $\mathcal{F}y\in C_{1-\gamma; \psi }\left[a, T\right].$ The proof will be given in two steps

Step(1): We show that the operator $\mathcal{F}$ has a unique fixed point $\widehat{y}$ in $C_{1-\gamma; \psi }\left[a, T\right].$ Let $y, y^{\ast }\in C_{1-\gamma; \psi }\left[a, T\right]$ and $t\in \left(a, T \right].$ Then, we have

where $K_{y}(s), K_{y^{\ast }}(s)\in C_{1-\gamma; \psi }\left[a, T\right]$ such that

By (H$_{2}$), we have

which implies

Then for any $t\in \left(a, T\right],$ we have

In view of Lemma 2.7, we obtain

Hence

which implies that

Due to Eq (3.12), we deduce that the operator $\mathcal{F}$ is a contraction mapping. According to Banach's contraction principle, we conclude that $\mathcal{F}$ has a unique fixed point $\widehat{y}\in C_{1-\gamma; \psi }\left[a, T\right]$.

Step(2): We show that such a fixed point $\widehat{y}\in C_{1-\gamma; \psi }\left[a, T\right]$ is actually in $C_{1-\gamma; \psi }^{\gamma }\left(a, T\right].$ Since $\widehat{y}$ is the unique fixed point of $\mathcal{F}$ in $C_{1-\gamma; \psi }\left[a, T\right],$ then, for each $t\in \left(a, T\right],$ we have

Multiplying both sides of the last equation by $D_{a^{+}}^{\gamma, \psi },$ using Lemmas 2.7 and 2.5, we have

Since $\gamma \geq \alpha,$ by (H$_{1}$), we have $D_{a^{+}}^{\beta (1-\alpha); \psi }K_{\widehat{y}}(t)\in C_{1-\gamma; \psi }\left[a, T\right],$ and hence $D_{a^{+}}^{\gamma, \psi }\widehat{y}\in C_{1-\gamma; \psi } \left[a, T\right].$ It follows from definition of $C_{1-\gamma; \psi }^{\gamma }\left[a, T\right]$ that $\widehat{y}\in C_{1-\gamma; \psi }^{\gamma }\left[a, T\right].$ As a consequence of the above steps, we conclude that the problem (1.1), (1.2) has a unique solution in $C_{1-\gamma; \psi }^{\gamma }\left[a, T\right].$

We present now the second result, which is based on Krasnoselskii fixed point theorem.

Theorem 3.3. Assume that (H$_{1}$) and (H$_{2}$) hold. Then the problem (1.1), (1.2) has at least one solution in $C_{1-\gamma; \psi }^{\gamma } \left[a, T\right].$

Proof. Defined the closed, bounded, convex and nonempty set

with

Set $N = \sup_{t\in \left(a, T\right] }\left\vert f(t, 0, 0)\right\vert.$ We split the operator $\mathcal{F}$ which defined by Eq (3.14) into two operators $\mathcal{F}_{1}, \mathcal{F}_{2}$ in $\mathcal{\Bbbk }_{\xi }$ as following

and

Note that $\mathcal{F}y(t)\mathcal{ = F}_{1}y(t)+\mathcal{F}_{2}y(t).$ The proof will be divided into several steps as follows:

Step(1):We show that $\mathcal{F}_{1}y(t)+\mathcal{F}_{2}v(t)\in \mathcal{\Bbbk }_{\xi }$ for any $y, v\in \mathcal{\Bbbk }_{\xi }.$

(ⅰ) For $t\in \left(a, T\right] \ $and $y\in \mathcal{\Bbbk }_{\xi }$, we have

From (H$_{2}$), we have

Multiplying both sides of the last inequality by $\left(\psi (t)-\psi (a)\right) ^{1-\gamma }$, we get

Then, for each $t\in \left(a, T\right],$ we have

Thus, the Eq (3.16) and Lemma 2.7, imply that

(ⅱ) In a similar manner, for $t\in \left(a, T\right],$ $v\in \mathcal{ \Bbbk }_{\xi }$, we get

Linking Eqs (3.17) and (3.18), for any $y, v\in \mathcal{\Bbbk }_{\xi },$ we obtain

which implies that $\mathcal{F}_{1}y(t)+\mathcal{F}_{2}v(t)\in \mathcal{ \Bbbk }_{\xi }.$

Step(2): We show that $\mathcal{F}_{1}$ is a contraction mapping$.$ From Theorem 3.2, we have already proved that $\mathcal{F}$ is a contraction mapping and hence $\mathcal{F}_{1}$ is a contraction mapping too in $\mathcal{\Bbbk }_{\xi }$.

Step(3): We show that $\mathcal{F}_{2}$ is a compact and continuous in $\mathcal{\Bbbk }_{\xi }$.

The continuity of $\mathcal{F}_{2}$ follows from the continuity of $f$. Now, we need only to prove that $\mathcal{F}_{2}$ is compact (i.e $\mathcal{F} _{2}$ uniformly bounded and equicontinuous). From Eq (3.18), for any $v\in \mathcal{\Bbbk }_{\xi },$ we have

This means that $\mathcal{F}_{2}$ is uniformly bounded in $\mathcal{\Bbbk } _{\xi }.$ Next, we show that $\mathcal{F}_{2}$ is equicontinuous in $\mathcal{\Bbbk }_{\xi }$. Let $y\in \mathcal{\Bbbk }_{\xi }$ and $t_{1}, t_{2}\in \left(a, T\right]$ such that $t_{1} < t_{2}.$ Then, we have$\ \ $

This means that $\mathcal{F}_{2}$ is equicontinuous in $\mathcal{\Bbbk } _{\xi }.$ Hence $\mathcal{F}_{2}$ is relatively compact on $\mathcal{\Bbbk } _{\xi }.$ By Arzelá-Ascoli Theorem, we deduce that $\mathcal{F}_{2}$ is compact on $\mathcal{\Bbbk }_{\xi }.$ According to Theorem (2.10), we conclude that $\mathcal{F}$ has at least a fixed

point $\widehat{y}\in C_{1-\gamma; \psi }\left[a, T\right]$ and by the same way of the proof of Theorem 3.2, we can easily show that $\widehat{y} \in C_{1-\gamma; \psi }^{\gamma }\left[a, T\right].$ Thus the problem (1.1), (1.2) has at least one solution in $C_{1-\gamma; \psi }^{\gamma } \left[a, T\right]$.

4.   $\delta$-Approximat solution

Definition 4.1 A function $y\in C_{1-\gamma, \psi }^{\gamma }\left[a, T \right]$ satisfying the $\psi$-Hilfer implicit fractional differential inequality

and

is called $\delta$-approximate solutions of $\psi$-Hilfer implicit fractional differential (1.1), (1.2)

Theorem 4.2. Let $f:\left(a, T\right] \times \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}$ be a continuous function satisfies the condition (H$_{2}$) for each $t\in J$ and. Let $z_{i}\in C_{1-\gamma, \psi }^{\gamma }\left(a, T\right],$ $i = 1, 2,$ be a $\delta$-approximation solutions of the following $\psi$ -Hilfer implicit fractional differential equation

Then

where

Proof. Let $z_{i}\in C_{1-\gamma, \psi }^{\gamma }\left(a, T\right],$ $i = 1, 2,$ be an $\delta$-approximation solutions of the problem (4.2). Then, we have

and

Applying $I_{a^{+}}^{\alpha, \psi }$ on both sides of the above inequality, and using lemma 2.8, we get

Using the fact $\left\vert x\right\vert -\left\vert y\right\vert \leq \left\vert x-y\right\vert \leq \left\vert x\right\vert +\left\vert y\right\vert$ in the above inequality, we have

In consequence, we have

where

Using Lemma 2.12, we obtain

Hence for each $t\in \left[a, b\right],$ we have

Thus

Remark 4.3 If $\delta _{1} = \delta _{2} = 0$ in the inequality (4.3), then $z_{1}, z_{2}$ are solutions of the problem (1.1) and the inequality (4.4) reduces to

which provides the continuous dependence of the problem (1.1). Also if $w_{1}^{\ast } = w_{2}^{\ast },$ we have $\left\Vert z_{1}-z_{2}\right\Vert _{C_{1-\gamma, \psi }} = 0,$ which provides the uniqueness of a solution of problem (1.1).

5.   Examples

In this section, we present illustrative examples to validate our results.

Example 5.1. Consider the following terminal value problem

Set $f(t, u, v) = \frac{t}{10}\left(1+u+v\right),$ for each $u, v\in \mathbb{R}$, $t\in \left(1, 2\right],$

with $\alpha = \frac{1}{2}, \beta = 0, \gamma = \frac{1}{2}, \psi (t) = e^{t},$ $\left(a, T\right] = \left(1, 2\right],$ $K_{y}(t) = f(t, y(t), K_{y}(t)).$ Clearly, the function $f\in C_{\frac{1}{2};e^{t}}\left[1, 2\right]$. Hence condition ($H_{1}$) is satisfied. For $u, v, u^{\ast }, v^{\ast }\in \mathbb{R}$, $t\in \left(1, 2\right],$ we have

Hence the hypothesis ($H_{2}$) is satisfied with $M = L = \frac{1}{10e}.$ By some simple calculations, the condition:

is satisfied with $T = 2$ and $a = 1$. Thus all assumptions in Theorem 3.2 are satisfied. It follows from Theorem 3.2 that the problem (5.1) has a unique solution in $C_{\frac{1}{3};e^{t}}^{\frac{1}{2}}[1,2].$

Example 5.2 Consider the following terminal value problem

Set $f(t, u, v) = \frac{1}{20e^{e+1-t}}\left(\ln t^{\frac{1}{2}}\cos u+v\right),$ for each $u, v\in \mathbb{R}$, $t\in \left(1, e\right],$

with $\alpha = \frac{1}{2}, \beta = 0, \gamma = \frac{1}{2}, \psi (t) = \ln t,$ $\left(a, T\right] = \left(1, e\right].$ Clearly, the function $f\in C_{\frac{ 1}{2};\ln t}\left[1, e\right]$. Hence condition ($H_{1}$) is satisfied. For $u, v, u^{\ast }, v^{\ast }\in \mathbb{R}$, $t\in \left(1, e\right],$ we have

Hence the hypothesis ($H_{2}$) is satisfied with $M = L = \frac{1}{20e}.$ By some simple calculations, the condition:

is satisfied with with $T = e$ and $a = 1$. Thus all assumptions in Theorem 3.2 are satisfied. It follows from Theorem 3.2 that the problem (5.2) has a unique solution in $C_{\frac{1}{2};\ln t}^{\frac{1}{2}}\left[1, e\right].$

Example 5.3 Consider the following terminal value problem

Set $f(t, u, v) = \frac{1}{10}\left(t^{2}\cos u+v\right),$ for each $u, v\in \mathbb{R}$, $t\in \left(1, 2\right],$

with $\alpha = \frac{1}{2}, \beta = 0, \gamma = \frac{1}{2}, \psi (t) = t^{\rho }$ $(\rho = \frac{1}{2}),$ $\left(a, T\right] = \left(1, 2\right].$ Clearly, the function $f\in C_{\frac{1}{2};t^{\rho }}\left[1, 2\right]$. Hence condition ($H_{1}$) is satisfied. For $u, v, u^{\ast }, v^{\ast }\in \mathbb{R}$, $t\in \left(1, 2\right],$ we have

Hence the hypothesis ($H_{2}$) is satisfied with $M = L = \frac{1}{10}.$ By some simple calculations, the condition:

is satisfied with $\rho = \frac{1}{2}$ $T = 2$ and $a = 1$. Thus all assumptions in Theorem 3.2 are satisfied. It follows from Theorem 3.2 that the problem (5.3) has a unique solution in $C_{\frac{1}{2};t^{\rho }}^{ \frac{1}{2}}\left[1, 2\right].$

Example 5.4 Consider the following terminal value problem

By Theorem 3.1, the implicit solution of problem (5.4) is given by

Here, we consider $K_{y}(t) = f(t, y(t), K_{y}(t)) = 1,$ $w = 1,$ $a = 1\ $and $T = 2$.

Case (ⅰ) If $\psi (t) = t,$ the exact solution of problem (5.4) is defined by

Case (ⅱ) If $\psi (t) = \log t,$ the exact solution of problem (5.4) is defined by

Case (ⅲ) If $\psi (t) = t^{\rho },$ $\rho > 0,$ the exact solution of problem (5.4) is defined by

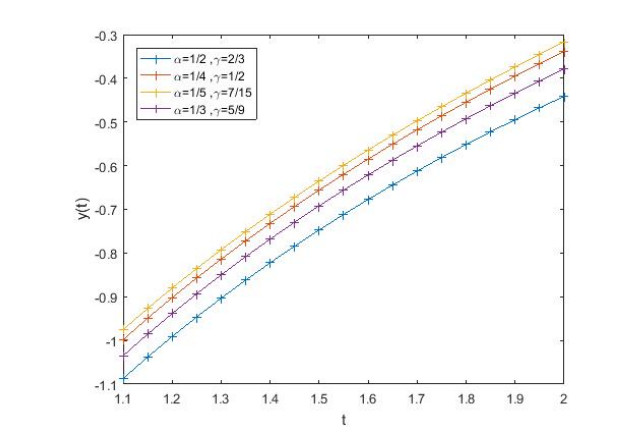
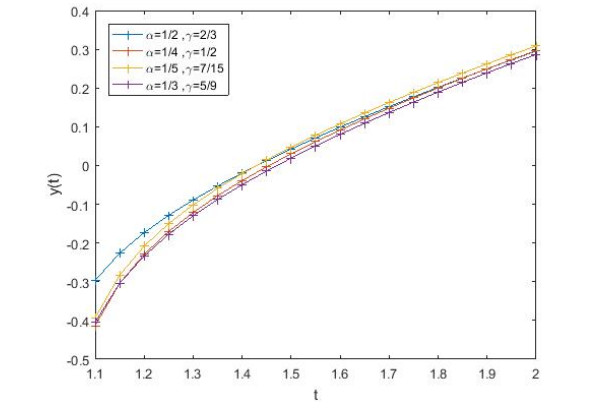
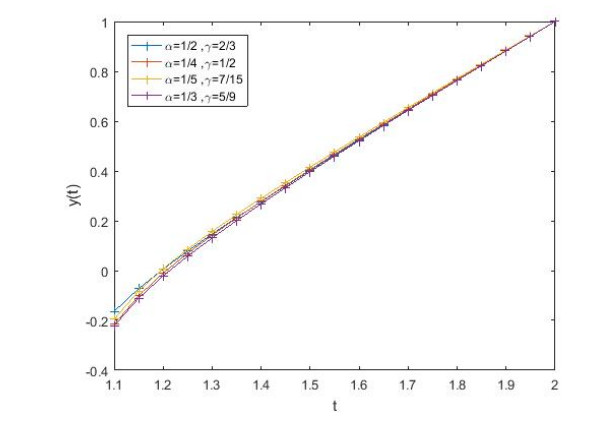
Figure 1, presents the solution curves with some values of $\alpha$ and $\gamma$, when $\psi (t) = t.$ Figure 2, presents the solution curves with some values of $\alpha$ and $\gamma$, when $\psi (t) = log(t).$ Figure 3, presents the solution curves with some values of $\alpha$ and $\gamma$, when $\psi (t) = t^{\rho}.$

6.   Conclusions

We have provided sufficient conditions ensuring the existence and uniqueness of solutions to a class of terminal value problem for differential equations with the $\psi$-Hilfer type fractional derivative. The arguments are based on the classical Banach contraction principle, and the Krasnoselskii's fixed point theorem. Moreover, we used generalized Gronwall inequality with singularity to established uniqueness and continuous dependence of the $\delta$-approximate solution. Four examples are included to show the applicability of our results.

Conflict of interest

All authors declare no conflicts of interest.