Biochar in cementitious material—A review on physical, chemical, mechanical, and durability properties

Abbreviations: ${\lambda }_{e}, {\mu }_{e}$: Lame elastic constants; $\rho$: Density; ${C}_{E}$: Specific heat at constant strain; $K$: Thermal conductivity; ${\alpha }_{t}$: Coefficient of linear thermal expansion; ${\gamma }_{e}$: $\left(3{\lambda }_{e}+2{\mu }_{e}\right){\alpha }_{t}$; ${\gamma }_{o}$: $\left(3{\lambda }_{e}{\alpha }_{o}+2{\mu }_{e}{\alpha }_{1}\right){\alpha }_{t}/{\gamma }_{e}$; ${\alpha }_{o}, {\alpha }_{1}$: Viscoelastic relaxation time; $t$: Time; ${q}_{i}$: Components of heat flux vector; ${\sigma }_{ij}$: Components of stress tensor; ${e}_{ij}$: Components of strain tensor; ${u}_{i}$: Components of displacement vector; ${T}_{o}$: Reference temperature; $\theta$: Temperature increment; ${\delta }_{ij}$: Kronicker delta; $e$: Cubical dilatation; $R$: Radius of the shell; ${\mu }_{o}$: Magnetic permittivity; $E$: Electric displacement vector; $J$: Current density vector; $H$: Total magnetic intensity vector; $h$: Induced magnetic field vector; ${H}_{o}$: Initial uniform magnetic field; ${F}_{i}$: Components of Lorentz body force; ${\pi }_{o}$: Coefficient connecting the current density with the heat flow density; ${k}_{o}$: Coefficient connecting the temperature gradient and electric current density

1.   Introduction

The traditional uncoupled hypothesis of thermo elasticity predicts two marvels not good with physical perceptions. In the first place, the condition of heat conduction of this hypothesis doesn't contain any elastic terms; second, the heat condition is of an parabolic kind, anticipating unending paces of spread for heat waves.

Biot ^[1] presented the hypothesis of coupled thermo elasticity to conquer the principal weakness. The overseeing conditions for this hypothesis are coupled, dispensing with the main oddity of the old style hypothesis. In any case, the two hypotheses share the second inadequacy since the heat equation for the coupled hypothesis is likewise parabolic.

Two generalizations to the coupled hypothesis were presented. The first is because of Lord and Shulman ^[2], who acquired a wave-type heat equation by proposing another law of heat equation to supplant the old style Fourier's law. Since the heat equation of this hypothesis is of the wave type, it consequently guarantees limited velocities of spread for heat and elastic waves. The staying administering equations for this hypothesis, to be specific, the equations of motion and constitutive relations, continue as before as those for the coupled and the uncoupled speculations. The second speculation to the coupled hypothesis of elasticity is what is known as the hypothesis of thermo elasticity with two relaxation times or the hypothesis of temperature-rate-dependent thermo elasticity. Müller ^[3], in a survey of the thermodynamics of thermo elasticity solids, proposed an entropy creation imbalance, with the assistance of which he thought about limitations on a class of constitutive equations. A generalization of this imbalance was proposed by Green and Laws ^[4]. Green and Lindsay got an express form of the constitutive equations in ^[5]. These equations were additionally gotten autonomously by Shuhubi ^[6] has acquired the fundamental solution for this hypothesis. This hypothesis contains two constants that go about as relaxation times and alter all the equation of the coupled hypothesis, not just the heat equation. The old style Fourier's law of heat equation isn't disregarded if the medium viable has a focal point of balance.

Later Green and Naghdi ^[7,8,9] proposed three hypotheses of generalized thermo elasticity. The primary model (G-N Ⅰ) is actually equivalent to Biot's hypothesis ^[1]. The second and third models are named as G-N Ⅱ and G-N Ⅲ model. In G-N Ⅱ and G-N Ⅲ models, the thermal wave engenders with limited rates which concur with physical circumstances. A significant component of G-N Ⅱ hypothesis is that this hypothesis doesn't suits dissipation of thermal energy though G-N Ⅲ hypothesis obliges dissemination of dissipation of thermal energy.

With the quick advancement of polymer science and plastic industry, just as the wide utilization of materials under high temperature in present day innovation and use of science and topography in designing, the hypothetical examination and applications in viscoelastic material has become a significant errand for strong mechanics.

The hypothesis of thermo-viscoelasticity and the solutions of some boundary value problems of thermo-viscoelasticity were researched by Illyushin's and Pobedria ^[10]. Crafted by Biot ^[11,12], Morland and Lee ^[13] and Tanner ^[14] mate extraordinary walks in the most recent decade in discovering answers for limit esteem issues for linear viscoelasticity materials including temperature varieties for both semi static and dynamic issues. Drozdov ^[15] inferred a constitutive model in thermo-viscoelasticity which represents changes in elastic moduli and relaxation times. Tasteless ^[16] connected the arrangement of linear viscoelasticity issues to comparing linear elastic solutions. Lion ^[17] studied the large deformation behavior of reinforced rubber at different temperatures. Thermo-viscoelastic experimental characterization and numerical modelling of VHB polymer were induced by Liao et al. ^[18].

The hypothesis of electro-magneto-thermo-viscoelasticity has stimulated a lot of enthusiasm for some mechanical applications especially in atomic gadget. Where there exists an essential magnetic field. Different examinations have been completed by thinking about the connection between attractive, magnetic, thermal and strain fields. Examinations of such issue additionally impact different applications in biomedical building just as in various geometric investigations. Fish et al. ^[19] has studied modeling and simulation of nonlinear electro-thermo-mechanical continua with application to shape memory polymeric medical devices.

Numerous applications of state space approach created for various sort of issues in electro-magneto-thermo-viscoelasticity ^{[20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]}.

2.   Basic governing equation

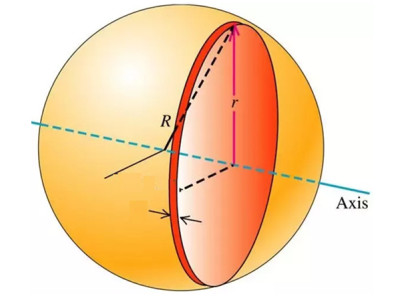
We shall consider a homogeneous isotropic thermo-viscoelastic medium occupying the region $R\ll r < \infty$ of a perfect electrically conductivity permeated by an initial constant magnetic field ${H}_{o}$, where $R$ is the radius of the shell.

Due to the effect of this magnetic field there arises in the conducting medium an induced magnetic field $h$ and induced electric field $E$. Also, there arises a force $F$ (the Lorentz Force). Due to the effect of this force, points of the medium undergo a displacement$u$, which gives rise to a temperature.

The linearized equations of electromagnetism for slowly moving media are:

The above field equations are supplemented by constitutive equations which consist first of modified ohm's law:

The second constitutive equation is the one for the Lorenz force which is

The third constitutive equation is the stress-displacement-temperature relation for viscoelastic medium of Kelvin–Voigt type:

The equation of motion is given by:

The generalized heat conduction equation is given by

The strain displacement relation is given by

Together with the previous equations, constitute a complete system of generalized-magneto-thermo-viscoelasticity equations for a medium with a perfect conductivity.

Let $\left(r, \psi, \varphi \right)$ denote the radial coordinates, the co-latitude, and the longitude of a spherical coordinates system, respectively. Due to spherical symmetry, all the considered function will be functions of $r$ and $t$ only.

The components of the displacement vector will be taken the form:

The strain tensor components are thus given by

From Eq 7 we obtain the components of the stress tensor as

Assume now that the initial magnetic field acts in the $\varphi$-direction and has the components$\left(0, 0, { H}_{o}\right)$. The induced magnetic field h will have one component h in the $\varphi$-direction, while the induced electric field E will have one component E in the $\psi$-direction.

Then, Eqs 1, 2 and 5 yield

From Eqs 17 and 6, we get that the Lorentz force has only one component ${F}_{r}$ in the $r$-direction:

Also, we arrived at

Equation 21 is to be supplemented by the constitutive Eq 13 and the heat conduction equation

Where ${\nabla }^{2}$ is Laplaces operator in spherical coordinates which is given by

In case of dependence on r only, this reduce to

Now, we shall use the following non dimensional variables:

Equations 14–19, 21 and 22 take the following form (dropping the primes for convenience).

Where, $\eta = \frac{\rho {C}_{E}}{K}, {C}_{1}^{2} = \frac{{\lambda }_{e}+2{\mu }_{e}}{\rho }$, $A = \frac{{k}_{o}}{{\mu }_{o}{H}_{o}}$.

Equation 32 can be written in the form:

3.   Laplace transform domain

Taking the Laplace transform of Eqs 26–31, 33 and 34 by using homogeneous initial conditions, defined and denoted as

We obtain

where

${L}_{1} = \frac{K\eta {C}_{1}^{2}{s}^{2}}{K+A+{K}^{*}\eta {C}_{1}^{2}{s}^{2}}, {l}_{2} = \frac{{\gamma }_{e}{C}_{1}^{2}\left(1+{\gamma }_{o}s\right){s}^{2}}{K+A+{K}^{*}\eta {C}_{1}^{2}{s}^{2}}, {a}_{1} = \frac{2{\mu }_{e}}{{\lambda }_{e}+2{\mu }_{e}}\left(1+A+{\alpha }_{1}s\right)$, ${a}_{2} = \frac{{\lambda }_{e}}{{\lambda }_{e}+2{\mu }_{e}}\left(1+A+{\alpha }_{o}s\right)$,

${a}_{3} = \frac{{\gamma }_{e}{\theta }_{o}}{{\lambda }_{e}+2{\mu }_{e}}\left(1+A+{\gamma }_{o}s\right), {M}_{1} = \frac{{\gamma }_{e}{\theta }_{o}\left(1+A+{\gamma }_{o}s\right){L}_{1}}{{\mu }_{o}{H}_{o}^{2}\rho {C}_{1}^{2}+\rho {C}_{1}^{2}+\left({\lambda }_{e}{\alpha }_{o}+2{\mu }_{e}{\alpha }_{1}\right)s}$, ${M}_{1} = \frac{\rho {C}_{1}^{2}{s}^{2}+{\gamma }_{e}{\theta }_{o}\left(1+A+{\gamma }_{o}s\right){L}_{2}}{{\mu }_{o}{H}_{o}^{2}\rho {C}_{1}^{2}+\rho {C}_{1}^{2}+\left({\lambda }_{e}{\alpha }_{o}+2{\mu }_{e}{\alpha }_{1}\right)s}$.

4.   State space formulation

Choosing as state variables the temperature of heat conduction $\stackrel{-}{\theta }$and the strain components $\stackrel{-}{e}$ then Eqs 35 and 38 can be written in the matrix form

where $\stackrel{-}{V}\left(r, s\right) = \left[\begin{array}{c}\stackrel{-}{\theta }\left(r, s\right)\\ \stackrel{-}{e}\left(r, s\right)\end{array}\right], A\left(s\right) = \left[\begin{array}{cc}{L}_{1}& {L}_{2}\\ {M}_{1}& {M}_{2}\end{array}\right]$.

The formal solution of Eq 43 can be written in the form

For bounded solution with large $r$, we have canceled the exponential part has positive power. And at $r = R$ the value of $C$ is given by $C = R\stackrel{-}{V}\left(R, s\right){e}^{\sqrt{A\left(s\right)}R}$, then Eq 44 reduces to

We will use the will-known Cayley–Hamiltonian theorem to find the form of the matrix $exp\left(-\sqrt{A\left(s\right)}\left(r-R\right)\right)$. The characteristic equation of the matrix $A\left(s\right)$ can be written as

The roots of this equation namely ${k}_{1}$ and ${k}_{2}$ satisfy the relations

The Tailor's series expansion for the matrix exponential of $exp\left(-\sqrt{A\left(s\right)}\left(r-R\right)\right)$ is given by

Using Cayley–Hamiltonian theorem, we can express ${A}^{2}$ and higher orders of the matrix $A$ in terms of $I$ and $A$ where $I$ is the unit matrix of second order.

Thus, the infinite series in Eq 49 can be reduced to

where ${b}_{o}$ and ${b}_{1}$ are some coefficients depending on $s$ and $r$.

By Cayley–Hamiltonian theorem, the characteristic roots ${k}_{1}$ and ${k}_{2}$ of the matrix $A$ must satisfy Eq 50, thus we have

Solving the above linear system of equations, we get

Hence, we have

where

5.   Applications

In order to evaluate the unknown parameters${\stackrel{-}{\theta }}_{o}\left(r, s\right)$and${\stackrel{-}{e}}_{o}\left(r, s\right)$, we shall use the boundary conditions on the internal surface of the shell, $r = R$ which are given by:

(Ⅰ) Thermal boundary condition at $\mathrm{r} = \mathrm{R}$, $\mathrm{\theta }\left(\mathrm{R}, \mathrm{t}\right) = {\mathrm{\theta }}_{\mathrm{o}}$

Taking the Laplace transform, this is defined as following:

(Ⅱ) Mechanical boundary condition

The internal surface $r = R$ has a rigid foundation, which is rigid enough to prevent any strain $e\left(R, t\right) = 0$. Taking the Laplace transform, this is defined as following:

Using the Eq 60 and 61 into Eq 45 and using Eqs 56–59, we get

To find the displacement, taking Laplace transform for Eq 32 using Eqs 62 and 63, we get

To find the radial stress, from Eq 40 and Eqs 62–64 we get

where ${B}_{4} = \frac{1}{{s}^{2}}+\frac{{\lambda }_{e}{\alpha }_{o}+2{\mu }_{e}{\alpha }_{1}}{\rho {C}_{1}^{2}{s}^{2}}$, ${B}_{5} = \frac{{\gamma }_{e}{\theta }_{o}\left(1+{\gamma }_{o}s\right)}{\rho {C}_{1}^{2}{s}^{2}}$.

6.   Numerical inversion of Laplace transforms

In order to invert the Laplace transforms in the above equations we shall use a numerical technique based on Fourier expansions of functions. Let $\stackrel{-}{g}\left(s\right)$ be the Laplace transform of a given function $g\left(t\right)$. The inversion formula of Laplace transforms states that

where d is an arbitrary positive constant greater than all the real parts of the singularities of $\stackrel{-}{g}\left(s\right)$. Taking s$= d+iy$, we get

This integral can be approximated by

Taking $∆y = \frac{\pi }{{t}_{1}}$we obtain:

For numerical purposes this is approximated by the function

where $N$ is a sufficiently large integer chosen such that

where $\eta$ is a reselected small positive number that corresponds to the degree of accuracy to be achieved Eq 69 is the numerical inversion formula valid for$0\le t\le {t}_{1}$. In particular, we choose$t = {t}_{1}$, getting

7.   Numerical results and discussions

The copper material was chosen for purposes of numerical evaluations and constants of the problem were taken as following (35) in SI units: $K = 386N/Ks, {\alpha }_{t} = 17.8{\left(10\right)}^{-5}{K}^{-1}, {C}_{E} = 383.1{m}^{2}/K, {T}_{o} = 293K, \rho = 8954kg/{m}^{2}$, ${\mu }_{e} = 3.86{\left(10\right)}^{10}N/{m}^{2}, {\lambda }_{e} = \mathrm{7, 76}{\left(10\right)}^{10}N/{m}^{2}, {\alpha }_{1} = 3.25{\left(10\right)}^{-2}, {\alpha }_{o} = 3.25{\left(10\right)}^{-2}$, $R = 1, {\theta }_{o} = 1$.

In order to study the effect of time t and study the comparison between two models on temperature, radial stress, shear stress, displacement and strain, we now present our results in the form of graphs (Figures 2–9).

Green and Naghdi ^[7,8,9] proposed three new thermoelastic theories based on entropy equality rather than the usual entropy inequality. The constitutive assumptions for the heat flux vector are different in each theory. Thus, they obtained three theories they called thermoelasticity of type Ⅰ, thermoelasticity of type Ⅱ and thermoelasticity of type Ⅲ. When the type Ⅰ theory is linearized we obtain the classical system of thermo-elasticity. The type Ⅱ theory (is a limiting case of type Ⅲ) does not admit energy dissipation.

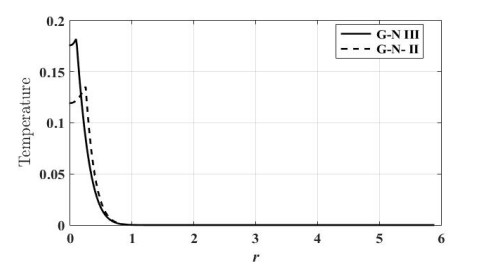
Figure 2 is plotted to show the variation of temperature $\theta$ against $r$for wide range of $r$ $\left(1\le r\le 3\right)$ at small time$\left(t = 0.07\right)$ for two theories (G-N Ⅲ) and (G-N Ⅱ). It is observed from this figure the magnitude of the temperature is greater for (G-N Ⅲ) model than (G-N Ⅱ). It can be noted that the speed of propagation of temperature is finite and coincide with the physical behavior of viscoelastic material. Also, we can see from this figure that the boundary condition (60) is satisfied.

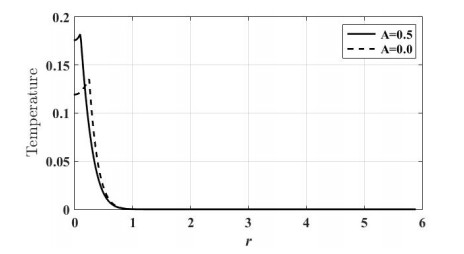
Figure 3 shows variation of temperature $\theta$ for the coefficient of Ohm and Fourier laws. It is noticed that the modified Fourier and Ohm laws influence is significant, the temperature in the modified model records value higher than these in the old model.

Figure 4 is plotted to show the variation of the radial stress ${\sigma }_{rr}$ against $r$for wide range of $r\left(1\le r\le 10\right)$, at small time$\left(t = 0.07\right)$, for two theories (G-N Ⅲ) and (G-N Ⅱ). It is observed from this figure the magnitude of the radial stress is greater for (G-N Ⅲ) model than (G-N Ⅱ). It can be noted that the speed of propagation of stress is finite and coincide with the physical behavior of viscoelastic material.

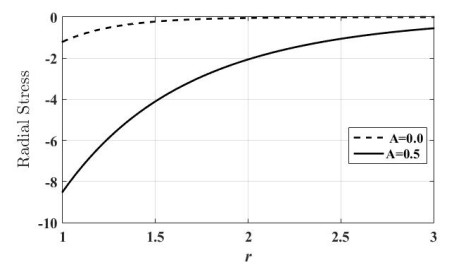
Figure 5 shows variation of radial stress for the coefficient of Ohm and Fourier laws. It is noticed that the modified Fourier^'s and Ohm^'s model effects on the radial stress by increasing their values.

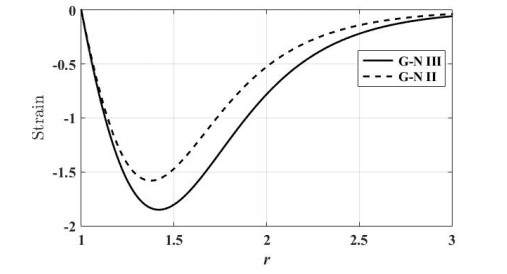
Figure 6 is plotted to show the variation of strain $e$against $r$for wide range of$\left(1\le r\le 3\right)$, at small time$\left(t = 0.07\right)$, for two theories (G-N Ⅲ) and (G-N Ⅱ). It is observed from this figure the magnitude of the strain is greater for (G-N Ⅲ) model than (G-N Ⅱ). It can be noted that the speed of propagation of strain is finite and coincide with the physical behavior of viscoelastic material. Also, we can see from this figure that the boundary condition (61) is satisfied.

Figure 7 shows variation of strain $e$ for the coefficient of Ohm and Fourier laws. It is noticed that the modified Fourier and Ohm laws influence is significant, the strain in the modified model records value higher than these in the old model.

Figure 8 is plotted to show the variation of displacement $u$against $r$for wide range of$\left(1\le r\le 3\right)$, at small time$\left(t = 0.07\right)$, for two theories (G-N Ⅲ) and (G-N Ⅱ). It is observed from this figure the magnitude of the displacement is greater for (G-N Ⅲ) model than (G-N Ⅱ). It can be noted that the speed of propagation of displacement is finite and coincide with the physical behavior of viscoelastic material.

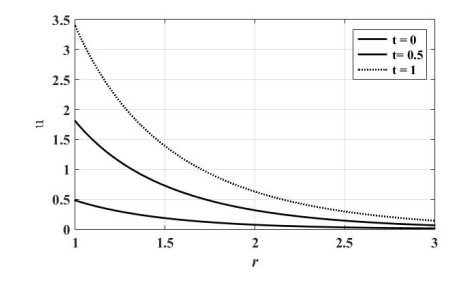
Figure 9 shows the variation of displacement $u$against $r$for wide range of$r$ $\left(1\le r\le 3\right)$, for different values of time$\left(t = 0.0, t = 0.5, t = 0.1\right)$. And we have noticed that, the time $t$has significant effects on displacement$u$. The increasing of the value of $t$causes increasing of the value of displacement $u$, and displacement $u$vanishes more rapidly.

8.   Conclusion

Green and Naghdi ^[7,8,9] developed a generalized theory of thermoelasticity which involves thermal displacement gradient as one of the constitutive variables in contrast to the classical coupled thermoelasticity which includes temperature gradient as one of the constitutive variables. An important feature of this theory is that it does not accommodate dissipation of thermal energy. On this theory the characterization of material response to a thermal phenomenon is based on three types of constitutive response functions. The nature of those three types of constitutive response functions is such that when the respective theories are linearized, type Ⅰ is same as classical heat conduction equation (based on Fourier's law), whereas type Ⅱ, the internal rate of production of entropy is taken to be identically zero, implying no dissipation of thermal energy. This model is known as the theory of thermoelasticity without energy dissipation. Type Ⅲ involves the previous two models as special cases, and admits dissipation of energy in general, in this model, introducing the temperature gradient and thermal displacement gradient as the constitutive variables.

From the above discussion, one can reason that the new model of generalized magneto-thermo-viscoelasticity predicts new qualities for the temperature, displacement, stresses and strain. The impact of the temperature gradient at adequately low temperature may cause new sorts of magneto-thermo-viscoelastic wave with explicit stability properties. The expansion in the estimations of temperature might be clarified as the lost heat producing from the development of electric flow; this heat might be the fundamental motivation behind why the deformation of the medium will in general be ordinary and the magnetic field records esteems more prominent than the qualities in the old model. As indicated by this work, numerous specialists in the field of generalized thermo elasticity have applied Green–Naghdi hypothesis (Ⅲ-Ⅱ) for thermo elastic problem and not many of them can effectively applied for magneto thermo Viscoelastic issue. Right now conclude that the greatness of the every single physical amount is more noteworthy for (G-N Ⅲ) model than (G-N Ⅱ). It very well may be noticed that the speed of spread of every single physical amount is limited and match with the physical conduct of Viscoelastic material.

Acknowledgements

The authors wish to acknowledge the approval and the support of this research study by the Project NO. SCI-2018-3-9-F-7795 from the Deanship of Scientific Research in Northern Border University, Arar, Saudi Arabia.

Conflict of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.