Nomenclature
| a | crack depth |
| a1, a2, a’ | the depths of crack 1, crack 2 and the combined crack, respectively |
| a0 | initial crack depth |
| a1,0, a2,0 | initial depths of cracks 1 and 2, respectively |
| c | half length of a crack |
| c1, c2, c’ | half lengths of crack 1, crack 2 and the combined crack, respectively |
| c0 | initial half length of a crack |
| c1,0, c2,0 | initial half lengths of cracks 1 and 2, respectively |
| C | material constant in Eqn. (1) |
| da/dN | fatigue crack growth rate |
| E | elastic modulus |
| H | half height of a plate |
| J | energy release rate |
| KI | stress intensity factor for mode I loading |
| K0 | normalized stress intensity factor |
| △KI | range of stress intensity factor |
| m | material constant in Eqn. (1) |
| R | stress ratio |
| s | distance between two adjacent flaws |
| s0 | initial minimum distance between two cracks |
| t | thickness of a plate |
| W | half width of a plate |
| v | Poisson’s ratio |
| σ | applied stress |
1. Introduction
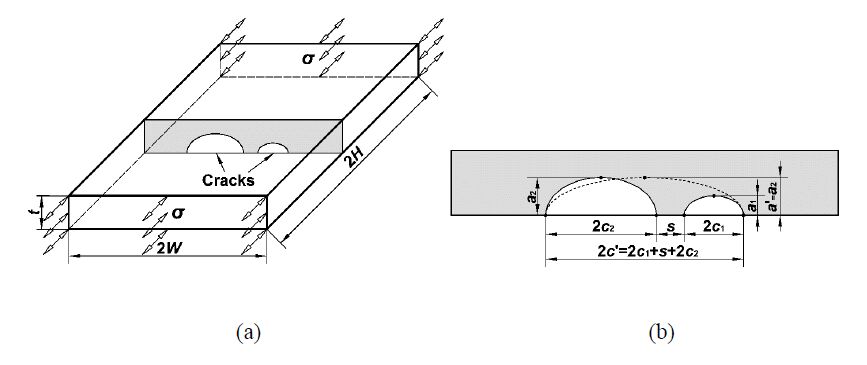
It is not uncommon to detect multiple flaws in structural components [1,2,3]. As reported by Nuclear and Industry Safety Agency, about two thirds of the stress corrosion cracks were existing as multiple flaws in a welded austenitic stainless steel pipe [4]. How to properly assess the structure containing multiple cracks is of great importance to preventing the potential catastrophic failure. For two coplanar surface cracks as shown in Figure 1, essentially based on the enhancement of stress intensity factor (e.g., [5,6]) and some experimental observations (e.g., [7,8]), guidance for the characterization of multiple flaws as displayed in Table 1, have been provided by the current fitness-for-service (FFS) procedures [9,10,11,12]. Although their basic concepts (i.e., when the distance between two adjacent flaws is equal to or less than a specific value, the two flaws will be combined into a virtual larger flaw) are similar, apparent discrepancy can be seen between various combination rules. Which of them is more reasonable and whether there are better options remain open questions [13].
Table 1. Combination rules for coplanar surface flaws in existing FFS codes.
| Sources | Combination rules |
| ASME [9] | Fatigue or stress corrosion: s = 0 |
| Others: s ≤ max(0.5a1,0.5a2) |
| BS7910 [10] | Fatigue: s = 0 |
| Others: s ≤ min(2c1,2c2) for a1/c1 or a2/c2 > 1 |
| s ≤ max(0.5a1,0.5a2) for a1/c1 ≤ 1 and a2/c2 ≤ 1 |
| API579-1 [11] | s ≤ c1 + c2 |
| GB/T 19624 [12] | s ≤ min(2c1,2c2) |
In the past four decades, a number of researchers have examined the interacting effect of adjacent cracks by fatigue crack growth tests. The pioneer experimental work of Iida et al. [8] in 1976 established an estimation procedure for fatigue life of a plate with multiple surface flaws. Soboyejo et al. [14] investigated the effects of stress ratio and initial crack separation on the interaction and coalescence of coplanar cracks under cyclic bending. By conducting complicated fatigue tests on specimens containing irregularly oriented surface cracks, Tu et al. [15] suggested a criterion for defect re-characterization. Kamaya [16] carried out fatigue crack growth tests for both coplanar and non-coplanar notches and argued that the growth of interacting surface cracks may be dependent on the area of crack face. Considerable efforts have also been devoted into finite element (FE) analyses which are obviously more cost-effective. It should be pointed that most numerical studies [17,18,19,20] only investigated the interacting effect on the crack tip parameters for stationary cracks, which are not necessarily relevant to the fatigue life of components. The attempts made by Lin et al. [21] and Kamaya [16] are notable exceptions that have simulated the crack growth behavior during the coalescence process for limited cases. However, how to rationalize a criterion for the re-characterization of multiple flaws from a series of numerical simulations remains a challenging task.
The purposes of this study is to assess the conservatism contained in different combination rules given by current FFS codes, and to develop a more rational one, based on the crack growth life of cracked structures. It should be noted that various failure mechanisms (cleavage, plastic collapse, fatigue, creep, corrosion, etc.) may significantly influence the flaw interaction criteria. To help clarify the description and obtain a clear understanding, our attention herein focuses specifically on the applicability of combination rules over the fatigue failure mode. In Section 2, the numerical method employed to simulate the fatigue crack growth is introduced, and then is validated by classic equations for stress intensity factors and by a fatigue test for a cracked plate. In Section 3, fatigue growth analysis of two identical cracks is performed. Furthermore, the conservatism contained in different combination rules provided by fitness-for-service codes and by the present study have been quantitatively assessed. Then, a numerical analysis for two dissimilar cracks is conducted in Section 4. Finally, several concluding remarks are drawn in Section 5.
2. Materials and Method
As depicted in Figure 1, a plate containing two coplanar surface flaws under cyclic loading was considered in this study. The surface flaws were idealized as semi-elliptical cracks. To eliminate the effect of the boundary on the calculation, the width and height of the plate were selected to be much larger than the crack dimensions. In this study, the number of cycles required for the re-characterized flaw to penetrate the plate was regarded as the life of the plate. The fatigue crack growth rate (mm×cycle-1) can be described by the well-known Paris equation
where C (mm×cycle-1 (MPa×mm0.5)-m) and m are material constants. △KI (MPa×mm0.5) denotes the range of stress intensity factor.
To trace the change of crack shape, local crack advance at an arbitrary point of crack front along the normal direction was computed. Two distinct methods were employed to predict the fatigue crack growth life the plate containing multiple cracks:
(I) Interaction Method:
A detailed step-by-step FE analysis was conducted to simulate the propagation, interaction and coalescence of multiple cracks. The interaction in the period of growth up to cracks touching, as well as the saturation of touching cracks to the achievement of a bounding crack, was taken into account. The routine of numerical simulations is described as follows:
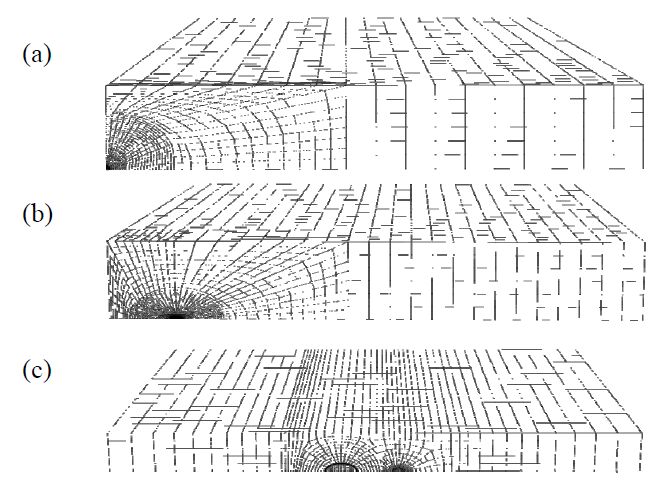
(a) Create the FE model. A fracture mechanics code, ZENCRACK [22], was adopted to create the FE model. In order to obtain accurate numerical results, extremely refined meshes are generated in the crack tip zone.
(b) Calculate KI. The values of energy release rate, J-integral, at a set of points that constitute the crack front was given by a FE code ABAQUS [23] using the domain integral method. For mode I loading, stress intensity factor, KI, with plane strain assumption can be obtained by
where E and v are elastic modulus and Poisson’s ratio, respectively.
(c) Calculate the increment of crack size. The fatigue crack growth at each point along the crack front in each step can be given by Eqn. (1).
(d) Establish a new crack profile. Based on the crack advancement at each node, the coordinates of a set of new nodes can be determined. The new crack profile was automatically created by ZENCRACK until the contact of two cracks. Note that at this moment the analysis would be suspended by the distorted mesh. A manual intervention was needed to slightly adjust the crack shape [24]. After that, ZENCRACK would continue to work.
(e) Return to stage (a). The cracks propagate through the stages from (a) to (d) until they penetrate the plate.
(II) Non-Interaction Method:
A similar step-by-step FE analysis was also performed but each crack was assumed to grow independently before the coalescence. Once a combination rule listed in Table 1 has been satisfied, adjacent cracks would immediately join together into a larger crack, with a depth of the deeper of the two pre-existing cracks and a length being equal to the sum of their lengths and minimum distance, as illustrated in Figure 1(b).
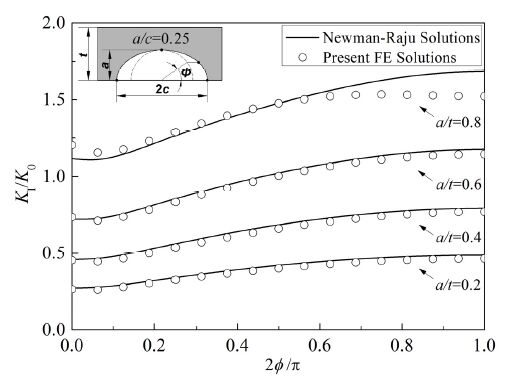
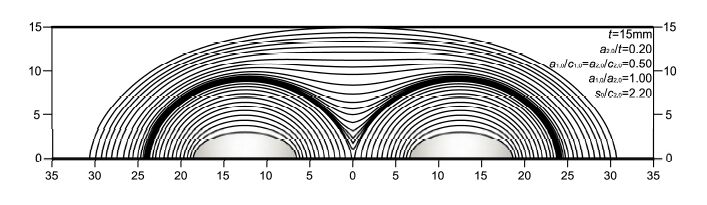
To check the validity of the FE model, stress intensity factors at a set of points that constitute the crack front calculated by ABAQUS have been compared with the Newman-Raju solutions [25], as shown in Figure 2, for semi-elliptical cracks (with aspect ratio a/c = 0.25 and depth ratio a/t = 0.2, 0.4, 0.6 and 0.8) in a plate (with thickness t = 15mm, half width W = 6.67t and half height H = 6.67t) subjected to a tension load (with stress σ = 200MPa). A typical FE mesh of a plate with an isolated crack is depicted in Figure 3(a). Elastic modulus and Poisson’s ratio are given in Table 2. The FE model contains 6517 eight-node isoparametric elements. Stress intensity factors have been normalized by K0=σ√πt. One can see that the present FE solutions agree very well with the Newman-Raju solutions for a/t = 0.2, 0.4 and 0.6, with errors less than 1.2%. For the case with a/t = 0.8 when 2ϕ/π>0.6, stress intensity factors from the Newman-Raju equations are slightly larger (within 7.0%) than the FE results. Similar difference between FE results and the Newman-Raju solutions for a/t = 0.8 has also been reported by Lei. It is believed that this discrepancy is due to the fitting error introduced by Newman-Raju equations.
Table 2. Material constants for a low carbon alloyed steel 16MnR [26].
| Elastic modulus | Poisson’s ratio | Coefficient in Eqn. (1) | Exponent in Eqn. (1) |
| E/MPa | ν | C/mm×cycle–1 (MPa×mm0.5)–m | m |
| 209000 | 0.28 | 7.30 × 10–15 | 3.42 |
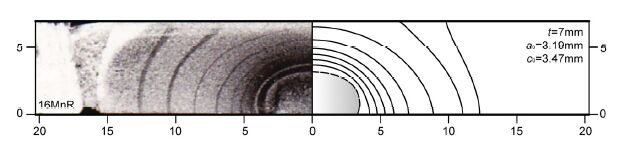
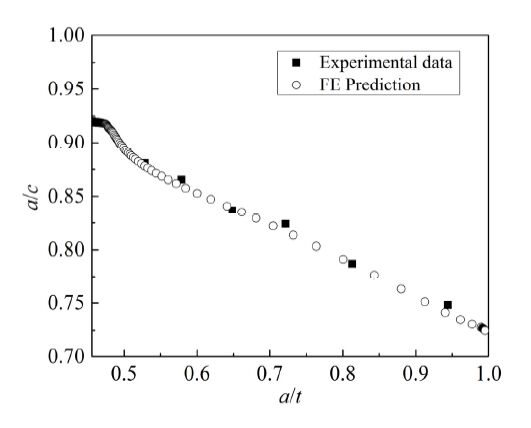
In order to validate the step-by-step numerical method employed, comparison between predictions and experimental results [26] has also been made for a plate (with half width W = 44.75 mm, half height H = 175 mm, and thickness t = 7 mm) containing a single crack (with initial depth a0 = 3.19 mm and half length c0 = 3.47 mm) under a cyclic loading (with maximum and minimum load, 140 kN and 0 kN, respectively). The initial surface defect was manufactured by electric discharge machining. The specimen was tested on a closed loop, servo-hydraulic testing system MTS 880. Sinusoidal tension loading at a frequency of 22 Hz was employed. To determine the crack shape evolution during the propagation, a crack front marking procedure was used at each interval of crack extension of about 0.5-1 mm, in which the maximum load was kept constant and the load range was reduced by one half. After the fatigue test was done, the specimen was opened and then heated to improve the clarity of the beach marks. The material of the plate is 16MnR, a widely-used low carbon alloyed steel for pressure vessels. Material constants used in this study are listed in Table 2 [26]. Due to the symmetry of both geometry and loading, only one quarter of the specimen has been created. As shown in Figure 3(a), the FE mesh contained a total of 7836 C3D8 elements. Figure 4 shows the comparison of predicted crack profiles with those on the fracture surface after test [26]. Clearly, the crack shapes predicted by the current step-by-step FE analysis are extremely similar to the experimental evidence, even after the plate thickness penetration of crack. A further comparison can be made on the variation of aspect ratio with depth growth throughout the plate thickness, as illustrated in Figure 5. The maximum error of aspect ratios, a/c, between prediction and test data for a given depth ratio, a/t, is only about 1.5%. These encouraging results prove the validity and predictive capability of the numerical analysis used in this study.
3. Fatigue Growth Analysis of Two Identical Cracks
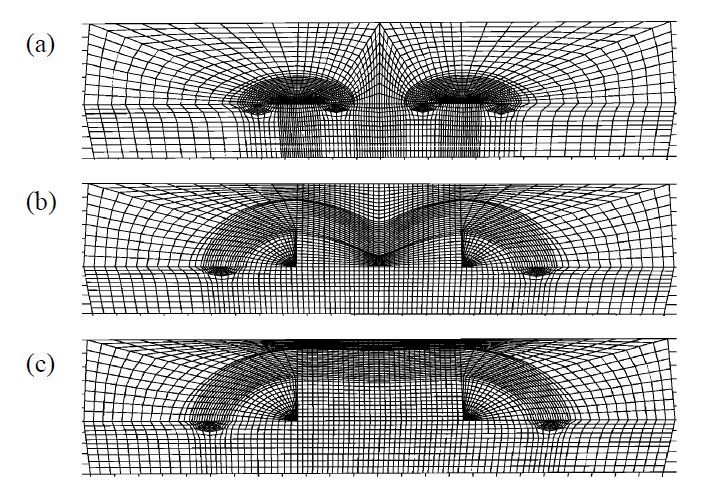
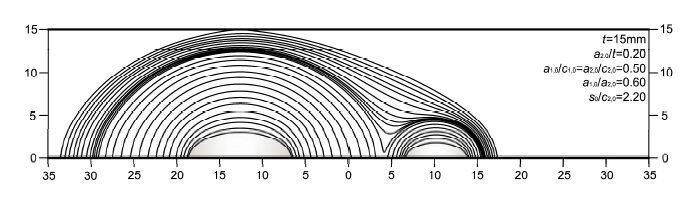
We started the investigation on multiple surface cracks with identical sizes. These cases may be regarded as probably more dangerous since the interaction effect is strong [5]. As shown in Figure 1, a finite thickness plate (with t = 15 mm, W = 6.67t and H = 6.67t) subjected to a cyclic load (with maximum stress σ = 200 MPa and stress ratio R = 0.1) was considered. The same material constants as listed in Table 2 were chosen. Two cracks (with a2,0/t = 0.20, a1,0/c1,0 = a2,0/c2,0 = 0.50, a1,0/a2,0 = 1.00 and s0/c2,0 = 2.20, where a1,0 and a2,0 are the initial depths of cracks 1 and 2, respectively; c1,0 and c2,0 are the initial half lengths of cracks 1 and 2, respectively; s0 is the initial minimum distance between two cracks; a0 = a1,0 = a2,0 and c0 = c1,0 = c2,0 where a0 and c0 are the initial crack depth and initial crack half length, respectively, when two cracks are identical to each other.) situated in the middle of the plate. With symmetry conditions imposed only one quarter of the plate model needed to be created using 13046 eight-node brick elements, as shown in Figure 3(b). Note that meshes were rebuilt in each step according to the updated crack profile. Meshes of selected finite element models (1/2 model) in various steps are shown in Figure 6. Figure 7 provides the shape development of two identical cracks predicted by the Interaction Method. It can be observed that the individual cracks propagate almost independently until the minimum distance between them becomes comparable with the crack depth. Then, crack grows at a higher rate in the neighboring zone than in other regions. When the coalescence begins, dented portions are formed, leading to a crack profile deviating from a semi-ellipse. In a short time, the concave points along the crack front disappear and the shape of newly-combined crack becomes smooth ultimately. The predicted shape evolution can be found to be in good agreement with many experimental observations (e.g., [16,26]).
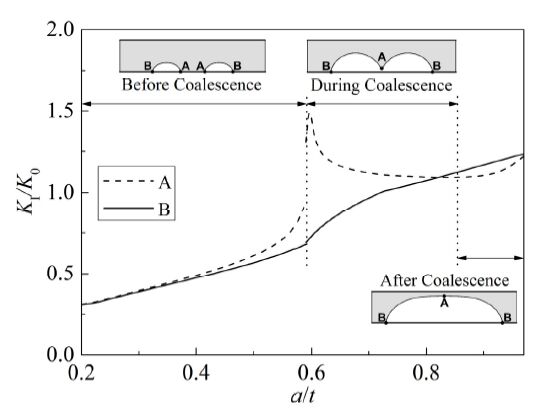
The phenomenon seen in the Figure 7 can be explained by investigating the developments of stress intensity factor at depth point and surface point in the crack growth process, as shown in Figure 8. Note that stress intensity factors have been normalized by K0=σ√πt. Locations of A and B are marked in the imbedded figures on different stages. It can be seen from Figure 8 that the stress intensity factors at A and B are identical initially, whereas their discrepancy gradually become significant as the two cracks get closer to each other. The stress intensity factor of the merging point, A, reaches a maximum value of approximately triple that at the surface point, B, soon after the contacting moment, and decreases until the crack shape become smooth again. On the final stage, the stress intensity factor at A rises due to the reduction of ligament area.
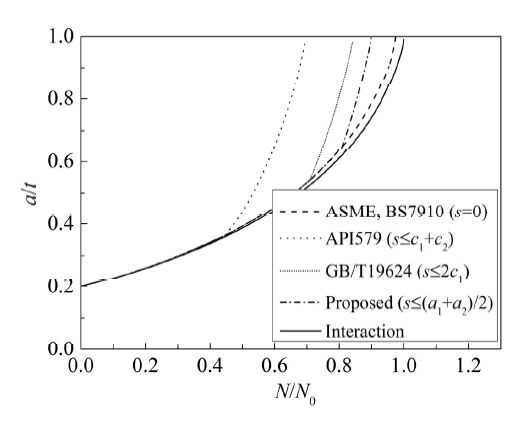
Figure 9 shows the comparison of crack growth curves predicted by the Interaction Method and the Non-Interaction Methods with different combination rules listed in Table 1, corresponding to the case of Figure 7. The fatigue cycles, N, has been normalized by the fatigue life, N0, taken for crack to penetrate the plate, given by the Interaction Method. One can find that the fatigue life predicted by the Non-Interaction Method with the combination rule, s = 0, in ASME [9] and BS7910 [10] is overestimated by approximate 15%. This indicates the interaction between two adjacent cracks cannot be ignored, otherwise the assessment may be unsafe. On the other hand, for the same case the criterion, s≤2c, provided by API579 [11] and GB/T19624 [12], leads to an excessively conservative estimation (only one half of the life given by the Interaction Method). None of the available combination rules is satisfying, at least in this case. Therefore, partly based on experience gained from the numerical solutions here and those to be presented later, we propose a new combination rule.
The result predicted by the proposed combination rule (degraded to s≤a for two identical cracks) is also shown in Figure 9. Clearly, the Non-Interaction Method with proposed combination rule gives a best estimation of crack growth curve.
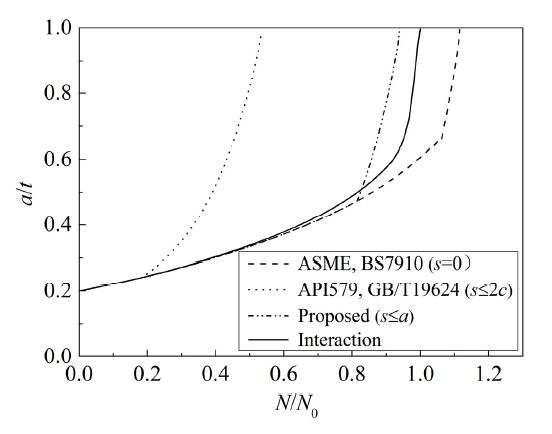
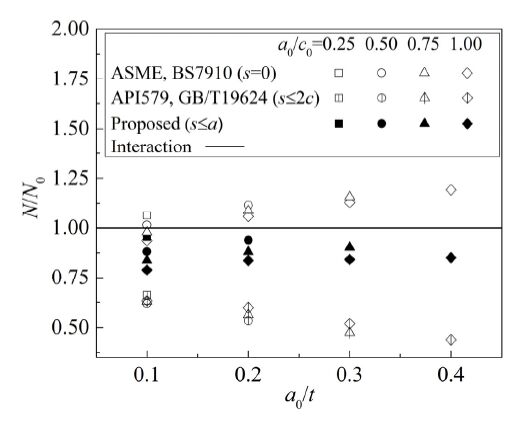
Numerical analyses were carried out for more cases with various initial crack shapes (a0/c0 = a1,0/c1,0 = a2,0/c2,0 = 0.25,0.50,0.75 and 1.00) and initial crack depth ratios (a0/t = a1,0/t = a2,0/t = 0.1,0.2,0.3 and 0.4). Note that the two cracks are initially separated at a relatively long distance (s0/c2,0 = 2.20). If the initial crack depth ratio, a0/t, is large enough, the cracks will individually penetrate the plate without coalescence. For this reason, the initial crack depth ratio was selected to be no larger than 0.4 in the present study. The normalized fatigue lives, N/N0, due to different combination rules are shown in Figure 10. As expected, the fatigue life obtained by the proposed combination rule is closer to the numerical results considering the interaction effect, whereas estimations given by ASME and BS7910 are essentially not conservative and those according to API579 and GB/T19624 are of excessive conservatism. It is remarkable that, with the increase of initial crack depth ratio, both non-conservatism due to s = 0 and over-conservatism from s≤2c rises, while the proposed combination rule always keeps a reasonable prediction.
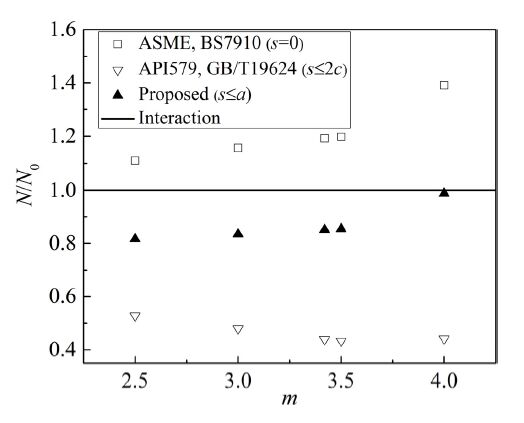
A parametric study was also performed for different materials with the exponent in the Paris equation, m, ranging from 2.5 to 4.0, which is the approximate range for most metals in the atmospheric environment [27]. As shown in Figure 11, for m = 4, the numerical results from the Non-Interaction Method with combination rule in ASME and BS7910 can lead to a maximum unsafe deviation of 40%, while API579 and GB/T19624 may underestimate the fatigue life by approximate 60%. Again, the results given by proposed criterion coincide with those considering interaction, and the ratio of the former to the latter is in a reasonable range of 80-100%.
4. Fatigue Growth Analysis of Two Dissimilar Cracks
The same finite thickness plate and loading condition, as described in Section 3, but with two dissimilar coplanar surface cracks were considered in this section. Due to symmetry one half of the plate was taken into account in the FE models using 13460 eight-node brick elements, as shown in Figure 3(c). Material constants of 16MnR listed in Table 2 were used again. Figure 12 illustrates the shape evolution of two dissimilar cracks (with initial sizes a2,0/t = 0.20, a1,0/c1,0 = a2,0/c2,0 = 0.50, a1,0/a2,0 = 0.60 and s0/c2,0 = 2.20) predicted by the Interaction Method. Crack propagation behavior similar to that shown in Figure 7 can be observed. What differs from the former is that the individual dissimilar cracks grow more independently as isolated flaws. It can be seen from Figure 7 that the spacing between the initial and touching crack shapes on the interacting side is significantly larger than that on the non-interacting side due to the interaction of two cracks. For the larger crack in Figure 12, by way of contrast, the intervals between crack profiles are almost the same on both interacting and non-interacting sides. That means the propagation of the larger crack seems less affected by the smaller crack. Obviously, the larger crack advance much more rapidly since the stress intensity factors at the crack front are always greater than those for smaller crack during the growth process. Similar shape development of two cracks with different sizes can be found in Ref. [14,28].
Figure 13 displays the comparison of crack growth curves, corresponding to the case of Figure 12, predicted by the Interaction Method and the Non-Interaction Methods with different combination rules. It demonstrates that, for this case, all combination rules lead to conservative estimations when compared with the results by the Interaction Method. Nonetheless, API579’s criterion (s≤c1 + c2) underestimates the fatigue life by approximate 30%.
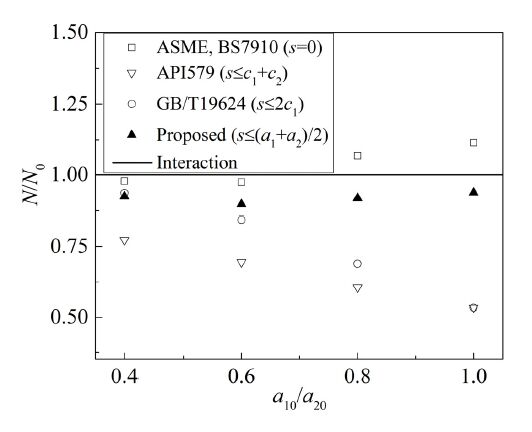
More cases with various crack sizes ratios (a1,0/a2,0 = 0.40, 0.60, 0.80 and 1.00) were also considered in the study. As can be seen in Figure 14, when the sizes of two cracks are considerably dissimilar (a1,0/a2,0≤0.60), the combination rule suggested by ASME and BS7910 (s = 0) will give estimations very close to the numerical results that considers crack interaction. This is because for these cases the two cracks can be regarded as independent to some extent during the propagation process up to cracks touching, as demonstrated in Figure 12. However, when the crack sizes are somewhat similar (a1,0/a2,0≥0.80), the effect of interaction between two adjacent cracks cannot be neglected, as illustrated in Section 3. In this circumstance, ASME and BS7910 will overestimate the fatigue life. By contrast, API 579 (s≤c1 + c2) always underestimate the results by at least 25%. Interestingly, conservatism of GB/T 19624 (s≤min(2c1, 2c2) or s = 2c1) is highly dependent on the crack size ratio. The noteworthy result is that, the proposed combination rule (s≤(a1 + a2)/2) always yields a reasonable estimation with necessary conservatism, no matter whether the crack sizes are similar or not.
5. Conclusions
The combination rules for multiple coplanar fatigue cracks provided by different existing FFS codes (ASME, BS7910, API579 and GB/T19624) have been examined by detailed step-by-step FE analyses. In addition, a new combination rule (s≤(a1 + a2)/2) based on the crack growth life of structure has been proposed. Conclusions can be drawn as follows:
(1) The amount of conservatism contained in the combination rules given by existing FFS procedures is dependent on the initial crack depth ratio, a0/t, and initial crack size ratio, a1,0/a2,0.
(2) Predictions using the re-characterization guideline (s = 0) provided by ASME and BS7910 can be non-conservative when initial sizes of two cracks are similar.
(3) Combination rules suggested by API579 (s≤c1 + c2) and GB/T19624 (s≤2c1) lead to excessively pessimistic predictions of crack growth for almost all the cases considered in the present study.
(4) The proposed combination rule (s≤(a1 + a2)/2) always yields a reasonable estimation with necessary conservatism, for various initial crack depths, material constants and relative sizes of two cracks.
Be aware of that the findings of this research may be only valid for fatigue failure mode. It would be interesting to undertake further studies for other failure mechanisms such as creep and corrosion, based on the same concept and similar numerical method.
Acknowledgements
Supports from National Natural Science Foundation of China (Grant Nos. 11472105 and 51505149) and the “111 project” are gratefully acknowledged. J.-F also wishes to thank the financial support provided by Shanghai Sailing Program (Grant No. 15YF1402900) and China Postdoctoral Science Foundation (Grant No. 2015M581543). Helpful discussion on the numerical technique with Mr. Chun-Lei Ma at Consys Ltd. And Dr. Ramesh Chandwani at Zentech Int. Ltd. is also greatly appreciated.
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.









 DownLoad:
DownLoad: